e-mail :

We continue the investigation of Vector Rosette of Actual Growth (and with them, Symmetry and Promorph) in crystals, focussing for the time being on 2-D crystals.
Recall that in the foregoing we've found out that we can, with respect to crystals, determine the Vector Rosette of Actual Growth that is necessary and sufficient for indicating the Shape of the given crystal, by giving only the vectors that point, from the center of that crystal, to its corners. Some of these vectors can be composed vectors (composed from the original growth vectors of the individual faces, which are perpendicular to the latter), indicating the effective relative growth, and (like all growth vectors) indicating the accomplished growth.
In organisms we will consider intrinsic Shape in a comparable way, where we have to realize that we can, and often will, encounter receding angles, and and also a dynamics causing variable shapes.
Intrinsic Symmetry of crystals is given by their Space Groups and (implied) Point Groups (For 2-D crystals by their Plane Groups and (implied) Point groups). In organisms their Point Symmetry is implied by their Promorph (as explained in the Series on Basic Forms -- Promorphology -- in Second Part of Website). Being aperiodic, they lack Space Group Symmetry.
The Promorph of crystals is determined by assessing the promorph of the microscopic translation-free chemical motif (or its analogue in 2-D crystals), and then adjudging this promorph to the crystal as a whole, because the latter is just a periodic repetition of the translation-free chemical motif. Organisms are not the result of a periodic repetition of some microscopic unit (that, as in crystals, already contained all relevant qualitative content), so their Promorph is only macroscopically present. In both cases -- crystals and organisms -- a n t i m e r s are crucial in constituting the promorph. In single crystal individuals the promorph follows from the point group symmetry (i.e. the Crystal Class), because that is the translation-free residue of the total symmetry, the Space Group, and as such the symmetry of the chemical complex that is being repeated in the crystal. But the promorph found in this way is often still a general promorph, which should be determined further on the basis of the number, the nature and arrangement of the antimers of that translation-free chemical motif. In the same way in organisms the promorph, insofar as following from the organism's point symmetry often is still a general promorph and must be determined further on the basis of the precize nature, etc. of the antimers.
These three properties, Shape, Symmetry and Promorph will be determined for a number of crystal species and organismic species (where the present documents are dealing with crystals, and later documents with organisms). They will eventually be expressed as If / Then Constants (generally treated in the foregoing documents), viz. (special) whatness categories and entitative constants. Also some other properties will be investigated as to their presence in crystals as well as in organisms. And by means of such a crystal-analogy we will discuss the constitutional transition from the Inorganic Layer to the Organic Layer. This transition will consist in a 'sudden' complexification, i.e. in a leap-wise increase in material complexity. Such a 'sudden' complexification should not be understood so much as a process that actually took place somewhere, but a leap in complexification that manifests itself when we compare crystals and organisms.
In the previous document we considered the Plane Groups P1 and P2.
In the present document we elaborate still further on the Plane Group P2, and started considering the Plane Group Pm. And in the documents to follow we will discuss all the remaining Plane Groups in this respect. There are in total 17 Plane Groups, and the study of them will prepare us for the study of three dimensional crystals with respect to their Shape, Symmetry and Promorph.
Antimers and Antisymmetry
So we are in the process of comparing Crystals with Organisms mainly with respect to intrinsic Shape, intrinsic Symmetry and Promorph.
As has been said, with respect to the Promorph or stereometric basic form the antimers play a decisive role.
Recall that the antimers or counterparts of a given body, be it a molecule, an atomic complex, a crystal or an orgamism, or even a part of an organism, are similar parts regularly arranged around the body's main axis (or around the body's central point, if such a main axis is not discernable). Important is the fact that the antimers do not have to be equal parts, i.e. they neither need to be congruent nor symmetric, and also not equiform (while differing in size). They should just be similar. In organisms such parts are, when present, often easily detectable by their similar internal and external morphologies and/or their organic functions, for example the petals of regular flowers ( The latter are parts of certain organisms, which, in organic Tectology are called persons (See Second Part of Website, Tectology Series), or the arms of starfishes. Or they (i.e. parts that are antimers) are detectable on the basis of homologies that can be assessed either on the basis of the individual development (ontogeny) or on the basis of the evolutionary development (phylogeny) of the given organism. Most animals, and also humans, have only two antimers, viz. their right and left body halves. And especially in higher animals and in humans we see that these two antimers are not equal, but just similar. They are, however, equal enough to be counted as antimers, in contradistinction to totally asymmetric organisms, like many unicellular organisms, that consequently do not have genuine antimers. But even the two totally different body halves of flatfishes can be counted as antimers, because they derive from equal body halves during the individual development of such a flatfish.
In inorganic beings like molecules or crystals, all this is much harder to assess, because individual development is virtually absent in such beings, and the phenomenon of functions is also absent (It is only present in machines and other artifacts, but they are not genuine beings, originated by self-organization of matter, they have extrinsic causes). But, with some effort, we can nevertheless detect -- when present -- antimers in inorganic bodies, which are similar parts, present in a definite number, and regularly arranged around the body's main axis or central point.
So antimers are more or less equal parts radially composing the given body. And despite of this inexact "more or less equal" we can describe them as antimers mathematically, namely by means of the concept of antisymmetry. To be more precise, if the antimers are equal (in the sense of related to each other by ordinary symmetry), we can describe them by (ordinary) symmetry groups, because they are transformed into each other by ordinary symmetries like reflections or rotations. But if the antimers are unequal (but still such as to be legitimately counted as antimers) they can be described by antisymmetry groups, because they can be transformed into each other by antisymmetry transformations.
For an explanation of a n t i s y m e t r y the reader should refer to, and -- within the Series on Group Theory (Second Part of Website) -- click on (the link) "SEQUEL TO GROUP THEORY", and then go to "Subpatterns and Subgroups Part II : Antisymmetry Groups Color Symmetry Groups", and then scroll down to "Antisymmetry Groups". To see this document in a separate window, click HERE.

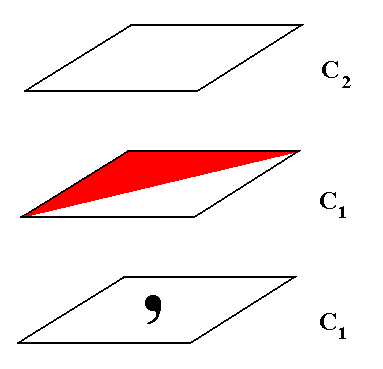
Figure 1.
Top image : A figure with C2 symmetry. Its only (non-trivial) symmetry element is a 2-fold rotation axis through the center of the figure. The g r o u p elements are the identity element and a half-turn ( = rotation by 1800 about the center of the figure).
Middle image : A figure with C1 symmetry.
The asymmetry is caused by the coloration of one half of the figure. The only group element is the identity element.
Bottom image : A figure with C1 symmetry.
The asymmetry is caused by the motif s.str. (comma). The only group element is the identity element.
The middle and bottom images of the above Figure are equivalent in the sense that their symmetry is according to the group C1. But if we look to them we see that the middle image at least suggests two antimers. And its coloration suggests that the symmetry of this image (figure) can be described by an antisymmetry group : This group then consists of the identity element and the antisymmetry transformation e1h , where e1 is the antiidentity transformation (as such not belonging to the [antisymmetry] group), which here is a permutation between two colors, red and white. This permutation can be written as (Red White) (cycle notation), meaning that when the color is found to be red, it must become white, and when it is found to be white, it must become red. h means a half-turn. Moreover the following relations hold :
e12 = e1e1 = 1 (where 1 is the identity element).
e1h = he1 (e1 commutes not only with h, but with every symmetry transformation of the original group (which is the group from which an antisymmetry group is about to be derived)).
From the group {1, h}, which has C2 structure, we can derive the antisymmetry group {1, e1h}, that can be denoted by C2 / C1 , by replacing the generator h (which is a half-turn) by the antisymmetry transformation e1h , which is a half-turn followed by a color change according to the color permutation (Red White). The resulting antisymmetry group C2 / C1 is isomorphic to C2 (which means that their algebraic structures are identical).
The next Figure shows the same images as above, but now with the group elements indicated and as representing areas of the image. Moreover the middle image is now interpreted as representing the antisymmetry group {1, e1h} denoted by C2 / C1 .
Figure 2.
Top image : A figure representing the group C2 . The two group elements 1 and h , represented by areas of the figure, are indicated.
Middle image : A figure representing the antisymmetry group C2 / C1 . The group elements 1 and e1h are indicated.
Bottom image : A figure representing the group C1 . The only one group element, viz. the identity element, 1, represented by the whole figure, is indicated.
To analyse these three groups still further, we give their group tables which indicate the combining of the group elements (Recall that each group element is a symmetry transformation. Combining two such transformations means their consecutive execution, i.e. first execute one, and then, on the result, execute the other).
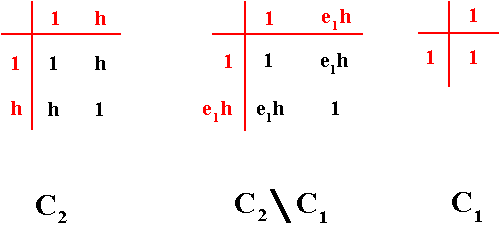
Figure 3. Group Tables of the above three groups : C2 , C2 / C1 and C1 .
From the above Tables it is evident that the groups C2 and C2 / C1 are isomorphic, i.e. their algebraic structure is identical.
Now it is possible to interpret the figure in the bottom image of Figure 2 also as representing the antisymmetry group C2 / C1 if we manage to interpret the geometric change of the comma in the same way as we did with the color change, i.e. if we manage to interpret this geometrical change as a to and fro of a dual quality. See next Figure.
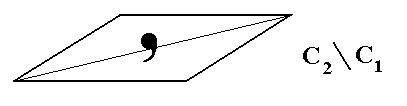
Figure 4. The figure in the bottom image of Figure 2 interpreted as the antisymmetry group C2 / C1 (isomorphic with C2 ). In this antisymmetry group we can interpret the antiidentity transformation e1 as the permutation (Head Tail) , which means that if it is a head, then it must become a tail, and if it is a tail, then it must become a head. The antisymmetry transformation will the be e1h , where h is a half-turn, and where e1 commutes with h.
But although we can interpret the bottom image of Figure 2, representing the group C1 , as an antisymmetry group isomorphic with the group C2 , we cannot correspondingly interpret the head and the tail (and including the corresponding surroundings) of the comma as two antimers, because they are far from being similar parts. So although antisymmetry can describe the presence of antimers, it cannot distinguish between true and false antimers. The latter is a purely qualitative distinction.
Figure 5.
Image A : A motif having, as its only symmetry element a two-fold rotation axis, and therefore having a symmetry according to the group C2 ( Its two g r o u p elements are the identity element and a half-turn). The motif consists of equal parts and thus allows to be interpreted as consisting of two antimers.
Image B : A desymmetrization of the motif of image A, resulting in a motif with similar (i.e. not equal) parts still allowing to be interpreted as antimers.
Image C : The motif of image B after it has been rotated 1800 about its center (half-turn, h).
Image D : Covering the initial motif (B) can be achieved by rotating the motif, as it is in C, again by 1800. We, however, will not do this. We will achieve covering of the initial motif (B) by letting the antimers remain where they are in image C, but subjecting them to the antiidentity transformation e1 which will be interpreted as follows :
If an antimer is found to be represented by a triangle smaller than those in image A, then it must change to a triangle equal the corresponding triangle of image A, and, reversely, if an antimer is found to be represented by a triangle equal to the corresponding triangle of image A, then it must change into a smaller triangle equal to the smaller triangle of image B.
For short, e1 stands for the (geometric) permutation (Big Triangle Small Triangle) (cycle notation).
Although the transformations e1 and h do not represent group elements of the antisymmetry group describing the motif represented by B, C and D, the antisymmetry transformation e1h does represent (together with the identity element) an element of that antisymmetry group. It represents the transformation from B to D (via C).
It is a genuine cover-operation, while being not identical to two half-turns, because -- while covering the initial motif (B) -- the p o s i t i o n s of the individual antimers are still different from those of the initial state (B) : The antimers have been geometrically changed, they have not been rotated (about the center of the motif). Only when we perform the antisymmetry transformation e1h two times we end up with the initial motif (B) again, i.e. only now also the positions of all the subareas are the same as they were in B :
e1he1h = he1e1h = hh = 1 (where 1 is the identity element).
So while the symmetry of the motif of image A is according to the group { 1, h } , denoted by C2 , and the symmetry of the motif of image B is according to the group { 1 } , denoted by C1 , the symmetry of the latter motif (viz. that of image B) can also be described by the antisymmetry group { 1, e1h } , denoted by C2 / C1 .
We will call o r d i n a r y symmetry "classical" symmetry, to distinguish it from antisymmetry (and also from color symmetry).
We will now place the motifs into an oblique lattice, viz. the motif as it is represented by two differently colored areas as in the middle image of Figure 2, into one such lattice, and the motif as it is represented by image B of the above Figure, into another such lattice.
Figure 6. From the symmetry group P2 (which can be represented by just an oblique point lattice) the antisymmetry group P2 / P1 is derived by partially coloring the meshes of the lattice.
The ordinary (i.e. classical) symmetry of the pattern of Figure 6 is, because of the coloration, that of the symmetry (plane) group P1, which means that the corresponding point symmetry is 1. And this in turn means that every possible crystal 'face' is at the same time a Form (in the crystallographic sense). Such a Form, consisting of one face only, cannot form a (2-D) crystal, but must be combined with at least two other such Forms ( The simplest 2-D crystal is a triangle). Which of the possible faces will finally combine to make up a crystal depends on the Vector Rosette of Actual Growth, which is itself depends on how much time was available to the face to grow (perpendicular to its plane) in relation to other faces, and on the relative growth rates of the 'faces' (in a direction perpendicular to them), which in turn depend on the geometry of the lattice (which here means how many lattice nodes are struck by a given face) and the 'chemical' 'atomic' aspect (s.str.) presented by the given face to the growing environment.
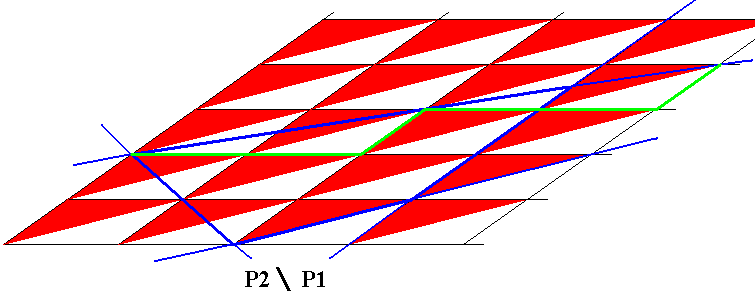
Figure 7. First stage in the construction of a 2-D crystal from the pattern of Figure 6.
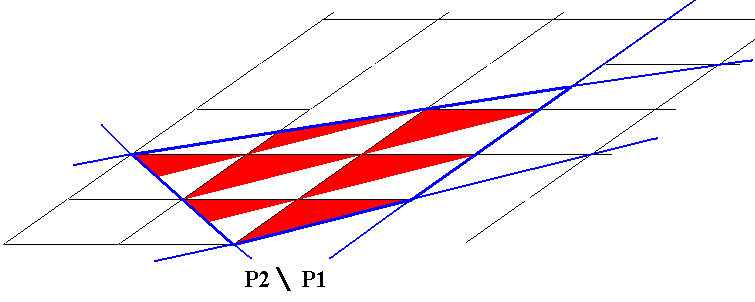
Figure 8. Second stage in the construction of a 2-D crystal from the pattern of Figure 6.
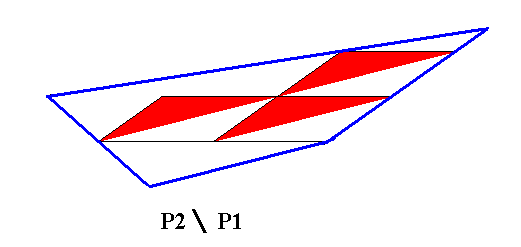
Figure 9. Final stage in the construction of a 2-D crystal from the pattern of Figure 6. The depicted crystal consists of only three building blocks, but of course we in fact have in mind a crystal consisting of a corresponding larger part of the periodic pattern of Figure 6.
Placing a motif similar to that of Figure 5, image A, in an oblique point lattice results in the following :
Figure 10. Periodic pattern (and at the same time a possible 2-D crystal) consisting of motifs (s.str.) as depicted in Figure 5, image A, i.e. motifs with C2 symmetry, resulting in the symmetry of the pattern to be according the Plane Group P2 . Because the point symmetry of this pattern is according to the Point Group C2 , each Form (in the crystallographic sense) consists of a pair of parallel crystal 'faces'. The 2-D crystal of the present Figure consists of two such Forms : aa and bb , resulting in four faces making up a parallelogram, which is the shape of the crystal.
Based on the tectological (i.e. in contradistinction to periodic) structure of the motif, the antimers of the crystal of Figure 10 can be indicated as follows :
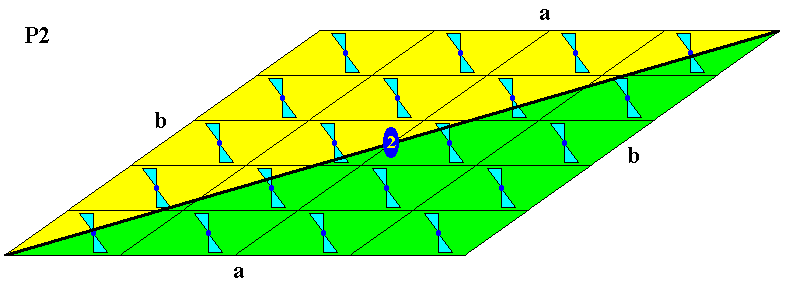
Figure 11. The two antimers of the crystal of Figure 10. The 2-fold rotation axis of the crystal (as a symmetry element of the crystal's point symmetry), by which the two antimers of the crystal are related, is indicated.
If the growth rate of a face c is low enough, three Forms will partake in the crystal's facial make-up, and the following shape could be the result :
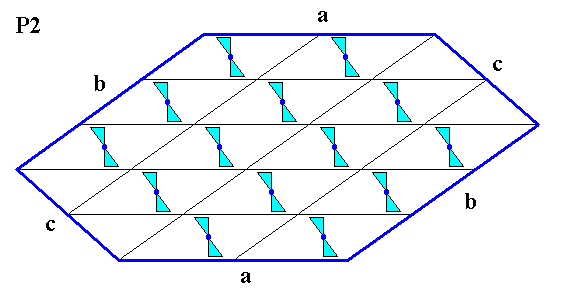
Figure 12. A two-dimensional crystal with the internal structure as in the previous Figure. The growth rate of a face c is low enough for the face to appear. But, because the point symmetry of the structure is according to the group C2 , another face parallel to c (and together constituting one Form) must also appear, resulting in a crystal bounded by six faces (two by two parallel).
Again, based on the tectological structure of the motif, the antimers of the crystal of Figure 12 can be indicated as follows :
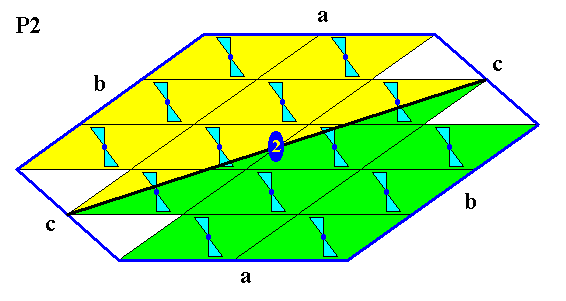
Figure 13. The two antimers of the crystal of Figure 12. The 2-fold rotation axis of the crystal (as a symmetry element of the crystal's point symmetry), by which the two antimers of the crystal are related, is indicated.
Based on Figures 11 and 13, the Promorph of the crystals of the Figures 10 and 12 is that of the 2-D analogue of the (3-D) Heterogyrostaura dimera (amphitect gyroid pyramids with two antimers).
Placing a motif similar to that of Figure 5, image B, in an oblique point lattice results in the following :
Figure 14. Periodic repetition of a motif, consisting of two unequal (but similar) antimers, like the one depicted in Figure 5, image B, results in a pattern that can be described by the antisymmetry group {1, t1 , t2 , e1h}, denoted by the symbol P2 / P1 , where t1 is the oblique translation, t2 the horizontal translation, 1 the identity element, and e1h the antisymmetry transformation consisting of the half-turn h and the antiidentity transformation e1 . The latter should be interpreted as stated in the subscript of Figure 5.
The pattern depicted in the present Figure can also already be seen as a possible 2-D crystal having the (internal) structure expressed by that pattern.
In the above Figure a 2-D crystal is depicted, consisting of four individual Forms, viz. a, b, c, d, which have alternately the same orientation. Each Form consists of only one possible crystal 'face', because the 'classical' point symmetry of the structure is that of the group C1 (implying absence of true symmetry, and therefore absence of any multiplication of a given face. In the present case we have four given faces).
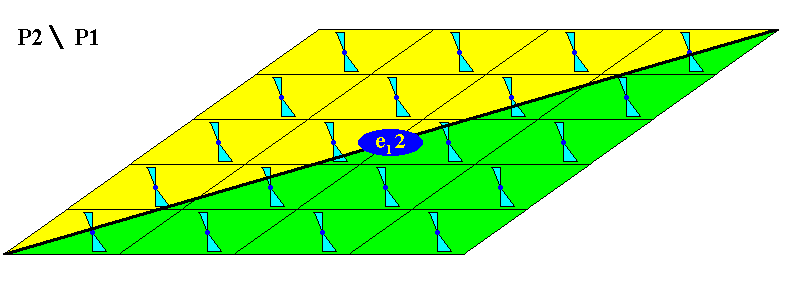
Figure 15. The two antimers of the crystal of Figure 14. The antisymmetry 2-fold rotation axis (e12) [where 2 is a half-turn] is indicated. It relates the two antimers. It is, however, not a classical symmetry element, like a rotation axis or a reflection line, because its effect is not macroscopically apparent, but relates to the translation-free motif. And, moreover, the antiidentity transformation e1 (which is a part of the antisymmetry transformation e12) is not itself an element of the antisymmetry group, nor is it an element of the classical symmetry group.
The antimers in Figure 15 look similar, i.e. they look exactly symmetric with respect to each other, seemingly related by a 2-fold rotation axis, while the antimers of the corresponding translation-free motif are not symmetric with respect to each other. A like phenomenon is common in crystals, where the latter can geometrically show a higher symmetry than they actually possess, like in the 2-D crystal of Figure 14, the outline of which has C2 symmetry, while its true (classical) symmetry is according to C1 ( Its non-classical symmetry, which here means its antisymmetry, is, however, that of the antisymmetry group C2 / C1 ).
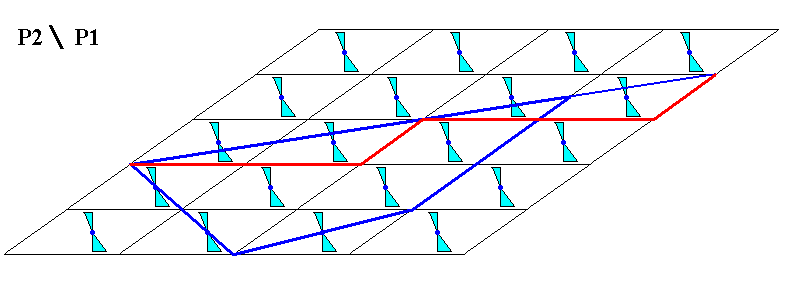
Figure 16. First stage of the construction of a 2-D crystal having the internal structure as given in Figure 14.
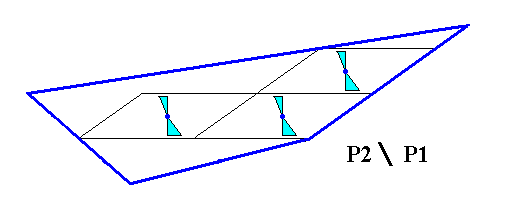
Figure 17. Final stage of the construction of a 2-D crystal as indicated in the previous Figure. The crystal consists of four Forms (in the crystallographic sense). Each Form consists of only one possible crystal face, because such a possible face will not be multiplied by any classical symmetry element in virtue of the absence of classical symmetry, i.e. the classical point symmetry group is C1 [while the antisymmetry point group is C2 / C1 , which is isomorphic with C2 ].
The antimers of the crystal of Figure 17 can be depicted as follows :
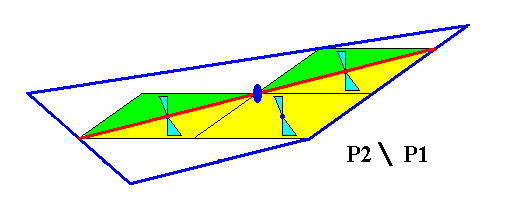
Figure 18. The two antimers of the 2-D crystal of Figure 17. The boundaries separating and delineating the two antimers are more or less arbitrary, because in crystals the Promorph is based on microscopical structure, i.e. on the number, nature and arrangement of the antimers of the translation-free (chemical) (microscopic) motif.
The asymmetry of the pair of (macroscopic) antimers of the crystal, as depicted in Figure 18, reveals the (classical) asymmetry of the pair of microscopic antimers, as they are in the translation-free motif. There, in one and the same motif, one antimer is different from (but similar to) the other antimer of the motif.
Based on the above, we can say that the Promorph of the 2-D crystals of the Figures 14 and 17 belongs to the 2-D analogue of the Heterogyrostaura dimera, although they are less clear representatives of this promorphological Class. We can, however, expect that because the motif involved here is very close to that of Figure 10, the respective atomic aspects presented to the growing environment by the possible faces, will be much alike, and consequently result in similar growth rates patterns, ending up in identical shapes of the corresponding crystals.
The Plane Group Pm
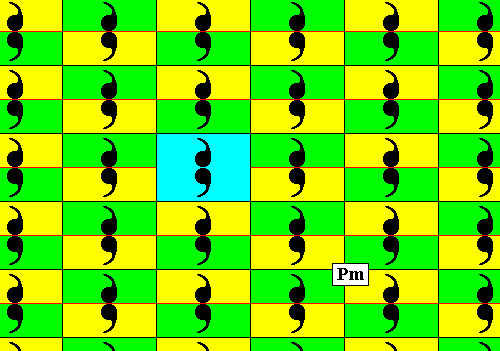
Figure 19. Two-dimensional periodic pattern according to a primitive rectangular point lattice (net), provided with reflectionally symmetric motifs (dual commas) resulting in a total symmetry according to the Plane Group Pm. A unit cell (unit mesh) is indicated (blue). The yellow and green halves of the meshes plus content (comma) represent group elements.
The next Figure depicts half a Rhombic Pyramid and makes clear some of its elements.
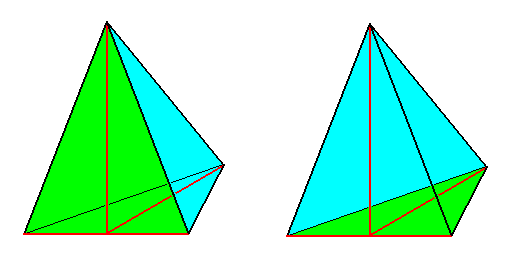
Figure 20.
The basic form of the Heterostaura allopola, illustrated by half a Rhombic Pyramid (which itself is the basic form of the Allopola zygopleura eudipleura) .
Left image : bisection face (originated by the bisection of the whole Rhombic Pyramid) emphasized (green).
Right image : Base emphasized (green).
Main axis (vertical), lateral axis (horizontal) and dorso-ventral axis are indicated in red. The only symmetry element is the mirror plane, which contains the main axis and the dorsoventral axis. It separates the two antimers.
The next Figure again gives the pattern of Figure 19, but now without indication of the areas representing group elements. The pattern is a periodic stacking of the unit mesh containing a mirror symmetric motif (s.str.) consisting of two antimers (commas).
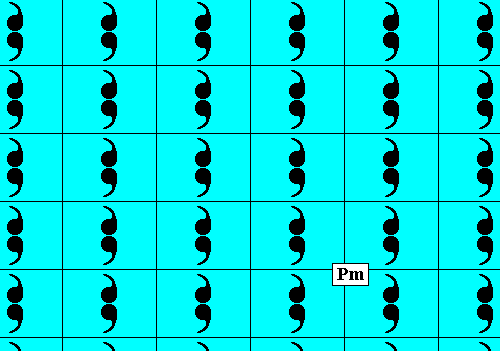
Figure 21. Pattern according to the Plane Group Pm.
It consists of mirror symmetric motifs repeated according to a primitive rectangular point lattice (net). The (translation-free) motif is such that it allows for two (equal) antimers to be distinguished.
The point symmetry of the pattern of Figure 21 (and also of 19), i.e. the translation-free residue of of the total symmetry (plane group), is m, which is isomorphic with the symmetry group D1 (which is itself isomorphic with C2 and also with Ci ). So the only symmetry element of this point symmetry as it will manifest itself in the intrinsic symmetry of the crystal macroscopically, is a mirror line. Every possible 'face' of a crystal with this structure that is perpendicular to this mirror line will not be multiplied when subjected to the whole set of point-symmetry elements (which here is just a mirror line) of the given pattern. So such a face is already a Form. All other possible faces, except when coinciding with the mirror line, will be duplicated resulting in a Form consisting of two faces that are mirror symmetrically placed with respect to each other.
The next Figure illustrates a possible crystal having the above structure.
Figure 22. A possible two-dimensional crystal having the structure of the pattern of the previous Figure.
It is a combination of three Forms (in the crystallographic sense) :
See also next Figure.
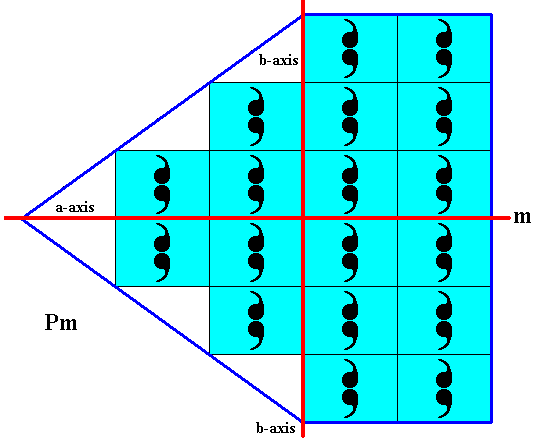
Figure 23. The 2-D crystal of the previous Figure.
The red lines are the two crystallographic axes (a and b). One of them coincides with the mirror line (m), while the other is perpendicular to it and aligned along the vertical translation vector of the pattern.
The next Figure indicates the Vector Rosette of Actual Growth of the crystal.
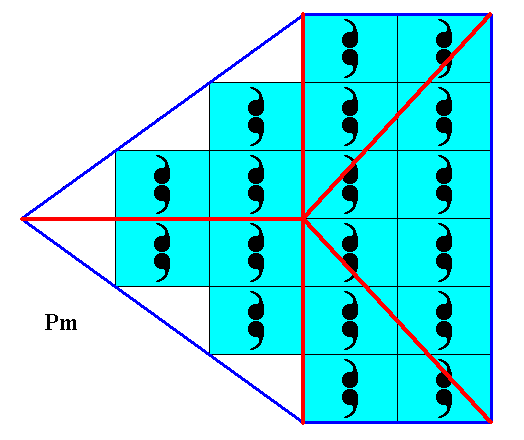
Figure 24. Vector Rosette of Actual Growth of the 2-D crystal of the previous Figures.
The two antimers (as such based on the morphology of the translation-free motif) of the above 2-D crystal are indicated in the next Figure.
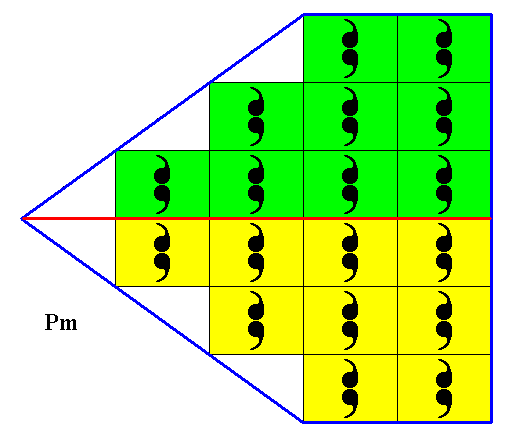
Figure 25. The two antimers of the crystal of Figure 24, 23 and 22 are indicated. They are separated by the crystal's mirror line.
The symmetry of the translation-free motif, expressing the intrinsic point symmetry (Crystal Class), already determines the crystal's general Promorph, namely that of the Heterostaura allopola (Stauraxonia heteropola, or single pyramids). The presence of two equal antimers determines the Promorph further, namely to that of the Zygopleura eudipleura (Heterostaura allopola).
Instead of the motif used above, we can think of all kinds of other motifs having the same symmetry, which is the symmetry according to the Point Group D1 . And when we replace our initial motifs by such other motifs, the symmetry of the pattern will stay the same, which is the symmetry according to the Plane Group Pm.
Figure 26. A (two-dimensional) motif with D1 symmetry (i.e. a motif having as its only symmetry element a mirror line), like the motif of the previous Figures. The motif consists of four similar antimers.
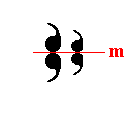
Figure 27. The above motif is mirror symmetric according to the reflection line m.
As can be seen in the previous two Figures, the motif allows for f o u r antimers to be distinguished. Although these antimers are different among each other, they are nevertheless similar. The next Figure illustrates this.
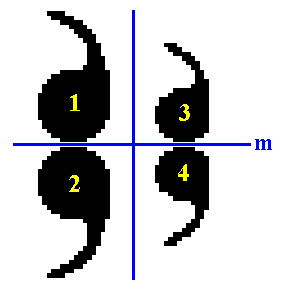
Figure 28. Enlargement of the newly chosen motif. It has D1 symmetry (crystallographically denoted as m) , and has four similar antimers, 1, 2, 3 and 4 (commas). The presence of the smaller antimers does not influence the symmetry of the motif at all, but changes its promorphology, from the 2-D analogue of the Zygopleura (eu)dipleura to that of the Zygopleura (eu)tetrapleura.
In the motif depicted in the above Figure we can see that the four radii are represented by the four antimers. The two perpendicular blue lines represent the two directional axes of the motif. They lie between the radii, and are therefore called interradial directional axes.
If we (repeatedly) place the motif of Figure 26 in a primitive rectangular point lattice we get the following pattern, the symmetry of which is still according to the Plane Group Pm :

Figure 29. A pattern according to the Plane Group Pm .
It consists of mirror symmetric motifs, repeated according to a primitive rectangular lattice. Each motif consists of four similar antimers.
We can now construct a crystal having the above internal structure.
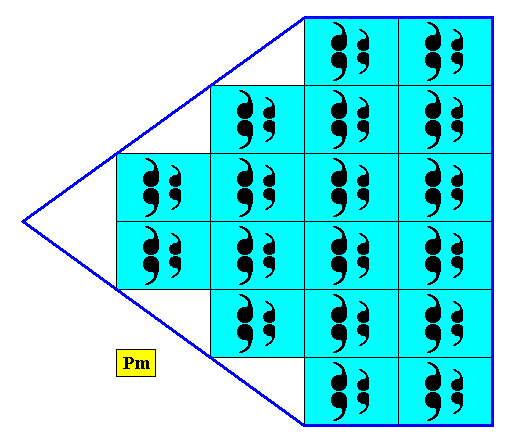
Figure 30. A two-dimensional crystal with internal structure as depicted in the previous Figure.
The antimers of this crystal are indicated in the next two Figures.
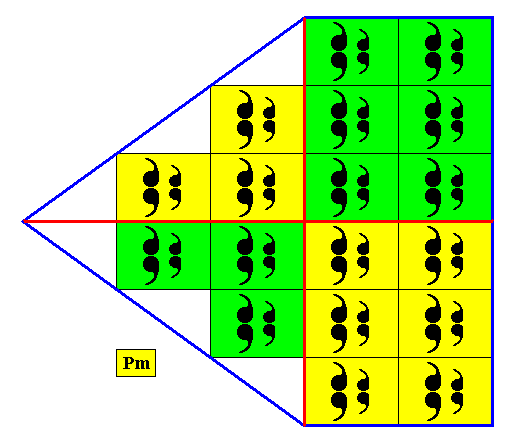
Figure 31. The four antimers of the two-dimensional crystal as depicted in the previous Figure. The boundaries separating these antimers are more or less arbitrary.
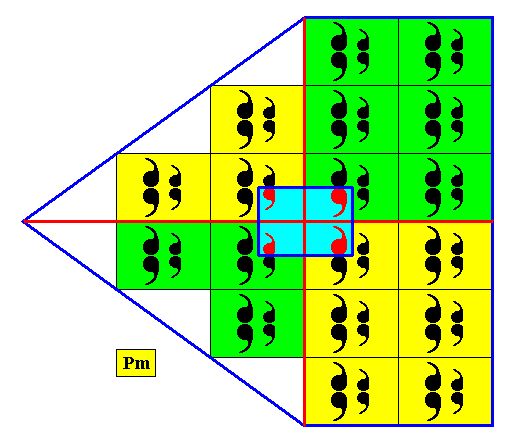
Figure 32. An alternative, but equivalent way, to indicate the motif. This way of indicating the motif helps visualizing the configuration of macroscopic antimers.
Om the basis of the structure of the translation-free (microscopic) motif we assess the Promorph of the crystal to belong to the two-dimensional analogue of the Eutetrapleura interradialia (as a species of the Allopola zygopleura). The directional axes of the translation-free motif are interradial, i.e. lying between the radii, which are represented by the antimers (See Figure 28). Therefore the corresponding crystal promorphologically belongs to the interradial eutetrapleurals. See next Figures.
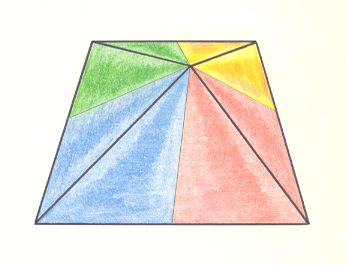
Figure 33. Oblique top view of a trapezoid-pyramid ( = antiparallelogram pyramid) as the basic form of the Eutetrapleura interradialia. The four antimers are indicated by colors.
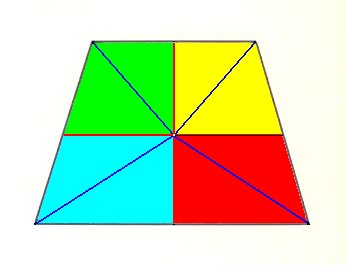
Figure 34. Base of the pyramid of Figure 33.
In that base we have indicated the (traces of the) directional planes (one horizontal and one vertical line in the drawing), and the four radii contained in the median planes of the antimers. The four antimers are indicated by colors.
In the next document we will consider still other motifs that have D1 symmetry and that can therefore also constitute a Pm pattern. But these different motifs also, although not changing any symmetry, imply different Promorphs (i.e. different species of the Heterostaura allopola or half amphitect pyramids).
To continue click HERE for further study of the Theory of Layers, Part XXXIII.
e-mail : 