General Ontology
Cosmos and Nomos
Theory of Ontological Layers and Complexity Layers

Part II
e-mail : 

Back to Homepage
This document continues the investigation of categories and complexity layers.
Ontological Status of Whatness Categories

We will now discuss  whatness categories  as to their way of being.
Conventionally the whatness of something is expressed as a definition. In it the meaning of some concept is given. As such a definition is a logical or gnoseological entity, not an ontological entity, and thus not a category or  If / Then  constant, because the reference is to concepts, not to things, materials or their properties. The direction of 'movement' is from unanalysed (not understood) to analysed (and therefore understood), for instance in

Man is a featherless biped.

In a whatness category, on the other hand, the direction is from analysed to unanalysed. And here we have, moreover not to do with concepts and their meaning, but with beings (which can be either physical or mathematical), materials and properties .
The whatness category (eidetical constant) can first of all determine the intrinsic whatness of a genuine being (When this being is mathematical there is no difference between intrinsic and extrinsic whatness). In the physical case such a whatness category or eidetical constant is the dynamical law of the physical dynamical system that generated that being ( This dynamical law is at the same time a nexus category, connecting states of the dynamical system).
The whatness category can also determine the intrinsic whatness of some given material, and, finally it can determine the whatness of some property of a given being or of a given material.
In the case of a whatness category, the "unanalysed" does not refer to something-not-understood, but to something-being-just-there. And the latter is necessarily what it intrinsically is, i.e. it is determined as to what it intrinsically is by the "analysed", where the latter does not mean analysed by us. It means the ontological 'machinery' that determines something as to what it is in itself.

As an example of a whatness category we take the  Category of 3-fold Cyclic symmetry  that was discussed earlier ( Part I ).

Category of 3-fold Cyclic Symmetry (whatness category) :

If all cover-operations (let us call them)  1,  p,  p2  of something form the group (as given by a group table) :

then that something has 3-fold cyclic symmetry.

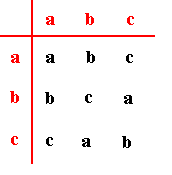
Let us analyse this particular whatness category.
It is supposed to determine 3-fold cyclic symmetry as to what it necessarily is. Roughly and generally it is a property, either of some mathematical figure or of some physical object. In itself, however, it is a certain coherent pattern. So we must look for this pattern. To begin with, the very kernel of this pattern is a certain abstract group. This group (in the mathematical sense) consists of three elements that are fully abstract, i.e. not interpreted. What they are is wholly contained within the group table which establishes the relations between them :

From this table we see that the following relations between the elements  a, b  and  c  hold :

aa = a2 = a
ab = b
ac = c
ba = b
bb = b2 = c
bc = a
ca = c
cb = a
cc = c2 = b

These relations show that the element  a  is the identity element of the group. It does not bring about a change when combined either with itself or with any other element of the group. And, again, what the other elements, viz.  b  and  c ,  are, is laid down completely and exclusively by their relations to the other elements, where these relations are given in the group table. There is no object (neither a mathematical object, nor a physical object (thing)) involved in this abstract pattern. The latter is just an algebraic pattern.

So with this algebraic pattern we have now established the kernel of the whatness category of 3-fold cyclic symmmetry. This kernel must now be 'upholstered' in order to arrive at symmetry. To begin with we must interpret the group elements as cover-operations.  A cover-operation is a transformation of an object (mathematical or physical) such that the result is precisely superposed upon the object as it was in its initial state. So now at least some object is involved. But this object is still not the (3-fold) symmetry. To involve cover-operations we can interpret the group elements  a, b, c  accordingly. First we saw that  bb = b2 = c .  So we can express  c  in terms of  b ,  i.e. we can replace  c  by  b2 .  Further, we had seen that the element  a  was the group's identity element, so, to indicate this, we can replace the symbol  a  by the symbol  1 .  The result is the following :

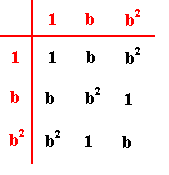
If we interpret these elements  1, b  and  b2  as cover-operations, then (I) the element  1 , the identity element, is indeed a cover-operation (because 'not doing anything to the object' or, equivalently, a rotation of the object by 00 or 3600 about any axis, results in the 'transformed' object to be exactly superposed upon the object as it initially was), (II) the element  b  must then be a rotation (let's say anticlockwise) of 1200 about some axis, and (III) the element  b2  must then be an anticlockwise rotation of 2400 about that same axis. If we now rename the elements such that the symbol  b  is replaced by the symbol  p ,  we get our original group table as it figured above in the Category of 3-fold Cyclic Symmmetry :

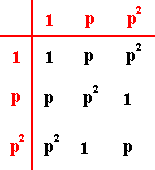
The group elements (which constitute the above mentioned algebraic pattern) are now cover-operations, and that means that they are symmetry transformations.  But as such they are still abstract, in the sense that they are transformations  of something.  And only the latter, or its parts, are beings.  So we must see what we can do with these (still abstract) group elements. See next Figure.

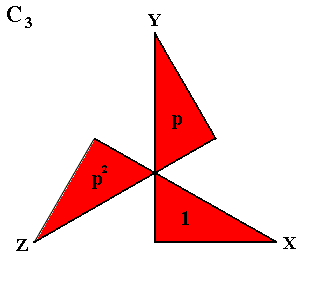
In the above Figure we see a two-dimensional object (and thus surely just a mathematical object), consisting of three parts  X, Y  and  Z ,  that will be superimposed upon itself when it is rotated either 00 or 1200 (anticlockwise) or 2400 about an axis perpendicular to its plane and going through its center. In fact what we see, when performing these rotations, that the parts  X, Y  and  Z  of this object are transduced into each other by the symmmetry transformations  1, p  and  p2  according to the following scheme :

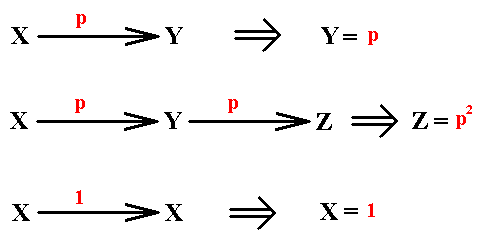
The above shows that we can identify part  X  of the object with group element  1 ,  part  Y  with the group element  p  and part  Z  with the group element  p2 .  So now the group elements of our group not only signify symmetry transformations, but can also be represented by parts of an object.  And it is clear that the configuration of these parts -- as such being the object's overall structure -- is now eidetically determined by the symmmetry group  {1, p, p2} ,  which as such is the group of  3-fold cyclic symmetry (C3), with generator set {p} and the defining relation  p3 = 1 ,  and explicitly given in the above group table .  And with "eidetically determined " we mean a determination that is not of a causal nature, but nevertheless an ontological determination, i.e. a determination by way of a whatness category, which here is the mentioned symmetry group. In the next Figure we see our object again, with its three parts, representing the three group elements. It is a two-dimensional Figure, and, as such still a mathematical object. If we make the object three-dimensional without altering its symmetry, we still have a purely mathematical object (a pyramid), involving three-dimensional geometric space. However, if we interpret this three-dimensional space of this three-dimensional object as physical space, then we have a physical object, a physical pyramid, the three parts of which still represent the same three group elements  1, p  and  p2 .  So now the whatness of the symmetric structure of this physical object is indeed the group C3 as given above. And the elements of the whatness category, that is represented by this group, are now indeed pointing not to concepts or their meanings, but to objects or their parts, which objects and parts can be either purely mathematical or physical.

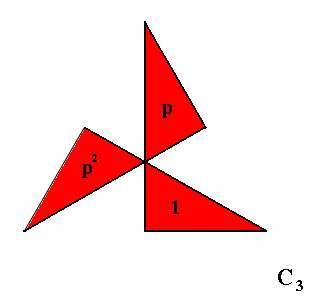
Figure 1.  The group  C3  interpreted, meaning that its elements are represented by parts of an object. In order to let the image represent  a  p h y s i c a l  object with the same symmetry, this object must be transformed into a gyroid pyramid (See next Figures). We can do this by erecting a line in the center of, and perpendicular to, the plane figure, and then connecting the top with all the angle points of that figure, and interpreting the 3-D space as physical space. The group elements  p,  p2  and  1  are represented by the parts of the 2-D figure as indicated, but at the same time (they are represented) by the implied irregular pyramids together making up the whole gyroid pyramid. The rotations are about an axis represented by the mid-point of the figure.

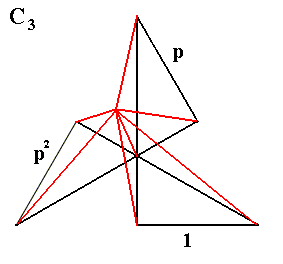
Figure 1a.  Construction of the gyroid pyramid from the gyroid polygon of the previous Figure. Black lines belong to the pyramid's base, while the red lines are going up, i.e. leave the plane of the base.
The next two Figures give the finished construction of the gyroid pyramid. It has the same symmetry -- C3 -- as the two-dimensional figure depicted in Figure 1 ,  and it can be interpreted as a physical object.

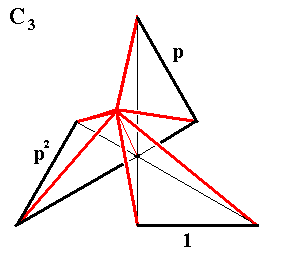
Figure 1b.  Three-fold gyroid pyramid, constructed from its base (Figure 1 ). See also next Figure.

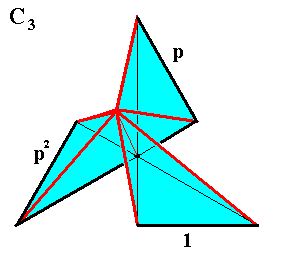
Figure 1c.  Same as previous Figure. Visible areas colored. The pyramid consists of three parts that can represent the three elements  1, p, p2  of the above discussed 3-fold cyclic group.
Every coherent object in the Physical Layer possesses a specific identity, viz. its ESSENCE. The latter is the object's genotypical whatness, while its phenotypical expression is the phenotypical whatness consisting of the complete set of intrinsic properties as analysed to their content. The latter is equivalent to the total set of entitative constants of the given object. In fact, entitative constants include, in addition to the corresponding properties, also the whole disjunctive set of their conditions. So the mentioned total set of entitative constants do include (at least) the object by which these properties are implied. In this total of entitative constants each corresponding property is presupposed as analysed. This being analysed comes about by the whatness category of that particular property. So all the intrinsic properties of the object are -- in the context of the total of the object's entitative constants -- being analysed in virtue of the corresponding whatness categories, i.e. their whatness is explicated, which here means determined. To determine the whatness of a property is to explicate it as it is  in itself,  i.e. what it is in itself. But of course a property does not have a self. It has only a self  in a certain sense,  and this wholly in virtue of the whatness of the thing of which it is the (intrinsic) property. So the 'self ' of the property derives from the self of the thing.
Indeed, in all this, it is just presupposed, to be sure, that such 'itselves', with respect to certain things, do really objectively exist. This presupposition could, however, be false, because it could also be (true) that the 'specific identity', as referred to above, of any object (thing) is completely determined by the total of all  relations  it has to (all) other objects. And that would amount to assume that the identity of a given object involves at least a whole Layer of existence. But this in turn would imply that such an object does not have any identity of its own :  Its identity would be either that (of the) entire Layer (for example the whole physical universe), or (that of) several such Layers as a whole, or (of) all Layers as a whole, or it would be nothing at all. And, moreover, the mentioned relations that it has with other objects vary all the time (certainly in the temporal Layers), and so would not point to a definite identity or self of such an object.
The most convincing argument that genuine objects do have a definite identity, can be taken from the fact that organisms do exist, especially human beings. Such an argument establishes that at least certain 'selves' do exist. And such selves are not absent in other objects, but probably grade down as we descend into the inorganic domain.
Another argument is the fact that materials do have certain constant properties, which we discussed as material constants, and thus referring to intrinsic properties, presupposing a kind of self of the material -- the latter as an integrated summation of all the individual constituent objects that make up this particular material (e.g. individual crystals or individual molecules) -- the material, of which they are intrinsic properties.
So despite the all-permeating  r e l a t i o n a l i t y ,  which -- as real relationality -- is one of the general categories of the Real Sphere of existence ( The temporal Layers), there must be things (genuine objects, beings) themselves. If we do not suppose this, i.e. if we let everything to consist of relations only, we end up in an infinite regress, of things being related to each other, where those 'things' 'themselves' are just relations, .  .  .  of (other) things, where these things are again just .  .  .  . 
So ultimately there must be things (objects) that have their identity not radiating out of it, but have it within. And this means that they are determined as to what they are all by themselves (not in virtue of relations with other such things). Determined by what ?  By whatness categories, .  .  . ultimately those that determine properties as to what they are, constituting in this way the (phenotypical) whatness of the given object, which as such is the phenotypical expression of the ESSENCE of that object, which (essence) is its genotypical whatness.
The expression of whatness categories in the form of  If / Then  constants shows that a whatness as such cannot change or vary. Only the thing that has this whatness can change, namely by replacing this particular whatness by another, because change involves a process, and only things can enter into a process.
So (to take an example) 3-fold cyclic symmetry will always remain 3-fold cyclic symmetry, because it is definitively  d e t e r m i n e d  as being the group of three rotations (00, 1200, 2400).
Determinative threads revisited

The next Figure illustrates how objects are connected to each other by entitatively determinative threads.

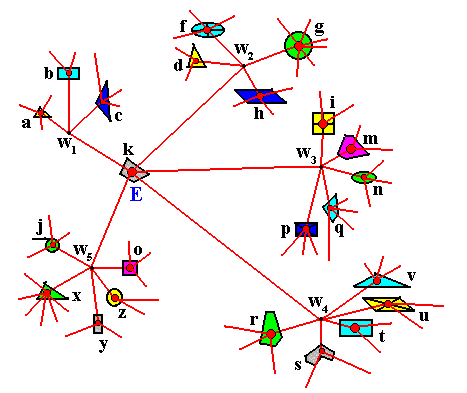
Figure 2.  Physical objects -- symbolized as discs, triangles, polygons, rectangles, etc. -- connected by entitative threads. The red dots in the objects symbolize their ESSENCE, and from the latter the intrinsic properties of the relevant object are phenotypically expressed. See also Figure 13 of the previous document.
Let us explain the above Figure.
The objects  a, b, c, k  imply an intrinsic property  w1  (i.e. intrinsic for these objects). This property is determined as to what it is (as analysed) by the corresponding whatness category (not drawn), and, as so analysed, presupposed by the entitative constant (which determines the implication of this property). The mentioned objects represent the disjunctive set of sufficient grounds (disjunctive set of If-components) for the implication of the property  w1 .
In the same way the objects  d, f, g, h, k  imply an intrinsic property  w2 . 
Further, the objects  i, m, n, q, p, k  imply an intrinsic property  w3 . 
And also the objects  r, s, t, u, v, k  imply an intrinsic property namely  w4 . 
And, finally, the objects  j, o, x, y, z, k  imply an intrinsic property  w5 . 
So the object  k  possesses all the intrinsic properties  w1 ,  w2 ,  w3 ,  w4  and  w5 .
Let these five properties, that are intrinsic to  k  -- while  w1  is also intrinsic to the objects  a, b, c ,  and  w2  is also intrinsic to the objects  d, f, g, h ,  etc. -- be the total of properties intrinsic to  k .  Then we can say that they represent the phenotypical whatness of the object  k ,  i.e. the whatness that results when the ESSENCE (genotypical whatness of object  k) is phenotypically expressed (which happens when the object is generated by a dynamical system, implying the dynamical law of the latter to be(come) the ESSENCE of that object).

The above drawing is about the ontological constitution of things. As such this is a static state of affairs. Now we want to involve nexus categories in that drawing, that is to say we now are going to add a dynamical element.
A nexus category determines the necessary connection between states of a dynamical system. When we consider only two consecutive states, we have -- in the Physical Layer -- to do with causality. If we consider all possible sequences of states, going out from all possible initial states (initial conditions), then we have to do with a certain special nexus category in the form of a dynamical law (which presupposes causality).
A part of a dynamical trajectory (i.e. a part of a sequence of states of the dynamical system) can be exemplified by a series of larval stages during the individual development of some insect. When we concentrate on two consecutive larval stages, Stage n  and Stage n+1, we can say that the former is the cause of the latter.
What we see when such an individual insect develops, is in fact the successive phenotypical expression and suppression of intrinsic properties by the insect's ESSENCE (i.e. some properties appear first, and later on some other properties, while some disappear again, etc. In all this the insect's ESSENCE remains the same.).
The next diagram repeats the previous one and shows where a nexus fits in, a nexus, between a concretum and a(nother) concretum, determined by a (special) nexus category.

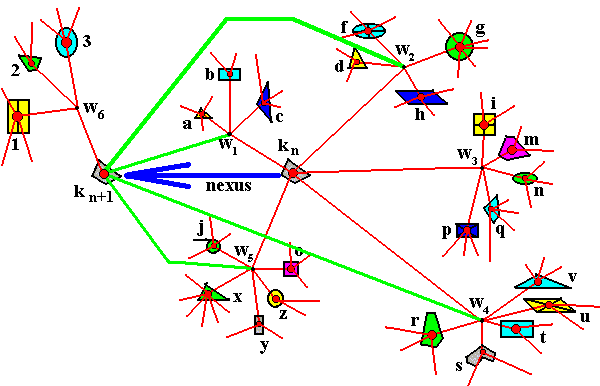
Figure 3.  Insertion of a  n e x u s  into the previous diagram (Figure 2).  The objects  kn  and  kn+1  are two consecutive states (or stadia) of a dynamical system. While the intrinsic properties  w1 ,  w2 ,  w4 ,  w5  are retained (i.e. they keep being expressed), the intrinsic property  w3  is suppressed (i.e. its former expression is annihilated), and intrinsic property  w6  is now expressed.
The nexus is indicated by a blue arrow. It is determined by a nexus category (presupposing causality), which is the dynamical law of the dynamical system of which  kn  and  kn+1  are consecutive states.
Until now we have discussed mainly some special categories. There are however also totally general categories of which the domain of relevance is the whole system of Layers, the Mathematical, Physical, Organic, Psychic and Super-psychic Layers. These are the fundamental categories, which are given by HARTMANN in the form of pairs of opposites, like Element--System, and, of course, Category--Concretum (Principle--Concretum). Further there are categories that have their domain of relevance to be one particular Layer as a whole, i.e. they determine everything within that Layer. The latter categories can either spill over into the next Layer, but are then over-formed, or they break down completely in that next Layer.
For such categories HARTMANN has established inter-categorical laws. These laws in fact describe positively what such categories really are and how they are related to each other.
Before we look into those categories and the corresponding inter-categorical laws, we will first continue to concentrate on special categories in order to see them in the context of a definite research program, which will later include the mentioned (more) general categories. Our "special" categories are very specific indeed, such as the Category of Intrinsic D6xC2 Symmetry (entitative constant), the Category of Hexagonal Bipyramidal Symmetry (whatness category), the Category of 3-fold Cyclic Symmetry (whatness category), etc. They are not common to all entities of a specific Layer (say, the Physical Layer), and because of this they are not investigated by HARTMANN.
In the next document we will continue with these special categories, and define the scope of the investigation.

A great many documents will follow, all concentrating on just a few (but interesting!) special categories, namely  Intrinsic Shape,  Symmetry  and  Promorph,  accompanied with some ontological discussions.

But if the reader is more interested in an overall view of the  Ontological Structure of the World  in terms of the Layer Theory, categories and categorical laws,  he or she can skip all the documents about shape, symmetry and promorph, and can pick up the theoretical discussion again at  Part XXIX Sequel-24 .  There the Theory of Ontological Layers is fully developed, and will form the philosophical context of an extensively worked-out Crystal Analogy.

If, however, the reader wishes to continue the study of the (special) categories Intrinsic Shape, Symmetry and Promorph, he or she should use the LINK directly below.
To continue click HERE for further study of the Theory of Layers, Part III.

e-mail : 

Back to Homepage

Back to Contents

Back to Part I