

e-mail :

Sequel-4 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-4) is a pictorial extension of the preliminary investigation into the 'phyllotaxis', symmetry, promorphology and ontology of snow crystals, as
When a snow crystal grows rapidly, it develops outgrowths. Such outgrowths are likely to start off from edges or corners, because they can be supplied from more directions, in our case supplied by water molecules present in the air. But, as far as I can see from the many microphotographs taken from snowflakes, these outgrowths do not appear at the edges that separate the upper face, as well as the bottom face of the (flat) hexagonal prism, from its sides. The outgrowths appear to develop only at the edges separating the sides of the prism. See next Figure.
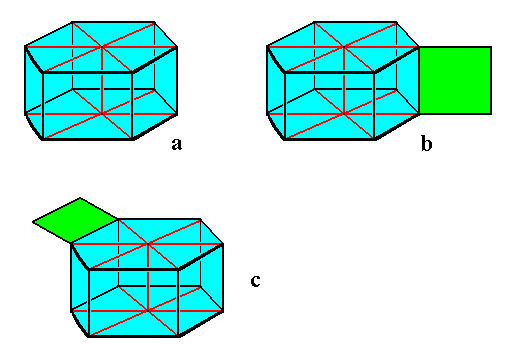
Figure above : Diagram of a snowflake, with and without outgrowths.
The snowflake is depicted here as a hexagonal prism, which indeed it is. In reality, however, the prism is much more flattened.
Image a : Hexagonal snowflake prism without outgrowths.
Image b : Hexagonal snowflake prism with outgrowths (one shown) at the vertical edges separating the sides of the prism, where they (i.e. the outgrowths) are indeed actually found.
Image c : Hexagonal snowflake prism with outgrowths (one shown) at the horizontal edges separating bottom and top face from the vertical sides. Such outgrowths are not found in snowflakes.
So the development of a snow crystal seems to be subjected to strict rules : symmetrical outgrowths only at the prism's vertical sides, resulting in a very flat crystal. The forms of these crystals are not the result of 'evolutionary crafting and engeneering', i.e. a sifting out of viable versions, versions that can perfrom the necessary functions for survival. They are just the result of initial configurations direct sliding off to configurations that are energetically stable, which is a direct and spontaneous process.
Point group symmetry, involving the repetition of macroscopic morphological structures (which are not (also) translationally repeated), can also be obtained by mathematical models involving chaotic dynamics. The next Figure is an example where this repetition is, as it is also in snow crystals, six-fold.

Figure above : A pattern having D6 symmetry obtained by mathematical chaotic dynamics (iteration of a symmetric mapping).
(After STEWART, I. & GOLUBITSKY, M., Fearful Symmetry, 1992 / 1993.)
The above symmetric pattern shows, like in branched snow crystals, a six-fold repetition of a complex morphology. It seems, however, in contradistinction to snow crystals, to be the result of local interactions only (instead of a global, i.e. holistic, process). However, it is just a mathematical model. And if it has any relevance to real processes at all, we must think of electrical oscillators or the like, and not of crystallization. Moreover, the symmetry of such patterns -- symmetric patterns resulting from chaotic dynamics -- exists only on average. That is to say that the symmetry is only apparent if we consider enough data points.
From this it is clear that there are many opportunities for setting up theoretical research plans for finding out the basics of pattern formation in Nature.
Back to snow crystals.
What follows is a selection of microphotographs of snow crystals from the book Snow Crystals of BENTLEY and HUMPHREYS (1931), where we see the above mentioned outgrowths, and get an idea of their endless variation.

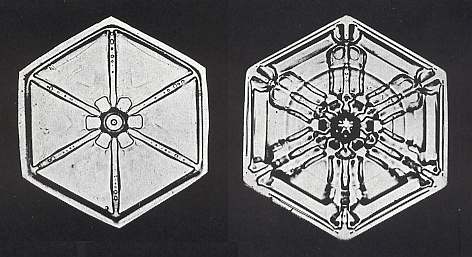
Figure above : Two snow crystals.
We see that they are hexagonal plates (thin hexagonal prisms). If these crystals were crystals without outgrowths, then, macroscopically, they should look homogeneous, possibly with some randomly distributed inclusions, irregularities, etc. What we see, however, is a symmetrical distribution of these features. So we must conclude that these crystals are in fact branched crystals, but where the branches have finally occupied all space between them. See also next Figure. In the left image we see an indication (three elongated oval marks parallel to three sides) that the crystal is (only) trigonal instead of hexagonal, which means that the crystal seems to have a lower symmetry than what we usually see namely 6/m2/m2/m. This phenomenon is often encountered in snow crystals.

Figure above : Two snow crystals.
The six branches or outgrowths have nearly invaded all space between them.

Figure above : Two snow crystals.
Also here the six branches or outgrowths have nearly invaded all space between them.
The following Figures show still more snow crystals, their multiplicity of possible branches or equivalent symmetrical structures, and occurring irregularities.

Left image : Morphology of arms not precisely repeated. Such a phenomenon must be attributed to local external conditions (and thus to extrinsic causes).
Right image : The interior of the crystal, as well as the distribution of its six arms, is three-fold instead of six-fold.

Left image : Large extension of the six almost perfectly repeated arms.
Right image : One of the six arms deviates from the others. Extrinsic cause.


The crystal of the left image shows indications of (only) three-fold symmetry.




Left image : Two identical snow crystals penetrate each other. It could be a genuine crystallographic twin.
Right image : A triangular snow crystal, apparently indicating trigonal symmetry.
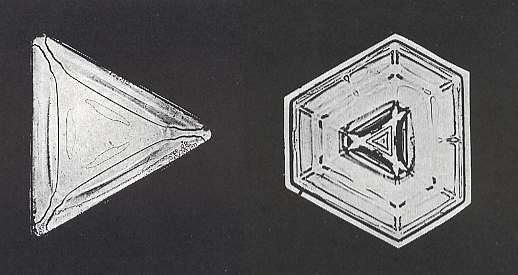
Left image : Triangular snow crystal.
Right image : A sexangular snow crystal. It seems to be an interpenetration of two different triangular (crystallographic) Forms (not two crystals), indicating trigonal symmetry.

Snow crystals consisting of a hexagonal prism capped with broad hexagonal plates.
In some of these the main axis is equipolar, in others non-equipolar.
According to 6/m2/m2/m symmetry (Dihexagonal-Bipyramidal Class) the main axis should be equipolar. So in the cases where this axis seems not to be equipolar, we must assume either a different symmetry (but same Crystal System) to be possessed by these crystals, for instance, 6mm (Dihexagonal-Pyramidal Class), or a case of twinning, or the non-equipolarity of the axis to be caused by extrinsic causes.
This concludes our investigation concerning snow crystals. However, as such it was just a cursory exploration about the significance of snow-crystal growth for ontological theory. It is clear that snow crystals deserve much more attention. They will get it in the next to next document (Part XXIX Sequel-6), after the ontological theory is summarized and extended (present document), and after the existence of the impetus, and thus the existence of a holistic feature (namely a variable quality), is demonstrated (Part XXIX Sequel-5).
Summary and Extension of Ontological Theory
Theory of the Implicate Order and the Categorical Novum : Categorical Nova on a smaller scale (Special Categorical Nova).
We have solved the vexed problem of the categorical novum -- i.e. the appearance of an entirely new ontological principle when changing from one Layer of Being to the next higher one -- or, generally, we have solved the problem of holism, by the theory of the coupling of two Orders playing a part in pattern generation :
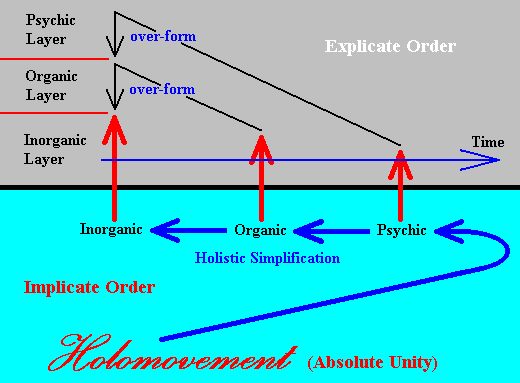
In Part XXIX Sequel-1 we have exemplified all this with the structural relationships between the Inorganic and the Organic : As we go, in the Explicate Order, from Inorganic to Organic, we encounter the appearance of a categorical NOVUM. This NOVUM, then modifies all or at least many of the other categories that have entered the Organic Layer from the Inorganic. And in this way clearly lets stand out the Organic Layer with respect to the Inorganic Layer.
The connection between higher irreducible entities to lower entities is mediated by holistic simplification (from these higher to lower entities) in the Implicate Order. The nature of this Order is not precisely known. It will have many different aspects, and it is almost certain that one of these aspects of the Implicate Order is its being field-like. The Explicate Order then is not fundamentally different : It consists of field singularities. And indeed a field has holistic properties. See, for example a magnetic field : If a magnet is cut in half, each half of it does not have half the original field, abruptly ending where the magnet was cut. It becomes a whole magnet, surrounded by a complete magnetic field.
In the field, representing the Implicate Order, v i b r a t i o n s will undoubtedly play an important role, concerning the interplay between Implicate and Explicate Order. A holistic interpretation of Reality rejects the assumption that there is one particular kind of collection of basic ultimate entities from which all higher (i.e. complex) entities are generated. Each type of higher entity is a holon in itself and is not reducible to lower entities, at least according to our brand of holism. They only relate to each other, i.e. are derived from each other, by holistic simplification within the Implicate Order, while in the Explicate Order they relate through the addition of a NOVUM, or, according to reductionist science, they relate to each other by reductionistic complexification. All holons together form a hierarchy of inclusion, i.e. inclusion of lower ( = simple) holons within higher holons, which hierarchy we can call a holarchy. So a higher holon structurally c o n s i s t s of lower holons, it is true, but a higher holon can nevertheless not be reduced to those constituent lower holons, which means that such a higher holon is not already implicitly, or potentially, present in (the collection of) its parts or elements. Each holon exists in itself as a basic and fundamental structure. There is no ultimate fundamental level or holon.
Of course there are 'things' that can totally be reduced to their elements, which is the case in all extrinsic beings, like sand dunes or human artifacts. But these are in fact no things or beings at all. Only their (ultimate) constituents are things in the sense of holons. And so we discriminate between aggregates and totalities . And the latter we also call intrinsic beings , substances (in a metaphysical sense) or holons.
As to the Implicate Order, we should realize that this Order is not transcendent with respect to the Explicate Order. It is not a Platonic domain of eternal Forms. The Explicate Order consists of projections from the (higher-dimensional) Implicate Order, or said differently, it consists of temporal singularities of the underlying field which is the Implicate Order. Noëtic processes within the Implicate Order can result in successive projections that represent the mentioned singularities. Some of these singularities are stable, others are not. The injections of these singularities influence the Whole, i.e. influence the Implicate Order plus Explicate Order.
Holistic communication between structures in the Explicate Order takes place via the Implicate Order by some resonance phenomenon. The latter is -- in our case -- a non-energetic transfer of information, and takes place on the basis of rhythmic patterns of activity, and their similarity. Space and Time are derived phenomena, derived from projections and injections, and characterize the Explicate Order. So when the Implicate Order is involved, resonance -- morphic resonance -- is neither a temperal, nor a spatial phenomenon.
The six sectors of a snow crystal communicate with each other via the Implicate Order (which is of a much higher dimension than is the Explicate Order, and which makes seemingly separated parts to be in fact strictly correlated, as we saw it expressed in the Figure in Part XXIX Sequel-1 ), and this type of communication we call -- following SHELDRAKE -- morphic resonance. It establishes, or represents, the crystal as a holon, i.e. as a holistic whole. In any such whole its apparent separate parts or sectors are non-locally connected, which is possible because this connection goes, as has been said, via the Implicate Order. There the parts are not unfolded (explicated) anymore, but totally enfolded, i.e. those parts are wholly within each other. The mentioned resonance between parts of one and the same holon can be called a form of self-resonance. Another form of self-resonance is that with the holon's own past, insofar as these past stages were similar. In addition to these kinds of self-resonance we have resonance of a certain part of a holon with a similar part of a specifically different holon, or a resonance between a presently existing holon and similar holons, be they in the presence or in the past.
The intrinsic and non-local connectedness of the parts of a holon makes it a genuine whole. Being such a whole, such a total unity, must necessarily entail that its parts or elements do not actually exist, as long as they are parts or elements of that whole (or of any whole whatsoever). These parts or elements exist v i r t u a l l y, and only become actual when the whole disintegrates, but then they are no longer parts or elements, but themselves holons (for example the melting of an ice crystal, resulting in individual H2O molecules).
So the new properties of a holon (new with respect to those of its constituents) are, of course, the properties of that holon. But also the "preserved properties" of the elements (parts, constituents) of that holon are properties of that holon (and thus not properties of the elements anymore). While all the properties of an aggregate (i.e. not a holon) are so-called aggregational resultants (HOENEN, 1947, pp.397), many properties of a holon are so-called totality resultants (Ibid.) (In First Part of Website we discussed all this in terms of the "Mixtum ( = holon) and its Elements ( = parts, constituents)"). There the term "mixtum" was meant to represent a "Mixtum Perfectum", or "Totality", in the sense of "holon" (for example a single crystal), in contradistinction to just an aggregate (which is just a mixture or extrinsic collection of elements, like any human artifact, and also like, say, a sand dune).
Whereas the elements of an aggregate exist actually, the elements of a mixtum perfectum exist only virtually. And only when these elements exist virtually, and not actually, the mixtum can be a genuine u n i t y, i.e. a true c o n t i n u u m or whole. And this whole (this holon) is something new with respect to its (virtually existing) elements, and therefore it cannot be derived from those elements. All this should be so if the holon really 'wants to be' a genuine whole, i.e. an absolute unity without any 'concessions'.
In every written text on HOLISM the very paradigm of such a holon is the individual organism. But, while in atoms, molecules and crystals we could, without too much difficulty, assume that their parts, their elements, have, as parts or elements only virtual existence (and appear as qualities of the holon), in organisms this is hard to accept. Are the organs and cells of an organic body only existing virtually? They seem in all respects to exist actually. And the same can be said of our arms and legs as actually existing parts of our body. But then also, say, the arms of a snow crystal must be actually existing parts of the crystal, not virtually so.
So we have a dilemma : If we interpret a crystal or an organism as being a holon, i.e. a true whole, which is therefore not completely derivable from its parts or elements (while consisting only of these parts or elements), then we must deny these parts or elements any actual existence within that holon (because otherwise that holon would not be a true unity anymore, but a collection of things, i.e. a plurality, albeit in a more or less integrated way) : The existence of all parts and elements in such a holon is only virtual, and as such their properties are nothing more than qualities of that holon. But, as we can see, especially in organisms, this cannot be true. The parts exist actually in the holon.
It is here where the Implicate Order comes in.
In the empirical world, i.e. the world of entities and processes as they are encountered in observation and measurement, the entities are separate from other entities, and the parts of entities, their elements, are also seen as discrete from one another, albeit connected to each other by physical interactions or chemical bonds. This is the Explicate Order, in which things are arranged within space and time. But according to the theory of the Implicate Order the Explicate Order consists of projections from the multidimensional Implicate Order, in such a way that every single thing is constantly created anew as it were, by the incessant projections and injections. Seen in this way, observable entities are just reflections or expressions of the Whole, and more directly of the corresponding particular holon within that Whole (Such a holon, in so far as it resides within the Implicate Order, differs from other such holons only with respect to specific content, implying that they can be perfectly well enfolded into one another). So the holons are not separated from other holons, and especially the parts of, and within, any such holon are not separated. They are tightly enfolded into each other. The fact that these parts project and inject together and do so repeatedly, indicates that the entity of which they are parts is a holon in itself. We say that the parts of one and the same holon have, insofar as they reside in the Implicate Order, approximately the same degree of implication, or said differently, such parts have approximately the same implication parameter, causing them to be projected (and injected) more or less together. And the fact that its parts are tightly enfolded within each other -- only apparently to be separated temporarily in the Explicate Order during projections into that Order -- makes their existence-as-parts only virtual.
Even when apparently separated, they are connected (which accounts for the holistic properties), not by some other entity or force, but by themselves, i.e. part A of a particular holon is connected to part B of that same holon, not by some medium, not by some other entity, say, C, and not by a force, but by themselves, implying that they do not have an identity of their own, and thus only v i r t u a l l y exist as parts in and of that holon. See next diagram, that expresses this in a simplified way, and to which was referred to already earlier.
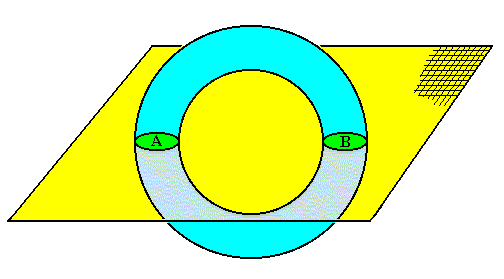
Figure above : A three-dimensional donut-shaped solid object (blue) is intersected by a plane (yellow). The product of the intersection is two areas A and B, which are each two-dimensional. While one cannot unequivocally derive the donut-shaped object from the areas A and B (they give us not enough information as to what the corresponding three-dimensional object will be), we can derive the areas A and B from the donut-shaped object, because those areas are already implicitly present in that object. If we intersect this object by a plane containing its axis of rotation, we obtain the areas A and B. This operation is nothing less than obtaining the areas A and B by holistic simplification of the donut-shaped object. Also here the latter is more than the former, and cannot be derived from it.
Within the two-dimensional plane (of intersection), i.e. seen from within this plane, the areas A and B seem to be separated. As such they appear to be two separately existing mutually independent (two-dimensional) holons, or they could be two parts, separately existing within one two-dimensional entity (this entity is then supposed to consist of only two parts, A and B, the relative positions of which expressing some dynamical equilibrium). In fact, however, they belong to a three-dimensional donut-shaped object. And when this object moves vertically through the plane, the areas A and B, as seen from within that plane, seem to be tightly correlated to one another, because their behavior shows strong coordination. Seen from the Whole, however, they clearly are no parts at all . Apart from their boundary that is determined by the boundary of the whole object itself, they have no boundary of their own. Within the whole object they are not delineated. They are only delineable. And their apparent connection with each other goes via the higher-dimensional Order.
We can visualize the Implicate / Explicate Order only by analogies. And each analogy only captures one or a few aspects of this Order, while it fails to express all other aspects. Some effects of the multidimensionality of the Implicate Order (i.e. it having more dimensions than the Explicate Order) are shown in the above diagram. Other, but related, effects of multidimensionality are shown in the next.
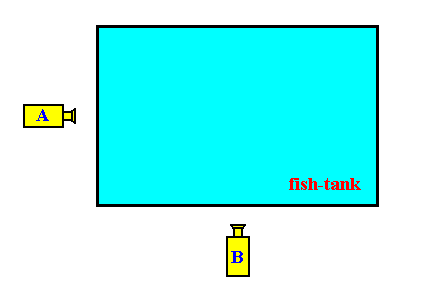
Figure above : Fish-tank analogy of the Implicate / Explicate Order, with respect to the multidimensionality of the Implicate Order with respect to the Explicate Order (As given by David BOHM, 1980). The Implicate Order is here represented by three-dimensional space, while the Explicate Order is represented by two-dimensional space.
One, and only one, fish (i.e. a three-dimensional fish) is brought into a fish-tank. Two TV-cameras, A and B, are pointed to the interior of the fish-tank under an angle of 90 degrees. To each camera is connected a TV screen. Both TV-screens are placed side by side in another room (i.e. another room than the one in which the fish-tank was placed). When looking at the two TV-screens we see two similar fishes moving about independently. However, on closer inspection we see that their movements are highly correlated, i.e. the movements of the one fish in some way correlate to the movements of the other. So there must be some connection between the two fishes. And in fact this is the case, because our two fishes are just two-dimensional projections of one single three-dimensional fish.
We can let the two fishes stand for two p a r t s of some larger whole. These parts then seem to be somehow correlated with each other (like the six outgrowths of a snow crystal). And the reason that they correlate (whether behaviorally or morphologically) is that they are enfolded into each other in some higher dimensional space. This mutual enfoldment of the two (2-dimensional) fishes results in one single (3-dimensional) fish. And this fish represents a holon.
We can use this analogy when thinking how parts of some whole can be mutually connected in such a way, that when one is changed, the other changes correspondingly and immediately. But after such thinking the space aspect must be subtracted again, because we assume that the Implicate Order has no extension (i.e. no spatial aspect). All the logic of extension (including dimensions) is, however, present in the Implicate Order, but only in a noëtical form (like the fact that all geometric features can be described algebraically).
The Implicate Order and the Virtual Existence of Parts or Elements of a Holon
Because of its apparent irrationality, the concept of virtual existence of parts or elements of an actually existing holon should be clarified still further. So before we pick up the general discussion again, we first try to make clear what this virtual existence precisely means, and how precisely the Implicate Order is involved in this.
In First Part of Website we have argued that any individual true substance (in its metaphysical sense), or, equivalently, any intrinsic being, is the result of interaction of certain elements, i.e. certain initially given material entities, an interaction according to a dynamical law immanent in this collection of elements and triggered into action by certain specific circumstances. Such an intrinsic being -- say a crystal or an organism -- can be considered to be a unity in virtue of that one dynamical law, which now constitutes its genotypical domain. But with respect to its (i.e. the intrinsic being's) phenotypical domain, i.e. the visible product of the corresponding dynamical system of interacting elements, it is not a strict unity, but merely a collection of entities -- which are the mentioned elements -- now organized into a certain pattern. This means that this intrinsic being is reducible to its elements, i.e. to the particular set of entities (elements) harboring the dynamical law. As such this intrinsic being is not a strict holon. Within the general theory in the mentioned First Part of Website this was no problem. But in the present discussion, it is, because here we have assumed (on the basis of some more or less convincing arguments or indications) that at least molecules, (single) solid crystals and organisms are true holons, i.e. entities that are not reducible to lower (i.e. less complex) entities, or to their elements (i.e. those entities that were the elements of the dynamical system that generated the molecule, crystal or organism). We then investigated how such a holon -- as holon -- must look like.
So now the alleged fact that any intrinsic being -- as the product of a dynamical system -- is reducible to the set of elements, the interaction of which, according to a dynamical law immanent in them, lead to that being, poses a problem.
In a given organism we see organs, bones, cells, etc., which are, in all probability, actual and discrete entities.
Alternatively, however, we could say that we see actual and discrete qualities (or, generally, properties), not of these entities (organs, bones, etc.), but qualities directly of that organism as a whole, causing the mentioned entities to be only virtually present in that given organism. And it is this brand of virtuality which we above called an "apparent irrationality". In the present discussion we try to circumvent such a brand of virtuality, by involving the Implicate Order. The second reason to invoke the Implicate Order is the fact, that even when we accept this apparent irrationality of 'virtual organs, bones, cells, etc.' we still have to do with genuine distances between qualitatively determined sites within one and the same organism (or crystal for that matter), which, in a way destroys its assumed strict unity.
And although organs, bones, cells, etc., seen as actual discrete entities, are not identical to the very elements of the dynamical system that generated that given organism, they can be seen as 'complex elements' or 'derived elements' (or elements after the fact) of the organism, because it is constituted by these organs, bones, cells, etc. And if we now demand a strict unity of the given intrinsic being (this demand based on certain features, like the arms of snowflakes, or holistic features in organisms), then we must declare all directly or indirectly visible discrete parts of it, not as being actually there, but existing only virtually in that intrinsic being, which means that some p r o p e r t i e s of those parts or elements are virtually preserved, i.e. preserved in a virtual way, because these parts or elements are themselves now virtual. So while these properties are virtually preserved, they are -- now as properties of the whole (intrinsic being itself) -- actually present, and thus now appear, not as genuine entities anymore, but as actual q u a l i t i e s of that intrinsic being, whether it be an organism or a crystal. All this results in the strict oneness or unity of that intrinsic being.
But what precisely does this 'virtually existing' of parts and elements mean? And why we still see, in the case of organisms at least, discrete parts?
Well, as already explained above, we assume these parts or elements are enfolded into each other within the Implicate Order. The 'discrete parts' we see are nothing more than a projection from the multi-dimensional Implicate Order onto the three-dimensional Explicate Order. One should realize in all this that the parts or elements, as they are conceived of in the Implicate Order, namely as enfolded into each other, are not some sort of second version, or duplication or copy of those (same) parts-or-elements-as-they-are-seen-in-the-Explicate-Order. They are one and the same, as the next diagram illustrates.
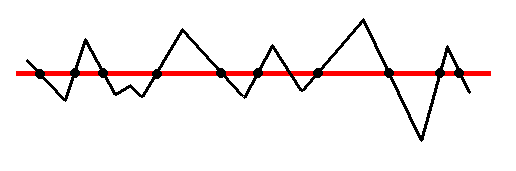
Diagram above : A structure (depicted as a zig-zag line) in the Implicate Order (here depicted as 2-dimensional space) is projected onto the Explicate Order (depicted as a one-dimensional space, a straight line (red)). The result of the projection is a collection of discrete points, each of which stands for a discrete part of that collection. This collection is, as it is seen in the Explicate Order, itself a certain being or thing (because we assume that these points -- parts -- appear together (not successively) in the Explicate Order, or, in different words, we assume that these parts have approximately the same implication parameter which means that their degree of enfoldment (when still residing within the Implicate Order) is approximately the same (and also not much different from the other parts of the whole structure [zig-zag line], but different from that of other structures).
The 'discrete' parts, as they present themselves in the Explicate Order aren't discrete, as indeed the 'full picture' reveals. So these (discrete) parts aren't parts or elements afterall : We call such 'parts' or 'elements' 'virtually existing parts or elements'. All these 'parts' are not in any way separated from each other. Only by cutting the whole (the zig-zag line) into chunks, we get discrete parts. But then these are not parts of that whole, because that whole doesn't exist anymore, they are all by themselves now, and thus no parts or elements at all.
Remark : We can assume that a given structure or part of it, when it is unfolded, and thus then present in the Explicate order, is also still present in an enfolded condition in the Implicate Order, in such a way that we have to do with a constant unfolding and enfolding, or, equivalently, with a constant projection and injection, where, and because of it, the mentioned structure is constantly being projected and injected, and thus -- as seen within the Explicate Order -- constantly being created, 'de-created' and re-created. So such a structure is then intrinsically dynamic on a fundamental level (See Third Part of Website , MODEL OF ENFOLDING AND UNFOLDING : The Ink-in-Glycerine Model ).
An intrinsic being (or, equivalently, a mixtum perfectum, or, shortly, mixtum) which is the product of the interaction of elements of a dynamical system (like what is a billion times taking place in a (bulk) chemical reaction), is -- now ex hypothesi -- one entity, and as such a c o n t i n u u m. Nevertheless such a continuum is not necessarily homogeneous, it can be heterogeneous, and thus a heterogeneous continuum, because of the following reasons :
Generally such an intrinsic being is generated from a set of different kinds of elements. These elements end up at different locations within the resulting intrinsic being, and become virtual. Some properties of these elements are preserved after the intrinsic being has been generated, resulting in a spatial mozaic of properties across that intrinsic being. These properties are actual (not virtual), and as such they only can derive from actual natures or essences. But this would imply that the intrinsic being consists of actual elements (representing these natures), denying it to enjoy strict unity. So these properties are not preserved properties of the elements, but just properties of the intrinsic being. And these properties are very similar to the corresponding properties of the elements, because the intrinsic being (mixtum perfectum) is, of course, very closely related to its elements.
So the elements of a mixtum perfectum, or, shortly, mixtum, are only virtually present in the mixtum (because they are folded within the Implicate Order, as explained above), while those properties of the elements that are preserved after the mixtum has been generated, are now properties not of these elements, but of the mixtum, resulting in a heterogeneous continuum, which as such is a true holon.
Continuation of the general discussion about the existence of genuine Holons
Also for molecules we must expect that they are such holons, i.e. such heterogeneous continua. Although they consist of atoms, or ions, they, until this day, do not seem to be reducible to those atoms, i.e. they cannot -- again, until this day -- be calculated from the (properties of) constituent atoms. Even the simplest of all molecular systems, the hydrogen molecule-ion, containing two protons and one electron, presents insuperable problems (SHELDRAKE, 1988, p.122). Its properties can be calculated only by making a series of simplifying assumptions. For complex molecules and crystals, even more drastic approximations and simplifying assumptions have to be made in order to apply a mathematical analysis. These calculations have given an increased understanding of some of the properties of molecules and crystals, but this is a very different matter from predicting their forms and properties from first principles (SHELDRAKE, 1988, p.122).
So it is not yet demonstrated that the structures of molecules or crystals are implicitly contained, or potentially present, in the (set of) constituent atoms. And consequently all this could be an indication that molecules and crystals are non-reducible entities, i.e. holons. Moreover, for molecules and crystals chemical bonds are crucially involved, which means that quantum conditions are imposed on them, implying that molecules and crystals are in no sense mechanical entities. Also for the atom we must conclude that it is a totality or holon, not reducible to its constituents : The hydrogen atom (to be precise, its lightest isotope), for example, consists of one positively charged proton and one negatively charged electron that is somehow associated with that proton. If we have just a mixture (i.e. an aggregate) of individual and independent protons and electrons, we can expect it to emit a continuous spectrum (perhaps caused by emission of electromagnetic energy wherever the trajectories of these particles happen to be accelerated or curved in whatever rate or intensity). If, on the other hand, we have a collection of hydrogen atoms, we see its spectrum to be a discontinuous one, i.e. a spectrum of discrete colored lines. These spectral lines of the collection of hydrogen atoms are precisely predicted by a theory that is supplemented by BOHR's quantum conditions. Several possible different energy states are divided (i.e. distributed) over the many individual atoms of the mentioned collection, which explaines all the different lines in the spectrum. The mentioned quantum conditions cannot be applied to an aggregation, i.e. just a collection, of protons and electrons, because in the case of such an aggregate it is assumed that, while calculating the energy, Coulomb's electrostatic law and the mechanical laws are valid, while at the same time this is denied by the quantum conditions. So it is clear, that when (formally) changing from an aggregate of protons and electrons to hydrogen atoms (or, from a proton and an electron to a hydrogen atom, for that matter), we must necessarily invoke BOHR's quantum conditions (which transforms the atom into a non-mechanical system). And it is these quantum conditions that constitute the NOVUM when we change from proton-electron aggregate to hydrogen atom. And this means that the hydrogen atom is a non-reducible entity, a genuine holon or totality. And such a totality is therefore a unity, in the present case a heterogeneous continuum (See HOENEN, P., [in Dutch] Philosophie der Anorganische Natuur [Philosophy of the Inorganic Nature], 1947 ). The quantum conditions are the folowing :
Molecules consist of atoms that are connected to each other by chemical bonds (See First Part of Website : The Chemical Bond ). Many molecules involve so-called covalent bonds, described by the theory of orbitals, and they surely entail quantum conditions. So such molecules are, like free atoms, totalities or holons.
Crystals can be considered as giant molecules (but now with a reticular or, equivalently, periodic structure, where often also covalent bonds are present, as in diamonds. In other crystals, however, ionic bonds prevail, which just consist of electrostatic attraction between ions, as we see it in salt crystals (NaCl). Again, in other crystals whole molecules are elements of a crystal. This is the case in ice crystals (H2O). Here these water molecules are held together in the crystal by hydrogen bonds (explained in the previous document). Also here we have a case of electrostatic attraction. Whether in ionic and hydrogen bonds quantum conditions are involved I am not sure, but we must realize that generally these bonds (at least covalent, ionic and metallic bonds) occur in mixtures (i.e. occur in mixed forms) in which one type of bond dominates in the given chemical bond). I think it is not unreasonable to assume that in all cases of chemical bonds quantum conditions are involved, implying that every chemical compound, and every single solid crystal is a genuine totality or holon.
Organisms consist of a host of chemical compounds and ions. Most of these are taken up into higher (i.e. more complex) structures, and although chemical bonds can be involved in such higher structures, this is generally not so. And this means that if we consider organisms as holons, they are so by other reasons : capacity to regeneration, to regulate, to reproduce, etc.
And so we could theorize that already within the Inorganic Physical Layer of Being there are genuine holons. And each such holon involves a NOVUM as we change from their constituents (their parts, or their elements) to that holon itself. This NOVUM is a new principle, a new category or If / Then constant, not to be found among those of the constituents. And indeed the appearance of a new principle causes the corresponding concretum to be an i r r e d u c i b l e entity and thus a holon. But it does not define a new ontological layer, as is the case with the NOVUM connected with the living state. It is a physical If / Then constant, which at the most, co-defines some sub-layer within the Inorganic Layer. And something comparable occurs within the Organic layer, based on the presence of many irreducible (living) entities, i.e. certain living entities that cannot be reduced to other (simpler) living entities (As the many failed attempts of the historical derivation of one animal group from another show).
In the Implicate Order such a NOVUM (those that are responsible for the emergence of a whole new Layer of Being, as well as those that are not) is represented by the corresponding holistic simplification, as explained earlier.
And, again, within the Inorganic Layer we see protein molecules and bimolecular complexes (of them), that show a morphological structure that is not derivable from the given amino acid sequence of such a molecule (SHELDRAKE, 1988, p.123--127). So also these are true holons, i.e. wholes not reducible to their parts or elements.
This non-reducibility must be specified as follows :
If all properties of a compound are either additive resultants, or constitutive resultants, and if the constitutive resultants can in principle be calculated from the corresponding properties of the elements ( The additive resultants can of course always be calculated ), all these properties can then together be called aggregation resultants , and the compound is then just an aggregate, i.e. it is an entity that can be fully reduced to its elements.
If we go from free atoms to the corresponding chemical compound, we can distinguish two general main kinds of properties of the compound with respect to its elements :
There are further two kinds of aggregation resultants :
An additive resultant is a property of the compound that results from adding up the corresponding properties of the elements. An example is mass (and if we want to press it, mass-energy, which does not change before and after a chemical reaction (and here we consider a reaction which results in a chemical compound from interacting atoms). So the mass of the compound is equal to the sum of the masses of the atoms that constitute the compound.
A constitutive resultant is a property of the compound that is absent in its elements (An analogous case can serve as an explanation what this means : Pressure of a gas is a property that is absent from any individual gas molecule, because this notion does not make sense for a molecule. So pressure of a gas is a constitutive resultant).
If, on the other hand, at least one constitutive property cannot, even in principle, be calculated from the corresponding properties of the elements, then this property should be called a totality resultant and the compound is then a totality or, equivalently, a holon, which, in virtue of its being a holon involves (as seen in the Explicate Order) a NOVUM, because it is not fully derivable from its elements.
But although such a holon or totality generally does involve a new (but special) principle or, equivalently a new category or If / Then constant, i.e. a (special) categorical NOVUM, it does not entail a new main Layer of Being (like we see when going from the Inorganic to the Organic, which involves a more general NOVUM). Like in the other cases we referred to, the NOVUM that is associated with such a holon does not entail the modification of one or more other categories.
And, as has been found out earlier, although the structures of many kinds of crystals have been described in detail, so that one exactly knows of what parts the crystal consists, the ways in which such a crystal takes up its structure as it crystallizes, is very obscure. In the first place, just as in the case of protein structures, it is not possible to predict from first principles, i.e. from the constituents as they are in themselves, the way in which the molecules, atoms or ions will pack themselves together in the crystal lattice. Even with quite simple chemical compounds there are many possible lattice conformations that are expected to be equally stable thermodynamically, and there is no clear reason why one rather than any of the others is actually taken up during crystallization. And, like in protein folding, there is no way of empirically testing the assumption that the actual lattice structure is uniquely stable from an energetic point of view. The molecules (in the sense of the given chemical compound) simply will not crystallize into the other theoretically possible lattice structure (within the same range of thermodynamic conditions), and therefore their energies cannot be measured and compared (SHELDRAKE, 1988, p.129). The second difficulty arises -- as has been discussed at length earlier -- in trying to understand the way in which the crystal grows as a whole. Somehow, as molecules in solution (or in a vapor) come close to the growing surface of the crystal, they 'snap' into place in the growing bulk crystal. But the way in which they do this cannot be directly observed, and attempts to model the process mathematically are still very crude and have not been very successful so far (SHELDRAKE, 1988, p.129, where, with respect to this, he cites MADDOX, 1985, No pattern yet for snowflakes, Nature, 313 : 93.). Such models take into account only local effects on the molecules, atoms or ions, joining the growing crystal. But crystals (each) as a whole show patterns of symmetry -- and here we mean not only crystallographic point symmetry, but also morphological point symmetry -- which cannot possibly arise from a sum of local effects. Such symmetry we see very clearly in star-shaped crystals, especially in snow crystals as discussed earlier. Snow crystals generally have a six-fold symmetry, but each is unique. Within a snowflake (which is a snow crystal), the intricate structure of the six arms is very similar, if not identical, and these arms are themselves symmetrical according to the group D2 : one mirror plane coinciding with the equatorial plane of the whole crystal, and a second mirror plane coinciding with one of the mirror planes of that same crystal (which itself has a point symmetry according to the product group D6 x C2, while this symmetry is denoted crystallographically as 6/m2/m2/m ).
Although the differences among snowflakes may be explained in terms of random variations, the symmetrical development within each snowflake, i.e. the six-fold repetition of some complex morphology (namely that of the arms), cannot be explained in this way. Lattice vibrations could be significant in this respect, but whether they are specific enough, with respect to the special morphologies, as we see them in the arms, is, according to me, not demonstrated. Maybe these lattice vibrations resonate with certain enfolded structures in the Implicate Order, and so establish a (non-local) connection between corresponding sites of the growing snow crystal. And such direct connections then guarantee the symmetrical repetition of morphologies within the crystal.
A Speculative Note on the Implicate Order
It is possible that in the whole of Reality, which here means not only in the Explicate Order, but especially also in the Implicate Order, there is a historical aspect present, and therefore, a contingent aspect. If this is correct, then it would seem that the Implicate Order is embedded within Time. But that contradicts our initial assumption. It is the Explicate Order where things appear (as) separated in time and /or space, because of the unfoldings that take place during projections from the Implicate order. So the Implicate Order is timeless. And changes in it (in fact, of it) -- expressing its historical aspect -- will only be evident in the Explicate Oder. If there have taken place certain projections followed by corresponding injections, then the Implicate Order is not precisely the same anymore, which can become visible in subsequent (as seen in the Explicate Order) projections. If all this is correct, then the Implicate Order is not a Platonic static transcendent domain of all possible -- one might say ideal -- structures or Forms (which are only formally being derived from each other), but is immanent in all explicate structures. The structures in the Implicate Order are potentially present in the Explicate Order. In given particular explicate structures, some specific implicate structures are present in near potency. And these implicate structures are timeless, despite the fact that they are immanent in temporal structures. The Explicate Order expresses (i.e. explicates or unfolds) the Implicate Order. And only from within the Explicate Order we can see 'how things are' in the Implicate Order. But if this were all, then the Implicate Order is -- with respect to its content -- what it is, and remains what it is, and so does not have a contingent aspect. But this aspect is necessary to preserve the unity of the Implicate-Explicate Order, i.e. the unity of the world. So there also must be events that originate in the Explicate Order, like the application of a series of ink drops into the ink-in-glycerine model device (as discussed in Third Part of Website). And injection of these applied ink drops changes the Implicate Order. A patterned series of ink drops, applied to the model device is injected (re-projected, re-injected etc.) into and from the glycerine, and could as such stand for, say, a crystallization event. And if a crystal of some totally new substance is formed for the first time (comparable to a certain definite and new pattern of applied ink drops), the Implicate Order is changed because of the ensuing injections. If we express all this in terms of morphic fields, we can say that the newly appeared crystal (i.e. the first crystal of a totally new substance) creates a field : A solution of the new substance becomes supersaturated, and thus becomes unstable, and, finally, finds a lower-energy state in virtue of the packing of the corresponding particles into an array, resulting in some stability of the system. Injection of such an array changes the Implicate Order correspondingly, which means the creation of a morphic field. Subsequent projections, which we can identify with resonances triggered by subsequent cases of supersaturated solutions of this new substance, now result in the formation of this particular kind of array (of constituents of the mentioned new substance) again and again, and thus the establishment of h a b i t, i.e. a habit of that substance to always crystallize in that particular array (within a given range of thermodynamic conditions). And from now on crystallization of that new substance will get started easier, because of resonance with the newly evolved morphic field.
If we adopt these speculations, the theory of the Implicate Order is brought closer to the hypothesis of formative causation of Rupert SHELDRAKE (first proposed by him in 1981).
Let's elaborate a little further on these additions to the theory.
A certain array of packing of particles of the new substance, representing a state of lower energy, can be arrived at by the system, and then -- in the sequel -- becomes a habit in virtue of the stabilization of the newly evolved implicate structure or field associated with this array of packing. From now on the substance always easily and quickly finds this particular array of packing, i.e. it crystallizes more readily. However, it must be emphasized, that a true holon cannot emerge spontaneously from the system of its constituents for the first time, when no morphic field has yet been formed, because, by definition, a holon cannot be reduced to that system ( It is more than that system alone, and this 'more' is not yet present in the Implicate Order, so no holistic simplification in this Order and the corresponding appearance of the NOVUM in the Explicate Order can yet take place). But it can emerge (for the first time) by pure accident. Such an accident is a one-off event, and so does not mean a reducibility of the result to the pre-existent system of elements, because this result did not emerge by intrinsic necessity. It could have been co-generated by (additional) extrinsic causes. As such, i.e. according to its history of generation, this result is not a holon, but its actual structure is the same as those entities, which will come after it, i.e. which will later be generated anew, and which we will interpret as holons : As soon as the habit of formation is firmly established by morphic resonance, this (particular kind of) result now emerges with necessity from the initial (not meaning the very first) system of elements, and represents, from then onwards, in every such case, a holon, because the necessity (which would otherwise entail it not to be a holon, but something that is fully reducible to its elements) is a necessity via the Implicate Order, where holistic simplification is taking place. It is now a holon, because its generation involves wholeness :
Of course a (pseudo) holon (as it comes about for the first time) never emerges completely by accident. First of all a sliding-off to lower energy states is 'for free', and thus spontaneously and repeatabe : Every system that is unstable will do that, because it is always being perturbed and thus never remains in such an unstable state (Often there is some small energy barrier to overcome before the system can plunge off into the lower energy state. The barrier can be taken when the strength of the perturbation is sufficient. If it is not, then the system is metastable.). Further, the system of interacting elements (ultimately leading to a new (pseudo) holon) will have many parts, or substructures, that will resonate with similar structures already present in the Implicate order, implying that many aspects of the new holon have not emerged by accident.
Lastly, we must realize that the accidental aspect comes wholly from without, i.e. from fluctuations of the environment, that are extrinsic and random with respect to the developing holon ( In a broader context these fluctuations are -- when they are not quantum fluctuations -- not random at all, but completely determined).
Continuum or Tight Contiguum?
While, according to our earlier considerations, free atoms, free molecules and single solid crystals seem to be (heterogeneous) continua, and snow crystals (and then with them, all solid crystals) seem to point to, we could say, an even stronger sense of continuum, namely where the parts and elements are non-locally connected, organisms seem to be different, although they can reasonably be interpreted as continua, even in the just mentioned stronger sense.
Because to see all these entities (atoms, molecules, crystals and organisms) as continua of some sort is intuitively difficult, but nevertheless very intriguing, it is perhaps instructive to summarize and further elaborate on the notion of "holon as (heterogeneous) continuum".
In his interesting book "Philosophie der Anorganische Natuur (1947), referred to earlier, HOENEN shows that the results of classical physics do not decide whether any given intrinsic being (i.e. a being which has the specific causes of its generation all within itself) is a continuum or a contiguum, i.e. whether it is (1) a strict continuum , and thus a holon in its strongest, but one, sense ( The stongest sense is that of a non-local continuum), in which its elements exist only virtually -- the continuum is, as continuum, not divided, but only divisible -- and are -- in a physical continuum -- just a spatial distribution of qualities of the holon, or (2) (whether such a being is) at most a tight contiguum, i.e. an entity consisting of well-defined tightly packed material parts and elements that exist actually in it, and are not qualities of something, but beings (i.e. things) themselves, and so resulting in a unity, it is true (because it is organized and patterned), but not a unity in the strict sense.
All results of classical physics and chemistry, about molecules and crystals (which are the supra-atomic intrinsic beings of the Inorganic World) are, according to HOENEN -- for which he advances strong arguments -- not in fact aimed to answer this question, and consequently do not decide on it. However, as we have seen above, quantum mechanics seems to point to continua and not to contigua. Further, as we saw above, dendritic snow crystals point in the same direction.
With organisms, however, things are a bit different, because they show -- it seems -- actually existing parts (like organs, bones, cells, etc.). Nevertheless organisms, and especially organisms, are considered to be true holons by many authors. We ourselves also consider it very likely that organisms, it is true, have been naturally evolved from inorganic precursors, but that they are nevertheless not derivable from these precursors, which means that during the emergence of organisms from the mentioned inorganic precursors a NOVUM has appeared. And this NOVUM we explained by means of holistic simplification within Implicate Order. So when we accept that an organism is a true holon, it seems to be so in a different way as it is in inorganic entities. And, as has been already found out, it is this way by which an organism is a continuum, that forces us to interpret the continuous nature of all intrinsic beings, be they organic or inorganic, in a special way : Their continuity (i.e. each one of them being a (heterogeneous) continuum) is so (i.e. is what it is), always in virtue of their parts being non-locally connected. But for this we need the Implicate Order : The parts of a holon are non-locally connected via (and in) the Implicate Order ( In an 'ordinary' continuum -- a local continuum -- there are still distances present between given areas or points of it).
In fact the two metaphysical interpretations of the unity status of any given intrinsic being -- absolute continuum [local or non-local] or (tight) contiguum -- left open by natural science (more or less decided for inorganic beings in favor of continua by quantum mechanics, left open for organisms), are, in a sense, both realized :
The fact that these intrinsic beings are, in the Implicate Order at least, non-local continua, can be seen to be expressed in the Explicate Order as follows : Intrinsic beings appear in the Explicate Order ultimately as h e t e r o g e n e o u s l o c a l c o n t i n u a , i.e. continua with a spatial distribution of qualities of the given intrinsic being.
This "spatial distribution of qualities of the given intrinsic being" is, first of all a pattern of different qualities across that being. Secondly, it can be a pattern of different intensities of a same quality across that being. The extension of the mentioned qualities is not something of these qualities themselves, but derives from the extension of that given being. So while a quality intrinsically has intensity (i.e. it has intensity per se), it has extension only per accidens. Where a given quality is prominent in a certain area or site of the given intrinsic being, we are persuaded to say that it is the quality of the corresponding part of that intrinsic being. However, if we consider the latter as a holon, then it is the quality of that holon. It is then heterogeneously distributed across that holon with a maximum of intensity at the mentioned site of that holon.
If we interpret, then, also organisms as heterogeneous local continua, then there seems to be an additional problem : In organisms we see movements of parts, which (parts) then seem to be ontologically independent entities all by themselves (instead of just qualities), destroying the continuum. Although many of these movements are real, e.g. the movements of our arms or legs, or the contractions of our heart, other 'movements' need not to be genuine movements at all. The a priori given possibility of heterogeneous (local) continua makes clear that many such 'movements' allow to be interpreted as just a change in the distribution of heterogeneity across the body (i.e. across the local continuum), without any movement at all. This interpretation sounds strange and unfamiliar, but metaphysically it is sound, and has no implications for biology or medicine ( The latter are neutral with respect to both interpretations).
One should realize that sense observation and the result of processing it theoretically, namely natural science, can never discriminate between (1) a given stable being that is a continuum with a heterogeneous and variable distribution of qualities-and-their-intensities of that being , and (2) that same being , equally stable, but now consisting of concrete parts -- which are themselves beings, and which cause that being not to be a continuum anymore, but a contiguum -- representing those qualities (i.e. parts that, with all their features exactly correspond to the mentioned qualities).
This implies that aggregates and totalities (intrinsic beings) cannot be distinguished by their appearances alone. They must be distinguished by the way they are generated. But, of course, this way of generation leaves its visible trails in the resulting beings.
A continuum is an extensum (i.e. something which is spatially extended) that is intrinsically one. And this means that a true continuum has no actual parts, that constitute it by their addition, because if a continuum as continuum were to have actual parts, these parts would then be points. But points can never lead to a continuum (which is an extensum) by addition. So a true continuum has, as continuum, no actual parts, it is not divided. It has, however, virtual parts, because it is divisible.
Of course there do exist also processes that directly and mechanistically lead to certain patterns, which are then patterns that are wholly reducible to initially present elements, and thus are not holons. Indeed they figure in our scheme of two main types of ontologically independent beings : aggregates and totalities.
True aggregates come into being by a purely mechanical process, which here means that the entities that now figure as elements of that aggregate are actually existing (as beings themselves) in that aggregate. They are in every respect separated from each other ( They at most touch each other, i.e. are immediately adjacent to each other). That these parts are beings themselves is, however, just a metaphysical interpretation. It means that every part is ontologically independent (as contrasted with accidents, say, qualities, which are ontologically dependent on a carrier, which ultimately is that being of which they are qualities). And we consider this to be so when the causes of the aggregate are extrinsic with respect to this aggregate. And of course in the process of aggregation the initial elements could be transformed by their interaction resulting in a collection of holons, while these themselves are driven together, resulting in the aggregate.
Variable Qualities and the Reductionism-Holism Problem.
Introduction.
In the present and previous documents we investigated what it is supposed to mean that Reality contains h o l i s t i c a s p e c t s, and looked into some evidence in favor of such aspects. Some of this evidence we found in crystals, especially in the morphology of snow crystals, other evidence seems to come from quantum theory describing the structure of the atom, the chemical bond, molecules and crystals. Still other evidence (in favor of holistic aspects) came from the consideration of organisms, especially their individual development.
However, in addition to this there is also metaphysical evidence that points to holistic aspects : The existence of variable qualities.
Metaphysically a q u a l i t y is not an ontologically independent being, it is an 'additional being', or, perhaps better, an 'appended being'. Its being wholly reduces to the being of the s u b s t a n c e (in the metaphysical sense, as explained in First Part of Website ) of which it is a quality, and which (i.e. the substance) is ontologically independent. The substance, i.e. a given substance, is the substrate of possible 'appended beings', like qualities. Equivalently we can say that a substance is the carrier of accidents. So we can say that the concept Quality signifies a certain type of property or accident (of one or another substance, or intrinsic being). Another such type is Quantity . As such they represent two important general categories or If / Then constants. While quantity is an extensive property or magnitude, like number, length, etc., quality is an intensive property or magnitude, and is extensive only per accidens, depending on the extension of the given substance of which it is a quality. To see the difference between extensive and intensive, think of temperature. Temperature is a quality, and thus an intensive magnitude (despite the fact that it is just the mean kinetic energy of a mass of molecules). It can be measured by means of an extensive effect of it, namely the thermometer. It nevertheless remains an intensive magnitude. The difference between an extensive magnitude and a magnitude like temperature, can be seen for example by the fact that they add up differently : While two lengths, say 5 cm and 3 cm, of metal bars easily add up to 8 cm by placing the bars one immediately after the other, a volume of water with a temperature of 5 degrees centigrade going to be mixed with, say, a same volume of water of 3 degrees centigrade, will not result in water of 8 degrees centigrade, but to a value between 5 and 3.
So qualities, quantities, etc. are accidents (in the sense of ontologically dependent) of a substance. And an accident cannot change. Only a substance can. And it does so by replacing the present value of some accident (say, length x) by another value of that accident (say, length x+1). In this process of change, which is called accidental change, the substance remains what it was, but some accident is replaced. And just because the substance remains what it was, the mentioned replacement is not essential to it (i.e. to it as seen from itself). To it the replacement is something accidental. That's why these features (color, length, etc.) are called accidents. There are, however, cases where some such features are necessary implications of the substance's essence, and so causing them to be essential for the substance's identity. But because of their ontological dependence they still are called accidents. In addition to accidental change there is substantial change, which penetrates deeper into the substance, it affects the substance all the way down to its prime matter (which is just pure potentiality). For all this, see First Part of Website).
So far so good with respect to qualities as they are in themselves.
For our general problem whether there really exist genuine holistic complex entities, not reducible to corresponding simpler entities, the general study of qualities and especially variable qualities can be very revealing, i.e. an attempt to answer the question of the possible existence of variable qualities can significantly contribute to solving and thus deciding the Reductionism--Holism problem. For this to determine clearly, we need -- to begin with -- some thinking about the relation between Reductionism and Mechanicism. Much of what follows is inspired, and partly based on, the discussions of HOENEN, P., in his book Philosophie der Anorganische Natuur (Philosophy of the Inorganic Nature) (written in Dutch), 1947.
Reductionism, Mechanicism, Variable Qualities and Holism.
As has been said, according to the Naturalism of ARISTOTLE and St Thomas AQUINAS a quality (and any other property or accident) -- all by itself -- cannot change, because a quality [and any other accident] has no katallel structure, that is, it does not consist of two ontological principles. And genuine change can only take place when one such principle is replaced by another, while the other remains the same. It is (only) the substance that can change in this case (because it indeed has a katallel structure), and this (change) manifests itself by the replacement of one quality by another, or by a decrease or increase of intensity of one particular quality. When we say, for example, that red is changed into green, we should say that the substance changed from being red to being green. And when we say that the red has become more intense red, we should say that the substance became more intense red. With respect to the substance we say that in these cases the substance changes per accidens. When, on the other hand, the very essence of some given substance is replaced by another, we have a new substance, and it is called substantial change.
Now, the fact of the existence of at least one genuine quality, namely electric charge, definitely rules out strict Mechanicism. And as soon as we have discovered even only one variable quality, we then have refuted all Mechanicism, i.e. in its strict as well as in its broader sense. And indeed we have found such a quality (Above we saw that electrical charge is not such a quality, i.e. is not such a variable quality) : the Impetus ( That this is indeed such a quality will be demonstrated in the next document).
The impetus of a particle is the active cause of its motion insofar as this motion is uniform (which itself is, as motion, passive, and because something is being moved, there must be an active cause for it to undergo so).
As we will see, this "impetus" is neither representing , nor an element of, some obsolete kinetic theory. It is a metaphysical interpretation of observed facts, and is not contradicting the formulae of classical kinetic theory (which are about the motion and acceleration of macroscopic bodies). These formulae involve forces. And although the impetus is a(n active) cause, it is not a force.
The impetus is, as has been said, the active cause of (motion insofar as it is) uniform motion, i.e. motion with constant velocity and along a straight line or path (Non-uniform motion, including curved motion, insofar as it is non-uniform, is caused by some external force applied to the moving particle).
Two aspects of the impetus are the momentum of the particle (i.e. the amount of motion) mv, where m is the particle's mass and v its speed), and its kinetic energy 1/2 mv2, magnitudes, well known in kinetic theory. It is clear that, in virtue of the application of a force in the direction of the movement of such a particle, the speed v of it will increase, while the mass m remains constant (provided the speed is within the 'ordinary' range, i.e. when it does not approach the speed of light). So the momentum and the kinetic energy, both increase, which implies that the impetus of that particle increases too. So to increase the impetus (which is a quality) of a given particle it is not necessary and thus not indispensable, and even devoid of any sense, to aggregate more (moving) particles (as it was necessary and indispensable with respect to negative electrical charge). To increase its impetus we simply need to apply an appropriate force to that particle. It will then accelerate (and is then non-uniform), and from the moment that force is disengaged again from the particle, the latter will continue its motion with a different speed, while this motion has again become uniform, and this means that it has acquired a different impetus (a different intensity of impetus). In this way the impetus turns out to be an existing variable quality, and this fact refutes not only strict Mechanicism, but also its broader version.
In the next document we will fully derive the essence and existence of the impetus, because of its importance as one of the indications pointing to the existence of holistic entities. For this (viz., existence and essence of the impetus) we need to show the (ultimate) asymmetric-relativity of motion (i.e. movement ultimately with respect to a universal immobile medium), because the impetus, as the active cause of (uniform) motion, is supposed to be a quality of the given particle. We will do this on the basis of the Contact Theory of Place (where "place" is meant in the sense of "location of a physical body").
If all this succeeds we have, as has been said, refuted Mechanicism (strict and broad) But in order to fully grasp the meaning of having refuted Mechanicism , we must ask ourselves whether that also means that Reductionism is refuted, and thus the presence of definite cases of Holism demonstrated. It is easy to see that Mechanicism implies Reductionism. But does Reductionism imply Mechanicism (i.e. are Mechanicism and Reductionism equivalent)? This is a tough question.
Surely, Reductionism means that complex entities can be fully reduced to simple entities : If we change from simple entities to corresponding complex entities we see, according to Reductionism, no NOVUM apppear. So the complex entity IS in fact wholly its elements (i.e. IS in fact nothing but these simple entities). And indeed all mechanical entities (things) are like that.
But can there be non-mechanical complex entities that are nevertheless reductionistic, which here means that we have a complex entity as a result of non-mechanical interaction of simpler entities? This non-mechanical interaction should not express some NOVUM, it should be fully understandable, at least in principle. Thereby it is not relevant whether the elements -- i.e. the simpler entities -- are themselves reductionistic or not.
Well, from all this it seems to follow that the "non-mechanical" interaction, if it results in a reductionistic (complex) entity, must be mechanical afterall. If this is correct, then Reductionism is equivalent to Mechanicism. And if we have succeeded to rule out Mechanicism (in all its senses, and especially in the sense that all generative processes would necessarily be mechanistic), then it follows that also Reductionism (in the sense that all entities, except the most fundamental, are reducible to simpler entities) is ruled out, and that we, accordingly, must turn, not to the metaphysics of DEMOCRITUS, or other reductionists, but to the metaphysics of ARISTOTLE and St Thomas AQUINAS, because this is a metaphysics that perfectly well accounts for variable qualities, and, generally, for the existence of holistic aspects. It was extensively treated in First Part of Website.
As has been said, in the next document (Part XXIX Sequel-5) we make an attempt to demonstrate the existence of the impetus as a variable quality, which then allows us to rule out all Mechanicism and -- if what was just stated above was correct -- with it (we can rule out) all Reductionism (in the sense that, if it were true, all generative processes should, with respect to their results, be reductionistic). And this finding then implies that not all complex entities can be fully reduced to simpler elements. All cases where they can be so reduced result in just aggregates, and where they cannot, they result in holons.
Summary
So with all this we have, a union and integration of several holistic theories, namely that of Nicolai HARTMANN (1940), of P. HOENEN (1947), of Adolf MEYER-ABICH (1948), of David BOHM (1980), of Rupert SHELDRAKE (1981), and of course, of ARISTOTLE (4th century BC) and St Thomas AQUINAS (13th century AD).
First of all, a theory of Layers of Being (inspired by Nicolai HARTMANN), each of which involving -- as seen from within the Explicate Order (from the theory of David BOHM) -- the appearance of a major categorical NOVUM or principle of Being (HARTMANN), i.e. a novum that draws with it a modification of many other categories that pass over into that Layer, and in doing so defines this particular Layer with respect to the lower Layer beneath. The counterpart of the appearance of the NOVUM as seen in the Explicate Order is the Holistic Simplification (MEYER-ABICH) within the Implicate Order ( The latter from the theory of BOHM). And within this theory we have a theory of individual intrinsic beings or Totalities (holons) as heterogeneous local continua (HOENEN, ARISTOTLE, St Thomas AQUINAS) which are embedded within the mentioned (appropriate) Layers of Being. Such an individual holon, or intrinsic being, involves, in addition to the categorical NOVUM of its Layer, also those categories that have crossed the boundary from below, i.e. those categories of the next lower Layer that also enter into (i.e. that are shared by) the present Layer (however, not just like that, but modified by the categorical NOVUM). This means that, for example an organism, is not an entity that is ontologically layered (a position we could be persuaded to hold on the basis of the chemical and physical processess that take place within each organism). An organism wholly belongs to the Organic Layer, because its 'physical' categories are not just physical categories anymore, but modified by the categorical novum of the Organic Layer.
Each such holon all by itself, also involves (as seen from within the Explicate Order) a NOVUM. But this NOVUM is highly specific, and doesn't therefore entail modifications in other categories of the Layer in which this holon resides. As has been said, such a holon appears in the Explicate Order often as a (tight) contiguum, i.e. an entity that has parts, which are themselves beings. Such a holon is, however, not a holon at all, but a product of Reductionistic Complexification. But in fact many of them (especially atoms, molecules, crystals and organisms) turn out to be heterogeneous local continua, and thus true holons. There are, however, indications that these continua are in fact, i.e. are on a deeper level, non-local continua, implying the existence of an implicate order. The mentioned Layers of Being appear as a result of projection or explication, from the Implicate Order, of structures that (then) over-form pre-existing substrates, i.e. substrates that have already been projected from the Implicate Order. The projection is always one from a higher-dimensional reality onto a lower-dimensional one (which here is the three-dimensional space of the Explicate Order). The fact that a given complete holon appears, by projection, in the Explicate Order, i.e. a given holon together with all its features, not mixed up with different features of other holons, can be explained by the fact -- as it is assumed for holons -- that all the features of that holon have approximately the same implication parameter, implying that they appear together (as an ensemble) in the Explicate Order.
We equate the lowest Layer of Being, the Mathematical Layer, with the Implicate Order (roughly this means that we identify HARTMANN's Ideal Sphere of Being with BOHM's Implicate Order), in which everything is enfolded into everything else, resulting in a non-local continuum. And this mutual enfoldment causes the Implicate Order to be a noëtic -- i.e. thought-like -- Layer.
All the supra-mathematical Layers taken together (HARTMANN's Real Sphere of Being), that are consequently above the Mathematical Layer, are Layers involving Time and Materiality, and are, as a complex, equated with BOHM's Explicate Order. These two Orders are, as has been said, assumed to be inextricately wound up into each other, and in this being wound up vibrations and resonances play an essential part, because we assume that the Implicate Order has a field-like aspect. All given Explicate morphological structures are, in a certain respect, vibration phenomena, which enable a contact of these structures with corresponding enfolded structures in the Implicate Order in so far as it is a vibrating field. This vibrational contact is called morphic resonance (SHELDRAKE).
The holons we spoke about are extensively treated in First Part of Website as to their ontology. These holons possess a vast number of intrinsic special properties, i.e. properties different from, and in addition to, those that are implied by something being a holon. In our websites we have chosen from this large set of (special) properties a few for further study : Shape, Symmetry and Promorph, and these are studied, not only for their own sake, but also because they reveal much about the general ontology of holons and of Existence as a whole.
We admit that our metaphysical (or ontological) theory, which is a holistic theory, so far developed, is complicated and more or less speculative. Further it is, according to me, certain that any holistic theory, including our own (synthesis), can never become totally consistent. It will always contain irrational elements. Most of these will be due to inconsistencies that can, in principle, be solved, and, of course, should be solved, but many will have some sort of fundamental nature. Indeed, any holistic theory is in fact founded on one or more encountered irrational elements, i.e. elements or aspects that principally defies explanation, and thus negates full rationality.
In contrast, the mechanistic theory ('mechanistic' in the sense of reductionistic) is as such, i.e. as deductive explanatory system, wholly rational, because it bans all irrational elements and aspects. It holds that every higher, i.e. complex, entity is completely reducible to its elements, in the sense, not only that it has actually emerged directly from them without any mediation, or guidance of a more or less global nature, but also that such a complex entity can, in principle, be completely understood in terms of its elements, and is therefore these very elements. It can therefore be subjected to a fully rational explanation, and is therefore itself fully rational. This reductionistic approach is fruitful and necessary, because it is directly aimed at the elimination of pseudo-irrationalities, i.e. irrationalities that turn out not to be irrationalities because they can be solved.
Holistic approaches can be deceiving, because they often are keen to have discovered fundamental irrationalities, which then are going to live a life of their own, resulting in pseudo-science (which I equate with self-deception or intellectual suicide).
So a true and honest follower of holism must continually test his theory by applying a mechanistic or reductionistic approach as far as possible ( In quantum theory a purely mechanical approach is probably out of the question, but it can, I think, still be reductionistic). Afterall, as we have said already earlier, true understanding is reductionism. Natural science should indeed continue to proceed reductionistically, but it must be prepared to embed its findings into a general holistic framework (not necessarily the one proposed here), as long as certain relevant irrationalities turn out to persist tenaciously.
There are, of course, several different possibilities as to what such a holistic framework we should conclude, i.e. to specifically what holistic theory. To a large extent metaphysical studies should decide this. But such a metaphysical theory (or ontological theory, if one prefers to call it) must be such that all more or less secured findings of natural science can be seen as specifications of this more general metaphysical theory, i.e. a theory of Being-as-such. And it is in the present and foregoing documents that we try to develop such a theory, which we call General Ontology to distinguish it from a metaphysical theory that also includes things like human values, morality, esthetics, etc. Considering some general properties, like Shape, Symmetry and Promorph, in more detail, has proven productive and instructive for setting up such an ontology.
In the next document we will, as has been said above, try to demonstrate the existence of the impetus as a variable quality, which as such then constitutes a metaphysical indication pointing to the existence of holistic aspects in the fabric of Reality.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-5.