

e-mail :

Sequel-6 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-6) supplements the investigation of snow crystals as was done in Part XXIX Sequel-3 and Sequel-4.
Sequel to the Significance of Snow-Crystal Growth for the General Holistic Ontological Theory
In Part XXIX Sequel-3 and Sequel-4 we investigated snow crystals as to their importance for a holistic theory. It is especially the star-shaped snow crystals that appeared to demonstrate the holistic character of snow crystals, and then, with them, of all (solid single) crystals. The detailed six-fold repetition as we see it in the arms of such a stellar crystal appeared to be the result of some global (and thus holistic) factor within the crystal, or, in other words, this repetition results from the crystal-as-a-whole, and not from local factors within or without the crystal. In the present document we're going to test this conjecture still further.
Because I am not a specialist on snow crystals, the ensuing discussion heavily rely on some authorities on the subject :
Habitus change in snow crystals.
The phenomenon of branching.
Analysis of the shapes of snowflakes, [. . .] often suggests that a similar succession of especially fast growths has occurred at the corners of a hexagonal plate. But the symmetry of these growths on a snowflake remains extraordinary; whatever one corner does, the others do too, at the same time and to the same extent. Several explanations have been offered for this unanimity in the detailed behavior of a snowflake in the six directions, but none has yet been generally accepted.SHELDRAKE, R., The Presence of the Past, 1988, also addresses this problem (p.129) :
The second difficulty arises in trying to understand the way in which the crystal grows as a whole. Somehow, as molecules in solution come close to the growing surface of the crystal, they "snap" into place in the growing aggregate. But the way in which they do this cannot be directly observed, and attempts to model the process mathematically are still very crude and have not been very successful so far. Such models take into account only local effects on the molecules joining the growing crystal. But crystals as a whole show patterns of symmetry which cannot possible arise from a sum of local effects. Consider snowflakes. These crystals generally have a sixfold symmetry, but each is unique. Within a snowflake, the intricate structure of the six arms is very similar, and these arms are themselves symmetrical. Although the differences among snowflakes can be explained in terms of random variations, the symmetrical development within each snowflake cannot be explained in this way.He then cites from MADDOX, J., 1985, No pattern yet for snowflakes, Nature, 313 : 93 :
[This] must be the consequence of some co-operative phenomenon involving the growing crystal as a whole. What can that be? What can tell one growing face of a crystal . . . what the shape of the opposite face is like? Only the lattice vibrations which are exquisitely sensitive to the shape of the structure in which they occur (but which are almost incalculable if the shapes are not simply regular).In his book "H2O , a biography of water", 1999, BALL, P. writes (p.177/8 of the 2000 Phoenix edition) :
A continuing mystery about dendritic snowflakes is why all six of their branches seem to be more or less identical. The theory of dendritic growth explains why the side branches will develop at certain angles, but it contains no guarantee that they will all appear at equivalent places on different branches, or will grow to the same dimensions. Indeed, these branching events are expected to happen at random. Yet snowflakes can present astonishing examples of coordination, as if each branch knows what the other is doing. One hypothesis is that vibrations of the crystal lattice bounce back and forth through the crystal like standing waves in an organ pipe, providing a degree of coordination and communication in the growth process. Another is that the apparent similarity of the arms is illusory, a result of the spatial constraints imposed because all the branches grow close together at more or less the same rate. But for the present, the secret of the snowflakes endures.That the latter explanation (involving spatial constraints) is incorrect is proven by the two snow crystals that we already depicted earlier in Part XXIX Sequel-4, the right image in one Figure and the left image in the next, Click HERE to see them.
"Several explanations have been offered for this unanimity in the detailed behavior of a snowflake in the six directions, but none has yet been generally accepted " wrote HOLDEN & MORRISON as we saw above. Such an explanation could involve lattice vibrations, or focus more on external conditions of snow-crystal growth. The latter kind of explanation is offered by I. PETERSON, Islands of Truth A Mathematical Mystery Cruise, 1990, p.131 :
Given the tremendous variations among different snowflakes, why do the six arms of a single snowflake look so much alike? Experimental studies reveal that environmental conditions at the six tips are a lot more similar than the environmental conditions between one snowflake and another. The six arms of a snowflake, each less than a millimeter long, tend to see the same temperature distribution and vapor density. Two neighboring but separately drifting snowflakes are far enough apart to encounter significant differences. However, the conditions surrounding even a single, tiny snowflake aren't completely uniform. A close look at any real snowflake reveals that its six arms aren't identical. There are always some imperfections.This kind of explanation was also given by LIBBRECHT, 2003, p.47, where he discusses the genesis of a stellar snow crystal while it is blown to and fro by the wind :
As it reached snow crystal adolescence, the crystal blew suddenly into a region of the cloud with high humidity. The increased water supply made the crystal grow faster, which in turn caused the corners of the plate to sprout small arms. Because the humidity increased suddenly, each of the six corners sprouted an arm at the same time. The arms sprouted independently of one another, yet their growth was coordinated because of the motion of the crystal through the cloud.However, when discussing branching (as an instability phenomenon) LIBBRECHT, writes the following (p.52) [comments between square brackets, emphasizing (bold) is mine] :
The crystal subsequently blew to and fro in the cloud while it grew, following the will of the wind. As it traveled, the crystal was exposed to different conditions. Since a snow crystal's growth depends strongly on its local environment, each change of the wind caused a change in the way the crystal grew. Again, each change was felt by all six arms at the same time, so the arms grew synchronously while the crystal danced through the clouds.
As the crystal grew larger and ever more ornate, it eventually became so heavy that it floated gently downward, out of the clouds to land on your mitten. The exact shape of each of the six arms reflects the history of the crystal's growth. The arms are nearly identical because they share the same history.
Consider a simple hexagonal plate crystal as it floats through a cloud. Because [in case of the commencing of rapid growth, that as such is (only) limited by the rate of diffusion of water molecules to the surface of the growing crystal] the hexagon's six points stick out a tiny bit [while their direction is that of the growth direction of a fast growing face type that had grown itself out of existence], water molecules are a bit more likely to diffuse to the points than to anywhere else on the crystal. The points then tend to grow a bit faster, and before long they stick out farther than they did before. Thus the points grow faster still. The growth becomes an unstable cycle : the points stick out a bit, they grow faster, they stick out more, they grow faster still.This latter statement about the random bumps is more or less badly compatible with the assumption (as stated by LIBBRECHT, and given above) that the morphological near-identity of the six arms of a single snow crystal is accounted for by near-identical conditions of temperature and humidity : If the structure of an arm is determined by the occurrence of random bumps (which then amplify during further growth), then the six arms would not be near-identical, because, as r a n d o m l y occurring bumps, these bumps cannot be expected to exhibit the same pattern of distribution (of these bumps) along each branch. The distribution pattern must turn out to be different on each of the six arms, resulting in arms that are significantly different with respect to their detailed morphology, because the bumps will amplify during growth. We will return to this matter shortly.
This kind of positive feedback produces what is called a branching instability -- even the tiniest protruding points will grow faster than their surroundings and thus protrude even more. Small corners grow into branches; random bumps on the branches grow into side branches. Complexity is born. Instabilities like this are the heart of of pattern formation, and nature is one unstable system heaped on top of another. [...] Instabilities are responsible for many of the patterns you see in nature, including snowflakes.
The explanation of the near-identity of the six arms of a single stellar snow crystal (which is often actually the case if we exclude all instances of distortion by local external agents, resulting in asymmetric crystals), in terms of their near-equal 'falling history', and thus in terms of their being subjected to near-equal conditions of temperature and humidity, sounds pretty convincing. And indeed, as it were not for the just mentioned discrepancy, that could be what actually happens. If true, the near-equality of the six arms is caused by l o c a l factors, and not by the crystal as a whole, implying that then there is no evidence of any holistic factor involved in the formation of snow crystals. But this would not lead to a diminishing of philosophical interest that snow crystals offer, because our statements as they are put down in Part XXIX Sequel-3 and Sequel-4 show, by means of studying those snow crystals, what the ontological consequences (which are huge) are if holistic factors were indeed at work, be it in crystals, organisms, or whatever. These consequences are so radical that they, in a way, represent a 'pro' for the reductionistic character of all of Reality. So even when we advocate (in our relevant documents) a holistic interpretation of Reality, we do so critically. And if this Reality turns out to be wholly reductionistic, that's fine. Only the truth matters. Theory may not transform into ideology.
The genesis of the different morphology of the branches of stellar snow crystals, and their near-identity in a single crystal.
Let's investigate these four factors more closely.
Crystal lattice.
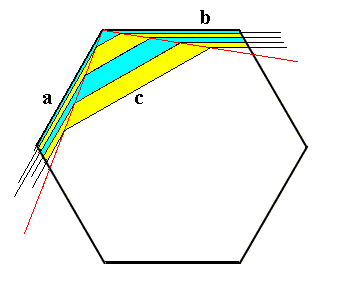
Figure above : The face c grows fast with respect to the faces a and b (ultimate prism faces of the snow crystal). And because the latter faces taper, the face c will eventually grow itself out of existence.
The lattice structure, as a co-determinant of the form of snow crystals, is not a variable, but a constant factor.
Temperature of the immediate surroundings of a developing snow crystal.

If we only consider the crystals as viewed along the c-axis, i.e. if we only consider a projection of the crystal onto the plane parallel to the basal faces of the prism, this habit change is not visible.
Temperature is a macroscopic variable. It cannot apply to a single molecule or a smal cluster of individual molecules. So it doesn't act in a strict local fashion.
Humidity of the immediate surroundings of a developing snow crystal.
The occurring r a n d o m b u m p s on the branches and sidebranches, as a result of the fact that the formation of stellar snow crystals is a non-equilibrium crystallization process, involving runaway growth at certain locations in the crystal.
The appearance of random initial bumps at one or another location on the growing crystal is a local variable, and is mainly responsible for the d e t a i l e d morphology of the arms of a stellar snow crystal. This is implied by what LIBBRECHT says on p.52 of his book, where he discusses the branching instability.
LIBBRECHT generated snow crystals in a convection chamber. He created small snowfalls at several temperatures. The most dramatic snow crystal growth was obtained at minus 150 Celcius and at high supersaturation, resulting in the growth of plates and stellar dendrites (snow crystals with ramified arms). About them he writes on his website :
These crystals were all grown under quite similar conditions, although some grew for a longer period of time before falling onto the observation window. The longest growth time was about two minutes. Even the small variations in temperature and supersaturation within the growth chamber resulted in the great variety of forms seen. This demonstrates that the final snow crystal shape is very sensitive to growth parameters, especially at minus 150 C when the supersaturation is high.The temperature of the chamber was held at minus 15 degrees Celcius, and, generally, the conditions were "quite similar" as LIBBRECHT informed us. And of course "small variations in temperature and supersaturations within the growth chamber" occur, but I assume that these are not actually measured. On his website LIBBRECHT shows the following crystals as a result of this experiment at minus 15 degrees Celcius :
The first image of this series shows a crystal with a tip-to-tip diameter of 140 microns (0.140 mm), and all the other images of this same series (as results of the minus 15 degree experiment) are shown at the same scale.
The next image shows a mosaic of snow crystals grown at minus 15 degrees Celcius.

I think it is reasonable to surmise (as a possibility) that it is not the above mentioned "small variations in temperature and supersaturation" that are (mainly) responsible for the difference in the (detailed) morphology of the resulting snow crystals. I propose to consider the possibility that the occurrence of random bumps on the growing crystal, especially when it grows rapidly (and therefore sprouting arms), is far more important in determining the detailed morphology of the branches. But naturally that would mean that these random bumps, and their ensuing amplification, are then copied onto equivalent sites on the growing crystal, which in turn would mean that the crystal ultimately grows as a whole, and not entirely by local factors.
Of course, the morphological effect of the occurrence of local random bumps on the growing crystal is dependent on the degree of humidity, because unstable growth (necessary for these bumps to become morphologically effective) only occurs at high levels of humidity. The degree of humidity indeed determines the overall 'wispiness' of the crystal, and the six branches probably experience the same degree of humidity. We might then think that the randomness of the distribution pattern of the random bumps in one single arm is also expressed by the fact that any single arm is not perfectly symmetric, and in the fact that the six arms of a single crystal are not exactly identical. And this would mean that the crystal does not grow as a whole afterall, but grows as a result of local factors only. However, I think that the six-fold symmetry (or, more precisely, the D6 symmetry) of snow crystals, as seen along their c-axis (as they are usually depicted), is far to 'good' for growth by local factors alone to be true.
With the same experimental devices LIBBRECHT also grew snow crystals at minus 2 degrees Celcius. They are again plate-like, although the growth rates are not as high as at minus 15 degrees Celcius. Thus the plates are smaller, but they also show significant differences in their detailed morphology. The following images, as results of this experiment, were given at LIBBRECHT's website :








As LIBBRECHT notes, the larger crystals (at the far right), which [apparently] grew at the highest supersaturation levels, show distinctive rounded arms. These reflect the (microscopic) roughening transition that occurs near the melting point -- the ice surface becomes microscopically rough, so the crystal boundaries are no longer faceted.
The random nature of the morphology of the arms of stellar snow crystals.
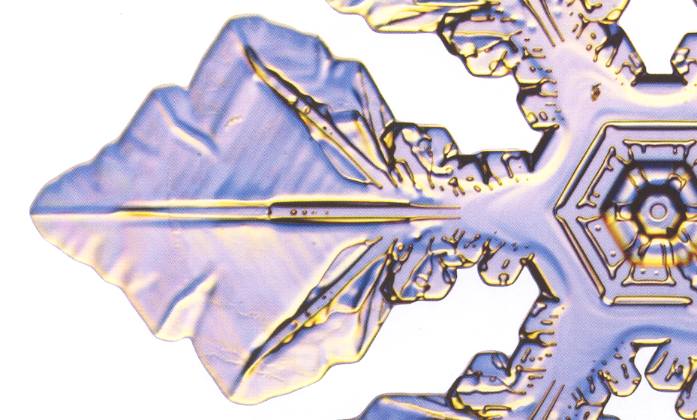
Figure above : Arm of a stellar snow crystal.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : Same as previous Figure. Only (about) one half of the arm depicted, to emphasize the mentioned sequence of freezing events.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
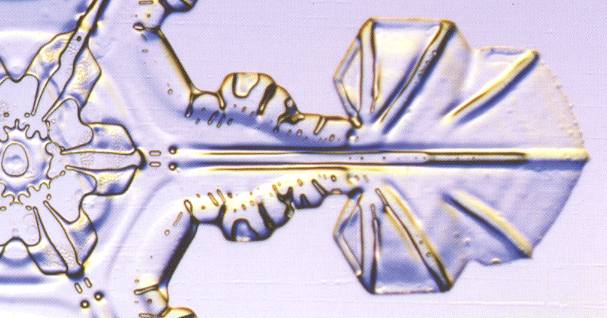
Figure above : Arm of a(nother) stellar snow crystal.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : Same as previous Figure. Only (about) one half of the arm depicted, to emphasize the mentioned sequence of freezing events.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : Arm of yet another stellar snow crystal.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : Same as previous Figure. Only (about) one half of the arm depicted, to emphasize the mentioned sequence of freezing events.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
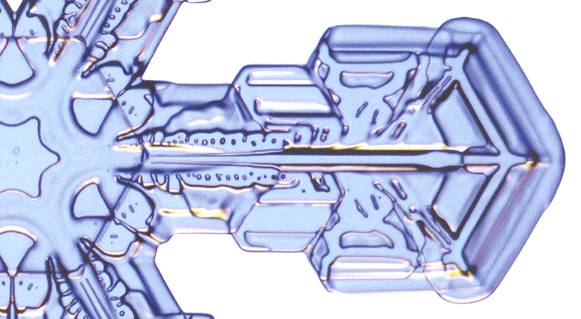
Figure above : Arm of yet another stellar snow crystal again.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
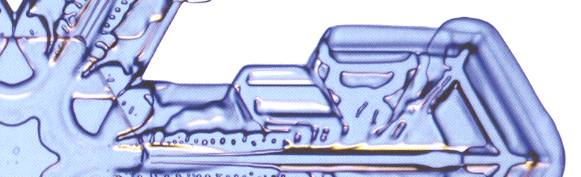
Figure above : Same as previous Figure. Only (about) one half of the arm depicted, to emphasize the mentioned sequence of freezing events.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
The whole crystal, to which the arm, depicted in the last two Figures belongs, can be seen HERE (to return, close window). (Image from LIBBRECHT, The Snowflake, 2003.)(Photography by Patricia Rasmussen).
As one can see in these Figures (and those to follow), there is a more or less random sequence of freezing events along one side of a (main) branch, and these are copied by reflection of them in the median plane of the branch. And then the whole resulting bilateral symmetric structure is then copied by rotation about a 6-fold axis. The copying is not totally exact, but exact enough to be astonishing. Many fine details are so copied.
As has been said, the overall structure of an arm, especially its degree of spikiness or wispiness, is determined by its history of experienced humidity changes during the snow crystal's fall through the cloud. But it is hard to believe that the almost infinite diversity of fine detail, i.e. a diversity of morphological design that we encounter when going from one snow crystal to another even within one and the same 'wispiness class' (so to say), is caused by the varying microclimatic conditions (temperature and humidity) constituting the crystal's falling history.
The mentioned "almost infinite diversity of fine detail" is a fingerprint of local randomness : In one given crystal a certain distribution of random bumps appears along one (main) branch (and is then copied across the crystal), while another crystal in the same (part of the) snowstorm obtains a different distribution of random bumps, different because of the inherent randomness that prevails in non-equilibrium crystallization. And this distribution is also copied across this (other) crystal.
As a typical snow crystal measures about 1-2 mm (0.04-0.08 inches) in diameter (LIBBRECHT, 2003, p.22), the morphological details, that are repeated across the crystal, are very small indeed, 0.1 mm or smaller. They clearly are the result of local randomness within the crystal, i.e. within one median half of a branch. The same applies to details that we see within many hexagonal snowflake plates which have not developed arms. See next Figures.

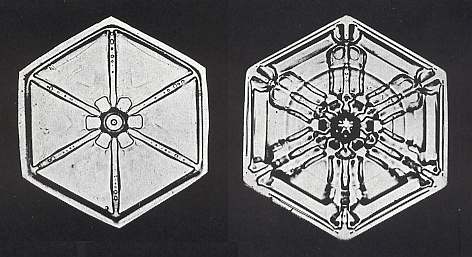
Four images above : Snow crystals as hexagonal plates. Branches not developed.
One can clearly see the D6 repetition of fine detail.
Although these crystals are just hexagonal plates, their growth must, like that of branched crystals, also have been unstable, otherwise more or less homogeneous hexagonal plates would have been developed.
(After BENTLEY & HUMPHREYS, Snow Crystals, 1931, 1962.)
Talking about the smallness of morphological details in snow crystals, they can even be much smaller than 0.1 mm, as is evident from the laboratory-made crystals shown above, which themselves are only 140 microns (0.140 mm) in diameter, implying morphological details smaller than 0.07 mm.
The next six images are snow crystal photographs as they are depicted in the website of FURUKAWA, Y. Fascination of Snow Crystals. How are their beautiful patterns created? , Institute of Low Temperature Science, Hokkaido University, Sapporo, 060 JAPAN.
The original subscript for these six pictures reads :
Microphotographs of natural snow crystals, which were taken under the condition below minus 150 C at the Mt. Asahidake locating in the central area of Hokkaido, Japan.






(After FURUKAWA (Website))
Small irregularities can often be observed in snow crystals, including some 3-foldness within an otherwise six-fold crystal.
In the present series of Documents we spoke about the analogy between crystals and organisms from a morphological point of view. Well, in the realm of insects we see a huge number of species (up to one million or more) all having bilateral symmetry, but apart from that, all possessing different morphologies.
Something like this we also see in natural snow crystals, especially those that are the result of non-equilibrium growth : If we, when considering these crystals, concentrate on one 600 sector only, we also have to do with bilaterally symmetric entities of roughly the same size as very many insects. And also these entities come in a bewildering variety of morphologies, even more so than in insects. And both are the result of unstable growth. So it is certainly interesting to dig deeper into the structure of snow crystals.
In the next document we continue the investigation of snowflakes and their significance for our holistic ontological theory.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-7.