

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Sequel-1 to the Summary and Evaluation (of the Parts XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
In the present document we will place our investigations concerning Shape, Symmetry and Promorph (as they were studied in two-dimensional crystals) in a broader and philosophical context, by investigating their ontological status.
On the Mathematical, Inorganic Physical, and Organic Layers of Being
Introduction
In Part I of the present Series of Documents we have established (as an ontological hypothesis) that the world of Being is layered. It consists at least of three ontological Layers, viz., the Mathematical Layer, the Inorganic Physical Layer and the Organic Layer. And perhaps, in addition to these, there exist (as also hypothesized in Part I) even two more Layers, namely the Psychic and Superpsychic Layers, as the philosopher Nicolai Hartmann claims. The existence of the latter two Layers is, however, according to me, very speculative and far from certain. Maybe it is a remnant of the old belief that humans consist of body and soul, where "soul" is some immaterial and independent entity. But perhaps we could see these two layers (the psychic and superpsychic) as s u b l a y e r s of the Organic Layer.
What is certain is that there is a genuine and fundamental o n t o l o g i c a l difference between the Mathematical Layer on the one hand, and the material Layers (Inorganic Physical Layer and Organic Layer) on the other. Whether there is also such a truly fundamental ontological difference between the Inorganic Physical Layer and the Organic Layer is, according to me, less certain : While it is clear that there is some very abrupt complexity jump to be seen when we formally go from the Inorganic Physical Layer to the Organic Layer, it is not certain whether this entails a fundamental ontological difference between these Layers. We'll come back to that later, and for the time being we assume such a difference to be present.
The transition from the Mathematical Layer to the layers above it, involves the appearance of materiality which in turn implies energy. The appearance of energy, and therefore of energetic relations, brings with it the phenomena of stability and instability of structures and patterns, i.e. of material structures and patterns. Purely mathematical structures, i.e. structures that are not in any way physically interpreted, are not dynamic, because movement is something physical ( The concepts of movement, like for instance rotation, are used in mathematics, but there they are just mathematical analogues of physical movements, not genuine movements). And thus mathematical systems can never be dynamical (only by analogy) and do not involve energy, meaning that the concepts of stability and instability do not apply to mathematical systems (again, at the most analogically so). In the material layers, on the other hand, stability and instability ultimately decide which mathematical systems and patterns can be physically materialized under given physical conditions. So the occurrence of particular patterns and structures in the material layers must be understood in terms of their (physical) stability.
That the transition from the Inorganic Physical Layer to the Organic Layer could indeed be as dramatic as we assume it to be (although much more speculatively so), can be seen from the fact that until now no forms, evolutionarily mediating between inorganic structures and organisms, have been found, nor somehow produced in the laboratory. This could be an indication that such intermediate forms have never existed, and that the evolutionary transition from inorganic to organic was an abrupt one.
One could think of virusses as intermediate between the inorganic and the organic (especially because many virusses occur, when outside their host, as crystals). However, virusses are only formally more or less intermediate, not evolutionarily, because they already presuppose the existence of genuine organisms like bacteria. Consequently they came after genuine life had already appeared. So virusses are secondarily formed, prompted by the existence of these genuine organisms, which could then be their potential hosts.
The present Series of Documents considers crystals (studied by means of investigating two-dimensional crystals) as representatives of macroscopic i n o r g a n i c (i.e. non-living) beings, because they occur as genuine individuals, and are stable and repeatable, and thus not accidental entities. They are, accordingly, intrinsic beings, and as such representing the Inorganic Physical Layer. Organisms, on the other hand, are considered to be macroscopic o r g a n i c (i.e. living) beings. They also occur as genuine individuals, and are relatively stable and in principle repeatable entities that actively maintain themselves. So also they are intrinsic beings, and, naturally, represent the Organic Layer.
One could wonder why we have chosen crystals to represent, as intrinsic beings, the Inorganic Physical Layer, instead of other inorganic intrinsic patterns as we see them for example in the Belousov-Zhabotinsky reaction, which is, like any organism, a dissipative dynamic system far from thermodynamic equilibrium, and, also like organisms, remaining dynamic during all of its existence, while the crystallization process is not such a system, because it tends towards thermodynamic equilibrium. Moreover the resulting crystal is a more or less static entity.
The reason that we have chosen crystals to represent inorganic beings is based on the fact that crystals, as the products of crystallization processes, are endowed with true individuality, i.e. they not only are individual, but are genuine individuals, showing definite, specific, constant, and repeatable boundaries that separate them from their environment. Also their internal structure is specific, constant and, as a whole, repeatable. In contrast, the target and spiral patterns generated by the Belousov-Zhabotinsky reaction do not possess such individuality, and the same goes for many other inorganic systems that generate intrinsic patterns. Also the boundary of the reaction as a whole is not definite, not specific and not constant. And of course the container of the reaction, for example a petri dish, is just an extrinsic boundary of the reaction. And the lack of this aspect of individuality is not replaced by some other aspect.
The documents of the present Series study Shape, Symmetry and Promorph in crystals and organisms in the context of the layered world of Being, especially how they figure in the Inorganic Physical Layer and in the Organic Layer, and how they connect crystals and organisms. In this way they're going to figure in a General Ontology (general theory of being).
A Promorphology of organisms (and anticipating that of crystals) is treated in Second Part of Website : BASIC FORMS (Promorphological System).
The theory and justification of a Promorphology of crystals is given in the final Series of documents in that same Second Part of Website : BASIC FORMS OF CRYSTALS.
The present Series of Documents (here, in Fourth Part of Website) develops this theory still further (by applying promorphology to two-dimensional crystals).
Shape, Symmetry and Promorph as they occur in the Layers of Being.
The complexity jump (i.e. a sudden, dramatic and untraceable increase of complexity), occurring at the transition from the Inorganic Physical Layer to the Organic Layer can be illustrated by the difference between crystal formation and individual development of an organism (organic morphogenesis), because crystals represent intrinsic macroscopic inorganic beings, while organisms represent intrinsic macroscopic living beings. Both types of beings are the result of dynamical systems.
In crystals the dynamics consists of the aggregation of atoms, ions or complexes of them, into ordered macroscopic entities. And because such a system is allowed to proceed to an absolute minimum of potential energy, it results in a closest packing of equal chemical motifs, which in turn results in a p e r i o d i c pattern of these motifs. Whithin the already generated crystal there is, apart from vibrations, generally no dynamics anymore. The crystal is a fairly rigid structure (when not considering liquid crystals and crystals built up by the periodic stacking of large elongated molocules, such as protein crystals, i.e. proteins in crystalline condition). Only at its perifery and within some area around it, there still is a dynamic going on as long as the crystal is allowed to grow. The whole system is tending to a thermodynamic equilibrium. The potential energy of the crystal becomes zero : The potential energy of the solution or melt has been transformed into actual energy that performs work (movement of particles to the crystal surface) and is being dissipated.
In organisms, on the other hand, we have to do with far-from-thermodynamic-equilibrium dynamical systems. An organism is such a system also after it has been generated. Energy from without is constantly being imported, while entropy is exported. Work is being done all the time, in virtue of this imported energy. All this is possible because the organism remains in a semi-liquid state, and thus allowing movements and transitions to take place within its interior. Because of this far-from-equilibrium state (and thus not involving an absolute minimum of potential energy to be established), and because of the presence of a vast diversity of chemical compounds and complexes, there can generally be no closest packing of motifs. These motifs are, as it were, held apart from each other. And this is a precondition for something being organic, because a closest packed arrangement of motifs would preclude virtually every internal dynamics. So in organisms it is natural that the motifs are not periodically packed, and so do not form a lattice. Moreover, in organisms the motifs that should pack are not equal.
If we concentrate on Shape, Symmetry and Promorph, we see them emerge in crystals as a result of the dynamics of crystal growth. In organisms we see them emerge as a result of organic growth. But organic growth is different from, and especially much more complex than, crystal growth. And this means that the way Shape, Symmetry and Promorph appear in organisms is much more complex than the way they appear in crystals. So here we have an instance of the complexity jump at the (formally understood) transition between inorganic and organic. In fact all the analogies between crystals and organisms (See Part IV of the present Series) represent such complexity jumps :
In the next document (which is an appendix to the present ontological discussion) we will elaborate further on the symmetry and promorph of p l a n t s as they are based on their phyllotaxis.
Many specific symmetries and many promorphs, encountered in inorganic beings, especially crystals, also occur in organisms. Their way of emergence, however, is -- as has been said -- generally different. This difference is rooted in the difference between inorganic and organic growth. The latter is vastly more complex than the former. Probably DNA just encodes dynamic rules or only some parameters, rather than encoding for the whole form at once. The mentioned difference in the way symmetry and promorph appear in organisms and inorganisms is directly evident in the difference between organic s h a p e s and inorganic s h a p e s. Symmetry and promorph represent only a tiny aspect of form and structure, especially the organic structures. We can see this in the fact that most organisms have D1 symmetry (i.e. having only one mirror plane and no other symmetries) with only two antimers, implying their promorph to belong to the Allopola Zygopleura eudipleura. This particular intrinsic symmetry and promorph is shared by almost all Vertebrates and Arthropods (together forming the bulk of all animals), but their intrinsic s h a p e s are all different, varying endlessly and being 'hopelessly' complex. Moreover, the ultimate units of symmetry and promorph are asymmetric and defy mathematical description in terms of Group Theory and Promorphology, apart from (being described by) the Asymmetric Group C1 and the (promorphological category of) Anaxonia acentra. To understand the morphological patterns represented by these units, we must, in the case of organisms, resort not to Mathematics, but to dynamics, organic function, adaptation and natural selection. Especially robust dynamical systems, operating in morphogenesis, play a very important role, not only in understanding these asymmetric units, but also the generation of a whole symmetric structure consisting of the regular repetition of such units. And this also holds for organic shapes (Recall that, for instance, a regular sea-urchin and a common starfish have the same intrinsic symmetry and the same promorph, but their intrinsic shapes are different nonetheless). The dynamics must tell us about transient form states, and especially about organic growth. Undoubtedly the appearance of intrinsic shape, symmetry and promorph are consequences of the deep simplicities of natural laws. But they are generally not direct consequences of them. This is certainly true of organic shapes, symmetries and promorphs, but even already of some inorganic ones. These simple natural laws operate on the wrong level for directly creating these forms. Especially in organisms there is a long long way leading from these simple laws up to those forms. It is a complicated causal route that is not yet disentangled by natural science. Maybe it never will. It represents the complexity jump occurring at the (formal) transition from the Inorganic Layer to the Organic Layer, or, formally, from crystals to organisms.
Apart from analogies between crystals and organisms, there are also analogies between phenomena in fluid flow (for example a splash, many flow patterns, or whatever other movements resulting in forms) in inorganic systems, and the movements of organic matter constituting a multicellular organisms such as a jelly fish, or of cytoplasm within a single independently living cell. Let's consider the latter case. A cell of a single-celled creature does have a definite shape, symmetry and promorph, especially when it has a constant skeleton, often silicon-, or calcium-based. But even then its cytoplasm moves within the cell, in order for the cell to function. Unicellular organisms without such a skeleton, often change their shape, like we see in amoebas. But, with or without a mineral (or otherwise) based (constant and rigid) skeleton, there is (according to my knowledge) always a so-called cytoskeleton present, a tangled network of tubes that resembles a bale of straw and provides the cell interior with a rigid scaffolding. Ian STEWART, writes the following about this cytoskeleton in his Nature's Numbers, p. 148 / 149 :
The cytoskeleton is amazingly flexible and dynamic. It can disappear altogether, under the influence of certain chemicals, or it can be made to grow wherever support is required. The cell moves about by tearing down its cytoskeleton and putting it up somewhere else.In the light of all these considerations we can, as an example of inorganic and organic pattern formation, c o m p a r e the crystallization of a radiate crystal with the formation of a flower whorl. And so we do : we're going to consider the formation of (some) radiate structures in crystals and in organisms, and see what we can learn from them.
The main component of the cytoskeleton is tubilin, which I mentioned earlier in connection with symmetries. As I said there, this remarkable molecule is a long tube composed of two units, alpha- and beta-tubilin, arranged like the black and white squares of a checkerboard. The tubilin molecule can grow by adding new units, or it can shrink by splitting backward from the tip, like a banana skin. It shrinks much faster than it grows, but both tendencies can be stimulated by suitable chemicals. The cell changes its structure by going fishing with tubulin rods in a biochemical sea. The rods themselves respond to the chemicals, which cause them to extend, collapse, or wave around. When the cell divides, it pulls itself apart on a tubulin web of its own creation.
Conventional fluid dynamics this is not. But it is undeniably some kind of dynamics. The cell's DNA may contain the instructions for making tubulin, but it doesn't contain the instructions for how tubilin should behave when it encounters a particular kind of chemical. That behavior is governed by the laws of chemistry -- you can no more change it by writing new instructions in the DNA than you can write DNA instructions that cause an elephant to fly by flapping its ears. What is the fluid-dynamics analogue for tubulin networks in a chemical sea? Nobody yet knows, but this is clearly a question for mathematics as well as for biology. The problem is not totally unprecedented : the dynamics of liquid crystals, a theory of the patterns formed by long molecules, is similarly puzzling. Cytoskeleton dynamics, however, is vastly more complicated, because the molecules can change their size or fall apart completely.
(And in 2-dimensional crystals all are radiate structures (regular or amphitect), except the asymmetric crystals, having just C1 symmetry, and those belonging to the [2-dimensional] Crystal Class m , i.e. crystals having D1 symmetry, which for 2-dimensional crystals in turn means that their only symmetry element is a mirror line).
(With respect to the point symmetries of three-dimensional crystals, see First Part of Website, Special Series ).
Let us elaborate on that for a while.
A flower whorl -- as an example of an organic radiate structure -- can, in principle possess any rotation axis, i.e. a 2-, 3-, 4-, 5-, 6-, 7-, 8-, 9-, 10-, 11-, etc. -fold rotation axis. But in reality, with the exception of a 4-fold axis (and possibly some other n-fold axes) only Fibonacci numbers define the foldness of the rotation axis : 2, 3, 5, 8, 13, etc ( 4-fold axes are typical for the large plant Family of Crucifers).
In a radiate crystal structure -- as an example of an inorganic radiate structure -- there is also one single main axis of rotation, which can, however, only be 2-, 3-, 4-, or 6-fold, because of the periodic structure of crystals. In Isometric crystals there is no single rotation axis that stands out, but always several of them that are totally equivalent. So these crystals cannot be regarded as true radiate structures. In (3-dimensional) crystals of the Orthorhombic System there are three axes of which each one could figure as main axis. In contrast to Isometric crystals these three axes are, among themselves, different in length. So we could choose the longest (or shortest, or the one that is intermediate, for that matter) as being the main axis, and can then speak of a radiate crystal structure. Crystals of the Pedial Class of the Triclinic Crystal System, i.e. crystals that are (intrinsically) totally asymmetric with respect to point symmetry (while their plane group symmetry is according to the group P1), cannot be regarded as radiate. The only symmetry element they have is a one-fold rotation axis that can be set anywhere with respect to the crystal. Also crystals of the other Class of the Triclinic Crystal System, the Pinacoidal Class, cannot be regarded as radial structures, because such crystals, just like the crystals of the Pedial Class, do not have an n-fold rotation axis with n greater than 1. Their only symmetry element is a center of symmetry. Finally, crystals of the Domatic Class of the Monoclinic System, having as their only symmetry element a mirror plane, cannot be regarded as true radiate structures.
All other three-dimensional crystals are radiate.
In what follows we present a comparison between the formation of radiate crystals and that of radiate flowers, or, more generally a whorled arrangement of leaves on a stem. We will be brief by not presenting too many technical details, in order not to interrupt the present general ontological discussion. In the next document (Part XXIX Sequel-2) we will provide these details, include spiral and distichous leaf arrangements, and discuss the (different) promorphs involved in all three types of plant phyllotaxis.
Crystallization from a melt or a solution takes place when the Gibbs free energy of formation is, with respect to that of the melt or solution, negative for the crystal, and stays negative even when surface energy, which is always positive, is added, which means that in this case the crystalline state represents a lower energy than that of the melt or solution : An initial crystal embryo satisfying these conditions will then spontaneously grow, according to the then prevailing form potential difference or form-potential field. What is taking place is a symmetry-breaking leading from a state of maximal symmetry -- which has become unstable -- to a state of lower symmetry which is, under the particular circumstances, stable.
The formation of a flower whorl appears when two or more primordia (buds of the members of the whorl, originally leaf buds) appear at the same time at the plant meristem (growing tip) and repel one another. Then another such cluster of primordia appears, then another, etc. If the rate of appearance of these clusters is sufficiently low, then only the repelling influence of the previous cluster is experienced by a given cluster. Then each cluster of primordia (unfolding into sepals, petals, etc.) would take up positions at maximal distance from each other, and successive clusters would be arranged in the spaces (as seen from above) of the previous cluster, resulting in a pattern with alternating whorls. The same goes for leaves of higher plants in decussate phyllotaxis (See for phyllotaxis, and the symmetries and promorphs it can produce, next document). Another way of formation of whorls, as it probably goes on in some giant unicellular algae (Dasycladales), can be described by a growing tip (of the one cell of which the alga consists) that flattens, and then forms a ring or annulus, which is as such unstable and therefore transforms (in virtue of the slightest perturbation) into a stable state by the transformation of it (i.e. of this annulus) into of a crown of spikes (as can also be seen in a splash, which as such then represents a simple fluid-dynamics analogue). (See for whorl formation in these algae, as well as in higher plants, GOODWIN, B., How the Leopard Changed Its Spots, 2001). As in crystallization, also in these latter two cases (whorl formation in higher and in lower plants), we can say that we have to do with a form-potential field which is as such unstable and consequently slides off into a stable configuration which is a whorl.
So in crystallization, initially, there is maximal symmetry (solution or melt without crystals). And this symmetry breaks, resulting in the point symmetry of the crystal, i.e. a symmetry according to one or another of the 32 (three-dimensional) Crystal Classes (And for two dimensions, we first have Dinfinity ( = maximal symmetry), which breaks to Dn or Cn symmetry, where n = 1, 2, 3, 4 or 6 ). In the same way we must assume that the relevant (excitable) medium of a generating plant whorl (comparable to a supercooled melt or a supersaturated solution) has, seen from above, Dinfinity symmetry, which breaks to Dn or Cn , where n could, in principle, be any whole number, although the number of petals (forming a whorl) is often either 2, or 3, 4, 5, 8, 13, etc. If we neglect the number four (which we see in all Crucifer flowers), then we have the sequence 2, 3, 5, 8, 13, etc., which belongs to the Fibonacci Series, which can be obtained by starting with 1, 1, and then adding numbers that are equal to the sum of the previous two numbers. So the number of petals stands, in a way, in connection with this number Series. Even closer zeroing in on the comparison between crystals and organisms : The initial annulus, that (in the unicellular algae mentioned above) appears before the whorl arises (and being highly comparable to the annulus that rises up in a splash), corresponds to the supercooled melt or supersaturated solution in the vicinity of the crystal embryo. Both are unstable and lead to a symmetry-breaking process, resulting in some kind of whorl, i.e. a radiate structure. The formal transition from the splash (where the spiked crown develops from the annulus, that rises up after impact), to the plant whorl (especially as it occurs in the mentioned unicellular algae) or maybe even to all whorled organisms or parts thereof, involves a complexity jump, and as such can represent the transition from the Inorganic to the Organic Layer of Being. While crystallization is a process tending toward thermodynamic equilibrium and thus to a static condition, the organic form generation is a process involving non-linearity, energy flow through the system, a displacement from thermodynamic equilibrium and chaotic patterns of fluctuation at bifurcation and transition points, they, nevertheless have much in common. Both involve a medium that initially is, or becomes, unstable. They then slide off onto a stable state which involves the formation of a definite pattern. But whereas in inorganic systems there generally is just one level involved, or at most a microscopic level and a macroscopic level, and maybe one level in between, in organic systems many more levels are intercalated between the ultimate lowest level and the appearance of (organic) macroscopic structures, i.e. these macroscopic structures are not, as they are in crystals, direct consequences of lower or lowest levels, but very indirect ones. This is because many regulatory processes intervene, going about in efficient cooperation and resulting in robust structures that are stable against a broad range of external perturbations, whereas in crystallization a change in temperature, pressure, concentration, etc. could terminate and even reverse (i.e. undo) the pattern-generating process.
Now it could be, that, as already the eminent philosopher Nicolai Hartmann proposed in 1940 (Der Aufbau der realen Welt), the formal transition from inorganic to organic involves the appearance of a 'novum', a "categorical novum" as he calls it, that is to say the emergence of one or more totally new p r i n c i p l e s o f b e i n g , i.e. new ontological categories. While on this subject more than a whole book is required to evaluate the 'pros' and 'cons' of such a position, let us assume this position to be basically correct (We have argued for such a position, and proposed some additions and amendments, in Part I of the present Series of documents).
Let us assume that there appears one new category (i.e. a new fundammental ontological principle) when formally going from the Inorganic Physical Layer to the Organic Layer. This new category (categorical novum) is undoubtedly very complex and not directly definable. So we can only give it a name : the state of something BEING ALIVE (loosely 'definable' as an integrated all-out cooperation between that something's parts, in such a way that the whole is in some way prior to its parts). This category then generally influences many inorganic categories as they (formally) pass over from the Inorganic to the Organic Layer of Being. For instance the category "to be an individuum passes over from the Inorganic to the Organic (where we find it respectively at the macroscopic level of the Inorganic Layer as crystal individuals (in the case of single, not twinned, crystals) and at the macroscopic level of the Organic Layer as living individuals, including bacteria an other unicellular organisms). Although both types of beings (i.e. crystals and organisms) can indeed be considered as genuine individuals, the way in which they are individuals is totally different : Where this way is more or less static in inorganic individuals, without active self-maintenance, it is eminently dynamic and regulatory in organic individuals, which actively maintain themselves, and which finally culminate in self-conscious beings. So although the category of "being an individual" (or possessing individuality) does not, when coming from the Inorganic, stop at the boundary where the Organic begins, but passes over from the Inorganic Layer to the Organic Layer, it is significantly transformed as a result. The cause of this transformation can be found in the presence of the categorical novum -- the state of being alive -- in the Organic Layer (and absent not only in the Inorganic Layer but also in the Mathematical Layer). In fact the essence of this novum totally consists in (or is totally exhausted by) all the transformations themselves that categories undergo when, while coming from the Inorganic, crossing the boundary between the latter and the Organic Layer. In fact these categories are not transformed into other categories, which means that they are not actually trans-formed, but (only) 'over - formed' : such a category, while keeping its identity as to what particular category it is, it is nevertheless changed when passing into a higher Layer of Being. And all these over-formed c a t e g o r i e s lie at the base of the corresponding jumps in complexity when b e i n g s cross that boundary, as can be visualized in crystals, formally (not evolutionarily) passing over into organisms.
As with being an individuum, the same can be said about being in a state of growing, being in a state of regeneration, etc. In fact all crystal analogies (See Part IV) can be seen as transitions from the Inorganic to the Organic, involving complexity jumps, and categorical over-forming.
However, we must emphasize that this is just a hypothesis, not a proven fact.
GOODWIN (How the Leopard Changed Its Spots, p. xiv) writes :
I take the position that organisms are as real, as fundamental, and as irreducible as the molecules out of which they are made.Although this statement does not propose the introduction of some immaterial and independent component in organisms that is absent in inorganic beings, i.e. it certainly denies a form of dualism that was assumed in earlier theories, it nevertheless maintains that organisms are irreducible. And the latter is not meant only epistemologically (i.e. referring to our inability to derive organisms from purely inorganic basic structures, which is, up to now, true), but also ontologically, i.e. it means that organisms are all by themselves not ultimately equivalent to inorganic processes and structures. The truth of the latter is not at all proven, and there are many biologists maintaining that organisms are nothing more than rather very complex and integrated inorganic structures, having a behavior that we call 'alive', and that have evolved from inorganic beings or processes.
And also our principal objects of study (but serving a general ontology), viz.,
having an intrinsic shape A,
having an intrinsic symmetry B, and
having a promorph C,
pass over into the Organic Layer without being over-formed. They even are already present in the Mathematical Layer, where many more of them are present (that can symbolically be indicated by D, E, F, G, etc.). In order to exist in the material Layers (i.e. Inorganic and Organic) they must satisfy energetic stability. The fact that, when passing over into higher Layers of Being, (intrinsic) shape, (intrinsic) symmetry and promorph are not over-formed, is because they are as such already very specific (in contrast, for example, to individuality, growth and the like). They do not admit of higher and lower forms : C3 symmetry, for example, can only manifest itself in precisely the same way in whatever Layer it appears, i.e. it is exactly the same in the Mathematical, in the Inorganic Physical and in the Organic Layer. There is no ' higher ' C3 symmetry. Likewise shape can only mean exactly the same in all these three Layers. The promorph, which in fact is just a geometric pattern, is in the same way present in all these three Layers.
Let's give an example to clarify this.
A mathematical figure, say a pyramid can have a definite shape, a definite symmetry and a definite promorph. Consider the following mathematical figure :
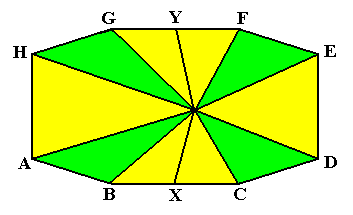
Figure above : Slightly oblique top view of an amphitect octogonal pyramid.
The lines, originating at the pyramid's apex and ending up at A, B, C, D, E, F, G and H are the eight ribs of the pyramid. This pyramid is, in the present example, provided with two additional lines, namely the ones that also originate at the pyramid's apex, but end up at X and Y. So the present three-dimensional mathematical figure, depicted here, consists of eight lines constituting an amphitect octogonal polygon (the base of the pyramid), eight lines, representing the pyramid's ribs, running from the apex to the corners of the octogonal polygon, and two lines connecting the pyramid's tip with the centers of the lines BC and GF. It is this mathematical figure -- we can call it a mathematical solid -- that we're now going to examine with respect to shape, symmetry and promorph.
The next Figure depicts the same mathematical solid (amphitect octagonal pyramid, with two extra lines (not ribs)) as the previous Figure, but viewed from an even more oblique angle.
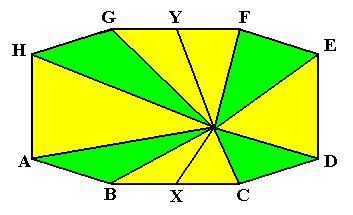
Figure above : A little more tilted top-view of the amphitect octogonal pyramid of the previous Figure. As in that previous Figure, the sides of the pyramid are indicated by the colors green and yellow.
The next Figure depicts the same, but now emphasizing an interpretation of this mathematical solid as consisting, not of eight, but of two antimers.
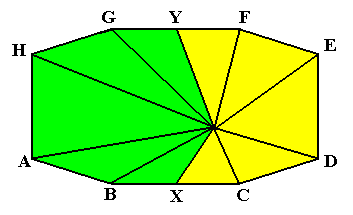
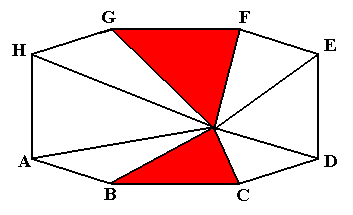
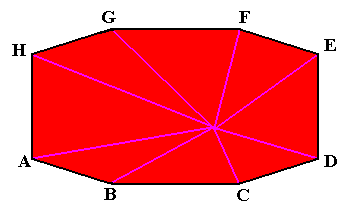
Figure above : The same mathematical solid as was depicted in the previous Figure. The lines running from the pyramid's tip to the points X and Y suggest an interpretation of this particular mathematical solid as possessing not eight, but two antimers (Generally, an amphitect octogonal pyramid, i.e. an amphitect 8-fold pyramid, is interpreted as having eight antimers).
The shape -- In mathematical figures the distinction between intrinsic and extrinsic is irrelevant -- of this solid is an amphitect octogonal pyramid.
This promorph is depicted in the next Figure :
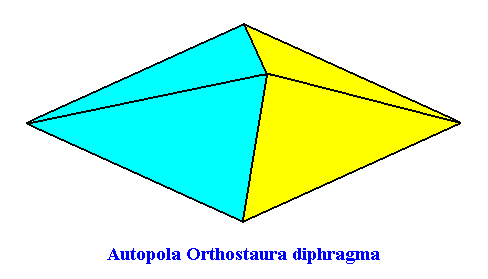
Figure above : Slightly oblique top view of a four-fold amphitect pyramid (rhombic pyramid) as the basic form of the Autopola orthostaura diphragma. This configuration as such possesses t w o antimers. These a n t i m e r s are indicated by colors (yellow, blue). It is the promorph of the mathematical solid (amphitect octogonal pyramid) as depicted earlier . To express the presence of just two antimers, we could call the pyramid (representing the promorph, and depicted in the present Figure) a ' two-fold amphitect pyramid ', or an ' rhombic pyramid with two antimers '.
All this, i.e. an amphitect octogonal pyramidal shape, a D2 symmetry , and a promorph belonging to the Autopola Orthostaura diphragma (represented by a two-fold amphitect pyramid), as such present in the Mathematical Layer, is also represented by objects in the material Layers (inorganic and organic), because there can be, and indeed are, conditions that allow them to be (energetically) s t a b l e configurations (of material elements).
Representation (by objects) in the I n o r g a n i c Layer of Being of the shape, symmetry and promorph of the amphitect octogonal pyramid as it was given above .
The D2 s y m m e t r y as represented in the Inorganic Layer :
The D2 s y m m e t r y of our mathematical solid is found as intrinsic point symmetry in the Inorganic Layer, for example in crystals of the mineral
Hemimorphite, Zn4Si2O7(OH)2 . H2O . See next Figure.
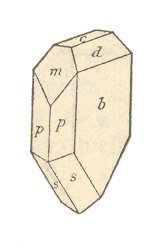
Figure above : A crystal of the mineral Hemimorphite.
The actual color of the crystal is white, in some cases with faint bluish or greenish shade. Also yellow to brown. Transparent to translucent.
This crystal belongs, according to its intrinsic D2 point symmetry, to the Rhombic-Pyramidal Class (mm2) of the Orthorhombic Crystal System.
Representation of the p r o m o r p h belonging to the (Heterostaura) Autopola Orthostaura diphragma in the Inorganic Layer.
Because I do not have relevant information as to the morphology of the translation-free residue (which has D2 symmetry) of a Hemimorphite crystal, I cannot assess the number of antimers, and so the assessment of the p r o m o r p h of these crystals can, for the time being, only point to a more general promorphological category, namely that of the Heterostaura Autopola (amphitect pyramids). Of course there is nothing that would forbid beforehand the possible existence of D2 three-dimensional crystals -- having shapes like we see in Hemimorphite crystals, or having other shapes, or even having the same shape as our mathematical amphitect octogonal pyramid -- that promorphologically belong to the (Heterostaura) Autopola Orthostaura diphragma, meaning that in that case the promorph of our mathematical amphitect octogonal pyramid as the latter was drawn earlier , is indeed represented by objects in the Inorganic Layer of Being.
Representation of the amphitect octogonal pyramidal s h a p e in the Inorganic Layer.
The s h a p e of our above mathematical solid, namely that of an amphitect octogonal pyramid, can be expected among the same Class of Orthorhombic crystals as to which the above hemimorphite crystal belongs, viz., the Rhombic-Pyramidal Crystal Class (mm2). A crystal having this shape is made up of a combination of four crystallographic Forms, viz., one rhombic pyramid, two domes and one pedion. Each Form is generated from some initially given crystal face in virtue of the action of the symmetry elements of the crystal, depending on the orientation of such an initial face with respect to the crystallographic axes (a, b, c). These latter are taken such as to align with the crystal's symmetry elements (mirror planes and rotation axis) : The c-axis coincides with the line of intersection of the two mirror planes (and thus coincides with the crystal's 2-fold rotation axis). The a-axis lies in one mirror plane, while the b-axis lies in the other, and both are perpendicular to the c-axis. See next Figure.
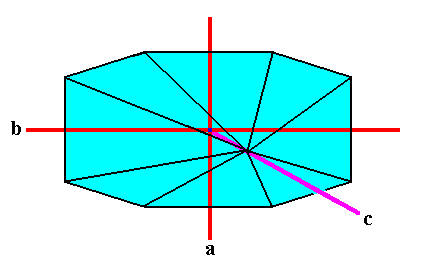
Figure above : Position of the crystallographic axes a, b and c of a three-dimensional crystal (oblique top view) having the shape of an amphitect octogonal pyramid, and belonging to the Rhombic-Pyramidal Class (mm2) -- and thus having D2 intrinsic symmetry -- of the Orthorhombic Crystal System. The c-axis connects the apex of the pyramid with the center of its base (where the latter is an amphitect octagon). We will now list and depict the four crystallographic Forms (indicated by red color) that together constitute our amphitect octogonal crystal.
So this was the s h a p e of the above mathematical solid, depicted earlier , as that shape can be represented in the Inorganic Physical Layer as an Orthorhombic crystal of the Class mm2 (Rhombic-Pyramidal Class) consisting of nine faces and as such a combination of four crystallographic Forms (Of course such a crystal also represents D2 symmetry in the Inorganic Layer).
The crystal example that has been given earlier (hemimorphite crystal) representing (only) i n t r i n s i c p o i n t s y m m e t r y ( D2 ), has a more complex shape than that of an amphitect octogonal pyramid. This particular (hemimorphite) crystal, as depicted above , consists of six crystallographic Forms, together making up 15 crystal faces. Let's list the Forms that participate in constituting this crystal :
See, with respect to crystallographic Forms of three-dimensional crystals, First Part of Website , In Special Series : "The Morphology of Crystals" and "Orthorhombic Crystal System II, Class mm2".
Representation (by objects) in the O r g a n i c Layer of Being of the shape, symmetry and promorph of the amphitect octogonal pyramid as it was given earlier .
Let's start with the symmetry and the promorph.
Representation of D2 symmetry and of the (Heterostaura) Autopola Orthostaura diphragma in the Organic Layer.
As for occurrence in the Organic Layer we can, as an example, advance the flower of the plant Circaea lutetiana (enchanter's nightshade, Family Onagraceae (Oenotheraceae)), that indeed has intrinsic D2 symmetry and a promorph belonging to the (Heterostaura) Autopola Orthostaura diphragma. See next Figures.
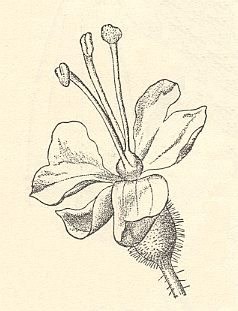
Figure above : Flower of Circaea lutetiana. It has two sepals, two (incised) petals, two stamens and one pistil. It is a two-fold structure.
After WETTSTEIN, R., Handbuch der Systematischen Botanik, 1924
The next Figure shows a promorphological analysis of this flower as done by Ernst Haeckel, in his Generelle Morphologie der Organismen, 1866, where he first proposed Promorphology as the Science of Basic Forms in organisms.
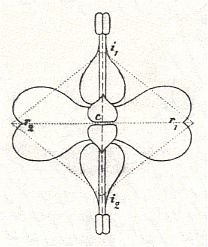
Figure above : Promorphological analysis of the flower of Circaea lutetiana.
After HAECKEL, E., Generelle Morphologie der Organismen, 1866.
Representation of the amphitect octogonal pyramidal s h a p e (by objects) in the Organic Layer.
While our presently discussed shape can occur as crystals in the Inorganic Layer of Being, it will be hard to find it represented as the intrinsic shape of entities of the Organic Layer. This is because our shape, the amphitect octogonal pyramid, consists of straight lines and plane surfaces, which are relatively rare among organisms, because of their semi-liquid state (allowing surface tension to play some role, i.e. allowing it to partake in the generation of shape). Generally such a shape (consisting of straight lines and plane surfaces) is to be expected only as an extrinsic shape, as for instance in certain cells making up certain organic tissues. The pyramidal shape has then come about by extrinsic forces with respect to such a cell. But maybe we can find it -- as intrinsic shape -- in certain pollen grains or other unicellular organic entities such as Radiolarians. One could also think of some virusses having this shape, when they are in their crystalline state. But virusses are, especially in this state, not really alive, they are, so to say, fragments of life, presupposing genuine life for their bioactivities, especially their reproduction.
But of course, s h a p e itself, i.e. shape just as shape, including intrinsic shape, occurs everywhere in the organic realm.
So far so good, with respect to the occurence of certain shapes, symmetries and promorphs in the Mathematical Layer of Being, and their representations in the Inorganic and Organic Layers. Later, in a new Series of Documents, we are internded to present many more examples.
The above had illustrated that the categories of Shape, Symmetry and Promorph can pass from the Mathematical Layer into the Inorganic and from there into the Organic Layer, without being over-formed. The concepts expressing them have exactly the same meaning in all three Layers. But the way Shape, Symmetry and Promorph are generated is different in these Layers :
In the present Series of Documents we emphasize the aspect of continuity between the three Layers, by studying Shape, Symmetry and Promorph in crystals and organisms (For the latter this is done extensively in Second Part of Website, Basic Forms ).
Further we will study the continuity and difference between the Inorganic Physical Layer and the Organic Layer by evaluating crystal analogies. There we will see that many properties that we see in crystals, return in organisms. However they there appear in a sort of 'elevated' state, i.e. they appear in a much more complex fashion than they do in crystals, embodying in this way the complexity jump that occurs at the (formal) transition between the Inorganic and the Organic.
Until now we have studied real crystals by way of imaginary two-dimensional crystals, because three-dimensional crystal structure is hard to depict on a two-dimensional screen. The geometrical structure of two-dimensional crystals is easier to grasp and reveals most of the structural principles of three-dimensional crystal structure. Moreover, in themselves, two-dimensional crystals are true inhabitants of the Mathematical Layer of Being, as long as we stick to their geometry (shape, symmetry and promorph), without interpreting their constituents as atoms or molecules. In fact we do so interpret, but after that discard it again. This we do to maintain the difference that obtains between two-dimensional crystals and other geometric plane figures.
But as soon as we want to fully evaluate all existing crystal analogies, we will have to deal with stability questions, and these necessarily involve energy considerations. And this can, of course, only be done with real, i.e. three-dimensional crystals. Therefore we will study their structure as well (but in a concise and algebraic fashion -- Group Theory -- and only in a very limited way in a geometric fashion).
This concludes our (preliminary) Ontological Discussion concerning the role that Shape, Symmetry and Promorph play in the layered structure of Being.
But before we go to the next document, we'd like to think an rethink the idea of a layered structure of Reality as presented in this website, because it could entail some remarkable consequences as to the overall and global structure of the whole of Existence, Reality, the World, or whatever we care to name it.
On the Transformation of the Organic into the Inorganic :
The theory of Layers of Being, as presented on this website (and inspired by, and partly based on, the philosophy of Nicolai HARTMANN ), can still be discussed further, as to its general validity or falsity, when we concentrate on the division between the Inorganic and the Organic. These can be related to each other in four different ways :
The Theory of the Implicate Order is extensively considered in Third Part of Website .
The theory boils down to the assumption that all things, apparently separated in space and / or time, are manifestations of one single dynamic whole, like the waves of an ocean. These things are projections from that whole -- which is called the Implicate Order -- into their states of separatenes, which collectively is called the Explicate Order. The mentioned things can also return from the Explicate (unfolded) Order to the Implicate (enfolded) Order, which is called injection. The Explicate Order is our observable world of things, space and time. What we see happening in this Order are physical processes and transformations. But these are only manifestations of a much more fundamental 'process', namely the dynamics of sustained projection and injection of aspects of the Implicate order. So all things in the Explicate Order are connected with each other in subtle ways via the Implicate Order. The way of being of this Implicate Order is not that of a material world with things separated in space and / or time, but a world in which everything is folded together, i.e. a world in which every 'thing' interpenetrates every other 'thing'. We will call this way of being noëtic which means 'thought-like'. We can think of it as being some kind of proto-intelligence. We can also compare it to Nicolai HARTMANN's Ideal Sphere of Being (See Part I of the present Series) or to our Mathematical Layer of Being (See also Part I of the present Series). So all the transformations that take place within the Implicate Order are 'thought-like'. Moreover, we assume them to be timeless (especially with respect to our (physical) time). So in fact those transformations are of a logical nature, not of a physical one. At its most fundamental, the Implicate Order is represented by the 'Holomovement' which is absolute unity.
This whole philosophical idea is mainly from the quantum physicist David BOHM, and it is, in its bottom line, very akin (though not mentioned by him) to the metaphysics of the Greek philosopher PLOTINUS in the third century A.D. In the latter metaphysics it is assumed that from "The One", which is unity in an absolute sense, some lower 'hypostases' (reality levels) emanate, ending up in the lowest 'hypostasis', namely that of the material world. So also here we see that the lower forms evolve from higher forms.
Well, the above assumed transition from Organic to Inorganic, cannot, as established above, take place within the physical universe, which we now can translate as such a transition not being possible in the Explicate Order (which is, it is important to realize, just an aspect of the Whole). But it can take place in the Implicate Order, because a transition from Organic to Inorganic can now be seen as a (logical) d e r i v a t i o n , namely by just eliminating the NOVUM and (automatically) with it, all that it entails. This we call Holistic Simplification from the Organic to the Inorganic, i.e. the Inorganic is a holistic simplification of the Organic (as was first proposed by MEYER-ABICH, A., in Naturphilosophie auf neuen Wegen, 1948). This simplification is thus a noëtic process, taking place in the Implicate Order in a space- and timeless fashion. The explicitation of this process, i.e. its appearance in the Explicate Order, must take place in r e v e r s e order : namely from Inorganic to Organic, because (as we now assume) the explicate Organic presupposes explicate Inorganic : To become explicate Organic, the implicate Organic needs an appropriate material substrate. This latter substrate must already be present in the Explicate Order and can now be over-formed by the implicate Organic, resulting in explicate Organic. So what we see in the Explicate Order (observable world) is the apparent emergence of the Organic from pre-existent Inorganic, while in fact the Inorganic was derived from the Organic in the Implicate Order by Holistic Simplification. In this way we have circumvented the problem of the NOVUM (but, of course, at a price of introducing a hypothetical entity, the existence of which must be demonstrated).
Because Holistic Simplification will play an important role in the ensuing discussion, let us give some instructive examples :
We can never derive the corresponding colored version from a given black-and-white picture (that intended to express a scene that originally had certain colors). The corresponding colored picture is more than its black-and-white version . We can, however, easily derive the black-and-white version from the corresponding colored picture, namely by taking a photograph of the latter with a black-and-white film. The latter process -- from colored picture to black-and-white version -- is a genuine holistic simplification.
A second example of holistic simplification concerns geometry. See next Figure.
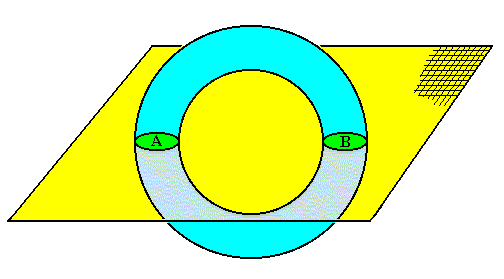
Figure above : A three-dimensional donut-shaped solid object (blue) is intersected by a plane (yellow). The product of the intersection is two areas A and B, which are each two-dimensional. While one cannot unequivocally derive the donut-shaped object from the areas A and B (they give us not enough information as to what the corresponding three-dimensional object will be), we can derive the areas A and B from the donut-shaped object, because those areas are already implicitly present in that object. If we intersect this object by a plane containing its axis of rotation, we obtain the areas A and B. This operation is nothing less than obtaining the areas A and B by holistic simplification of the donut-shaped object. Also here the latter is more than the former, and cannot be derived from it.
The general line of argument here is in fact the following : If it can be shown that the Organic cannot in any way be reduced to the Inorganic, which here should mean not only epistemologically, but also ontologically, then we must assume the appearance of a NOVUM when we formally go from the Inorganic to the Organic. In all this we must realize what precisely "cannot in any way be reduced" means, a slogan that is often enough heard, without, however, any discussion about what such a position entails. One speaks about dynamical systems that are self-organizing, and create patterns and structures that are not to be found in the initial conditions of the system. Such patterns are called emergent. And of course the Organic contains such emergent properties which are absent in the Inorganic. But when these properties have ultimately been produced from inorganic dynamical systems, they can be called "emergent" but they do not represent a genuine NOVUM, because they have (physically) been derived from the dynamical system, i.e. totally from within the dynamical system, which means that such properties were already present in the Inorganic, albeit only implicitly so. And in this case, of course, the Organic -- as represented by its emergent properties -- is reducible to the Inorganic, because it was actually produced by (and thus derived from) the Inorganic (which was represented by the dynamical system that produced these properties). So if one claims to adhere to a true holism, i.e. to an anti-reductionism, in the case of organisms, as many authors do, then they must admit the appearance of a genuine NOVUM when we formally change from the Inorganic to the Organic. But then we must also admit that the Organic cannot have been evolved from the Inorganic, despite the fact of the many indications that it did so originate. We thus have a problem, but this problem can be solved by assuming the above mentioned Implicate order. So if we are forced to assume a genuine NOVUM to appear when formally going from the Inorganic to the Organic, and if the only outcome from the then implied dilemma is the assumption of something like an Implicate Order (where the holistic simplification takes place), then we have a fairly good argument in favor of the existence of such an Implicate Order.
HARTMANN, N., Der Aufbau der realen Welt, 1940.
MEYER-ABICH, A., Naturphilosophie auf neuen Wegen, 1948.
BOHM, D., Wholeness and the Implicate Order, 1980, 1983.
SHELDRAKE, R., A New Science of Life, 1981.
DAVIES, P., The Cosmic Blueprint, 1987, 1989.
BOHM, D. & PEAT, F., Science, Order, and Creativity, 1987.
PEAT, F., Synchronicity, 1987.
ROSE, S., Lifelines, 1997.
GOODWIN, B., How the Leopard Changed its Spots, 1994, 2001.
This list could be extended by many more examples of authors that maintain the irreducibility of the organic world to the inorganic world. Of course, we can judge such a position as a capitulation with respect to relevant scientific research. Organisms turn out to be so stupefying complex, that one is giving up any serious investigation that could finally reveal the reducibility of organisms to inorganic beings and processes. All these authors acknowledge the general validity of the Theory of (organic) Evolution, where it is stated that higher organisms have evolved from lower, and ultimately from lowest ones. From this it seems legitimate to extrapolate, and maintain that these lowest organisms evolved from inorganic entities. (We continue our list of indications that point to te presence of a NOVUM as we go from Inorganic to Organic).
All of Existence forms an undivided Whole. Nothing in it is isolated, neither in time nor in space. However, this Wholeness is like an ocean that carries various waves, that are seemingly separated from each other. These waves are, however, totally integrated within the Whole, and therefore not actually separated from each other. They emerge from the Whole, without actually leaving this Whole, and are again absorbed by the whole. The seemingly separated waves are a manifestation of the inner dynamics of the Whole. Conceptually we can separate the waves from the ocean, and especially from each other, but ontologically, i.e. realiter or actually, we cannot. So when we consider the waves as separate entities, and view their dynamics and interactions, i.e. if we erect a theory about them, this theory is only an abstraction of, or approximation to, the actual and true state of affairs, which latter involves all there is, i.e. it involves the Whole.
In fact this (i.e. the waves and the ocean) is just a crude analogy of the Explicate and Implicate Order. While the Implicate Order enfolds all things within each other, and thus represents global and non-local order, the Explicate Order unfolds all things in space and time, and so represents local order. It is an unfolded successive dynamic whole, and as such only an aspect of the Whole. The Implicate Order is an enfolded whole, it contains all totalities and structures implicitly, and at once. It is timeless. As such it is a multidimensional domain, having many more dimensions than the Explicate Order into which it is constantly unfolding itself (or, equivalently, onto which it is constantly projecting itself), while at the same time the Explicate order is enfolding itself back into the Implicate Order, in a continuous dynamics of projection and injection. While in the explicated (i.e. unfolded) state things are physical and local, and materially interact with each other, resulting in spatial and / temporal patterns, in the implicate (i.e. enfolded) state their way of being is not material or physical, not spatial, but noëtical , i.e. thought-like. The 'processes' 'taking place' there are not material processes but logical deductions. They do not -- as they do in human thought -- proceed in time, neither they 'take place' in space. The explicate entities, on the other hand, are manifestations of the Whole, i.e. each explicate entity is a manifestation and effect of all that is going on in the Whole. And this is just another way of saying that each of them 'holographically' contains that Whole. In order for this to be possible, matter must have a far more subtle inner structure than is normally assumed.
Within the Implicate Order several domains contain each other holistically and are related to each other by noëtic holistic simplification :
The Psychic Domain (if we acknowledge such a domain at all, and which should then be noëtic in a way appropriate to the way of being within the Implicate Order), holistically simplifies into the Organic Domain, i.e. the latter Domain is a holistic simplification of the Psychic.
The Organic noëtic Domain holistically simplifies into the Inorganic Domain, i.e. the latter Domain is a holistic simplification of the Organic.
These three noëtic Domains can successively be explicated, roughly as in the ink-in-glycerine model of the Implicate and Explicate Orders, as discussed in the mentioned Third Part of Website. Thereby we assume that (elements of) the Psychic noëtic Domain can only be explicated when (they) it can over-form an appropriate organic substrate that already is explicate. In the same way we assume that (elements of) the Organic Domain can only become explicate when (they) it can over-form an appropriate inorganic substrate that already is explicate. Finally we assume that the Inorganic (i.e. physical) can become explicate all by itself. It has so much substrate quality already all by itself, that it does not need a pre-existent explicate substrate.
We are now ready to summarize all this into a diagram of the holistic world :
Diagram above : Implicate Order (light blue) and Explicate Order (grey-brown).
What we actually see in our observable world is a manifestation of a dynamics of continuous projection (from the implicate into the explicate), injection (from the explicate into te implicate), re-projection and re-injection. Only the explicate condition of being is accessible to observation. We then see (or can deduce from theory and observation) successive stages of processes, for example crystallization, individual organic development, phylogenetic sequences, etc. What we surely see (or, again, can deduce from theory and observation) is that from initially given inorganic entities organisms emerge, and that these latter develop in more and more complex forms. As a latest development, a latest complexification, we see conscious beings emerge from non-conscious animal ancestors. So what we see is that an initially given inorganic substrate is being over-formed by organic structure, or in other words, we see something novelty appearing that harnesses the inorganic, creating dynamic and functional wholes, organisms. In the same way we see novelty appearing where conscious beings evolve from initially given organisms lacking consciousness. This mentioned novel aspect expresses the appearance of one or more totally new principles or categories. So we call it, with HARTMANN, (the appearance) of a categorical novum , that modifies all other categories. This, indeed, is what we see in the Explicate Order. As a result we see three Layers of Being, viz., the Inorganic, Organic, and Psychic Layer.
The events, as we see them in the Explicate Order, are no less fundamental. They reflect the events, not of the Implicate Order, but of the W h o l e. The fact that we see (in theory or observation) organisms evolve from inorganic entities, and not the other way around, is fundamental in its own right, because of the mentioned substrate-form relationship. Every aspect of the observable world is an aspect of the Whole. And every primary aspect of that observable world is a primary aspect of that same Whole.
In the above diagram depicting the Whole as consisting of the Explicate and Implicate Order, we see how, in the Explicate Order three Layers of Being are constituted, by a process of explication and substrate over-forming. Well, it is further reasonable to interpret the Implicate Order itself as the Mathematical Layer of Being, because, indeed, mathematics is noëtic, i.e. thought-like. If this is correct then, if we accept the Psychic Layer in addition to the other Layers, we have four Layers of Being, viz., the Mathematical Layer, the Inorganic Physical Layer, the Organic Layer and the Psychic Layer. In fact our scheme, as depicted in the diagram mentioned, represents a further elaboration of our Theory of Layers. And it especially elaborates on the transition from the Mathematical Layer to the other Layers (i.e. to the Temporal Layers). This transition is one of explicitation (in conjunction with substrate over-forming).
The introduction of the Implicate Order (and interpreted as the Mathematical Layer), as contrasted with the Explicate Order (consisting of the Inorganic, Organic, etc. Layers), brings our ontological scheme still more closer to that of HARTMANN : For him, our Mathematical Layer was a separate sphere of Being, the Ideal Sphere, which has its own way of being (its own modality), different from that of his "Real Sphere of Being" which, according to him consists of four Layers of Being, viz., the Inorganic, Organic, Psychic and Super-psychic Layers. Well, by identifying our Mathematical Layer with the Implicate Order, we now, like HARTMANN, contrast it with all the rest of Existence (i.e. the temporal Layers) taken together. And indeed, the Mathematical Layer, also in the form of the Implicate Order, has a fundamentally different way of being (a different modality), namely t i m e l e s s, i.e. different from that of the other Layers taken together, because these are t e m p o r a l.
We must realize that when it would unequivocally turn out that science is finally able to entirely reduce organisms to inorganic entities (and psychic organisms to non-psychic organisms), the idea of ontological Layers and the idea of the Implicate Order probably become superfluous, and should be abandoned. What is left at the most is the Mathematical Layer and the Time Layer, i.e. the former non-mathematical Layers taken together. And within the latter we still can see, it is true, some layering, but only in the form of complexity l e v e l s without ontological significance. Moreover, the Mathematical Layer then probably loses its ontological status : It will become just a way of description of Reality. Quite frankly, I personally am inclined to consider r e d u c t i o n i s m as being a way of seeing things closest to the truth, and thus adhering to an ontological reductionism (where the NOVUM turns into reductionistic complexification). There is, however, no hard evidence for it, apart from the fact that we know for sure that, as a temporal sequence, the Inorganic was first, while only after it the Organic had appeared (and, even later, the Psychic).
We should further realize, that r e d u c t i o n i s m is the only m e t h o d by which natural science can proceed, because a genuine u n d e r s t a n d i n g of any observed phenomenon is reducing it to simpler phenomena. In the individual development of organisms, and also in crystal growth, there are some indications of n o n - l o c a l i t y (distant parts being somehow correlated, however not by any sort of chemical or physical signal), implying w h o l e n e s s. Such phenomena are not intelligible (at least not when they occur in the macroscopic realm). And in such cases, altering the relevant scientific theories and methods will not help. The only thing one can do is to place the (reductionistic) scientific theories and methods in a broader philosophical or metaphysical context that admits of wholeness to be the case, and concede that all scientific theories are always, and in principle, no more than approximations, because they are necessarily reductionistic in character. A possible metaphysical context, fully allowing for Wholeness, is the Theory of the Implicate Order, as outlined above, and in the mentioned Third Part of Website.
In the next to next document (Part XXIX, Sequel-3 to the Summary and Evaluation [of Parts XVI--XXVIII ] ) we will add some more considerations about the holistic nature of Reality, when we discuss symmetry and promorph of snow flakes (i.e. single crystals of the substance H2O).
In the next document (Part XXIX, Sequel-2 to the Summary and Evaluation [of Parts XVI--XXVIII ] ) we append a discussion -- as is provoked by the Ontological Discussion -- about the Promorphology of Plants, considering their way of leaf (or flower organs) arrangement (phyllotaxis). The goal is to compare in more detail the inorganic form-potential field in crystallization and that in leaf pattern formation in plants, including the arrangement of sepals, petals, stamens and carpels in flowers, which are originally derived from (ordinary) leaves (which are now their 'ground state'). As a corrollary result we will find two new promorphs.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX (Sequel-2).