e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Summaries and some theorizing (Sequel-1)
In the previous document we distinguished between Holomorphic crystals and Meromorphic crystals. Because this distinction is important for what follows, we repeat the relevant Section dealing with it :
Let's say something more about the relationship between the symmetry of the crystal's intrinsic shape and that of the crystal itself, i.e. that between the geometric and crystallographic symmetry.
We call a crystal h o l o m o r p h i c when the point symmetry of its intrinsic shape is the same as the intrinsic point symmetry of the crystal. If, on the other hand, the crystal's point symmetry is l o w e r than that of its intrinsic shape we call the crystal m e r o m o r p h i c.
So in holomorphic crystals their whole shape reflects the intrinsic symmetry of the crystal, while in meromorphic crystals only a part of their shape reflects the intrinsic symmetry of the crystal.
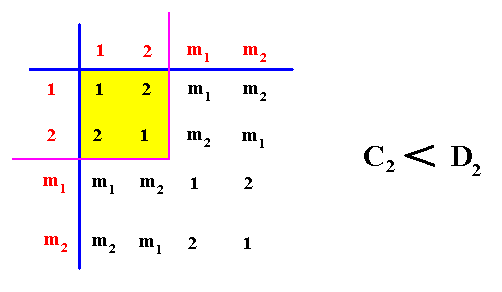
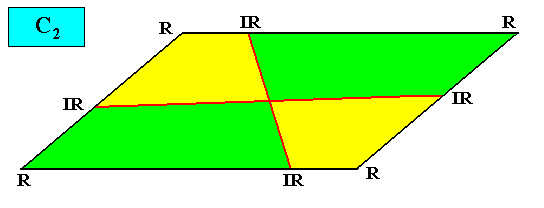
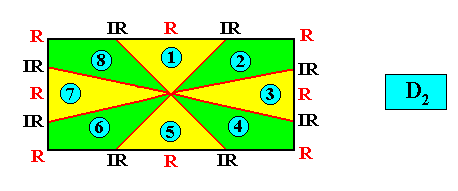
If we have, for example, a (two-dimensional) crystal with intrinsic C2 symmetry, and possessing as its intrinsic shape that of a rectangle, then only a part of this rectangle indicates the true symmetry of the crystal, namely the 2-fold rotation axis of the rectangle. In different but equivalent words : The symmetry of the rectangle is according to the group D2 , while the true symmetry of the crystal is according to the group C2 , and the group C2 is a subgroup of the group D2 what we denote as follows : C2 < D2 , and which is shown in the next diagram (group table) :

Diagram above : The Cyclic Group C2 (yellow) is a subgroup of the Dihedral Group D2 (whole table).
So in general meromorphic crystals have an intrinsic (point) symmetry that is represented by a subgroup of the group representing the symmetry of their intrinsic shape, while in holomorphic crystals their intrinsic symmetry is the same as the symmetry of their intrinsic shape.
Meromorphy, holomorphy and eupromorphy can also occur in o r g a n i s m s : There are organisms whose shape neatly expresses their symmetry, i.e. the symmetry of their shape is compatible with the internal structure of the organism, and such organisms are then holomorphic. But there are also organisms whose symmetry according to their internal organization is lower than that of their shape ( There are, for example, spherical organisms with asymmetric or lower symmetric internal organization), and such an organism is then meromorphic.
Further there are organisms whose shape not only neatly expresses their intrinsic symmetry (when their internal organization is taken into account), but also their promorph, as in many Radiolarians belonging to the subdivision Spumellaria, and also in most star-fishes.
In the previous document we listed (as second summary) the promorphs that had appeared in earlier Parts (V -- XIV) together with some examples of two-dimensional crystals, each having one of our six simple (intrinsic) shapes : Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon. Among these we found Holomorphic as well as Meromorphic crystals. In the following we have selected all the h o l o m o r p h i c cases from that summary. While all of them indeed have a symmetry that is identical to that of their shape (holomorphy), some of them are even more special : Their shape, as represented by the Vector Rosette of Actual Growth (vectors from the center of the crystal to its corners), also precisely reflects the number and arrangement of antimers, that is to say, the vectors of the mentioned rosette either coincide with interradial or with radial axes, or at least are in some way related to them. We shall call crystals where this is the case, i.e. crystals of which their intrinsic shape fully expresses their promorph, e u p r o m o r p h i c crystals. In the following list of holomorphic crystals (from the mentioned second summary) we have indicated these eupromorphic crystals.
Planimetric Basic Form, representing this promorph :
Example of holomorphic crystal :
Planimetric Basic Form, representing this promorph :

Example of holomorphic crystal :
Planimetric Basic Form, representing this promorph :
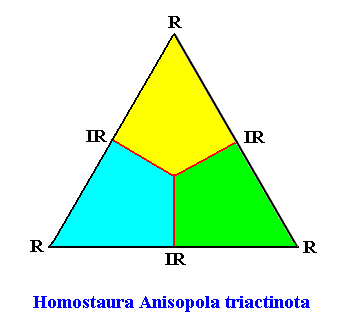
Example of holomorphic crystal :
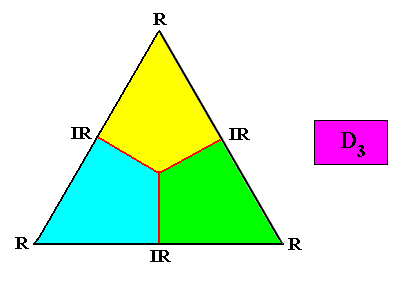
Planimetric Basic Form, representing this promorph :
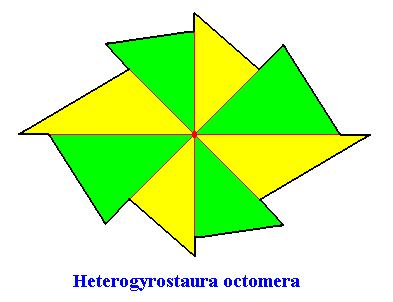
Example of holomorphic crystal :
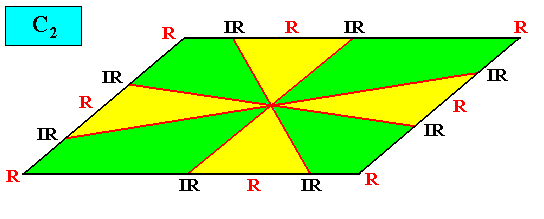
Planimetric Basic Form, representing this promorph :
Example of holomorphic crystal :
Planimetric Basic Form, representing this promorph :
Example of holomorphic crystal :
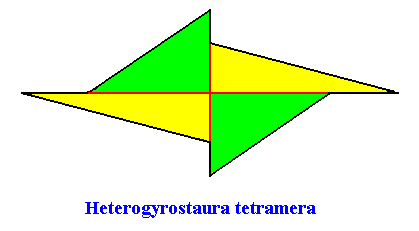
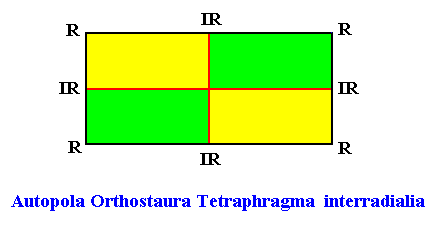
Heterostaura Autopola (amphitect polygons),
Planimetric Basic Form, representing this promorph :
Examples of holomorphic crystals :
Planimetric Basic Form, representing this promorph :
Examples of holomorphic crystals :
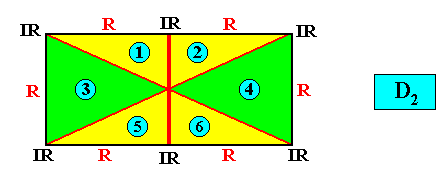
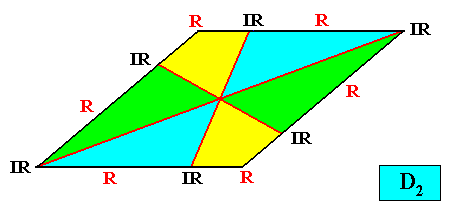
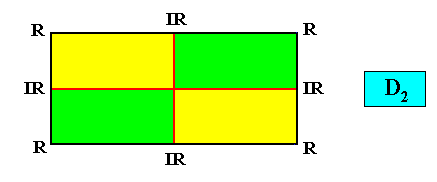
Heterostaura Autopola (amphitect polygons),
Planimetric Basic Form, representing this promorph :
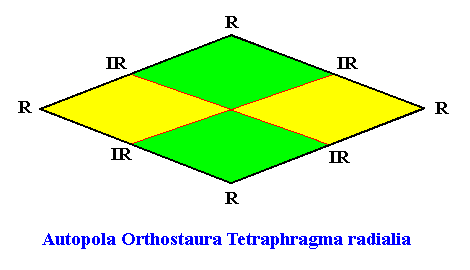
Examples of holomorphic crystals :
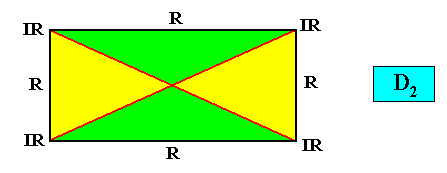
Planimetric Basic Form, representing this promorph :
Examples of holomorphic crystals :
Planimetric Basic Form, representing this promorph :
Examples of holomorphic crystals :
This concludes the summary of all the holomorphic crystals with respect to the six simple shapes (Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon) discussed in the previous documents.
In the following we will pick up all the eupromorphic crystals from the above, and let them be accompanied by their corresponding figures in which the Vector Rosette of Actual Growth (with its vectors a, b, c, . . . ) has been added.

With vector rosette added :

With vector rosette added :
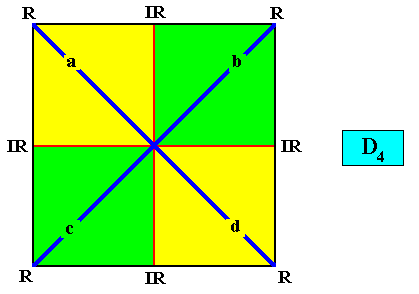

With vector rosette added :
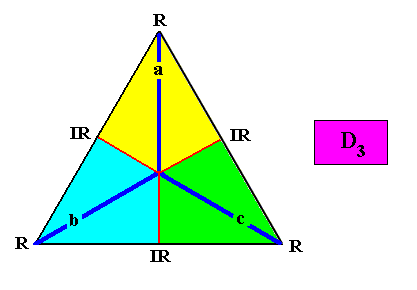

With vector rosette added :
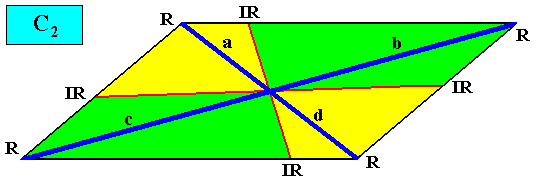

With vector rosette added :
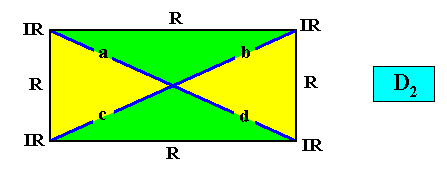

With vector rosette added :
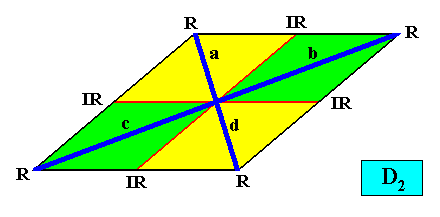

With vector rosette added :
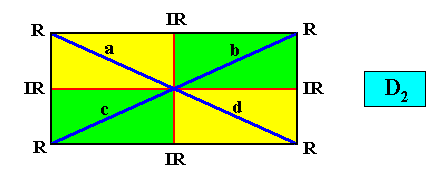

With vector rosette added :
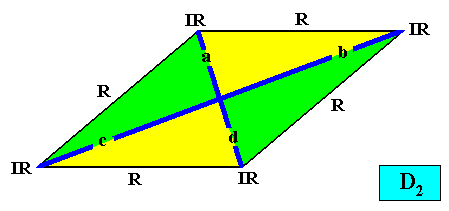
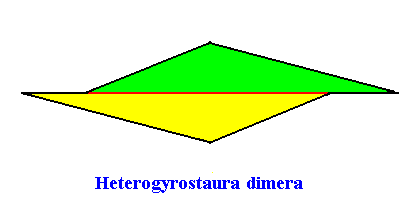
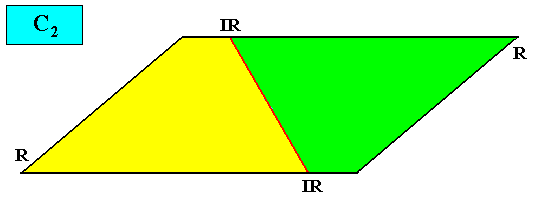
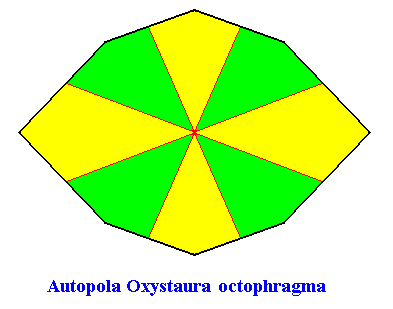
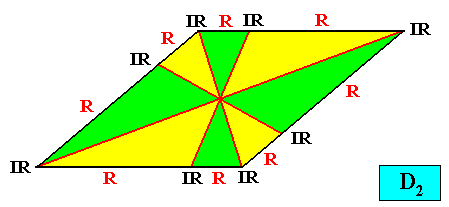
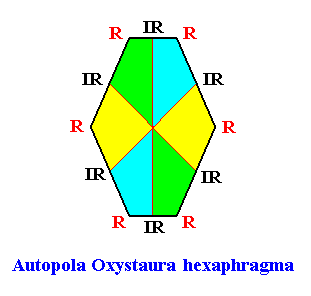
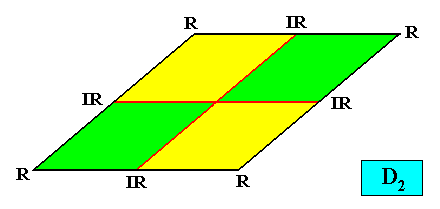
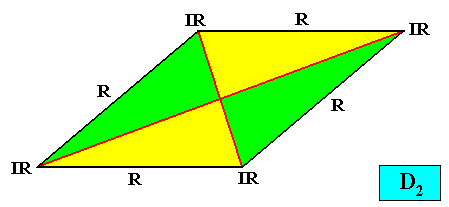
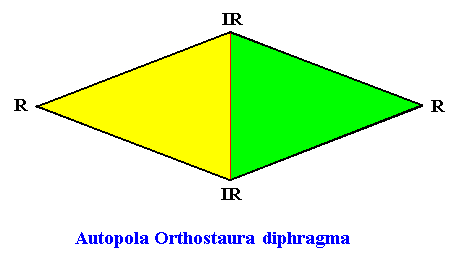
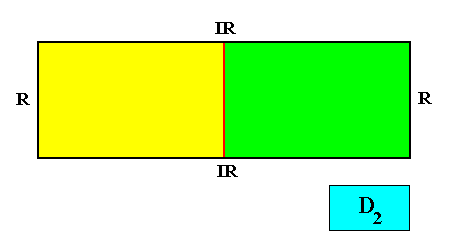
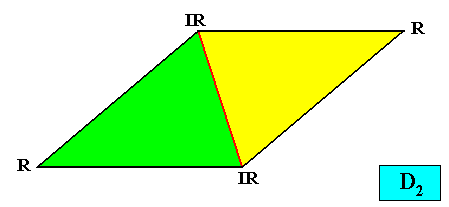
As we can see, by listing all eupromorphic crystals from the crystal shapes so far discussed (Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon), we get only a few promorphs out of the many possible. Obviously more (intrinsic) crystal shapes are required to cover all possible promorphs by eupromorphic crystals. Or, in other words, to let crystal shapes fully express all possible promorphs (here of course all crystallographically possible promorphs), we need much more shapes. For example we need the six-sided gyroid rectangle to let the intrinsic shape of the crystal express the Heterogyrostaura hexamera, and we need the elongated hexagon to express the Autopola Oxystaura hexaphragma. And letting express, by the intrinsic crystal shape, the promorph of D1 crystals (i.e. crystals possessing as their only symmetry element a mirror line) with two symmetrically arranged antimers (Zygopleura eudipleura) represents an aberrant case, because there are no plane straight-edged figures with only two corners. The straight-edged figure with the least number of corners and having D1 symmetry is the isosceles triangle. So this shape must somehow express the mentioned promorph, despite the fact that its Vector Rosette of Actual Growth (vectors from the center to the corners) does not reflect this promorph as in other eupromorphic crystals. Nevertheless we must call D1 crystals with two antimers and having the isosceles triangle as their intrinsic shape, eupromorphic crystals, just because this shape neatly expresses an instance of the Zygopleura eudipleura (which, as promorph are indeed geometrically represented by an isosceles triangle). The same applies to D2 crystals with two antimers and having the rectangle or rhombus as their intrinsic shape. The rectangle as well as the rhombus then are considered to neatly express an instance of the Autopola Orthostaura diphragma. And among the above considered crystal shapes we indeed had two of them (rectangle and rhombus) that were considered to be already holomorphic crystals, but not eupromorphic ones, and which must now nevertheless be considered to be eupromorphic crystals. It was a rectangular D2 crystal with two antimers, and a rhomb-shaped D2 crystal also with two antimers :


The same applies to C2 crystals with two antimers and having the parallelogram as their intrinsic shape :

Relations between internal structure and geometric shape in two-dimensional crystals.
Intrinsic symmetry and intrinsic shape of two-dimensional crystals are determined by a number of factors :
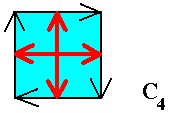
Figure above : Diagram of a C4 crystal (i.e. a crystal with intrinsic symmetry consisting of a 4-fold rotation axis only, and no mirror lines). The four growth vectors indicated (red) are equal and represent directions of slowest growth. The result is a square crystal. So the intrinsic symmetry group -- C4 -- of the crystal is a subgroup of the symmetry group of its shape -- D4 .
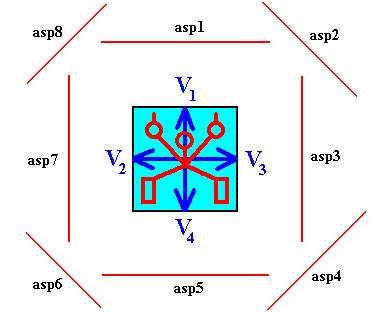
Figure above : Diagram of a quadratic two-dimensional crystal with motif (red) inserted (to indicate the crystal's D1 symmetry) and with four of its growth rate vectors indicated (blue). Atomic aspects (asp) indicated.
Symmetry of Intrinsic Shape (Square) : D4 .
Intrinsic Point Symmetry of Crystal : D1 .
Promorph : Pentamphipleura, i.e. bilateral forms with five antimers (and not Tetractinota, and also not Homogyrostaura tetramera for that matter).
Even when, of the above depicted crystal, the atomic aspects asp1, asp2, asp3, asp4 and asp5 (and also asp1, asp8, asp7, asp6 and asp5) are d i f f e r e n t (while asp2 = asp8, asp3 = asp7, asp4 = asp6), corresponding growth rates could be the same nevertheless, in virtue of a certain configuration of determining factors : Different atomic aspects generally will entail different growth rates, but not necessarily so (unless we define atomic aspects according to the resulting growth rates). And indeed in the above depicted case, with respect to the growth rate vectors, V1 (asp1) = V3 (asp3) = V4 (asp5) = V2 (asp7). And the same applies to the corresponding diagonal growth rate vectors (equal among themselves, different from, and higher than, the non-diagonal growth rates), resulting in a case where the intrinsic shape is a square, and as such not reflecting the promorph (and even also not the intrinsic point symmetry) of the crystal.
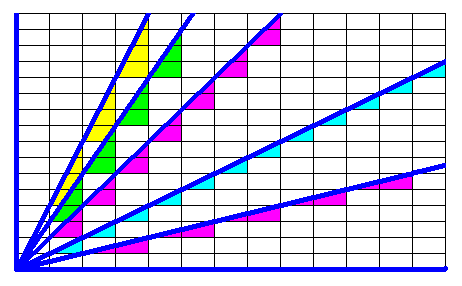
Figure above : Some possible faces in a given rectangular crystal lattice.
The next Figure shows again the oblique possible faces, but now they are drawn as thin lines, in order to enhance accuracy.
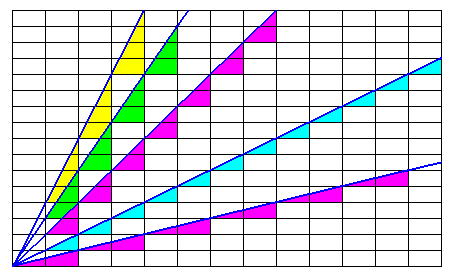
Figure above : The same possible (oblique) faces of the previous Figure, now drawn as thin lines.
The next Figure shows three 'faces' that are impossible.
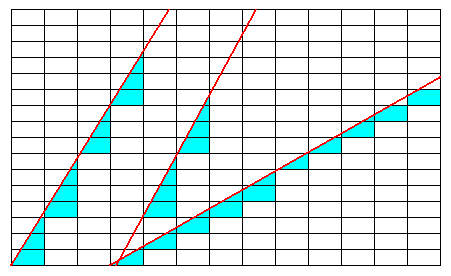
Figure above : Some impossible faces in the given (in previous Figure) rectangular crystal lattice. They do not climb up by a whole number of building blocks and at the same time just toughing the corners of the building blocks involved. See also next Figure.
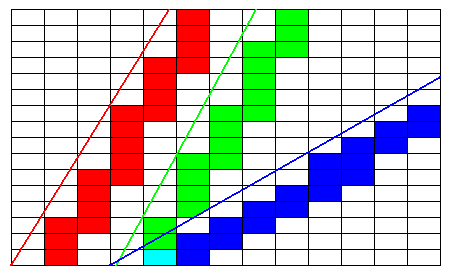
Figure above : The same impossible faces as in the previous Figure.
Only whole building blocks can be involved in constituting the crystal. To the right of each impossible face whole building blocks are indicated that are closest to it. One can see that irregular crystal faces (i.e. not straight ones) are implied, i.e. not genuine faces.
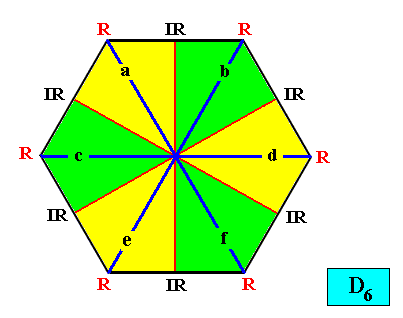
Let us now then discuss the above mentioned crystal shapes. For each shape a possible Vector Rosette of Actual Growth (with vectors a, b, c, . . . ) is indicated :
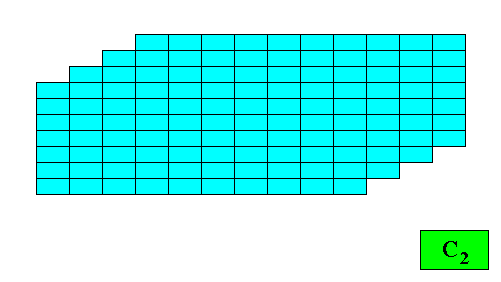
Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in a amphitect gyroid hexagon (six-fold gyroid amphitect polygon). If the motifs (not drawn) in the building blocks have C2 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group C2 . The growth rates of the six faces are supposed to be such that they balance, resulting in the persistence of all of them.

Figure above : Resulting crystal shape (amphitect gyroid hexagon) from the above stacking of rectangular building blocks.
And with its Vector Rosette of Actual Growth added :

Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in an amphitect gyroid octagon (eight-fold gyroid amphitect polygon). If the motifs (not drawn) in the building blocks have C2 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group C2 . The growth rates of the eight faces are supposed to be such that they balance, resulting in the persistence of all of them.
Figure above : Resulting crystal shape (amphitect gyroid octagon) from the above stacking of rectangular building blocks.
And with its Vector Rosette of Actual Growth added :
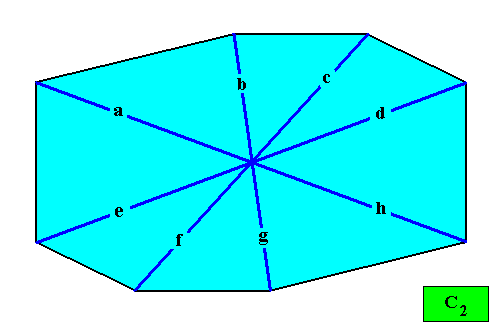

Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in an amphitect hexagon (elongated hexagon). If the motifs (not drawn) in the building blocks have D2 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D2 . The growth rates of the six faces are supposed to be such that they balance, resulting in the persistence of all of them.

Figure above : Resulting crystal shape (amphitect hexagon) from the above stacking of rectangular building blocks.
And with its Vector Rosette of Actual Growth added :
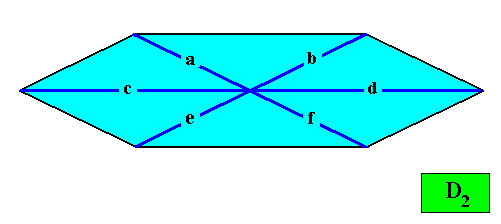
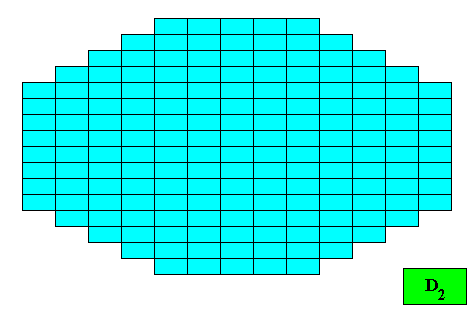
Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in a amphitect octagon. If the motifs (not drawn) in the building blocks have D2 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D2 . The growth rates of the six faces are supposed to be such that they balance, resulting in the persistence of all of them.
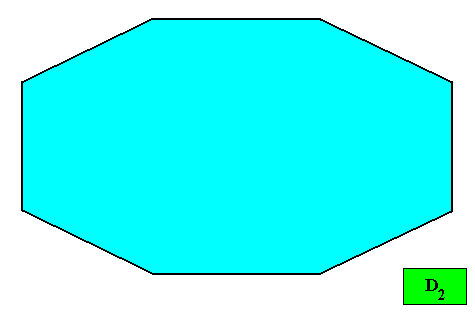
Figure above : Resulting crystal shape (amphitect octagon) from the above stacking of rectangular building blocks.
And with its Vector Rosette of Actual Growth added :
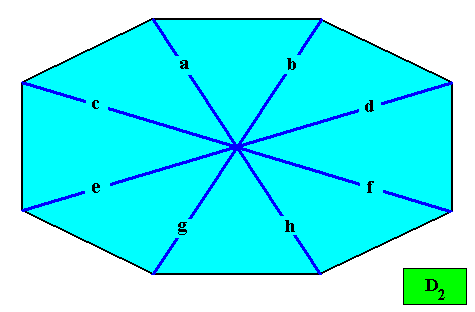
Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in an bi-isosceles trapezium (bilateral hexagon). If the motifs (not drawn) in the building blocks have D1 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D1 . The growth rates of the six faces are supposed to be such that they balance, resulting in the persistence of all of them.
Figure above : Resulting crystal shape (bi-isosceles trapezium) from the above stacking of rectangular building blocks.
And with a possible Vector Rosette of Actual Growth added :
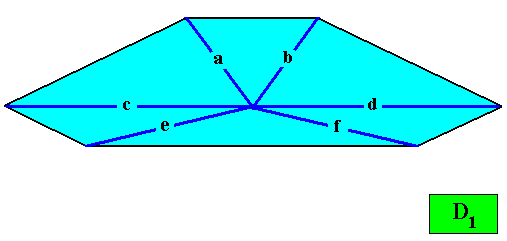
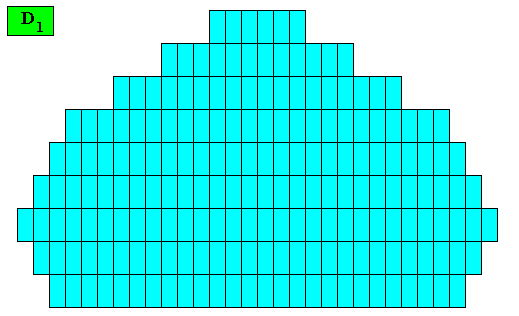
Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in a bilateral octagon. If the motifs (not drawn) in the building blocks have D1 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D1 . The growth rates of the eight faces are supposed to be such that they balance, resulting in the persistence of all of them.
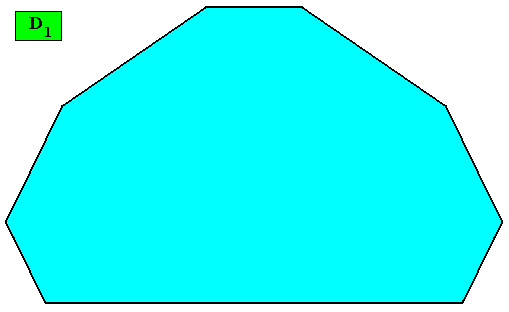
Figure above : Resulting crystal shape (bilateral octagon) from the above stacking of rectangular building blocks.
And with a possible Vector Rosette of Actual Growth added :
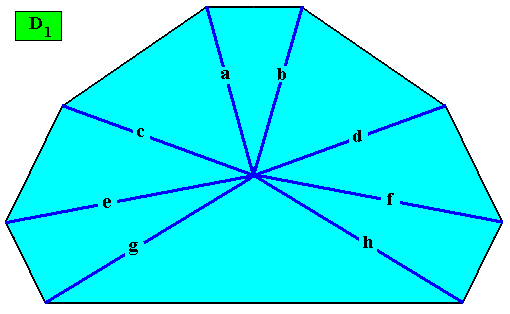
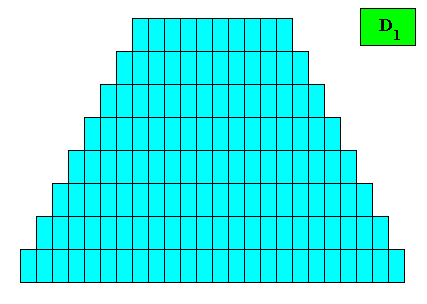
Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in an isosceles trapezium (bilateral tetragon). If the motifs (not drawn) in the building blocks have D1 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D1 . The growth rates of the four faces are supposed to be such that they balance, resulting in the persistence of all of them.

Figure above : Resulting crystal shape (isosceles trapezium) from the above stacking of rectangular building blocks.
And with its Vector Rosette of Actual Growth added :
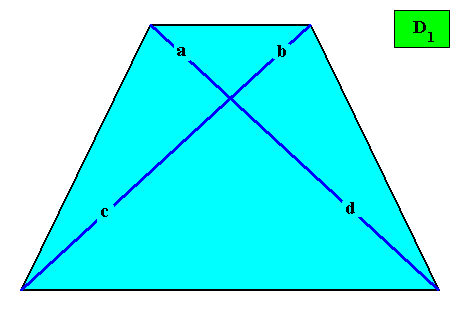
Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in an isosceles triangle (bilateral trigon). If the motifs (not drawn) in the building blocks have D1 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D1 .
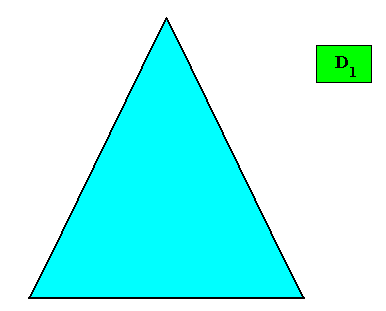
Figure above : Resulting crystal shape (isosceles triangle) from the above stacking of rectangular building blocks.
And with a possible Vector Rosette of Actual Growth added :
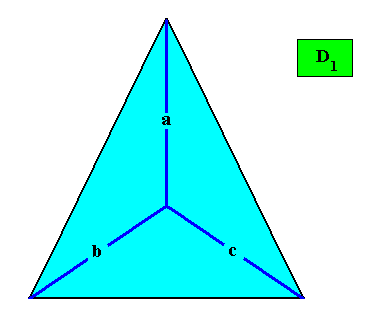
Figure above : Possible Vector Rosette of Actual Growth of the above depicted crystal. It indicates the presence of three antimers.
The next Figure adds the growth vectors (red) of the three faces of the above isoscelesly triangular crystal.
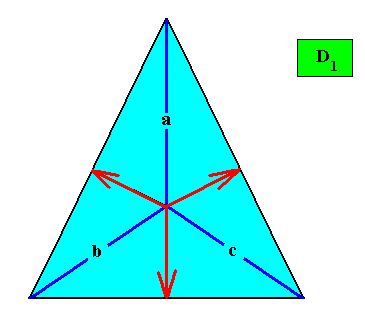
For the case of only two antimers the following Vector Rosette of Actual Growth can be suggested :
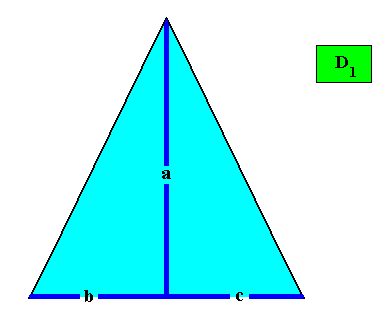
Figure above : A possible Vector Rosette of Actual Growth for the above depicted isoscelesly triangular crystal, indicating the presence of only two antimers.
The next Figure adds growth vectors (red) of the faces, growth vectors of which, in the present case, there are supposed to be only two.
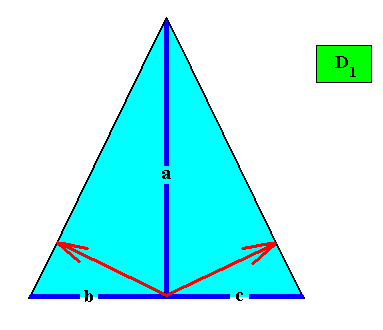
Figure above : The isoscelesly triangular crystal of the above Figures. It has only two facial growth vectors. The third face is just implied by the other two without actually having grown (in a direction perpendicular to it). See also next Figure.
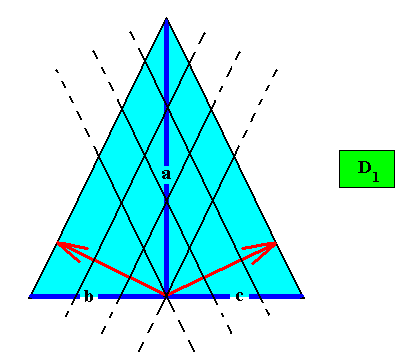
Figure above : In the present case the isoscelesly triangular crystal (D1 , two antimers) of the above Figures has grown two faces, while a third is automatically implied, without actually having grown from the center of the vector rosette. All this is a more or less symbolic way to indicate that the crystal has only two antimers.
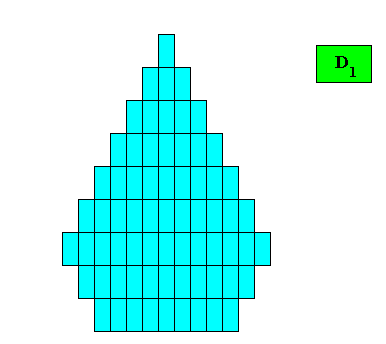
Figure above : Two-dimensional crystal built up from a stacking of rectangular building blocks, resulting in a bilateral pentagon. If the motifs (not drawn) in the building blocks have D1 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D1 . The growth rates of the five faces are supposed to be such that they balance, resulting in the persistence of all of them.
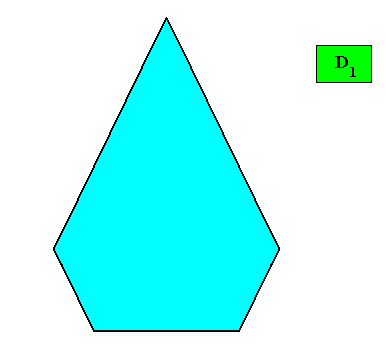
Figure above : Resulting crystal shape (bilateral pentagon) from the above stacking of rectangular building blocks.
And with a possible Vector Rosette of Actual Growth added :
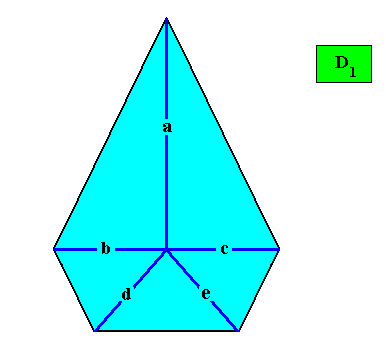
Another possible Vector Rosette of Actual Growth of this crystal could be the following :
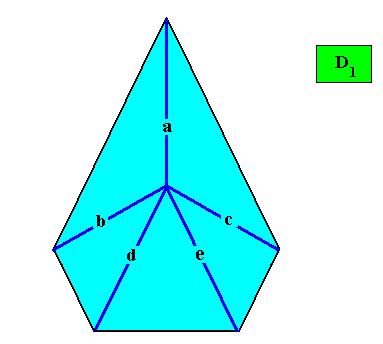
Figure above : Another possible Vector of Actual Growth for the above crystal (shape). The crystal has a vertical mirror line (as its only symmetry element) and thus the center of the vector rosette must lie on this mirror line. Where on this mirror line depends on the growth that has actually taken place in several directions from the starting point of the crystal, i.e. from the initial (microscopically small) crystal seed.

Figure above : Two-dimensional crystal built up from a stacking of quadratic building blocks, resulting in a regular gyroid ditetragon. If the motifs (not drawn) in the building blocks have C4 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group C4 . The growth rates of the eight faces are supposed to be such that they balance, resulting in the persistence of all of them.
This shape could also, and equivalently, be called regular gyroid octagon, because 'regular' and 'gyroid' already determine the nature of the octagon, namely that it is composed of two different squares (expressed by 'regular') -- and thus that it is a ditetragon -- that are superimposed upon each other and involving a rotation such that all mirror lines disappear (expressed by 'gyroid'). But because the term 'regular' is as such more or less vague, and because the term 'gyroid' is probably not so familiar, we prefer to call this shape regular gyroid ditetragon.
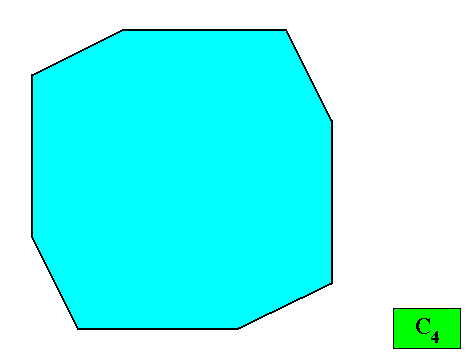
Figure above : Resulting crystal shape (regular gyroid ditetragon) from the above stacking of quadratic building blocks.
And with its Vector Rosette of Actual Growth added :
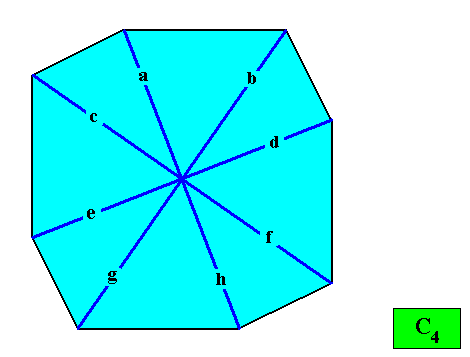
Figure above : Two-dimensional crystal built up from a stacking of quadratic building blocks, resulting in a regular ditetragon. If the motifs (not drawn) in the building blocks have D4 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D4 . As one can see, the depicted crystal shape is an octagon, but not a regular octagon (it lacks the equality of all its sides). According to the four-fold symmetry the number of antimers must be four, while the crystal has eight corners. So although the crystal is holomorphic (symmetry of shape is equal to intrinsic symmetry of crystal -- both D4 ), it is not eupromorphic. The growth rates of the eight faces are supposed to be such that they balance, resulting in the persistence of all of them.
Although this shape is an octagon, it is not a regular octagon, because the length of an oblique side is to that of a horizontal or vertical side as 4(square root)2 to 5 . It can be thought of as a combination of two different (i.e. differently sized) squares such that all existing symmetry is preserved. And this is what the term regular ditetragon expresses.
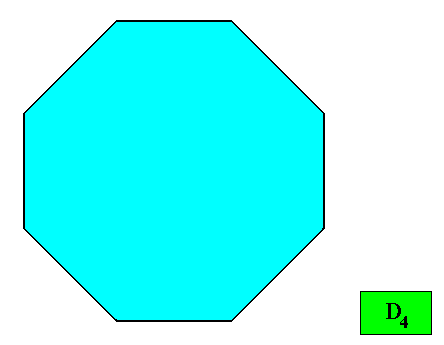
Figure above : Resulting crystal shape (regular ditetragon) from the above stacking of quadratic building blocks.
And with its Vector Rosette of Actual Growth added :
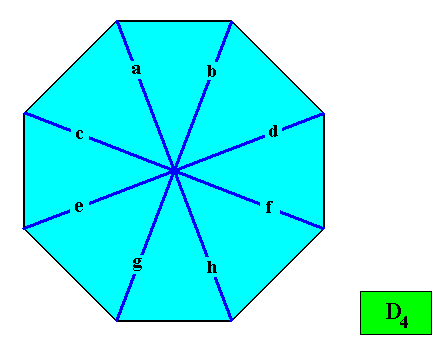
Figure above : The vectors of the Vector Rosette of Actual Growth are eight in number ( a, b, c, d, e, f, g, h ), but are only alternately equivalent, implying four (and not eight) antimers to be present, meaning that the crystal, although holomorphic, is not eupromorphic.
Our final crystal shape to be discussed is the Regular Gyroid Hexagon. But because of the same reasons as were put forward above with respect to the (term) regular gyroid octagon, we will replace the name Regular Gyroid Hexagon by the name Regular Gyroid Ditrigon, because this shape can be thought of as a composition of two equilateral triangles. We will construct it from a hexagonal lattice or net, consisting of the periodic stacking of 60/1200 rhombi. First we give the outline of an equilateral triangle consisting of three possible faces. After that we will obliquely cut off its three corners, resulting in Regular Gyroid Ditrigon. The symmetry of this shape is according to the group C3 , and we will assume that the intrinsic symmetry of the crystal is also C3 so that the crystal is holomorphic. But because a C3 object can only have three antimers (if antimers are present at all), the crystal is also eupromorphic. The next Figures show the derivation of such a crystal (shape) in several steps.
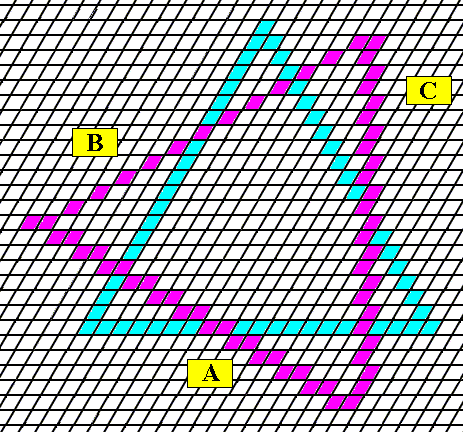
Figure above : Outline of equilateral triangle (blue) as it is supported by a hexagonal net. In order to construct the regular gyroid ditrigon the corners of the equilateral triangle are obliquely cut off, by a second equilateral triangle. The sides of the latter are indicated by A, B and C.
The next Figure shows that the angle between the faces A and B is indeed 600 .
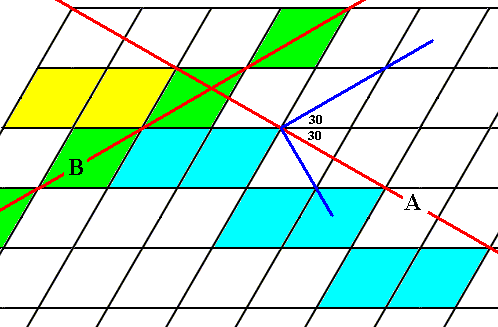
The next Figure shows that the angle between the faces A and C is indeed 600 :
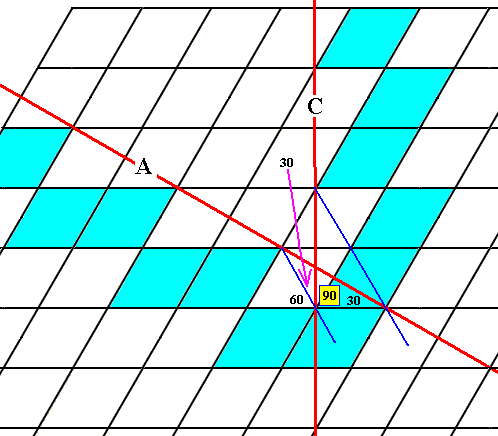
So the second triangle (which was) used to cut off the corners of the first is indeed an equilateral triangle guaranteeing the three-foldness to be preserved.

Completing the isolation gives :

Figure above : Two-dimensional crystal built up from a stacking of 60/1200 rhombic building blocks, resulting in a regular gyroid ditrigon. If the motifs (not drawn) in the building blocks have C3 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group C3 . The growth rates of the six faces are supposed to be such that they balance, resulting in the persistence of all of them.
The next Figure indicates the morphological outline of our C3 crystal with the intrinsic shape of a regular gyroid ditrigon.
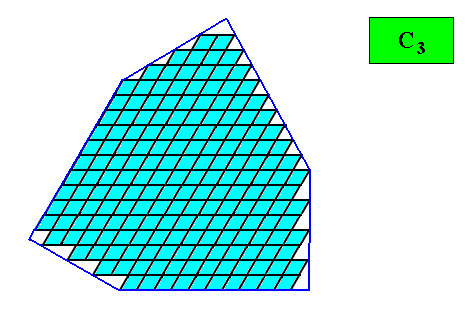
The resulting crystal shape is given in the next Figure :
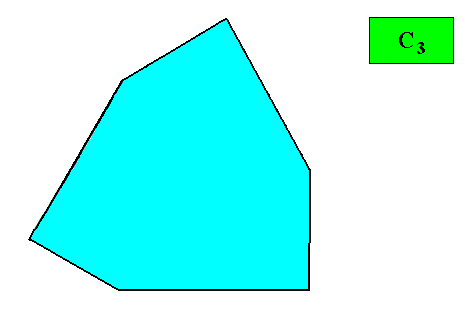
Figure above : Crystal shape (regular gyroid ditrigon) resulting from the stacking (as shown above) of 60/1200 rhombic building blocks.
An with its Vector Rosette of Actual Growth added :
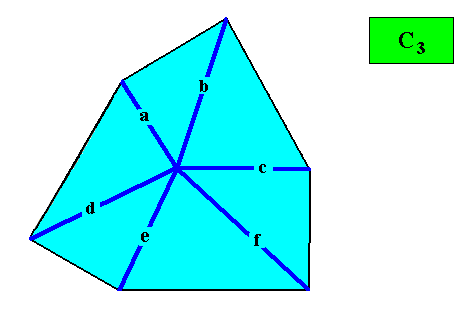
Figure above : Crystal shape (regular gyroid ditrigon) resulting from the stacking (as shown above) of 60/1200 rhombic building blocks. Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f added. The center of the rosette is fixed, i.e. only one location is possible, namely at the center of the figure, because of the presence of the 3-fold rotation axis.
Let us list the above crystal shapes (and include still one more to be studied) :
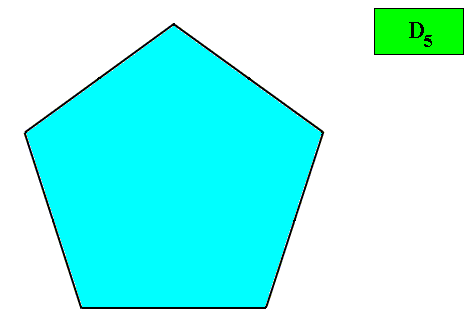
Figure above : Pentagonal shape (regular pentagon), which cannot result from any periodic stacking of building blocks, and cannot therefore occur in crystals. It does, however, occur (as promorph) in organisms.
An with its Vector Rosette of Actual Growth added :
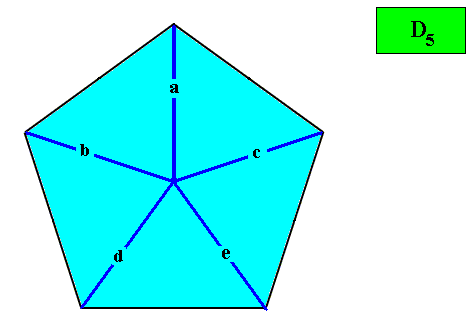
Figure above : The five vectors here are not vectors of crystal growth, but of organic growth.
The next Figure provides an organic example of a form of which the promorph is a regular five-fold pyramid (of which the base is a regular pentagon).

Figure above : Test of a regular sea-urchin (Echinoderms). One can clearly see its five-foldness.
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XV (2nd Sequel).
e-mail : 