General Ontology XXIXe

General Ontology Cosmos and Nomos

Theory of Ontological Layers and Complexity Layers

Part XXIX (Sequel-5)

Crystals and Organisms

Theory of intrinsic Shape, intrinsic Symmetry and Promorph

e-mail :

Back to Homepage

Sequel-5 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).

This document (Part XXIX Sequel-5) supplements the ontological discussion of the previous document. It tries to demonstrate the impetus of a material entity as a variable quality of that entity. If it succeeds we possess an important metaphysical indication that points to the existence of holistic aspects in Reality.
The following discussions are heavily inspired by HOENEN, 1947, in his wonderful book (written in Dutch) "Philosophie der Anorganische Natuur" (Philosophy of the Inorganic Nature). So full credit of these discussions is acknowledged to him. Another author I drew upon is Van MELSEN, A., especially with respect to his book Natuurfilosofie (Natural Philosophy), 1955 (written in Dutch).
The argument, as I have given it here, was not as such presented by the mentioned authors (or any other authors), but is compiled by me from their several considerations, and from additional ideas of myself.

Overview of the Argument

The argument, leading to the demonstration of the existence of at least one variable quality is structured as follows :

The first, and thus most fundamental relevant datum is the ens extensum (the spatial being, generally considered). Every intrinsic being is an ens extensum that is intrinsically one, and therefore a continuum, often a heterogeneous continuum.
The possibility of continua to be (mutually) penetrable is demonstrated.
Fundamental necessary general conditions are found for something to have a place (i.e. a position). From this the Contact Theory of Place (first contact, then neighborhood or distance) is developed, as contrasted with the Position Theory (first position, then contact or distance). The contact theory turns out to be the more plausible theory of place, distance and motion.
The Ether of Lorentz can figure in the contact theory as a universal medium of localization (placed ojects on the one hand, and ether on the other, are mutually penetrable continua). The medium of localization, precisely as medium of localization, is further specified ontologically.
Resulting from the existence of such a medium is the fact that place (and consequently motion) is absolute (though not as such objectively measurable).
A second argument in favor of absolute place, now without invoking an ether, is presented on the basis of the existence of absolute simultaneity as it turns out to be presupposed by the theory of relativity. It is argued that although the theory of relativity correctly demonstrates the fact that, even in principle, absolute simultaneity cannot be objectively measured, its existence is nevertheless presupposed by that same theory of relativity, in virtue of the assumed possibility of transformation with respect to different frames of reference that move with respect to each other.
From the established absolute simultaneity, absolute place and therfore absolute motion (i.e. asymmetrical relativity of motion) is derived, paving the way for demonstrating and characterizing the impetus of a moving body or particle as a variable quality of it.
With the demonstration of absolute place we have obtained yet another confirmation of the existence of some universal medium of localization.
Demonstration of the existence of an impetus, as a variable quality of a moving body or particle. The existence of such a variable quality in turn demonstrates the existence of holistic aspects of the fabric of Reality.

The complete argument, leading from the ens extensum to the existence of the impetus as a variable quality, will now be presented :

Ens extensum

With respect to the material world the subjectively and objectively first datum is the ens extensum , i.e. the spatial being, the spatial thing (whether it is a simple particle, a complex thing, or a physical field, and whether it is an intrinsic thing or aggregate). The term "ens" (latin) means "being" in the sense of " any (particular given) being insofar as it is being" . The term "extensum" stands for the english "spatial extendedness" (in Dutch : "uitgebreidheid").
The study of the general ens extensum (but then just) as extensum, and as extensum alone, is the province of Geometry. In the present document, however, we study the extensum as ens, and that means we are doing metaphysics.
Because of its primary nature the ens extensum cannot be defined, because every 'definition' of it will already contain directly or indirectly the concept of ens extensum (To see this, just try it!).
An ens extensum can come about in two varieties, viz. a contiguum or a continuum (and we have already shown that the latter can be heterogeneous).
An (ens) extensum is a continuum if it is intrinsically one. If it is not, then it is a contiguum.
In the previous document we have established that every given intrinsic being or ens per se, or, equivalently, every 'totality' -- which kind of being is, in what follows, the focus of the discussion -- is a (local) continuum, and in most cases it is a heterogeneous continuum. Our ensuing discussions will relate therefore to (physical) continua, homogeneous or heterogeneous.

Possibility of penetrable continua

The concept of extensum, and by implication that of continuum, implies the concepts of inside and outside. So, when not speaking metaphorically, only with respect to extensa (plural of extensum) we can talk of impenetrability of one body A with respect to a body B (which means that the body B must stay outside A), or of penetrability of a body A for a body B (which means that body B can go inside A).
Consider a moving body that meets another body, and collides with the latter (We here speak about central collision).
If they are mutually penetrable then they would continue their course, they fly just through one another. If, on the other hand, they are not mutually penetrable they are, when colliding, being deformed, resulting in so-called restoring forces (elastic forces) acting on them and changing their motion. So the primary cause of this change of motion is the impenetrability, and this entails an a c t i v i t y . What we see is that impenetrability of something (for something) has an effect on the situation and motion of another thing. And this is not possible without an effective cause.
From this we see that an extensum (and by implication a continuum) alone is, it is true, a condition for impenetrability, but it is not a sufficient condition, because it also demands activity. On the basis of this, the possibility of the absense of such an activity in or at an extensum is given, which means that there are no a priori objections against the existence of an extensum that is penetrable. This is an important result.

Place and Space

From the primary notion of ens extension some possibilities can be derived. In a spatial world (here we're not talking about space, but of a world of spatially extended things or bodies), which indeed is 'our' world, the capacity for contact is automatically given : two bodies can touch each other. They are then in each other's immediate neigborhood. They can touch a third body on either side (i.e. such that this third body fits exactly between the two other bodies). They then are at a certain distance from each other. If this contact changes continuously (i.e. when there is flowing contact) then there is motion. The general study of these relations is the philosophy of Place (in the sense of the location of something) and Space (the latter is a (further) derived concept, derived from the concepts that flow from the concept of ens extensum).

Place
We will now develop the concept of Place in the sense of where a given body is. It is clear that the place of a body A is, to begin with, the immediate vicinity of the body A. And for this the concept of extensum is presupposed. The body as well as its place must be an ens extensum. If this being in a certain place (and also change of place) is to be real, then not only the thing that is in such a place, but also the place itself must be real. And in addition to it the place must be something different, i.e. different from the thing that is in that place. So both the body and its place must be real material entities, and, as has been said, they must be different from one another. And in order for the place not to be just a general place (like me being in Athens, where also other people are, and which (place) could still be specified further, as to the particular street say), we demand that the place of a body is its immediate neighborhood.
But a genuine place demands still more : If this (immediate) neighborhood, as the place of a given body, changes (moves, resulting in its substitution by another neighborhood), then the place of that body would have become a different place, which contradicts our intuitive notion of the place of that body. So the place must be absolutely unmovable (immobile), or, generally, unchangeable. One might think of the equivalence of (1) the body moving with respect to its surroundings, and (2) the motion of these surroundings with respect to that body. But this only relates to equivalent mathematical descriptions, i.e. this only means that the mathematical descriptions are equivalent. Physically (and also metaphysically) these descriptions are not necessarily equivalent. And indeed we will see that they indeed are not equivalent.

Relativity of place.
In virtue of the foregoing findings, it is clear that to be somewhere is relative. For a body to have a place there must be another entity that is its place. If there were only one body or entity, it would not have a place. It would be nowhere, but existing nonetheless.
So the place of a body consists of a surface of something that immediately surrounds it, and which is immobile and unchangeable. And so place involves contact. We will later see that it is possible to find surroundings that are in contact with the given body more intensely, and in such a way that the place, like the body, is three-dimensional.

Contact Theory of Place
Now we can ask the following question : Suppose that two bodies are immediately adjacent to each other, and thus touch each other, or (as a second case) that they touch the opposite sides of a third body, and so are at a certain distance from each other. What then is primary : (1) Their situation of being maximally close to each other, (or) repectively, their being at a distance of each other, or (2) their mutual contact, (or) respectively, their contact with the third body (i.e. their contact as mediated by [contact with] the third body)? Or in other words, do bodies first of all have their position and then (as a consequence of that and of their sizes) contact, or do they first have contact and then position? Of course with "first.....then" no time order is meant. What is meant is ontological priority, order according to nature.
When we assign ontological priority to position, then space provided with some coordinate system is presupposed. But these have not yet been defined. Or (again considering this same case of position-first) we must assume that bodies having a place, have this in virtue of some innate quality, some innate position, which sounds at best dubious.
But we see that by what is already established so far, we can already define place (not needing to use the concept of space or of innate position : The place of a given entity A is constituted by its contact with an immobile entity, different from A. Indeed, in this definition there are no unintelligible notions. The definition is clear. So now we can legitimately say that contact comes (ontologically) first, and only then we have position. Because of certain contacts bodies have definite positions (relative to other bodies). And they have a place in virtue of contact with the mentioned immobile body or entity. This is the contact theory of place, i.e. a brand of localization theory. One will ask, where and what this particular immobile body is. Well it is, as we shall see, the ether of Lorentz, which will be interpreted as the one universal medium of localization (by contact), and it, as characterized by LORENTZ, perfectly fulfils the demands of the place (of any given body) to be real. And with this ether we can assign in an absolute way a uniform motion (where it occurs) to a given particle or, generally, to a given material body. And this directly entails that we can assign in this same way an impetus (which is the active cause of that motion, and will be discussed below) to that given particle or material body. And with the impetus we then have demonstrated the existence of at least one variable quality, which as such directly implies the existence of holistic aspects of the fabric of Reality.
Directly below we will discuss this ether as having this localization function, and work out the argument more fully.

Investigation of the contact theory.
Let us repeat : The ens extensum , or the spatial, necessary implies the capacity of contact, which in turn implies the possibility of place. And place is position. And position automatically implies the possibility of distance (including zero distance). Finally, smoothly changing place (and thus position) results in motion.
Let us consider some of these in more detail.
Two extensa, say, two cubic bodies can touch each other by two faces. They are then at a minimal distance from each other.
And now another case (which possibility is certain) : We have two such cubes, A and B, that are in contact with opposite sides (faces) of a rectangular parallelepipedum, C (i.e. a bar with rectangular faces) :

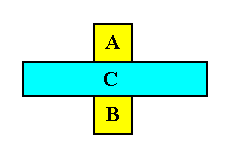
Again, it is immediately evident that from this double contact a distance results, which has the length of a face of the parallelepipedum, i.e. a distance between the contacting faces of the two cubes.

And yet another case is equally possible :

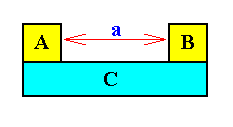
Two cubes A and B are in contact with a rectangular bar C, such that the two faces of the cubes, facing each other, are parallel. Again it is immediately clear that the mentioned faces of A and B (or there mid-points) have a distance from each other measured by the length a. This distance again results from the contacts.
Now let the contact of A with C be changing smoothly (also this possibility is immediately clear, and we can call it a flowing contact). Again it is clear that motion of A with respect to C results, and also, because there is indirect flowing contact, motion with respect to B. The distance from A to B becomes larger or smaller. Purely mathematically this motion can also be described such that the system BC moves with respect to A. Whether this (equivalence) also holds physically, will be looked at later.
Let us again consider this system of three bodies, A, B, and C. And let us suppose that no other bodies exist. Then between A and B there 'exists' an empty space of certain dimensions. But this 'existence' should not be taken literally, because space is not an ens, i.e. it is not a being, which is so because we had supposed only three beings (three entia) to be present. And that this space is not a being whatsoever, means that it is nothing. And a nothing cannot exist. So with this "empty space -- being nothing -- between A and B " we, in fact, mean the following : Between A and B we can place a fourth body (if available) with a maximum length of a . If this length is greater, then it cannot be placed (i.e. it cannot exist) between A and B, if it is smaller, then still an additional body can be placed there. Also this is immediately evident.
Also outside this 'three-body universe' an empty space 'exists' which potentially extends into infinity. But also this statement means the following : The number of bodies can be increased and brought into physical contact with the three bodies already present, and this potentially into infinity.
Indeed, all fundamental relations, that are found with respect to place, space and motion, are completely intelligible within the framework of the contact theory. And they are intelligible from the primary datum, the ens extensum or spatial thing (HOENEN, 1947, p.140). And, especially, these things remain intelligible when we advance the ether of Lorentz as a universal medium of localization (in our above example of a three-body universe the bar C could represent this ether, while the cubes A and B represent bodies that are in contact with this ether. And when we assume the contact with this ether to be total, i.e. such that the bodies are totally submerged in this ether, the contact is three-dimensional, because the ether is assumed to be penetrable for all bodies, the possibility of which was established above.

A possible difficulty of the contact theory, and its solution.
If we hold that indeed the contact between real bodies is the only source of local relations, then two bodies that neither touch each other, nor touch each other via some other body, or via a series of other bodies, will not relate to each other locally. They are then neither (minimally) near each other, nor at a certain distance from each other. One can say "the two bodies touch to nothing", but this only means "they do not touch something", and from these two negations one cannot produce a positive result. And, having no distance, they also cannot be at changing distances, implying that also motion with repect to each other is impossible, it is even senseless.
But this seems to contradict our intuition : In the space of our imagination we so easily place two completely separated objects -- this is in fact what the position theory expresses, as opposing the contact theory -- which then have a certain distance between them, a distance that can vary, implying the possibility of motion.
But before we jump to the conclusion that the contact theory is in trouble, we should analyse this matter still further.
What in fact is our intuition, our imagination, of space? Well, we see ourselves within a space surrounding us. And this space we experience as real, not as empty. It has to be traversed in order to reach out to something successfully. We cannot ignore it. An additional reason why we experience space as something real is the fact that we cannot imagine pure nothingness. Our intuition of nothingness always refers to things that are there, i.e. we refer to nothingness only with respect to the absence of certain things among other things that are present. So it is clear that we do not intuit empty space. Indeed our intuition of real space has much in common with the theoretical ether of Lorentz.

The position theory.
From the viewpoint of the contact theory a world of particles flying about in empty space is absurd, because each such a particle would be a world, and these worlds would not be in any sense interrelated. This is true when departing from the contact theory as the only intelligible way of seeing things, especially meaning that the position theory is not.
Let's investigate this position theory.
While the contact theory says : first contact, then position, which here means that position cannot exist without (existentially presupposing) contact, and with minimum distance (i.e. neighborhood) resulting from immediate contact and distance resulting from mediate (i.e. indirect) contact, the position theory says : first position, then either contact resulting from neighborhood, or distance.
Place (which in the position theory is called position) and motion can never be such that they exclusively involve only one body, i.e. involve one body in an empty space, while the whereabouts of all other bodies are totally irrelevant for the place and motion of that one body. As we have seen, and will show further down, a certain place and a certain motion can belong to just one particular body A, and not equivalently to all non-A, but this still means that a place always demands two entities, and so does motion. Given all this we can now formulate the position theory as follows : It assigns to every body a position, which is an intrinsic determination, accident or modality of such a body, resulting in a relation of the latter to other bodies or entities (that possess their own intrinsic position). This relation can then be either contact (resulting from neighborhood) or (a certain) distance.
If the possibility of distance between bodies embedded into an absolute vacuum, without mediate contact by (contact with) other real extensa, really exists, then, indeed, one should, in order to explain this possibility, resort to the position theory. But does such possibility exist? As we saw above, with respect to intuition or imagination, we cannot construct this possibility a priori. We do not and cannot intuit or imagine empty space.
We could, however, try a different construction.
Suppose two bodies that touch a third one on both sides. They then will be at a certain distance from each other measured by the dimension of that third body. Now suppose that this third body is annihilated while nothing else happens. Then, so one could argue, there is no reason why this particular distance should vanish. But this argument is false. First of all, in the beginning the contact theory was presupposed : from the double contact distance resulted. Then the third body was annihilated, whereby it was supposed that nothing else was changed, i.e. it was supposed that this annihilation did not entail other changes. But this cannot be, because when the third body is annihilated then the two contacts are also annihilated, which means that then the conditions -- as presupposed by the construction -- for the distance between the two bodies also disappear, implying the disappearance of this distance itself. Ans so no local relation between the two bodies exist anymore. So this construction, devised for the demonstration of the possibility of empty space, and a distance not based on contact, fails.
While the implication of the possibility of place or position and of motion by the ens extensum (i.e. by the presupposed presence of spatial entities) by means of contact, is totally intelligible, and as such expressed by the contact theory, the position theory must assume bodies with intrinsic positions, whose nature eludes us totally. But in spite of this such a theory could still be true. Or does it contain a contradiction? It does.

The contact theory wins.
Recall that we have found the following : From the content of the concept of ens extensum the possibility of contact between two extensa necessarily results. And this is completely intelligible. It is not just concluded from a broad experience, it can be concluded a priori.
If the position theory were right, then the possibility of contact would not directly result from the nature of the extensa (as extensa). From the latter would first follow intrinsic position (with respect to other bodies) and only then the possibility of contact or distance. Well, this could be so, but something else not. Possessing insight in the ultimate emergence of possible contact, namely via the link position, entails that we then also should possess insight of that link itself. But this insight is totally absent. So if this link really would exist we only conclude as to its existence on the basis of a broad experience. But then also our conviction of the possibility of contact were only based on broad experience, and nothing more. But, as we have seen, this is not so. The possibility of contact is a priori clear, as soon as the ens extensum is presupposed. It follows therefore that the link -- i.e. the intrinsic position -- does not exist, which in turn means that the position theory is impossible. Consequently we accept the contact theory.
The contact theory was first proposed by St Thomas Aquinas in the 13th century. It is further worked out by HOENEN, 1947, the result of which is reproduced here. But, remarkably, HOENEN found it more or less expressed by EINSTEIN (Forum Philosophicum I, 1930, p.173). He cites :

Ihm (dem Raume) geht die Bildung der objektiven Körperwelt voran. Ich kann Körper durch sinnliche Merkmale wiedererkennnen, ohne sie bereits räumlich zu erfassen. Ist in solchem Sinne der Körperbegriff gebildet, so zwingt uns die sinnliche Erfahrung dazu, Lagen-Beziehungen zwischen den Körpern festzustellen d.h. Relationen der gegenseitigen Berührung. Was wir als räumliche Beziehungen zwischen Körpern deuten is nichts anderes. Also : ohne Körperbegriff kein Begriff räumlicher Relationen zwischen Körpern und ohne den Begriff der räumlichen Relationen kein Raumbegriff.

(The italics are from HOENEN)

Let us translate this important passage into English, and provide it with some comments, placed between square brackets :

The objective world of bodies [which we can represent by the ens extensum] precedes it (space). I can recognize bodies by means of sensible features, without grasping them spatially [here meaning : without presupposing space]. When in this way the concept of body is formed, then sensible experience forces us to determine local relations between the bodies, i.e. Relations of mutual contacts. And what we signify as spatial relations between bodies is nothing else. So : without the concept of body there is no concept of spatial relations between bodies and without the concept of the spatial relations there is no concept of space.

Some might argue that this is all about concepts, but the reference to sense experience says otherwise.

The Ether of Lorentz
So it is safe to fully accept the contact theory concerning place, position, distance and motion. And this theory demands that the place of a body comes about by a region of contact of this body with another real entity that is unchangeable and immobile. And if we now ask ourselves what this immobile entity would be, we can say that the ether of Lorentz is a good candidate. It fulfils perfectly well all five conditions for a place of a body : (1) It (i.e. the ether) is (supposed to be) real, (2) it is (supposed to be) an ens extensum, (3) it is different from the body, (4) it makes contact with the body (the area contact is three-dimensional, because the ether is supposed to be penetrable by the body, the principal possibility of which was established above), and finally, (5) it is unchangeable and immobile. This ether was, although for other reasons, established and proposed by LORENTZ. HOENEN cites him from his The Theory of Electrons, 1909, p.10 :

One of the most important of our fundamental assumptions must be that the ether not only occupies all space between molecules, atoms or electrons, but that it pervades all these particles. We shall add the hypothesis that, though the particles may move, the ether always remains at rest.

From this statement of LORENTZ it is clear that his ether neatly fulfils the demands of place. And this we consider to be a fairly good indication of its actual existence. So although it cannot, it seems, make motion with respect to it observable, its existence as a medium of localization is now fairly well established.

HOENEN, pp.150, sets out to demonstrate that physical motion is not necessarily symmetrically relative, which means that although mathematically it makes no difference when we say A moves with respect to B, or B moves with respect to A, physically it makes a difference. However, he does this by invoking the ether of Lorentz, i.e. he presupposes the existence of this ether. We cannot accept this as a demonstration that motion is not symmetrically relative.

Fortunately there is a metaphysical indication that points to this asymmetry, when we consider uniform motion : When a particle moves uniformly (i.e. with the same velocity), no force is acting upon it (otherwise the motion becomes non-uniform). But motion is change, namely change of place. And, moreover, the body-moving-uniformly is something passive (and it should therefore, to express this, be called "body-being-moved-uniformly"). So there must be an active cause. But this cause cannot be a force. And it must reside either (1) in the body's surroundings, and then moving these surroundings (with respect to the body) or (2) in the body itself, and then moving the body (with respect to its surroundings), or (3) in both, body and its surroundings. I think it is fair enough to rule out the first and third possibilities, because they imply a large extension or realized expansion of this cause, affecting many many bodies or particles. So when a body is moving uniformly, it does so in virtue of an active cause residing in the body, not in the surroundings ( this active cause will later be identified with the impetus).
All this is at least some indication of motion not being symmetrically relative, without invoking an ether like that of Lorentz.

The contact theory, which we have found to be correct, demands an immobile and unchangeable medium as a medium of localization. And if we look for such a medium we see that the ether of Lorentz fits these demands. It is pervading all non-ethereal bodies, and so is indeed a medium for them, implying three-dimensional contact with every such body. It is permanently at rest (according to LORENTZ's hypothesis), which means that the place of any non-ethereal object immersed in this ether is immobile. It is the non-ethereal object that moves and therefore changes place.
However, this ether, in its function of universal localization medium, must be specified further, for its own sake as well as in order to assess the plausibility of its existence :

Ontological analysis of the Ether as universal Medium of Localization.
Every real full-fledged being can be considered to consist of Substance and Accident, or, in other words, of properties (accidents) plus that (substance) of which they are properties. If it were not so constituted, it would be difficult to consider it as real. The ether, if it is to be a medium of localization, must be a real being (as established earlier). So it must ontologically be constituted by substance and accident. But as such the ether can change, and would not be an appropriate localization medium. A way out of this dilemma could be the following : Precisely the 'naked' substance, i.e. its substance without accidents, i.e. that which remains the same during (accidental) change, is the medium of localization. This medium would not be real if it did not have accidents (properties). But it does have accidents. It is only that these accidents do not participate in the ether being a universal medium of localization. Only its substantial aspect does. That this, not seen as a being, but as an aspect of a being, is real enough can be illustrated by the substantial aspect of any ordinary physical body that is an intrinsic being. Let's take snowflakes. They all differ in appearance, even when grown in uniform conditions. Especially they differ in morphology. But their chemical composition is the same, and also their crystallographic symmetry (expressed by their Space Group) is the same. As was established in First Part of Website (Crystals and Metaphysics) the Essence of a single crystal is its Chemical Composition plus its Space Group (symmetry). And this Essence represents the substance and was called the genotypical domain of the given being, which here is a crystal. From this Essence flows part of the crystal's phenotypical domain, consisting of intrinsic properties, like the crystal's point symmetry, its electrical and other physical properties, and also its chemical properties. In addition to these properties the crystal also displays extrinsic features (constituting the other part of its phenotypical domain) such as resulting from irregular growth, caused by fortuitous irregularities of the growing environment.
This description should, however, be a little amended : In fact the mentioned crystal's chemical composition plus its space group symmetry -- because as such this is already a full-fledged physical structure -- already belongs to the crystal's phenotypical domain, the domain of the observable consequences of the crystal's Essence (its genotypical domain), and the latter can be identified with the particular relevant crystallization law (as dynamical law of a dynamical system, which is the growing crystal in its nutrient environment). It is this crystallization law that, as Essence of this particular crystal, cannot change, because in that case we would obtain a specifically different crystal (Realize that the Essence, insofar as it is this particular Essence, cannot change. Only the crystal can change, and when this change is a substantial change -- and thus not an accidental change -- we have to do with a specifically new Essence of the crystal. This could happen, for instance, when a given crystal metamorphoses its intrinsic structure as a result of change of certain external conditions like temperature and pressure.). In the same way the direct (phenotypical) consequences of the Essence of the crystal, for example the space group symmetry and point group symmetry as intrinsic properties (and only as intrinsic properties) remain the same, while other features like the particular shape and morphology that the crystal has actually taken up, changes, when say, ice crystals are concerned, from snowflake to snowflake. Of course the intrinsic properties could change, but only as properties, not as intrinsic properties of the initially given crystal, and then they become intrinsic properties with respect to another species of crystal, for instance, with respect to chemical composition, when Oxygen is replaced by Sulfur (at low temperatures), or, when its space group symmetry turns into another space group symmetry ( These are substantial changes, about which we spoke just above). But in a snowfall this does not happen. And it is this case we consider illustrative for something remaining the same within something that changes constantly. And the ether is now considered to be something that remains the same -- and can as such serve as a medium of localization -- within an ontologically broader entity that can and does change all the time. This ontologically broader entity, which as such must be a full-fledged being, is composed of (a particular) substance plus (its) accidents, intrinsic or extrinsic, and could, or even should be -- because a universal medium of localization not only demands just extension, but extension in and around all objects that obtain place -- some physical field. Maybe several physical fields are involved, that, however, ultimately unite to be one field after all, and the ether would then be that aspect of this field that remains the same. And this aspect will then consist of the (unified) field's Essence plus that what necessarily flows from it, i.e. that which is immediately implied by it, which is the set of intrinsic properties. What we observe however, is neither this Essence, nor the intrinsic properties insofar as they are intrinsic properties, but only actually existing features. The Essence plus intrinsic features does not change as long as the substance does not change, i.e. is not annihilated. This means that our unchangeable entity, demanded by the contact theory, is a theoretical construct, not a physical entity. And this goes someway to explain why the Michelson-Morley experiment failed to demonstrate it : Motion can only be measured when it is motion of a body, i.e. of an ontologically complete entity, with respect to another such body.
This interpretation, here presented, of the nature of the localization medium differs from that of HOENEN, because he maintains that this medium is a full-fledged substance, i.e. a complete being, its substance plus its accidents. We say that the medium of localization is only an ontological part of such a complete being. It is the theoretical construct (or, equivalently, the ideal entity) as outlined just above. And its reality wholly derives from the reality of the complete being of which it is an ontological part.
If our medium of localization by means of which a body obtains its place, were uniform and homogeneous, then every place would be the same, which means that motion with respect to this medium would be impossible. But our medium is not necessarily homogeneous. We have said that this medium of localization (insofar as it is a universal medium of localization), is the constant structure that is immediately implied by the Essence or intrinsic nature of the complete entity of which the medium is just an ontological part. And if we now assume that this constant and permanent structure is non-periodic (otherwise many places separated by certain distances are exactly the same with respect to local structure as well as to orientation), then our medium is a true universal medium of localization. It is an abstract heterogeneous continuum.
If there really exists such a universal medium of localization, then the place of a body is a unique place when it is related to this medium. But can a place really be unique, i.e. can we demonstrate this without assuming this medium ? Yes we can. We will derive it from absolute simultaneity. So the first thing we must do is to derive the latter :

The Theory of Relativity presupposes the possibility of Absolute Simultaneity.
What the theory of relativity demonstrates is that absolute simultaneity, when it occurs, cannot, even in principle, be m e a s u r e d. Observers, which are observing two events as to their simultaneity or non-simultaneity, will not agree about this when their frames of reference (each represented by a particular coordinate system) move with respect to each other with a high speed (approaching the speed of light). This, however, does not mean that, according to the theory of relativity as a theory of natural science, absolute simultaneity does not e x i s t, because then the following philosophical position (and thus not a result of natural science) has been smuggled in : That what cannot in principle be measured -- and thus cannot be observed -- does not exist. Of course that still doesn't demonstrate the possibility of absolute simultaneity, but it also doesn't disprove it.
Before we continue, we must elaborate a little more on the just given philosophical position. And to begin with, there is another philosophical position to which we like to adhere, the principle of intelligibility :

If something is not intelligible, then it cannot exist.

We will now show when the first mentioned philosophical position applies, and when it does not.
Suppose there is something of which we definitely (i.e. in the sense of direct intellectual insight) know that it has quantity. And suppose we can establish that this quantity cannot, even in principle, be measured, while this impossibility is neither caused by imperfect measuring devices, nor by fundamental physical constraints, but comes about by a cause within that entity itself, then such a something (i.e. this entity) is unintelligible. And, according to the just given principle of intelligibility, it then cannot exist. So in this case the first philosophical position --- not observable in principle ==> cannot exist --- is valid.
Indeed this position is only valid if the "in principle non-observability" relates to the object itself, i.e. to the object in question.
It is not valid when this in principle non-observability relates either exclusively to technical imperfections of the instruments (but this is aggreed upon by everybody), or exclusively to absolute, i.e. in principle, physical impossibility of observing and measuring, because here we can imagine cases where we know beforehand the presence of, say, a property (of something) by evident intellectual intuition, while this property is not observable because of fundamental physical reasons. And in such a case the philosophical position --- not observable ==> cannot exist --- does not hold. A simple example could be the following : Suppose that it is impossible, even in principle, by physical reasons, to position measuring devices such that they can inspect the rear side of the moon. Then we cannot conclude that the moon doesn't have a rear side, because we intuitively know, that the moon, being an extensum, i.e. a spatial thing, must necessarily have a rear side.

Let's continue with the problem of the existence of absolute simultaneity.
We should realize that we here are trying to determine something of the nature of time, not how it can be measured. What is then time? Well, we could, with ARISTOTLE, define time as follows :

Time is the numerable aspect of change (for instance motion) with respect to the before and after.

Let us supplement and elaborate on this definition.
Every change unequivocally determines an order of before and after. This temperal order does not exist apart from of the different changes, it is within these changes, but is not a privilege of some particular change or motion. When a given moment of one or another change (motion, or, generally, process) corresponds, i.e. is simultaneous, with a certain moment of another change, then all that precedes that moment of the first change, also precedes that same moment of the second change. And if the end of a given change coincides with the beginning of another change, then the whole order of before and after resulting from the second change, comes after the order of before and after of the first change. In this way all changes contribute to one and the same order of before and after in the whole universe. It is because of this that we are entitled to speak of one universal time, one universal order of before and after. This does not mean that time proceeds independently from change. What exists is nothing else than the order of before and after in concrete moving or changing matter.

The above given definition of time and also the just given elaboration on it, seems to be contradicted by the theory of relativity, especially the notion of simultaneity. But, there is a caveat here : While the philosophical definition of time admits of the possibility of the existence of objective and absolute simultaneity and therefore holds that there is just one universal time, the theory of relativity says, and rightly so, that absolute simultaneity cannot, even in principle, be measured. And, as has been said, it is now important not to jump to the conclusion that it then doesn't exist. On the contrary, absolute simultaneity, is, although not measurable, presupposed by the theory of relativity :
This is because in the theory of relativity the possibility of transformation is assumed. Transformation here means that the location (place) and moment in time of a given event, i.e. one and the same event in the universe, can be determined in more than one system of reference (coordinate system). And this means that observers in different systems of reference that move with respect to each other, all can observe and record this event, be it that they will find different values of place and time, at which this event takes place. Transformation formulae admit to express time and place as measured within one particular reference system to be expressed in terms of another reference system that moves with respect to the first one.
The ensuing argument, demonstrating that absolute simultaneity is -- because transformation is (by the theory of relativity) supposed to be possible -- presupposed in the described situation, was first given by Van MELSEN, A., 1955, Natuurfilosofie (written in Dutch). There is an English edition of this work -- not a translation -- preceding Natuurfilosofie : Van MELSEN, A., The Philosophy of Nature, 1954).

If we, for the sake of convenience, limit ourselves to two systems of reference, I and II, that move with respect to each other with a uniform motion (i.e. with constant speed), then the possibility of transformation presupposes that every event, recorded in I, can also be recorded in II. The transformation equations then exactly determine what the values of registration in II will be, when given in I, or vice versa. One can now express the presupposition, based on every transformation-possibility, also as follows : The two systems (which move with respect to each other) should be constantly in contact with each other (i.e. penetrate each other), otherwise not every event could be recorded in I as well as in II. This being constantly in contact, however, means that at whatever chosen moment of time all points of II coincide with certain (though unknown) points of I. After all, there must be a constant correspondence ( = transformation possibility) between the two reference systems.
Precisely the existence of such correspondence presupposes something with respect to time, still apart from its measurement. It is, namely, presupposed that at the same moment when, say, point P₁ in system I coincides with point P'₁ in system II, another point P₂ (in system I ) necessarily coincides with one or another point in system II. Otherwise the two systems would not be in contact with each other at that particular moment, implying that there does not exist any sensible application of the transformation equations. See next Figures.

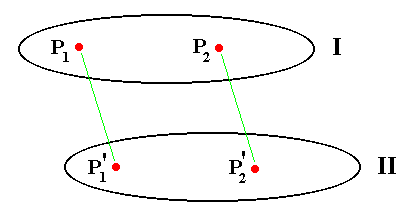
Figure above : Two systems of reference, I and II, moving with respect to each other. Both systems must be imagined to be extended indefinitely. See also next Figure.

The systems of reference (with respect to the assessment of place) should be understood as coordinate systems (For three-dimensional reality they must be three-dimensional) :

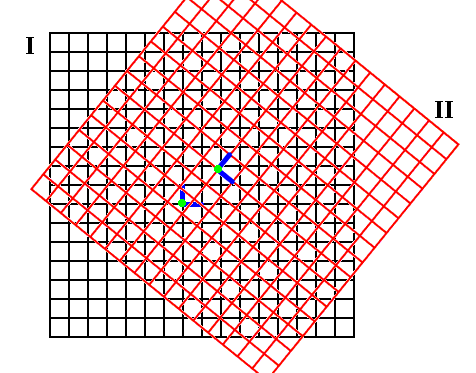
Figure above : Two systems of reference, I (black) and II (red), moving with respect to each other. Both systems must be imagined to be extended indefinitely. They are coordinate systems, each provided with an origin (indicated by a green point). From such an orgin the location of some object can be indicated (with two coordinates), i.e. it can be measured.

So the application of the transformation equations presupposes that at every given moment, let us say the moment that is marked by a certain event at point P₁ in system I, all points of I, whatever their distance is from P₁ , coincide with certain points of system II. And in this fundamental sense (and only in this sense) one can legitimately speak of absolute simultaneity. This simultaneity does not mean that clocks indicate a same point in time. It means that a given moment in time is not limited to one place, one point in a system. Or, expressed in other words : Absolute simultaneity, according to its fundamental philosophical meaning, expresses nothing more than the fact of the coexistence of the parts of the universe (Van MELSEN, 1955, p.236).
In fact, in virtue of the discovery of the presupposition, a simultaneity is discovered, that is objective (partly) due to the fact that the simultaneity was not found by means of signals (such as light). The simultaneity is, in this case, found in a direct way, and therefore it is absolute.

REMARK : In the above argument we considered two events that occurred simultaneously, viz., the coincidence of point P₁ of system I with point P'₁ of system II on the one hand, and of point P₂ of system I with point P'₂ of system II on the other. But these are not really events in a physical way. So one could conclude that the implied simultaneity is not of a physical nature either, and therefore not real. And thus the argument, which was supposed to be about real simultaneity, seems to be invalid.
However, I don't think that things are that bad. The systems of reference, I and II, of the argument, m o v e with respect to each other, making them enough physical for the argument to be relevant.
Moreover, we could tentatively add the following : Suppose that at the location and moment of the coincidence of point P₁ of system I with point P'₁ of system II, there happens to take place some physical event, and that at the location of our point P₂ of system I, while coinciding with point P'₂ of system II, there also happens to take place a physical event. Then from the fact of the simultaneity (here in the sense of [mathematical] coexistence) of the two coincidences (P₁ with P'₁, and P₂ with P'₂ ) it follows that also the two physical events took place simultaneously.

It is of great importance to realize that the above described presupposition (present in the theory of relativity, and based upon the supposed possibility of transformation) of the simultaneous coincidence of points of one reference system with those of another (that moves with respect to the first), does not mean that this coincidence can be objectively registered. To see this, let us analyse the following case :
Suppose we have two systems of reference, I an II, as described above, which uniformly move with respect to each other. If we take into account the possibility that the (constant) speed involved in this motion can be very high, i.e. can approach the speed of light, then the transformations that relate these two reference systems must be (according to the theory of relativity) the so-called Lorentz transformations for place and for time.
Suppose further (see this Figure above ) that at a certain moment point P₁ of system I coincides with point P'₁ of system II, while this moment of coincidence is recorded as t₁ . If we further, for the sake of convenience, suppose that system II moves in the direction of the x-axis of system I, then, with respect to the position of P₁ in system I only the x-coordinate counts. We suppose that, by measurement in system I, it is assessed that the involved coordinate is x₁ . And now, according to what has been said above, at the same moment when t₁ is measured, another point P₂ of system I will necessarily coincide with one or another point of system II. Let us call this point P'₂ . (a little later we say something about its position). The difficulty, now at hand, is that observers in I and II will not agree among each other as to which points P₂ and P'₂ of both systems will coincide at the time t₁ . The position of point P₂ of system I and with respect to I, at the time t₁ is measured to be x₂ . This point will coincide with a point P'₂ of system II. This point thus becomes identical to the point with location x₂ , but the location of this point as assessed within system II is different. It is different according to the Lorentz transformation of a coordinate. The new coordinate (x'₂) then is :

What we, until now, have is that the observer in system I maintains that point P₂ with the coordinate x₂ coincides, at time t₁ with a point P'₂ of system II.
However, the observer in system II sees the coordinate of the point P₂ as being not x₂ , but x'₂ (the value of which is given by the above formula). So they disagree about the position of the point P₂, and they explain this by maintaining that the measurement of the coinciding of the points P₂ and P'₂ was not done at the same time.
Observers in system II, that find themselves at the points corresponding with P₁ and P₂ of system I will maintain that their colleagues in system I at P₁ and P₂ did not assess the point in II, that coincides with P₂ in system I, at the same moment as that moment in which P₁ and P'₁ coincide. According to the observers in system II the time t₁ , that the observer in system I at point P₁ uses, has (according to the Lorentz transformation for time) the value :

while the time used at P₂ (by observers in system I ) according to them (i.e. the observers in system II) has the value :

So according to the observers in II these moments differ, and they conclude therefore that the observers in system I were wrong about the simultaneity of the two events, viz., the coincidence of P₁ with P'₁ on the one hand, and the coincidence of P₂ with P'₂ on the other.
The observers in I will, however, maintain that they have measured at the same moment. So according to them the coincidence of P₁ with P'₁ took simultaneously place with the coincidence of P₂ and P'₂ (Van MELSEN, 1955, p.236--237).

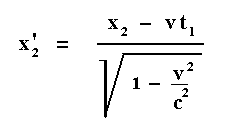
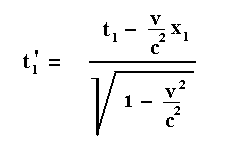
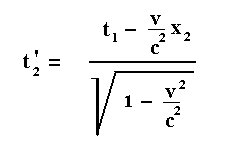
So indeed we see that the necessary presupposition of the existence of objective simultaneity, in the sense of being implied by every accepted possibility of transformation between systems of reference, namely that the places of one given coordinate system are continually in contact with those of another coordinate system, doesn't say anything about the possibility to actually and objectively measure this simultaneity.
There is no possibility to measure this simultaneity. And this is a true result of the theory of relativity. Therefore the concept of simultaneity does not make sense in natural science, but it does make sense as one of its presuppositions, and as such it is a truly philosophical concept.

So in our metaphysical (and thus philosophical) analysis of reality, which is a consideration of the way and status of Being and beings, we can accept the existence of absolute simultaneity.
And such a simultaneity implies the existence of absolute place (absolute position), because of the following reason :
If at location x₁ an event g₁ takes place, then a simultaneous event g₂ cannot take place at location x₁ . It can, however, in principle, take place at any other location (i.e. at any location which is not x₁ ). And this shows that the location x₁ is unique with respect to a given event. In the same way we can couple a different event to another point, say x₂ , and so on with respect to every point whatsoever. All this means that place is something absolute. And this means that we have found with all this a second indication of the truth of the contact theory ( The first indication was conceptual in nature, it drew from the concept of ens extensum). And after having established objective place, absolute motion follows as a consequence, because motion is continuous change of place.
As we have said, absolute simultaneity cannot be objectively measured, and so, consequently absolute place and absolute motion cannot be so measured. And that's why the outcome of the famous Michelson-Morley experiment was negative.

Now that we have, finally, established the absolute nature of time, place and motion (and knowing that they cannot as such be objectively measured, but are necessarily presupposed), we can turn to the phenomenon of the impetus . We will show that it exists, and that it is a variable quality (And all this is done to obtain, by means of the demonstration of the existence of at least one variable quality, another indication of the existence of h o l i s t i c a s p e c t s in the fabric of Reality).

The Impetus as a Variable Quality.
To demonstrate the existence of the impetus as a variable quality of a body or particle, we must start with the principle of inertia, which is a highly important principle of classical mechanics. In this principle uniform motion plays an important role, and that's why we will first define it. And we shall ultimately define it without involving the notion of time, because we want to let relate uniform motion totally to the body itself that moves uniformly. But let us first give a definition that does involve time :

The motion is uniform, if in randomly chosen equal time intervals, equal distances are traversed (HOENEN, 1947, p.287).

We shall now work towards a definition not involving time.
Suppose we have two bodies, say two metal spheres, that are moving in such a way, that they begin to move together, and end their movement together, or, if we do not want to involve the complexities of the starting and ending of movement, we consider just a segment of this movement, cut out out somewhere between begin and end. The motion of the two bodies is further supposed to be such that they always stick together, resulting in the fact that the motion of the one is an exact copy of the other. We will call these two motions congruent. That this is possible is immediately clear. It is also clear that these two motions can be connected to each other, end of first to begin of second, resulting in one motion. While the first case can be observed and verified easily, the second is harder to observe unequivocally. But here we're talking about concepts, and these are clear. The possibility of the second case results from the fact that the successive continuum, like the static extension, is, what could be called a principle of individuation in the following sense : It is immediately clear that a figure, that is here realized in an extensum, can also be realized in another extensum, or in another appropriate part of the same extensum, which means that congruent figures can exist. These figures only differ with respect to position, that is to say, they only differ individually or (equivalently) numerically. And the same holds with respect to the flowing continuum (dynamic continuum), which is motion (also in its broader sense of change). So evidently motions are possible that only differ in successive position, i.e. they only differ purely individually or numerically. These motions then are mutually congruent.
Well, what is valid for two (or more) motions, also holds for successive parts of one and the same motion. And again, evidently, a case is possible where two or more of these parts only differ with respect to successive position, i.e. they can be congruent. And this evidently holds for larger and smaller parts. So a motion is possible of which randomly chosen parts that are equal among themselves are, no matter how large or small they may be, congruent. The equality of these parts is defined by the equality of corresponding pieces of the trajectory. And such a motion we define as uniform. And then we can, now without circularity, define uniform motion by involving time (as in the definition given above ) : equal parts of time correspond to equal parts of a uniform motion.

Now the principle of inertia.
This principle, consisting of two parts, reads as follows :

If a body is not subjected to any external factor, then it will, if it is in a state of rest, remain in that state. And if a body, that is not subjected to external factors, (already) has a velocity, then it will have it continually, with the same direction and magnitude, i.e. also in this case it will remain in the same state of motion as it initially was. This motion, then, is uniform motion..

The first part of this definition of the principle of inertia, does not raise problems. But the second part does. First of all we will ( following HOENEN, 1947 ) argue that the principle of inertia is not an a priori principle, but in fact an empirical principle, i.e. it follows from and is confirmed by, observation.
The second part of the principle says that in the absence of external influences a moving body continues to do so with unaltered velocity. This means that its motion is along a straight line with constant speed, which we call uniform motion. But what does that exactly mean? And, specifically, what does it mean that the body moves in a straight line? We know that "motion" first of all means : motion with respect to another extensive entity (where motion is the continuous change of place). So motion along a straight line means : motion along a straight line residing in that other (extensive) entity. But this very same motion can, with respect to another extensum, be different, i.e. can be a motion not along a straight line. For example :
If we find ourselves in a uniformly moving train, and if we throw a ball straight up, it moves, first up (where it decelerates), and then down (where it accelerates), along a straight line. But to an observer outside the train (i.e. an observer that is at rest with respect to the railroad track), the ball does not move along a straight line, but along a parabola. And if the motion of the ball was uniform with respect to the train, it would proceed along a straight line also with respect to the railroad track. But if the motion of the train in this latter case was not uniform (the train accelerating or decelerating), then the motion of the ball with respect to the railroad track would be non-uniform. So when the principle of inertia speaks about a "linear uniform motion" one should indicate with respect to what other extensum this motion is linear and uniform. What extensum would that be? A partial solution of this problem was given by MACH (as HOENEN tells us), by demanding that the motion -- as described in the (second part of the) principle of inertia -- is along a straight line with respect to the world of the stars as a whole. And indeed the principle is then found to be true in the application of mechanics to the celestial bodies (Newton's theory of planetary motion). But then the principle of inertia is an empirical principle, and not a principle a priori found (to be necessary).
But still everything isn't yet allright.
If the uniform motion, as described in the principle of inertia, is ascribed to the combined gravitational influence of all the stars, in the sense that all these influences cancel each other, resulting in zero influence, then we already presuppose the principle of inertia. We don't know whether this net influence is zero. And if we nevertheless say that it is, we have already used the principle of inertia.
So, empirically, it is established that when a body is moving uniformly (and thus along a straight line) with respect to the world of the stars as a whole, it will keep on doing this, i.e. it continues this motion. And maybe it is reasonable that the net gravitational force is zero (if the moving body is not too close to some large gravitational mass). And so we have empirically (or one might say experimentally) found that when a body is moving uniformly, it will continue to do so if no (net) external forces act upon it. And this is, of course, the (second part of the) principle of inertia. So we now know, on the basis of extensive observations, that any material body obeys the principle of inertia. The question, however, is w h y it is obeying this principle. And this boils down to the question about the intelligibility of motion, which means that we want to know the cause of motion. Thereby we know that change of motion, i.e. acceleration or deceleration, is caused by a force, applied to the body, whether its motion is zero or otherwise. The motion is then changed from zero to some positive motion, or from a given positive motion to another positive motion. But motion itself, i.e. uniform motion, is, as such not intelligible.
Motion, and thus also uniform motion, is a certain kind of change, namely a (continuous) change of place. And motion as such is passive : a body is being moved. So, also in the case of uniform motion, it needs an active cause. And because, according to the empirically confirmed principle of inertia, uniform motion does not involve a force , the active cause, that sustains uniform motion, is not a force. Therefore the postulate of such an active cause, does not contradict the formulae of classical mechanics, because these formulae only concern forces and their effects. It does, however, contradict the current interpretation of classical mechanics. The latter says, that where no force is active, all active causes are excluded. It identifies all activity with force (where "force" is meant in its technical sense as cause of change of motion).
We will now dig a little deeper into the problem of the intelligibility of uniform motion.
Uniform motion is only partly intelligible :
We have two extensa, the body and the place. And we immediately understand that motion of the first with respect to the second is possible in principle.
Further, it is immediately clear that when a body passes point A, then, if it is to arrive at point C, it must necessarily pass some point B closer to A than is C.
But, when that body is in A, or is even in the process of passing A, it is not in itself (i.e. without any additional data) clear, that it will reach point B or C. We cannot say that because the body is now at A, it will be at B or C (or any other point) later. As the case stands, it will not be at B or C at all, because we only consider (i.e. we only have) motion, which is a passive phenomenon, and which means that we do not yet consider (i.e. have) an active cause.
Another reason that motion as such is not intelligible is the following : A body that moves, displays, because it moves, activity : If it collides with another body it exerts a force, if it carries an electric force, it causes change elsewhere, etc. So motion encloses, together with the passive 'becoming' of the motion, also an active capacity, and both are related to each other. Two aspects of this activity are important magnitudes in classical mechanics, viz., momentum (i.e. amount of motion) mv (where m is the mass of the (moving) body and v its speed), and the kinetic energy 1/2 mv² . Both aspects of this activity relate to the speed (v) of this 'becoming' with which they increase or decrease.
Now we can ask the following question :
Does the activity depend on the motion, or
does the motion depend on that activity, or
do both depend on a third, yet unmentioned, entity?
The first case supposes dependence of an activity on a purely passive 'becoming', which is absurd.
So it is the second case which we ought to adhere to [ The third case is equivalent to the second : Some cause causes the activity (for instance, the shooter causes the explosion of the charge of the bullet), and this activity in turn causes the motion) ].

Our result so far is that motion, also uniform motion, must have an active cause, in order for it to be intelligible (and thus in order for it to exist), while this cause is not a force (in its technical sense). But what then is this active cause?

In finding this cause we must adhere to the principle that there is no action at a distance. This is why in physics the field concept is introduced. Further, the active cause does not seem to reside wholly in the medium of motion, because it does not exert a noticeable influence onto other bodies as long as the moving body doesn't collide with them. So this cause must reside chiefly in the moving body.
So we have found that the active cause of sustained motion, as this motion is expressed by the empirically verified principle of inertia, lies chiefly in the moving body, and that this cause is not a force, but a quality. Further we have learned that when a force is applied to the moving body it accelerates if the force is applied in the direction of the initial motion, or decelerates if it is applied in the opposite direction. Such a force thus changes the speed, and consequently changes the momentum and kinetic energy which are the aspects of the active cause. So this active cause itself increases or decreases when a force is applied to the moving body, which means that this active cause is a v a r i a b l e quality of the moving body. And this variable quality as the active cause of motion (not the cause of change of motion) is called the i m p e t u s of the moving body. This impetus, thus, belongs (mainly) to the moving body, which implies that the motion of this body is asymmetrically relative (i.e. the impetus is asymmetrically distributed among the body and its surrounings whatever these surroundings may be). And this means that we cannot maintain that we could equally say that these surroundings move with respect to the body in question. And this asymmetrically relative motion demands a universal medium with respect to which the body moves, which in turn implies the existence of absolute place. And for this a universal medium of localization is demanded. And we found this medium earlier. It was the ether of Lorentz in the form of the theoretical construct given above .

So now we've finally found at least one variable quality, and this fact refutes all forms of Mechanicism (and probably also all forms of Reductionism) in their sense that ALL complex entities are mechanical, respectively reductionistic, i.e. totally reducible to simpler entities. This is because the increase of such a quality, such a variable quality, is not exclusively dependent on the increase of the number and of the arrangement of relevant particles or elements. An entity having such a quality, can acquire an augmented 'version' of this quality. This means that inner change of such a particle is possible, which is denied by Mechanicism.
Let us specify this a little more.
The total impetus of a body consisting of many particles of course increases when, while everything else remains the same, this number of constituent particles increases, say by accretion of additional particles initially outside this body. But this does not refute our position, because of two reasons :

The total impetus of a body consisting of many particles can also increase when the impetus of each constituent particle increases in the same degree, without the need to include more such particles into that body.
The smallest and most fundamental entities that can still be called particles, can, each for themselves, only increase their impetus by getting it replaced by an increased impetus, not by accretion of additional particles, because then the result (of such an accretion) is not a fundamental particle anymore.

So the existence of at least one variable quality is for certain.

In the next document we pick up our investigation of snow crystals again : Their significance for the holistic ontological theory is further examined.

e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX.