

e-mail :

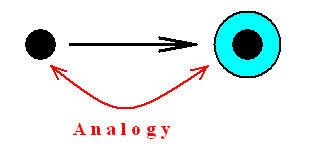
This document (Part XXIX Sequel-27) further elaborates on, and prepares for, the analogy between crystals and organisms.
Philosophical Context of the Crystal Analogy (IV)
In order to find the analogies that obtain between the Inorganic and the Organic (as such forming a generalized crystal analogy), it is necessary to analyse those general categories that will play a major role in the distinction between the Inorganic and the Organic : Process, Causality, Simultaneous Interdependency and the general natural Dynamical Law. This was done in the previous document. In the present document we will consider the category of Dynamical System. Thereby we have realized that Thermodynamics must be involved, and that, as a result, our earlier considerations of Causality may be in need of supplementation and amendment.
Introduction
The foregoing analysis of inorganic categories (previous document) did not consider actual ' t h i n g s ', i.e. the stable local dynamic patterns such as molecules, crystals, stars and the like. There it was about the continua, and with them the unlimitedness. Also the general simultaneous interdependency still has this trait. With the ensuing study of the natural (inorganic) dynamical systems this primacy comes to an end. They are the special cases of simultaneous interdependency. From now on we will consider the domain of bounded patterns, the domain of the finite, the domain of (intrinsic) things.
The (relatively) Stable Pattern (as subpattern and dynamic system, that stands out against the overall dynamic real-world background) as such must be understood in opposition to Process. It is akin to the State, shares its dissolvability in the process, but has the natural closeness and a certain constancy that distinguishes it from a mere state. A stable pattern is something that has external, but intrinsic, boundaries, an intrinsic shape, symmetry and promorph and an internal intrinsic structure. They are intrinsic beings. They are not being, but beings ( They were, by the way, the very subject of First Part of Website ). A thing is not necessarily an intrinsic being : An example of a thing, which (in this particular case) is definitely not an intrinsic being, is illustrated in the next Figure.

Figure above : Conglomerate. Found on the beach in northern Israel.
A pebble (length 3.6 cm) consisting of fragments of rocks cemented together. The fragments are not orderly distributed in the pebble. The latter once was a part of a larger formation, that had formed by deposition of coarse rock fragments. These (primary) fragments were once elements of a (geological) dynamical system. Later this formation of tightly cemented rock fragments was broken up again, resulting, not in these same fragments again, but in new fragments, each containing original fragments (i.e. the primary rock fragments mentioned above). Such a new fragment, eventually resulting in the one that is depicted here, came under the influence of running water (or blowing wind) itself containing many small but hard particles (e.g. sand grains) that have polished the new fragment, resulting in a smooth pebble.
It is clear that the external shape of this pebble is extrinsic, its causes were wholly external. Also its internal structure consists of irregular, randomly (with respect to the pebble and its shape) distributed primary fragments. There is no all-out intrinsic relationship between the pebble's (overall) shape and its internal structure. At most, only a few minor aspects of its internal structure have influenced its external shape. So it is clear, that although this pebble is a genuine thing , it is not an intrinsic thing, not an intrinsic being, but an extrinsic being. As it was found, it was an element of a dynamical system, which we could call "beach", but it is not itself a (complete and uniform) dynamical system. And as we know, certain other geological products can certainly be intrinsic things : crystals. If their individual development took place in a uniform medium, their internal structure fully determines their external shape. And that's why such a crystal is repeatable (i.e. it can originate again and again), while the pebble is unique, with respect to its (precise) internal structure as well as to its external shape.
An intrinsic being (or, equivalently, a dynamical system) has, as has been said, an external boundary and a shape of its own, it stands out from other co-ordinated beings and from its surroundings. It does not spatially or temporally fade out into something different. It maintains itself pretty well amidst the overall cacophony of the real-world flow.
Bounded area of simultaneous interdependency as dynamical system.
Much richer than the general simultaneous interdependency of the overall cosmos, is, therefore, the special simultaneous interdependency of the bounded intrinsic beings in themselves. At large distances this general simultaneous interdependency becomes vanishing small anyway. It is then a magnitude which can be legitimately neglected in considering local dispositions. On the other hand, in the narrow domains of limited but strong degree of interconnection, the simultaneous interdependency is the dominating factor. Here it condenses into a tight system of mutual conditioning. By virtue of the appearance of such domains, the special activity system -- the dynamical system -- rises up from the general simultaneous interdependency, rises up as intrinsic being. And with it also its special form of being distinguishes itself from the overall simultaneous interdependency as a new category. The name "dynamical system" means that here everything is based on the mutual force relationship of parts or members, and that consequently the unity and wholeness of this being is conditioned from within. The latter is also well expressed by the alternative and equivalent name "intrinsic being".
A mere state of a (local) process is just a simultaneity section. It hasn't duration. But if we look to the content of the state, its morphology, structure, etc., then, although in many cases the content also rapidly, but smoothly, makes place for another content, in many other cases a given content has a certain duration, that is to say, the content largely remains the same in a long sequence of consecutive states. Here either the (local) process runs slowly or its components sustain each other, resulting in a more or less constant overall structure or in a definite collocation of elements. Such 'states' (i.e. sequences of true states) do have a certain intrinsic resistence, in virtue of which they enjoy some stability.
The intrinsic being, characterized here as a more or less independent dynamical system, largely coincides with "substance + accidents" of First Part of Website . What we have here is some relatively constant substrate carrying properties that can replace each other.
Natural intrinsic dynamical systems (intrinsic beings).
When we call dynamical systems "intrinsic beings" they must be natural, which here means that their generation and their duration comes from within. So human artifacts, such a houses, spoons, and machines, are not intrinsic beings, because their generation and duration (maintenance) comes from without. On the other hand, a newly synthesized molecule is an entity that has generated itself on the basis of the properties of its constituents. What man has done in this case is just the setting up of the right conditions and then letting Nature do her job. But in a certain respect such a molecule is the product of the higher entity, the objective spirit, which has consciously intervened in the overall real-world process.
Although no one thing is truly independent, there are things (beings) that enjoy a relative independency with respect to the environment. Such a thing cannot, however, do without the environment, because with it it has to exchange matter and energy in order to be generated and sustained.
From all this it should be clear what kind of inorganic things are intrinsic beings. They are cosmic entities like stars, galaxies, spherical star heaps, and other more exotic entities. Further they are single crystals (sterro- and rheocrystals [i.e. solid and liquid crystals] ) and maybe things like raindrops, oildrops and flames, and other self-sustaining chemical systems ( like the famous Belousov-Zhabotinsky Reaction) (See for all this, First Part of Website, referred to earlier). In the organic domain the self-containedness of certain dynamical systems is even much more pronounced : individual organisms.
Dynamic boundary delineation in dynamical systems (relatively independent beings, intrinsic beings).
Knowing that the general simultaneous interdependency comprises all spatially co-existing entities, it is clear that the basic phenomenon in dynamical systems is that they draw for themselves a boundary of some kind at all, by which they contrast themselves against other co-existents. They mark themselves out 'against' the general simultaneous interdependency. However, they cannot do so by cancelling out the latter within their own spatial range. They do it rather by outstripping the broader active dynamical coherence that pervades them, by the force of internal connectedness. By virtue of this they contrast themselves from the overall wholeness in which they stand, as intrinsic things, without withdrawing from its broader connection with the rest of the world. They stay within it, while at the same time contrasting with it. They do not cut off the threads of the all-pervading overall simultaneous interdependence, but outstrip them as a result of the fact that their internal coherence, within the limits of its range, dynamically surpasses the coherence of the next higher whole.
So the marking out, or boundary, of a dynamical system is a function of its internal forces insofar as these oppose the dissolving influence coming from without. The external shape of such systems is thus not secondary, is not an extrinsic matter for them, but is eminently intrinsic. It is the essential shape for it, determined by itself, and maintained by it against deforming influences.
This phenomenon of dynamic delineation, of dynamic boundaries, as distinguished from merely material boundaries, is clear when one realizes that the boundary (delineating the system from its surroundings) in the majority of dynamical systems does not form sharp spatial surfaces, but that these systems spatially more or less fade out into their surroundings. This is, for instance, the case in all larger cosmic systems like galaxies and spherical star heaps. We cannot unequivocally indicate a sharp external boundary, and even when we could indicate with certainty the outermost members of such a (large cosmic) system, they would not form an external boundary, but rather be mere outposts of the system. The unity of such systems is only apprehensible from within, and only from a central zone outwards one can distinguish zones of lesser density (because when we want to start from the outside we wouldn't know where precisely to begin). In reality, however, this spatial sectioning is already based on an intrinsic dynamical coherence. In the mentioned cases this is the system's own gravitational coherence.
Perhaps one can say that solid bodies (which have definite surfaces as their boundaries) are more or less rare in the cosmos anyway. The large mass of matter in space is probably gaseous, be it extended in nebulas across large distances, be it condensed into spherical gas balls. Among the natural inorganic dynamical systems, perhaps only the (single) crystals can be considered to be solid bodies, sharply delimited with respect to the surroundings. When one, however, considers their complicated conditions of generation, involving special partial conditions in much larger systems, they also seem to be less independent. On the other hand we must realize that a crystal of the same species can be generated in a variety of (geological or chemical) conditions, making it possible to unearth the strict conditions (the absolutely necessary and sufficient conditions) of their generation, and then they turn out to be self-contained, that is to say they turn out to be genuine intrinsic beings.
In all cases of genuine dynamical systems, representing intrinsic beings, there always is a broader overall dynamic coherence that works through the given dynamical system and beyond it, but which is not as such differentiated within that dynamical system, because, although it is not neutralized, it is surpassed by the intrinsic coherence. The dynamical system only comes about by this non-differentiation (while at the same time developing it). That's why its external form is determined by its dynamic boundary zone.
For the overall coherence of the cosmos the effect of such dynamic delimitations -- also there where they occur in a relative way [the system becoming larger or smaller according to the degree of strength of the overall force field] -- is the division of the cosmic whole into dynamical domains or ranges, and with it the articulation of the cosmos into relatively stable closed beings (things, objects). The structure of the physical world is not based on the pervading continua only, also not on pervading lawfulness alone, but also essentially on the delimitation of closed beings. That is one of its basic rules. Delimitation and closeness are, however, functions of dynamic undifferentiation of the overall simultaneous interdependency inside dynamical systems ( HARTMANN, 1950, p.456 ). On this the primary discretion of the physical world, codetermining all the more special articulation, is based. The large mass of secondary systems rests already on the primary dynamical systems.
Yet another rule determining the structure of the cosmos becomes evident : The largest intrinsic beings, that originate in this way, are in no way always the highest. They are neither necessarily the most differentiated, nor necessarily the most stable. With respect to differentiation (internal diversity) the cosmos as a whole is an instructive example : It is built upon some few dynamical foundations, but already with respect to the structure of the Earth, although the latter is vanishing small as compared with the cosmos as a whole, the basic structure of the cosmos falls short. And even still higher forms of dynamical systems, but much smaller, can be found on the Earth's surface. Surely one should not conclude the other way around : Also the smallest intrinsic beings (dynamical systems) are not the highest, although enjoying a high degree of stability. The truly highest forms seem to lie in moderate orders of magnitude. For this the domain of organisms speaks for itself. But these systems are already not mere dynamic anymore ( HARTMANN, 1950, p.457 ).
General theory of dynamical systems.
With the dynamical system, especially with the "totality-generating dynamical system", we have -- as it was already found out earlier -- arrived at intrinsic beings.
While the states of a causal process as such, and even those of a regular causal process as such, can together form a continuously changing sequence without some specific content temporarily, but nevertheless definitely, enduring, the dynamical system, on the other hand, either is a local and finite unity, delimited from the overall simultaneous mutuality or interdependence, and as such being an intrinsic being, or generates one (or more) intrinsic beings. Anyway, the process, that we call "dynamical system" always involves intrinsic beings, while a causal process as such not necessarily involves intrinsic beings, because the states in such a process could be just fragments of intrinsic beings, or an aggregate of intrinsic beings. In the dynamical system the states are, or eventually become, a whole intrinsic being (when a dynamical system produces many intrinsic beings, we -- in our considerations -- concentrate on just one of them).
And with the dynamical system, and, by implication, with intrinsic beings, we have, in our theory of category layers, finally arrived at the category of Substance, in the sense of the Substance-Accident Structure of an intrinsic being.
We, accordingly, consider Substance in a different way than HARTMANN, 1950, pp.280, has done : While the latter considers substance not exclusively in connection with intrinsic beings, we do so consider it.
Substance in our view is that (having still content) what remains the same during (accidental) change of an intrinsic being, and which is at the same time a substrate (i.e. 'carrier') of those determinations that do not belong to the intrinsic being's essence. These determinations are collectively called 'Accidents'. And the Essence of such an intrinsic being is the physically interpreted dynamical law (and nothing else and nothing more) of the dynamical system which is or generates that intrinsic being.
So what we have done is interpreting the Aristotelian-Thomistic Substance-Accident structure dynamically (as also HARTMANN has done, but not in the context of the classical substance-accident metaphysics (Aristoteles, St Thomas Aquinas). As has been said this is fully developed in First Part of Website .
The dynamical system is a principle of discretion (in contrast to continuity) and of the finite. With this, one comes closer to the observable. Categories of the finite should be the preferred categories of sight (not necessarily that of the eyes alone) (Anschauung). But the domain of the finite is still an infinitely wide domain. Only a small section of it is given for observation and experience : as regards order of magnitude a section of moderate things. And exactly this section is almost entirely devoid of natural dynamical systems (intrinsic beings). It mainly consists of fragments, parts and artificial things, at least so when we do, for just a moment, not consider crystals and organisms. The latter are, or are products of, genuine finite dynamical systems. They have, what HARTMANN calls, a central core (in German : Inneres). And this central core we call the Essence of the intrinsic being.
In itself, observation and experience are more than anything geared to apprehend wholes. But these are only wholes of sight, of image, of impression, not of ontological structure. And nothing comes more close to the naive consciousness than to attribute to each and every thing a central core, and interpret such a thing as something that is independent. This consciousness bestows soul, and anthropomorphizes recklessly. But this bestowed central core is just something made up, not something natural, real and dynamical.
With respect to all this, we can say : Wholeness and Central Core are within the confines of consciousness hybrid categories (i.e. not pure categories).
The incipient understanding should first run down its copious proliferation, in order to arrive at ontological wholeness and natural central core. For naive consciousness is, in virtue of its 'thing-idea', almost exclusively about fragments and parts. It does not see the natural wholes. And where they are at last shown to it, it doesn't distinguish them as such. Anyway, the 'thing-consciousness' is only seemingly concrete. In fact it floats, without knowing it, over and above, and away from, the true diversity of things. It is blindly isolating and generalizing, and thus in this respect an abstract consciousness (i.e. abstractly apprehending things). Categorically expressed : Its wholes lack the central core that legitimately belongs to them, and of which these wholes are the outside, and this irrespective of whether they have it inside or outside them (i.e. whether the wholes, as seen by naive consciousness, have their true central core within them or outside of them). In short, the viewpoint of the dynamical system is lacking in naive consciousness.
The inorganic world shows us a hierarchical system of dynamical systems, that is to say, the elements of a given dynamical system can themselves be dynamical systems, while the given dynamical system can be an element of a still larger dynamical system.
The elements of a dynamical system are, seen in a first approximation, the passive carriers of the system as a whole of which they are elements. They indeed play here the role of 'matter'. Their function in the system is as such a dynamical precondition. But this does not exhaust them, for they become, as existing within the system, its 'members' with a specific function. And in virtue of this 'member function', which they do not possess all by themselves (i.e. do not possess in virtue of what they are in themselves), they become something different from what they were. So the atom in the molecule, the atom in the crystal, the molecule in the raindrop, have different functions as when existing in isolation. So also the planetary body in the solar system, the star in the system of a star heap, etc. Whether the element also occurs freely or not, is initially immaterial : It is not the literal 'addition' of the member function that counts, but only the dynamic origin of this function in the system.
The member function of the element contrasts with its matter function. As matter it determines the system (of which it is an element), it therefore is a determining factor, albeit a subordinated one. As member, on the other hand, it is determined by the system as a whole and is subject to the centralized determination of the system.
HARTMANN, 1950, pp.457 discusses the internal dynamics and stability of dynamical systems.
However, since 1950 a great deal of work is done and discoveries are made in dynamical systems, especially in the context of the modern chaos theory. So we here temporarily leave HARTMANN, and turn to these relatively recent considerations. But this is already extensively done in First Part of website , so the reader should, if necessary, consult the many documents on dynamical systems, where they are largely explained by means of computer simulations (Cellular Automata, Boolean Networks, L-systems, etc.).
One of the documents there gives a general exposition of dynamical systems and their ontological status, especially with respect to the Substance-Accident structure of intrinsic beings : Non-Classical Series, "Metaphysics and Dynamical Systems".
Because its considerations are highly relevant in the present context, we reproduce it here in full [with some extra indications between square brackets] :

But to clarify and deepen those observations we need something to know about DYNAMICAL SYSTEMS. Of course that means : natural dynamical systems, i.e. concrete, material, physical or biological systems. We shall discuss them. But we must emphasize that those natural systems are generally very complex, and only partially understood, especially the biological ones. Therefore we shall concentrate our expositions on abstract dynamical systems in the form of computer simulations. Which in fact means that when we discuss real dynamical systems, we are inspired by those abstract systems. Such systems are fully defined, and because of that better understood. Maybe they can supply us with the proper concepts needed for a revised Substance-Accident Metaphysics. We must thereby keep in mind, however, that those simulations are relatively simple and are not able to supply all the concepts needed.
By means of the study of dynamical systems we hope to find out more about the status of Substance, Accident, Essence, Individual, the per se and the per accidens. Maybe we can do this by means of conceps like Dynamical Law, System State, Initial Condition, System elements, Attractors, Phase-portraits, Attractor Basin Fields, Dynamical Stability, and so on, which in fact means the following : an ontological interpretation of those concepts.
"Ontology " means here : The study of Being as such, the way of being of an individual thing, the status of being of the Essence, the status of being of the Universal, the status and way of being of properties in relation to Substance, the status of a process in terms of being or becoming, etc.
A DYNAMICAL SYSTEM is a process that generates a sequence of states (stadia) on the basis of a certain dynamical law.
Such a dynamical law, together with a starting-state (initial condition) is already the whole dynamical system.
When the system states together form a continuous sequence, the dynamical law will have the form of (i.e. will be described with) one, or a set of, differential equations, which describe, and dictate as a law, the changes of one or more quantities in time (and in space), and so (describe and dictate) the continuous sequence of states.
When, on the other hand, those states together form a discrete sequence, then the dynamical law will express a constant relation between (every time) the present state and the next state, and this relation is of such a nature that no infinitesimals are involved (in other words, the differences between successive states are nowhere infinitely small).
Every process state (system state) is a (certain) configuration of, ultimately, system elements , which (configuration) is generally different with each successive process state. The dynamical law according to which those configurational changes proceed, is immanent in the (properties of the) system elements (For where else should it be seated?). The changes in the element configuration, and so also the (implied) succession of process states, is the effect of (i.e. is caused by) interactions between system elements (In such a process it is possible that some system elements disintegrate to other elements or form compounds with other elements, and then those products will interact with one another). These interactions are the concrete embodiment of the dynamical law in action.
The changes of configuration could be such, that we can (after the fact) speak of SELF-ORGANIZATION of the system elements towards a coherent stable PATTERN. This pattern can be a final configuration of the system elements, to which the system clings, i.e. never leaving this configuration anymore. But the above mentioned pattern can also be a dynamical pattern, which also is coherent in itself, but which moreover alternates in a regular and coherent way.
Both cases of self-organisation can be interpreted as the formation of an organized whole, and this we will call a Totality (in all cases of real systems, that means a Uniform Being ), especially when the generated (dynamic or otherwise) pattern shows an intrinsic delimitation (a boundary) with an environment. When this all happens we speak of a Totality-generating dynamical system.
An ontological interpretation of a macroscopic Totality (a uniform thing) in terms of dynamical systems will proceed along the following lines :
We will first of all presuppose (the presence of) a Totality-generating dynamical system.
The process stadia of such a system now imply the corresponding process
stadia of the Totality. A process stadium of a Totality is the ' Here-and-now Individual ' -- we can call this also : the Semaphoront -- while, all those stadia taken together, form the ' Historical Individual '.
Generation of a Totality means that the system elements, or a part thereof, together form a coherent whole, a totality-resultant of the dynamical system, coherent, either in space, or in time, or in space and time, and having an intrinsic boundary with an environment. So not just any (arbitrarily chosen) process (dynamical system) generates a Totality. Especially for abstract ' dynamical ' systems -- which are moreover just simulations of dynamical systems -- applies the following : They cannot supply all the revised metaphysical concepts, needed for the establishment of a revised Substance-Accident Metaphysics. The dynamical systems that are involved in the generation of full-fledged Totalities thus have some special properties.
Every process stadium is a certain configuration of system elements and can be considered as an initial state , meaning that the system will be observed from that state onwards.
The real , actual (= ' historical ') initial state also is a configuration of system elements, but as configuration it originates from outside the system. It could even be a configuration which in principle cannot be generated by the system from other configurations (i.e. from other states). Such an actual initial state can also be random (i.e. a random arrangement of elements, or / and random states of the elements themselves). But the system can transform this random configuration, once given, into a (following) PATTERN (= a not-random configuration), and in turn into a next pattern, etc., and so leading to a sequencing of patterned process stadia. In other words the system is then able to organize the constituents into a real pattern. The elements (constituents) are going to take part in (the formation of) a Totality. The sequence of process stadia, taken as a whole, also can be considered as a pattern when it gives a reason to do so. But a real Totality is only formed when such a pattern has a, for the system intrinsic, boundary with an environment.
A local, individual action originating from the environment, thus coming from outside a running dynamical system, can be considered as a perturbation of a current process state. The perturbation then creates, as it were, a new initial state with respect to that process.
The relevant properties of the constituents (the system elements) of that process determine the nature of their interactions. Thus that which determines those interactions as such and such (a way) taking place, is immanent with respect to the constituents. The whole system, and thus the whole process, is further constrained by the general (global) state of the environment and thus by the general nature of physical matter, described by Natural Science in the form of general -- i.e. everywhere operating -- Natural Laws. These global (i.e. operating on a global scale) Laws of Nature are immanent, i.e. inherent in the general properties of physical matter.
The mentioned -- (mentioned) with respect to the taking place of the interaction process -- relevant properties of the system constituents can also in this non-global case -- thus in the case of a special process, taking place somewhere, generating a Totality -- be interpreted as a law, namely the law that is valid for specifically that (type of) dynamical system : The Dynamical Law. This law is, as has been said, immanent in the relevant elements of the system. The pattern, i.e. the arrangement -- at a certain point of time -- of these elements is extrinsic with respect to that Dynamical Law. It even could, as have been said, be an arrangement (configuration of system elements) which cannot even in principle be reached by the system itself from whatever initial condition. Such an unreachable state, which as such can only originate from outside the system (= from outside being imposed on the system), is called a ' Garden of Eden State ' of the system (Theoretical models learn that many systems each for themselves have a large proportion of such Garden of Eden States). Such an unreachable configuration (of system elements) either is a real starting state of the dynamical system (i.e. the system happened to start just with such a configuration), and so is coming from outside the system, or such a state is the result of a perturbation, which took place at some point in time during the running of the system, and so is also coming from outside the system, a perturbation of a process state (situated) higher up in the sequence. Thus by actions from outside, a current process state, itself also being a configuration of system elements, can be changed, resulting in a new, i.e. other, configuration of system elements, which then functions as an initial state with respect to the further history of the process.
So a dynamical system implies a number of types (meanings) of : " outside the system " :
Before we explain these two ways, something must first be said about the status of element :
With " elements coming in from outside the system (and therefore quasi elements) " I mean elements which are not imported by the dynamical system itself, but which, by accident end up within the active domain of the system. If a Totality, or more generally, a pattern (of a higher order than that of the system elements themselves) is being generated within the active medium of the dynamical system, then it is possible that the elements belonging to that active medium, as well as possibly elements coming from without (that active medium), are going to participate in the formation of the Totality (the unified pattern, being generated by the dynamical system). The insertion into that Totality, in this last mentioned case (elements coming in from without), does not happen by virtue of the Dynamical Law of the relevant dynamical system, but is a perturbation from without. The present context is concerned with the effect of elements-coming-from-without on the stability of the dynamical system.
Now we are ready to discuss the above mentioned two ways by which the system tries to maintain itself :
If a given real dynamical system generates a full-fledged Totality, for instance (generating) a crystal from a solution, then this Totality is a Substance (in the metaphysical sense of the term), more specifically, it is a First Substance.
The Essence or (ontological) Second Substance, is the Dynamical Law of such a system.
All the observable properties of such a Totality are generated by the system. These properties are called Accidents (although they do not all have a status of 'generated by accident' ), and will be all kinds of quantitative properties like length, volume and the like, but also qualitative properties like configuration (which can end up as colors, densities and the like).
All these observable entities, the First Substance and its properties, are, as has been said, generated.
Borrowing terms from Genetics, we could say that those generated entities are seated in the 'phenotypical' domain (a domain of being, a way of being), while the corresponding Dynamical Law is seated in the 'genotypical' domain (another domain of being, another way of being). We discriminate between these domains, because the Dynamical Law as such is not observable. It abides in the collection of system elements, i.e. it is dispersed over those elements, without being the same as those elements because it is only dispersed over some (not all) aspects of every system element. Therefore the Dynamical Law is neither a thing, nor a property. It is abstract.
The First Substance and its properties are, on the contrary, concrete and directly observable.
The mentioned accidents belong to that first substance of which they are accidents. Some of them belong to it per se, others only per accidens.
All those accidents together make up the first substance [NOTE 2]. They can only exist as a first substance. They cannot exist on their own, because they are, each for themselves, just a determination of a first substance.
Remark : A different initial condition does not correspond to a different settling pattern in a per se manner. So, often a certain set of different initial conditions exists, each member of which bringing the system to the same settling pattern. But such a set need not be the total set of possible initial conditions with respect to the system.
The total set of states, belonging to, and arranged according to, all possible trajectories, all leading to a certain attractor, say attractor A(1), forms, together with the attractor states themselves, the basin of attraction of the attractor A(1) (analogous to all the rivers that drain a certain area and all end up in the same lake).
The total of all possible basins of attraction belonging to (i.e. corresponding to) a certain dynamical system is called the phase portrait (this term is used in the case of continuous systems) of that system, or the attraction-basin field (term used for discrete systems).
The attraction-basin field represents all possible systemstate-transitions of that dynamical system, and is, in a way, equivalent to the Dynamical Law of that system.
The Dynamical Law is the system law (seated) at a low structural level, while the corresponding attraction-basin field is this same law, but now (seen) from a global structural level.
There exist dynamical systems, for instance abstract Boolean Networks (and their real counterparts), where the dynamical behavior depends on a whole set of dynamical laws, but which nevertheless have only ONE attraction-basin field. It seems reasonable to interpret this attraction-basin field as THE (one) Law of the system, and so also as the Essence of the Totality (when a Totality is indeed generated by the system). But of course the mentioned set of dynamical laws can also be interpreted as THE (one) Dynamical Law and so as the Essence of the (generated) Totality.
Just the set of all possible system states corresponding with a certain dynamical system is called the phase-space (term used for continuous systems) or the state space (term used for discrete systems) of the system. The system thus organizes its state-space into (a relatively small number of) basins of attraction, the attraction-basin field, by establishing all its possible state transitions (which means that the possible states are now related to each other in a specific way). And so the dynamical system ' categorizes ' the state-space and because of that the resulting attraction-basin field can be considered as the ' memory ' of the system, especially when such a system is a Boolean Network. A Boolean Network is a discrete dynamical system with only two-valued variables. Such systems constitute a possible basis for the study of genetic and neural networks (See the Essay on Random Boolean Networks [ First Part of Website, Non-Classical Series ] ).
The above given interpretation of the notions Totality, Identity, Essence, Here-and-now Individual ( Semaphoront ), Historical Individual, etc. is inspired by the study of simple abstract models of dynamical systems (in the form of computer simulations), which pretend to represent processes, and aspects thereof, in the Real World, especially those processes which show self-organisation of system elements towards stable coherent patterns. Such are for instance crystallisation processes and ontogenetic processes (the last mentioned are processes relating to the formation of an individual organism).
But we must realize that we, in proceeding along these lines, make use of formidable simplifications of natural real processes (natural real dynamical systems), resulting in such models, i.e. reducing them to such models. This is, according to me, inevitable because the processes in the Real World generally are much too complex and much too strongly interweaved and intertwined with other processes, as to allow directly from them (i.e. them serving as a theoretical point of departure) a definitive ontological interpretation of such Totality-generating processes. The models must be part of the point of departure of such an attempt to an ontological interpretation.
In the present context (theory of category layers) "dynamical system" is a general category ( If / Then constant) of the Inorganic Layer : Every concretum in this Layer is determined by it : Everything in the physical domain is either a dynamical system (or more of them), or is a fragment of one or more dynamical systems. Only a being that is one single dynamical system is a genuine intrinsic being.
|
About the Analogy between Crystals and Organisms (or, more generally, between Inorganic and Organic) ( Analogy and Over-forming ) |
|
It is perhaps useful to remind the reader whereto all this is supposed to lead. |
| Let us symbolize the phenomenon of over-forming by a 'core' ( = that which becomes overformed) which is 'clothed' by something else ( = that which overforms the core) :

With this phenomenon of over-forming a fundamental difference, viz., the difference between that what becomes over-formed and that which is the result of the over-forming, is involved.
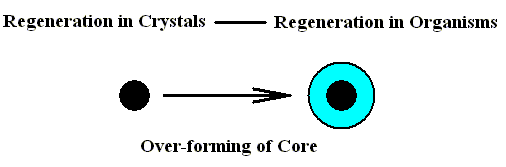 The common possession of the categorical core,  , in category change, i.e. over-forming, is assumed by HARTMANN only for all general categories that he has established for the Inorganic. All other new features that appear in the domain of organisms he assumes to be determined by n e w categories, not occurring at all in the Inorganic. So HARTMANN is expected to deny any more or less far-reaching crystal analogy (and, more generally, any far-reaching Inorganic-Organic analogy), which can be symbolized by : , in category change, i.e. over-forming, is assumed by HARTMANN only for all general categories that he has established for the Inorganic. All other new features that appear in the domain of organisms he assumes to be determined by n e w categories, not occurring at all in the Inorganic. So HARTMANN is expected to deny any more or less far-reaching crystal analogy (and, more generally, any far-reaching Inorganic-Organic analogy), which can be symbolized by :
 With respect to categories determining specifically organic (but still general) functions or structures (but not with respect to the categories 'Causality', 'Simultaneous Interdependence', and other such categories), HARTMANN in fact does not hold : 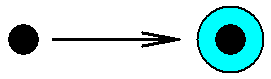 , ,  , ,which means the appearance of a totally new category, determining such an organic function (or structure). |
|
As has been said, according to HARTMANN all categories of the Inorganic (as established by him) pass over into the Organic. No one of them breaks off. But in doing so they are modified, i.e. they are over-formed, as a result of the presence of the organic NOVUM. Surely, the NOVUM itself is a new category, but (in contradistinction to a new category that is the result of over-forming) one that has originated as a result of a fortuitous (and therefore irrational) fluctuation of an existing category, as explained earlier. |
|
Some -- maybe all -- organic functions can be simulated. This means that they can be 'mimicked' with inorganic means, which can be certain (laboratory-based) chemical reaction systems, but, most importantly, computers. Epistemologically, i.e. methodologically, such simulations are (called) models. The possibility of simulation is based on the assumed fact that at least the core of the organic function to be inorganically simulated exists in the Inorganic, or can be set up with exclusively inorganic means. Insofar as being set up by conscious human activity, such a simulation is a 'product' of the human mind, and belongs to the Super-psychic Layer of categories, i.e. it is a concretum whose determining categories belong to that category Layer. However, seen, all by or in itself, the product or result of such a simulation is an inorganic entity, totally determined by inorganic categories. This is so because the simulation and its product is (as has just been said), first of all, a product of a final nexus as it operates in the super-psychic Layer. But such a nexus works as follows :
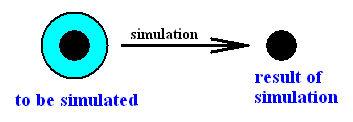
We see, simulation is the reverse of over-forming, and over-forming creates true analogy. Simulation of Intelligence ? I n t e l l i g e n c e, as a concretum, belongs to the Psychic Layer of Being (i.e. the category which determines it belongs to this Layer). If intelligence can be simulated with exclusively inorganic means, for example with a computer, then its core not only must be already present in the Organic but also in the Inorganic. Genuine complete intelligence, i.e. intelligence as we know it, only occurs in the highest organisms, where the Organic is over-built, resulting in a third category Layer added on top of the Organic (which itself lies on top of the Inorganic). So, when simulating intelligence, it is assumed that intelligence, although not naturally occurring in the Inorganic (and also not in the Organic [s.str.] ), can be constructed with purely inorganic means. It is not, and therefore maybe cannot, spontaneously (be) generated by natural inorganic processes. But when it is actually constructed, say, in the form of a computer, it is, despite the detour necessarily involving -- yes -- intelligence, now a property of an inorganic being or system. When actually constructed, intelligence, from now on, occurs in the inorganic world. Surely, it is constructed by a final nexus, but, as we've said, the final nexus' core is causality. So its actual generation is causal. If we interpret "intelligence" as a case of "being-so", we can express it as an If / Then constant. The If-component then consists of a disjunctive set of sufficient grounds for intelligence (which means -- recall -- that each one of these grounds is already enough to imply the appearance of intelligence). Let us give three of such grounds :
But if every member of the whole disjunctive set of (formally) sufficient grounds is as such impossible, even in principle, then the category does not in any way exist, and is therefore invalid.
Maybe the third sufficient ground of the above list can never occur in the real World, which means that it (i.e. a series of natural causal inorganic events leading to inorganic intelligence) is a physical impossibility. And even the second sufficient ground may never occur, because an intelligent computer is a physical impossibility. If both of these (formally) sufficient grounds are physically impossible in principle, then the Inorganic category Layer does not harbor a category of intelligence (inorganism-based or machine-based intelligence). Simulation of Consciousness ? As regards the Psychic Layer, its NOVUM certainly is (or can, collectively, be called) C o n s c i o u s n e s s . Consciousness of a given being (an animal, or whatever) is an active reflection (carried out by that being) on (in the sense of a pondering about) the content of its interior world. In fact, it could be that this act of reflection is the very cause of this interior world's existence at all, i.e. its existence in such a being. So consciousness is, in a certain degree, self-referential. If such an active reflection is, in addition, be able to focus on the "its" of "the content of its interior world ", i.e. when it is completely self-referential, then this given being possesses Self-consciousness. And a given being is either constituted (or constructed) in such a way that it is able to carry out such reflections, or it is not (so constituted). There is no in-between. And it seems to be impossible (even in principle) that consciousness, let alone self-consciousness, can be simulated by means of inorganic dynamic patterns such as computers. So the Inorganic does not contain a primordial state of consciousness, nor even potentially so. Does the Organic contain such a state? This seems unlikely, because the interior world of consciousness is not spatial. And this is the reason why the Psychic Layer over-builds, instead of over-forms, the next lower Layer. And even if the category determining consciousness were the result of (just) over-forming of a lower-Layer category (in virtue of some NOVUM that has appeared in the Psychic Layer), this lower-Layer category itself is expected to be new with respect to the Inorganic Layer, that is to say it is expected to be a category only insofar as it is organically over-formed (in virtue of the organic NOVUM). So also then consciousness cannot be traced all the way down to the Inorganic, and thus cannot be simulated by inorganic means. The latter situation is symbolized in the next Figure.
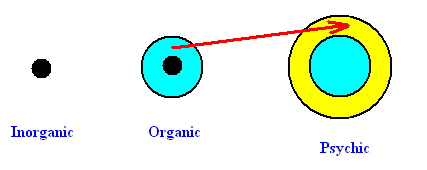 We need not go further with these considerations concerning Intelligence and Consciousness, because our main topic is the Inorganic-Organic comparison, i.e. it is about the first two (lower) real-world category Layers only. The reason that we did consider Intelligence and Consciousness nevertheless, is that such a consideration throws some more light on the essence and ontological nature of simulation (which will play a major role in the Inorganic-Organic comparison). Simulation, not of organisms, but of individual organic functions or structures. In the comparison of the Inorganic with the Organic (i.e. in the ensuing 'crystal-analogy'), crystals will be compared with organisms, and simulations of organic functions and structures are being discussed. In order to see this in the appropriate light, the following consideration is important : The corresponding concretum of the o r g a n i c NOVUM can (also) be expressed as follows : Organisms are primarily unstable material configurations that are secondarily stabilized by flexible regulations ( In this way the causal nexus is over-formed, resulting in the nexus organicus). All processes, such as (chemical) assimilation, dissimulation, reproduction, death and phylogenesis (by genetic mutation and natural selection) are a necessary implication of the fact that organisms are primarily unstable structures. The fact that organisms, despite their unstable nature, nevertheless exist is due to these processes, which effect recreation at several levels and, in addition, transformation (when external conditions have changed).
Crystals, on the other hand, are relatively stable configurations (because they are lowest-energy configurations while organisms are not). They do not, therefore, need the above processes in order to remain existent at all. Especially they do not need natural selection, because crystals, taken generally, can (in contrast to organisms) be generated and maintained in a great variety of conditions. And because they are not products of a long evolution, they can easily be recreated after temporarily adverse conditions have returned to more favorable conditions again. But, as a result of them being so, crystals cannot evolve. Liquid crystals (discussed in Part XXIX Sequel-14 ) are an example of inorganic intrinsic beings that, probably, are -- like organisms -- more or less unstable.
|
Having concluded the above (long) intermezzo, we continue with our considerations about inorganic dynamical systems.
HARTMANN, 1950, pp.491, assumes the presence, already in the Inorganic, of the phenomenon, of "wholeness determination" :
There are, according to him, inorganic dynamical systems (and maybe this applies to all such systems) that not only show a determination from the elements (which generally are themselves dynamical systems) to the system (i.e. the system is determined by its elements), but also a determination from the system as a whole to its elements (i.e. certain aspects of the elements are determined by the system as a whole).
According to me this is not so, at least not in inorganic dynamical systems : Here the system is its elements. Of course the system is not identical to any single element of it, and, generally, also not to just their summation. The system wholly consists of its elements, (but having these elements) not in the form of isolated entities, but as they relate to each other, and interact with each other, such that they together form a configuration that represents a possible state of the dynamical system. So in this way a dynamical system is wholly its elements. And in this way too there is no (backwards) determination from the system to its elements, because the system is not something apart from its elements. And the elements determine the system because the system intrinsically contains these elements. The system is the immediate result of the elements. And because we must interpret "elements" as we did above, i.e. including their patterned distribution (reflecting the simultaneous interdependence) and their interaction (reflecting their causal -- and thus non-simultaneous reciprocal action) -- because only then they are true elements -- it is to be expected that the system as a whole can show features that are not present in any one of its elements, and are also not just the result of aggregation, but are the result of integration , for instance as we saw it in star-shaped snow crystals : Such a crystal, together with its growing environment, can be seen as a dynamical system, consisting of elements, in this case water molecules (H2O). When such crystals grow very fast in a uniform environment, they develop six arms. In one and the same crystal individual these arms are always of precisely the same morphological type (See Part XXIX Sequel-6 ), which points to some global communication within the snow crystal, more or less in the sense that each arm 'knows' what the others are doing (i.e. how they grow). It is clear that this phenomenon cannot be derived from the properties of water molecules as they are in themselves. This peculiar feature obviously comes from water molecules that are e l e m e n t s in a crystal lattice, and some others that are in the immediate growing environment of the given (branched) snow crystal. In short, this feature wholly comes from the elements of the dynamical system. So, as regards inorganic dynamical systems, we should not see the system as something separate from its elements, i.e. we should not consider the system as one thing, and its (set of) elements as another (which would then result in the possibility that the system acts on its elements, and which HARTMANN calls "wholeness determination" (Ganzheitsdetermination)). The latter -- HARTMANN's wholeness determination -- is, in the case of inorganic dynamical systems, just the total of external conditions within which the system is embedded. These conditions constrain the system, and make it possible (or impossible) for the system to exist there at all. If these conditions, initially sustaining the system, change, in such a way as to make prolonged existence of the system no longer possible, then the system disintegrates and its elements are taken up by larger systems.
In o r g a n i c dynamical systems, on the other hand, we can expect such a wholeness determination, because here we have to do with the presence of a categorical NOVUM : the nexus organicus.
So we can, on the basis of all this, distinguish inorganic beings (inorganic dynamical systems) from organic beings (organic dynamical systems) by the absence or presence of "wholeness determination".
Apparently teleological nature of inorganic dynamical systems
Before we proceed further, we again remind the reader that our First Part of Website ( First Series of Documents) , contains much for an up-to-date insight into the generalities of dynamical systems (involving "states", "initial conditions", "trajectories", "attractors", "attractor basins", "attractor-basin field", "dynamical law", "chaotic systems", etc.). We especially recomment the following four documents :
Terms like "aiming to equilibrium", "attractor", "having a tendency", etc. which are used in the theory of dynamical systems, are just convenient images, convenient to visualize and compactly describe complex relationships. But basically they are misleading. For here, i.e. in inorganic dynamical systems, there are no "goals" or "purposes" toward which a system would "tend to go", "aim", or (toward which a system would) "be attracted". Instead of these goals or purposes there are equilibria. But these are not preset.
Energy
Let me be honest with the reader. All the remaining part of this document tries to analyse causality further by involving thermodynamics. Now thermodynamics is a very vast and difficult body of enquiry. And I am certainly not an expert in those matters. Moreover my intellectual training (which is mainly philosophy and geometrical symmetry) does not admit to quickly catch up in thermodynamic matters. Certainly, I am more or less in possession of the main lines, but my knowledge even of these is predominantly qualitative. So in what follows the reader should not interpret my text as some sort of scientific textbook on thermodynamics. For that he or she must consult a real textbook on the subject. And because I am not technically acquainted with thermodynamics, errors (in my text) are possible. The reader should be aware of this. The only thing I have tried to do is use the thermodynamic things I know, or think I understand, for the benefit of an extended categorical analysis of causality. I hope that every amendment the reader finds necessary will be communicated to me. In this way this document (and the next) could increase in quality and consistency.
It must have striked the reader that we, when discussing Causality and Dynamical Systems, spoke little about energy, in spite of the evident fact that energy relations, energy conversions, and difference between energy levels (energy fall), must play a decisive role in Determination and Process. We will now rectify this shortcoming.
Considerations about energy are especially important in the case of dissipative systems or structures. And moreover, while some, but not all inorganic processes are dissipative, all organic dynamical systems, without exceptions, are dissipative systems. And being 'dissipative' means that these systems import matter and energy and export matter and entropy, and are therefore in a state of far-from-thermodynamic-equilibrium (and will as such be contrasted with systems that are in a state of thermodynamic equilibrium or near-equilibrium, as the latter is the case in crystallization).
Entropy, as it was just mentioned, can be described as the degree of ' leveling out ' of energetic differences, which in turn means that work can no longer be performed, despite the presence of energy.
In the next Sections of the present document we will again discuss Causality, but now how it is related to energy, and further how energy is related to the mentioned dissipative systems. The purpose of all this is to obtain still more insight into the inorganic analogues of organic pattern formation, i.e. we do not limit our discussion of these inorganic analogues to just the formation of crystals, which are thermodynamically near-equilibrium systems, but will also discuss the very important inorganic d i s s i p a t i v e systems, which are thermodynamically far-from-equilibrium systems (As such they are treated in First Part of Website, first Series of Documents : Non-living Dissipative Systems ).
Here, in the present document, we will concentrate on the general categorical elements involved in the thermodynamics of dissipative systems (as compared to non-dissipative systems), especially the types of determination (i.e. the determinations -- nexus categories -- that are involved in pattern-generating inorganic dissipative dynamical systems).
Causality, Energy, and Entropy.
This Section discusses in what way and to what extent e n e r g y is involved in causality (as we see the latter at work in dynamical systems). So in doing so it further investigates the nature of causality.
However, I must urge the reader not to take this Section too seriously, because I, unfortunately, am not an authority in Thermodynamics. So the content of this Section is only a qualitative and intuitive attempt to understand the role that energy plays in causality. Maybe the reader can improve on it, or refute it all together. Please let me hear!
Earlier we had established that causality connects, to begin with, two states : the cause and the effect. The effect is different from the cause, in the sense that it is creatively different : the (pure) effect is produced from and by the cause as something totally new, and consequently the difference of the effect is as it is, i.e. it is not intelligible.
Now, one could surmise that the difference of the effect could consist in the effect being a state of lower potential energy (as compared with the cause). And so the difference is intelligible after all. However, there exist energetically up-hill processes (for example the morphogenesis of an organism), which means that if we want to understand these processes energetically, we must include the environment from which energy is taken up by the (up-hill) process. But this implies that we must extend our process to the whole Universe, because the energetic environment of such a process is in fact not bounded. And while the total amount of energy (potential + actual energy) of the Universe stays the same (First Law of Thermodynamics), the total amount of potential energy of the Universe will decrease. So we could characterize our process as effecting a decrease of the potential energy.
This, however, can perhaps be better expressed by means of a related concept, namely that of entropy.
According to the Second Law of Thermodynamics, whatever process takes place, the total amount of entropy (of the Universe) cannot decrease, where, as has been said, "entropy" is a measure of the degree of leveling-out energy differences. We can imagine a configuration of particles that attract one another, but repel when they come very close to each other. When the particles are far apart, the configuration possesses potential energy, but when they are pressed more or less closely together, the configuration also possesses potential energy. In both cases we have to do with stress so to say, and the system wants to get rid of this stress. So when left alone, the result will be that the particles, when far apart are moving toward each other (potential energy will be converted into actual (in this case kinetic) energy). But when they come, as a result of this movement, too close to each other (potential energy being built up again) they will repel each other and thus move apart again, resulting in a configuration of equilibrium with zero potential energy. This is just a mechanical system which will settle at its equilibrium. Dissipative systems, however, do not settle at or near equilibrium, but are held far from equilibrium. And this means that it has a low entropy with respect to its surroundings. But according to the Second Law of Thermodynamics such a system would not be able to get off the ground in the first place, because a decrease of entropy is involved. This is solved by nature as follows : While the entropy in a dissipative pattern-generating dynamical system decreases (which as such is a local decrease of entropy, and a local increase of order), the netto entropy increases nevertheless (i.e. if we include the dissipative system's environment, and, if necessary, the whole Universe, the total amount of entropy always increases). So the Second law is not violated. Thus we could surmise that causality is, in all cases, necessarily linked up with entropy increase.
However, entropy increase can be accomplished in many ways. So we can understand only one single aspect of the effect (i.e. the state that follows from the cause), namely that the netto entropy change must be positive, or, equivalently the total entropy of the Universe must increase, in order for this effect to be realized. In other words, when whatever process has taken place, the total entropy of the Universe has then been increased as a result of this process. So we now have at least a partial understanding of what (kind of) effect must follow from a given cause.
We could perhaps make the production of the effect from the cause completely (instead of only partially) intelligible by assuming that the effect is necessarily that state which involves the largest increase of entropy (i.e. increase as seen from the cause). In that case the effect would be totally determined (provided there is only one single configuration -- making up the effect -- that involves the largest entropy increase), and thus totally intelligible. The decrease of entropy as a result of the generation of a dissipative patterned structure can be neutralized by a same increase of entropy of the surroundings, and of course also by a still larger increase of the entropy of the surroundings. But a largest increase would only take place when all the other energy falls everywhere in the Universe are leveled out. But although it is evident that Nature locally tends to leveling out things, because this means relaxation (accounting for the spontaneity of processes that bring about this relaxation), this tendency is perhaps not so evident at the global scale, i.e. at the scale of the Universe as a whole.
If we accept the latter, i.e. if we indeed hold that the Universe-as-a-whole does not necessarily tend to maximally relax when it is locally stressed, but that for it just a little more than cancelling out the locally originated stress is sufficient to allow for the effect to take place, and if we moreover realize that entropy increase as such can be accomplished in many different ways, then entropy increase is only a conditio sine qua non (an indispensable but not necessarily sufficient condition) for causality (to take place). All other aspects of causality, i.e. all other aspects of the production of the effect, still remain unintelligible. Given a certain cause, its effect is (only) partially conditioned (and thus only partially understood) as a result of the demand that the netto entropy change be positive, realized either directly by the system itself (for instance in the case of a falling body), or by its immediate surroundings. The latter case is the one where the (pattern-generating dissipative) system enters into a state of higher order (and thus lower entropy), implying a definite pattern, and thus differences. And these in turn mean (increase of) stress, which, more generally can mean an increase in potential energy, for example when we stretch out a spring ( In this particular example the increase in stress already takes place without the increase of order, namely just because attracting particles come to lie farther apart and in this way increasing the potential energy ). The entropy decrease, that took place within the (pattern-generating) dynamical system, generally becomes a little more than (just) cancelled in virtue of an entropy increase of the immediate surroundings of the system. And because the netto change of entropy is positive (entropy increases), the area containing the system is relaxed (as compared with its state before the pattern was generated). And this is already sufficient (for the effect to take place, where the cause is, for example, the initial state of a pattern-generating dissipative dynamical system, and the effect is the generated pattern and its surroundings where the entropy increase has taken place). The relaxation does not need to be maximal (i.e. is not extending across the whole Universe). Therefore this relaxation can be accomplished in many different ways, which implies that the specific and constant way of relaxation (the specific effect) which is produced by a particular cause in a repeatable way (same cause, same effect) is still not intelligible. Therefore causality is still inherently creative, even when energy restrictions are included.
In the next Section we will elaborate still more on the relationship between causality and entropy.
Causality and the spontaneity of entropy increase.
Entropy increase is a transition from an unstable (more) ordered configuration of material elements to a more disordered configuration. Two examples are given.
An example, taken from (near) equilibrium systems, is the following : A supersaturated solution of a given chemical compound is an unstable configuration of material elements. Its overall orderliness is higher than that of the next configuration which is : crystal and solution, i.e. the generated crystal, now situated in a (just) saturated solution (which belongs to the system). Although the crystal is more ordered than any solution, heat was given off into its surroundings, the solution. This causes an increase of the thermal agitation of the molecules in the solution, and thus an increase in entropy of that solution. And this increase must -- according to the Second Law of Thermodynamics -- be such that the netto change of the entropy is positive, i.e. the entropy of the system as a whole -- crystal + solution -- must increase (despite the local increase of order in the system : the crystal (lattice)). The same applies to the phenomenon of solidification (crystallization) of some molten material after super-cooling, making the configuration unstable : a more ordered state appears during crystallization, it is true, but heat is given off to the environment, increasing its entropy, and this environment belongs to the system.
See (for 'authorization') NOTE 4 .
An example, now taken from far-from-equilibrium systems, is the death and decomposition of an organism : The ordered configuration passes over into a disordered state, as soon as the barriers against decomposition are removed, resulting in an increase of entropy. In itself the far-from-equilibrium structure is ordered, but unstable.
The fact that entropy increase is spontaneous, can be understood, because it is equivalent to 'leveling things out', and therefore to 'relaxation'.
So it is clear that an unstable (more) ordered configuration (intrinsically unstable, because it is actively upheld or forced into the (more) ordered state) will, when all possible barriers are removed, spontaneously transform into a (more) disordered state of the system as a whole (netto increase of entropy), because in such a state everything is leveled out (at least more so than in the initial state), which means that the system-as-a-whole now finds itself in a (more) relaxed overall condition.
So it is at least intuitively evident that the system will spontaneously pass over into this more relaxed condition as soon as relevant barriers are removed (When we let go a stretched spring, it will spontaneously contract).
This spontaneous transition from an ordered state to a disordered state is sometimes explained as follows :
Because, with respect to a given set of (different) elements, there generally are many many more mathematically possible disordered configurations (of the elements of the set) than there are ordered configurations, the chance that, in the case of a re-configuration of the elements, an ordered configuration will (after the fact) be seen to have been followed by a disordered configuration is much much larger than the chance that an ordered configuration will (after the fact) be seen to have been followed by another ordered configuration, and certainly also when a disordered configuration is seen to have been followed by an ordered one.
Such an explanation would only make sense when the initial configuration or state were indeterminate as to the nature of the next configuration (state), i.e. if every mathematically possible configuration were equally possible physically. Then indeed the chance is very big that an ordered configuration (state) (or a disordered configuration for that matter) will (after the fact) be seen to have been followed by a disordered configuration (state) ( Where "followed by a disordered configuration" in fact means : " followed by one or another disordered configuration" ), because there are so many more disordered configurations (of the elements of the given set) than there are ordered ones.
There is, however, no reason to believe that any given configuration of (an intrinsic dynamical system of) material elements is indeterminate as to the nature of the next state (configuration), i.e. it is not so that, given a particular state (configuration), there is more than one next state that can emerge from this given initial state. On the contrary, we'd better assume that in all such cases causality rules over things. So the initial state (initial configuration of material elements) is the cause of the next state (next configuration), which is the effect. This next state is completely determined by the previous state (of that same dynamical system). One aspect of this "being completely determined " is that the system will necessarily relax as soon as barriers (to do so) are removed. So in our case of an unstable ordered configuration of material elements (where the barrier for (spontaneous) transformation is removed) -- which is the cause -- we will obtain a disordered configuration -- which is the effect. This is the part of the "effect being completely determined " demanded by thermodynamics. The other part of this being determined consists in the fact that from a particular (i.e. given) initial configuration (of material elements) a particular disordered configuration will follow (instead of any other disordered [or ordered for that matter] configuration), i.e. one specific (disordered) configuration out of the many that are mathematically possible. This constant relation between a particular initial ordered configuration and a particular disordered configuration (instead of some other [disordered] configuration) is the creative, genuinely productive, and therefore non-intelligible aspect of causality. In accordance with this, another particular initial configuration will give another particular configuration as its next state.
All these considerations are based on the (validity of the) Second Law of Thermodynamics (What follows is taken from a university manual written by Van MIDDELKOOP, 1971, pp.58). This Second Law can be expressed in terms of heat engines in the following way :
Q1 (heat supply to engine) = Q2 (heat fiven off to the environment) + W (work done by ideal machine).
The work done by the machine would be maximal when Q2 = 0. Then we would have Q1 = W, which means that all the imported heat were transformed in work. But this is never the case because in, say, a steam engine, the used steam always still possesses a considerable amount of heat.
Q2 is a function of T2. If T1 and T2 are absolute temperatures, then it turns out that
And if T2 = 0 (absolute zero temperature), then Q2 = 0.
Only in that case in the ideal engine (no heat leakage, no friction) all heat is transformed into mechanical work. Apart from this, there is (even in an ideal engine), after work has been done, always some heat left that must be exported.
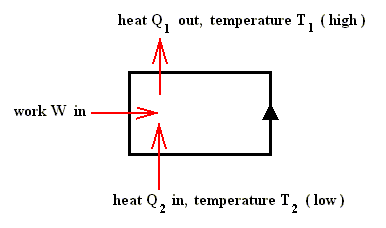
Carnot (1796-1832) defined the ideal heat engine, which has no internal friction, and working only on the basis of a temperature difference. Schematically :
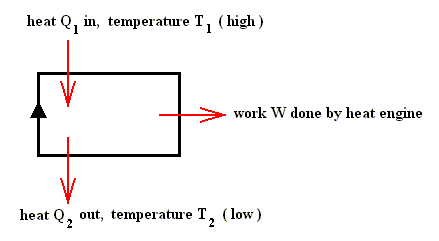
Let us now calculate the efficiency of an ideal steam engine (using the above relation Q1 / Q2 = T1 / T2).
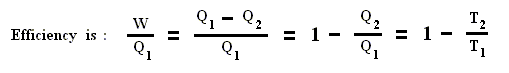
T1 = 3730K, T2 = 2880 K, so the efficiency is : 1 - 288 / 373 = 0.23, that is to say, the efficiency of even an ideal heat engine is only 23% (!).
A real engine will, as a result of losses, have a still lower efficiency.
The carnot engine can also be reversed : By supplying mechanical work the exit temperature T1 is higher then the entrance temperature T2. Schematically :
This is the case of the refrigerator and the air-conditioner. A refrigerator cools its contents (and heats the room in which it stands), thus reversing the flow of entropy and increasing the order within the refrigerator, but only at the expense of the increasing entropy of the power station producing the electricity that drives the refrigerator motor. The entropy of the entire system, refrigerator and power source, must not decrease -- and, in practical matters, will increase ( Here there is a flow of heat from lower temperature to higher temperature, but this flow is not accomplished in a self-acting way, i.e. it is not spontaneous, it is driven.).
Now we can formulate the Second Law very concisely by means of the concept of entropy. The following discussion will result in this formulation.
The entropy S is a quantity that is only dependent on the amount of transported heat and the temperature T at which this transport takes place, and can be defined by its change :
The change of entropy dS is then equal to the amount of transported heat dQ divided by the temperature T at which this change occurs.
The Second Law of Thermodynamics now is equivalent to the following statement :
In a physical or chemical process the entropy S i n c r e a s e s, until equilibrium has been reached.
And this statement is equivalent to :
Heat only s p o n t a n e o u s l y flows from higher to lower temperatures.
This latter statement will be made clear as follows :
Consider two systems with initial temperatures T1 and T2 , where T2 > T1 (where > means : greater than, whereas < means : smaller than), and where these systems are in contact with each other. Suppose that initially S = S1 + S2 (i.e. the total entropy is the entropy of the first system plus the entropy of the second system).
Because of the temperature difference there is a flow of heat of system 2 to system 1. This means that S1 increases with an amount dS1 = dQ / T1 when there is an amount of heat dQ transported from 2 to 1.
And because system 2 loses heat we have dS2 = - dQ / T2 (i.e. dS2 is minus dQ / T2 ).
So dS ( = the change of S with respect to the total system (1 + 2)) =
dS1 + dS2 = dQ / T1 - dQ / T2 = (1 / T1 - 1 / T2)dQ. And this is a positive quantity, i.e. dS > 0, because T2 > T1 , therefore 1 / T2 < 1 / T1 and therefore 1 / T1 - 1 / T2 > 0.
Further we know that dQ > 0, so (1 / T1 - 1 / T2)dQ = dS > 0.
So the entropy increases, until T1 = T2 (equilibrium). If the heat had spontaneously flown the other way around (from something having a lower temperature to something having a higher temperature) dS would be negative and thus contradicting the Second Law.
Indeed, when T1 = T2 , 1 / T1 = 1 / T2 , so 1 / T1 - 1 / T2 = 0, and therefore
(1 / T1 - 1 / T2)dQ = 0, and thus dS = 0 (the entropy has become constant).
Entropy can be considered a measure of chaos (disorder) (Van MIDDELKOOP, G. 1971, p.58-60).
Entropy figures in the Second Law of Thermodynamics. What then is the First Law?
(In fact we should write dQ and dA with the greek letter delta, because only dU is a complete differential).
For the sum of a series of successive small quantities (increments) like these, we use integrals,
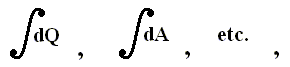
because the series of increments need not to be regular. We can also say that expressing them as integrals is a generalisation of dQ, dA, dU, etc.
If the change of the system not small, for instance when we add much heat and compress the gas strongly, then the added heat Q and the added work A will be expressed as these integrals, and we get
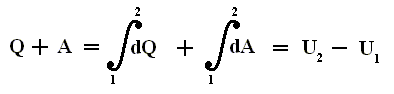 ........................ (1)
........................ (1)where 1 and 2 respectively indicate the initial state and the end state, and where the sum of the small energy changes
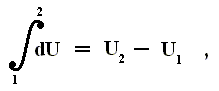
is the energy difference between the end state and initial state.
This, i.e. expression (1), is called the First Law of Thermodynamics, which formulates the law of energy conservation in the science of heat. It says that an increase in energy of a system must be the result of the addition of heat energy or of work, it can not come out of the blue. It also says that if we want to obtain work from some given system, the energy of the system must be increased. It is therefore impossible to give off work from nothing (to yield work from nothing). A machine, which could realize this, is called a perpetuum mobile of the first kind.
The First Law of Thermodynamics is thus equivalent to saying that such a perpetuum mobile is impossible.
Causality and the probabilistic approach to entropy.
Above we discussed the relation between causality and spontaneous entropy increase. Entropy, however, is often explained in terms of probability. We already stated that this approach is inconsistent with the notion of causality, which notion implies strict determinism : A particular cause has a particular effect in a repeatable way : same cause, same effect. The (particular) effect thus necessarily comes out of the given cause. The cause produces its effect. The nature of this production is ultimately unintelligible, because it is essentially creative. The probabilistic approach, on the other hand, presupposes indeterminism. It is correct as a method, but incorrect as an ontology. In fact it is an epistemological approach : It sets out with a given state of a certain kind of system, namely a system consisting of an astronomical number of interacting particles (for example molecules), and because it is impossible to assess the adventures of each molecule, a statistical consideration, involving probabilities, is necessary in order to predict the change of macroscopic features of the system, such as temperature, pressure, volume, etc.
Before elaborating on this point, let us first emphasize a few things :
The problem, as it is stated above, namely the problem of the relationships between causality, relaxation, determinism and probability, turns out to be a very difficult one. It certainly cannot be settled here once and for all.
During the ensuing investigation of the mentioned relationships it might turn out to be necessary to slightly change our earlier notion of causality (and with it the role attributed to relaxation), in order to eliminate the above mentioned inconsistency between the probabilistic approach and the nature of causality.
Regarding this probabilistic approach we will show (below) that at first the presupposed indeterminism is not seen as a truely ontological indeterminism, but only as an epistemological indeterminism, i.e. not expressing an objective and intrinsic (partial) indeterminism between the states of a real-world dynamical system, but (expressing) a degree of unpredictability for some investigating mind : Although individual outcomes cannot be predicted, the chances that certain behaviors will actually materialize can be assessed, often with great precision, by such an investigating mind, on the basis of statistical methods. But, as we will see shortly, there are indications that the partial indeterminism (as presupposed by the probabilistic approach) might turn out to be an intrinsic aspect of real-world dynamical systems, and therefore also of causality, which means that it might be an ontological (partial) (not just epistemological) indeterminism after all. The reason that -- in solving the above mentioned inconsistency -- we resort to amending our concept of causality, instead of rejecting the ontological significance of the probabilistic method, is the very nature of chaotic dynamical systems (unstable dynamic systems). The slight change in our notion of causality (as held on this website), will consist in the assumed fact that relaxation is not as such the driving force, nor is it as such a conditio sine qua non (necessary condition), for causality, i.e. for an effect to be produced by the cause : It is this only in a statistical sense. Unfortunately, if the latter is true, it decreases still more the understanding of the nature of causality.
Let us now work out in more detail the things we've just succinctly suggested.
The probabilistic approach, and its explanation of the increase of entropy, is itself often explained by using a system of colliding billiard balls, while supposing all friction to be absent, implying that the system, once set in motion, continues to run indefinitely (and having in the back of one's mind a system of physically interacting molecules of a gas).
Because we do not know precisely the momenta (NOTE 5 ) and the positions of the balls (molecules) at any one moment in time, we cannot follow each ball (molecule, particle) as it is moving (and colliding) in relation to the other balls, because there are supposed to be so many of them, and also because they are supposed to have microscopic dimensions. So we cannot predict the ensuing sequence of spatial patterns of the balls (as a result of their motion and collisions). Therefore we subdivide the billiard table into a number of equal areas (boxes), within which we do not specify the exact positions of the balls and also not the pattern of momenta associated with these balls. The pattern of the balls (configuration of system elements), specified as to which balls are present in which box (sub-area of the billiard table), is considered as having appeared after the previous pattern, while the present pattern appears before the next pattern. We assume that, when the system of balls is set in motion (by shaking the table for example), every mathematically possible configuration of elements (the distribution of the balls over the boxes [equal sub-areas] of the billiard table) has an equal chance to show up after some predetermined running time of the system. This "equal chance" is connected with the fact that the system is randomized by the collisions of its elements (each collision involves the leveling-out of momenta of the colliding balls). When we now categorize the possible patterns of the balls (expressed by their presence in one or another box of the billiard table) such as to distinguish between ordered configurations (for example all balls in one box) and disordered configurations (balls more or less uniformly distributed over all the boxes), we will find that there are many more mathematically possible disordered patterns (i.e. patterns that are disordered in one way or another) than there are ordered patterns (i.e. patterns that are ordered in one way or another). And it is now possible to assign a corresponding chance to each of these categories, a chance that they will actually appear after some predetermined running time. And indeed, the chance that we will see (at that prespecified time) one of the disordered configurations of balls is much greater than the chance that one of the ordered patterns will appear (at that prespecified time). So statistically a system will move from an ordered state to a disordered state (which is equivalent to the relaxation of the system).
This then is the statistical (probabilistic) approach, which makes it possible to do predictions after all.
In and by this approach we invoke some degree of indeterminism of a next state (i.e. next distribution of the balls over the boxes) with respect to the present state, that is to say this next state is not totally determined by the nature of the present state (present distribution of the balls over the boxes). But this indeterminism is just the expression of the fact that we do not possess detailed relevant knowledge. It is just epistemological indeterminism, and not the assumption of an ontological indeterminism. Many offered (textbook) explanations of what entropy actually is, have not always been clear on this point, i.e. whether the encountered (partial) indeterminism is just epistemological or whether it is ontological as well (in the sense of objective and intrinsic indeterminism of the processes as they are in themselves ).
Statistical Mechanics compresses all the information of the molecular level into a few macroscopic (thermodynamic) variables, such as temperature, pressure, volume and entropy. Thermodynamical behavior originates from, or is a manifestation of, atomic and molecular events. The latter can only be described (and indeed, very well) statistically, because of their smallness and vast numbers.
A system of molecules of a gas ultimately visists every possible state (i.e. every configuration of positions and momenta that is relevant to the given dynamical system of interacting molecules), and thus visits every point of its phase space (See note 7). And because an initial condition (initial state) can never be assessed exactly (NOTE 6 ), and also because of the often occurring high sensitivity of initial conditions with respect to the system's subsequent behavior (thus the occurrence of unstable systems), a statistical approach must be followed :
The initial condition of such a dynamical system must then be represented, not by a point in the phase space (NOTE 7 ) of the system, but by a 'blob', that is to say, by a certain volume within phase space. Epistemologically we have (partial) indeterminism, but not ontologically. And, when we have an ergodic system (which is a system that explores all its phase space), we can detect an arrow of time, but only when we treat such a system statistically : evolution of the initial' blob' (which represents the initial probability distribution function of possible states) in the phase space of such a system. In a single trajectory, thus departing not from a blob but from a single point in phase space, no time [going in one direction only] is visible, because in an ergodic system this trajectory (apart from the fact that a single trajectory cannot be 'seen' in [the practice of] natural science) is not (necessarily) representing a successive sequence of system states which become more and more disordered, but roams about in phase space in a more or less erratic manner, i.e. not smoothly from ordered to more and more disordered states. Only the average behavior (that is to say the behavior having the highest chance to be materialized by the system) indicates a steady increase in disorder of the successive states represented by the system's average trajectory expressed by the evolving blob.
Systems that are confined to a small area of their phase space (non-ergodic systems) will eventually repeat their behaviour (' Poincaré's return'), which means that there is no arrow of time, and no ultimate relaxation of the system. This is the case in an ideal pendulum, i.e. a pendulum without friction. Its evolution can be depicted by a trajectory in its phase space, and this trajectory has the form of an ellipse. Once the (ideal) pendulum has received energy, it keeps on swinging indefinitely, exchanging within it potential energy and kinetic energy. So this is a purely dynamical system (in contrast to a thermodynamic system). No entropy increase is involved. Such a system, however, does not occur in reality ( There we have friction, and thus dissipation of energy to the environment, resulting in the total energy of the pendulum to steadily decrease until it has become zero and the pendulum comes to rest).
The investigations of Boltzmann (end 19th century), Prigogine (second half of 20th century) and many others, boil down to an objective derivation of the irreversible from (reversible) mechanics, that is to say from the behavior of (large numbers of) atoms and molecules. Roughly they amount to the detection of leveling-out tendencies already in the atomic/molecular behavior. The processes of mixing and diffusion (and other like processes) involve an enormous number of particles. Further such processes can be super-unstable where infinitesimal differences in starting conditions result in exponentially diverging trajectories in phase space (and thus in totally different end states of such a process). Therefore, in studying the behavior of such systems, as they are in the real world, statistical methods cannot be avoided. And this we see in the works of the above mentioned authors.
If we want to understand causality at work in these systems (where it is expected to appear in its most general and naked form), we must reduce the macroscopic behavior of the system to the interaction of its constituent particles (elements of the system).
But all we are able to know about the behavior of those interacting particles is based on the results of statistical investigations (observations and simulations [mathematical simulation and computer simulation] ), because this is all we have.
We depart from the idea that a system evolves, from an initial state, to equilibrium. Equilibrium here means that maximally leveled-out states follow one after another, that is to say the system goes (at equilibrium) from one maximally leveled-out state to another such state. The entropy is then maximal.
If we want to investigate the relationship between causality and dynamic behavior (because somewhere in the latter we are expected to find causality), it is best to investigate all this there where this relationship, certainly at first sight, is most obscurely represented, in order not to be misled by investigating 'tidy' systems.
Well, this is the case in unstable systems (chaotic systems, such as so-called K-flows, which as such are probably wide-spread in nature) (NOTE 8 ) . In such systems even very small differences in initial conditions (initial states) lead to very large differences in the system's long-term evolution (Statistically this is expressed by the fact that upon evolution the initial (small) blob, statistically representing the system's initial state in phase space, and covering only a small area of that phase space, drastically changes shape [while maintaining its volume] : with a twisting shape and long branches it now reaches all areas of phase space).
Important for our problem (i.e. the relationship between causality and dynamic behavior, including entropy [increase] ) is the just mentioned fact of the divergence of trajectories in the phase space (not to be confused with the actual trajectories of particles in 3-dimensional space) of such a chaotic system. These trajectories can be simulated, but only in a limited way, because also in the computer only rational numbers are possible ( For simulating stable systems we can happily round off to rational numbers, but not for simulating unstable systems).
In the case of molecules (which form real, and chaotic systems, like the interacting molecules in a gas), however, the concept of trajectories (in phase space), implying point-like starting conditions, must be abandoned. Instead, the starting condition of such a system must be indicated by a small area (a 'blob') in phase space. This blob represents a large number (in fact an infinite number) of point-like starting conditions of the system which differ only slightly from each other ( The blob in fact represents a probability distribution of these point-like starting conditions). When the system starts to run, this blob evolves, i.e. a bundle of probable trajectories (with different probabilities) emanates from the blob : While its volume remains the same, its shape changes (as has been stated earlier), eventually resulting it to be almost everywhere present in phase space, that is to say, there is no longer a large area of phase space representing possible states that are never visited by the system (as in non-ergodic systems). This results from the strongly diverging phase space trajectories of such an unstable system, where a "trajectory" (in phase space) is a sequence of system states, states that are successively passed through ('visited') by the system.
Regarding causality, this divergence is rather strange : The cause is a give state (of the system), while its (immediate) effect is the next state. But because the states are coupled by each other by the causal nexus -- A ==> B ==> C ==> D ==> E ==> F ==> -- we can also say that A is a cause and E the (longer-term) effect of A.
Now, the effect comes out of the cause, and thus we would expect that causes that are very similar to each other (especially the very simple causes like "spatial configuration of positions and momenta" [determining the next configuration] ) will have correspondingly similar effects (In our case we must think as follows : While A (eventually) causes E, a cause that is very similar to A should cause something that is very similar to E ).
But unstable dynamical systems show that this need not necessarily be so : Very similar causes can have very dissimilar effects (in the sense of effects that differ very strongly from each other), reflected by the diverging trajectories in phase space.
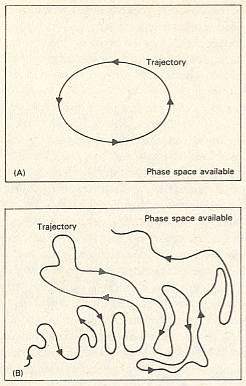
Figure above : (A) Phase space portrait of a pendulum for small swings, which constitutes an integrable dynamical system. The trajectory is confined to a very small region of phase space. (B) Phase space portrait for a collection of molecules in a gas. Here the trajectory probes every part of phase space -- the motion is ergodic. The trajectory of a chaotic system (and a collection of molecules in a gas can be assumed chaotic) in phase space does not in fact visit every point of phase space, but the system will eventually come arbitrarily close to every point of the energy surface [which I take to be phase space] (PRIGOGINE, I., From Being to Becoming, 1980, p.33).
(After COVENEY & HIGHFIELD, The Arrow of Time, 1991)
The fact that two initial states, howsoever similar to each other, can give rise to strongly diverging trajectories in phase space, demonstrates that the effect is not immediately and exclusively implied by the structure or nature of the initial state (the cause). This is the irrational (unintelligible) aspect of causality, that is to say, of the production of the effect by and from a given cause.
Before we continue, we must, first of all, say something more about the phase space of a dynamical system. In NOTE 7 above , we already explained some characteristics of this concept. Here we add some illustrations in order to be more clear.
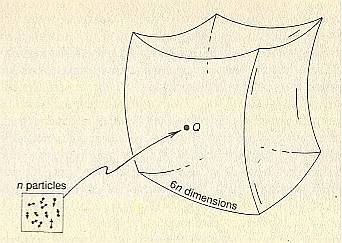
Figure above : Phase space. A single point Q of phase space represents the entire state of some physical system, including the instantaneous motions of all of its parts.
(After PENROSE, R., The Emperor's New Mind, 1990)
Each point in phase space represents a possible state of the dynamical system. With respect to each of these points a next point is defined by the equation(s) of that dynamical system, and with respect to these latter points, again a next point is defined. So from each point in phase space possible trajectories depart, and the very beginning of such a trajectory can be represented by a vector, giving the initial direction of the departing trajectory. So the equation(s) of the dynamical system define a vector field on phase space. This is illustrated by the next Figure.
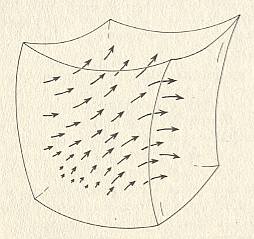
Figure above : A vector field on phase space, representing time-evolution of a given dynamical system according to its dynamic equation(s).
(After PENROSE, R., The Emperor's New Mind, 1990)
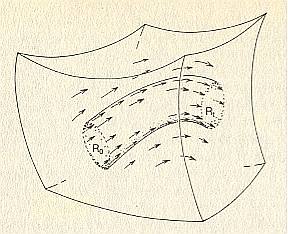
Figure above : Stable system. As time evolves, a phase space region R0 is dragged along by the vector field to a new region Rt . This represents the time-evolution from one set of probable system states to another. Small differences in initial conditions (within the initial phase space region) lead to correspondingly small differences in later phase space regions evolving form the initial region.
(After PENROSE, R., The Emperor's New Mind, 1990)
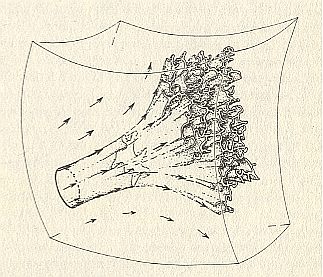
Figure above : Time-evolution of an unstable system. Despite the fact that Liouville's theorem tells us that a given phase-space volume does not change with time-evolution, this volume will normally effectively spread outwards because of the extreme complication of this evolution.
(After PENROSE, R., The Emperor's New Mind, 1990)
The next Figure shows three phase space portraits, representing three different types of dynamical system. The starting condition (starting state) of each of these systems is represented by an area (instead of a point) in phase space. Upon evolution of the system this area evolves : while maintaining its volume in all cases, it changes its shape in mixing systems (moderately chaotic systems) and all other chaotic systems.
Figure above : Time evolution of phase space probability densities : (A) non-ergodic. (B) Ergodic. (C) Mixing.
In the non-ergodic case (A) the system remains cycling within a limited area of its phase space. Small differences in initial conditions imply small differences in the evolution of the system (non-chaotic system, stable system).
In the ergodic cases (B) (stable) and (C) (unstable), where C is not only ergodic, but also moderately chaotic (moderately unstable), which is called "mixing", the system eventually explores all of phase space.
(From COVENEY & HIGHFIELD, The Arrow of Time, 1991)
Having further expounded the concept of phase space, and the way it can characterize several types of dynanic systems, we continue our discussion about the ontological status of probability as it figures in statistical mechanics, and in what way this dynamic probability is connected with causality.
When we consider one single trajectory in the phase space of a given chaotic system (i.e. an unstable system), thus a trajectory departing from one particular point in phase space, then the trajectory ends up somewhere in this phase space (with "ends up" we mean that we look where its 'head' is after the system has run for some considerable time), while a trajectory starting from another point ( These two starting points represent two possible histories of the system out of many possible histories), even when this second initial point lies infinitely close to the first initial point, ends up somewhere else in phase space, often far from where the first trajectory ends up. Thus the trajectories diverge. Such trajectories do not say anything about the leveling of the system, because one of them could indeed end up in a leveled state (a point in phase space that represents a leveled state of the dynamic system), but the other might not do such a thing, it could have ended up in a much less leveled, or even ordered, state (while their respective initial points were [ex hypothesi] very close together, and thus representing very similar system states). And even the first mentioned trajectory, initially ending up in a leveled system state, could, upon further evolution return to less leveled system states. So again, such single trajectories do not say anything about a final leveling-out of the system, although observation shows the ultimate leveling-out (relaxation) of such a system, when it is left on its own (i.e. if we only consider its spontaneous evolution). So there must be something more than just deterministic and reversible trajectories each departing from a single point in phase space. And this could mean that in one way or another the probability is fundamental (not only invoked by our ignorance). If this is true, then -- we already did state it earlier -- such systems are not only epistemologically indeterministic (i.e. indeterministic as a result of our ignorance as regards to the precise nature of, and values of variables involved in, the states of such systems), but also ontologically so (i.e. intrinsically indeterministic). This does not mean a total indetermism, because the chances for certain outcomes are definitely determined. And all this arguing is the result of a consideration of a genuinely intrinsic and objective property of such systems, namely their instability. This could mean that causality is in most cases only statistically determinative, and that the tendency toward leveling is only a statistical tendency : By far the most trajectories that are consistent with the system, i.e. trajectories in its phase space, and thus possible series of successive system states, lead to leveled states. Not, however, all trajectories (consistent with the system).
The simple notion of causality, as described and analysed by HARTMANN, and, following him, by us in earlier documents, might be incorrect, or at least not general enough. However, it remains very difficult to acknowledge the presence (in nature) of an intrinsic and objective probability.
If we consider one particular 'given' trajectory, departing from one point in phase space, then we cannot say that there is a definite chance that this trajectory evolves toward a particular (end) state. No, this (end) state is then already totally fixed. If we want to introduce probability as an intrinsic aspect of nature, then we cannot consider one single trajectory (departing from one point in phase space) : such a trajectory then cannot exist. Or, in other words, point-like starting states, and with it, point-like states whatsoever, do not exist. Only small areas of probability, as to where this state lies (in phase space), do exist. And it is the evolution of such an initial area (now ontologically interpreted) -- i.e. an evolution of probabilities (also now ontologically interpreted) -- that manifests the behavior of the system.
How can we make the notion of "no point-like states do exist" intelligible?
Well, let's think of a (mathematical) line (finite or infinite). It is said that it is built up by (mathematical) points. But this cannot be so, for points do not add up to anything. Their 'length' is zero, and how many zeros we add together, the result remains zero. So the line must be built up, not by points, but by elementary very small segments (which do add up to a line). These elementary segments can be visualized by letting any finite segment approach zero length as close as we want to, without ever reaching it.
This would mean that exact physical quantities, corresponding to single numbers (not approximated numbers), do not exist. Such a quantity, if it is involved in characterizing a state of a dynamical system, must then be seen as 'smeared out' over a small area or volume.
The leveling (relaxation), of which we have spoken so much on earlier occasions, is, also in our new insights, still considered to be the 'driving force' of causality, but this driving force is now intrinsically and objectively probabilistic. The dynamical laws of mechanics must be replaced by statistical laws. The probability aspect of these laws is, however, different from that of the laws of quantum mechanics.
It is now time to ask ourselves more precisely what " i n t r i n s i c probability in dynamic systems " should in fact mean, and whether such a thing (intrinsic probability) is possible at all. We'll do this in the next (colored) Section.
|
Epistemological and Ontological Probability ( Ontological Status of Probability in Dynamical Systems ) |
| In earlier documents we have analysed Causality. And causality must be looked for within (real-world) dynamical systems. But now, while studying such dynamical systems, especially highly unstable systems, we encounter p r o b a b i l i t y, which as such seems to oppose causality. However, as long as this is only epistemological probability (i.e. resort to the application of statistical methods solely by reason of ignorance of relevant facts and values), it has no ontological significance, and consequently no bearing on the nature of causality. But if it is ontological probability, i.e. intrinsic and objective probability inherent in the real-world processes themselves, independent of their being studied, then it is to be expected that the concept of causality, as it was developed earlier on this Website, must be amended. So this question -- epistemological or ontological probability -- is very important for any ontological evaluation and interpretation of real-world processes, and must be decided as good as possible. So let us analyse the phenomenon of probability as it emerges from the study of dynamical systems.
PRIGOGINE & STENGERS, in their book Order out of Chaos, 1984, and COVENEY & HIGHFIELD, in The Arrow of Time, 1990, and, it seems, many, if not, all other authors writing on the subject, hold that the probability, as it is more or less recently introduced into the (classical) physics of thermodynamic processes, is "fundamental", because (now) based on the intrinsic instability of many dynamical systems.
Statistical procedures (and thus procedures involving probability) are adopted everywhere in classical science (we do not here consider quantum mechanics and its inherent probabilistic features) where it is, at least in a practical sense, impossible to know the values of relevant variables and parameters with sufficient accuracy. One then resorts to the study of averages and chances or probabilities, that is to say to methods that can calculate these chances (for something to occur, or something to be in a certain state). However, as technical procedures more and more improve, it becomes possible to abandon those statistical procedures, as soon as one can assess the values of relevant variables with sufficient accuracy (surely not with infinite accuracy, but sufficiently so). And for non-chaotic, i.e. stable systems, one can determine the initial conditions and predict the future behavior of the system (necessary to test a theory), because in such systems a small error in the assessment of the starting condition only implies correspondingly small errors in the dynamical system's evolution, including its long-term behavior.
Figure above : Initial and later states of a dynamical (stable or unstable) system. If this is so, then the starting-off from this (volume-like) initial condition is intrinsically probabilistic (inherently probabilistic). And then of course also the outcome of the system, i.e. its later states, is also probabilistic. It is only deterministic as seen with respect to the particular trajectory that actually started off from the volume-like initial condition. If we repeat this system from the same volume-like initial condition, then most probably another potential trajectory will emanate from this initial condition, but, of course, only a trajectory that is consistent with that initial condition (i.e. one of its potential trajectories). And science is able to assess, or at least characterize, the initial probability distribution of potential trajectories, that is to say the probability distribution of initial point-like states (together forming the volume-like starting condition). And because in chaotic (i.e. unstable) systems the potential trajectories diverge strongly, the probability distribution of possible later system states changes significantly (in stable systems these trajectories do not diverge). If this is correct, then we can say that intrinsic instability implies intrinsic probability, provided that point-like initial conditions are forbidden in all real-world dynamical systems, and only volume-like initial conditions can exist, and provided further that such a volume-like initial condition (which cannot be taken apart) is a collection of point-like initial conditions, where each such point-like initial condition is intrinsically connected with a definite probability of becoming the starting point of a (deterministic) trajectory (in phase space). And, as has been said, this initial probability distribution changes while the system proceeds. Indeed, if we follow (in theory) all potential trajectories that can emanate from the initial phase space volume, then we can see a blob changing its shape (but not its volume), becoming more and more branched, until, at equilibrium, it is infinitely close to every point in phase space : The probability distribution function is now uniformly present all over phase space, which means that every possible state (every state consistent with the system) is now equally probable, equally probable thus when the system is in equilibrium. And because there are so many many more disordered potential system states than there are ordered potential system states, we always see systems, when they are allowed to go their way spontaneously, end up in a (more) disordered state. And because the initial condition has this inherent probability as to the emanation of this or that potential trajectory, the particular outcome of the system, as assessed (by us) after the fact, must ontologically be seen as not significant (i.e. as ontologically secondary) : The system was not determined to reach this particular outcome, it could have been any other outcome, because of the probability inherent in the initial condition. So the observed particular outcome, and any particular outcome, of the system (Such an outcome can be assessed with fairly high, but, of course, not with infinite, precision by the methods of natural science) must ontologically be seen in some intrinsic and objective probabilistic context or background. And it is only in this way -- namely as a result of assuming the intrinsic and objective impossibility of a point-like intial condition -- that we can go along with PRIGOGINE's and others' assertion that the probabilism in (at least chaotic) dynamical systems is intrinsic. Of course we must still figure out what exactly, and especially ontologically, our statement " So the observed particular outcome, and any particular outcome, of the system [...] must o n t o l o g i c a l l y be seen in some intrinsic and objective probabilistic context or background " actually should mean, especially with respect to the nature of causality. To begin with, we can say (as stated earlier) that the particular outcome of a chaotic dynamical system, as can be assessed after the fact, is not significant (or at least less so) ontologically. What is ontologically significant is the time evolution of the 'blob' in phase space, as it is depicted in the Figure given earlier . The right image depicts the phase space evolution of a (moderate) chaotic system ('mixing' system). The central image depicts the phase space evolution of a stable ergodic system, while the left image depicts that of a stable non-ergodic system. Each image in fact depicts a successive series of probability distribution functions (or we can say, the evolution of a probability distribution function). But - we emphasize again -- this conclusion cannot be reached by the arguments of PRIGOGINE, and other authors writing in the same vein, alone, because, as they stand, their conclusions are only epistemological, not ontological. Only when we, in addition, assume the intrinsic and objective non-pointlike nature of initial states (and any other state), can the arguments of the mentioned authors lead to the conclusion of intrinsic and objective involvement of probability.
REMARK :
When we assume that point-like initial conditions cannot exist in real-world dynamical systems, then we mean it for every dynamical system, stable or unstable. Thus also for a stable dynamical system the initial condition (initial state, but of course also any other later system state) is not point-like, but a small volume in phase space (See the Figure given earlier, left image ). And also here we have to do with a probability distribution of potentially emanating trajectories. And different trajectories (which we can obtain by repeating the system) imply different later states. But for stable (real-world) systems the (small) difference in potentially emanating trajectories only imply correspondingly small differences in the course of the trajectories, that is to say the potential trajectories (obtained by repeating the system several times) do not (significantly) diverge, meaning that repeating the system several times yields later states, say at time tn (where n is some definite number), that do not differ from each other significantly (See yet another Figure given above ). So here it seems, that upon repeating the system from the same volume-like initial condition leads (also in the long run) to the same volume-like tn state, giving the impression of
: same cause, same effect. Causality thus seems deterministic in the case of stable dynamical systems (but in fact isn't : We just cannot detect a probabilistic nature in causation in the case of stable dynamical systems). Causality is inherently probabilistic. Thus although this probabilistic nature of causality is not detectable (but is nevertheless present) in stable systems, it is detectable in unstable systems. So if we accept the objective impossibility of point-like initial conditions in real-world dynamical systems, our analysis of causality, as was done in the previous document (Part XXIX Sequel-26 ), must be amended. |
After having made clear a possible position (i.e. a point of view) with respect to the intrinsic probabilistic nature of causality, and (having made clear) the difference between epistemological and ontological status, we can now proceed further with expounding the philosophical context and categorical content of dynamical systems. Much attention will be devoted to a mathematical model (two versions) of a chaotic dynamical system to clear up the notion of objective randomness, unpredictability and the evolution in phase space of an area where the dynamical system is represented.
Dynamical systems and randomness.
In statistical mechanics it is assumed that molecular collisions occur at random (DAVIES, P., 1987, The Cosmic Blueprint, p.31 of the 1989 UNWIN edition). This "random" is meant epistemologically by DAVIES. But after this, DAVIES asks himself : The puzzle is, if randomness is a product of ignorance, it assumes a subjective nature. How can something subjective lead to l a w s of chance that legislate the activities of material objects like roulette wheels and dice with such dependability? (In these latter cases randomness is assumed by the theory of statistical mechanics).
The search for the source of true randomness, not based on ignorance, but producing ignorance, has been drastically transformed long after Boltzmann had introduced probability into classical mechanics (in order to deal, from a microscopic point of view, with systems consisting of a very large number of interacting elements such as gases and their thermodynamic behavior). It (i.e. the search for the source of true randomness) has, namely, been transformed by the discovery of mathematical 'dynamical' systems which generate truly random behavior (mathematical chaotic systems), and in which no use is made of the phenomenon of large numbers of elements (being large populations and so allowing to study averages), and in which one does not involve ignorance of unknown forces (that is to say the ignorance of all [ordinary physical] forces acting within and on the system). Such a mathematical system is in itself deterministic but eventually unpredictable.
The following example of such a system involves one 'particle' only, which moves according to a certain algorithm (which is the mathematical equivalent of some deterministic real-world dynamical law). And this 'dynamic' proces is every bit as random as tossing a coin, but not based on ignorance. And because we unanimously call the behavior involved in tossing a coin r a n d o m (At every toss we do not know the outcome -- head or tail -- because we, so we could argue, have total ignorance of the precise initial condition and all the forces acting on the coin, but we do know that the probability [chance] is exactly 0.5 for either outcome), in whatever way this randomness may have arised, either by ignorance or in virtue of intrinsic randomness, or in virtue of the involvation of large numbers of molecules, we can attribute to the mathematical system (as one of the many possible examples of a mathematical unstable 'dynamical' system) that is about to follow, genuine, that is to say objective and intrinsic randomness.
Let us now describe such an unstable (chaotic) discrete mathematical dynamical system (taken from DAVIES, P., The Cosmic Blueprint, 1987, 1989). While the states of a real-world dynamical system are connected by causality, the states of a mathematical dynamical system are connected by logic. In this way the mathematical system is supposed to mimic a possible real-world dynamic system.
A mathematical example of a discrete chaotic dynamical system : Clock Doubling on the line interval [0, 1] : Iteration of a non-linear transformation.
Clock doubling on the line interval between 0 (inclusive) and 1 (inclusive) means the following : to a point x belonging to this interval is assigned another point y of that interval such that when 2x is equal or greater than 1, y = 2x-1.
Another way of expressing this arithmetical algorithm is : x ==> 2x (modulo 1), which means that we double the point (its value or position on the line interval) but then only retain its remainder under division by 1.
If we think of decimal numbers between 0 and 1, then this algoritm boils down to doubling the number, and, after this has been done, removing the 1 when it appears before the decimal point ( This means that when we, upon doubling, get past 1, we start evaluating from zero again, in the same way as we do while reading a clock : If we pass 12 (or 24), we start counting all over again). When we repeat this transformation on the result(s) over and over again, it is said that we iterate our transformation. The overall result is a sequence of numbers, which we can call a trajectory of the system, althoug the sequence is discrete.
Let's give some examples of one step of such a transformation :
0.4 ==> 0.8
0.6 ==> 0.2
0.9 ==> 0.8
0.0 ==> 0.0 (where 1.0 = 0.0)
0.5 ==> 0.0
etc.
A trajectory of this system could be the following :
0.6 ==> 0.2 ==> 0.4 ==> 0.8 ==> 0.6 ==> 0.2 etc.
As we see the trajectory forms a loop, we get the repeating sequence :
0.6, 0.2, 0.4, 0.8
that is to say a cycle of period four.
Now let us interpret this system geometrically (which is important because we will discuss such systems in the context of phase spaces). We consider the line segment [1, 0]. This line segment contains an infinity of points, where the position of such a point can be specified by the real number (of the number line) that corresponds with this point. The geometric equivalent of our aritmetical algorithm will be applied to the whole line segment, i.e. to every one of its points (as did the arithmetical algorithm (apply) to every number between 0 (inclusive) and 1 (inclusive)). This geometrical algorithm reads : stretch the (whole) line segment till it has become twice as long, and then cut the result in half and shift the right half over the left half till it covers the latter completely. In doing this we follow one chosen point on the line, and see where it ends up after one such transformation. See next Figure (four images, (a), (b), (c), (d) ).
Figure above :
(a) The line interval 0 to 1 is stretched to twice its length : each number in the interval is doubled.
(b) The stretched line is cut in the middle.
(c) The two segments are stacked.
(d) The stacked line segments are merged, thereby recovering an interval of unit length again. This sequence of operations is equivalent to doubling numbers and extracting only the decimal part. Shown as an example is the case of 0.6, which becomes 0.2.
(After DAVIES, P., The Cosmic Blueprint, 1989)
If we repeat the just depicted procedure again and again (i.e. if we iterate the transformation) and if we follow the fate of just one point, we can think of this point as being a particle that jumps about on the line between 0 and 1. Its itinerary can be determined by the repeated application of the algorithm, that is to say we can compute this itinerary. As an example, let us compute the itinerary for a particle starting at 0.17, and let us omit the " 0." part :
17, 34, 68, 36, 72, 44, 88, 76, 52, 04, 08, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, etc.
So the starting value 0.17 ( = starting position of the jumping point on the line, and which is a rational number), when subjected to the iteration of our clockdoubling algorithm, yields an itinerary which ends up with a loop of period 20 : We see 17, 34 and then 68. When we follow the next numbers of the itinerary we eventually bump into 68 again, and now we know, because the system is deterministic, that all the numbers we already know that came after 68, will appear again, until 68 is reached again, etc.
In spite of the simplicity of this algorithm it generates behavior which is so rich, complex and erratic that it turns out to be completely unpredictable. In fact, in most cases (these involve the irrational numbers) the particle jumps back and forth in an apparently random fashion. To demonstrate this, it is most convenient to reformulate the same system in terms of b i n a r y numbers (instead of the conventional decimal numbers). Let us explain what such binary notation of numbers means.
While decimal numbers (which are just numbers, but written in decimal notation) are sums of powers of 10, binary numbers (numbers in binary nitation) are sums of powers of 2.
Let's give some examples, where Nten means the number N expressed in decimal notation, and where Ntwo means that same number N, but now expressed in binary notation.
425.26ten = 4 x 102 + 2 x 101 + 5 x 100 + 2 x 10-1 + 6 x 10-2
0.27ten = 0 x 100 + 2 x 10-1 + 7 x 10-2
While the digit string of a decimal number is composed of symbols from the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, the digit string of a binary number has only the symbols 0 and 1 at its disposal.
101.001two = 1 x 22 + 0 x 21 + 1 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3
Which is 4 + 1 + 2-3 = 5 + 1/8 = 51/8ten
0.011two = 0 x 20 + 0 x 2-1 + 1 x 2-2 + 1 x 2-3 = 1/4 + 1/8 = 3/8ten
When decimal numbers are multiplied by 10, one only needs to shift the decimal point one place to the right. Thus 643.215 x 10 = 6432.15.
Binary numbers have a similar rule except that it is multiplication by 2 rather than 10 that shifts the point. So 0.1011, when doubled, becomes 1.011. The rule adapts naturally to our doubling algorithm : successive applications applied to the number 0.1001011, for example, yield 0.001011, 0.01011, 0.1011, 0.011, 0.11, and so on (remembering to drop the 1 before the point if it appears).
The numbers in our interval will now be expressed by means of the binary notation. And if this interval 0two to 1two (which is equal to 0ten to 1ten) is represented by a line (i.e. to each number of the interval a point is assigned), then numbers less than half (0.5ten , 0.1two) lie to the left of the line's center, while numbers greater than half lie to the right. We can now envisage two equal compartments of our line, a left one (L) and a right one (R). Each number of the interval now belongs to either L (left compartment) or R (right compartment), while, in addition, we set that half itself (0.5ten , 0.1two) belongs to R.
In binary, these correspond to numbers for which the first entry after the (binal) point is 0 or 1 respectively. Thus 0.1011two (which is equal to 11/16ten , itself equal to 0.6875ten ) lies in the right compartment (R), and 0.01011two (which is equal to 11/32ten , itself equal to 0.34375ten ) lies in the left compartment (L). The clock doubling algorithm causes the 'particle' to jump back and forth between L and R, and the resulting LR sequence is exactly equivalent to the binary expansion of the initial number (expressing the initial position [state] of the jumping particle).
Suppose that we start with the number 0.011010001, which corresponds to a point in the left hand cell because the first entry after the binal point is 0. The particle therefore starts out in L. When doubled, this number becomes 0.11010001, which is on the right, i.e. the particle jumps into R. Doubling again gives 1.1010001, and our algorithm requires that we drop the 1 before the binal point. The first entry after this point is 1, so the particle stays in R. Continuing this way we generate the jump sequence LRRLRLLLR. So the binal expansion of the initial number precisely specifies the itinerary of the particle in terms of its position either in L or in R.
It will be clear from the foregoing that the fate of the particle (i.e. whether it is in L or in R) on the nth step will depend on whether the nth digit is a 0 or a 1. Thus two numbers which are identical up to the nth binal place, but differ in the n+1 entry, will generate the same sequence of L and R jumps for n steps, but will assign the particle to different compartments on the next step. In other words, two starting numbers that are very close together, corresponding to two points on the line that are very near to each other, will give rise to sequences of hops that eventually differ greatly.
It is now possible to see why the motion of the particle is unpredictable. Unless the initial position of the particle is known exactly the uncertainty will grow and grow until we eventually lose all ability to forecast.
After intervals expressed by binary numbers have been explained, we give two examples of the unpredictability (Several Figures, further below).
Intervals in the 0 to 1 line segment [0, 1].
The Interval 0.010
The next Figure gives this interval. Further below it is derived.
Figure above : The 0 to 1 line segment [0, 1]. Positions on this line are defined by the corresponding numbers. Some numbers are explicitly indicated and expressed in binary notation. The dots, ... at the tail of a digit sequence means that the last digit repeats itself indefinitely, thus specifying a number, not an interval. Intervals are specified by a binary sequence of digits without a ... tail.
The interval 0.010 is indicated (red).
The next Figure derives and explains this interval ( 0.010 ). In order to do so we read the relevant binary numbers by following their digits one by one. The Figure can be accessed (and seen in full screen) by clicking HERE , [and, after inspection, close the window to return to main text].
The Interval 0.01
To see how we can find the interval 0.01 (as contrasted with the interval 0.010 ) click HERE [and, after inspection, close the window to return to main text].
Clock Doubling of the line segment [0, 1].
We are now ready to give the first example that demonstates that the clock doubling algorithm yields an unpredictable behavior unless the intial condition is known with infinite precision. We'll do this by setting up, on the 0 to 1 line segment, a small interval (which stands for a number with a small uncertainty attached to it, an uncertainty as to its precise value), and follow this interval when the clock doubling algorithm is repeatedly applied to the 0 to 1 line segment (and thus to all its corresponding numbers). We will see that the uncertainty rapidly increases when the algorithm is repeatedly applied (always to the last obtained result). So what we do is apply the algorithm (doubling and : "1." becomes "0." ) to the whole 0 to 1 line segment, and follow the fate of a small part of it, namely the mentioned interval. In the next Figure we see, in addition to the interval (0.0110101) figuring in the first example, also the interval (0.0110111) that is going to figure in the second example. These intervals are first derived. :
Figure above : The 0 to 1 line segment. Positions on this line are given by the corresponding numbers in binary notation.
To emphasize again, " u v w 0 . . ." means that the last digit 0 is repeated indefinitely
The interval 0.10010 expresses the fact that the next digit that should come after the sequence 0.10010 is unknown. So it could either be a 0 or a 1. And these possible digits determine the begin and end numbers defining the interval.
These numbers are thus : 0.10010 0... (which is equal to 0.10010...) and is the minimum value (left extreme of the interval), and 0.100101... (which is equal to 0.100110...) and is the maximal value (right extreme of the interval).
In the same way the interval 0.010 expresses the uncertainty as to the value of the next digit (0 or 1), so the minimum value is 0.010 0... (which is equal to 0.010...) and the maximum value is 0.0101... (which is equal to 0.0110...).
Finally, the interval 0.01 expresses the uncertainty as to the value (0 or 1) of the next digit after 0.01, so the minimum value is 0.010... and the maximum value is 0.011... (which is equal to 0.01... and also to 0.10...).
In the Figure (i.e. the drawing) just given above, we have indicated (and explained) the interval 0.0110101 which lies between 0.01101010... and 0.01101011... . It is the interval that we are about to follow when it is subjected to the clock doubling algorithm (or, in other words, which is the algorithm's initial condition). Also here, the interval expresses the uncertainty of the next digit, so the minimal value (representing the left extreme of the interval) is 0.01101010... and the maximal value (representing the right extreme of the interval is 0.01101011... (which is equal to 0.0110101... ) and also to 0.0110110... ).
The Figure below will show the fate of this interval under the clock doubling algorithm.
0.0110101, 0.110101, 0.10101, 0.0101, 0.101, 0.01, 0.1 .
We have thus obtained these intervals by successively shifting the binal point one place to the right (which is the effect of doubling) and have dropped the 1 before the binal point (when there appeared such a 1). If, after having obtained the interval 0.1 , we again shift the binal point one place to the right and change (the resulting) "1." into "0.", then we get " 0.---", which means that we know that the interval is still in the 0 to 1 line segment, but we have no idea where. And because our 'universe' was the 0 to 1 line segment (and nothing more), the uncertainty has grown to 100 percent.
We can also say that we had an initial number (which could represent our jumping particle at its start) given with a small uncertainty (and therefore given as a small interval). Upon running the clock doubling algorithm the uncertainty of the successively resulting numbers increases rapidly. Already after seven iterations (i.e. after having applied the algorithm seven times [always to the result of the previous application] ) we have no idea anymore into what number the intial number has finally been transformed. We don't even know in what compartment ( L orR ) of the 0 to 1 line segment the number, and thus the jumping particle, will end up after (only) seven iterations. So, unless we know the initial condition with infinite precision, this clock doubling is totally unpredictable as to its more or less long-term outcomes.
The next Figure depicts all this geometrically. It can be accessed (and seen in full screen) by clicking HERE (and, after inspection, be closed to return to main text).W
And for a more compact overview of this dynamics click HERE (and, after inspection, close the window to return to main text).
What comes next is the second example of the unpredictability (and instability) of Clock Doubling : We follow an interval that is very close to the interval (0.0110101) just investigated, namely the interval 0.0110111 . We will see that the evolutions emanating from these two very similar initial conditions differ strongly. And also in the case of this new interval the uncertainty grows rapidly till it becomes 100 percent.
And for a more compact overview of this dynamics, and a comparison with the previous result (first example) (by scrolling further down), click HERE (and, after inspection, close the window to return to main text).
So we have now shown the unpredictability of the clock doubling process when the initial condition is not known exactly. Generally, if we know the initial position of the particle to an accuracy of n binary digits after the point, we will not be able to forecast whether it will be on the left (L) or right (R) of the 0 to 1 line interval after n jumps. Because a precise specification of the initial position requires an infinite binary expansion, any error will sooner or later lead to a deviation between prediction and fact.
All this is quite clear from what has been found above.
Now we must ask ourselves : What is the ontological status of this unpredictability? Is it just epistemological or is it truly ontological? The latter case would mean that the unpredictability is not only an unpredictability for us (as researcher), but also for Nature herself. And that in turn means that the course of the clock doubling process is, where it is materialized in some way in Nature, not deterministic.
If the unpredictability is only epistemological, then the process is (also as it is materialized in Nature) still deterministic. In either case, of course, the system is highly unstable, because the slightest, even infinitely small, difference of starting conditions can produce totally different long-term behaviors of the system.
Earlier we have stated that such a form of instability, when it occurs in real-world systems (and it indeed does), could point to the impossibility of point-like starting states (and indeed any other state) (Other reasons for this impossibility may come from the mathematical and metaphysical analysis of a continuum, such as a line segment, where one could argue that an actual infinity of digits specifying a number, and with it a position, is impossible : the infinity is only potential, which means that there is no end of the digit string. The digit string keeps on expanding, while nevertheless being finite (and thus always being just an interval) at whatever stadium along the way of this expansion. Never is the totality of the infinite number of digits (which are specifications or conditions) present together as a whole. And infinity of the number of parts of a continuum only being a potential infinity, follows from the wholeness nature of every continuum : its parts are only potentially there, not actually.). If this is correct, then the unpredictability of real-world versions of systems like clock doubling is an ontological unpredictability (i.e. an unpredictability because of ontological reasons). Of course a starting condition in its ontological limit, i.e. holding the ontologically smallest possible volume in the phase space of the corresponding dynamical system, can by far not be reached by our observations and measurements, so where science now stands we have to do with the epistemological limit, representing a much larger volume in phase space than that belonging to the ontological limit. And in both cases a statistical approach is necessary.
Phase Space of the Clock Doubling System.
Generally within a volume-like initial condition the number of potential trajectories (in phase space) that can (one at a time, according to a certain probability) emanate from this volume is potentially (but not actually) infinite. Such a trajectory is a series of successive system states each represented by a same volume (somewhere in phase space).
Clock doubling can be interpreted as the jumping motion of a single 'particle'. And this particle possesses -- in the context of clock doubling -- with respect to its state (which thus is here also the state of the system) only one variable, namely its position in the line segment [0, 1] (i.e. in the 0 to 1 line segment). And this position can be expressed by a number lying between 0 (inclusive) and 1 (inclusive, but which is set equal to 0 again, because our system is in fact a 'clock', that is to say the [0, 1] line segment is bent back to form a circle -- the dial of a 'clock' [ If we include this circular form of the line, then, in the algorithm we do not need the "drop the 1 before the point" command anymore] ). So we have one particle and one particle-state variable, and that means that we can describe our clock doubling system with a phase space which has 1 x 1 = 1 dimensions (Generally a particular system state is the particular configuration of all the particle-states (element states) at a certain moment in time, and such a system state can be represented in phase space by a single point). And this implies that the line segment [0, 1] is not only the (one-dimensional) space in which the particle actually jumps to and fro, but at the same time the phase space of the system. So the actual position of the particle in the line segment [0, 1] is at the same time the position of the system in its (one-dimensional) phase space.
Rational and Irrational Numbers.
The line segment [0, 1] is, as any line segment, a continuum, and so also the set of numbers corresponding to points of that line segment, that is to say these numbers also form a continuum. The numbers (which we here consider in their binary notation) of this line segment are all so-called real numbers. The real-number set of this line segment consists of two varieties of real numbers, namely rational numbers and irrational numbers, which are totally intermixed with each other : both varieties can be found in any interval of the [0, 1] line segment howsoever small.
A rational number is a number that can be expressed by the ratio of two integers (whole numbers). This includes all fractions, but also all integers because they also can be expressed as a ratio of whole numbers, namely the number itself and the number 1. There are infinitely many of these rationals (in any interval). They themselves can be indexed by whole numbers (i.e. they can be counted), so it is said that there are as many rationals as there are intergers (there is a one-to-one correspondence between the members of the two sets). When expressed as a decimal or binal expansion a rational number either ends up with a repetition of one digit, or with a repetition of a segment of the digit chain.
As has been said, there are infinitely many rational numbers, but strewn between these rationals are the irrationals.
An irrational number is a number that cannot be expressed as the ratio between two integers. Its decimal or binary expansion does not end up with a repetition of some particular digit, neither does it end up with a repetition of some segment of the digit chain. The irrationals cannot be indexed by integers, and thus it is said that, in a given interval, there are more irrational numbers than there are rational numbers, despite the fact that such an interval contains infinitely many rational numbers. In fact there are infinitely many more irrationals than there are rationals in any given interval, that is to say, rational numbers are extremely rare in such an interval.
The nature of trajectories in clock doubling.
The numbers which we have used thus far in our clock doubling system (for instance those that indicated the boundaries of intervals) were such that their binal expansion ended up with a repetition of digits, so these were all rational numbers. But even with them, if we only have, as initial conditions, intervals (starting with a rational number and ending with one) at our disposal, we get an increase of uncertainty.
Only if we have a precisely expressed and completely and explicitly known number (and thus a rational number) as (specifying) an initial condition (and thus not a mere interval), for instance 0.110010... or 0.001101 (the digit string 1101 repeated indefinitely), then the system ends up in a stationary state or in a cycle respectively, which means that the total behavior of the system is precisely known.
Every irrational number as initial condition (for the clock doubling system) results in an increase of uncertainty (as to the behavior of the system), because an irrational number is never completely and explicitely known, despite the fact that some of them, like SQUARE ROOT (x), or PI, can be defined exactly. Thus an irrational number is itself only given by a truncated digit string (which means by an approximation) and thus is given only by an interval. While square roots, pi, and the like can be calculated, resulting in an ever better approximation, the digit sequence of irrational numbers such as the one given below, can even be imagined. But neither of these irrational numbers, although 'known', can be written down completely (these numbers are never complete(d)).
A study of the theory of numbers reveals an important feature about the clock doubling system. To expound this we agree on indicating the numbers (in their binary expression) within the [0, 1] line segment only by their binary expansion that comes after the binary point (because all numbers of the [0, 0] line segment start with "0." , even the number 0, which is 0.0..., and even the number 1, which can be written as 0.1111... ).
Suppose we pick a finite digit string, say 101101 . All binary numbers (Recall that "binary numbers" are just ordinary numbers expressed in binary notation) between 0 and 1 that start out with this particular string lie in a narrow interval of the line bounded by the numbers 1011010... and 101101... . If we choose a longer string, a narrower interval is circumscribed. The longer the string the narrower the interval. In the limit that the string becomes infinitely long, the range shrinks to nothing and a single point (i.e. number) is specified.
Let us now return to the behavior of the jumping particle. If the example digit string 101101 occurs somewhere in the binary expansion of its initial position then it must be the case that at some stage in its itinerary the particle will end up jumping into the above line interval (because, at every step in the running of our system, we shift the binal point one place to the right and drop the 1 before the point when it appears there, so sooner or later we arrive at 0.101101----- ). And a similar result holds, of course, for any finite digit string.
Now it can be proved (See DAVIES, P., The Cosmic Blueprint, 1987, p.33 of the 1989 Unwin edition) that every finite digit string crops up somewhere in the infinite binary
expansion of every irrational number (strictly with isolated exceptions such as :
0.010010001000010000010000001000000010000000010000000001 etc.).
It follows that if the particle starts out at a point specified by any irrational number (and most points on the line interval are specified by irrational numbers), then sooner or later it must hop into the narrow region specified by any arbitrary digit string. Thus, the particle is assured to visit every interval of the line, however narrow, at some stage during its career.
In phase space terminology we can say that the clock doubling system visits every 'volume' of its phase space at some stage during its career, however small this volume.
Such a behavior we can indeed call random (and, especially objectively random) because every volume, however small, of phase space has the same chance of being (eventually) visited (incontrast to cases where the system only moves around in a very limited part of phase space, while never visiting the other parts, for instance where the system quickly settles onto a small cycle, or to a point.
One can go further (Ibid., p.33). It turns out that any given string of digits not only crops up somewhere in the binary expansion of (almost) every irrational number, it does so infinitely many times. In terms of particle jumps, this means that when the particle hops out of a particular interval of the line, we know that eventually it will return -- and do so again and again. As this remains true however small the region of interest, and as it applies to any such region anywhere on the line interval, it must be the case that the particle visits every part of the line again and again, there are no gaps.
REMARK :
In the described case the particle does not visit a same number (point on the line) twice, because in that case the whole trajectory lying between this point and its second visit will be repeated, and repeated indefinitely, implying that the initial condition (starting number) is rational, whereas we were describing the case of an irrational starting number.
The particle visits every preconceived interval (not every preconceived point) however small. Only in that sense it explores the whole of phase space (if the starting number was irrational).
This "exploring the whole of phase space" (again and again) is the property of ergodicity (of unstable systems).
Algorithmic complexity theory provides a means of quantifying the complexity of infinite digit strings in terms of the amount of information necessary for a computing machine to generate them. Some numbers, even though they involve infinite binary expansions, can be specified by finite computer algorithms. Actually the number pi belongs to this class, in spite of the apparently endless complexity of its binary expansion.
However, according to DAVIES, Ibid., p.34, most numbers require i n f i n i t e computer programming information for their generation, and can therefore be considered infinitely complex. It follows that most numbers are actually unspecifiable! They are completely unpredictable and completely incalculable. Their binary expansions are r a n d o m in the most fundamental and objective sense.
Clearly, if the motion of a particle is based on such a number it too is truly random.
To analyse this phenomenon further, we must define what randomness actually is. For this we must first know what coincidence is. Well, coincidence is an event that is the result of several cause-and-effect chains, without these chains being structurally connected to each other. For instance, when there is some accident, like colliding automobiles, an explosion can take place. If so there were two causal chains, namely one that resulted in the presence of a spark at some spot, and another in the presence of inflammable fuel at the same spot. These two chains are not regulatively connected to each other, in the way that they always happen together (as they are so connected in a combustion engine). So the explosion is a coincidence. However, we are not at all surprised when an explosion occurs when two cars collide. This we express by the saying that the probability of the simultaneous presence at the same spot, of a spark and an inflammable substance, and thus the probability of an explosion, is fairly high, despite the fact that such an explosion is, strictly considered, a (result of a) coincidence. So probability is the chance that a coincidental event actually happens.
If we now conceive of a large number of possible events that are each for themselves coincidental, then we can assign a chance (value) to each of these events to actually take place. And if these chances for all of these events are exactly the same (because of the absence of some special organizing factor, causing a bias in these chances), then these events occur randomly.
Let's now go back to our jumping particle. A jump of it from one point of the line to another is an event. When the initial number is given, then each event necessarily follows from the previous event, for example the transition : 0.0110... ==> 0.110... . So the sequence of events, that is to say the sequence of resulting binary strings is not random, because they are determined by the binary expansion of the initial number. All the time a next binary digit string is ultimately determined by the intial number.
If we think in terms of the two compartments of the 0 to 1 line segment, namely the left-hand half (L), consisting of numbers of which the first binary digit after the binary point is a 0, and the right-hand half (R) consisting of numbers of which the first binary digit after the binary point is a 1, then in which of the two compartments the particle will jump depends on the value of the first digit after the binal point of the number that resulted from the previous number by the clock doubling operation.
So if we have an initial number and apply the clock doubling algorithm repeatedly, then for every step -- every iteration -- we must just shift the binal point one place to the right and drop the 1 before the binal point if there appears one. And thus we can read off the particle's itinerary in tems of compartments L and R directly from the binary expansion of the initial number. And because this initial number is supposed to be given, the sequence of events (hopping in L, hopping in R) is not random, that is to say the chance that the next compartment (in which the particle will be) is R is not equal to the chance that the next comparment is L, because the compartment in which the particle will be is already totally determined, and so to one of them a zero chance is attached.
But now the case of an irrational starting number (for the clock doubling system).
For this there are two possibilities, namely a specifiable irrational number (like, say, SQUARE ROOT (2ten) , which can be defined to be that number that when it is squared results in the number 2ten), or a non-specifiable number (about we spoke above).
When we apply the clock doubling algorithm to the 0 to 1 line segment, starting from a specifiable irrational number, and follow the sequence of the resulting L's and R's, we have the following situation.
As long as we know the next digit of the initial number, we know in which compartment the particle will be, that is to say that comparment, L or R, is determined. As we continue to shift the binary point (and drop the 1 when it appears before that point) we finally are at the end of the known digit string of the (specifiable) irrational number. So in order to know in what compartment the particle will be at the next step, we have to compute the next digit of our initial number. Having computed it, we know the compartment in which the particle will be. Then the next digit of the starting number must be computed, etc. So also in this case the succession of L's and R's is completely determined (in the sense that each next L or R is determined, not, however, in the sense that all L's and R's are determined). Every time, one of the possibilities, L or R, has a zero chance of appearing while the other has a 100 percent chance to appear, so the sequence is not random.
When, on the other hand, we appy the clock doubling algorithm to the 0 to 1 line segment, starting from a non-specifiable irrational number, and follow the sequence of the resulting L's and R's, we have the following situation.
Because the initial number cannot be specified (except for being in the 0 to 1 line segment), and thus not, digit for digit, be computed, the chance of every next digit is 50 percent for being a 0 and 50 percent for being a 1. And, of course, the same applies for the resulting L's or R's. So the sequence of digits and that of corresponding compartments (L, R) are each totally and objectively random. The appearance of a next digit after an existing digit, and also a next compartment (in which the particle will be) after that in which the particle presently is, can be considered a coincidence, for example after a 0 (of the initial digit string) there happened to appear a 1, and thus, if we look at the system, after the particle was in L, it now happened to appear in R. While the LR sequence does depend on the 01 sequence in the initial string, this string itself is not determined, and thus the LR sequence is ultimately also not determined. In fact the initial digit string (the unspecifiable irrational starting number) 'develops' gradually while the system goes its way, that is to say the system's initial state is not in any way fixed but developes. But it develops randomly. The gradual completion (which never comes to a conclusion) of the unspecifiable irrational initial number is, with respect to every newly attached digit, an event that is fortuitous (50 percent chance for 0, and 50 percent chance for 1). A certain digit is attached to a previously attached digit, without there being any principle or law that connects these two digits. Precisely the same can be said with respect to the ensuing string of L's and R's. So indeed, clock doubling, starting from an unspecifiable irrational number (and most of the numbers are unspecifiable irrational numbers) gives a totally and objectively random sequence of L's and R's, or in other words, the behavior of such a system is totally and objectively random, while for clock doubling starting off from a specifiable initial number it is not.
Let us now follow trajectories that start out from the most common type of number, namely the unspecifiable number. And if we apply to such a number (or to the small interval in which it lies) the clock doubling algorithm (that is to say, if we repeatedly apply this algorithm to the whole 0 to 1 line segment, i.e. to every one of its points [or sub-segments], or, equivalently, to every one of its numbers [or intervals]), and follow the fate of the number or interval that we had named "starting number", or "starting interval" representing that number, then we have to do with causality in its least recognizable form. And it is from this form that its true and general nature can be derived. So clock doubling (as an instance of an unstable dynamical system) from an unspecifiable irrational starting number is expected to uncover the bare bones of causality, or at least some of them.
Thereby we can, as shown above, see the 0 to 1 line segment as the phase space of the clock doubling system, where thus the actual location of the jumping particle (on the line) is at the same time the actual state of the system (i.e. the position of the system in its phase space). And what we then in fact do is repeatedly applying the clock doubling algorithm to the whole of phase space and follow the fate of one point or of one (small) 'volume' of it.
To begin with we could depart from a small interval (within the 0 to 1 line segment), representing the ontological limit, i.e. representing the ontologically smallest possible area that can represent a number. It is best to consider this interval as being an open interval, which means that its two boundary points (numbers) do not belong to the interval.
From this interval -- the initial condition of the system -- can emanate potential trajectories. One of them will actually appear, according to a distribution of chances over those possible trajectories. Of course such an appearing 'trajectory' is not actually a true trajectory, i.e. not a succession of point-like system states, but a succession of 'volume-like' system states of which, say, the centers represent the trajectory.
Now suppose that this initial condition or state of the clock doubling system is represented by the interval 0.0101 of which the boundary points 0.01010... and 0.01011... do not belong to the interval. So this interval is supposed to represent the ontological limit of an initial condition (a condition represented by an ontologically minimal area of phase space).
The evolution of this interval -- the intial 'blob' in phase space -- under the clock doubling algorithm, can be depicted as follows : Click HERE .
From this intial interval ('blob') can emanate potential trajectories, one of which could be for example a trajectory starting from the unspecifiable number 0.010101---- , where we consider this number to reside in the sub-interval 0.010101, bounded by 0.0101010... and 0.0101011... (We can say that most numbers in the sub-interval 0.010101 (as in any interval) are unspecifiable numbers, and our number, 0.010101---- , is one of them). See the following magnification :
Figure above : The interval 0.0101 (red and purple). The boundary points are (here) supposed not to belong to the interval. Some other points are indicated. Also the sub-interval 0.010101 is indicated (purple) in which our unspecifiable number 0.010101---- lies.
REMARK :
Before we continue, let us summarize our notations of numbers and intervals by digits, to avoid misunderstandings :
Because the size of the present document is bound to become too large, we continue our discussion in the next document.
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-28.
e-mail : 