

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Equilateral Triangle
Let us consider a fully developed two-dimensional crystal having as its intrinsic shape the equilateral triangle :

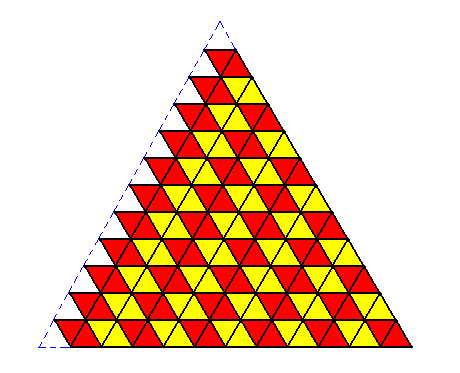
A regularly-triangular crystal could, at first sight, be conceived of as being built up by a stacking of microscopic regularly-triangular units, as the next Figure illustrates.

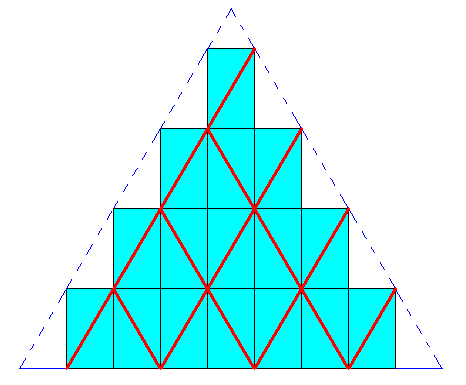
However, the plane group underlying this triangular tiling of the plane is the plane group P6mm : The pattern (conceived to be extended indefinitely over the plane) possesses mirror lines in six different directions and 6-fold rotation axes. One such axis is highlighted in the next Figure.
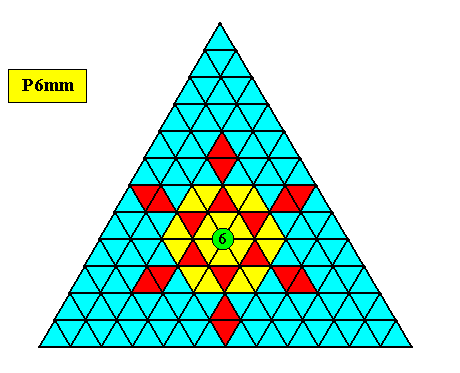
Because the 6-fold rotation axis, and three of the six mirror lines, implied by this plane group (P6mm) and as such belonging to its point symmetry, do not occur among the symmetries of the Equilateral Triangle as such, a triangular tiling of the plane, as given above, cannot support regularly-triangular crystal shape. And moreover, the small triangles, making up the large triangle, are not genuine building blocks of crystals at all, because their stacking is not periodic. So we will not encounter triangular building blocks in crystals at all.
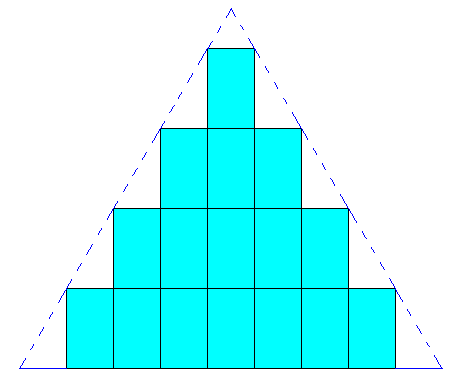
But a regularly-triangular crystal can, in appropriate cases (in fact they are equivalent), also be accomplished by the periodic stacking of rectangles, but only of rectangles of which the proportion of the longer and the shorter side is such that the diagonals involve angles of 600. See next Figure.
These rectangles, however, are directly related to the above mentioned rhombi (viz. those with 60 and 120 degrees angles) by their diagonals, as the next Figure shows.
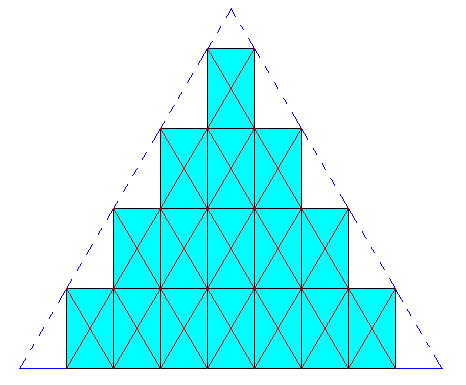
The next Figure analyses this relation of the rectangles to the rhombi formed by their diagonals.
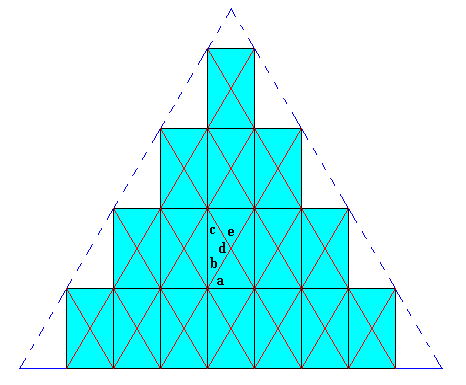
Figure above : The rhombi formed by the diagonals of the rectangles are rhombi with 60 and 120 degrees angles, and therefore appropriate building blocks for a regularly-triangular crystal. To see this, consider the angles a, b, c, d and e . First of all a is 600 (in virtue of the special dimensions of the rectangle). b is therefore 300. But then c is also 300. It then follows that d is 1200 and from this follows that e is 600.
The next two Figures show the rhombic net formed by the diagonals of the rectangles.
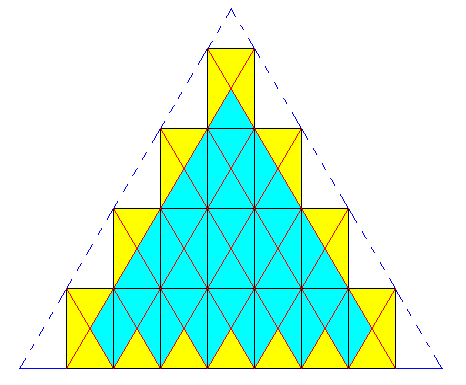
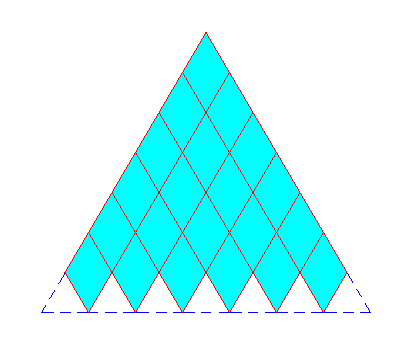
Figure above : Two-dimensional intrinsically regularly-triangular crystal built up by the periodic stacking of rhomb-shaped (empty) building blocks. The rhombi possess 60 and 120 degrees angles. As such these rhombi together constitute a hexagonal lattice.
When motifs are inserted we will need larger rhombi (but with the same angles) to represent (filled-in) unit meshes. See next Figure.
The true point symmetry of such a regularly-triangular two-dimensional crystal is either according to the Dihedral Group D3 (crystallographically denoted as 3m , and full point symmetry of the Equilateral Triangle), or to the Cyclic Group C3 (crystallographically denoted as 3 ), or to the Dihedral Group D1 (crystallographically denoted as m ), or, finally, to the Asymmetric Group C1 (crystallographically denoted as 1 ), all depending on the crystal's internal structure.
That a regularly-triangular crystal (i.e. a crystal having as its intrinsic shape the equilateral triangle) can have these intrinsic symmetries can be explained succinctly as follows (and will be further evident in the sequel) :
An Equilateral Triangle as such has the following (point) symmetries, i.e. it will be superposed upon itself by the following transformations (which are therefore symmetry transformations) :
The regularly-triangular crystal originates by development of crystal faces. These faces will appear in accordance with the available symmetry, i.e. according to the set of symmetry transformations available in each case. And this set is dependent on the symmetry of the motif. An initially given face will imply copies of itself according to this set of available symmetry transformations. The configuration of faces so obtained then constitutes a Form (in the crystallographic sense). So it is clear that :
| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 3 |
| Pm Cm Pg |
D1 ( m ) | 2 |
| P3 | C3 ( 3 ) | 1 |
| P3m1 | D3 ( 3m ) | 1 |
* The plane group P31m does not support regularly-triangular crystals, as we will see in the sequel.
For each of these plane groups we will show how it supports a regularly-triangular crystal shape. The intrinsic shape of the crystal, i.e. the shape a crystal adopts when fully grown (i.e. fully developed) under uniform conditions, in the present case its regularly-triangular shape, depends on the Growth Rate Vector Rosette, which in turn depends on the atomic aspects (chemical nature of motifs and geometry of lattice) presented to the growing environment by the possible crystal faces. The regularly-triangular crystal can be formed by the periodic stacking of rhomb- or rectangularly-shaped building blocks (unit meshes) containing a motif s.str. compatible with the point symmetry implied by the given plane group. The point symmetry is indicated in each case. Recall that the point symmetry of a crystal is the translation-free residue of its plane group symmetry.
An equilateral triangle, which has a point symmetry according to the group D3 , will be supported by those plane groups of which all the implied point symmetries (i.e. implied by the plane group) are also symmetries of the Equilateral Triangle. This does not necessarily hold the other way around : A crystal can have an intrinsic shape that is an equilateral triangle, but nevertheless some, or even all, symmetries of this triangle can be absent in the crystal, resulting in the fact that the intrinsic symmetry of the crystal is lower than that of its intrinsic shape.
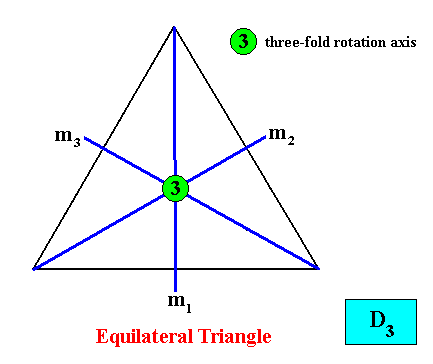
Figure above : The symmetries (indicated by symmetry elements) of the Equilateral Triangle : Three mirror lines and a three-fold rotation axis at their point of intersection.
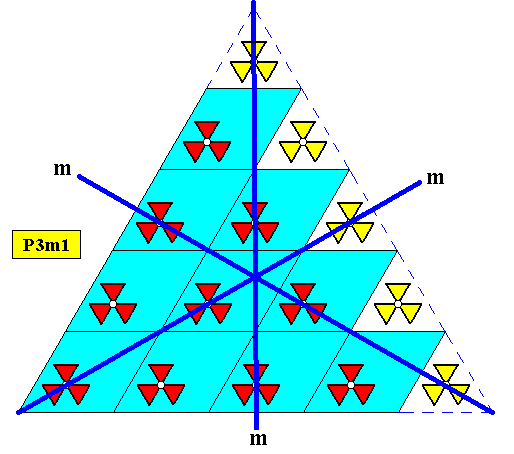
Plane Group P3m1.
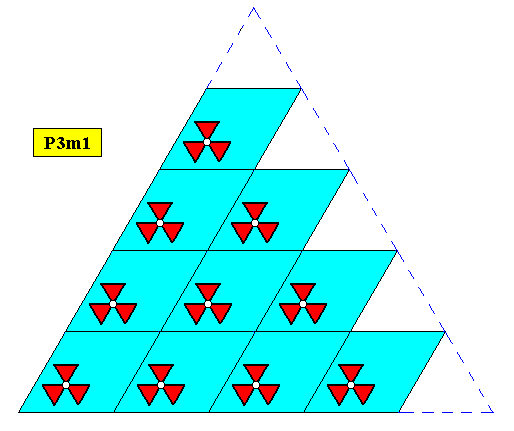
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D3 , and supported by a hexagonal point lattice (indicated by connection lines). A hexagonal point lattice consists of rhomb-shaped meshes, where the rhombi are special : they have 600 and 1200 angles. And in the present case the crystal is built up by the periodic stacking of such rhombic building blocks.
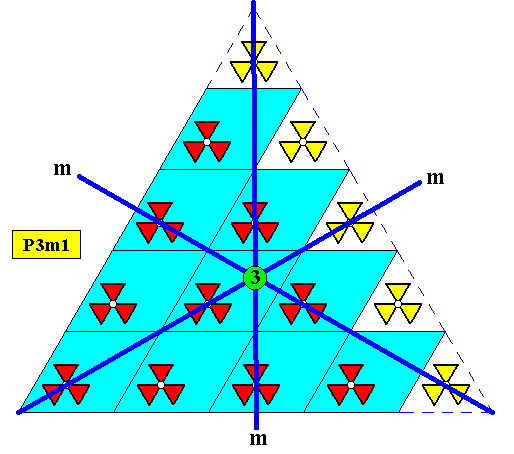
For convenient overview of shape we give yet a smaller version of the same crystal type :
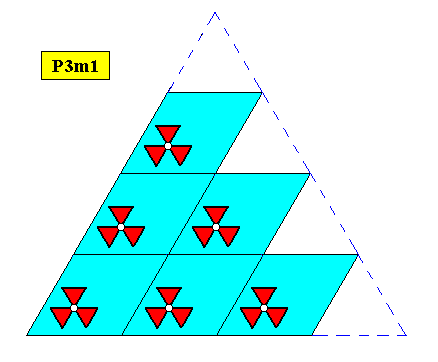
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D3 , and supported by a hexagonal point lattice (indicated by connection lines). Smaller version.
The next Figures show that the point symmetries of of the plane group, viz. three mirror lines and a 3-fold rotation axis, are also symmetries of the equilateral triangle representing the shape of the crystal. The pattern of motifs s.str. is extended a little bit in order to let the symmetries be evident (Recall that the microscopic structural pattern of motifs s.str. of a (two-dimensional) crystal must be imagined to extend indefinitely over the plane). Also recall that the lattice connection lines do not as such belong to the pattern.
In the above Figures we had extended the pattern of motifs s.str. a little bit, which is allowed, because the pattern is supposed to be already extended indefinitely -- (the latter) by reason of the fact that in crystals the translations are very very small indeed, and thus allowing the number of repetitions to be considered infinite (and only as such these patterns will represent genuine (plane) groups). We performed this (partial) extension in order to show the point symmetry of the crystal. But, in order to do so, we can just as well remove some empty space (which is part of the motif s.l.), as the next Figure illustrates.
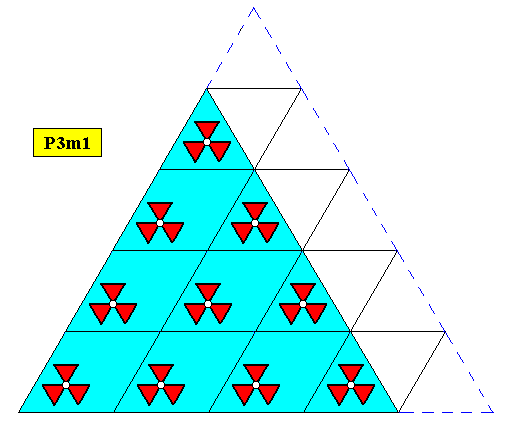
Figure above : Two-dimensional regularly-triangular crystal (blue), with point symmetry D3 , and supported by a hexagonal point lattice (indicated by connection lines). Compare with the Figure above , depicting the same crystal (which is, consequently a slightly larger version).
Plane Group P31m.
Here there is a snag : One would perhaps be tempted to let the plane group P31m support a regularly-triangular crystal shape according to the next two Figures :
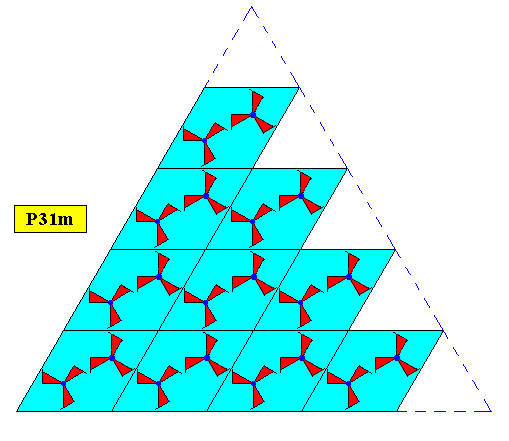
Figure above : Alleged two-dimensional regularly-triangular crystal, with point symmetry D3 , and supported by a hexagonal point lattice (indicated by connection lines).
For convenient overview of shape we give yet a smaller version of the same crystal type :
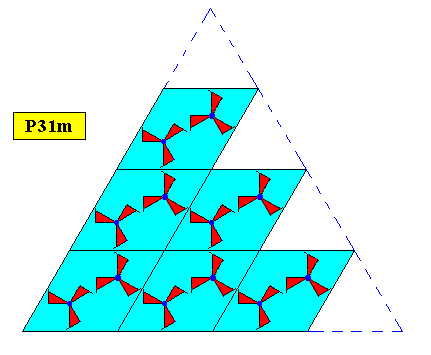
Figure above : Alleged two-dimensional regularly-triangular crystal, with point symmetry D3 , and supported by a hexagonal point lattice (indicated by connection lines). Smaller version.
The next Figure emphasizes the alleged possibility to form a regularly-triangular crystal on the basis of our plane group P31m.
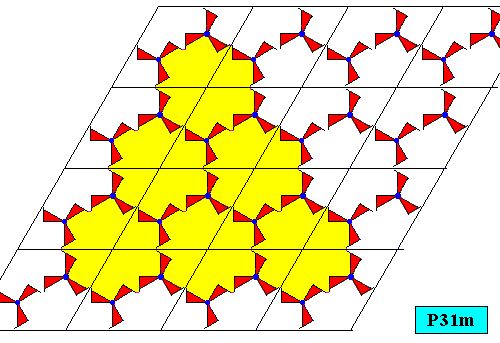
But the relevant internal symmetry elements do not align with those of the equilateral triangle allegedly representing the shape of the crystal, and so do not coincide with them. See next Figures.
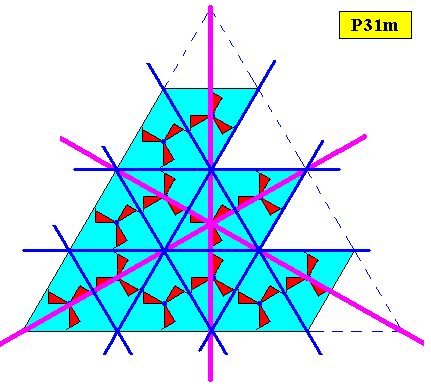
Figure above : The plane group pattern has mirror lines in three directions. No one of them coincides with a mirror line of the equilateral triangle allegedly representing the shape of the crystal.
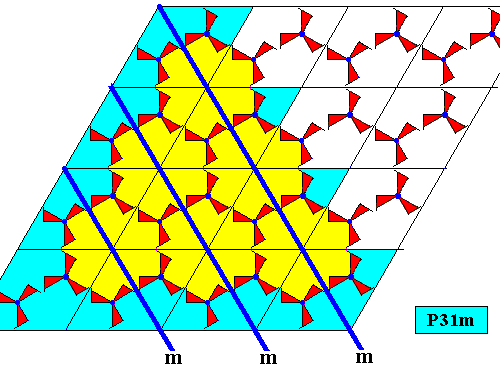
Figure above : In the direction shown there is no mirror line of the plane group pattern that coincides with a mirror line of the equilateral triangle allegedly representing the shape of the crystal.
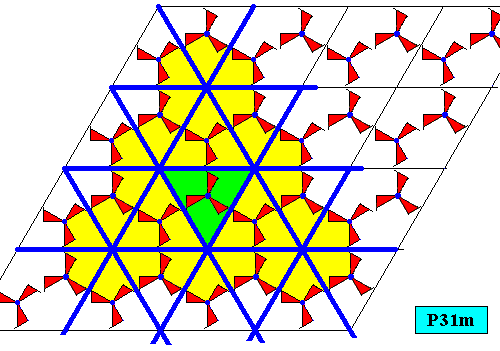
Figure above : Relevant (i.e. relevant with respect to the equilateral triangle allegedly representing the shape of the crystal) mirror lines of all three directions of the plane group pattern (plane group P31m). No one of them coincides with one of the mirror lines of the mentioned equilateral triangle. The center of the latter is highlighted. As one can see there is a 3-fold rotation axis of the periodic P31m pattern that does coincide with the 3-fold rotation axis of the (mentioned) equilateral triangle, but there are no three mirror lines of the periodic pattern such that their point of intersection coincides with the location of this axis. The symmetry of the triangular crystal, i.e. its intrinsic symmetry, is, consequently, according to the Cyclic Group C3 instead of the Dihedral Group D3 (which is the point group implied by the plane group P31m).
The next two Figures depict our regularly-triangular crystal without the lattice connection lines (which do not belong to the internal pattern as such). One can see that the intrinsic symmetry of this crystal is not D3 as should be expected (because it is the point symmetry implied by the present plane group, i.e. the group P31m), but C3 , i.e. its only symmetry element is a 3-fold rotation axis.
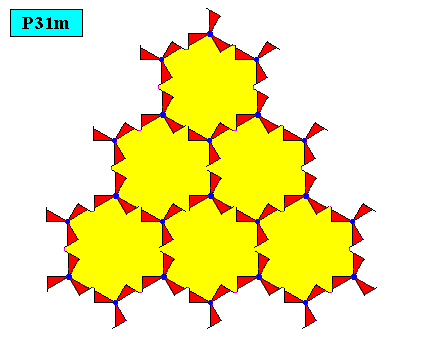
Figure above : Two-dimensional crystal with the intrinsic shape of an equilateral triangle as it was discussed above, drawn without lattice connection lines.
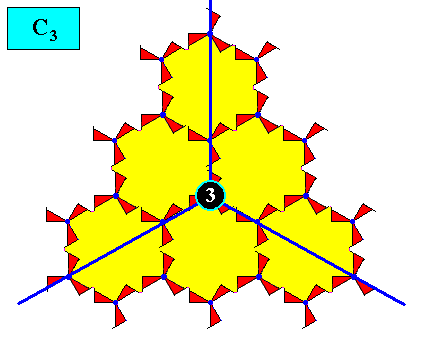
Figure above : Same as previous Figure. The 3-fold rotation axis as the only symmetry element of the triangular crystal, is indicated. The blue lines are not mirror lines of the crystal.
So the plane group P31m does not support crystals with the Equilateral Triangle as their intrinsic shape.
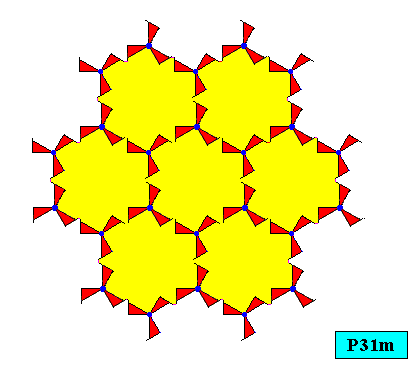
Figure above : Two-dimensional crystal with intrinsic (regularly) hexagonal shape, supported by the plane group P31m. The connection lines of the hexagonal point lattice not drawn. The next Figure shows its intrinsic symmetry.
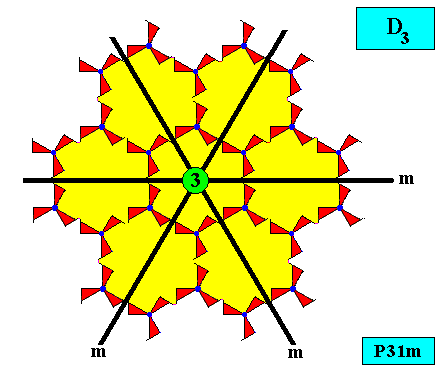
Figure above : Two-dimensional crystal with intrinsic (regularly) hexagonal shape, supported by the plane group P31m. The connection lines of the hexagonal point lattice not drawn. While the hexagon -- as being the shape of the crystal -- itself has D6 symmetry, the intrinsic symmetry of the crystal is lower, namely according to the group D3 : three mirror lines and one 3-fold rotation axis (while the hexagon, just as hexagon, has six mirror lines and one 6-fold rotation axis).
Plane Group P3.
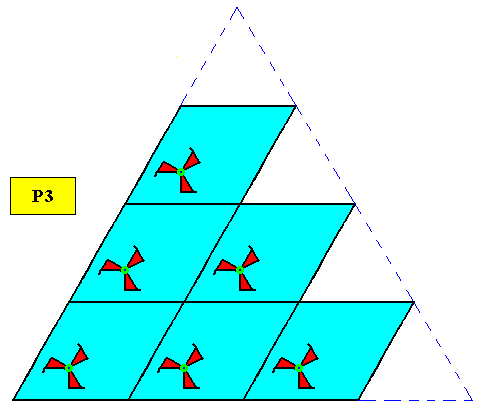
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry C3 , and supported by a hexagonal point lattice (indicated by connection lines).
The next two Figures show the symmetry -- C3 -- of the above crystal.
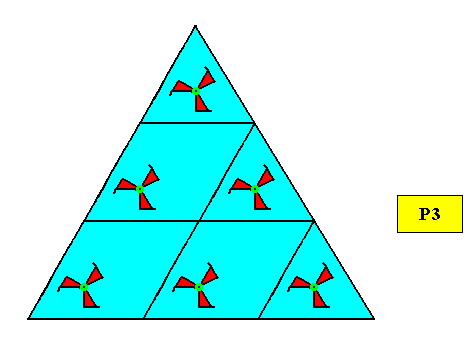
Figure above : The two-dimensional regularly-triangular crystal of the previous Figure, with point symmetry C3 , and supported by a hexagonal point lattice (indicated by connection lines). Empty spaces (right side) removed (resulting in a smaller version of the crystal, but wholly equivalent).
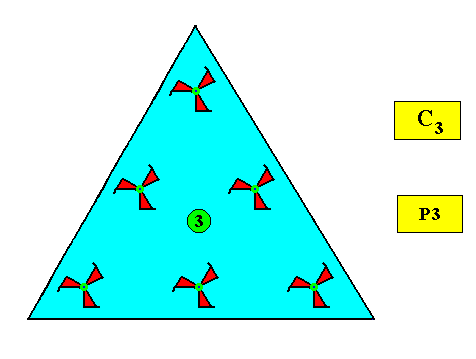
Figure above : Same as previous Figure. Lattice connection lines removed (they do not belong to the pattern), and the 3-fold rotation axis (as the only symmetry element of the crystal) indicated. The intrinsic symmetry of the triangular crystal is clearly according to the group C3 (which is implied by the supporting plane group P3 ).
The next Figure shows that the periodic stacking of rhombi is equivalent to a periodic stacking of corresponding rectangles (as was discussed above).
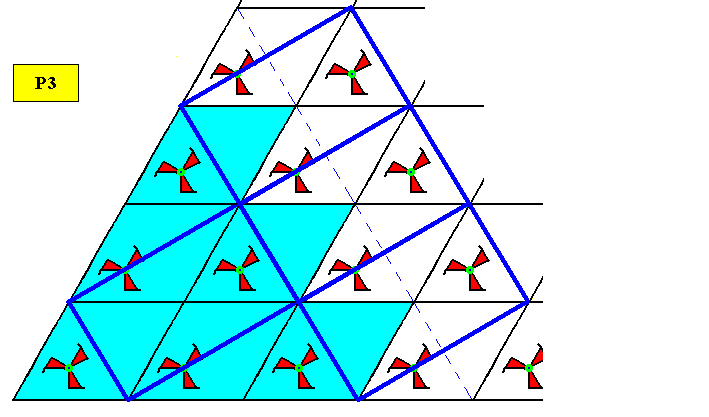
Plane Groups Pm and Pg.
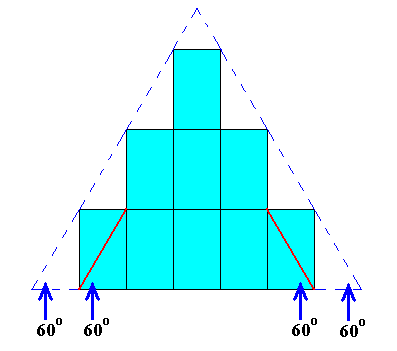
Figure above : Rectangular building blocks of special dimensions, namely such that their diagonals involve angles of 600, can be periodically stacked in such a way that possible crystal faces form an equilateral triangle. The next Figures provide these rectangular building blocks with appropriate motifs, resulting in the plane groups Pm (point group D1) and Pg (point group D1), both based on a primitive rectangular lattice. The latter is thus a special primitive rectangular lattice in virtue of the angles mentioned, and as such it in fact turns into a hexagonal lattice.
Plane Group Pm.
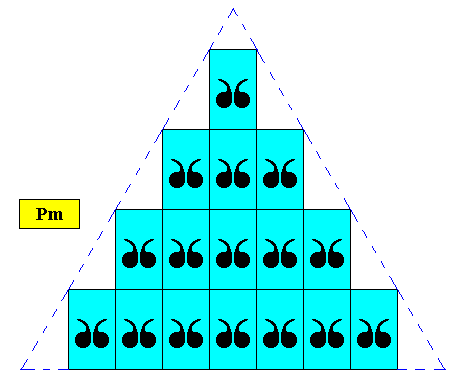
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines), with meshes of special dimensions, such that their diagonals involve angles of 600. As has been said, this point lattice is in fact a hexagonal point lattice.
For convenient overview of shape we give yet a smaller version of the same crystal type :
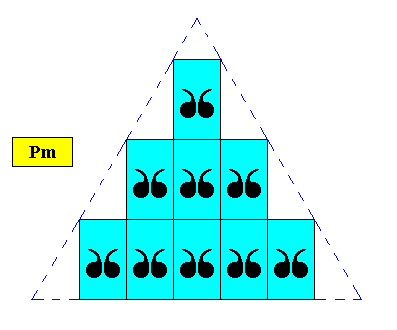
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines), with meshes of special dimensions, such that their diagonals involve angles of 600. Smaller version of triangle.
The next Figure shows the intrinsic symmetry -- D1 -- of the above triangular crystal (larger version).
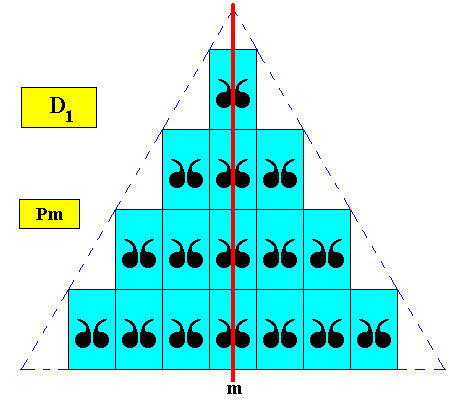
Figure above : The (larger version of the) two-dimensional regularly-triangular crystal considered above, with point symmetry D1 . Its only symmetry element -- a mirror line ( m ) -- is indicated. It is consistent with the crystal's intrinsic shape, because this mirror line is also present in the equilateral triangle representing this shape. It is also consistent with the crystal's internal structure.
In the rectangular point lattice of the above crystals we can inscribe a rhombic net (by drawing connection lines coinciding with the diagonals of the rectangles). But this rhombic net as drawn cannot be a lattice that underlies the mode of repetition of the motifs of the crystal, because it turns out that we then have two types of filled-in rhombi (instead of just one type), meaning that we do not then have one and the same filled-in rhombus that is periodically repeated all over the crystal. See next Figure.
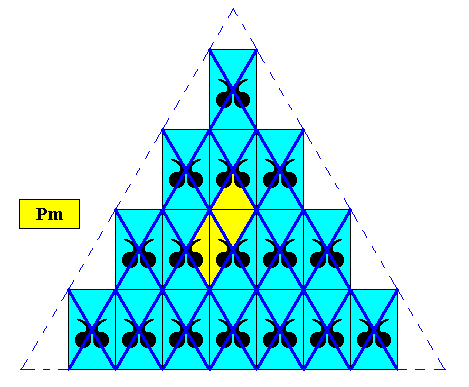
Figure above : Two types of filled-in rhombic meshes of the above discussed triangular crystal, meaning that the rhombus as drawn does not contain all the information of the pattern, i.e. it is too small for it to be a unit mesh .
In order to let a unit rhombus to contain all the (morphological) information of the motif we must choose a larger rhombus, as the next Figure shows.
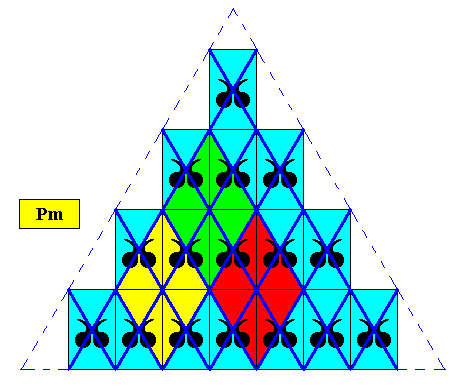
Figure above : A larger rhombus must be taken to represent a unit mesh (a filled-in building block) of the above triangular crystal. See also next Figure.
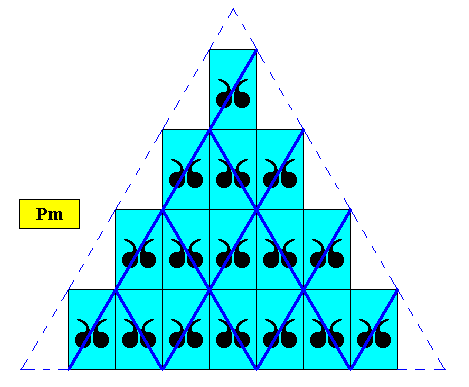
Figure above : The larger rhombus, as established in the previous Figure, is indicated to represent a unit mesh (a filled-in building block) of the above triangular crystal. See also next Figure.
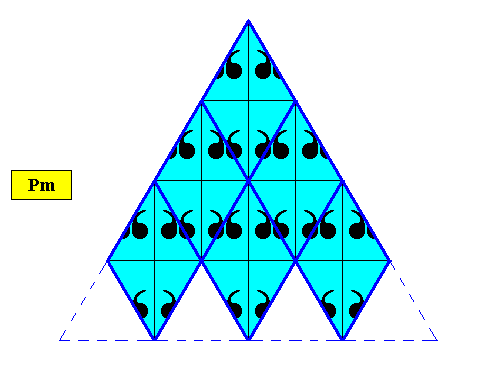
Figure above : Two-dimensional regularly-triangular crystal with D1 intrinsic symmetry (plane group Pm) based on the periodic stacking of filled-in rhombi (with 60 and 120 degrees angles). As such these rhombi directly represent the hexagonal point lattice of the crystal.
Plane Group Pg.
In order to get crystals with plane group symmetry Pg (and, consequently, with point group symmetry D1), and having their intrinsic shape to be that of the equilateral triangle, we start from the (special) rectangular building block of the previous Figures provided with a D1 motif consisting of two commas. By pulling the commas apart along the former mirror line ( m ) by an appropriate distance, we get a unit mesh still with two commas, but which is such that when repeated vertically a sequence of commas is obtained that relate to each other by a glide line ( g ). See next Figure.
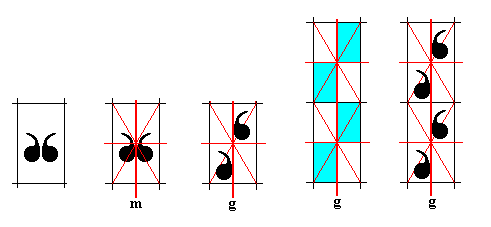
Figure above : Construction of a Pg pattern from a Pm pattern involving rectangular building blocks that can support a regularly-triangular shape. Repetition of this building block in the horizontal direction as well (i.e. in addition to a vertical repetition), results in a Pg pattern supporting a regularly-triangular configuration of possible crystal faces. See next Figure.
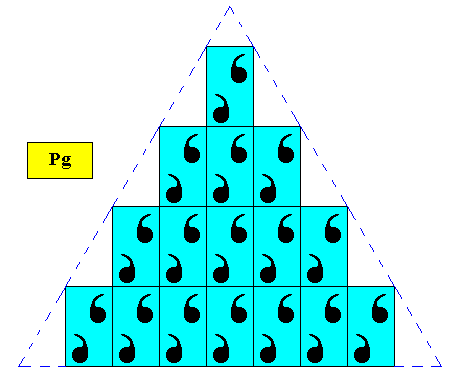
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines), with meshes of special dimensions, such that their diagonals involve angles of 600.
For convenient overview of shape we give yet a smaller version of the same crystal type :
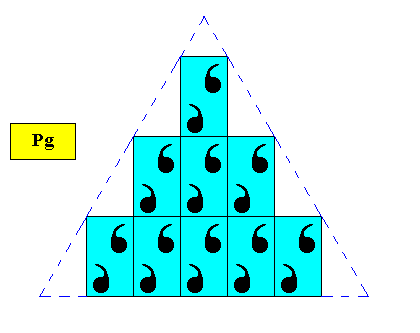
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines), with meshes of special dimensions, such that their diagonals involve angles of 600. Smaller version of triangle.
The next Figure shows the intrinsic symmetry -- D1 -- of the above triangular crystal (larger version).
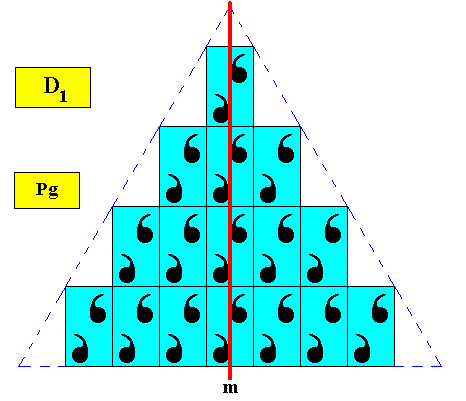
Figure above : The (larger version of the) two-dimensional regularly-triangular crystal considered above, with point symmetry D1 . Its only symmetry element -- a mirror line ( m ) -- is indicated. It is consistent with the crystal's intrinsic shape, because this mirror line is also present in the equilateral triangle representing this shape. It is also consistent with the crystal's internal structure.
Of course, in the crystal just depicted, there is, strictly speaking, no such mirror line present. The triangular crystal is based on the plane group Pg and the line m is in fact a glide line. The transformation associated with a glide line is a combination of a reflection and a translation. However, because of the fact that the translation involved here is very small indeed, it is macroscopically not visible. Also all other translations are not visible at the macroscopic level. So in considering the crystal's symmetry from a macroscopic perspective they can be neglected, resulting in a translation-free residue of the plane group symmetry, and this residue is the crystal's point symmetry. The translation-free residue of a glide reflection is a mirror reflection, so the glide line has then turned into a mirror line, and the point symmetry of the crystal is then according to the group D1 (while its shape is of a higher symmetry -- D3 ).
As we already know, the rectangular lattice of the above Figures (triangular D1 crystals, plane group Pg ) is in fact a hexagonal lattice (meshes having the shape of 60, 120 degrees rhombi), as the next Figures show.
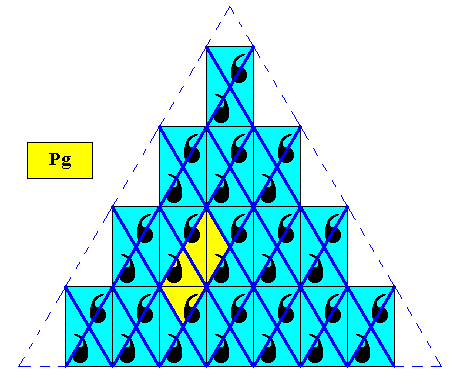
Figure above : Hexagonal net. As drawn it contains not one but two types of filled-in rhombic meshes of the above discussed triangular crystal, meaning that the rhombus is not exactly repeated : One rhombus as drawn does not contain all the information of the pattern, meaning that it is too small for it to be a (filled-in) unit mesh. .
In order to let a unit rhombus to contain all the (morphological) information of the motif we must choose a larger rhombus, as the next Figure shows.
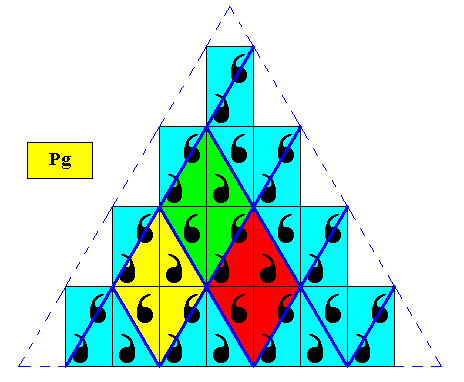
Figure above : A larger rhombus must be taken to represent a unit mesh (a filled-in building block) of the above triangular crystal. See also next Figure.
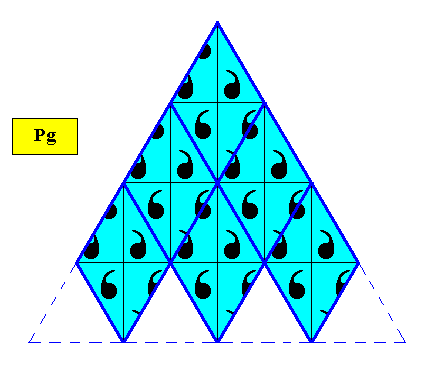
Figure above : Two-dimensional regularly-triangular crystal with D1 intrinsic symmetry (plane group Pg) based on the periodic stacking of filled-in rhombi (with 60 and 120 degrees angles). As such these rhombi directly represent the hexagonal point lattice of the crystal.
Plane Group Cm.
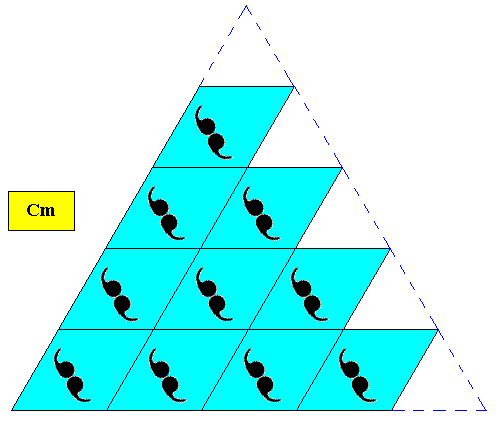
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D1 , and supported by a rhombic point lattice (indicated by connection lines), with meshes that happen to possess angles of 600. Because of these special angles the lattice is in fact a hexagonal lattice.
For convenient overview of shape we give yet a smaller version of the same crystal type :
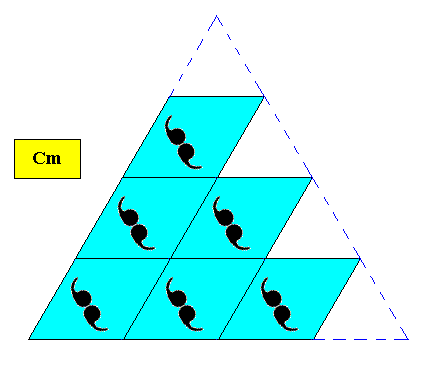
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry D1 , and supported by a rhombic point lattice (indicated by connection lines), with meshes that happen to possess angles of 600, implying the net to be a hexagonal lattice. Smaller version of triangle.
The next Figure shows the mirror line of the point symmetry of our D1 triangular crystal (plane group Cm). It is consistent with the crystal's intrinsic shape, i.e. this mirror line is also present in the equilateral triangle representing this shape. It is also consistent with the crystal's internal structure.
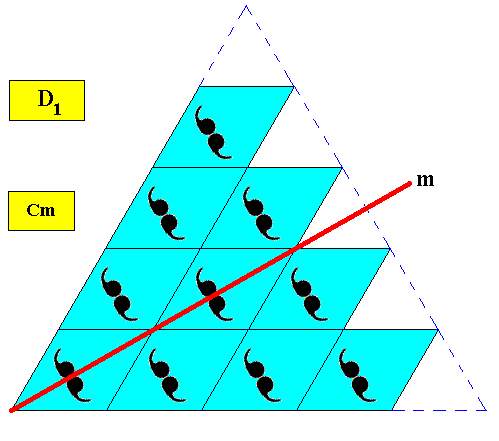
Figure above : Mirror line ( m ) of the two-dimensional regularly-triangular crystal, with point symmetry D1 , and supported by a rhombic point lattice (indicated by connection lines), with meshes possessing angles of 600, implying it to be a hexagonal point lattice.
The above crystal can also be seen as being built up by a periodic stacking of rectangular building blocks as long as the latter have diagonals involving 600 angles. See next Figure.
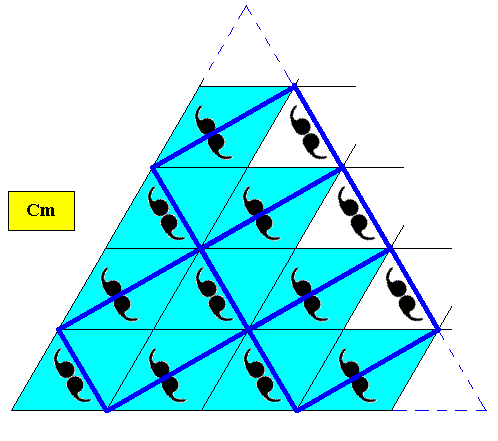
Figure above : Two-dimensional triangular D1 crystal (as discussed above). Instead of rhombic building blocks, also rectangular building blocks, of which the diagonals involve 600 angles, can be considered to build up the crystal by periodic stacking.
The plane group P1.
A regularly-triangular shape can, finally, be supported by the plane group P1 if the oblique lattice happens to be such that its two (independent) translations are perpendicular to each other and imply rectangular meshes with their diagonals making angles of 60 and 300 with the sides. As we know, such a (special) net is in fact a hexagonal point lattice. See next Figures.
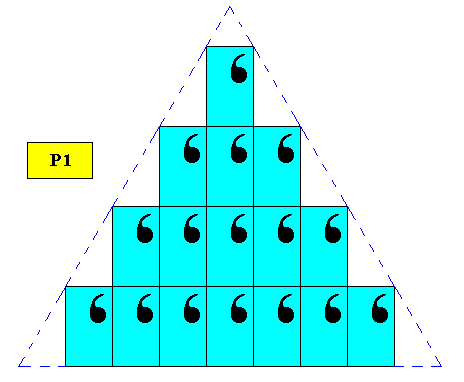
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry C1 , and supported by an oblique point lattice (indicated by connection lines), where the (independent) translations happen to be perpendicular to each other, while their lengths are such that they result in rectangles in which the diagonals involve angles of 600, turning the oblique lattice into a hexagonal lattice. But, of course, despite the hexagonal lattice (describing the repetition of the motifs), the crystal is intrinsically asymmetric (point group C1).
For convenient overview of shape we give yet a smaller version of the same crystal type :
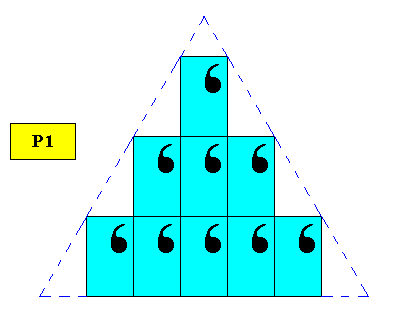
Figure above : Two-dimensional regularly-triangular crystal, with point symmetry C1 , and supported by a rhombic point lattice (indicated by connection lines), where the (independent) translations happen to be perpendicular to each other, while their lengths are such that they result in rectangles in which the diagonals involve angles of 600. Smaller version of triangle. As in cases discussed earlier, we also see here a crystal having an intrinsic shape that is symmetric, viz. that of the equilateral triangle, which has D3 symmetry, while its true symmetry is that of C1, i.e. no symmetry at all.
As we already know, the rectangular lattice of the above Figures (triangular C1 crystals, plane group P1 ) is in fact a hexagonal lattice (meshes having the shape of 60, 120 degrees rhombi), as the next Figures show.
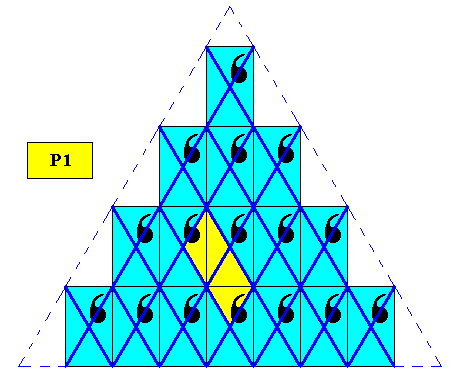
Figure above : Hexagonal net. As drawn it contains not one but two types of filled-in rhombic meshes of the above discussed triangular C1 crystal, meaning that the rhombus is not exactly repeated : One rhombus as drawn does not contain all the information of the pattern, meaning that it is too small for it to be a (filled-in) unit mesh.
In order to let a unit rhombus to contain all the (morphological) information of the motif we must choose a larger rhombus, as the next Figure shows.
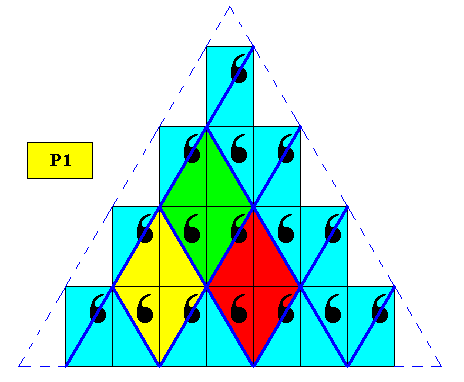
Figure above : A larger rhombus must be taken to represent a unit mesh (a filled-in building block) of the above triangular crystal. See also next Figure.
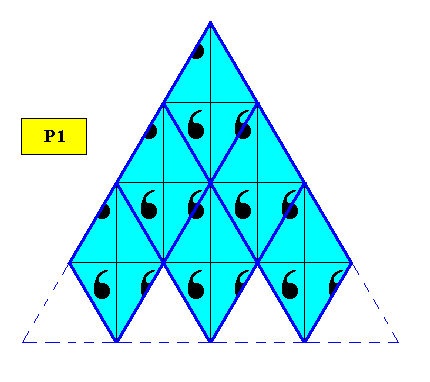
Figure above : Two-dimensional regularly-triangular crystal with C1 intrinsic symmetry (plane group P1) based on the periodic stacking of filled-in rhombi (with 60 and 120 degrees angles). As such these rhombi directly represent the hexagonal point lattice of the crystal.
As soon as we change the mode of repetition of the motifs, resulting in a different lattice, i.e. a lattice different from the hexagonal lattice, an intrinsically triangular shape (equilateral triangle) cannot be supported anymore. See next Figures.
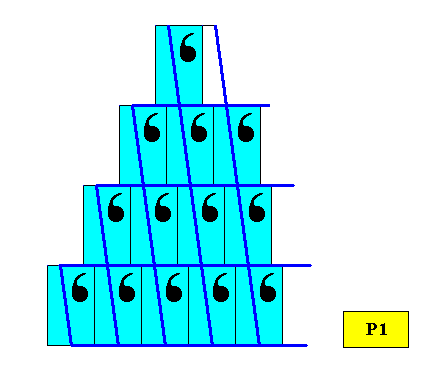
Figure above : By displacing the rectangles (with their motifs) of the above Figures, a different lattice results. In the case here depicted, an oblique lattice. This lattice consists of parallelograms. Periodic stacking of these parallelograms cannot result in a regularly-triangular crystal shape. See next Figure.
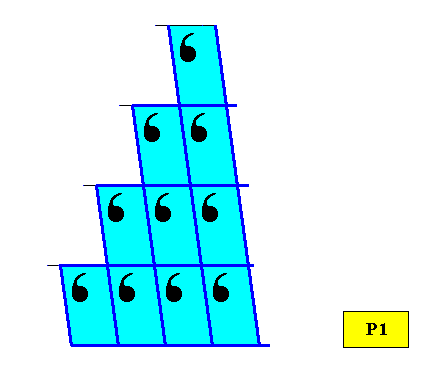
Figure above : Periodic repetition of asymmetric motifs according to an oblique point lattice resulting in a P1 pattern (point symmetry C1). A regularly-triangular shape cannot be accomplished by the periodic stacking of this pattern's unit parallelograms.
The plane groups P2mm, C2mm, P2mg, P2gg and P2 do not support a regularly-triangular crystal shape, because their 2-fold rotation axis is not compatible with the (symmetry of the) Equilateral Triangle, i.e. such a 2-fold axis does not occur in the Equilateral Triangle.
This concludes a summary, showing when and in what way, regularly-triangular two-dimensional crystals are supported.
The next document will investigate the possible promorphs of these two-dimensional regularly-triangular crystals.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XII.
e-mail : 