

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms. It, and the ensuing documents, brings crystals closer to organisms by demonstrating that promorphs are not typical only for organisms, but can also be established for crystals, despite their periodic nature.
In fact we have demonstrated this already in Second Part of Website , viz. in the Series "Basic Forms of Crystals" (which can be found by scrolling down the left frame associated with this Second Part of Website). There we could establish that crystals do in fact have a promorph (on the basis of the geometry of the translation-free residue), but, as thus established, this promorph was not expressed macroscopically in the crystal. In the present series of document we let it be so expressed, by showing the macroscopic regions of the crystal that represent genuine antimers. In this way we succeed in bringing crystals even more close to organisms (in which the promorph and its corresponding antimers are always macroscopically expressed).
Crystals and Organisms, Shape, Symmetry and Promorph.
Rectangle (Promorphs)
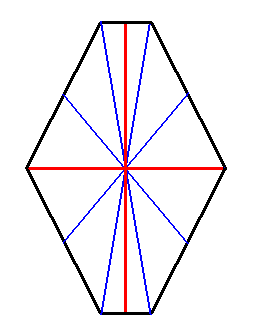
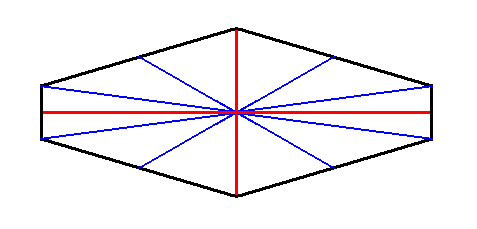
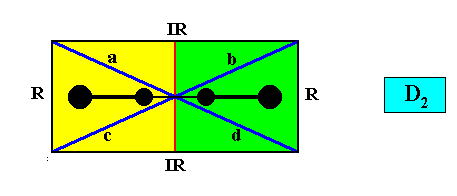
The Vector Rosette of Actual Growth of any intrinsically rectangular two-dimensional (fully developed) crystal of whatever (possible) intrinsic point symmetry (while the symmetry of a rectangle itself is always that of D2) is as follows (blue lines) :
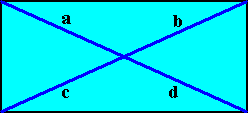
This vector rosette in fact consists of four lines (vectors), a, b, c, d, each originating in the center of the crystal and ending up at a corner. As such it encodes the crystal's shape. And the lines of this rosette generally point to the presence of four or two antimers (dependent on the chemico-geometric features of the crystal's motifs, expressed as the equivalence or non-equivalence of the vectors a, b, c, d in the rosette) where, of course, in addition to these four lines, also the boundaries between the antimers indicate special directions, as well as the mirror lines, if present, of the crystal (which can coincide with the boundaries between antimers, or coincide with the median lines of antimers).
In some cases the vectors of actual growth do not point to antimers at all, viz. in all (2-D) crystals with their symmetry group according to the plane group P1 (and therefore having C1 point symmetry). Here an asymmetric motif is repeated along two independent translations, that, in the case of a rectangular crystal (See the relevant Figure in Part V ), happen to be perpendicular to each other (In the Figure just mentioned only the way of the repetition of some motif -- symmetric or asymmetric -- is indicated). And because of the asymmetry of the motif the four vectors are not equivalent, and consequently do not point to antimers.
In other cases, different numbers, i.e. different from 2 and 4, antimers can occur in rectangular (2-D) crystals.
We will now consider several possible cases of the given example of a rectangular two-dimensional crystal as depicted just above .
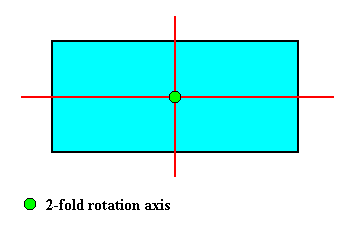
D2 symmetry.
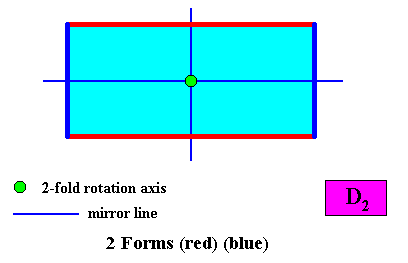
The shape of the rectangular D2 crystal consists of two crystallographic Forms : One consisting of a set of two parallel horizontal faces (indicated by red coloring), and one consisting of a set of two parallel vertical faces (indicated by dark blue coloring) :
If a rectangularly shaped crystal has intrinsic D2 symmetry, it has the full symmetry of the rectangle, i.e. it has the full symmetry of its shape, meaning that its (intrinsic) shape precisely expresses its intrinsic point symmetry.
D2 symmetry and four antimers.
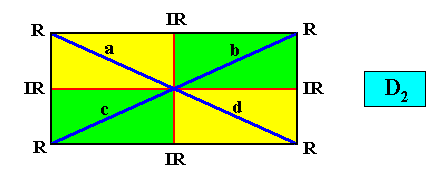
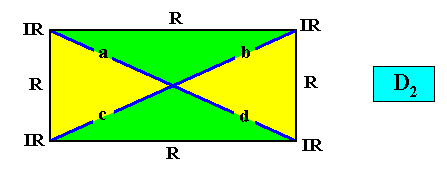
which choice is arbitrary in the absence of further 'chemical' information about the crystal. In such a case we prefer the first way of depicting. If, on the other hand, such information is available as to the geometry and orientation of the motifs, then we should assess which of these two possiblities is actually realized. They constitute two different types of configuration of the four antimers, and they correspondingly represent two slightly different promorphs.
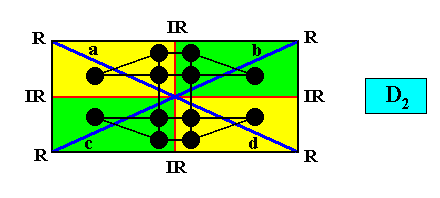
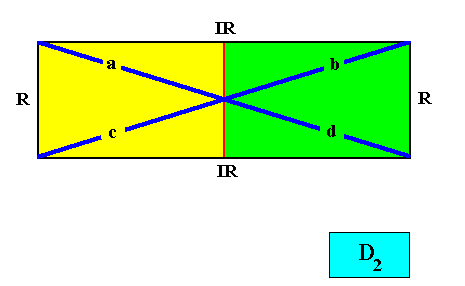
And the next Figure depicts the same, but with another, also compatible motif, i.e. we still have the case of a rectangular crystal having D2 symmetry and four antimers :
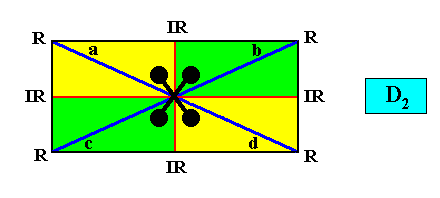
Both Figures also represent the first mentioned type of configuration of the four antimers , which we here depict again, but without the Vector Rosette :
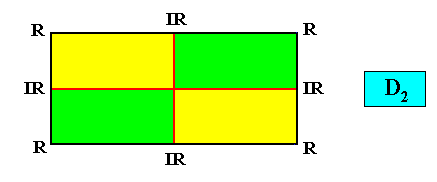
Figure above : Interradial configuration of the four antimers (green, yellow) of the above described rectangular two-dimensional crystal with intrinsic D2 symmetry.
The second mentioned type of configuration of the four antimers is depicted next, also without the Vector Rosette :
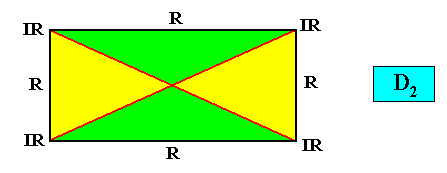
Figure above : Radial configuration of the four antimers (green, yellow) of the above described rectangular two-dimensional crystal with intrinsic D2 symmetry.
To symbolize this second type of configuration, we insert a motif (black) :
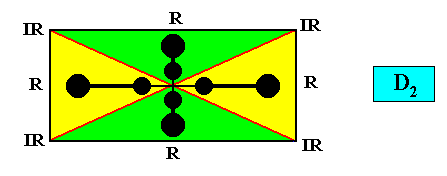
To see in what way the motif (shown by a comparable motif, also having D2 symmetry) is actually only microscopically present (and then periodically repeated) in the rectangular crystal, see the relevant Figure in Part V . Sometimes such a motif is 'smeared out' as it were because of glide reflections (of which only the reflection component is macroscopically visible, because the translations are very small). When, in addition to the simple translations, also the translational component of such glide reflections is eliminated (turning them into ordinary reflections, which is what we do when looking to the crystal macroscopically), we are, in the present case, left with a translation-free residue with D2 symmetry. See for this latter case the relevant Figure in Part V .
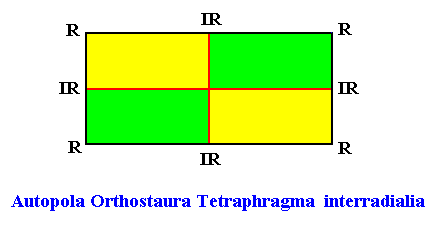
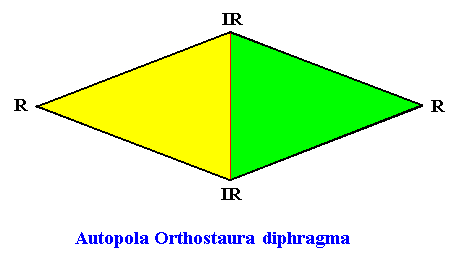
The next two Figures depict and name the promorph of the above considered two-dimensional crystals. It is either the 2-dimensional analogue of a rectangular pyramid (in fact it is its base) with four antimers (yellow, green) (first mentioned type of configuration of the four antimers ) :
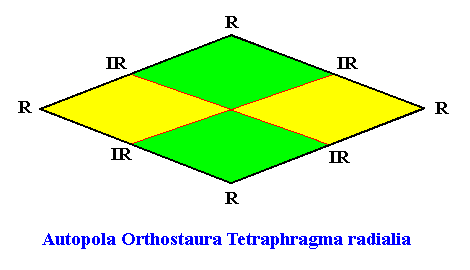
or, (second mentioned type of configuration of the four antimers ) (see for further explanation, below), the 2-dimensional analogue of a rhombic pyramid (in fact it is its base) also with four antimers :
The next Figure explains these two promorphological possibilities. They depend on how the motif lets itself be interpreted in terms of antimers.
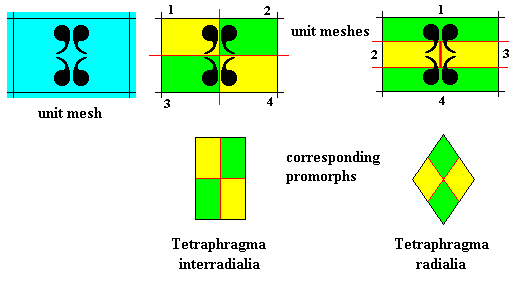
Figure above : The chemical and morphological features of a two-dimensional ('chemical') D2 motif determine which parts of it to be interpreted as antimers. In the case of a motif consisting of four antimers the promorph can then be either that of the (Autopola Orthostaura) Tetraphragma interradialia, or that of the (Autopola Orthostaura) Tetraphragma radialia. The spatial configuration of the four antimers (green, yellow, indicated by numerals) is different in each case (See for this difference also our Promorphological System of Stereometric Basic Forms (Promorphs) at "Autopola" in Second Part of Website : BASIC FORMS ). See also next three Figures.
The delineation of the four antimers can be expressed in several equivalent ways, as is shown in the next Figure for the radial configuration :

The next five Figures are about cross axes and directional axes.
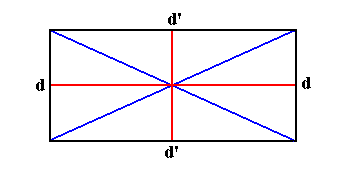
Figure above : System of cross axes of a rectangle.
A rectangle (but also all other amphitect [ = laterally compressed] polygons) possesses a special system of cross axes. Generally, cross axes are lines that go through the center, where each such line connects two definite parts (for example corners or centers of sides) of a polygon. When, as in amphitect polygons, there is one (and only one) pair of such axes of which the members are perpendicular to each other, we call them directional axes ( In the Figure the lines dd and d'd' ). And if the directional axes are radial, then we call the corresponding promorph radial, as in "(Autopola Orthostaura) Tetraphragma radialia". If, on the other hand, the directional axes are interradial, then we call the corresponding promorph interradial, as in "(Autopola Orthostaura) Tetraphragma interradialia".
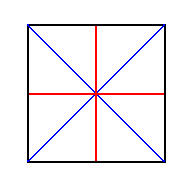
The next Figure shows the system of cross axes of a square. It consists of two pairs. The members, however, of each pair are perpendicular to each other, implying that we cannot distinguish one unique pair as representing the directional axes of the figure (which means that this figure doesn't have directional axes at all).
The next Figure, finally, shows the system of cross axes of a six-fold amphitect polygon.
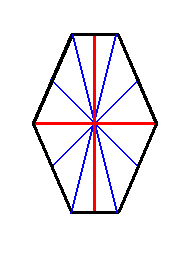
Figure above : System of cross axes (three pairs, red, blue, blue) of a 6-fold amphitect polygon. The perpendicular ones (red) are the directional axes of the polygon.
In the above drawing there is another pair of cross axes of which the members seem to be perpendicular to each other, in addition to the pair (red) mentioned earlier. But the perpendicularity of that second pair is only of an accidental nature, implied by the special demensions of this particular figure. Generally, in any amphitect polygon all cross axes involve angles different from 900 except for one pair of them. See next two Figures.
D2 symmetry and two antimers.
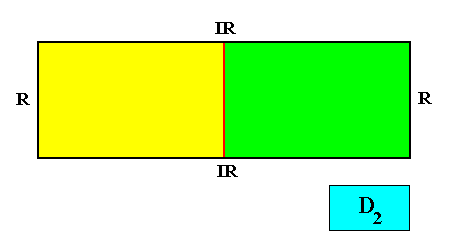
Figure above : A two-dimensional intrinsically rectangular crystal with intrinsic D2 symmetry and with only two antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
The next Figure is the same ( D2 crystal, two antimers), but now with an appropriate motif s.str. inserted (black) to show (more clearly) the equivalence of all the four vectors a, b, c, d of the Vector Rosette of Actual Growth (blue lines).
The next Figure gives the promorph (and its name) of this crystal (D2 , two antimers). It is a 2-D analogue of a rhombic pyramid with two antimers. Because there is only one way of arrangement of the two antimers possible, the simplest geometric figure to express this promorph is a rhombus ( The rectangle of the crystal has two types of sides -- long and short --, while the rhombus has only one)
There can in principle be any even number of antimers, dependent on the geometry of the translation-free chemical motif. The Figures below show the cases of six and of eight antimers.
D2 symmetry and six antimers :
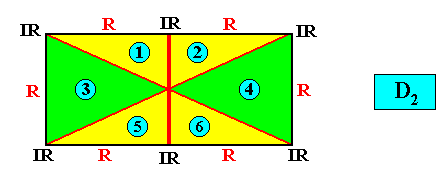
Figure above : A two-dimensional rectangular D2 crystal with six antimers (green, yellow, and indicated by numerals).
And with the Vector Rosette of Actual Growth added :
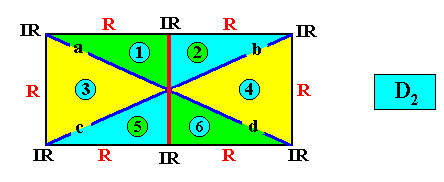
Figure above : A two-dimensional rectangular D2 crystal with six antimers (green, yellow, blue, and indicated by numerals). Vector Rosette of Actual Growth added.
The corresponding promorph and its name is given in the next Figure. It is a two-dimensional analogue of an amphitect pyramid with six sides. The amphitect polygon, representing the two-dimensional promorph, has two types of sides, as does the rectangle of the crystal. The amphitect polygon is, however, more appropriate to represent the promorph, because each of its six corners represents one of its six antimers, while in the rectangle we do not have six corners, nor six sides, to represent the antimers.
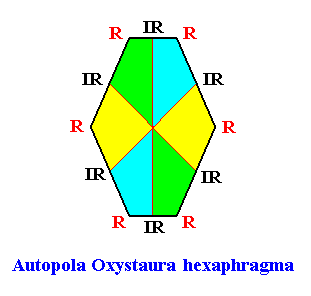
Figure above : Promorph of a D2 two-dimensional crystal with six antimers (green, yellow, blue).
D2 symmetry and eight antimers :
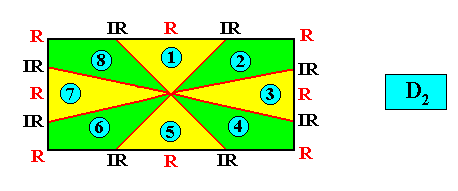
and with the Vector Rosette of Actual Growth added :
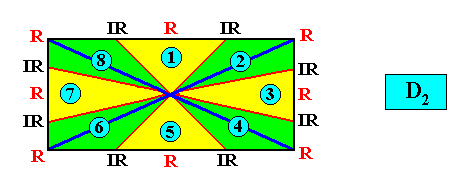
The next Figures give the promorph (and its name) of the above crystal (D2 , eight antimers). It is the 2-D analogue of an amphitect pyramid with eight sides.
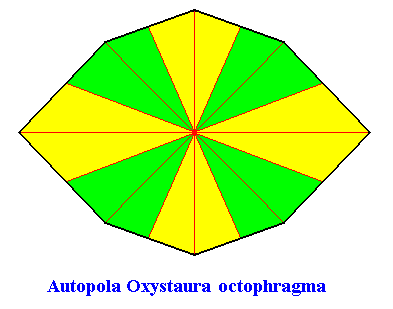
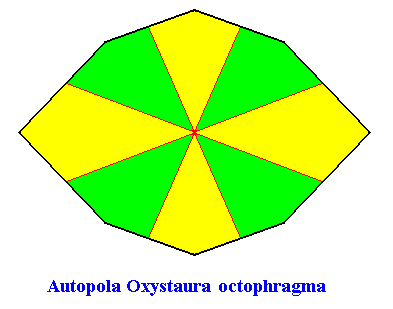
Figure above : Same as previous Figure. Median lines of antimers omitted, in order to let the latter stand out more clearly.
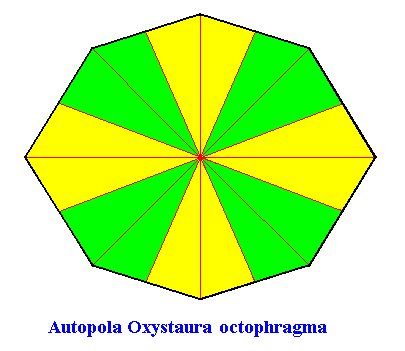
The degree of flattening of the amphitect polygon that depicts this promorph is arbitrary (as long as it remains flattened), so the next will do also :
C2 symmetry.
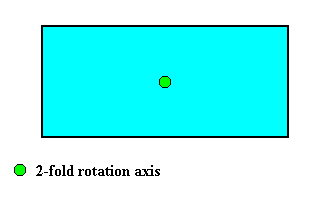
Its only symmetry element is then a 2-fold rotation axis (Its symmetry group therefore consists of two group elements, viz. the identity element and a half-turn p , where p2 = 1 (identity element)). In spite of this the shape of the crystal can still be rectangular : Two-fold motifs (i.e. motifs with C2 symmetry) arranged according to an oblique lattice where the angles between the translations happen to be 900, i.e. where the meshes of the crystal lattice happen to be rectangles (periodic stacking of which results in a rectangularly shaped crystal).
The shape of our rectangular C2 crystal consists of a combination of two crystallographic Forms : One consisting of two parallel horizontal faces (indicated by red coloring), the other of two parallel vertical faces (indicated by dark blue coloring) :
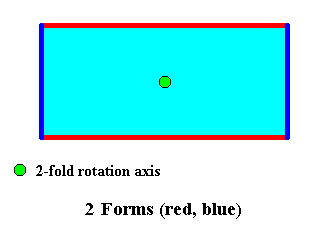
Crystals with intrinsic C2 point symmetry can, in principle, have any even number of antimers. We will give some examples.
C2 symmetry and four antimers.
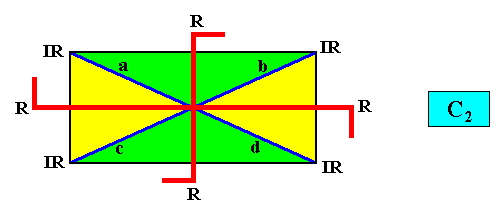
where the C2 symmetry of the rectangular crystal is indicated by red hooked lines. They indicate the equivalence of the vectors a and d , and of the vectors b and c , and the non-equivalence of the vectors a and b , and of the vectors c and d , and further the non-equivalence of the vectors a and c and, finally, of the vectors b and d of the Vector Rosette of Actual Growth of the crystal.
A somewhat better representation of an intrinsically rectangular two-dimensional crystal with intrinsic C2 symmetry and with four antimers, is the following :
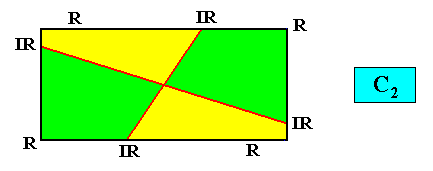
and with the Vector Rosette of Actual Growth added :
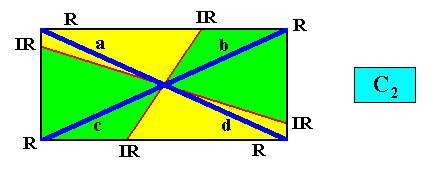
The next Figure gives the promorph (and its name) of the above crystal (C2 , four antimers). It is a two-dimensional analogue of the four-fold amphitect gyroid pyramid (i.e. it is its base). The four antimers are indicated (yellow, green).
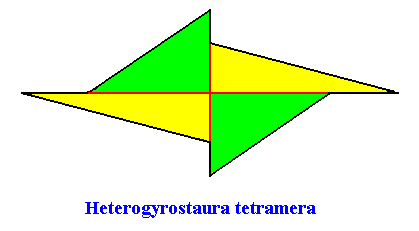
Its three-dimensional counterpart (i.e. the corresponding pyramid) is given in the next Figure (slightly oblique top-view) :
C2 symmetry and two antimers.
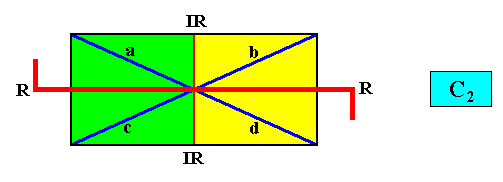
where the C2 symmetry of the rectangular crystal is indicated by red hooked lines. They indicate the equivalence of the vectors a and d , and of the vectors b and c , and the non-equivalence of the vectors a and b , and of the vectors c and d , and further the non-equivalence of the vectors a and c and, finally, of the vectors b and d of the Vector Rosette of Actual Growth of the crystal.
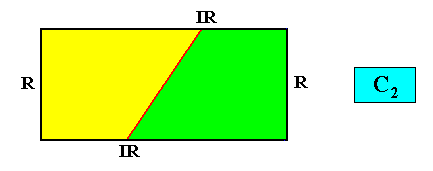
A slightly better representation of our two-dimensional rectangular C2 crystal with two antimers is the following :
and with the Vector Rosette of Actual Growth added :
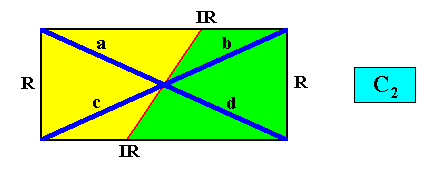
The next Figure gives the promorph (and its name) of the above depicted rectangular crystal (C2 , two antimers). It is a two-fold amphitect gyroid polygon, and as such a two-dimensional analogue of the corresponding three-dimensional two-fold amphitect gyroid pyramid.
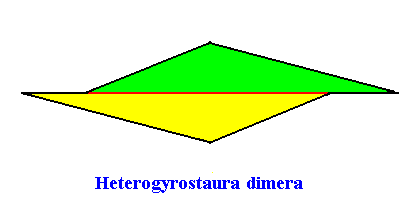
Its three-dimensional analogue -- the pyramid -- is depicted in the next Figure (slightly oblique top-view) :
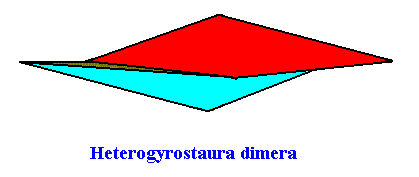
There can in principle be any even number of antimers, dependent on the geometry of the translation-free chemical motif. The next Figures show the case of eight antimers.
C2 symmetry and eight antimers.
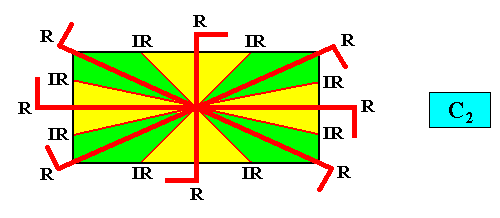
Or, the same symmetry -- C2 -- and number of antimers, differently expressed :

and with the Vector Rosette of Actual Growth added :
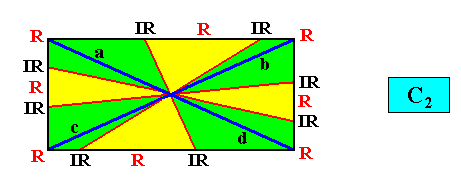
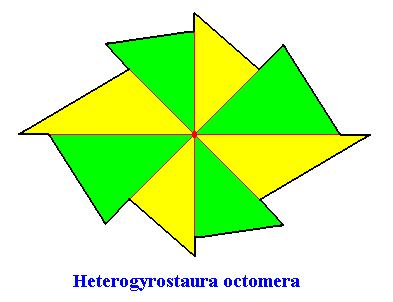
The next Figure gives the promorph (and its name) of the above rectangular crystal (C2 , eight antimers). It is an 8-fold amphitect gyroid polygon and as such the two-dimensional analogue of an 8-fold amphitect gyroid pyramid (i.e. it is its base). The eight antimers (green, yellow) are indicated.
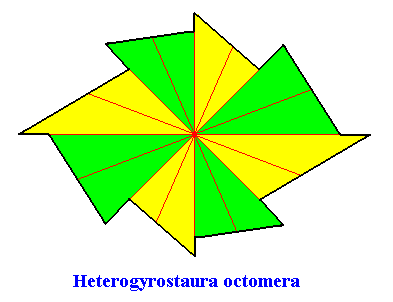
The next Figure gives this same promorph, but now with the median lines of the antimers omitted, in order to let the latter stand out more clearly.
D1 symmetry.
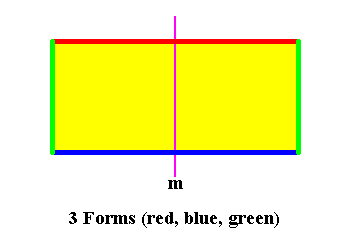
The rectangular shape of the crystal consists of a combination of three crystallographic Forms : One such Form consists of one horizontal crystal face (indicated by red coloration in the next Figure). The second Form consists of a horizontal crystal face (indicated dark blue) parallel to the first one. The third Form, finally, consists of two parallel vertical crystal faces (indicated green). See next Figure.
Such a D1 rectangular crystal in principle admits of any number (> 1) of antimers, as long as they are symmetrically arranged with respect to a mirror line. We give some examples.
D1 symmetry and two antimers.
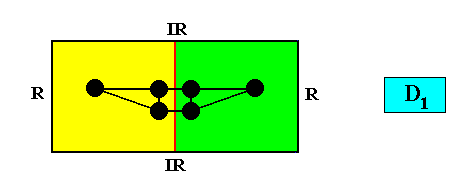
Figure above : A two-dimensional intrinsically rectangular crystal with intrinsic D1 symmetry and two antimers (green, yellow). The D1 symmetry of the crystal is expressed by the insertion of a motif (black).
With another way of expressing the D1 symmetry of the crystal (red hooked lines), and with the Vector Rosette of Actual Growth Added :
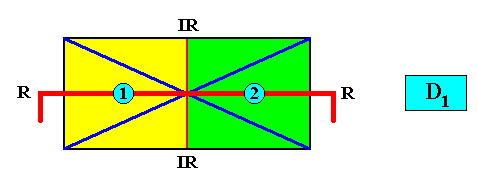
Figure above : Same crystal as in previous Figure. Vector Rosette of Actual Growth added. The two antimers (green, yellow) indicated by numerals.
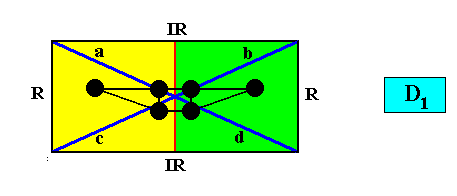
The next Figure is the same ( D1 crystal, two antimers), but with the former motif s.str. (black) inserted within the crystal to (more clearly) show the equivalence of the vectors a and b , the equivalence of the vectors c and d , and the non-equivalence of the vectors a and c , and, finally, the non-equivalence of the vectors b and d of the Vector Rosette of Actual Growth (blue lines).
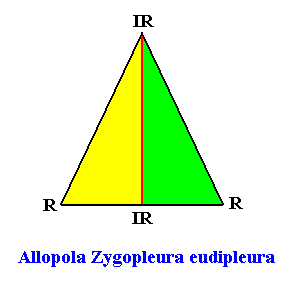
The next Figure gives the promorph (and its name) of the above rectangular crystal (D1 , two antimers). It is an isosceles triangle, and as such the two-dimensional analogue of half a rhombic pyramid. The two antimers (green, yellow) and radial and interradial directions are indicated.
D1 symmetry and four antimers.
Interradial :
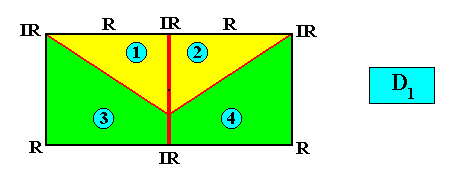
and with the Vector Rosette of Actual Growth added :
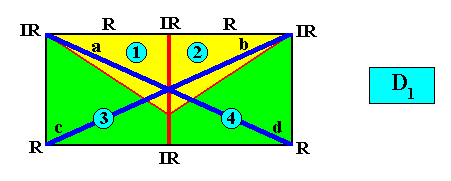
Radial :
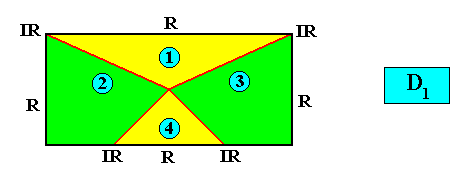
or, alternatively (but promorphologically equivalently) :
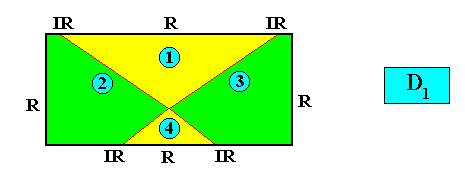
and with the Vector Rosette of Actual Growth added :
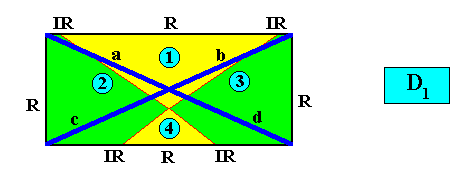
The next two Figures give the corresponding promorphs (and their name) of the above rectangular crystal ( D1 , four antimers). It is either (dependent on the above mentioned configuration of the four antimers) an isosceles trapezium, and as such the two-dimensional analogue of a trapezoid pyramid (i.e. it is its base), or a bi-isosceles triangle and as such the two-dimensional analogue of a bi-isosceles pyramid (i.e. it is its base). The four antimers (green, yellow) and the radial and interradial directions are indicated.
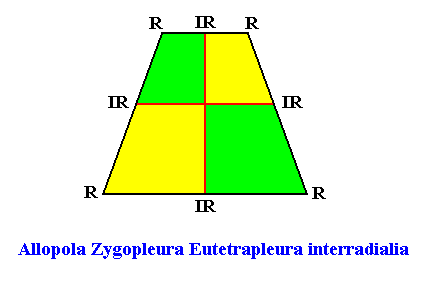
Interradial case (perpendicular directional axes interradially positioned) :
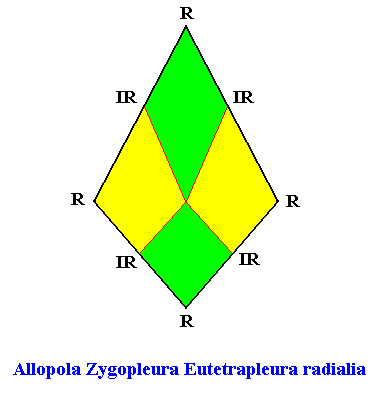
Radial case (perpendicular directional axes radially positioned):
The next three Figures elaborate a little more on the directional axes of D1 promorphs (Allopola) with four antimers ( Allopola Zygopleura eutetrapleura, in fact, their two-dimensional analogues). The two possible promorphs were given just above.
Figure above : Cross axes (two pairs, blue, red) of the isosceles trapezium, the basic form of the Eutetrapleura interradialia. The perpendicular cross axes (red) are the directional axes, while the other axes (blue) are just cross axes. The latter are bent, but this is neither typical, nor necessary as the next Figure shows.
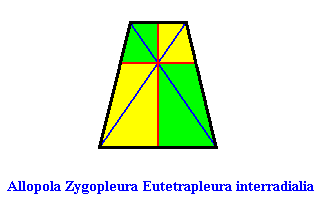
Figure above : Cross axes of the isosceles trapezium, the basic form of the Eutetrapleura interradialia. Two sets of (straight) cross axes (red, blue). The perpendicular ones (red) are the directional axes of the isosceles trapezium. The horizontal directional axis does not connect the centers of opposite sides, but this is to be expected because of the absence in the promorph of a horizontal mirror line.
Also the basic form of the Allpola Zygopleura Eutetrapleura r a d i a l i a can be depicted by a polygon, viz. a bi-isosceles triangle, such that it has straight cross axes :
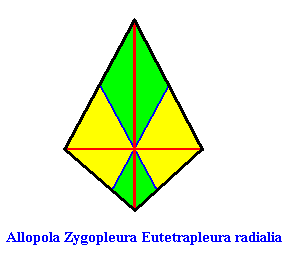
Figure above : Cross axes of a bi-isosceles triangle, the basic form of the Eutetrapleura radialia. All cross axes are straight. The perpendicular ones (red) are the directional axes of the bi-isosceles triangle.
D1 symmetry and six antimers.
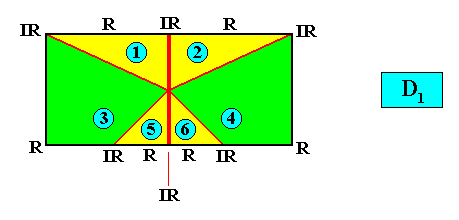
and with the Vector Rosette of Actual Growth added :
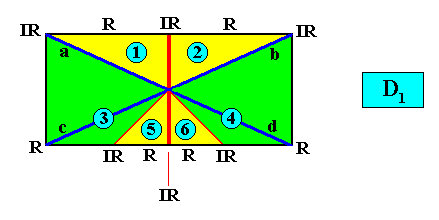
Indicating the arrangement and number of antimers, to express a certain promorph, often allows for some freedom. The next two Figures are wholly equivalent to the two Figures directly above. The six antimers are indicated by the colors green, yellow and blue (See also next Figure).
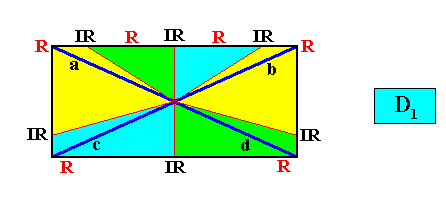
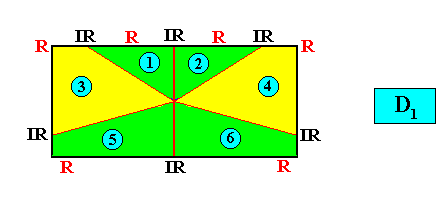
Figure above : Same as previous Figure. Vector Rosette omitted. Coloration of the six antimers (green, yellow) expressing the intrinsic reflectional symmetry of the crystal.
The next Figure gives (with two images) the promorph (and its name) of the above rectangular crystal (D1 , six antimers). It is half a 12-fold amphitect polygon, and as such a two-dimensional analogue of half a 12-fold amphitect pyramid (i.e. it is its base). In the right image the six antimers (green, yellow) and the radial and interradial directions are indicated.
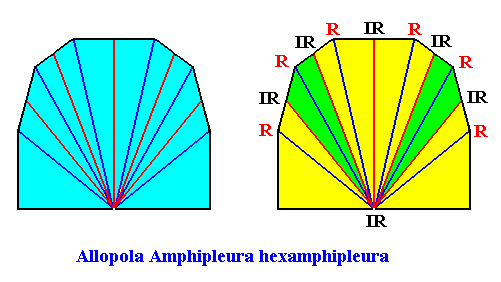
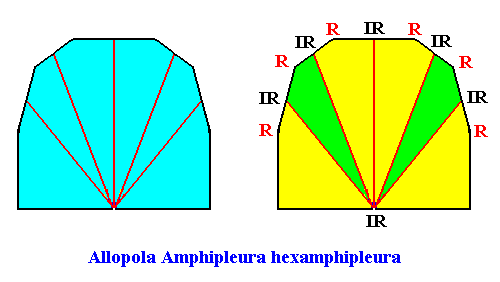
Figure above : Same as previous Figure. Median lines of antimers omitted, in order to let the latter stand out more clearly.
D1 symmetry and three antimers.
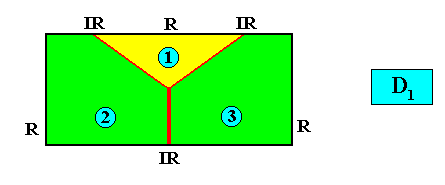
and with the Vector Rosette of Actual Growth added :
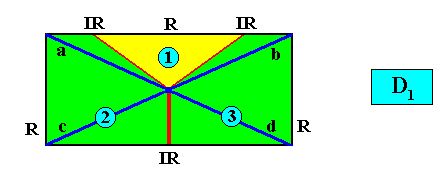
Also here there are alternative ways to indicate the three antimers in a rectangular D1 crystal. See next Figure.
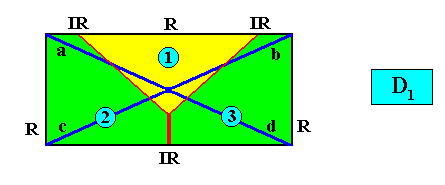
The next Figure gives the promorph (and its name) of the above rectangular crystal (D1 , three antimers). It is half a 6-fold amphitect polygon, and as such a two-dimensional analogue of half a 6-fold amphitect pyramid (i.e. it is its base). The three antimers (green, yellow) and the radial and interradial directions are indicated.
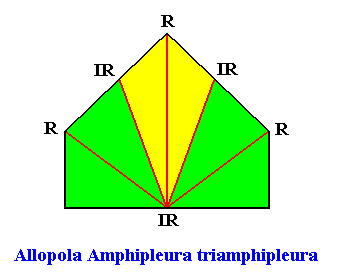
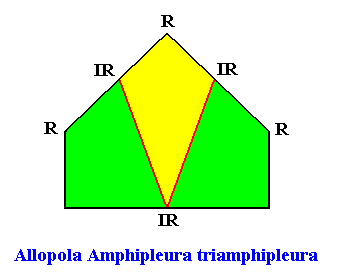
Figure above : Same as previous Figure. Median lines of antimers omitted, in order to let the latter stand out more clearly.
D1 symmetry and five antimers.
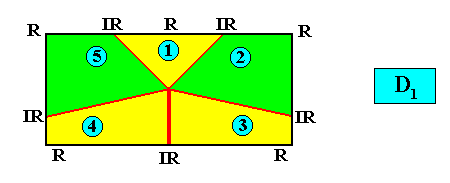
and with the Vector Rosette of Actual Growth added :
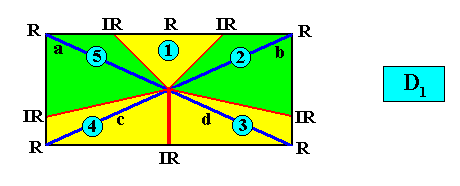
As before, there are several alternative ways to express five antimers in a rectangular D1 crystal. See next Figure.
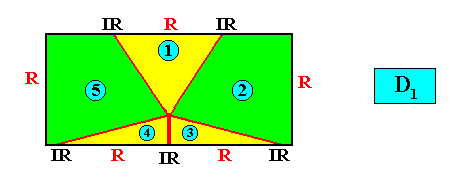
Figure above : Alternative representation of five antimers (green, yellow) in a rectangular D1 crystal.
The next Figure gives (with two images) the promorph (and its name) of the above rectangular crystal (D1 , five antimers). It is half a 10-fold amphitect polygon, and as such a two-dimensional analogue of half a 10-fold amphitect pyramid (i.e. it is its base). In the right image the five antimers (green, yellow) and the radial and interradial directions are indicated.
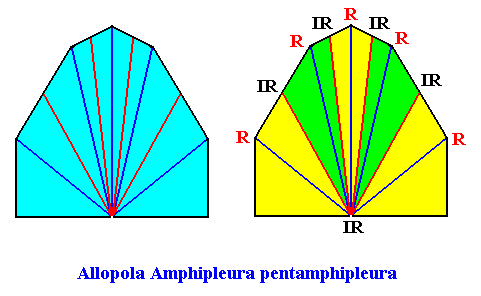
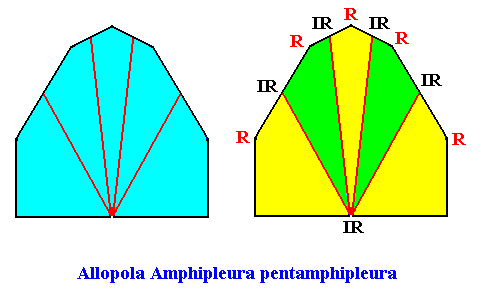
Figure above : Same as previous Figure. Median lines of antimers omitted, in order to let the latter stand out more clearly.
D1 symmetry and seven antimers.
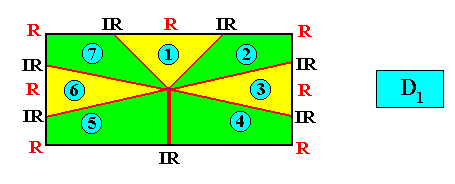
Figure above : A two-dimensional rectangular crystal with intrinsic D1 symmetry and seven antimers (green, yellow).
and with the Vector Rosette of Actual Growth added :
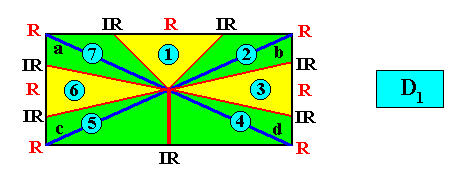
There are, of course, several different ways to express the presence of seven antimers in a rectangular D1 crystal. See next Figure.
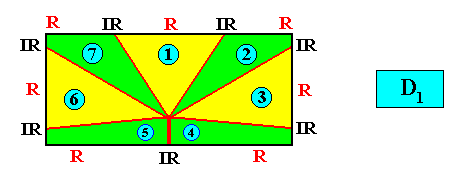
The next Figure gives (with two images) the promorph (and its name) of the above rectangular crystal (D1 , seven antimers). It is half a 14-fold amphitect polygon, and as such a two-dimensional analogue of half a 14-fold amphitect pyramid (i.e. it is its base). In the right image the seven antimers (green, yellow) and the radial and interradial directions are indicated.
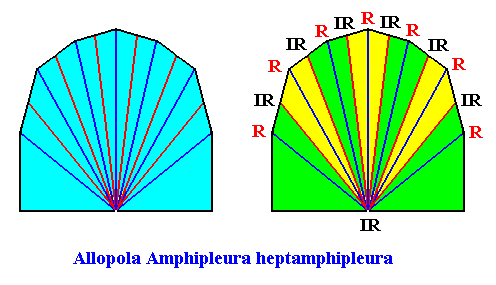
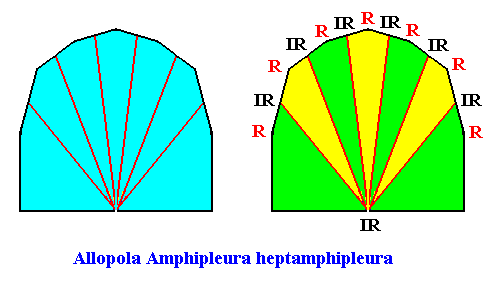
Figure above : Same as previous Figure. Median lines of antimers omitted, in order to let the latter more clearly stand out.
C1 symmetry and no antimers.

Figure above : A two-dimensional intrinsically rectangular crystal with intrinsic C1 symmetry. There are no genuine antimers. A motif (black) is inserted to clearly express the C1 symmetry of the crystal.
And with the Vector Rosette of Actual Growth added :
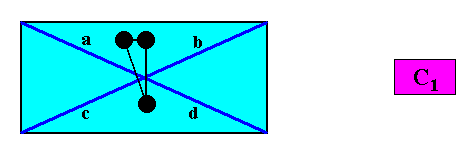
The inserted asymmetric motif (black) clearly shows that the vectors a, b, c, d are all non-equivalent, i.e. each of them is unique, and cannot be transformed into any of the other vectors by whatever symmetry transformation (Recall, that the equivalence or non-equivalence of the vectors takes into account their surroundings). Intrinsically rectangular C1 crystals can occur if the (asymmetric) motif s.str. plus its corresponding surroundings (together forming the motif s.l.) are stacked according to a rectangular net, which is in fact an oblique net in which the angles happen to be 900. See the relevant Figure in Part V .
The next Figure (two images) gives the possible promorphs (and their names) of this rectangular crystal. The promorph is either (left image) half an isosceles triangle (and, equivalently, a quarter of a rhombus), and is as such the two-dimensional analogue of a quarter of a rhombic pyramid, or (right image) an irregular triangle, indicating two unequal antimers (yellow, green), and is as such the two-dimensional analogue of an irregular pyramid (or, equivalently, a 1-fold pyramid).
This concludes our investigation concerning the relation of intrinsic rectangular (2-dimensional) crystal shape to intrinsic point symmetry and to promorph.
In the next document we will investigate the second shape from our above given list : rectangle, square, parallelogram, rhombus, equilateral triangle, regular hexagon.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part VI.
e-mail : 