e-mail : 

Back to Homepage

After having established a preliminary general ontology, in this case a Theory of Layers, in which we already considered some specific examples of categories and intrinsic properties, it is now time to elaborate all this, first of all in more detail, and secondly in a systematic manner. This, in order to test the preliminary theory, and, as a result, set up a more definitive general ontology. We have already seen that the Theory of Essence, as expounded in the First Part of Website (accessible by the back to homepage link), fits neatly into the proposed general ontology (but, of course, their respective points of departure are different). In this Theory the whatness of an intrinsic object is established as follows :  'Phenotypically' it is the total of intrinsic properties as they are simultaneously or successively expressed (and often suppressed again) by the Essence of the object (and as such it is a composed whatness), which (essence) is the 'genotypical' whatness of the object, and identical to the dynamical law of the dynamical system that has generated that object. So the Essence is a particular type of whatness category, different from that of a property (As dynamical law it is at the same time a nexus category).
In elaborating a more detailed ontology we have set certain limits as to the scope of the objects (things) and processes to be studied ( The reason will be given later) :
We will concentrate on three Layers, viz. the Mathematical, the Physical and the Organic Layer. However, with respect to organisms we will consider only some of their physical aspects, which in fact means that we go back again to the Physical Layer, which is the substrate of the Organic.
With respect to properties we will restrict ourselves first of all to general MATERIAL STRUCTURE. And within (investigating the phenomenon of) structure we will -- with respect to organic as well as to inorganic beings -- limit ourselves to some specific, but important aspects of it, namely intrinsic SHAPE ( = outer form), intrinsic SYMMETRY, and PROMORPH.  Recall that the latter is the stereometric basic form of some object, i.e. its symmetry expressed geometrically (as a solid), plus indication (also in a geometric way) of the number and configuration of antimers [bodily counterparts]. These forms are classified in our Promorphological System of Basic Forms [Second Part of Website]  and are treated together with symmetry and categories in an introductory document in the Series on Group Theory (Subpatterns and Subgroups, Part XIII) revealing their ontological significance. To see this document in a separate window, click HERE.
S t r u c t u r e,  and this always means microscopic structure, of  natural intrinsic bodies or objects implies, among other properties,  i n t r i n s i c   s h a p e,  i n t r i n s i c   s y m m e t r y   and  p r o m o r p h.  During the generation-from-within of a given object (which makes it an intrinsic body) its Essence expresses itself as  s t r u c t u r e,  i.e the integrated total of material features making up the fabric of that given body. This co-generation of structure boils down to the simultaneous and/or successive unfolding and enfolding of intrinsic properties, which are implied by this structure, and of which we here focus on intrinsic shape, intrinsic symmetry, and promorph.
With respect to  c r y s t a l s  it is possible to know the complete microscopic structure, insofar as the latter is seen as a configuration of atomic nuclei, i.e. a definite pattern of such nuclei, embedded in a cloud of electrons. And with that (crystal) structure we can see the properties that unfold from it.
For  o r g a n i s m s  on the other hand, we can in fact not know their complete microscopic structure because of their immense complexity (Even if we knew this complete structure, we could not survey it, and, as a consequence, could not deduce in an exact way all the properties that potentially unfold from it).
So in organisms we cannot actually derive Shape, Symmetry and Promorph from their microstructure because we don't know the latter. But we can, after the fact, assess their intrinsic symmetry and their promorph from macroscopic morphological data. To categorize mathematically the full (intrinsic) shape is, however, virtually impossible.
As has been said, in the case of  c r y s t a l s  we are in a better position.
From the (known) microstructure of a given crystal, i.e. from its microstereochemical structure, which is in principle assessible by X-ray analysis, we can derive its intrinsic Symmetry (Space Group and Point Group). We can also derive its Promorph, namely by analysing the symmetry and antimers of the chemical motif that remains after removing all translational elements from the crystal's structure. And, finally, from the microchemical structure we can also derive the intrinsic Shape of the crystal (i.e. its external outline or the form of the space that it occupies, insofar as this form is not considered to be distorted by external agents), by assessing the rosette of the rates of growth (Growth Rate Vector Rosette, more about it, next document). This rosette, as just a geometric rosette, then implies Shape and also the macroscopic geometric symmetry (not necessarily the crystallographic symmetry, which will be revealed when the atomic aspects are considered in detail) of the crystal (In organisms this rosette also determines the promorph), and is itself dependent on the geometry of the crystal  l a t t i c e  and on the  a t o m i c   a s p e c t  as presented to the growing environment by the several possible crystal faces. Both factors together determine the growth rate of crystal faces in different directions. The growth rate vector rosette shows the participation of Forms (in the crystallographic sense, where a Form is a set of equivalent crystal faces) in the constitution of the crystal. Each (crystallographic) Form represents a subrosette of growth rate vectors -- in those cases where a particular Form consists of only one face, only one vector is involved in such a subrosette -- while all the participating Forms together (which are called combinations) constitute the full growth rate rosette. And this latter rosette brings about the intrinsic shape of the given crystal ( This intrinsic Shape is often distorted by external agents, resulting in the extrinsic shape of the crystal). All this will be explained more fully below (but also presupposes what has been said in our exposition on the Morphology of Crystals, laid down in the First Part of Website).

We can see these three property types (Shape, Symmetry and Promorph) as category classes (i.e. classes of special If / Then constants) that in their generality, i.e. just as shape, symmetry and promorph, are common determinants in the three lowest Layers, viz. the Mathematical, the Physical and the Organic.
In the Mathematical Layer Shape, Symmetry and Promorph are not physically interpreted, while they are so interpreted in the Physical and Organic Layer (where "interpreted" is meant in an ontological sense).
Shape, Symmetry and Promorph in organisms are co-generated by higher-level dynamical systems, while lower-level systems co-generate them in inorganic beings like crystals.
In the Mathematical Layer we again see Shape, Symmetry and Promorph, but here only as geometrically interpreted (One or another Symmetry appears there as a geometric interpretation of the corresponding abstract group, while a Shape, and also a Promorph, is just a geometric solid). To limit ourselves still further, we will concentrate mainly on (single) CRYSTALS, because their structure and properties are relatively transparent. And by means of the example of the crystal we will analyse what precisely are intrinsic properties (insofar as intrinsic properties), how they relate to the Essence of the given crystal, and in what way they come together in the crystal structure. As has been said, this structure involves Shape, Symmetry and Promorph as main aspects. But, although concentrating on crystals and their properties, we will, as soon as we consider their shape, symmetry or promorph, involve those organisms that happen to possess the same shape, symmetry or promorph.

Crystals possess a periodic structure, which means that a certain (microscopic) unit is repeated in a regular way, viz. such that spatial orientation, size and shape reamain the same. This boils down to the repetition of some chemical unit according to one or another lattice.
Organisms on the other hand, do -- apart from some possible exceptions relating to some colony-like organismic beings -- not possess such a periodic structure. They have repeated parts to be sure, but the orientation of these parts is not the same ( Think of the five arms of a common starfish). The structure is, what I call, tectological (instead of periodic). When such a tectological structure has symmetry (other than C₁ ,  which is the asymmetric group), it is always point symmetry, implying a Point Group, i.e. a group, of which the symmetry transformations are such that at least one point remains invariant (while in a Plane Group at least the plane is invariant (although its points move), and in a Space Group the 3-D space).

So for a crystal the  s y m m e t r y  is first of all its total symmetry, i.e. its SPACE GROUP (which is a three-dimensional analogue to a Plane Group, and as such comprises, like the latter, in addition to rotations and reflections, also translational symmetries (simple translation, glide reflection planes, screw axes). It is geometrically explained for the -- much more simple -- case of imaginary two-dimensional crystals in the First Part of Website (Link HOMEPAGE) (Internal Structure of Crystals) and algebraically (i.e. grouptheoretically) for 2-dimensional crystals in Second Part of Website.
In some cases the symmetry of some Space Group can be further worked out by considering its actual symmetry as a desymmetrization by antisymmetry of a higher symmetry (See in Second Part of Website :  Part II of Subpatterns and Subgroups, where antisymmetry (and colored symmetry) is explained for the -- much more simple -- case of two-dimensional periodic patterns). The resulting antisymmetry group is isomorphic with this higher symmetry (i.e. their basic algebraic structure is the same). So the fact that we are in such a case allowed to interpret existing asymmetries within a periodic pattern of motifs as the result of antisymmetry, means that we have dug deeper into the crystal's structure.

Antisymmetry and colored symmetry are generalizations of (ordinary) symmetry. Let's consider the case of antisymmetry.  Recall that a cover-operation is an operation performed on some object, like a rotation or reflection, such that the object occupies exactly the same space as it did before that operation was applied to it.
While the elements of a usual symmetry group are ordinary symmetry transformations, i.e. ordinary cover-operations, but in fact special cover-operations, involving only reflection planes and points, rotation axes and translation vectors,  an  antisymmetry transformation  is a commutative combination of such an ordinary symmetry transformation, let us call it  S ,  and a transformation, let us call it  e₁ ,  of a totally different type, i.e. not a cover-operation, but nevertheless isomorphic with a reflection (At least so in so-called  junior antisymmetry groups. In such a group  e₁  is itself not an element of the antisymmetry group). The latter (e₁) is a permutation of two states. These two states can represent any bivalent quality whatsoever, including structural features. So the transformation  e₁  represents an alternating change between these two states, say from A to B, and from B to A. As has been said, the transformation  Se₁ ( = e₁S ) is an antisymmetry transformation, and this transformation is again a cover-operation, but of a different type, i.e. different from the cover-operations of usual symmetry ( The  e₁-component is, however, not a cover-operation). Well, if some particular symmetry transformation  S  of an ordinary symmetry group is replaced by an antisymmetry transformation  e₁S ,  the resulting set of transformations still forms a group, an antisymmetry group, which is isomorphic to the original symmetry group. According to usual symmetry, a pattern potentially representing an antisymmetry group has lower symmetry than when it is explicitly interpreted as antisymmetry group. Interpreting such a low-symmetric pattern as an antisymmetry pattern involves extra features of the structure, viz. the above mentioned dual qualities, i.e. extra features of the given structure are now taken into consideration, and so we dig deeper into that structure than by usual symmetry alone.

The same applies to colored symmetry (which is a generalization of antisymmetry).

All the Space Groups, including their anti- or colored symmetry versions, are infinite groups, which means that the number of elements of such a group is infinite -- the order of the group is infinite.

In addition to the space group symmetry we have the intrinsic point symmetry of the crystal, its POINT GROUP, which is the translation-free residue of the corresponding Space Group. Organisms, which all lack a periodic structure, have only point symmetry.

Here we must discriminate between  intrinsic  and  extrinsic  symmetry :  The external shape of a crystal, as such determined by its Essence, is 'in the wild' often distorted by external agents or by inhomogeneous growing conditions, resulting in a lower (extrinsic) symmetry.  By  i n t r i n s i c   s y m m e t r y  we here mean the symmetry, solely resulting from the crystal's Essence, which (symmetry) will appear under uniform growing conditions, free from biasing agents. The potential presence of such biasing elements is typical for the non-mathematical Layers. So only there the distinction between extrinsic and intrinsic is relevant.
In organisms this difference between intrinsic and extrinsic symmetry is even stronger pronounced, but in a different way than it is in crystals. In organisms not only perturbations from outside can distort their symmetry (for example in plants), but also, and more importantly, many functional demands involve deviations from a symmetry initially (primarily) present. Promorphology attempts to uncover and retrieve such primary symmetries :  It assesses the 'ideal' basic form of a given organism (and of all other (inorganic) non-periodic structures (for example molecules or atomic complexes, for that matter), or of those that can be reduced to non-periodic structures (for example crystals).

This point group symmetry can be of three types, of which only the first one appears in crystals :

• Isometric symmetries (distances preserved).
  They involve the usual symmetry transformations like reflection and rotation, and give rise to isometric groups, which are finite with respect to all discrete cases (as in all crystals). Equiformity, and even congruity are preserved. [Apart from isometric Point Groups, the mentioned Space Groups can also be isometric, and they even cannot be otherwise.]

• Similarity symmetries (distances not preserved).
  This type of symmetry is a generalization of isometric symmetry. In it congruity is not preserved, but equiformity is still preserved. Its typical symmetry transformations are reflection-followed-by-dilation (or contraction) and rotation-followed-by-dilation (or contraction). They give rise to similarity symmetry groups. They are infinite, and involve, in addition to the usual symmetry transformations, extra structural features (dilations and contractions) that supplement the description of structure done by just ordinary symmetry transformations. Similarity symmetry groups occur (as an approximation) in some organisms.

• Conformal symmetries (circles are preserved).
  This is a further generalization. It consists of circle preserving transformations of the plane E²\{O} (i.e. the 2-dimensional plane without the origin). For it the property of equiangularity has been preserved, but not that of equiformity, and gives rise to conformal symmetry groups. We have, as the elementary transformation of conformal symmetry in E²\{O}, the circle inversion isomorphic with a reflection, which will be explained later. When no similarity transformations are present, such a group is finite. It involves, in addition to the usual symmetry transformations, extra structural features that supplement the description of structure done by just ordinary symmetry transformations. Conformal symmetry could in principle occur in some organisms or parts of them when they are projected onto the plane, or when its 3-dimensional analogue is considered instead.

As has been related earlier, the point symmetry of a crystal (which here is always an isometry) is the translation-free residue of the corresponding Space Group of the crystal.
A particular Point Group, however, admits of several possible Space Groups :
The Point Group describes (and is) the symmetry of a chemical motif that remains when all translations, present as symmetry transformations in the crystal structure, are eliminated. But there are several different ways in which such a motif can be periodically arranged into a lattice :  For the 32 Point Groups this results in 230 possible Space Groups. So if we go from the crystal's Point Group to its Space Group, we dig deeper into the crystal's structure.
Further, a particular Point Group of a crystal as well as of an organism, generally admits of several possible Promorphs, depending on the number and configuration of the antimers. For crystals, knowing the symmetry of the chemical motif (the chemical motif that remains after elimination of all translations), we can dig still deeper into that motif's structure, i.e. deeper than by symmetry alone, by considering its chemical composition and configuration. As a result we can assess its Promorph (giving the number and arrangement of antimers of the given chemical motif, and, on the basis of this, adjudge this promorph to the crystal itself), and (assess) its chemical type, especially the precise distribution of certain atoms, ions or atomic complexes, within the crystal lattice.
For an organism we can assess its basic symmetry, by considering reflection planes and rotation axes. When these data are supplemented by the number and configuration of antimers, we can assess the organism's promorph, which in many cases supplements the information about the organism's structure as obtained by symmetry alone. See next Figures.

Figure 1.  Test of a recent sea urchin (sanddollar), with (natural) indications of the five antimers (extending also internally) which together build up the whole animal. Although almost regularly 5-fold, the animal is only bilaterally symmetric and possesses a mirror plane as its only symmetry element. Its symmetry therefore is that of  D₁ .  This group has two group elements, namely the identity element and the reflection in the median plane. The general  promorph  of the animal, is half a rhombic pyramid, or, still more generally, half an amphitect pyramid, and so belongs to the (general) (Heterostaura) Allopola. It has, however, five (similar) antimers, and so does not belong to the Allopola zygopleura. The true promorph of the body of this animal is half a 10-fold amphitect pyramid, expressing in this way the possession of five antimers and implying the promorph to belong to the  Pentamphipleura  (itself being a species of the Allopola amphipleura).   See next Figure.

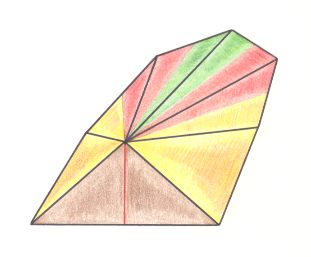
Figure 2.  Oblique top view of the promorph of the bodies of irregular sea urchins. It is half a 10-fold amphitect pyramid with the five antimers (corresponding to five body parts in the animal) indicated by colors. It therefore belongs to the  Pentamphipleura  (Allopola amphipleura). The brown plane facing the beholder is the bisection face associated with the bisection of the 10-fold amphitect pyramid.

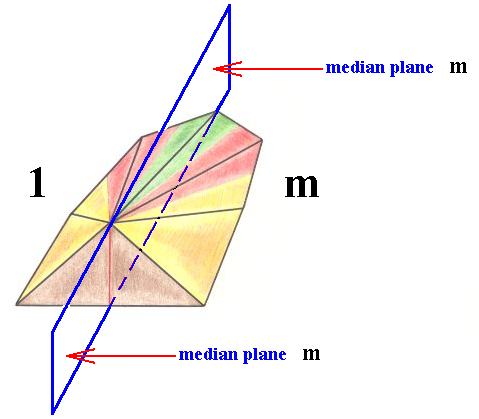
Figure 3.  Half a 10-fold amphitect pyramid representing the promorph of an irregular sea urchin. The latter's five antimers are indicated by colors. The median plane is a mirror plane and as such the only symmetry element of the sea urchin's symmetry. The symmetry group therefore is  D₁ .  This group has two group elements, namely the identity element  1  and the reflection in the median plane  m .  In the promorph they are represented by its two halves separated by the median plane. These halves are asymmetric units. But, as can be seen, each such a half -- representing a group element -- consists of two-and-a-half antimers, so each group element is -- in the present case -- interpreted as a certain set of antimers (more precisely, as a set of five half-antimers, or, equivalently, by two and a half antimer).

The symmetry of an organism, as formally implied by its promorph, evidently comes about, in spite of its one and definite grouptheoretical what-is-it, by a quite different process as is the case (for the same symmetry) in crystals. In the latter the actual generation (which is strictly just a co-generation) of their symmetry is based on lower-level processes that have to do with lowest-energy configurations of atoms, ions or atomic complexes, configurations that are going to make up the crystal structure. The higher-level processes in organisms, responsible for their basic symmetry, are the result of harnessing lower-level laws, as explained in Part I. The same applies to the phenomenon of growth. In crystals this consists in the apposition (deposition) of constituents (molecules, atoms, ions or atomic radicals) onto the surface of the growing crystal (without changing the crystal so far formed). This apposition takes place in order to reduce surface energy (caused by dangling chemical valences). So this way of growing is a low-level process. In organisms on the other hand, growth proceeds by intussusception, i.e. by the intake of nutrient constituents into the interior of the organism, accompanied by complex metabolic processes. This way of growth often changes the organism so far formed. It is a high-level process (a high-level growth). The mentioned intussusception is possible because an organismic body is in a semi-liquid state, in contrast to crystals which are solid objects ( There do exist so-called liquid crystals, it is true, and there intussusception is possible, but in that case it is a simple (low-level) process without being accompanied by genuine metabolic processes).
All the mentioned high-level processes embody a leap of increase in material complexity, elevating the inorganic to the organic. Functional demands, absent in inorganic beings -- where only energy demands count -- play a decisive role in constituting the organismic structure. They have to do with locomotion, suspension (in water), and even ornaments, the latter in connection with sexual reproduction. All these are high-level features, and many of them must be maintained against the tendency to lowest-energy states. Therefore organisms are not thermodynamically equilibrium structures, like crystals are, but are dissipative structures, held far from thermodynamic equilibrium. That's why organisms must feed themselves.

Functional demands are not the sole generators of organic forms. In all organisms we can find certain fundamental dynamic subsystems, that represent stable dynamics within the developing organisms, and result in some basic morphological structures (generic forms) as we see it, for example, in phyllotaxis in plants. These basic morphological structures often are expressed in the final promorph of the organism or part of it. See for all this, GOODWIN, B., 1994, and 2001, How the Leopard Changed Its Spots.

When all these analyses are done with respect to a given crystal or organism, we are left with two types of asymmetric units, units that cannot be further analysed grouptheoretically :

The first type of asymmetric unit is a symmetry left-over, i.e. it represents the ultimate motif representing in turn the ultimate group element, and consists (in the case of crystals) of two subtypes :

• The macroscopic left-over asymmetric unit resulting from considering the crystal's Point Group.

• The microscopic left-over asymmetric unit resulting from considering the molecular symmetry rosette (3-dimensional), obtained after all translations have been eliminated. This rosette has the same symmetry as the macroscopic intrinsic point symmetry of the crystal.

In the case of  crystals  it is an antimer or half an antimer of the molecular rosette [Macroscopically, single crystals do not have genuine antimers, because their structure is microscopically periodic. Macroscopically, these crystals are (structurally) homogeneous. Organisms on the other hand, are macroscopically heterogenous and definitely do have antimers macroscopically].

Crystals often occur as 'twinned' forms. In these cases two or more crystal individuals (of the same species) have grown together in a definite and regular way. Such a twinned condition sometimes allows for macroscopic antimers to be detected. These antimers are then represented by the crystal individuals which have grown together. Consequently such twinned crystals are, at a higher structural level, aperiodic. So in a formal morphological sense they represent a transition from single crystals (which are wholly periodic) to organisms (which are aperiodic, with some exceptions among Bryozoans and maybe some other colony-like organic individuals).
It should be realized that in most cases crystal individuals grow together in a totally irregular way resulting in crystalline aggregates as we find them in most rocks. Twinning, on the other hand, is the result of a regular process, according to some definite rules, yielding typical and repeatable forms.

In the case of  organisms  the ultimate promorphological unit is always a macroscopic antimer or half an antimer.

If such an antimer is symmetric (normally according to the symmetry group D₁), it can grouptheoretically be further analysed as to its parts, representing group elements. What is left then is (normally) half an antimer, which cannot be further analysed grouptheoretically.
If the antimer is already, all by itself, asymmetric, it is as such a left-over asymmetric promorphological unit and cannot be further analysed by Group Theory.
The structure of all these left-over asymmetric units can only be understood by means of a study of the dynamical systems or subsystems that took part in their generation. In organisms this involves consideration of organic functions and their evolution.

• Whatness Categories.
  In our introductory document (Second Part of Website, Series on Group Theory, Subpatterns and Subgroups, Part XIII) we distinguished them as just whatnesses, contrasting them with categories, but here we consider them as whatness categories. We have two subtypes :
  • Whatness Category of a given intrinsic object (being), viz. its Essence.
    As 'phenotypical' expression of the (genotypical) Essence it is a composed whatness, consisting of all the object's intrinsic properties. The latter are simultaneously or successively expressed or suppressed by the Essence as it acts as the dynamical law according to which the object is generated and maintained (Think of a caterpillar developing into a butterfly). As Essence it is the genotypical whatness of the object.
  • Whatness Category of an intrinsic property.
    As such it determines the what-is-it of that property, resulting in that property-as-analysed (in an ontological sense). The properties which will concern us most are, as has been said, intrinsic Shape, intrinsic Symmetry, and Promorph.

• Entitative Constant, i.e. a category determining the  implication  of an intrinsic property (of which its whatness is already presupposed)  by  a given intrinsic object.

• Nexus Category (causality, general and special laws).
  This category connects states of a dynamical system, and as such -- when all possible trajectories are considered -- is a dynamical law. The fundamental conservation laws of Physics are contained within such a law (If it is a dynamical law of a totality-generating system, i.e. a system that generates a genuine being, then this law becomes the Essence of that being and so is at the same time a whatness category).

( Further there are categories with respect to bulk matter (whatness categories, material constants and nexus categories). But these we will not consider, because we here investigate intrinsic beings only (atoms, molecules, crystals, and, at times, organisms). Bulk matter is, in this respect, less fundamental because it is an aggregate of intrinsic beings (atoms, molecules and crystals).

The beings (or whatever being-thuses) are signified by the Then-components. So one could think that these beings are already present with the  If / Then  constants. When we take such a constant, say, If X then Y, itself to be present, then, one would be tempted to say that Y is already present. But this is not so. To begin with, the  If / Then  constant is not and never present in an existential way :  it is not, but is valid. Further, the Y in it is not Y, but :  then-Y.  Y will only be existentially present when X is satisfied. Also the X as it figures in the constant is not X, but If-X.

We've said that we shall limit ourselves mainly to  crystals  (and to compare them with organisms, but only with respect to some features they have in common), which should figure as examples while clarifying the ontological structure of the world. But in fact all types of intrinsic objects -- at least crystals and organisms -- should be involved in such a clarification (Especially human individuals -- each one of them involving the total set of Layers -- should be included). The reason that we stick mainly to crystals is the fact that organisms are too little understood to serve as clarifying examples. It will be the task of future generations of investigators.
For setting up an ontology of  If / Then  determinants, it is not sufficient to superficially browse through the stock (or part of it) of the world's things and processes. This can only be a first tentative stage, as we have done in the foregoing. The next and present stage of the investigation must consider some chosen homogeneous well-known family of intrinsic objects, from which at least some of the most basic and general ontological relations can be read-off by analysing their special features. And having chosen the family of  c r y s t a l s,  we should, for instance, actually show the asymmetric ultimate chemical unit of a given (single) crystal, or show the antimers of the chemical rosette. Group Theory and Promorphology will then demonstrate formally in what way such a unit is found to be repeated to  c o n s t i t u t e  the crystal's structure or pattern, i.e. to reveal the whatness of such a pattern. Some Thermodynamics will help to clarify the actual  g e n e r a t i o n  of that pattern, i.e. to understand it as a lowest-energy configuration of system elements, a configuration realized by the crystallization process. The question of why such a configuration is indeed a lowest-energy configuration is expected to be answered by Quantum Mechanics. The generation of the asymmetric unit itself should be seen as being integrated in the whole process, not necessarily as a separate stage of the latter.
By concentrating systematically on a specific family of intrinsic objects, in our case crystals, we can closely study, on the basis of their intrinsic structure, their intrinsic properties as to what precisely they are in each case, and then evaluate them ontologically (which means knowing what they are, precisely and only insofar as they are intrinsic properties), leading to a better understanding of the determinative constants and of the interwoveness of COSMOS and NOMOS by determinative threads.
Certain aspects of Group Theory, Promorphology, Mineralogy, Crystallography, Chemistry, Biology (when comparing crystals with organisms) and even ornamental art, will be studied (partly already done so). Especially in the domains of Group Theory and Mineralogy we will find many in this respect important and interesting crystallographic features that will provoke ontological pondering, resulting in a detailed account of an ontology of determinants. And as a third stage of the investigation, organisms should be fully included, revealing still more details and challenges for such an account.

In fact, what we will do is the setting up of a general Pattern Theory.  Indeed all regularities involve repetitions of basic units. We can see this not only in Morphology, but also in Behavior and Chemistry. Here we will limit ourselves to a general theory of spatial patterns, which includes rosettes, periodic patterns, but also tilings (periodic and non-periodic). And because we are only out for generalities, the study of the much more easier two-dimensional patterns (2-D rosettes, 2-D periodic patterns, 2-D periodic and non-periodic tilings, etc.) will be prominent in our studies. Such a pattern theory will be mathematical in character. It will rationally classify patterns, and establish logical connections. And these latter will then be re-interpreted ontologically, and placed within a broader ontological context ( If / Then  constants, determinative threads, categorical laws, Layers of existence, etc.) as has been set out in the foregoing.

While in ancient times Ontology (as a metaphysics of beings and Being) could stand on its own feet, because genuine natural science was still absent,  it is clear that this is no longer the case. Ontology must now evaluate some general and specific results of Natural Science (and also of modern Mathematics and some other sciences as well) as to their ontological significance, which means that the whole undertaking becomes highly interdisciplinary (which is, by the way, a general trend nowadays). The necessity of such an interdisciplinary approach is emphasized throughout the present website.

But of the general categories there is such a discipline, established by the eminent philosopher Nicolai HARTMANN (first part of 20th century). These categories (not treated, however, in the form of  If / Then  constants) are of two main types (with respect to their generality) :

• Categories common to one particular Layer (either the Mathematical -- treated by HARTMANN as his 'Ideal Sphere of Being' -- or the Physical (inorganic) Layer, or the Organic, or the Psychic, or, finally, the Super-psychic Layer).

• Categories common to the whole series of Layers involving Time :  The Physical, Organic, Psychic and Super-psychic Layers, i.e. HARTMANN's Real Sphere of Being.

• Categories common to all Spheres and Layers of Existence, viz. the Fundamental Categories, given by HARTMANN in the form of pairs of opposites, like
  SYSTEM--ELEMENTS.

e-mail : 

Back to Homepage

Back to Contents

Back to Part I

Back to Part II