

(Takes a few minutes to load images)
e-mail :

Sequel-8 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-8) continues the investigation of snow crystals (and generally, on ice crystals).
Sequel to the Significance of Snow-Crystal Growth for the General Holistic Ontological Theory, and the Significance of Ice-Crystal-Growth-in-general for a consideration of Organic Pattern Formation.
The Branching Instability in Snow Crystals.
7. Mechanism of morphological instabilityAnother important point [ The previous point concerned habit change of snow crystals] about the pattern formation is the mechanism of morphological instability occurring on the polyhedral snow crystals [A polyhedral body is one that is bounded by flat surfaces]. In general, this problem relates to the interaction between the local distribution of supersaturation on the crystal surface and the growth kinetics along the surface. How does the morphological instability develop on the snow crystals as a function of supersaturation?
Now we consider the diffusion field of water vapor around the snow crystal. When a snow crystal is growing in the atmosphere, the water vapor near the surface is consumed by the growing crystal and the diffusion field conforms around the crystal, as shown schematically in Fig. 9.
Fig. 9. Schematic illustration of diffusion field around a polyhedral crystal. The water molecules are transferred through the vapor phase from the surrounding supercooled cloud droplets to the snow crystal.
The equiconcentration lines should be almost concentric, but the snow crystal has a polyhedral shape. Then the corners and/or edges of polyhedral crystals stand out toward the higher concentration region. This phenomenon is called Berg effect and very general for the diffusion field around the crystal. Consequently, the supersaturation along the surface should be the highest at the corner and/or edge but the lowest at the center of the facets. This configuration of the diffusion field allows the corners and/or edges of polyhedral crystals to grow faster than the central parts of facets and drives the development of unstable shapes. This process also can be simulated by numerical calculations. Fig.10 shows an example of the simulation results which were carried out for the two-dimensional ice crystals by Yokoyama and Kuroda. The development from a circular plate, to a sector crystal through a hexagonal plate, and then to a dendrite is clearly found in this illustration.
Fig. 10. Time-sequence illustration of a growing snow crystal, obtained by a computer simulation. A circular plate crystal, which is an initial shape in this simulation, grows into a hexagonal plate and finally the hexagonal dendrite develops. Numbers on the right hand side indicate the growth times in seconds. Supersaturations of environment are 0.17 and 0.34 for (a) and (b), respectively.
It is clear that this mechanism, as explained by FURUKAWA, is meant to explain the fact of dendritic growth in snow crystals. It is based on growth rates. And because the six points of a snowflake hexagon are equivalent, we can expect a same degree of extension at each of the six corners.
In branched snow crystals we see the interplay of two processes, viz., (1) the development of slow growing crystal faces, in our case, where we only consider the snow crystal as seen down along the c-axis, the six sides of the (flat) hexagonal prism, and (2) the rapid unstable growth in directions between those of the mentioned six prism faces, resulting in outgrowths or arms, extending from each edge of the flat hexagonal prism (or, as seen from above, extending from each of the six corners of the hexagon), and also the growth of side-arms emerging from the main arms at angles of 600.

Figure above : Part of a snow crystal.
We see branches (as the result of fast unstable growth), and, in addition to that, the formation of normal crystal faces. See next Figure.
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
The next Figure indicates the growth directions of the prism faces, at the prism itself, as well as at the branches.
Figure above : Same as previous Figure.
Growth directions of prism faces indicated.
(Adapted from LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
The next photograph is a snow crystal having the shape of a flat hexagonal prism (a regular hexagon when seen down along its c-axis).

Figure above : A hexagonal snow crystal that has the shape of a flat hexagonal plate. Unstable growth is just about to begin. The rounded contours are the result of melting.
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : This (partial) image of a snow crystal again shows the two growing phenomena, viz., branching and faceting.
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : Also here we see the two growth phenomena in a single snow crystal. One can see the six-fold repetition of fine details.
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : Branched and faceted growth in a snow crystal. The central part is out of focus, which means that a hexagonal column rises from the stellar base of the crystal. This column could be very thin and capped with a small stellar top. Also here the repetiton of fine detail is extraordinary (not extraordinary for snow crystals, but just extraordinary).
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)

Figure above : Whole snow crystal. The curved ridges point to local habit change, which is then six-fold repeated around the crystal's c-axis. Also here the repetition of fine detail is extraordinary.
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
With snow crystals we deal with WATER-ICE. While this document was being prepared, a successfull mission of unmanned spacecraft to Saturn and its moon Titan was accomplished. Photographs of the surface of Titan and other data, suggest the presence of water ice. See next image.
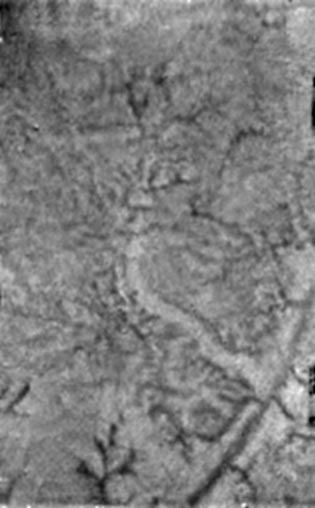
Figure above : A single Huygens Descent Imager/ Spectral Radiometer (DISR) instrument image shows two new features on the surface of Titan. A bright linear feature suggests an area where water ice may have been extruded onto the surface. Also visible are short, stubby dark channels that may have been formed by 'springs' of liquid methane rather than methane 'rain'.
The Descent Imager/Spectral Radiometer is one of two NASA instruments on the probe.
(Image and subscript from NASA)
(Credit : ESA/NASA/JPL/Univ. of Arizona.)
(Date : 21-01-05)
We have seen that in stellar snow crystals in all cases - also those where the crystals are distorted, resulting in asymmetric crystals (See next Figure) - the general morphology is neatly repeated six-fold around the center of the crystal, and that in nearly all cases most of the fine detail is also repeated.

But also in most non-stellar crystals we see their morphology repeated. This internal (but still macroscopic) morphology is certainly the result of more or less unstable, and thus fast, growth, but not fast enough to let branches appear.
For Figure 1 click HERE .
For Figure 2 click HERE .
For Figure 3 click HERE .
For Figure 4 click HERE .
While the above Figures show the repetition of morphological details even in (single) non-branched snow crystals, the next Figures concentrate on the diversity of morphology among snow flakes. The enormous diversity is already present in non-branched snow crystals, and continues to be so diverse in branched snow crystals as well :
From the booklet Snowflakes in Photographs by W.A. BENTLEY, 1931, I have again taken images (which are all copyright-free) of plate-like hexagonal snow crystals without branches, and have isolated an approximately radial segment from each of them, to show the diversity of morphology among such snow flakes, i.e. to show the change of morphology if we go from snow flake to snow flake (In the whole crystal this morphology is, in the vast majority of cases, repeated six-fold about the crystal's main axis). The series of Figures is then continued depicting branched snow crystals. See the next series of Figures :
For Figure 5 click HERE
For Figure 6 click HERE
For Figure 7 click HERE
For Figure 8 click HERE
For Figure 9 click HERE
For Figure 10 click HERE
For Figure 11 click HERE
For Figure 12 click HERE
What we see here, and in the following Figures, is the realization of the enormous form potential of ice. In fact this form potential, or form generator, is inherent in the system
Rhombic Prism + unstable (fast) growth .
This fast (i.e. so fast that it is unstable) growth must already be assumed for the above non-branched snow crystals, because they are not homogeneous (flat hexagonal) prisms. The mentioned rhombic prism is the unit cell of the hexagonal crystal lattice, where the latter is provided with water molecules, as can be seen in the Figure given above in the previous document. In fact we see here the molecules A, B, D, C, E, E', A', B', D', C', A'', B'', D'' and C''. But to give an exact count of the number of water molecules pertaining to the unit cell, we must realize that with the exception of E and E', all the other molecules are only partially belonging to the unit cell :
1/2 x 1/3 of A
1/2 x 1/3 of D
1/2 x 1/6 of C
1/2 x 1/6 of B
1/3 of A'
1/3 of D'
1/6 of C'
1/6 of B'
1/2 x 1/3 of A''
1/2 x 1/3 of D''
1/2 x 1/6 of C''
1/2 x 1/6 of B''
and in addition to these we have :
1 x E
1 x E'
This adds up to four molecules.
So one rhombic unit cell of ice contains four water molecules.
The next Figure gives such a unit cell (but still provided with whole molecules, part of which accordingly belong to adjacent unit cells).
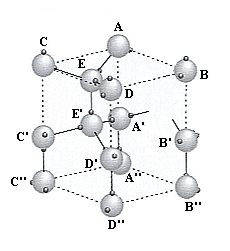
Figure above : (Single) Unit Cell of the structure of Ice. It contains four water molecules. The shape of this unit cell is that of a rhombic prism.
(Adapted from NESSE, 2000, p.52)
And it is this Rhombic Prism with four Water molecules, combined with the phenomenon of Rapid Growth (where this unit cell is going to be copied over and over again, such that a periodic structure results), that represents an extremely versatile form-generator, as is evident not only in snowflakes, but also in the varieties of shapes represented by ice-flowers (windowpane frost) that can be seen, for example, on windshields of parked cars on a humid night with a temperature of around 00 C. In such ice-flowers even curved structures (as long as 10 cm) can be seen. See next Figure.

Figure above : Ice-flowers (windowpane frost). One can clearly see curved structures.
(After BENTLEY, W., Snowflakes in Photographs, 1931, 2000.)
The next two Figures also show windowpane frost.


Figure above : Windowpane frost.
(After LIBBRECHT (from his website www.snowcrystals.com))
Window frost forms when a pane of glass is exposed to below-freezing temperatures on the outside and warm moist air on the inside. Water vapor from the inside air condenses as frost on the frigid window. The branches of the frost in the two above Figures are each about 3mm in length. These frosts form basically by the same crystal growth processes as those in snowflakes, except the frost crystal growth is heavily influenced by the window surface (LIBBRECHT, www.snowcrystals.com at : Natural Snowflakes, Frost Crystals).
Crude model for windowpane frost.
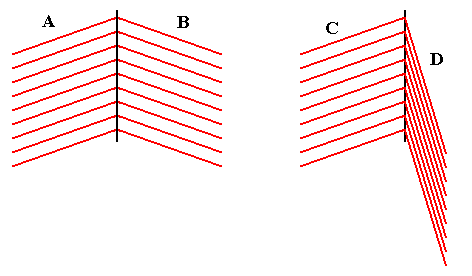
The next Figure again depicts the growth of two crystal faces, but here the growth rate of one of these faces changes during the course of growth. We can say that the Figure depicts an example of two faces that react differently to a change of temperature along the growth path.
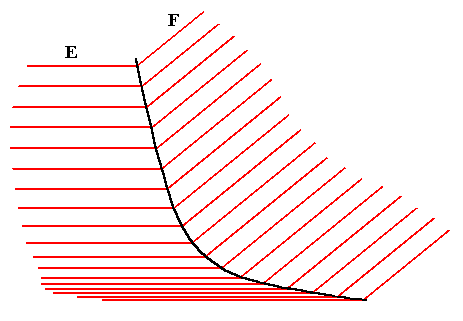
Figure above : Two crystal faces, E and F, growing in different directions, are subjected to a change in temperature. Because they are supposed to be (crystallographically) non-equivalent faces, their surface features are different, and they react to a change in temperature (here a smooth continuous change) in different ways, resulting in a continuing change of growth rate of one of them (in the present example). This automatically implies a continual change of habit of the crystal if they are faces of a crystal at all. If these faces belong to an ice-flower feather, then the curved mid-line is the most prominent feature. And indeed we see ice flowers that have a general morphology as the one diagrammatically depicted in the present Figure. In the latter, however, a more or less exaggerated temperature change is assumed, in order to illustrate the phenomenon. We suppose that in real ice flowers the change of temperature during the growth of a feather is very small, resulting in weak curves (as indeed they are in real ice flowers), in turn resulting in more or less equal distances between the successive traces of facial growth, so that indeed a feather-like structure emerges.
Of course all this is just an attempt at a more or less crude explanation of the formation of curved ice flowers.
As to the formation of ice flowers, whether curved or not, we can add the following :
They seem, when temperature and humity conditions are right, to be initiated, i.e. 'seeded' by existing scratches or abrasions in the substrate. They tend to follow these scratches.
About this BENTLEY, W. and HUMPHRYES, W., in their book Snow Crystals, 1931, 1962, p.21, write the following [comments between square brackets] :
Scratches, however, obviously do not account for all the beautiful fern and plume-like forms of windowpane, and kindred surface, ice and frost, and often appear to account for none of them at all, for they occur in great abundance and in the most graceful curves even on a smooth pavement where it would be preposterous to expect guiding grooves to exist in such artistic sweeps and whirls. Of course, inequalities in the availability of moisture, whether liquid or gaseous, is an important factor in determining the direction of growth of surface frost. But where such inequalities are not pronounced, the pattern assumed appears to be determined partly by grooves and scratches, if any, in the surface [ i.e. the substrate of the ice structure ], and partly by one or more other causes not definitely known. In addition to the curved forms there are at least two lattice types [ highly remarkable! ]. One in which the crystals go off at an angle of 60 degrees to each other and form a herring-bone pattern, as in 2, page 214 [ to see it click HERE ], and another, illustrated by 4, page 214, in which the angle of departure is 90 degrees, and the result a "Tannenbaum" (fir tree) figure [ to see it click HERE ]. [ See also the artificial tetragonal 'snowflake' generated in the Hele-Shaw cell, depicted in the bottom image in a Figure below ].
For more examples of windowpane frost (ice flowers) click HERE . They are taken from BENTLEY & HUMPHREYS, Snow Crystals, 1931, 1962.
When looking at these pictures of windowpane frost, one thing is clear : How exactly these frost structures are formed is not clear. And it is evident that the above model is indeed only a very crude one. It reminds me of the many theories or models trying to explain the more general features of organic morphogenesis, and their poorness with respect to real morphogenesis as it is actually observed in organisms.
Let's briefly discuss some of the images (labelled as A, B, C, etc.) of the just given Figure of windowpane frost structures (see LINK directly above) :
In image A we see a combination of linear and curved growth.
In image B we see irregular curved growth, which could be due to the following of a scratch in the substrate.
In image C we see strongly curved structures which are more or less symmetric.
In image D we see strongly and regularly curved forms, where at the same time several different angles are involved.
In image E we see fine feather-like structures. I have seen that such structures can easily reach lengths of up to 20 cm.
In image F we again see different angles (different from 600) involved. We even see the orientation of side-branches changing along one and the same (curved) main branch. The curved frost line (as visible in the image) is certainly not caused by a corresponding scratch, because the angle of the side-branches, insofar as it varies, varies smoothly as we go along that frost line. If the frost had followed a pre-existing scratch (which it certainly will do if there is one), then individual crystals would have been deposited along the scratch with random orientation with respect to each other (because of the random structure of the surface of the groove). And these crystals would then shoot off differently oriented branches.
In image G the frost structures look very 'organic' indeed.
The structures in image H could be the result of the frost following pre-existing scratches in the substrate. It is then to be expected -- and actually present in the image --that along the scratch differently oriented crystals are seeded, differently oriented because the surface of the groove is more or less randomly sculptured as we go along the bottom and side walls of the groove. And from these differently oriented initial crystals correspondingly differently oriented outgrowths will result.
In images I and J we again see a clear manifestation of a 900 off-shoot angle.
In image K, finally, we see 'good-old' sixfoldness to be clearly expresses in windowpane frost (Although, unfortunately, the scale of the photograph is not indicated, it is pretty sure that we here have to do with a large ice crystal, having the same general shape as a typical snow crystal).
We assume that, like in the case of branched snowflakes, the formation of ice flowers is a non-equilibrium crystallization process. The growth process is very fast. Particles that arrive at the growing surface of the ice already present (and which itself lies on a substrate, for instance a glass plate), and arriving there properly aligned, will be accepted and thus will be deposited onto that surface, while particles arriving at the growing surface, but arriving there not in the right orientation, will be rejected and, because of the rapidity of the process, do not have time to realign themselves. Where on the surface these initial depositions occur is fully by chance. And they will be preferred points for further growth because they stick out into the growing medium.
Form generator of organic entities.
One may speculate (but not more than that) that this form-generator (involving the rhombic unit cell, and thus representing the c-centered hexagonal lattice), together with its crystallographical cousins, that involve the remaining 13 types of (three-dimensional) crystal lattices (by which other substances crystallize), viz.,
primitive triclinic lattice,
primitive monoclinic lattice,
centered monoclinic lattice,
primitive orthorhombic lattice,
centered orthorhombic lattice,
orthorhombic body-centered lattice,
face-centered orthorhombic latice,
primitive tetragonal lattice,
body-centered tetragonal lattice,
rhombohedral lattice,
primitive isometric lattice,
body-centered isometric lattice
face-centered isometric lattice,
and, in addition to these, the possible quasi-lattices as is observed in certain 'crystals', also lie at the basis of the generation of organic forms.
The quasi-lattices just mentioned could account for 5-fold symmetry, which in genuine crystals cannot occur. It does, however, occur in quasi-crystals. The 'lattice' on which the structure of these crystals is based is in fact not a lattice at all, because it is not strictly periodic. It is however approximately periodic, and can be such as to need two units, that when repeated in a certain way result in such a quasi-lattice. The latter were studied in Part XX , at : Short Intermezzo on Crystals, Quasicrystals and Organisms. Here (in the present document) we reproduce an example of such a lattice (in the form of a two-dimensional analogue) :
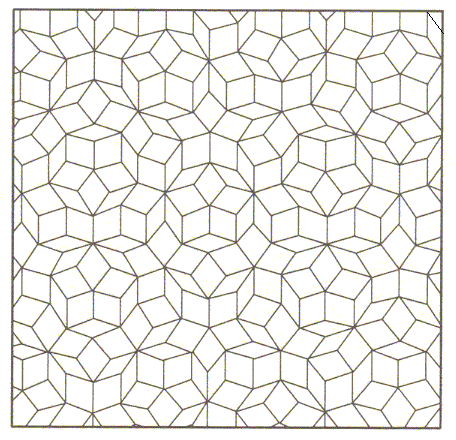
Figure above : A (rough) model of the internal structure -- in terms of building blocks -- of a two-dimensional quasicrystal.
(After BALL, Ph., 1994)
That perfectly-looking crystals can exist on the basis of such a quasi lattice is shown by the next Figure.
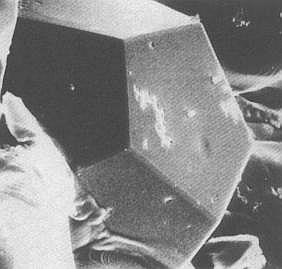
Figure above : A quasicrystal. They can have shapes that reflect the forbidden symmetries of the atomic structure. In this picture the quasicrystal has a dodecahedral shape.
(After BALL, Ph., 1994)
Examples of other materials that generate forms reminiscent of biological entities are presented by the next Figure. It was given by BALL, P., Designing the Molecular World 1994, p.293, Figure 9.1, with the following subscript :
When prepared by depositing the atoms from a vapor onto a cold surface, metal silicides such as (Cr,Fe)5Si3 crystallize into a variety of bizarre and dramatic shapes.
You can see this Figure HERE .
So it could be that the general form-generating system Lattice, or Quasi-lattice, plus Fast Growth lies at the basis not only of the morphology of crystals (and quasicrystals), but also of that of organisms. In the latter, however, we must assume that it only lies at the u l t i m a t e basis of organic form generation, or maybe, entirely within the Implicate Order, resulting in the fact that lattices have not been observed in organisms.
The possibility of the existence of organic lattices is discussed by PRZIBRAM, H., Die anorganischen Grenzgebiete der Biologie, 1926.
Generally it is clear that branched forms, as a result of unstable growth, will be irregular, not only with respect to their detailed morphology, but also with respect to their global features, unless either the expanding substance or its medium of expansion is prestructured, in the sense of it being anisotropic (i.e. showing preferred directions), which can be accomplished by the presence of a lattice.
It is instructive to again consider branched growth in crystals. Crystal growth is the increasing expansion of formed substance by supply of more and more material. The rate of this process determines the resulting shapes. Only in the case of slow growth the narrowly space-enclosing crystals will result. These crystals are therefore polyhedral bodies bounded by flat faces. The deviation from the best possible space filling, namely the sphere, which, with relative largest volume has the smallest surface area, can only be due to the anisotropy of the given material, of which the intrinsic growth rate is different in (certain) different directions (PRZIBRAM, 1926, p.96). And indeed the resulting crystals are enclosed by the slowest growing faces, and having thus accomplished a closest packing of their constituents (ibidem, p.96). The possible crystal shape with smallest possible surface area (which never reaches a sphere because of the mentioned anisotropy of the material) is the most stable configuration.
With increased rate of crystallization the particles that are about to be deposited onto the crystal's surface will first do so at protruding points of the crystal already formed, because these points are better exposed to catch particles. Moreover these protruding points came into being because they correspond to the directions of fastest growth. And when, upon further growth, the particles generally (still in the case of fast crystallization) do not have enough time to find the right sites at which to settle, those that, on approaching the crystal, happen to be oriented in the same direction as those that have already settled, provide preferential points for further growth. And these preferential points are the "random bumps" of which we spoke earlier.
In the case of extremely fast transformations, finally, there is no sufficient time for an orderly supply and deposition of oriented particles anymore, resulting in glasses or in colloidal forms (the latter in the case of solutions). All genuine structure is then lost. They are not expansion phenomena anymore, in the same way that a bullet leaves just a circular hole in a glass plate, and not a star-shaped figure of cracks (PRZIBRAM, 1926, p.96 -- 97).
The next Figure gives three examples of artificial unstable growth resulting in certain expansion structures to emerge with regular or irregular branches.
Figure above : Pattern formation in the Hele-Shaw cell (two flat plates -- one transparent -- between which is enclosed a layer of viscous liquid), in which a liquid (here the clear liquid) is injected into a more dense liquid (colored) under pressure. Depending on the injection pressure and other factors, different bubble shapes can be observed that are reminiscent of those seen in electrodeposition ( = the deposition of metal clusters by applying a voltage to an electrode dipped in a solution of metal ions).
Shown here are (1) DLA-like (top-left) -- "DLA" means diffusion-limited aggregation, (2) dense-branching (top-right) and (3) dendritic (bottom) growth. For the latter, some directional preference must be introduced, for example by scoring the face of one of the two plates with a lattice of grooves. The square lattice in this example generates a "snowflake" with fourfold symmetry.
(From BALL, P., Designing the Molecular World, 1994, Plate 14.)
In the artificial fourfold "snow crystal" of the previous Figure (bottom) we see the same morphology repeated four times about a central axis. This "snow crystal" is, of course, not a snow crystal, and, moreover, it is not a crystal at all. It is an expansion figure of a liquid, and a liquid does not possess a periodic structure, it is morphologically isotropic. In fact the generation of this structure is wholly mechanical. But, nevertheless it seems to display holistic features, expressed by the fact that the morphology of the four branches is more or less exactly repeated, as we see it also in the case of the six branches of many snow crystals. But in fact, this artificial fourfold structure is not holistic at all, which will be clear after considering the following : Whereas in the case of snow crystals only the developing crystal is structured (by an intrinsic lattice, i.e. a lattice pertaining to the material itself of the crystal), and the growing medium of the snow crystal is not so structured, in the case of the artificial fourfold figure not only this figure is pre-structured (and is so pre-structured by an extrinsic lattice), but also its medium is (in the same way) pre-structured. And so this medium (of the artificial fourfold structure) does not impose or bring about any randomness with respect to the developing figure, while in the case of a developing real snow crystal such randomness is inherent in its growing medium, resulting in a random pattern of properly oriented particles (arrived) close aboard the growing surface of the crystal (amidst not properly oriented particles) and directly adhering to that growing surface and so constituting preferential points of further growth.
Now it seems that the same laws of form generation prevail in organisms too. Often increased growth in plants of which the leaves are undivided or only a little split, brings about heavily branched or incised leaves (PRZIBRAM, 1926, p.97). Also in the animal kingdom such phenomena are observed. PRZIBRAM gives several examples.
So all this could indicate that the system pre-existing anisotropy plus fast growth, where the anisotropy can be due to the presence of a lattice, also determines (much of) organic form generation.
With this idea several problems pop up, viz., the wide-spread five-foldness in organic entities (many flowers and all Echinoderms), and the also wide-spread phenomenon of spiral forms within the organic world. While the first problem could be remedied by assuming the presence of quasi-lattices, the second problem is much harder to bring into harmony with something like the existence of organic lattices. The spiralling as we see it in many plants (as was discussed in Part XXIX Sequel-2 ) is discrete : the leaves are positioned on an imaginary spiral. This form of growth (in plants) could be interpreted as fast growth from a central point in horizontal directions, while this point is moving vertically. And where certain regularities are present (providing the resulting plant with a certain definite morphological aspect as presented to an observer), we could assume the presence of some pre-existing anisotropy, possibly in the form of some lattice.
The continuous spirals, on the other hand, as we see them realized in the shells of many snails, in Ammonites, etc., cannot, it seems, be due to the presence of some pre-existing lattice (although, given the fact of the many forms of ice-flowers -- which are the result of fast growth and a pre-existing lattice -- in which curved shapes commonly appear, "everything could be possible" on the basis of such a form-generating system). Although the shells of Ammonites and snails are themselves crystalline, they presumably consist of an aggregate of very small crystals, an aggregate without crystallographical continuity, which is moulded by the organism. And there are certainly many other organic shapes (and also even inorganic ones) that do not seem to be based on such a form generator.
Like unbranched crystals (and thus polyhedral crystals) do not involve fast (unstable) growth, many organic forms will also not be the result of fast growth. And many organic forms (branched or otherwise) are totally irregular, so they are certainly not the result of some sort of pre-existing lattice, unless we have a case comparable with the crystals belonging to the Asymmetric Crystal Class of the Triclinic System.
But however this may be, organic morphogenesis remains a mystery. Several models are proposed that purport to explain the generation of organic shape, but to my knowledge none of them is universally accepted up to the present day (year 2005). So although organic lattices have not been observed, the system "fast (unstable) growth plus lattice" must be taken as a serious candidate for explaining many organic shapes. The fact that these lattices are not observed can partly be due to the molecular dimensions of their unit cells, or to a host of secondary features and processes that completely mask the presence of such a lattice.
With respect to form-generation, especially by processes of unstable growth, often leading to very complex patterns, Philip BALL in his book Designing the Molecular World, 1994, writes the following (p.292) :
The real surprise is that there may be nothing in the fundamental elements of the mathematical description to warn us that these structures might appear. A reductionist sees only the most prosaic of interactions between the system's individual components, but the "holist" who considers the system as a whole discovers within it an unguessed capacity for intricate organization.So it is certainly worth the trouble to investigate the degree of universality of the above discussed form-generator : Lattice (or quasi-lattice) plus fast unstable growth, which here means considering the possibility of organic lattices to account for general pattern features in organisms. Indeed because of the discoveries about unstable growth in crystals, the crystal-analogy (i.e. the assumed analogy between crystals and organisms), as discussed in Part IV , becomes more 'tight' : while initially we had crystals as a result of equilibrium processes, and had organisms as a result of non-equilibrium processes, we now have, in addition to plain crystals, branched crystals which are the result of non-equilibrium processes. And while crystals generally do not show curved features (with the exception of the faces of diamond and the mineral Siderite), and organisms invariable do, we now also have these curved features in ice flowers (and also in some snow crystals). And because of the latter findings such curved features can also be expected in crystals of other materials when the conditions are appropriate.
Many of the patterns that arise out of complexity resemble the delicate and often beautiful "organic" forms of the natural world. Moreover, similar patterns may be found in systems that are ostensibly unrelated. There is a common thread, however : these systems tend to be undergoing processes of rapid or unstable transformation. This has led to hopes for a unified description of pattern formation in systems that are far from attaining equilibrium.
If we indeed assume that the general pattern formation in organisms is due to the presence of one or more organic lattices combined with varying degrees of non-equilibrium growth, what then is the role of the instructions in the DNA in such a pattern formation? Doesn't the DNA simply code for the pattern to be generated?
Well, with GOODWIN, B., How the Leopard Changed Its Spots, 1994, 2001, we say that DNA only provides chemicals, be it in a well orchestrated fashion, and as such provides parameter settings for certain dynamical systems. So, apart from creating certain chemical gradients (implying some vectoriality) in some cases, DNA only takes care of some scalar aspects of organic form generation, while the organic lattice takes care of its vectorial aspects, i.e. aspects involving spatial directions.
It is possible to illustrate (but only crudely so!!) the role of DNA and the role of randomness in organic pattern formation on the basis of lattice plus unstable growth , with the help of the above discussed Hele-Shaw cell (two plates enclosing a viscous liquid, into which a less viscous liquid is injected which doesn't mix with the enclosed liquid), especially the variant where one of the plates was scored with grooves (forming a square lattice) in order to impose preferred directions of expansion of the injected liquid. This cell was depicted earlier : bottom image of the Figure above .
The process that goes on in the just mentioned Hele-Shaw cell results, it is true, in an expansion figure, and thus implying growth, but in contradistinction to crystallization, this growth is not accomplished in virtue of aggregation of particles that come down to the expansion figure from its medium (which is the viscous liquid enclosed between the two plates of the cell), but come from within the injected (less viscous) liquid. This means that we can interpret the process as a passage of energy (embodied by the pressure by which the lesser viscous liquid is injected) that leaves behind an effect, a trail, after impact. Now it depends on the amount of energy of the impact, the amount per unit of time, whether or not the process is able to bring about the mentioned effect onto every point of the expansion space. And this availability of energy per unit of time is itself dependent on the speed of the expansion, the expansion rate, which in turn depends, among other things, on the nature of the medium in which the expansion takes place. While in the case of the effect being variable with respect to its intensity, this effect can, in certain cases smoothly peter out, resulting in fuzzy or indistinct boundaries of the expansion figure, the effect taking place in the Hele-Shaw cell -- intrusion of a liquid into another liquid without possibility of mixing -- cannot increase or decrease in intensity, but only in spatial extension, implying that in this case the boundaries of the expansion figure always remain definite and distinguishable.
If indeed we interpret the process that goes on within the Hele-Shaw cell in the just described way, then the general description of an expansion process as given by PRZIBRAM, H., in his book Die anorganischen Grenzgebiete der Biologie, 1926 (where he proposes the theory of organic lattices) is very appropriate and instructive. In what comes next we will paraphrase (not literally translate) what he wrote on p.91 -- 92 of the mentioned work.
Especially evident is the influence that (1) the mutual interaction of ordered confluence or flow-off and (2) supply of material has on the generation of certain patterns, namely expansion figures. And whether they are connected with the expansion of the effects of forces or with the convection of material particles, the resulting (expansion) figures obey the same laws. The study of these figures is a genuine part of general morphology.
If an effect of a force is expanding, such that it leaves behind visible traces, it depends on whether or not there are sufficient amounts of energy available to distribute -- during the passage of the force flow through larger and larger patches space -- these traces to all points (places) of the expansion space.
If the amount of energy is large enough to leave behind its effects at all sites during expansion, then, in the case of an ideal homogeneous and isotropic ( = no preferred spatial directions) m e d i u m a spherical advancing front line of the expansion (of the mentioned effects) is to be expected (or a circular one in two-dimensional cases). And at the same time a complete filling-in of the space enclosed by this boundary line, a complete filling-in with the effect, is also to be expected.
If the m e d i u m does not satisfy the mentioned conditions, then some inequalities, it is true, of the boundary line will appear, but the 'packing' will always remain more or less dense.
If, on the other hand, the amount of energy, that is, per unit time, available during the passage of the force through the expansion space of a certain radius, is too small to display visible effects at all sites, then, in a uniform medium, the distinctness of these visible effects must decrease more and more within a series of individual cases where, from case to case the mentioned amount of energy decreases steadily, resulting in the dwindling of the expansion figure (from case to case), without, however, losing its spherical contour (As has been said, in the case of the Hele-Shaw cell the effect cannot decrease in intensity, but only in its spatial extension).
But because in reality always small inequalities are present in the medium, the places having equal radial distance from the point of impact, do not receive equal amounts of energy, and instead of a spherical expansion figure we now get a rayed, i.e. a branched, figure. And as soon as such a differentiation into rays has taken place, then a more and more open figure will be the result during expansion, because an increasing number of places will not be supplied anymore (with the effect of energy passage). And although secondary and teriary branches will appear, again in virtue of random inequalities of the medium, they will not lead to a complete space filling.
Now the rate of expansion will decide whether at the places that are successively visited by the passing energy, enough of this energy is given off per unit of time.
If this expansion or propagation rate is low, then all places will be sufficiently provided (with the visible effect), and a perfect space-filling figure, enclosed by minimal faces, is obtained.
If, on the other hand, the expansion rate is above a certain limit (and thus is in any case higher than it was in the former case), then the described dilution (i.e. the appearance of a more or less open figure) and the formation of rays or branches, will appear in ever higher degrees of expression, because the time of the passage of the force is not sufficient anymore to provide all places with visible effect.
But it is only up to a certain limit of the expansion rate that the branching itself becomes more extensive. When this rate increases still further the delivery per unit time will not be sufficient anymore to sustain the formation of new branches at all. From case to case we see with the increase of expansion rate a corresponding decrease of branches, a shortening of them, and, finally, at the highest rates, a complete disappearance of them. In the latter case the resulting figure can be very similar again to that resulting from a lower rate of expansion, a rate sufficient to effect a complete space filling, namely a stocky, or even a rounded figure. But this figure is not an expansion figure anymore, but one that is created directly in a single moment, like we see in the case of a bullet hole in a glass window.
So we see, that fast (unstable) growth, radiating from a given point or site, generally results in a branched figure. If the medium is, apart from containing small accidental inequalities, uniform, the branching pattern as a whole will be more or less rotationally symmetric (i.e. the radii will be more or less equal), but each branch in itself is irregular, and differs in many of its details from any other branch of the structure.
But as soon as some pre-existing structure is present, the resulting branched figure will become more regular in the sense that the branches are also equal with respect to many of their details.
In the case of the Hele-Shaw cell where one of the plates is provided with a regular lattice of grooves, we have a case of a pre-structured medium. It effects two preferred directions of flow of the injected expanding liquid. This, together with the fact that the remaining conditions are absolutely homogeneous, or at least exactly equal along concentric circles (of which the common center is the injection site), we can expect a regular expansion figure, of which the branches are equal up to most of their details. Apart from very slight inequalities in the apparatus, there is no room for randomness to take place. And it is this kind of pre-structuring of the m e d i u m that in organisms is done by the DNA. The products of its instructions set the stage for growth of the organism. They either set parameters or initial conditions of certain pre-existent dynamical systems, and in this way do away with randomness. The resulting morphological strucures and patterns are now repeatable, because they are, in a sense, indirectly encoded in the DNA (i.e. the mentioned parameter and initial-condition settings are encoded in it), which itself replicates.
Back to the Hele-Shaw cell again, that produces the four-fold 'snowflake', we cannot predict the exact structure of a branch, because we have to do with unstable growth (as non-equilibrium process). But we can predict that the branches will be equal to each other even up to fine detail, because randomness is eliminated.
On the other hand, in the case of the development of a snow crystal, the medium, in any case that part of the medium immediately neighboring the crystal, is not pre-structured. It is a water-vapor medium with only extremely minor, if any, not patterned differences in humidity and temperature. Only as considered during the crystal's path of fall, this medium will be varying more or less smoothly and considerably. This will be expressed in the sequence of morphological or crystallographical growth-types appearing and preserved in the corresponding successive growth-stages of the crystal : faceting and branching growth-types are expected to alternate in a definite sequence on all six arms of the growing snow crystal.
REMARK : Successive growth stages of a branched crystal do not solely consist of further terminal growth of the arms, but also of lateral growth as long as the relevant sites are still easily within reach of the arriving particles. That we cannot expect to see a "falling-history" (and with it a history of development) to be clearly recorded in the snowflake, show the two examples in the Figure given HERE (After BENTLEY & HUMPHREYS, 1931, 1962.). It is clear that if the terminal plates were the result of slow growth in virtue decreased humidity at the end of the snowflake's descent, then this plate-like growth (i.e. the growth of the slow-growing crystal faces) should also be evident on most of the rest of the length of the arms, because of good accessibility for incoming particles.
And these possible growth-types are implied by the fact that the bulk material (H2O) is, when solidified, microscopically structured in a definite way. We could say pre-structured in a definite way, because this structure is intrinsic with respect to the material, in the present case H2O. So in snow-crystal development we have a case of the medium not being pre-structured, while the expanding material is. And it is here that randomness comes in : The medium of the developing snow crystal confers randomness in the follwing way : If the expansion rate or growth rate of the crystal is too fast to result in complete space-filling, then a branched crystal will be generated ( The primary branches will go off from the corners of the initial hexagonal crystal embryo). And when we assume that this growth, although fast and unstable, is nevertheless not fast enough to allow improper alignment of arriving particles onto the growing surface, resulting in totally irregular structures (because in many local cases, during the growth of a single crystal, there was in that case simply not enough time for proper alignment of arriving particles to be realized), i.e. if there is enough time for the arriving particles to properly align to the microstructure of the growing surface, then still a degree of randomness remains, namely the random distribution of places at the growing surface that happen to receive particles that happened to be already properly aligned with respect to the existing lattice of the developing crystal insofar already present. Such particles will be the first to adhere to the growing surface. And, as has been said already earlier, these places (of first adhering particles) will be preferential points for further growth, because they stick out farther into the nutrient medium than their immediate surroundings. These randomly distributed places, where growth continues preferentially, are expected to be on the main-branches, giving rise to side-branches emanating from these preferential points, and (are further to be expected) on the side-branches in turn, giving rise to tertiary branches, etc., resulting in the more or less fractal structure that is so well-known in many snow crystals. So the detailed structure of a snowflake branch is largely determined by random (microscopic) events. And now, in contradistinction to the 'snowflake' generated in the Hele-Shaw cell, it is not to be expected anymore that the detailed structure of such a snowflake branch will almost exactly be repeated in the same crystal, because the random microscopic events, eventually shaping the fine detail of the branch, are isolated local events. The microscopic random events on the other (main) branches of the crystal are not in any way correlated with the events of the first (mentioned) branch, just in virtue of the fact that they are random events. They are completely local, not global. So what is to be expected in a snow crystal is six branches, that are roughly similar, but differ significantly in detail. And because the development of a definite structure from a random, but just microscopical, bump, is a sort of runaway process, in which the developing side-branch will become more and more pronounced, we can expect a substantial difference of resulting morphology among the six branches of a single snow crystal.
But, on observation, such a substantial morphological difference between the branches of a same snow crystal is definitely not the case, as the many photographs of snow crystals, given in this website and elsewhere, clearly indicate. So while the detailed equality of the branches in the 'snowflake' generated in the above discussed Hele-Shaw cell is perfectly explicable (in mechanical terms), it is not so in the case of real snowflakes. The latter seem to develop as a whole. A snow crystal is thus not an aggregate of independently existing particles, and it does not develop by the local aggregation of particles, but by the global aggregation of particles orchestrated by the crystal as a whole.
So we see that the system "Lattice (provided with chemical motifs) plus Fast (unstable) Growth" is a h o l i s t i c form-generator, and that it is powerful. And because many facts appear to point to a prevailing holism in o r g a n i c morphogenesis, the just mentioned holistic form-generator -- lattice + fast growth -- that works so well for inorganic pattern formation, could be a good candidate to represent an o r g a n i c form principle as well. And this, as has been said, boils down to the assumption of o r g a n i c lattices as was first proposed by PRZIBRAM in 1926.
PRZIBRAM bases his theory on the many morphological and growth analogies that can be observed between crystals and organisms. He says that these analogies point to the same form-generating priciples at work in crystals and in organisms. In the case of organisms we must, however, assume that these form-generating principles are more hidden than they are in crystals. In organisms they are heavily 'over-formed' by other principles.
In the case of branched crystals (which PRZIBRAM only discusses very briefly) randomness plays an important role, while in organisms it is more or less eliminated by the encoding of dynamical parameter settings and settings of initial conditions. Randomness will play an important role, however, in the form of mutations in the DNA, which constitute an important factor in evolution.
Having discovered the enormous form-generating potential of non-equilibrium crystallization, we introduced the notion of organic lattices.
After continuing and concluding our investigation of snow crystals (next document) we will extensively work out a theory of organic lattices (Part XXIX Sequel-10).
In the next document we continue (and conclude) our investigation of ice crystals in connection with their form-generation capabilities.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-9.