

(Takes a little while loading the images)
e-mail :

Sequel-19 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-19) further elaborates on the analogy between crystals and organisms.
Sequel to the Preparations (VII) to the Repertoire of the Crystal Analogy
Sequel (II) to Special Features of Crystals
Triangular snow crystals (four documents)
One of the most puzzling phenomena in the world of snow crystals is the occurrence of definitely triangular crystals. See next Figures.

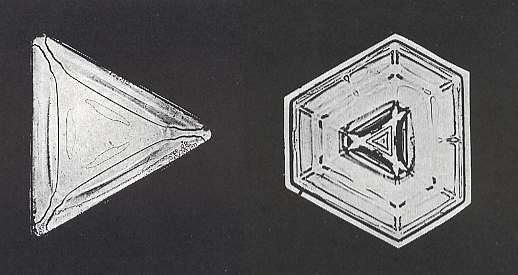

Figure above : Truncated triangle (ditrigon). These forms are nearly always small. The crystal is only 0.3 mm (0.01 inches) on a side.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : A trigonal snow crystal. The crystal started out as a triangular form. It tends to adopt a hexagonal shape while growing.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)

Figure above : Trigonal snow crystals. Both crystals have the shape of a ditrigon (a combination of two unequal equilateral triangles) and clearly show a three-fold symmetry.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)
Because the apparent symmetry of such crystals is decreased with respect to normal snow crystals, twinning becomes a less plausible cause of the formation of triangular crystals. In addition to triangular shapes (or those approaching such a shape) there are snow crystals with an intricate structure, like we see in ordinary branched crystals, while this structure now has a definite trigonal symmetry. The next Figure shows two such crystals, having very broad and more or less complex 'branches'. One of these two crystals even shows definite curved ridges, and also they are repeated three-fold according to, not the group D6 (as in ordinary snow crystals), but the group D3 : Reflection in a mirror line and multiplication of the result by a factor 3 in virtue of a three-fold rotation axis.
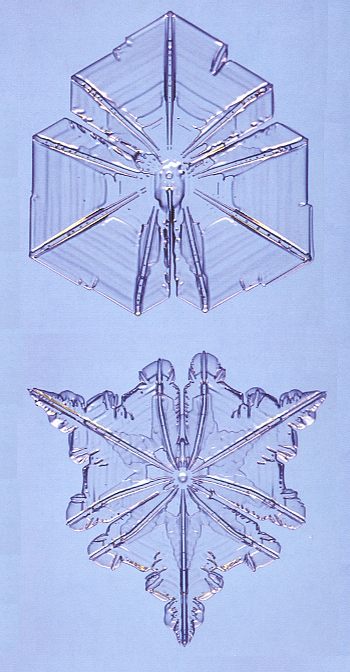
Figure above : Snow crystals with three roughly identical branches are unusual, and nice specimens tend to be small. These two each span about 0.6 mm (0.02 inches).
Note the curved ridges, especially in the bottom image.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : A complex three-fold snow crystal.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
In the subscript to the above Figure LIBBRECHT (p.96) writes :
ACCIDENTALLY TRIANGULAR.It seems to me rather unlikely that three alternate arms are in the same degree a little slower growing than the other branches.
The different branches of an ordinary stellar crystal don't always grow symmetrically. When three happen to lag behind by chance, a slightly triangular morphology results, as here.

Figure above : This triangular crystal appears to be one side of a broken split-star crystal.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
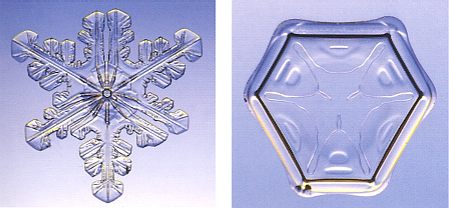
Figure above :
Left image : A three-fold branched snow crystal.
Right image : A three-fold snow crystal having a ditrigonal shape.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
About all these (different types of) three-fold snow crystals LIBBRECHT, Ibid., p.94 writes the following [comments of mine between square brackets] :
Occasionally one finds snow crystals that exhibit a distinctly triangular symmetry. It's not clear how these triangular crystals develop this symmetry, although it certainly has nothing to do with changes in the underlying symmetry of the ice lattice. The crystal maintains the usual hexagonal structure, as evidenced by the fact that the faceting on triangular crystals is no different than that on hexagonal crystals [ I do not understand what precisely is meant by this last statement about the faceting. Crystallographically trigonal crystals can have a hexagonal shape. See further below.] .
One scenario for making triangular crystals starts with a capped column that then makes a split star [ i.e. we have an incomplete first star (lacking some branches), and a second star, also incomplete, but consisting of the missing branches of the first ]. If each star has three dominant branches, and these alternate between stars [ A process of fast growing will tend to create exactly this constellation, because in such a constellation the individual arms minimally impede each other ] , then the split star will be like two three-armed crystals joined together [ by the central column ] . If the two stars break apart, you can be left with a pair of triangular crystals.
This split-star scenario likely plays out from time to time, and it probably explains some of the larger, elaborate triangular crystals. But many triangular crystals are too small to be thus explained [ because such small crystals have not yet reached a state of possible competition between arms ] , and in addition, we frequently observe smaller triangular crystals in the lab. It appears that some snow crystals simply decide early on to grow with three-fold symmetry [ Of course we should investigate what this precisely means ].
These plate crystals develop with varying degrees of triangularity, forming most commonly around -20 C (280 F). The initial move to triangularity is probably accidental, as there is always some variation in the growth rates of the different sides of a crystal [ The relevant sides here are the six prism sides, but these are -- if we assume the crystal symmetry still to be that according to the Class 6/m 2/m 2/m -- crystallographically equivalent, which means that their intrinsic growth rates are the same. The actual growth rates can, it is true, be different, but if so, it must be caused by some environmental bias. However, this bias would then be supposed to be triangular itself, which, I think, is highly improbable in all cases of non-branched crystals ]. The branching instability accentuates the process, so the triangular shape persists once it begins.
The intrinsic symmetry of triangular snow crystals
In this section we will discuss triangular snow crystals as to their intrinsic symmetry, and whether or not it differs from the usual intrinsic symmetry of snow crystals which is 6/m 2/m 2/m (point symmetry, Hexagonal System). If this symmetry differs, then it should be either 6-m2 or 3m (both 3-dimensional, also Hexagonal System). If we assume that such triangular snow crystals possess a mirror plane perpendicular to the c-axis (i.e. a mirror plane parallel to the plane of all the given photographs of triangular snow crystals), which assumption is reasonable, then the first of the two symmetries mentioned, viz., 6-m2, would be the symmetry of these crystals. The 6- rotoinversion axis of the just mentioned Class 6-m2 is equivalent to a 3-fold rotation axis plus a mirror plane perpendicular to it. Crystals having this 6-m2 symmetry, we will call crystallographically trigonal crystals (in contradistinction to the crystallographically hexagonal (s.str.) crystals belonging to the Class 6/m 2/m 2/m (the most symmetrical Class of the Hexagonal System) to which all snow crystals are supposed to belong.
First of all we should realize that crystallographically trigonal crystals can still have the shape of a regular hexagon as seen in a projection along the c-axis. The next Figure shows this by means of depicting a two-dimensional ionic crystal :
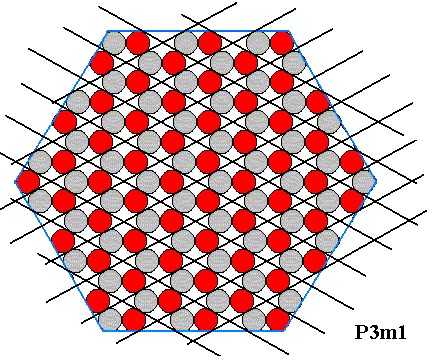
Figure above : A crystallographically trigonal (2-dimensional) crystal having the shape of a regular hexagon. The hexagonal lattice, underlying the structure, is indicated. The motifs, placed in this lattice, and their orientation, determine the total symmetry of the pattern to be that of the Plane Group P3m1. The symmetry of the motif is trigonal. The meshes of the hexagonal net are rhombs with angles of 600 and 1200. Each mesh contains two (different, or differently oriented) ions. The Figure represents a two-dimensional ionic sterrocrystal bounded by six A-faces (For these, see next Figure ). The crystal has mirror lines connecting opposite corners, but no mirror lines connecting the centers of opposite faces. So the symmetry is lower than that of a(n empty) regular hexagon, or of a regular hexagon filled with one type of chemical entity only. Whether also water molecules are able to somehow adopt such a trigonal structure, I don't know. The complete set of the six faces of this crystal can be generated from just one of them : If we subject one such face (chosen as initial face) to the actions of the symmetry elements of this crystal, then all six faces are generated as follows : First the initial face is subjected to the adjacent mirror line, resulting in a second face. Then these pair of faces is subjected to the operations of the 3-fold rotation axis, resulting in four more faces, adding up to a total of six faces forming a regular hexagon. This means that this set of six faces is one single (crystallographic) Form, which in turn means that these six faces are (crystallographically) equivalent ( Therefore growing at the same rate and consequently forming a regular hexagon). So this crystal has a morphological symmetry according to the group D6 (i.e. the symmetry of the regular hexagon), while its crystallographic symmetry is lower, namely according to the group D3 (i.e. the symmetry of the equilateral triangle). Generally, crystals that have a lower (crystallographic) symmetry than their shape suggests are called merohedric crystals. And because in the present case (only) one set of equivalent mirror lines is lost (A regular hexagon -- as most symmetric 6-fold shape -- has 3+3 mirror lines, while our two-dimensional ionic crystal has only 3), our crystal is called hemihedric (where, in two-dimensional crystals, crystal boundary lines are interpreted as faces).
Figure above : Some atomic aspects that can be found in the structure of the two-dimensional ionic crystal depicted in the previous Figure. They are the aspects of possible crystal faces.
In order to understand triangular and hexangular snow crystals, several shapes, i.e. two-dimensional figures, must be considered. These are, the equilateral triangle (regular trigon), the regular hexagon, the face-ditrigon and the angle-ditrigon. See next Figure.
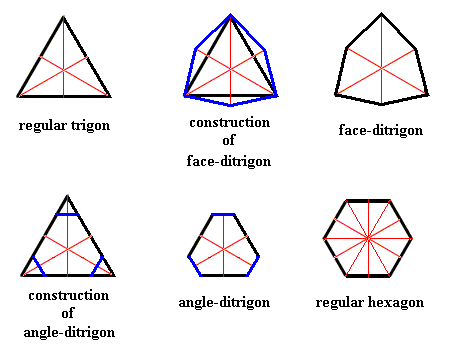
Figure above : Some two-dimensional figures (black) with their mirror lines (red) inserted : Regular Trigon, Face-ditrigon, Angle-ditrigon, and Regular Hexagon. The trigon and ditrigons have D3 symmetry (three equal mirror lines and a 3-fold rotation axis at their point of intersection), whereas the regular hexagon has D6 symmetry (a first set of three equal mirror lines, a second set of three equal mirror lines, and a 6-fold rotation axis at their point of intersection).
A face-ditrigon is a polygon with six equal sides and two alternating sets of angles (i.e. there are two different angles involved that alternate with each other). Crystallographically it is one Form.
An angle-ditrigon is a polygon with six equal angles (1200) and two alternating sets of sides (i.e. with respect to its sides (faces) there are two different lengths involved that alternate with each other). Crystallographically it is a combination of two Forms.
Snow crystals having the shape of a face-ditrigon were depicted above .
Perhaps snow crystals having the shape of an angle-ditrigon can give us a clue about the true intrinsic symmetry of triangular crystals. See next Figure.
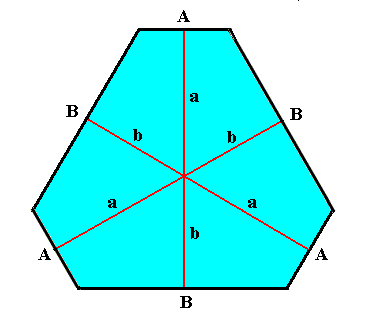
Figure above : A crystal having the shape of an angle-ditrigon ( The depicted crystal can be interpreted either as a projection of a snow crystal along its c-axis or as a two-dimensional crystal). See also the Figure referred to above by clicking HERE .
The distance (a) of the A-faces from the center of the crystal is longer than the distance (b) of the B-faces from the center. This means that, supposing a uniform growth environment, the A-faces intrinsically grow faster than the B-faces, which in turn means that the A-faces are not equivalent to the B-faces (while the three A-faces are equivalent to each other, and the three B-faces are also equivalent to each other). All this implies that the crystal is made up of two crystallographic Forms, each one of which is an equilateral triangle. And because such a triangle has D3 symmetry, the intrinsic symmetry of the crystal must be the same. And this is a lower intrinsic symmetry than that of normal snow crystals when projected along their c-axis. Or, in other words, if the above depicted crystal, having the shape of an angle-ditrigon, is a projection along the c-axis of a snow crystal, then this snow crystal has a lower symmetry than a normal snow crystal has. It belongs not to the highest symmetrical Class (6/m 2/m 2/m, Dihexagonal-bipyramidal Class) of the Hexagonal Crystal System (as do normal snow crystals) but to the Class 6-m2 (Ditrigonal-bipyramidal Class, also of the Hexagonal Crystal System), which has a lesser symmetry. When this is true for crystals having the shape of an angle-ditrigon, it will be expected to be true also of crystals having the shape of a face-ditrigon or having the shape of a regular trigon (equilateral triangle) (And then also some crystals having the shape of a regular hexagon could belong to this lower-symmetry Class, namely when the intrinsic growth rate of the A-faces happens to be equal to that of the B-faces, while at the same time, and for other reasons, these faces are still not equivalent).
This conclusion contradicts LIBBRECHT's assertion (see quote above) that all snow crystals, including all triangular forms, are based on the same lattice symmetry, meaning that they all belong to Class 6/m 2/m 2/m . I must admit that LIBBRECHT's assumption sounds nevertheless reasonable (Why would some snow crystals, while being in a normal environment, crystallize in a different crystal Class, different from that in which the other snow crystals crystallize?), meaning that my conclusion about a different intrinsic symmetry of triangular crystals is just something to think about, and to stimulate investigation into the matter.
The just depicted angle-ditrigon is crystallographically a combination of two Forms. Of these, each one is an equilateral triangle. They differ in orientation and size. See next Figure.
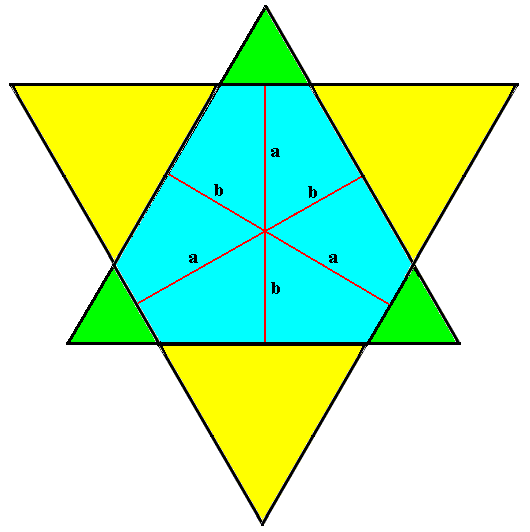
Figure above : The angle-ditrigon, depicted in the previous Figure, is a combination of two crystallographic Forms, namely equilateral triangles, that differ in size and orientation.
During growth of the corresponding crystal these triangles cut off each other's corners, resulting in the angle-ditrigon.
Generally a Form is generated from some initial face (which, in a two-dimensional case is represented by a line) that has a certain orientation with respect to the symmetry elements (mirror planes, rotation axes, center of symmetry, etc.) of the crystal Class to which the crystal belongs. This face is then copied (multiplied) in virtue of those symmetry elements. The result is a set of faces, which is called a Form (Obviously, the symmetry of such a Form is identical to that of the crystal Class to which it belongs). Such a Form can be some polyhedron (or, in two-dimensional crystals, a polygon), which is called a closed Form. As such a closed Form can be, all by itself, a crystal. In other cases the resulting Form is not closed, called an open Form. It consists of one, two, or more faces that together do not enclose a definite volume of space. Such a form cannot exist as a crystal. It must form combinations with other Forms such that the result is a polyhedron (or polygon in the two-dimensional case).
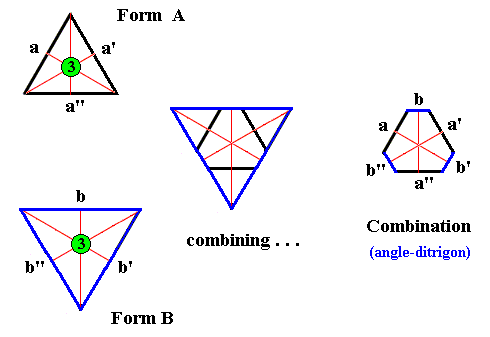
Figure above : Two Forms (A and B), together forming an angle-ditrigon.
Upper left : An intial face a has a certain orientation with respect to the three mirror lines and the 3-fold rotation axis. It is now rotated 1200 (which is a symmetry operation, in virtue of the 3-fold rotation axis), resulting in the face a' . The same intial face a is rotated 2400 (which is yet another symmetry operation in virtue of the 3-fold rotation axis), resulting in the face a'' . This second rotation (2400) is, of course also automatically applied to the already existing face a' , resulting in face a , which was already present. So now we have generated the Form A. In this Form, which is an equilateral triangle, the mirror lines are now automatically implied.
Of course we can generate this same triangle also by using the other symmetry elements, i.e. instead of the 3-fold rotation axis we can use two mirror lines : The initial face a is reflected in the vertical mirror line, yielding the face a' . When we now subject this face to the other (adjacent) mirror line we get the face a'' .
In the same way (bottom left) the second Form (B) is generated : An intial face b yields the faces b' and b'' , resulting in the Form B, which also is an equilateral triangle, but with an orientation that differes from that of the first Form, and with a larger size, expressing the supposed fact that the b faces (i.e. the three faces of the Form B) intrinsically grow faster than the a faces (i.e. the three faces of the Form A).
Although each of these Forms can exist as a (two-dimensional) crystal, they can also engage in a combination, resulting in an angle-ditrigon. This is illustrated by the middle and right images of the Figure.
During growth of the ditrigonal crystal the Forms cut off each other's corners. The faces of the resulting angle-ditrigon consequently are : a , b , a' , b' , a'' and b'' .
The next Figures illustrate the formation of an angle-ditrigonal crystal by the combination of two triangular Forms, using, as an example an ionic two-dimensional crystal.
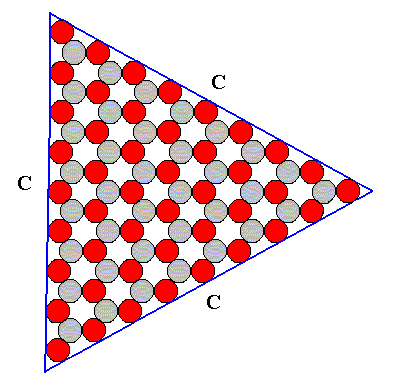
Figure above : A Form consisting of the C-faces as they are possible in an ionic two-dimensional crystal with D3 symmetry. See for the atomic aspects of the possible faces A, B and C, the Figure above . The shape of this Form is that of an equilateral triangle.
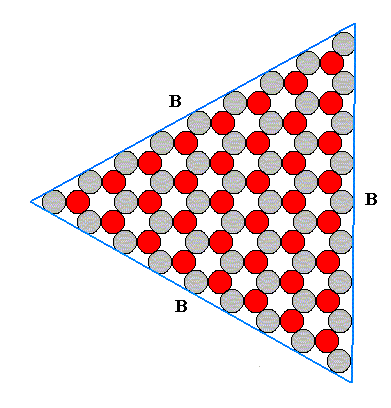
Figure above : A Form consisting of the B-faces as they are possible in an ionic two-dimensional crystal with D3 symmetry. See for the atomic aspects of the possible faces A, B and C, the Figure above . The shape of this Form is also that of an equilateral triangle.
These Forms can combine, resulting in an angle-ditrigonal ionic two-dimensional crystal :
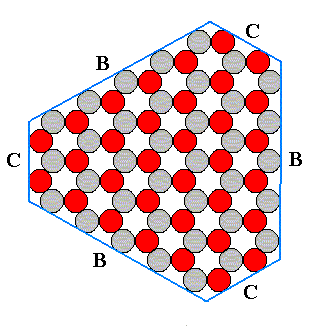
Figure above : An angle-ditrigonal ionic two-dimensional crystal (crystallographically) generated from the two triangular Forms depicted in the previous two Figures. The crystal is thus a combination of two Forms and consists of six faces, viz., the three B-faces, alternating with the three C-faces. Like its component Forms, this combination has also D3 symmetry.
The above exposition has shown us something about trigonal crystals, which could be either some 2-dimensional crystals, or a projection of certain 3-dimensional crystals along their c-axis onto the basal plane (i.e. the plane that is perpendicular to this c-axis, which itself is parallel to the prism faces of such trigonal or hexagonal crystals). We also considered the possibility that some snow crystals belong to a lower symmetry Class (some trigonal Class), a class, lower than the Class to which the majority of them belongs. This lower symmetry class would then be the trigonal hemihedric (6-m2) of (i.e. derived from) the Holohedric Class (6/m 2/m 2/m) ((both) of the Hexagonal Crystal System) to which latter Class the mentioned majority of snow crystals belongs.
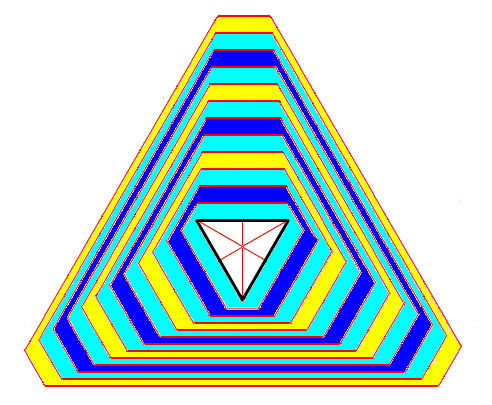
Figure above : An initial triangle develops into an angle-ditrigon, which eventually definitively develops into a reversed triangle. Two Forms (each consisting of three faces) are involved, one growing slower than the other, causing the latter to eventually disappear.
To see the end stage of this process (where the reversed triangle finally appears and stays) click HERE (Close window to return to text). See also the Figure further below .
If we look to the above Figure, we see that the dividing lines between the faces diverge for one set of faces, implying that those faces widen during development of the crystal. For the second set of faces these dividing lines converge, meaning that these faces diminish (i.e. narrow down) during development and will eventually disappear. See next Figure.
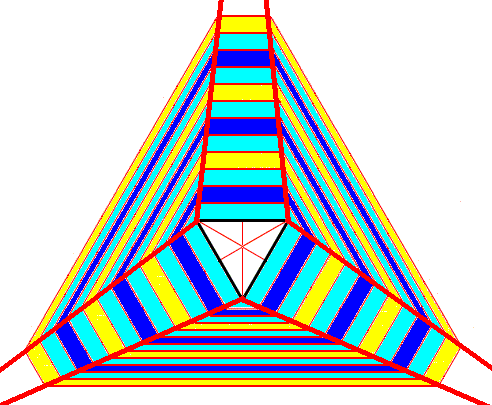
If we now look again to this Figure above which depicts a snow crystal having the shape of an angle-ditrigon (six equal angles and six unequal faces, of which three having one size and three others having a different size), we see that the structure of this crystal reveals dividing lines (See also next Figure) that all diverge, meaning that all six faces grow at the same rate, which in turn means that they together constitute one single Form. And because this Form consists of six equivalent faces, it must eventually assume the shape of a regular hexagon. And because a regular hexagon contains a 6-fold rotation axis (which is not the same as a 6- rotoinversion axis, and also not the same as just a 3-fold rotation axis) the crystal cannot be trigonal (because a crystal has the same symmetry as any of its Forms).

Figure above :
Left image : A snow crystal having the shape of an angle-ditrigon.
Right image : The same snow crystal, now with the dividing lines inserted. All dividing lines diverge, indicating that the growth rates of all the six faces are equal, meaning that they are crystallographically equivalent.
(Adapted from a photograph by LIBBRECHT, 2004, The Little Book of Snowflakes)
See also next Figure where we see an angle-ditrigonal snow crystal with developed arms.

Figure above : An angle-ditrigonal snow crystal. When inspecting the directions of the six arms, we clearly see that the above mentioned dividing lines between faces all diverge, implying that all six faces intrinsically grow with equal rates, meaning that all six faces are equivalent, which in turn means that the intrinsic shape of the (crystallographic) Form (as seen in projection) consisting of these six faces, is a regular hexagon. This implies that the crystal cannot be cystallographically trigonal, but belongs, just like the other snow crystals, to the Class 6/m 2/m 2/m.
(After LIBBRECHT, 2004, The Little Book of Snowflakes)
The next Figure shows the development of a crystal finally obtaining the shape of an angle-ditrigon and having an intrinsic symmetry of 6/m 2/m 2/m (or of 6mm for the 2-dimensional case or for the projection of the 3-dimensional crystal along its c-axis).
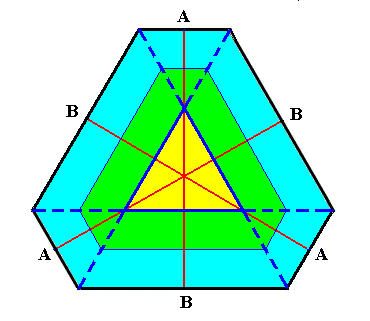
Figure above : An initially triangular crystal nucleus (i.e. the nucleus having the shape of a triangle) develops into an angle-ditrigon. Dividing lines between faces are indicated (dark blue). The angles between the dividing lines holding the A-faces are all 600. Also the angles between the dividing lines holding the B-faces are 600 but the origins of these latter angles start earlier than those of the dividing lines holding the A-faces (See next Figure). This implies that the B-faces will remain larger than the A-faces, meaning that the shape of the crystal will remain an angle-ditrigon.
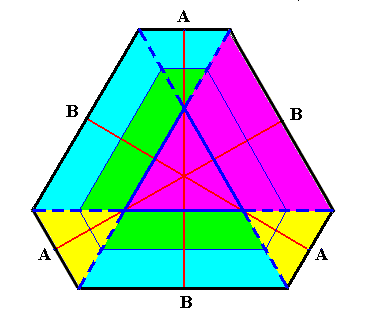
Figure above : Same as previous Figure. It is shown that the B-faces will always remain larger than the A-faces while the development of the crystal proceeds. Nevertheless the shape will approach (but never reach) that of a regular hexagon, because when the crystal has grown large the relative difference in distance from the origin of the dividing-line angle to the corresponding face dimishes from that of another face.
It seems that if a snow crystal, as (still) a nucleus, begins as a regular hexagon (in fact a regular prism), it will continue to have the shape of a regular hexagon. But if the nucleus, for some reason, happens to be a(n) (equilateral) triangle, then the final shape of the crystal can become that of an angle-ditrigon (as demonstrated in the above Figures). A snow crystal having the shape of an angle-ditrigon can, in virtue of this shape, be crystallographically trigonal, but the snow crystals, having this shape, actually observed (i.e. judged from the available photographs) happen to be 6-fold (i.e. with a genuine 6-fold rotation axis), not 3-fold. Their shape, just as geometrical shape, has D3 symmetry, but as actually observed crystals they have D6 symmetry (both symmetries referring to projections or to 2-dimensional analogs).
Let us now discuss the generation of the angle-ditrigon in terms of the hexagonal net underlying both the ice lattice as it is in at least the vast majority of snow crystals, and (underlying) a possible trigonal ice lattice. Recall that the regular ice lattice is represented by the following structure (next two Figures) :
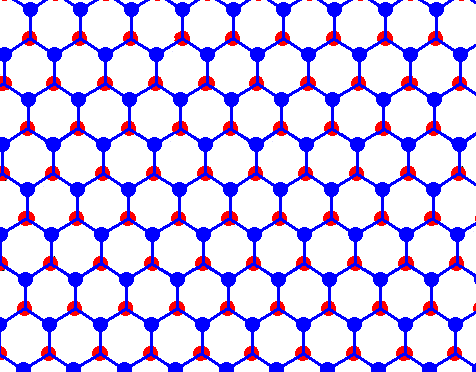
Figure above : Structure of ice, seen along the crystallographic c-axis.
Each dot (red or blue) represents a water molecule. Each such water molecule connects with four others by hydrogen bonds. Three such bonds shown for each water molecule. The fourth bond is perpendicular to the plane of the drawing. What we see here are two layers, distinguished by coloration. (Figure taken from Part XXIX Sequel-7 )
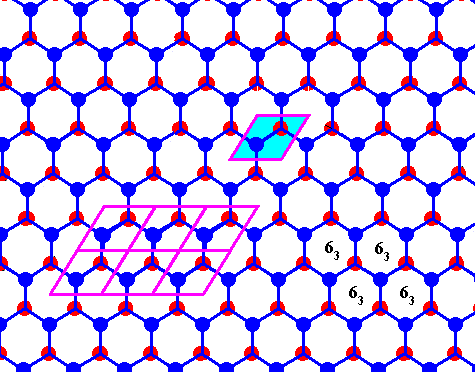
Figure above : Same as previous Figure.
Possible rhombic unit cell indicated. The the center of each hexagon is the location of a 63 screw axis (four of them indicated), if the Figure is interpreted as representing a 3-dimensional view (down the c-axis).
If the Figure is 2-dimensionally interpreted, then we see a rhombic unit mesh, containing two 3-fold rotation axes (coinciding with the two molecules of that mesh), and a 6-fold rotation axis at each of its corners. (Figure taken from Part XXIX Sequel-7)
The next Figure gives this same ice structure, but now explicitly with all vertical translations eliminated. The result is now one single layer of water molecules (which can now be indicated with one and the same color) lying at the corners (and not at the centers) of regular hexagons that are periodically stacked, such that their centers lie at the nodes of a hexagonal net (consisting of 600/1200 rhombs).
Figure above : Structure of ice, as seen in projection along the c-axis onto the basal plane.
The water molecules, represented by red discs, are (as seen in projection) ordered according to a hexagonal net. This net consists of a periodic stacking of 600/1200 rhombs over the plane. Each rhomb consists of two equilateral triangles, each provided with a water molecule. At the corners of each rhomb (i.e. each rhomb-shaped building block) there are 6-fold rotation axes, and at the center of each triangle there is a 3-fold rotation axis (so the interior of each rhomb-shape building block contains two 3-fold rotation axes). The Plane Group of this structure is P6mm . The point symmetry is according to the Point Group D6 (six mirror lines and one 6-fold rotation axis at their point of intersection). This point group symmetry is crystallographically indicated as 6mm (for the two-dimensional case, or, equivalently, for the projection).
The next Figure illustrates the trigonal case. The Plane Group is now P3m1 and the Point Group is D3 , crystallographically denoted by 3m . The structure is based on the same hexagonal net, i.e. it is based on the same empty building blocks (600/1200 rhombs), but now each rhomb contains, not two identical, but two different chemical motifs. The difference of these motifs could be solely a matter of orientation, i.e. two identical motifs but differing in orientation.

Figure above : Trigonal structure, as seen in projection along the c-axis onto the basal plane.
The structure is based on the same hexagonal net as is the projected ice structure. But now each rhomb-shaped building block contains two different motifs. This entails that now the corners of each building block harbor 3-fold rotation axes (instead of 6-fold). There are no 6-fold rotation axes present. The Plane Group is P3m1 and the Point Group is D3 .
One could surmise that instead of letting the two motifs of a rhomb-shaped building block be different (morphologically or orientationally), we could just as well do away with one of these motifs, also resulting in a trigonal pattern (We would then have the ice structure where alternate layers are absent), but this is not so. The reason is that we interchange one motif for an empty space, and this empty space is identical to already existing empty spaces in the original pattern. So the symmetry will be increased, resulting in P6mm symmetry instead of P3m1 symmetry, or, in other words, resulting in the loss of pure trigonality of the pattern. See next two Figures.
Figure above : If we omit the grey motifs from the trigonal pattern of the previous Figure, we are not left with (an alternative version of) a trigonal pattern, but with a hexagonal pattern, i.e. a pattern containing 6-fold rotation axes. See also next Figure.
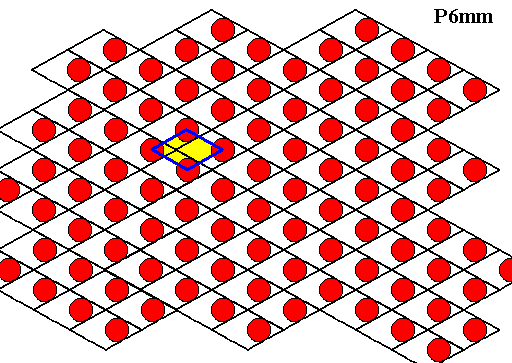
Figure above : Same as previous Figure. We can see that the motifs (red discs) are arranged according to an alternative, but equivalent, hexagonal net, and that at the corners of the rhomb-shaped building blocks of this alternative net are 6-fold rotation axes. So the structure is not purely (and solely) trigonal anymore.
We will now investigate the angle-ditrigon, departing from internal structure (as seen in projection, or equivalently, as two-dimensional). In order to do so we set up a hexagonal net (consisting of 60/120 degree rhombs). If we use this net as such, which means with empty building blocks (i.e. just rhombs, each geometrically consisting of two equilateral triangles), then we have to do with the maximal symmetry supported by this net. The next Figure shows that this symmetry is according to the plane group P6mm, implying a point group symmetry (i.e. translation-free symmetry) of 6mm (crystallographic notation) or, equivalently, D6 (group theoretical notation).
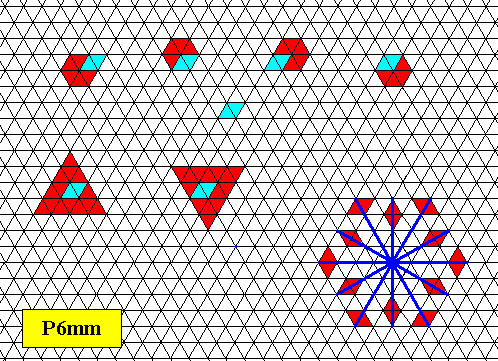
Figure above : The hexagonal net as such, i.e. with empty (rhomb-shaped) building blocks (empty, except for a line dividing the rhomb-shaped unit mesh or building block into two equilateral triangles), has a total symmetry according to the plane group P6mm, and therefore supports a D6 point symmetry. This is demonstrated by the fact that (1) each corner of a rhomb-shaped unit mesh contains a six-fold rotation axis (upper row of images), (2) each rhomb-shaped unit mesh contains two 3-fold rotation axes in its interior (bottom-left images), and (3) the net harbors mirror lines in six directions (bottom-right image).
This is the fingerprint of P6mm, resp. D6 symmetry (See for the theory of plane group symmetry : First Part of Website (see at end of document, "Back to Homepage" LINK) : the Series of Documents about The Internal Structure of Crystals, where in Part V the plane group P6mm is discussed).
First we will show that a two-dimensional crystal (or equivalently, a projection of a three-dimensional one along its c-axis), of which the internal structure is based on a hexagonal net, when starting from a hexagon-shaped nucleus, results (under uniform conditions) in a hexagon-shaped crystal, if the growth rates of the six faces are equal :

Figure above : Starting from a hexagon-shaped nucleus, a crystal, based on a hexagonal net, retains its hexagonal shape during growth. If we consider this to be an ice crystal, then in each little triangle there is a water molecule. In fact the triangles then represent water molecules. So the ice crystal grows by accretion of water molecules (by taking them up into a regular array). As implicitly indicated in the Figure, the growth rates of all the faces shown are supposed to be equal. Because the unit meshes (building blocks) are empty, they represent P6mm plane group symmetry and D6 point group symmetry. See also next Figure.
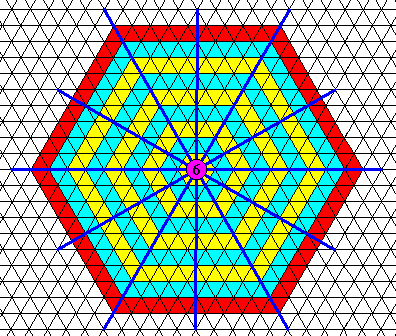
Figure above : Same as previous Figure. Symmetry elements indicated : six mirror lines and one 6-fold rotation axis in their point of intersection.
If the symmetry of a given two-dimensional crystal is trigonal, its plane group symmetry is either P3, or P3m1 or P31m, and its point group symmetry is for P3 3 (crystallographic notation), or equivalently C3 (group theoretic notation), and for P3m1 and P31m it is 3m (crystallographic notation), or, equivalently, D3 (group theoretic notation).

Figure above : Hexagonal net, where we have differentiated between the two triangles constituting a rhomb-shaped building block or unit mesh. This differentiation is indicated by different coloring (red, white) of these triangles, resulting in a pattern of alternately colored small equilateral triangles. This pattern is then trigonal : In the present case having P3m1 plane group symmetry and D3 point group symmetry. Compare this pattern with that of the ionic two-dimensional crystal depicted above . Both patterns have the same plane group as well as point group symmetry. Note, that when comparing these patterns, their respective nets are not drawn with the same orientation (with respect to the plane of the drawing).
The next Figure demonstrates that the colored hexagonal net of the above Figure has plane group symmetry P3m1, implying that its point group symmetry is D3 :

Figure above : Hexagonal net, where we have (as in the previous Figure) differentiated between the two triangles constituting a rhomb-shaped building block or unit mesh. Each corner of a rhomb-shaped unit mesh is the site of a three-fold rotation axis (upper row of images). The interior of each rhomb-shaped unit mesh contains two three-fold rotation axes (lower row of images). The pattern has mirror lines in three different directions, one of which is perpendicular to an edge of a unit mesh (bottom-right image). These properties form the fingerprint of the plane group P3m1, implying a D3 point group symmetry.
A trigonal lattice (as depicted above) cannot only support triangular shapes, but also hexagonal shapes. See next Figure.

Figure above : A hexagon-shaped two-dimensional crystal can be supported by a trigonal lattice, and can even be represented by one single (crystallographic) Form : by an initial face, making an angle of 600 with a mirror line of the structure, a second face is generated (by relection in the mentioned mirror line), and this pair is then tripled by the action of the 3-fold rotation axis lying on the mentioned mirror line, resulting in six faces making up a single Form which is a regular hexagon.
One can see that mirror lines exist from corner to opposite corner, but that no mirror lines exist that connect the centers of opposite faces. Compare with this Figure above , which has precisely the same symmetry.
The next Figure indicates the symmetry of the just depicted crystal.

Figure above : The symmetry elements of the crystal of the previous Figure are indicated : three equivalent mirror lines and a three-fold rotation axis at their point of intersection. This is the fingerprint of D3 symmetry.
In addition to the above hexagonal shape, a trigonal lattice can also support a hexagonal shape by means of the combination of two triangular (crystallographic) Forms. See next Figure.

Figure above : A hexagon-shaped two-dimensional crystal formed by the combination of two Forms, where each Form consists of three equivalent faces. The trigonal nature of the lattice is indicated in the last layer of the crystal, i.e. it is everywhere present in the structure, but as such indicated only in the last layer, where the two triangles making up a rhomb-shaped unit mesh are colored differently. One can see two different aspects as presented to the growing environment, corresponding to the two Forms. Generally faces with different aspects have different growth rates, but this need not necessarily be so. In the present case all the faces have the same growth rate. The symmetry of this crystal is indicated in the next Figure.
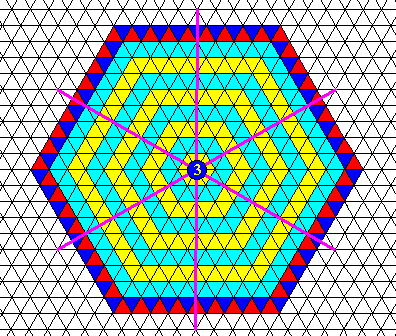
Figure above : The symmetry elements of the crystal of the previous Figure are indicated : three equivalent mirror lines and a three-fold rotation axis at their point of intersection. There are no mirror lines connecting opposite corners of the crystal. All this is the fingerprint of D3 symmetry.
Also a triangular shape can be supported by a trigonal lattice :

Figure above : A two-dimensional crystal having the shape of an equilateral triangle. The three sides (faces) of the triangle present the same aspect to the growing environment, so they must be equivalent, meaning that they together constitute one single crystallographical Form. The symmetry elements of this crystal are indicated in the next Figure.

Figure above : Symmetry elements of the triangular crystal of the previous Figure : three equivalent mirror lines and one 3-fold rotation axis at their point of intersection. This is the fingerprint of D3 symmetry.
While the above triangle represented one crystallographic Form, the next Figure shows the other Form consisting of three equal faces and constituting a triangle.

Figure above : A two-dimensional crystal having the shape of an equilateral triangle. The three sides (faces) of the triangle present the same aspect to the growing environment, so they must be equivalent, meaning that they together constitute one single crystallographical Form. The aspect of the faces of the present triangle is, however, different from that of the sides of the previously depicted triangle. The symmetry elements of this crystal are indicated in the next Figure.

Figure above : Symmetry elements of the triangular crystal of the previous Figure : three equivalent mirror lines and one 3-fold rotation axis at their point of intersection. This is the fingerprint of D3 symmetry.
The two triangles just discussed are indeed the two Forms that combined to give the hexagon-shaped crystal of the Figure further above . We can see there the two different aspects.
If in a 6/m 2/m 2/m crystal (vast majority of ice crystals) that particular possible prism face which grows at the slowest rate has a general (not special) orientation with respect to the symmetry elements, and more specifically, when the slowest growing face of such a crystal as seen in a projection along the c-axis has a general orientation wit respect to the six mirror lines, then a face-dihexagon will develop (See Figure in previous document , where we see it as the base of a dihexagonal pyramid). Such a face-dihexagon is a polygon with 12 equal sides and alternating angles. We should not confuse this face-dihexagon with a face-ditrigon. The latter has 6 equal sides.
The next Figure shows how an angle-ditrigon can develop from a triangular crystal nucleus. We surmise that when the crystal somehow happens to start with a triangular nucleus, but is such that all six faces grow at the same rate, a distorted hexagon is the result, distorted such that it becomes an angle-ditrigon (instead of a regular hexagon).

Figure above : Angle-ditrigon. Holohedric case.
Starting from a triangle-shaped nucleus, a crystal, based on a hexagonal net, can grow into the shape of an angle-ditrigon. As growth proceeds the shape approaches to that of a regular hexagon, whithout, however, ever reaching it.
This could partially explain why some snow crystals have the shape of an angle-ditrigon instead of that of a regular hexagon. See for such a snow crystal the Figure given earlier . As implicitly indicated in the Figure, the growth rates of all the faces shown are supposed to be equal. And because we have used here empty building blocks, we have to do with a crystallographically hexagonal (s.str.), i.e. holohedric crystal. In this holohedric case each rhomb-shaped building block contains two identical chemical motifs (which can, as such, be represented by empty meshes, or represented more explicitly, as is done in the Figure given earlier ). In the trigonal case (i.e. the trigonal-hemihedric case), we have to do with the same hexagonal net, but here a building block (rhomb) is provided with two different, or differently oriented, chemical entities (See this Figure above ). The trigonal case is depicted in the next Figure.

Figure above : Same as previous Figure. Trigonal-hemihedric case. The trigonal nature of the lattice is indicated (only) in the last layer of the crystal. In the depicted (trigonal) case the faces, although supposed to grow with the same rate, are nonetheless not equivalent. Their aspects, as they are presented to the nutrient environment, are different (which normally, but not necessary entails a difference in intrinsic growth rate). Therefore, two different crystallographic Forms are involved, i.e. the crystal is a combination of two different Forms.
When intrinsic growth rates within one and the same crystal are different, we can, starting from a triangular crystal nucleus, get the following :
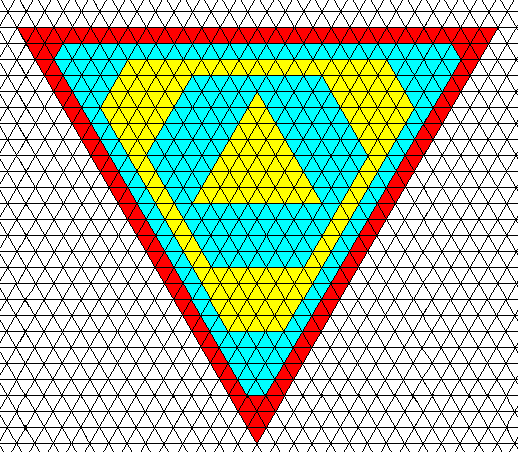
Figure above : Starting from a triangle-shaped nucleus, a crystal, based on a hexagonal net, can, when growth rates are different, initially grow into the shape of an angle-ditrigon. As growth proceeds the shape turns into a triangle again and remains so.
We see two types of faces, which differ in their intrinsic growth rates : If, during a certain time unit one layer of molecules (represented by small triangles) is laid down onto the growing crystal with respect to one type of face, four layers are (in the same time) laid down onto it with respect to the other type of face. As can be seen, the fast growing faces finally disappear, resulting in a triangle-shaped crystal. Because the growth rates of the faces are supposed to be different, they are not equivalent. This means that two different (crystallographic) Forms are involved, and because these Forms are equilateral triangles, the intrinsic (i.e. crystallographic) symmetry of the crystal must be, like such a triangle, according to the group D3 . The crystal is therefore (crystallographically) trigonal. The next Figure depicts the upper right corner of this crystal and shows further growth.

Figure above : Continued growth of the crystal of the previous Figure. Only upper right corner shown. As one can see, further growth does not change the crystal's shape anymore. The latter remains an equilateral triangle.
The next Figure depicts this same trigonal crystal, but now with the (crystallographic) trigonality indicated in some layers.

Figure above : The trigonal crystal of the Figure(s) above . The trigonality of the (filled-in) lattice is indicated in some (i.e. not all) growth layers (i.e. this trigonality is everywhere present in the crystal, but is indicated in some layers only). We clearly see that two crystallographic Forms are involved (recognizable by the different aspects that the present and earlier faces present to the growing environment of the crystal). The point symmetry of the crystal is clearly according to the group D3 . The next Figure shows that the trigonal indications (red and dark blue triangles) are drawn correctly : the indicated areas are crystallographically continuous with each other.

Figure above : Same as previous Figure.
The indicated areas (as drawn in the previous Figure) of the trigonal crystal are crystallographically continuous, as they should be.
Because genuine triangular snow crystals (i.e. plate-like crystals of which the plate has the shape of an equilateral triangle) are, it seems, without exception, very small (See Figure further above , and also this Figure further above (left image) ), it is doubtful that triangle-shaped snow crystals develop according to the Figures just above (which suggest the unlimited growth of a final triangle, preceded by an angle-ditrigonal intermediate state), i.e. it is doubtful that such crystals are crystallographically trigonal.
In the next document we continue our investigation of triangular snow crystals (as a crystallographic preparation and exercise to the systematic exposition of the crystal-analogy to come).
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-20.