

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Square
We now consider a fully developed 2-D (i.e. two-dimensional) (imaginary) crystal having the shape of a square :

Any square, i.e. quadratic, crystal can be conceived as being built up by a periodic stacking of microscopic square units, as the next two Figures illustrate :

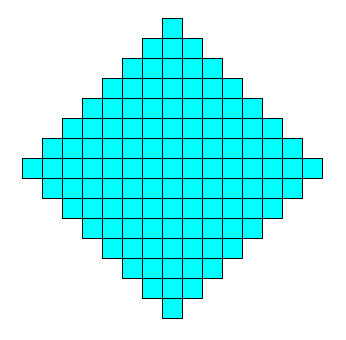
The true, i.e. intrinsic, point symmetry of such a crystal can either be according to the Dihedral Group D4 (crystallographically indicated as 4mm ), or to the Dihedral Group D2 (crystallographically indicated as 2mm ), or to the Dihedral Group D1 (crystallographically indicated as m ), or to the Cyclic Group C1 (i.e. the Asymmtric Group, crystallographically indicated as 1 ), or to the Cyclic Group C2 (crystallographically indicated as 2 ), or, finally, to the Cyclic Group C4 (crystallographically indicated as 4 ), all depending on the crystal's internal structure.
That a square crystal can have these intrinsic symmetries can be explained succinctly as follows (and will be further evident in the sequel) :
A Square as such has the following symmetries, i.e. it will be superposed upon itself by the following transformations (which are then for that reason symmetry transformations) :
The next table shows the plane groups that can support (two-dimensional) crystals having the Square as their intrinsic shape. Further the table shows the intrinsic point symmetry of the crystal, and, finally, the number of crystallographic Forms needed to generate such a square crystal :

| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 4 |
| P2 | C2 ( 2 ) | 2 |
| Pm Cm Pg |
D1 ( m ) | 2 |
| P2mm C2mm P2mg P2gg |
D2 ( 2mm ) | 1 |
| P4 | C4 ( 4 ) | 1 |
| P4mm P4gm |
D4 ( 4mm ) | 1 |
For each of these plane groups mentioned in the above table, we will show how it supports a square crystal shape. The intrinsic shape of the crystal, in the present case its square shape, depends on the Growth Rate Vector Rosette, which in turn depends on the atomic aspects (chemical nature of motifs and geometry of lattice) presented to the growing environment by the possible crystal faces. The square crystal can be formed by the stacking of square or rhombic building blocks (unit meshes) containing a motif s.str. compatible with the point symmetry implied by the given plane group. The point symmetry is indicated in each case. Recall that the point symmetry of a crystal is the translation-free residue of its plane group symmetry.
A square, which has a symmetry according to the group D4 , will be supported by those plane groups of which all the implied point symmetries (i.e. implied by the plane group) are also symmetries of the Square. This does not necessarily hold the other way around : A crystal can have an intrinsic shape that is a square, but nevertheless some, or even all, symmetries of this square can be absent in the crystal, resulting in the fact that the intrinsic symmetry of the crystal is lower than that of its intrinsic shape.

Figure above : Two-dimensional square (quadratic) crystal, point symmetry D4 , and supported by a quadratic point lattice (indicated by connection lines).
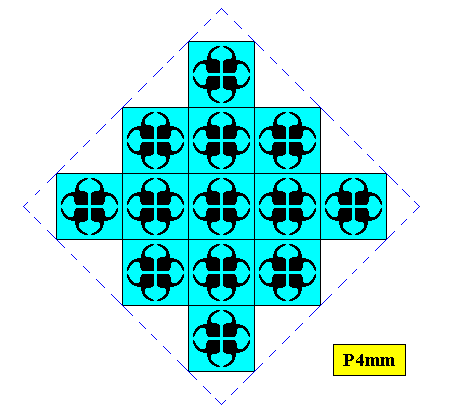

Figure above : Two-dimensional quadratic crystal, point symmetry D4 , and supported by a quadratic point lattice (indicated by connection lines).
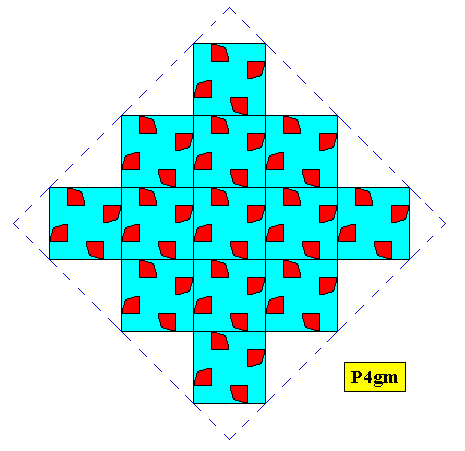

Figure above : Two-dimensional square crystal, point symmetry C4 , and supported by a quadratic point lattice (indicated by connection lines).
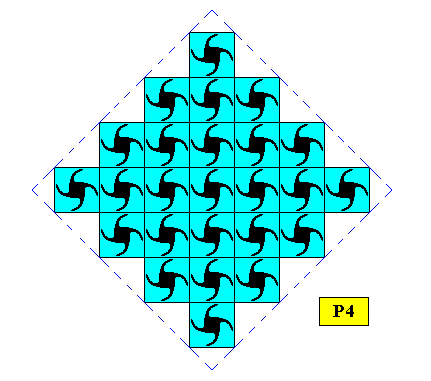
While a square mesh is intrinsic for the plane groups P4mm, P4gm and P4 (considered above), it is not intrinsic for the plane groups P2mm, C2mm, P2mg, P2gg, Pm, Cm, Pg, P2 and P1 (yet to be considered), but can, nevertheless occur. The general shape of the lattice mesh of the plane groups P2mm, C2mm, P2mg, P2gg, Pm, Cm, and Pg is a rectangle (for C2mm and Cm it can equivalently be a (general) rhombus). We can imagine that for these latter seven plane groups the chemical features of the motifs could be such that first they involve rectangular building blocks, and second, that the intrinsic growth rates with repect to possible crystal faces are such that stacking of these rectangular building blocks results in a square crystal. Let us consider such a case.

Let us, in the above Figure, denote the longer side of the unit rectangle lo and the shorter side sh . In the present case lo / sh = 3. Let us further denote the growth rate perpendicular to lo : Rate(lo) and perpendicular to sh : Rate (sh) . And let us express these rates in terms of the number of unit rectangles in a unit of time (and thus not in terms of units of distance). It is then clear that in the present case, in order for crystal growth to result in a rectangular crystal, Rate(lo) must be three times as big as Rate(sh) . And indeed generally we can say that if the stacking of rectangular building blocks should result in a square crystal, the relation
Rate(lo) = (lo / sh) Rate(sh) (measured in terms of numbers of building blocks)
must be satisfied.
Although such cases of the formation of square crystals out of rectangular building blocks can be imagined to occur, we will not pursue them further. Instead we consider the cases where the properties of the chemical motifs are such that, with respect to the plane groups P2mm, C2mm, P2mg, P2gg, Pm, Cm, Pg, P2 and P1, the lattice meshes become squares. See next Figures.

Figure above : Two-dimensional square crystal, point symmetry D2 , and supported by a primitive rectangular point lattice (indicated by connection lines) where the two translations happen to be of equal length.
The above Figure depicts a two-dimensional crystal with plane group symmetry P2mm and point group symmetry D2 . Earlier, viz. in Part V , we depicted a crystal with the same intrinsic symmetry, but having an intrinsic rectangular shape. The difference between the two must lie in the motif. But we have used the same motif. And we will keep on doing this, because our drawn motifs (commas or other figures) only symbolize the (point) s y m m e t r y of the actual 'chemical' motifs of the crystal.
The next two Figures also show a square P2mm crystal (as in the Figure directly above), but now with its motifs rotated anticlockwise by 450, implying that also the mirror lines are so rotated.

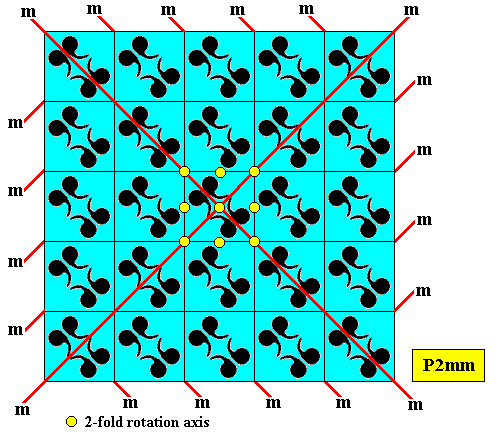
Figure above : Same as previous Figure. Some symmetry elements indicated : 2-fold rotation axes (small yellow solid circles) and mirror lines ( m ), demonstrating that the symmetry of the pattern is indeed according to the plane group P2mm.
The next Figures illustrate that a symmetry pattern having C2mm symmetry can nevertheless be such that it is consisting of s q u a r e building blocks (unit meshes).
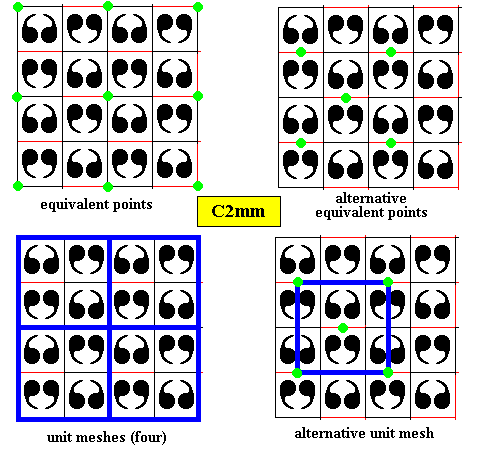
Figure above : Construction (by means of auxiliary lines) of a two-dimensional square crystal with C2mm plane group symmetry, and (consequently) D2 point group symmetry. See next Figures.

Figure above : Two-dimensional square crystal, point symmetry D2 , and supported by a centered rectangular point lattice (indicated by connection lines) where the two translations happen to be of equal length. Compare with its rectangular analogue of Part V .
The next five Figures analyse the above square crystal.
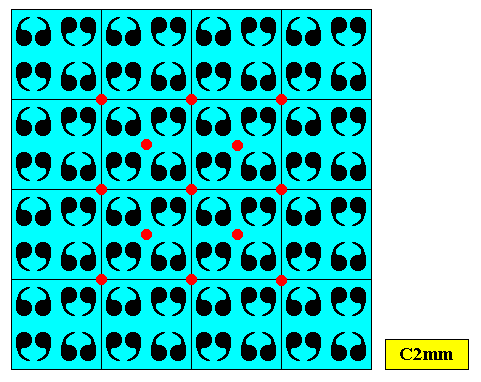
Figure above : Two-dimensional square crystal of previous Figure. Some equivalent points indicated. Together they form the centered rectangular point lattice of the crystal. In the present case the meshes happen to be squares (as a special kind of rectangle). Compare with its rectangular analogue of Part V .
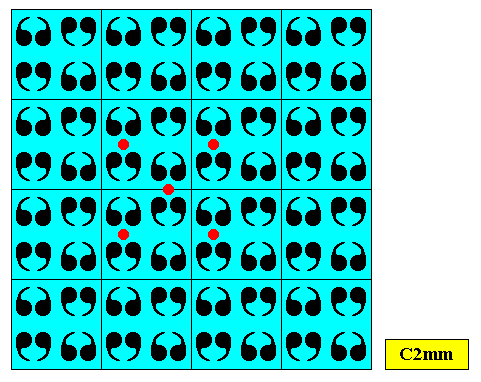
Above Figure : Some points of an alternative set of equivalent points of the crystal of the previous Figures. Like the set depicted above, they also form a possible centered rectangular lattice of the crystal. The next Figure shows how, according to this lattice D2 motifs are repeated.
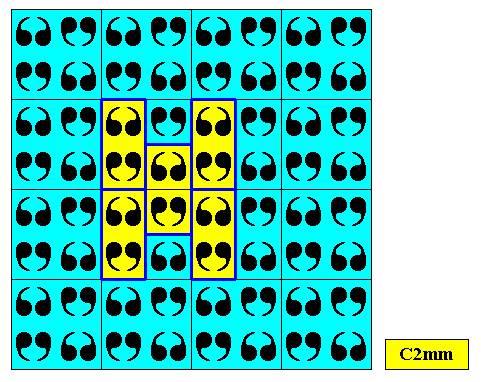
Above Figure : Two-dimensional square crystal of previous Figures. Some motifs highlighted. All this in fact shows D2 motifs being repeated according to a centered rectangular point lattice, which demonstrates that the pattern is indeed a C2mm pattern, despite its square meshes.
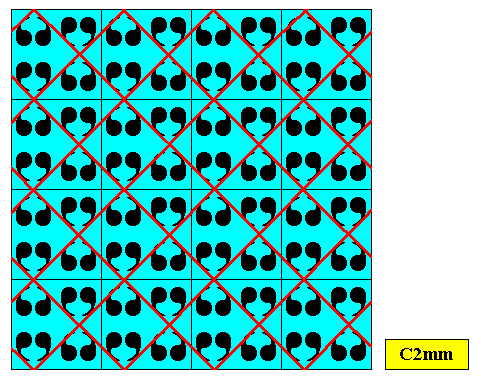
Above Figure : Two-dimensional square crystal of previous Figures. The repetition of the motifs can also be described with a rhombic point lattice (instead of with a centered rectangular lattice, as was done above). In our present case the rhombi of this lattice happen to be squares, which are a particular species of rhombus. Compare this square crystal with its rectangular analogue of Part V . Inspecting the present Figure, one would be tempted to see a D2 motif which is repeated by two independent translations perpendicular to each other, indicating that the plane group symmetry of the pattern is P2mm (instead of C2mm). But this is not so, because the reflection lines of the motif are not aligned with the edges of the square meshes, which should be so when the pattern's symmetry was according to P2mm, as can be seen in the earlier Figure depicting a P2mm crystal , where we see a D2 motif repeated according to a primitive rectangular point lattice (where in the present case the shape of the meshes has become a square). The next Figure shows this more clearly.
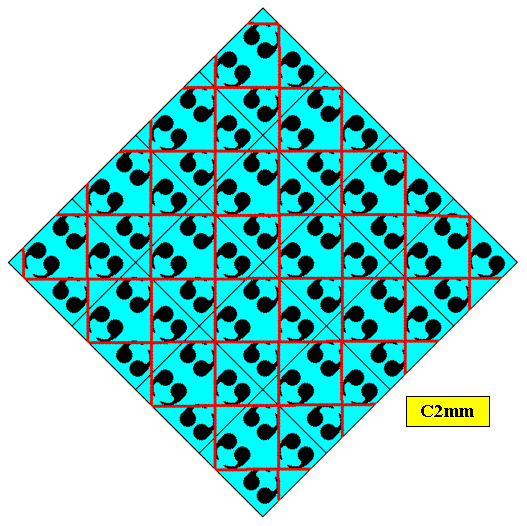
Figure above : Same as previous Figure (viz. 2-D square crystal with plane group symmetry C2mm and point group symmetry D2), but rotated 450 to clearly see the non-alignment of the motif's mirror lines with the edges of the square meshes. Compare with the earlier Figure depicting a P2mm crystal . The motif's mirror lines only aligns with the edges of the meshes when we have chosen to describe the repetition of the motifs by means of a centered rectangular lattice. See above , where such a repetition of the motifs, viz. a repetition according to the centered rectangular lattice (the meshes of which have in the present case become squares), is depicted, and where one can see that the mirror lines of the motifs do align with the edges of the (square) meshes.
To obtain the above pattern, i.e. a C2mm pattern allowing for s q u a r e lattice meshes, in particular that of the above Figure , from the corresponding pattern having rectangular lattice meshes as was depicted earlier, in Part V , it is not enough simply to change the rectangle, that outlines the rectangular unit mesh, into a square. If we do this we get the following pattern (next Figure), and when we inspect this pattern we see that its plane group symmetry is not according to C2mm anymore but to Pm : We see a D1 motif repeated according to two translations perpendicular to each other, and because the two points indicated (red) are not equivalent, the lattice is primitiv (i.e. not centered) :
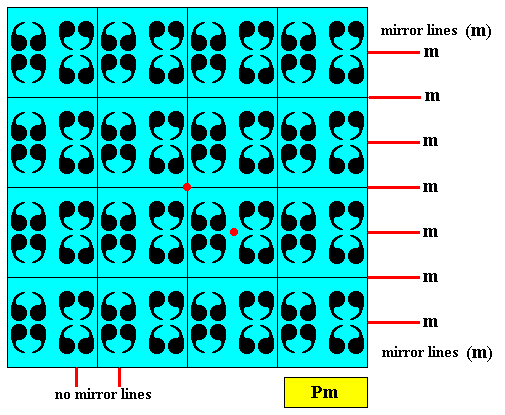
In order to get the correct pattern we must change the spacing between the motif units appropriately, as was done above .
After this analysis of our square C2mm crystal, we continue with the next plane group, viz. P2mg .
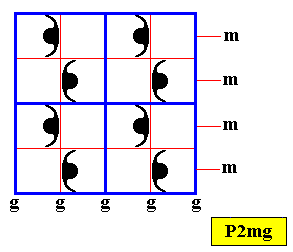
Figure above : Construction (by means of auxiliary lines) of a two-dimensional square crystal with P2mg plane group symmetry, and (consequently) D2 point group symmetry. See next Figure.
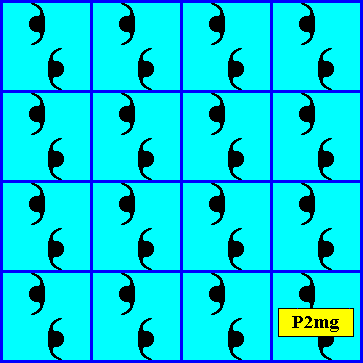
Figure above : Two-dimensional square crystal, point group symmetry D2 , and supported by a primitive rectangular point lattice (indicated by connection lines) where the two translations happen to be of equal length. Compare with its rectangular counterpart, as depicted in Part V .
Now we're going to derive a P2gg pattern with square lattice meshes from the corresponding pattern with rectangular meshes, as was depicted earlier, in Part V . See next Figure.
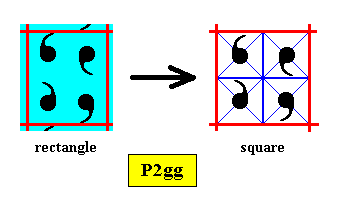
Figure above : Construction of a two-dimensional square crystal with plane group symmetry P2gg and (consequently) with point group symmetry D2 , based on a primitive rectangular point lattice, in which the meshes happen to be squares (as a particular species of rectangle). The rectangular mesh as it was so in the corresponding rectangular version, depicted earlier, in Part V , is transformed into a square mesh with the motif units at the appropriate locations. The next Figure completes the pattern.

Figure above : Two-dimensional square crystal, point symmetry D2 , and supported by a primitive rectangular point lattice (indicated by connection lines) where the two translations happen to be of equal length. Compare with its rectangular analogue as depicted earlier, in Part V .
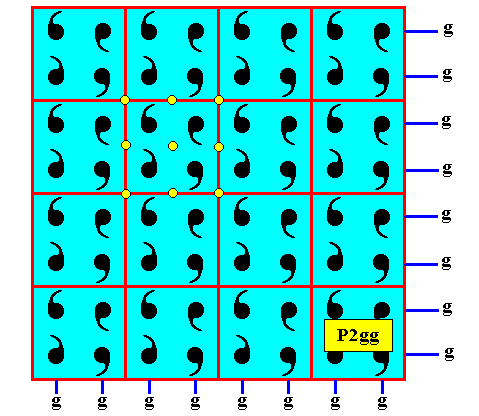
The next Figure analyses the just obtained pattern. As one can see it has vertical and horizontal glide lines ( g ) and two-fold rotation axes (some of them indicated (green)), together forming a pattern of symmetry elements that is the fingerprint of the plane group P2gg.
The next plane group to be discussed as to how it supports square crystals is Pm .
Figure above : Construction of a two-dimensional square crystal with plane group symmetry Pm and (consequently) with point group symmetry D1 , based on a primitive rectangular point lattice, in which the meshes happen to be squares (as a particular species of rectangle). The rectangular mesh as it was so in the corresponding rectangular version, depicted earlier, in Part V , is transformed into a square mesh with the motif units at the appropriate locations. The next Figure completes the pattern.
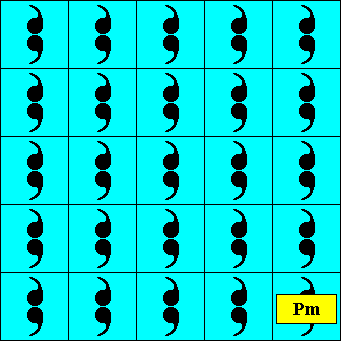
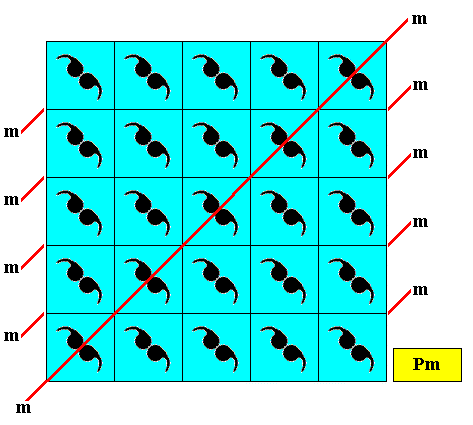
Figure above : Two-dimensional square crystal, point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines) where the two translations happen to be of equal length. Compare with its rectangular analogue as depicted earlier, in Part V .
The next two Figures also depict a square Pm crystal, but with its motifs rotated anticlockwise by 450, implying that also the mirror lines of the pattern are so rotated,

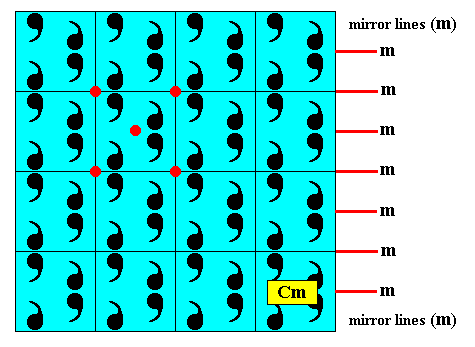
The next plane group to be discussed as to how it supports square crystals is Cm .
Figure above : Construction of a two-dimensional square crystal with plane group symmetry Cm and (consequently) with point group symmetry D1 , based on a centered rectangular point lattice, in which the meshes happen to be squares (as a particular species of rectangle). The rectangular mesh as it was so in the corresponding rectangular version, depicted earlier, in Part V , is transformed into a square mesh with the motif units at the appropriate locations. The next Figure completes the pattern.

Figure above : Two-dimensional square crystal, point symmetry D1 , and supported by a centered rectangular point lattice (indicated by connection lines) where the two translations happen to be of equal length. Compare with its rectangular analogue as depicted earlier, in Part V .
The next Figure analyses the just constructed square crystal. One can see the mirror lines ( m ), and (one can see) also the fact that a D1 motif (four commas) is repeated according to two equal translations perpendicular to each other. Further one can see that the unit mesh is not primitive but centered. All this demonstrates that the pattern has indeed Cm plane group symmetry.
The next plane group to be discussed as to how it supports square crystals is Pg .
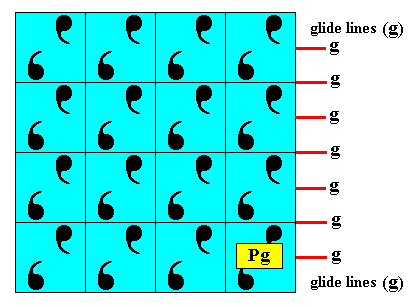
Figure above : Construction of a two-dimensional square crystal with plane group symmetry Pg and (consequently) with point group symmetry D1 , based on a centered rectangular point lattice, in which the meshes happen to be squares (as a particular species of rectangle). The rectangular mesh as it was so in the corresponding rectangular version, depicted earlier, in Part V , is transformed into a square mesh with the motif units at the appropriate locations. The next Figure completes the pattern.

Figure above : Two-dimensional square crystal, point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines) where the two translations happen to be of equal length. Compare with its rectangular analogue as depicted earlier, in Part V .
The next Figure analyses the just constructed crystal (but a smaller version of it) as to its symmetry. One can see that the pattern's only symmetry elements are horizontal glide lines, demonstrating that the plane group symmetry of the pattern is indeed that of Pg.
The next Figure is about the plane group P2 . A C2 motif (two commas) is repeated according to two equal translations perpendicular to each other.

Figure above : Two-dimensional square crystal, point symmetry C2 , and supported by an oblique point lattice (indicated by connection lines) where the angles happen to be 900 and the two translations to be of equal length.
The next Figure, finally, is about the plane group P1 . An asymmetric (C1) motif is repeated according to two equal translations perpendicular to each other.

Figure above : Two-dimensional square crystal, point symmetry C1 , and supported by an oblique point lattice (indicated by connection lines) where the angles happen to be 900 and the two translations to be of equal length.
This concludes a summary, showing when, and in what way, square-shaped two-dimensional crystals are supported. As can be seen in the above Figures, in many cases the actual point symmetry of the (square-shaped) crystal is lower than that of the Square.
The next document will investigate the possible promorphs of these two-dimensional square crystals.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part VII.
e-mail : 