

(Takes a little while loading the images)
e-mail :

Sequel-18 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-18) further elaborates on the analogy between crystals and organisms.
Sequel to the Preparations (VI) to the Repertoire of the Crystal Analogy
Sequel to Special Features of Crystals
Twinning
The phenomenon of twinning is very wide-spread in the world of crystals, so it is to be expected in snow crystals too. Under normal atmospheric conditions H2O crystallizes in the most symmetric Class (6/m 2/m 2/m) of the Hexagonal Crystal System, whereas a projection of such a crystal down along the c-axis results in a two-dimensional crystal belonging to the Class 6mm (symmetry group D6) of the Two-dimensional Hexagonal Crystal System (plane group P6mm). So whenever we see a snow crystal where two (or more) faces stand to each other at an angle that is not compatible with the intrinsic symmetry of ice, then, if we are sure that we do not have to do with two crystals accidentally and randomly glued together, a twin could be involved. Twins can be considered to be two (or more) individual crystals that are grown together in a regular way, i.e. according to a rule (as one of the several twin laws). They often are recognizable by the presence of receding (reentrant) angles. Generally twinning brings with it an increase in the symmetry of the result.
Let us hear what LIBBRECHT, K., has to say about twinning in snow crystals (The Snowflake, 2003, p.85) [comments of mine in square brackets] :
Twinning is a crystallography term referring to two [ or more ] separate crystals joined together in some precisely incorrect fashion. Compare it to buttoning up your shirt wrong : you make just one mistake in the beginning by putting the first button in the wrong buttonhole, and then you button up as usual and find the whole shirt askew. Twinning works the same way. There's one molecular defect in the beginning, and then the whole crystal goes together wrong.
There are several ways ice crystals can get buttoned-up wrong, and one way makes a pair of twin columns. The defect starts in the crystal's nucleus, producing what looks like an ordinary columnar crystal. But a columnar twin is two crystals, one with a 60-degree twist relative to the other. The 60-degree twist means that the facets on one side [ i.e. one end, one half ] of the prism are positioned exactly the same as the facets on the other side, so the twins appear as a normal column when they grow. But if you let the column evaporate a bit, it shows its true nature. The molecular bonds connecting the two crystals are weaker than the bonds in either of the twins. Thus the molecules at the join are more likely to evaporate. After some evaporation, the column displays a characteristic evaporation groove around its middle. You have to look for it, but it's common in columnar snowflakes [ See next Figure ] .

Figure above : Evaporation groove. A columnar crystal (which is in fact an elongated hexagonal prism, whose edges are rounded off by incipient evaporation) sometimes contains an evaporation groove that runs around the middle of the column. The presence of such a feature reveals that the two halves are crystal twins, incorrectly joined together at the molecular level.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
In what comes next I will try to explain this kind of twinning (involving a 600 twist in a columnar snow crystal).
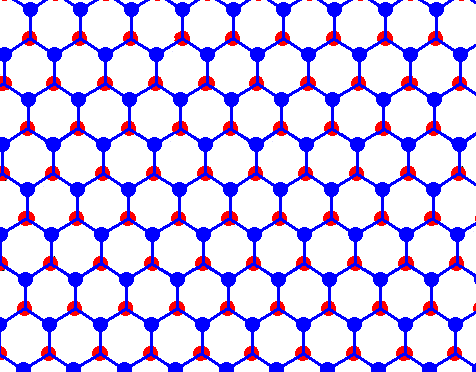
Figure above : Structure of ice, seen along the crystallographic c-axis.
Each dot (red or blue) represents a water molecule. Each such water molecule connects with four others by hydrogen bonds. Three such bonds shown for each water molecule. The fourth bond is perpendicular to the plane of the drawing. What we see here are two layers, distinguished by coloration. (Figure taken from Part XXIX Sequel-7 )
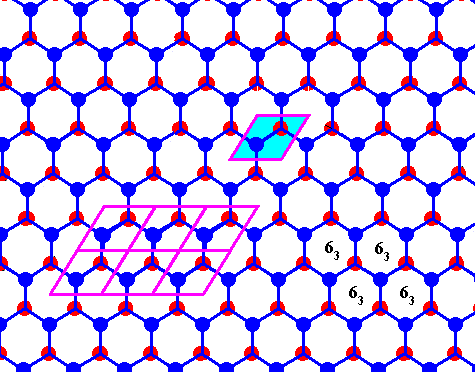
Figure above : Same as previous Figure.
Possible rhombic unit cell indicated. The the center of each hexagon is the location of a 63 screw axis (four of them indicated), if the Figure is interpreted as representing a 3-dimensional view (down the c-axis).
If the Figure is 2-dimensionally interpreted, then we see a rhombic unit mesh, containing two 3-fold rotation axes (coinciding with the two molecules of that mesh), and a 6-fold rotation axis at each of its corners. (Figure taken from Part XXIX Sequel-7)
The next Figure depicts such a 63 screw axis.
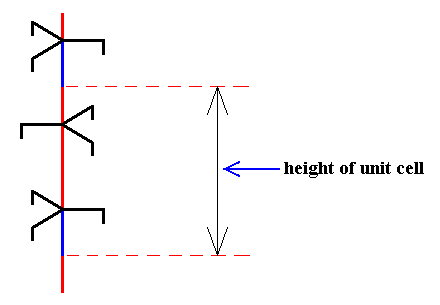
Figure above : 63 screw axis.
The three arms of each trigonal motif unit (along the axis) are congruent and make angles of 1200 with each other.
If we imagine this structure to extend indefinitely upwards and downwards, then if we rotate it by 600 about the axis and then translate it by half a unit translation (i.e. half the vertical length of the unit cell) along the axis, then the whole structure will coincide with itself, which means that this structure contains a 63 screw axis.
In the vertical direction the above structure -- if it is extended upwards and downwards -- is periodic, and it is thus possible to select a part (and we have many equivalent possibilities to do so) that can build this structure by being repeated periodically along the direction of the axis. The next Figure has chosen such a part and a copy of it.
Figure above : A periodic unit is selected from the structure depicted in the previous Figure, and then copied.
If we place this part and its copy on top of each other, then we are building up our structure :
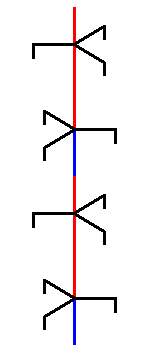
Figure above : A copy of the selected unit part is placed on top of that unit part. By repeating this operation we build up our structure, i.e. we build up the ice structure in the vertical direction ( = direction of the crystallographic c-axis)
If, on the other hand, the copy of the unit part is 600 rotated about the axis with respect to the initial unit part, and then placed on top of that unit part, then we see that at their junction are two equally oriented trigonal motif units, which is at odds with the screw axis symmetry. See next two Figures.
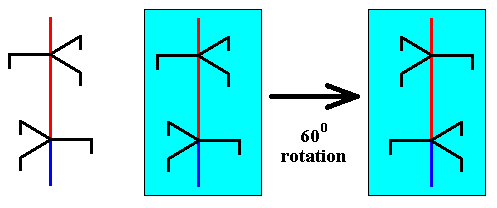
Figure above : A copy of the selected unit part is rotated 600 about the axis.
This rotated copy is now placed on top of the initial unit part :
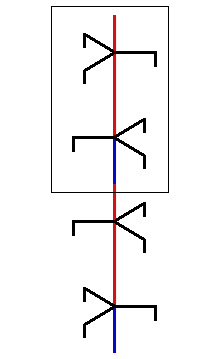
Figure above : A copy of the selected unit part is, after it has been rotated 600 about its axis, placed on top of the initial unit part. The result is a structure which contains a region that is at odds with the 63 screw axis structure. See also next Figure.
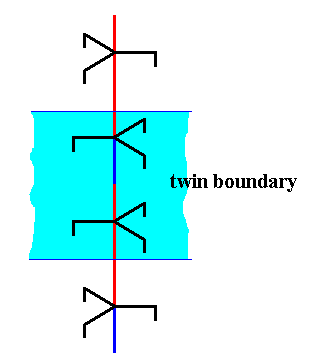
Figure above : The junction area of the above twinning construction is indicated.
I assume that the above described twinning of a hexagonal columnar snow crystal proceeds along the lines just sketched. An ice structure, of course, contains a great many of 63 screw axes. In a 60-degree twist twin each such screw contains the just described juncture at the same height, i.e. all these junctures lie at the same level in the crystal. And it is to be expected that the chemical bonds involved at this juncture are distorted or strained, and the relevant molecules are more likely to escape from the solid than others, resulting in an evaporation groove as evidence of twinning.
In many other cases, twinning can be directly identified by the presence of odd angles, i.e. angles that are incompatible with the intrinsic symmetry of ice crystals. In next Figure we see that the facet angles of the diamond-shaped crystals are not right for the usual hexagonal symmetry of the ice crystal, but a close look often shows an evaporation groove bisecting the form, indicating another example of twinning. And here we see also that in this case twinning increases the symmetry.
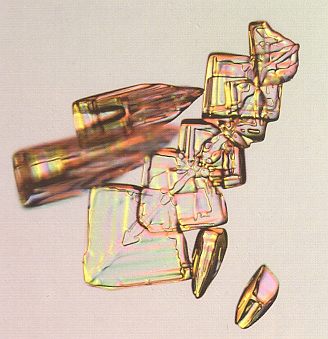
Figure above : Arrowhead snow crystals. These unusual diamond-shaped plates fall along with columnar crystals, and the evaporation grooves show they result from crystal twinning. See also next Figure.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
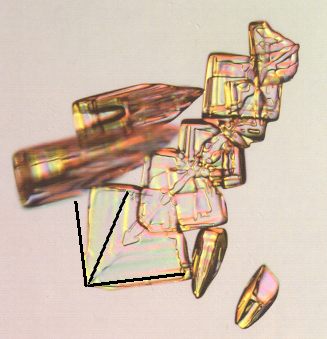
Figure above : Same as previous Figure. Here we investigate the angle between two adjacent faces of the arrowhead-shaped snow crystal individual, which is a plate, meaning that the crystal's c-axis is perpendicular to the plane of the photograph. Allowed angles are then angles having a value between 1800 and 1200, implying that this angle is in all cases obtuse (See next Figure). The inserted black lines, depicting angles of 900 and 600, show that the two (adjacent) crystal faces (which are seen as edges, or represented by parallel faint ridges in the photograph) make an angle smaller than 900 (but not 600, which is an angle that could be expected to turn up somehow in the Crystal Class (6/m 2/m ) in which water crystallizes), that is to say the angle between these faces is acute. So the crystal is a twin.
(Adapted from a photograph (previous Figure) by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
The next Figure shows the possible angles between adjacent faces seen in projections down along the c-axis of crystals of the Dihexagonal-bipyramidal Class (6/m 2/m 2/m) (to which ice belongs) of the Hexagonal Crystal System. The mentioned projections either are regular hexagons in different orientations (representing the proto- or deuteropyramids or prisms) or a possible dihexagon. Every two adjacent faces in these projections (seen as lines) make an obtuse angle with each other. See next Figure.
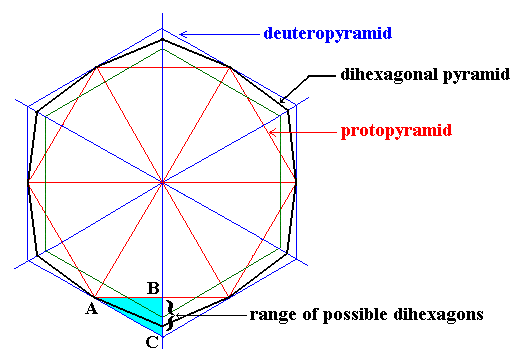
Figure above : [ Taken from First Part of Website ( = "Back to Hompage" link), Hexagonal Crystal System I, Fig. 13 ] Range of possible dihexagons (the general ones, but also the special (regular) case). The possible intercepts (i.e. cut-offs from the line running from the center of the figure to B and C) related to a representative side of the dihexagon (corresponding to a representative face of the associated dihexagonal pyramid or prism) can vary between those of the Protopyramid and those of the Deuteropyramid. It can be seen that the angle between two adjacent faces of the dihexagon, as seen in projection, is obtuse, it lies between 1800 and 1200.
The next Figure illustrates an instance of twinning as seen in the context of the crystal lattice (In this particular example an orthorhombic lattice is used as seen in cross-section).
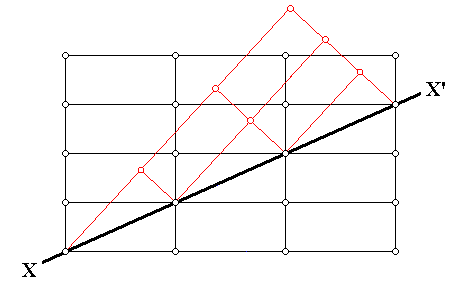
Figure above : Cross-section through an orthorhombic lattice (which as such is then a primitive rectangular net) showing a twinned relationship (indicated by red lines) about the direction XX' . Along this direction atoms (or lattice nodes) are compatible with the regular as well as the twinned relationship. The twin may be viewed as the result of a 1800 rotation about XX' , or of a mirror along XX' . We can also see here that the twinning results in an odd angle between (adjacent) faces.
(Adapted from C. HURLBUT, Jr. & C. KLEIN, Manual of Mineralogy, 1977.)
The next Figure is the same as the previous Figure, but at some lattice nodes letters are inserted.
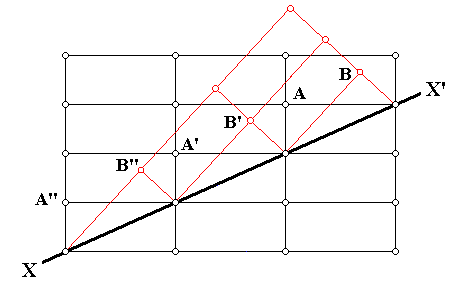
Figure above : Same as previous Figure : Cross-section through an orthorhombic lattice (which as such is then a primitive rectangular net) showing a twinned relationship (indicated by red lines) about the direction XX' . At some lattice points letters are inserted in connection with the next discussion.
(Adapted from C. HURLBUT, Jr. & C. KLEIN, Manual of Mineralogy, 1977.)
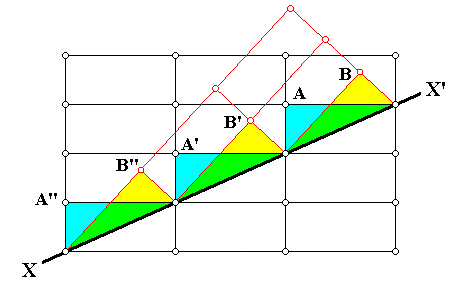
Figure above : Same as previous Figure : One can see the alternative choices (A or B) that can be made by atoms (ions, or molecules) as they are about to appose (deposit) on the surface XX' (as possible (growing) crystal face). However, these two choices are not equivalent : to continue the original orientation of the lattice is expected to be energetically more favorable. The chemical bonds connecting the twin partners will therefore be expected to be weaker.
The above three Figures illustrate a particular kind of twinning, resulting in what is called growth twins. About these HURLBUT & KLEIN, Manual of Mineralogy, 1977, p.100, report the following (referring to the above Figure) [comments of mine between square brackets] :
Growth twins are the result of an emplacement of atoms, or ions (or groups of atoms or ions) on the outside of a growing crystal in such a way that the regular arrangement of the original crystal structure (and, therefore, its lattice) is interrupted. For example, in the above Figure, the line XX' may be considered a side view of an external face of a growing crystal. An ion, or atom (or group [ of atoms or ] of ions), would have the choice of attaching itself at structural sites represented by lattice nodes A, A', A'', or B, B', B''. In the former case the original structure is continued without interruption but in the latter a twinned relationship results. Growth twinning therefore reflects "accidents" during free growth ("nucleation errors") and can be considered as primary twinning. Growth twins can be recognized in mineral specimens by the presence of a single, often somewhat irregular boundary between the twinned units or [ in other cases of growth twins ] by the interpenetration of two twinned units.
There are also other kinds of twinning, resulting in transformation twins or in gliding (or deformation) twins.
Columns and needles
Many snowfalls consist primarily of columns and needles. They appear when the temperature is such that the ratio between the growth rate of the basal faces and that of the prism sides becomes high. There is thus a considerable change in habitus when we go from plate-like crystals to columnar or needle-like crystals. Columns generally grow at temperatures around -50 C (230 F) and also at temperatures below a frigid -250 C (-130 F). Long columns look a bit like thin ice needles, and these grow only in a narrow temperature range around -50 C (230 F) when the humidity is high (LIBBRECHT, The Snowflake, 2003, p.76). The next Figure depicts a column.

Figure above : Columnar snow crystals are common. They range from short, cylindrical blocks to long, thin needles. The small block crystal here is 1.8 mm (0.07 inches) long. While LIBBRECHT doesn't mention it explicitly here (later he does), it is clear that the smooth cylindrical shapes of the columnar snow crystals is a product of incipient evaporation of sharp-edged hexagonal prisms as they are as such seen in cold climates (See the snow crystals from Antarctica depicted earlier (Part XXIX Sequel-16) )). The features visible in the depicted columnar crystal are probably related to air inclusions.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
Hollow columns
The growth of columnar crystals is controlled by the interplay between faceting and branching ( The latter is, as we saw earlier, a growth of fast-growing faces while their surface area remains very small). When the crystals are small (meaning that the nutrient material can easily reach all parts of the crystal) and the humidity is low (meaning that actual growth will be slow, so that the nutrient material can have the chance to supply all sites of the crystal), then faceting dominates (i.e. the slowest growing faces are prominent, while the fast growing faces -- where tapering of adjacent faces is the case -- grow themselves totally out of existence). In this case (small crystals, low humidity) the crystals grow into simple hexagonal prisms (LIBBRECHT, Ibid., p.76).
When a hexagonal prism grows larger, the rate of diffusion becomes a limiting factor, and the branching instability takes on a new role. The basal edges (at top and bottom) of the prisms grow more rapidly than the face centers, and soon a column will start to hollow. Hollow column crystals are common when the cloud temperatures are near -50 C (230 F). See upper-right image of next Figure.

Figure above : Snow crystals : Bullet cluster (left image), bullet crystal (bottom-right), and hollow column (top-right). A (partially) hollow column originates when the edges of the basal faces of the prism grow faster than the face center. In fact it is a form of branching.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
In Part XXIX Sequel-4 we in fact already distinguished between outgrowths emanating from the prism edges (perpendicular to the bottom and top faces) (as we see it in stellar crystals), and outgrowths emanating from the top and bottom edges of the snow crystal prism (as we see it in partly hollowed columns) (Text and Figure taken from the mentioned Part XXIX Sequel-4 with alterations) :
When a snow crystal grows rapidly, it develops outgrowths. Such outgrowths are likely to start off from edges or corners, because they can be supplied from more directions, in our case supplied by water molecules present in the air. But, as far as I can see from the many microphotographs taken from snowflakes, these outgrowths do not appear at the edges that separate the upper face, as well as the bottom face of the (flat) hexagonal prism, from its sides. The outgrowths appear to develop only at the edges separating the sides of the prism. See next Figure.
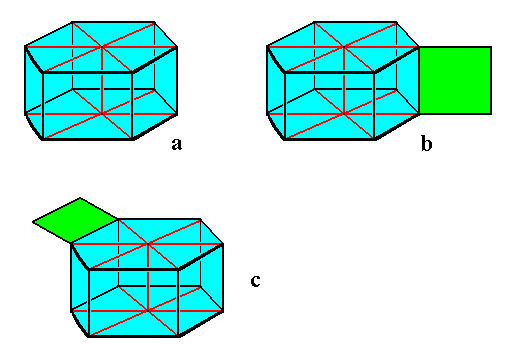
Figure above : Diagram of a snowflake, with and without outgrowths.
The snowflake is depicted here as a hexagonal prism, which indeed it is. In reality, however, the prism is much more flattened or elongated.
Image a : Hexagonal snowflake prism without outgrowths.
Image b : Hexagonal snowflake prism with outgrowths (one shown) at the vertical edges separating the sides of the prism, where they (i.e. the outgrowths) are indeed actually found in stellar snow crystals.
Image c : Hexagonal snowflake prism with outgrowths (one shown) at the horizontal edges separating bottom and top face from the vertical sides. Such outgrowths are not clearly and unambiguously found in snowflakes. However the "hollow columns", described by LIBBRECHT, p.76, could be a manifestation of such outgrowths.
Evaporation does often remove material from snow crystals after they've stopped growing. Sometimes this happens in flight, and it certainly occurs once they hit the ground. The crystal edges often appear a bit rounded from evaporation. We see this frequently with columns because evaporation occurs more rapidly when the temperature is close to ice's meling point (columns generally grow at temperatures around -50 C, as stated earlier). At colder temperatures ( The second optimum for growth of columns is below -250 C, as stated earlier), the facets are more robust (LIBBRECHT, p.77), as we saw in the Antarctic crystals.
Needles and bullets
If the humidity is high and the temperature is close to -50 C (230 F), then the rim of a hollow collumn can become so thin that its growth is also unstable (We see this also in the splash : After the drop has hit the liquid surface a shallow very thin cylinder of liquid rises up. After that the rim of this cylinder breaks up into long extensions, and when these extensions finally become themselves very thin, each one of them breaks up, resulting in a droplet splitting off from the extension).
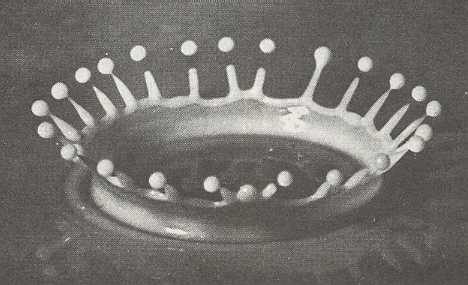
Figure above :
An instantaneous photograph of a splash of milk (See Part XXIX Sequel-3 ). (After D'Arcy THOMPSON, On Growth and Form, 1942.)
Some parts of the rim (of a hollow column crystal) grow faster than others (so the rim breaks up), and these parts soon grow out into a number of needle-like extensions. This is yet another manifestation of the branching instability. Once one part of the rim grows ahead of the rest by just a bit, it then enjoys a better water vapor supply and grows faster still (i.e. faster actual growth relative to the other parts, because it grabs all the nutrient material). Soon it leaves the rest behind. When the humidity is very high, this plays out repeatedly, and the result can end up looking like a cluster of thin needles (LIBBRECHT, p.77), although such a form is in fact one single crystal.
Bullet-shaped crystals are another variant of columnar growth. They form in clusters, with several bullets emanating from a single center. A cluster begins when a cloud droplet freezes into a jumble of several crystals, called a polycrystal. The resulting bullet clusters (see left image of Figure above ) often come apart to yield isolated bullet crystals (see bottom-right image of Figure above ). A typical bullet crystal is a column that tapers at one end. I assume that this has to do with the way of originating from a common point resulting in a cluster.
Capped columns (tsuzumi crystals)
Capped columns are remarkable snow crystals. They generally are not twins. They are like many other snow crystals the result of fast unstable growth. They consist of a short columnar element (originally a short hexagonal prism) capped on both ends with plates. Dependent on the (absolute) rate of growth these caps either are more or less like hexagonal plates, or are branched plates like we see in ordinary branched crystals. These plates must, according to me be seen as localized extensions of the edges separating the prism faces, i.e. the edges that are perpendicular to the top and bottom faces of the prism. The localization is such that only the upper and lower parts of the short columnar prism grow out. This is so because those regions stick out, so they collect most of the nutrient. And when the caps extend, they more and more shield the region between them from collecting nutrient material. As a later Figure clearly shows, such a capped column generally is one single crystal, which means that it is crystallographically continuous and uniform througout its body. See next Figures.
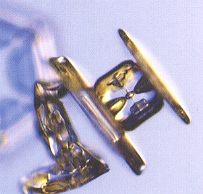
Figure above : A capped column. Such a crystal started out as a stubby column (hexagonal prism), and then switched to plate-like growth. (Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : Capped columns. (After BENTLEY and HUMPHREYS, 1931, 1962, Snow Crystals.)

Figure above : Capped columns.
The crystal in the left image appears (to me) to reveal the presence an evaporation groove around the middle of the column, indicating that the crystal is in fact a twin.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)
The next Figure very clearly shows that the depicted form (and many other capped columns) is one single crystal, because of the exact centering of the top cap, column, and bottom cap.

Figure above : A capped column with competing plates (caps). A surprising number of stellar snow crystals are actually capped columns with one dominant plate. Here the camera is focused on the smaller of the two plates.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
Let us quote LIBBRECHT, when he discusses capped columns on p.78 of his The Snowflake, 2003 :
Thin, flat plates and long, slender columns are the two extreme cases of snow-crystal growth. They each occur within a fairly narrow temperature range -- the longest needles (i.e. long hexagonal prisms) form near -50 C (230 F) and the thinnest plates (i.e. very short hexagonal prisms) form near -150 C (50 F). At intermediate temperatures, crystals grow into blockier forms. Since temperatures in the atmosphere can vary dramatically from place to place, a snow crystal may change its morphology [ but not its intrinsic symmetry, neither its promorphology ] substantially while it grows.
Often a snow crystal begins growing into a stubby column at intermediate temperatures and is subsequently carried by the wind to a region of the cloud at -150 C (50 F), where plates develop. In such cases, plates begin growing at both ends of the crystal, and we end up with a stout column capped by two thin plates. Nakaya [ a japanese researcher who was the first one to investigate scientifically under what circumstances the several snow crystal types develop ] called these tsuzumi crystals, after the japanese drum with a similar shape. The more common name is capped columns.
Capped columns come in various shapes and sizes. The initial column can be long and thin or short and stubby, and the plates in turn can range from thin to thick. It all depends on the growth history of each crystal.
If the initial column is long enough, then two nearly independent plates [ independent from each other because they are relatively far apart ] can grow on its two ends, giving a symmetrical[ly] capped column. Often, however, the plates interfere with each other's growth, particularly on a short column. Then we run into yet another manifestation of the branching instability, resulting in a column capped with plates of unequal sizes.
If a capped column starts wit two identical plates, then for a while they both grow at the same rate because they are growing in the same conditions. But if one of the plates grows just a bit larger than the other, the larger plate will stick out farther and find a better water supply, which causes it to grow faster. Soon it sticks out even farther, and thus it grows faster still. So the cycle goes until one plate wins out over the other. What results is an asymmetric capped column. This competition is inevitable with capped columns, although a given crystal may not have enough time to develop a large asymmetry between its plates.
When LIBBRECHT speaks about different growth rates of the two plates, we should realize that these plates are equivalent, implying that their intrinsic growth rates are the same, and stay the same. One plate can, by chance nevertheless become a little larger than the other plate of the crystal. It then sticks out better and thus can better grasp nutrient material, at the expense of the other plate. It therefore gathers more material, so that it now sticks out even better, etc. The involved growth rates of which LIBBRECHT speaks are then not the intrinsic growth rates (as they are at specified conditions), but the net effective growth rates. In fact all this is equivalent to the distortion a growing crystal undergoes when its supply of nutrient is not uniform but spatially biased. So the resulting asymmetry (large plate on one end, small plate on the other) is definitely not an intrinsic asymmetry, but extrinsic. The true, i.e. intrinsic, symmetry is always 6/m 2/m 2/m, i.e. the symmetry of the highest symmetrical Class of the Hexagonal Crystal System. It is the symmetry of the regular hexagonal bipyramid (which is the simplest solid having this symmetry).
Split stars and split plates
About these special forms of snow crystals LIBBRECHT, 2003, The Snowflake, p.81, writes the following :
The most dramatic example of a capped column with competing plates occurs when the plates develop dendritic branches. [ Dependence on ] Diffusion causes the branches of one star to compete fiercely with the corresponding branches of the other, in yet another manifestation of the branching instability.
The competition between branches can produce a split star crystal. It starts on the ends of a small column, where two stellar crystals begin growing and branching. The scene soon becomes one of six growth races -- each of the six arms of one stellar crystal [ i.e. one plate of a (capped) crystal ] compete with the corresponding arms of the other. Eventually the six races prodice six separate outcomes. If the winning arms are from different ends of the column, then we have a split star.
Many of these bizarre morphologies, such as asymmetric capped columns or split stars, are not all that unusual. If you look at a typical snowfall you will probably see a substantial number of these forms. These special types reveal a great deal about how snow crystals develop [ like the latter in turn instruct us well about the crystallization process in general ].

Figure above : Stellar construction
This crystal began as a small capped column -- two plates joined by a thin column. As the plates competed for water vapor, the arms of the plates raced for dominance. Two arms from one plate and four from the other were the eventual victors. These winning arms grew into a stellar dendrite, while the defeated arms were left behind. The crystal broke apart (i.e. its axle broke) when it hit the collection board.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : Split plates.
If the growth does not produce branching to make a stellar crystal, a snow crystal can end up with split plates. [As could be implied by the Figure, we have two incompletely developed hexagonal plates connected by a short (hexagonal) column].
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
Twinned snow crystals revisited : Twelve-fold snowflakes
Earlier we spoke about twinning in snow crystals. Here are some other examples. Because they involve angles of 300 between adjacent equivalent structures, and in this way implying 12-foldness, which is impossible in crystals, we expect this to be the result of twinning (which indeed often increases the symmetry).
About these LIBBRECHT, Ibid., p.86, writes the following [comments of mine between square brackets] :
Twelve-sided [ I prefer the term "twelve-folded" ] snowflakes are one of nature's fascinating anomalies. Occasionally the process of turning a cloud droplet into a nascent snow crystal produces an unusual columnar twin consisting of two ordinary columns connected with a 30-degree twist, a variation of the 60-degree twinned column [ that we saw earlier ].The next Figures show some twelve-fold snow crystals.
When a 30-degree twin column moves to -150 C (50 F), it grows two end plates that each follow the crystalline structure of their respective underlying columns [ These crystalline structures only differ in orientation ] , resulting in two separate six-branched plates rotated relative to each other. If the branches of the two plates are narrow, then after they grow out a bit, the tips are separated from one another. The separated branches do not compete with each other as vigorously as do the branches of a normal capped column. All twelve can then grow in a relatively normal fashion, creating a double star. Sometimes these look like symmetrical twelve-sided snowflakes.
I call this a snowflake, and not a snow crystal, because the whole structure is made of not one distinct crystal, but two. Although they are not common, twelve-sided snowflakes can be found if you keep your eyes open. Their abundance is not random. Some storms produce a fair number of twelve-sided specimens, whereas other storms produce almost none. No one knows why.

Figure above : A twelve-fold snow crystal.
It is in fact a twin, consisting of two single-capped columns, rotated 300 relativ to each other.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : A double star.
How did this constellation form? It's unlikely they collided in midair, since both exhibit rare sectored-plate extensions. The stellar pair probably started out as a twelve-fold snowflake in which the two stars were connected by a thin axle, as in a normal capped column. The 30-degree twist left room for both stars to develop independently, without a strong competition between the arms. Then at some point the axle broke and the assembly collapsed into the configuration you see here.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : A twelve-fold snow crystal.
Also here, the crystal is in fact a twin, consisting of two single-capped columns, rotated 300 relativ to each other.
Sometimes the centers of teh two stars do not exactly coincide, as in this example.
As we can see from the photograph, all the twelve branches are of the same morphological type. There is, however, a small, but systematic, difference between the two : The tips of the branches of the star that lies behind the other one are slightly broader than those of the front star. And because the two stars are very close together, as evidenced by the almost equal focusing, this difference can certainly not be accounted for by environmental differences (because then the environment would, at the time of the formation of this crystal, be itself 12-folded in some respect). This means that the two stars are more or less independent. We have here in fact two crystals (connected by twinning) that each follow its own slightly different branching morphology. Maybe the slightly acentric connection also has to do with twinning.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
The next Figure shows a capped column that is a twin. Here, however, we cannot decide whether the twinning is according to a 30-degree twist (giving rise to double stars), or to a 60-degree twist.

Figure above : Capped-column snow crystal. Around the middle of the column one can see (with sufficiently high brightness setting of the monitor) an evaporation groove, indicating that the crystal is a twin. If the twinning is according to a 30-degree twist, then a twelve-fold crystal will result (And because in all these cases there is in fact no genuine 12-foldedness of a crystal involved at all, but a twinning of two six-fold crystals, a 30-degree twinned capped column with branching plates can better be called a double star).
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)
The next document continues the discussion of special features of sterrocrystals, still using snow crystals as examples. Special attention will be devoted to triangularity in snow crystals.
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-19.