

(Takes a little while loading the images)
e-mail :

This document (Part XXIX Sequel-33) further elaborates on, and prepares for, the analogy between crystals and organisms.
Sequel to morphological development of dendritic ice crystals. Sectored Plates.
Growth Centers in Snow Crystals.
Before discussing the morphology and genesis of Sectored Plates in snow crystals we first must talk about the possibility of more than one growth center in a single snow crystal.
In the previous document we discussed distorted ice hexagons, either as isolated single crystals or as substructures in one and the same individual snow crystal. There we let such hexagons develop from a given growth center, which in fact means that we cannot discover the growth center -- and on the basis of this determine the relative growth rate rosette -- of such a distorted hexagon simply by studying the geometry of its extant faces (for example by reconstructing a regular hexagon on which the distorted hexagon was supposed to be based, and then finding the growth center of the latter by determining the location of the center of the regular hexagon), because if we do so, we already presuppose what the relative growth rates of the faces of the distorted hexagon are. So in order to find the distorted hexagon's rosette of relative growth rates, which can be found on the basis of the location of the growth center, we must proceed in a different way. We must find the growth center of the distorted hexagon (present as shovel in a crystal) by investigating morphological and geometrical features of that hexagon, for example how (morphologically and geometrically) it is attached to the rest of the crystal. And, having thus determined the location of the growth center of the distorted hexagon -- which lies at a different location as does the growth center of the crystal-as-a-whole to which the distorted hexagon is attached (in a crystallographically continuous way) -- we can find the rosette of relative growth vectors, by drawing lines departing from the growth center and ending up perpendicularly onto the distorted hexagon's faces or their extensions (when a line falls beyond the face actually developed).
We will now demonstrate that more than one growth center can indeed exist in branched (snow) crystals.
Normal crystal faces, for example the six faces of a plain ice hexagon (a six-sided ice tablet without branches or any other extensions) grow away from the geometric center of such a crystal. Judging from the morphology and geometry of the ice hexagon, this center can legitimately be considered to be the growth center of the crystal. It is its very origin.
But because in snow crystals, that grew with branching and faceting, we see, at many places in the crystal, faces that grow, not away from this center, but (obliquely) toward this center (see next Figure), such faces, evidently, cannot be considered as the result of growth from this center as their origin. They have grown, instead, from other growth centers in the crystal.

Figure above : A snow crystal having grown in branching as well as in faceting mode (first branches, then faces). We see many distorted hexagons (crystallites) with clearly developed faces (perpendicular to the plane of the photograph, and seen as lines). Many of these faces do not grow away from the center of the crystal, but (obliquely) toward it. Two of them are explicitly indicated.
So it is certain that in branched snow crystals there can, in addition to the main growth center (the geometric center of the crystal-as-a-whole), exist other, that is, secondary, growth centers in the same crystal.
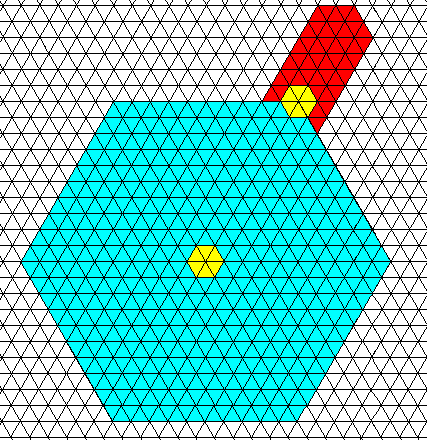
Figure above : Model of the two-dimensional aspect (perpendicular to the c-axis) of a hexagon-shaped snow crystal based on a hexagonal net.
The small central part the hexagon can be interpreted as representing the growth center of the crystal-as-a-whole, that is, the primary or main growth center.
At one of the hexagon's corners there is another growth center, a secondary growth center (in real snow crystals such a second center [and all what it entails] is repeated six times around the crystal). From this secondary growth center a crystallite has grown (red). It turns out to have the shape of a distorted hexagon (all 1200 angles preserved), that is, a partially developed elongated hexagon, crystallographically continuous with the rest of the crystal.
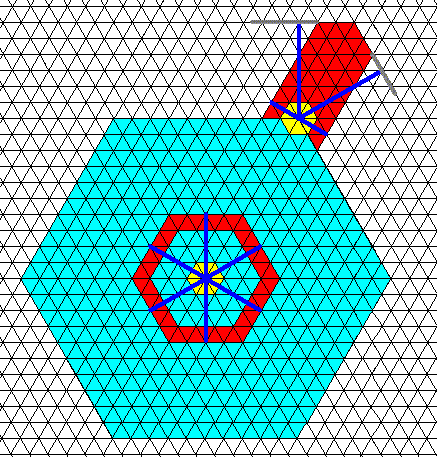
Figure above : Same as previous Figure.
Rosettes of actual relative-growth vectors added.
Each growth center is associated with a rosette of relative-growth vectors. That is to say, we can, after the whole crystal has been formed, or after the crystallite (such as a distorted hexagon) has been formed at some location in the (branched, or incipient branched) snow crystal, draw lines starting at the growth center and ending up perpendicularly onto a developed face or extension of it. The set of lines, so obtained, we call the Rosette of Actual Relative-Growth Vectors. It indicates the pattern of relative growth and directions, of actually developed faces, that is, the relative lengths of the lines indicate the relative growth rates of the developed faces to which the growth center belongs, while the direction of growth is indicated by the direction of these lines.
We see a rosette of actual relative-growth vectors which (rosette) belongs to the main or primary growing center (that is, the growing center of the snow-crystal as a whole). The absolute length of the lines of this rosette is arbitrarily chosen (we could also have them extended to the edge of the crystal). What they should, and indeed do, express is only the relative-growth pattern and directions.
In addition to this primary rosette we see another rosette at one of the corners of the hexagon. It is the rosette of actual relative-growth vectors belonging to a secondary growth center. We clearly see that the pattern of relative lengths of the lines of this rosette is different from that of the rosette associated with the primary growth center of the crystal. Their directions, however, are exactly the same (indicating crystallographically continuity between the crystallite and the rest of the crystal). The different lines of the secondary rosette indicate direction and relative growth rates of the faces of the crystallite (having itself the shape of an elongated [partially developed] hexagon) that has grown from the secondary center at one of the corners of the hexagon. Of course also here the lines of the rosette are obtained by starting them out from the growth center of the crystallite and letting them land perpendicularly onto a facet or its extension. The difference of the length of the lines of the secondary rosette indicate a difference in the relative growth rate of the facets of the crystallite.
So while the relative growth rates of the actually developed faces of the initial hexagon-shaped snow crystal were equal (indicated by the relative-growth rate rosette of the primary growth center), the relative growth rates of the actually developed facets of the crystallite have changed (indicated by the relative-growth rate rosette of the secondary growth center of the snow crystal, that is, the growth center of the crystallite that grows from the snow crystal. Two examples from real snow crystals are presented in the next two Figures.

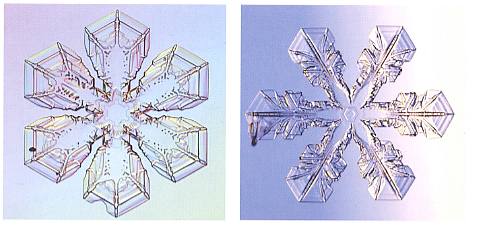
Figure above : Snow crystal having the form of a regular hexagon, that is, initially it was a regular hexagon. Subsequent appearance of six new growth centers at the corners of the hexagon, resulted in six more or less distorted, partially developed, small hexagons.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004)

Figure above : A snow crystal having the form of a regular hexagon with shovels (elongated hexagons) at its six corners, indicating six new growth centers.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004)
It is also possible that several new growth centers appear one after another on the same branch (and, generally, being then repeated six times) :
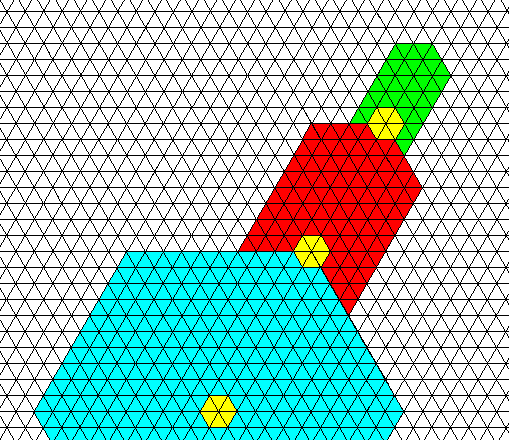
Figure above : A new growth center had appeared, but after this, another one on the same branch appeared with the distorted hexagon (crystallite) determined by it. Each growth center is characterized by its specific location in the snow crystal, and by its specific rosette of actual relative-growth vectors that determines the shape of the crystallite.
A nice example, in real snow crystals, of the subsequent development of growth centers along one and the same branch (and so for each one of the six branches) shows the next photograph. In this case the crystallites are not shovels but sectored plates.

Figure above : A branched snow crystal in which the crystallites are sectored plates.
On each of the six (main) branches three sectored plates have subsequently developed, one after the other. They correspond to three secondary growth centers (so in all we have 18 secondary growth centers present in the crystal).
Sectored Plates
In many snow crystals we see so-called sectored plates. These are crystallites of a certain nature developed on the branches of a snow crystal. Just as in the case of the appearance of shovels, they are the result of predominantly faceting growth, setting in after a period of (predominantly) branching growth. We have discussed these structures already earlier, but here we go deeper into their genesis and morphology. Let us first depict some real snow crystals possessing such sectored plates.

Figure above : A snow crystal with sectored plates developed on its branches.
(After BENTLEY, W., Snowflakes in Photographs, 2000 (1962, 1931))

Figure above : A snow crystal with sectored plates developed on its branches.
(After BENTLEY, W., Snowflakes in Photographs, 2000 (1962, 1931))

Figure above : A snow crystal with sectored plates developed on its branches.
(After BENTLEY, W. & HUMPHREYS, W., Snow Crystals, 1962 (1931))

Figure above : A snow crystal with sectored plates developed on its branches.
(After BENTLEY, W. & HUMPHREYS, W., Snow Crystals, 1962 (1931))

Figure above : A snow crystal with sectored plates developed on its branches.
(After BENTLEY, W., Snowflakes in Photographs, 2000 (1962, 1931))

Figure above : A snow crystal with sectored plates developed on its branches.
(After LIBBRECHT, K., The Snowflake, 2003)
(Photography by Patricia Rasmussen)

Figure above : A snow crystal with sectored plates developed on its branches.
Here the structure of a sectored plate is very clearly displayed. It consists of a median ridge which is the extension of the main branch, two symmetrically placed conspicuous lateral ridges, and, more proximally, two more lateral ridges, which often are less prominent. Between these ridges vertical prism faces have extended themselves. The growth of these prism faces can be seen by the parallel and smooth elevations extending between the ridges. The finally developed vertical prism faces are seen as lines connecting the tips of the ridges. The ice areas between the ridges correspond to the basal prism faces (that is, top or bottom face of the ice prism). It is the nature of the ridges that distinguishes sectored plates from shovels, as we will see below.
(After LIBBRECHT, K., The Snowflake, 2003)
(Photography by Patricia Rasmussen)

Figure above : A small sectored plate has been developed onto a snow crystal (and then repeated around the crystal).
(After LIBBRECHT, K., The Snowflake, 2003)
(Photography by Patricia Rasmussen)

Figure above : Sectored plates are developed on the unequal branches of a snow crystal.
(After LIBBRECHT, K., The Snowflake, 2003)
(Photography by Patricia Rasmussen)

Figure above : Artificially grown snow crystal with subsequently developed sectored plates on each branch.
This designer snowflake's pattern was determined by controlling the growth conditions. It was grown on the end of an ice needle that is out of sight directly behind the crystal. Tip to tip, the crystal is about 1.5 mm (0.06 inches).
(After LIBBRECHT, K., The Snowflake, 2003)

Earlier we discussed shovels, that is plate-like extensions (crystallites) generally having the shape of an elongated hexagon. Each one of these crystallites has its own (secondary) growth center with its rosette of actual relative-growth vectors determining the shape of the crystallite.
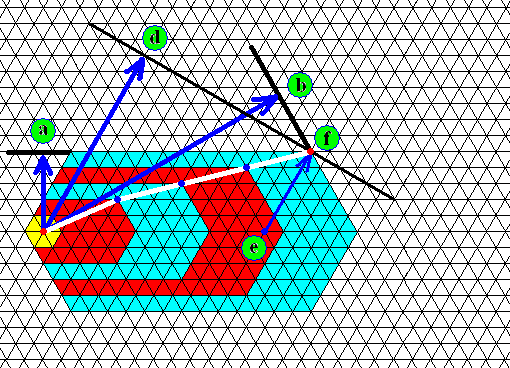
Figure above : Model of a shovel, given earlier (previous document). The lines associated with a and b belong to the rosette of actual relative-growth vectors of the shovel's growth center. The line e-f (and its symmetrical counterpart) is often developed as a side-ridge of the main ridge. The curve going from the growth center to f is, in shovels, not developed as a ridge, or, more generally, it is not present as some structure. So a shovel generally looks like this :
Figure above : Model of a shovel attached to a main branch, showing its ridges.
The ridges of the shovel involve 600 and 1200 angles, and are (thus) completely compatible with the crystal lattice.
Sometimes the side-ridges are not at all developed in shovels (at least not in the non-terminal shovels), as can be seen in THIS snow crystal . And also this feature (this absence of side-ridges in a lateral shovel) is then everywhere evident throughout the crystal.
Because of the compatibility of the ridges of a shovel with the crystal lattice, we will call them structural ridges.
They are not lines that just separate actually developed (slow-growing) facets. They are intrinsic structures of ice crystals, intrinsic as to their directions. With a terminal, that is, apically placed, shovel the stage is set for the further development of the branching system of the snow crystal, namely by the extension of these ridges. See next two Figures.

Figure above : A shovel (elongated hexagonal crystallite) is formed at the end of each main branch of the snow crystal. Here the structural ridges of the shovels (one median ridge and two side-ridges making angles of 600 with the median ridge) are clearly visible.
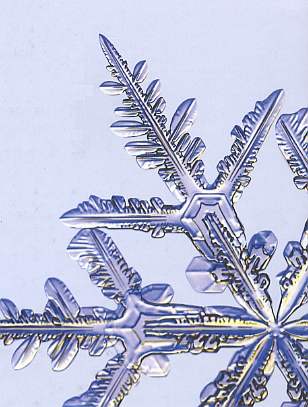
Figure above : Part of a branched snow crystal. Here we can see that at first a shovel was formed at the end of each main branch of the crystal. By extending their structural ridges (which here are only weakly developed, or at least poorly or not at all visible), these crystallites are involved in the further development of the branching system of the crystal.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004)
In other crystallites, however, we see, apart from the median ridge, ridges of a different nature. They follow a course as does the white curve in the above Figure . These ridges, if actually present as ridges, are not intrinsic structures of ice crystals (while the median ridge is such a structure). They record the history or lifeline of some individual ice crystal or of a part of it, and I call them history lines. The exact course of this 'history' (that is, the history of the crystal or of one of its parts) is not intrinsic for ice, but is the result of local environmental conditions.
The just mentioned impossibility of the conditions being different from one facet of a crystallite to another (adjacent facet of that same crystallite), is, of course, only true for the case of terminal (that is, apically placed) crystallites (often so placed in the case of shovels, and probably without exception so placed in the case of sectored plates), that is crystallites sticking out well into the nutrient environment because developed at the end of the six main branches of the snow crystal, or from the six corners of the ice hexagon (as the most recent structures developed from these corners). Here, indeed conditions cannot differ as we go from one (apical) facet to another of the same crystallite.
But when we consider a crowding of many crystallites inside a snow crystal as the one depicted earlier (see HERE to see it), we can expect small-scale but significant differences in, for example, the local supply of nutrient material (water molecules) to the surfaces of the crystalline structures already present, resulting in a difference of the length of the facets of any one individual crystallite, and in a difference of the shapes of the crystallites when compared with each other.
The angles involved in the history lines of sectored plates are often close (if not, equal) to 600, which could result in a difficulty to distinguish them from shovels. But somehow they look different, despite the fact that also the ridges (history lines) of sectored plates can (like the ridges of the shovels) become extended and in this way give rise to the extension of the branching system of the crystal.
It seems that when a ridge makes an odd angle with the longitudinal axis of the plate, it causes a change in the growth-rate ratio of the adjacent facets. Or is it the other way around? We will address this question below.
If we talk about crystal faces having grown fast or slow, we should not see these faces (or facets) as individual entities that go their business all by themselves : Normally, different faces (or facets) are not as such distinguished in the interior of a crystal (or crystallite), especially when it was allowed to grow slowly, that is, we don't see faces there. It is only a matter of different growth rates in different directions of one and the same crystallizing substance. Only at the outer edge of the resulting crystal, or of the crystallite, these different growth rates manifest themselves as different faces or facets.
Analysis of the snow crystal depicted in LIBBRECHT (The Snowflake, p.75) and reproduced here.
In his book The Snowflake LIBBRECHT shows a photograph of a crystal, that at first sight looks puzzling with respect to its morphology :

Figure above : A snow crystal with some form of sectored plates developed at each of its straight main branches or ridges. For a blow-up of a part of it click HERE (if necessary, click on the image to see it in full size).
(After LIBBRECHT, K., The Snowflake, 2003)
(Photography by Patricia Rasmussen)
For an understanding of what has actually happened when a snow crystal has developed sectored plates on each of the six main branches (themselves developing along the six directions of intrinsically fast growth), an analysis of this remarkable snow crystal could be revealing, but is at the same time also a challenging case for the ice morphologist.
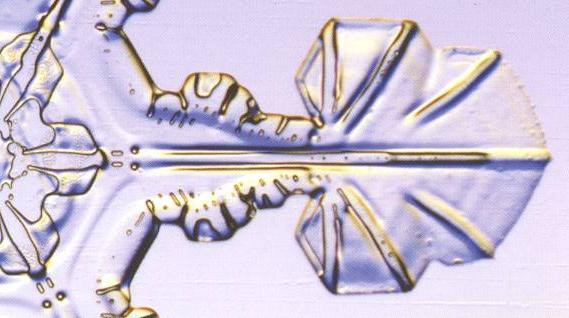
Figure above : A branch of a snow crystal with two successively developed sectored plates. Compare with our crystal under investigation . Clearly we see a smaller sectored plate grown on top of another larger one.
(After LIBBRECHT, K., The Snowflake, 2003)
(Photography by Patricia Rasmussen)

Figure above :
A branch of a snow crystal with two successively developed sectored plates.
(After LIBBRECHT, K., The Snowflake, 2003)
(Photography by Patricia Rasmussen)

Figure above :
A snow crystal with two successively developed sectored plates on each branch.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004)
In these crystals we clearly see a second sectored plate grown on top of a first one. So while the first sectored plate originated from a secondary growth center, the second sectored plate (on the same branch) developed from a new secondary growth center originated a little farther up along the branch of the snow crystal. This has happened on all six branches of the crystal, in all resulting in 2 x 6 = 12 sectored plates.

Figure above : A snow crystal, that could represent the type of crystal from which the crystal under investigation can be derived morphologically.
or (looked initially like) some of the earlier depicted crystals. To see these crystals, click HERE and HERE . Then, on top of the initially developed sectored plates a second one developed by virtue of a second secondary growth center that came to lie on the same branch.
The concept of the formation of secondary growth centers in one and the same snow crystal is crucial for this interpretation (As we have indicated earlier, also shovels can develop second shovels on top of them in virtue of the formation of a second growth center, after the first [secondary] growth center, farther up the branch. See HERE for an example [the roundings we see there are the result of evaporation] ). In this way all the many crystallites of a single given branched snow crystal originate. And all of them are crystallographically continuous with each other and with the snow crystal as a whole. The next Figure (already given earlier) shows that even three sectored plates can grow on top of each other, that is, successively develop along one and the same direction, and thus all having the same orientation. To see it click HERE (if necessary, click on the image to see it in full size). However, it cannot be ruled out that at least the most proximal 'sectored plate' in reality consists of two laterally oriented sectored plates (which is as remarkable and as interesting anyway).
Why do these secondary growth centers (whether in the case of sectored plates or other cases) appear?
As we know, snow crystals develop branches, side-branches and side-structures (crystallites) in order to cope with the large energy well they represent as a result of prevailing high supersaturation levels : They grow in such a way that their surface of contact with the environment will increase rapidly to ease the energy discharge. So the development of secondary growth centers is part of the snow crystal's strategy to realize as large an energy discharge as possible per unit time. These secondary growth centers originate at points in the crystal that stick out well into the nutrient environment. These points can be the corners of hexagons, or randomly appeared ice bumps on branches. It results in the extension of existing branches, development of side-branches, and, when the conditions are such that faceting still plays a role (together with branching), the development of crystallites.
The origin and development of sectored plates.
" If the Lord Almighty had consulted me before embarking on Creation, I should have recommended something simpler."
- Alphonso the Wise (1221 - 1289)
But, "Never make anything simple and efficient when a way can be found to make it complex and wonderful."
- Unknown
Very often, if not, always, a sectored plate is observed to originate from a pre-existing terminal shovel, as can be seen in the many photographs depicting snow crystals with sectored plates. We show two of them, both after BENTLEY & HUMPHREYS in Snow Crystals, 1931, 1962 :


Especially they develop from terminal shovels possessing a median and two lateral ridges (the latter making angles with the former of 600 ) :

Figure above : Model of a terminal shovel, that is a shovel whose main axis is the extension of a main branch, or a shovel that is directly attached to a corner of the initial ice hexagon (blue) and whose main axis is the extension of the line connecting the center of the initial ice hexagon with that corner. The shovel has developed three ridges (brown), all compatible with the crystal lattice. Its growth center indicated (yellow).
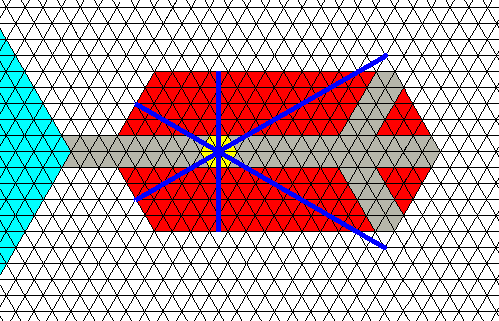
Figure above : Same as previous Figure. The rosette of actual relative-growth vectors of the shovel's growing center (yellow) added.
I assume that sectored plates, when originating from a pre-existent shovel, can do that in several ways. One way is that a new growth center appears at the tip of the shovel (or on the tip of an extension of its median ridge) :

Figure above : A new growth center (green) appears at the tip of the shovel. This growth center will give rise to a (terminal) sectored plate.
The next Figure depicts a possible first stage in the development of a sectored plate on the basis of this pre-existent shovel.

Figure above : Around the pre-existent shovel (red) the first stage (blue) of a sectored plate has been completed. At the left the structure has not developed facets because of diffusion problems (this is because on both sides of the structure the same such structures develop nearby). The growth center of the sectored plate is indicated by a white spot (earlier indicated with green). If we draw lines from this center perpendicular onto the four new facets we obtain the rosette of actual relative-growth vectors of this growth center. The three ridges of the shovel have been carried along with the growth of the structure. In the Figure the beginning of the curvature of the two lateral ridges, that is, their angles becoming odd, is shown. It is shown rather crudely because we have so strongly magnified the lattice. The change of direction of the course of these ridges indicates a change of the rosette of actual relative-growth vectors of the growth center of the sectored plate. Often the first stage is marked by a border, either in the form of a weak lining or in the form of a more or less pronounced ridge.
This phase or stage of the development of the sectored plate can be seen on page 130, image 10 in the book Snow Crystals of BENTLEY and HUMPHREYS, and reproduced here :

It can also be seen in the following snow crystal, depicted by LIBBRECHT in the book The Snowflake and reproduced already earlier :
In the latter photograph we can clearly see the lining-off of the first stage, and the beginning of the third phase. This beginning of the third stage is modelled in the next Figure. To see it click HERE (if necessary, click on the image to see it in full size).
The next Figure shows further growth of this sectored plate. See it (and read the subscript) HERE (close window to return to main text).
The development of our sectored plate can stop here. But it can also develop further. Its end-state is then a large more or less elongated sectored plate. To see this end-state in a real snow crystal (already depicted above) click HERE . To preview how the model will develop, I first present two reductions of the large Figure to come. These reductions are not a precise diminution, but only serve to give an easy orientation of the subsequent large Figure.
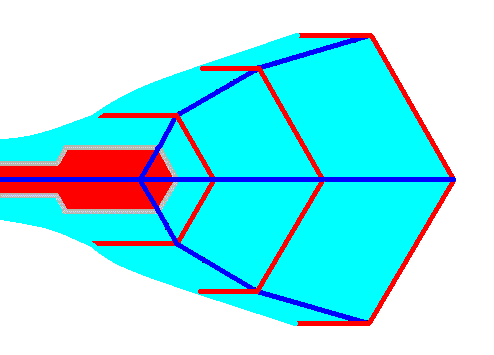
Figure above : A more or less fully developed sectored plate. The plate's history lines are indicated (dark blue) : two lateral ones and one median. In many sectored plates two lateral (but less conspicuous) history lines are developed more proximally in addition to the mentioned ones. Three stages of development of the sectored plate from a (terminal) shovel (red) are shown.
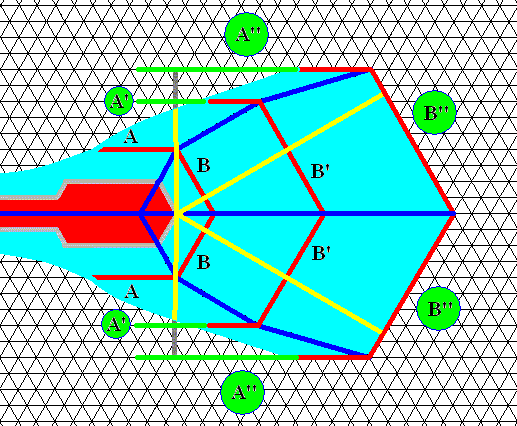
Figure above : Same as previous Figure. The network of lines outside the structure can serve as lines of orientation, especially in regard of the angles.
Two morphological types of facets are developed : A, A', A" and B, B', B" .
All these facets are crystallographically equivalent (so they represent only one crystallographical type).
From the growth center of the sectored plate radiate the vectors (yellow) of actual relative-growth rate. Together they form the rosette of actual relative-growth rate vectors of that growth center. Each vector originates in the growth center and lands normal to the facet or its extension.
The next Figure gives this further development in terms of our large model. To see it click HERE (if necessary, click on the image to see it in full size, and close window to return to main text). The image does not yet represent the end state. On further growth the lateral ridges will continue their bending toward the median ridge till they, finally, come to end up at nearly 900 to the boundary of the crystal (see the just mentioned photograph).
The next Figure indicates the (changing) rosette of actual relative-growth vectors for three stages of the sectored plate's development. The rosette is about developed facets, and in the Figure only one half of it is depicted because the other half is identical. What it expresses is the relative growth rate of two adjacent facets of the sectored plate. To see it click HERE (if necessary, click on the image to see it in full size, and close window to return to main text). Each vector starts at the growing center of the sectored plate and ends up perpendicularly to the facet.
From the relative length of the vectors of the facets A and B (facets of the first stage) we obtain the relative growth rate of these facets (that is, how fast they grow with respect to each other).
From the relative length of the vectors of the facets A' and B' (facets of the second stage) we obtain the relative growth rate of these facets.
From the relative length of the vectors of the facets A'' and B'' (facets of the third stage) we obtain the relative growth rate of these facets.
That is we get three ratios belonging to three successive stages of development of the sectored plate :
Metaphysical analysis of branched snow crystals (and crystals in general).
As we can see in all the photographs of branched snow crystals, crystals that is, that were allowed to develop undisturbedly, we invariably find six-fold symmetry : Seen from above, that is, along the crystal's c-axis, we see a symmetry according to the point group D6 (crystallographically denoted by the symbol 6mm).
At first sight this is not remarkable : We just expect such crystals having 6mm symmetry.
It is, however, remarkable.
In Part XXIX Sequel-3 we discussed the difference between crystallographic symmetry, morphological symmetry and intrinsic shape of a crystal, and found that the faces of a crystal (grown in uniform conditions) are not morphological units, because they just represent the direction of certain atomic aspects as they are presented to the growing environment. And these aspects are not unique, because they are translationally repeated throughout the crystal (i.e. such an aspect has parallel copies of it in the crystal). The number of their copies is thus not limited and thus not definite. As they are (translational copies), their number could well be infinite, that is, their number could well approach infinity. Therefore they are not morphological structures of the crystal.
A genuine morphological structure in a crystal on the other hand -- such as an arm of a snow crystal -- is also repeated it is true, but it is not repeated translationally, but only rotationally and reflectionally, which implies that the resulting number of copies is limited anyway, and indeed limited to a small number, because of the rotational restrictions in periodic structures ( There, only 1-, 2-, 3-, 4-, and 6-fold rotation axes are possible), which in turn limit the number of non-parallel reflections.
If necessary, the reader should consult the mentioned document (Part XXIX Sequel-3) for a good understanding of all this.
The intrinsic six-fold point symmetry of snow crystals is just the point symmetry of the ice-crystal lattice (that is, the lattice has six-fold point symmetry), and nothing more. This symmetry -- as seen along the c-axis -- means only that there are six directions of intrinsically fast growth, and six other directions of intrinsically slower growth (and these directions are lines, it is true, but lines with no particular origin). The only way this symmetry will macroscopically manifest itself is when an ice crystal has grown, not too fast, in a uniform medium and under uniform conditions : The result is then a hexagonal prism or tablet. Seen along the c-axis we see a regular hexagon : six equal sides and six equal angles between them. And that is all that is macroscopically manifested. And, as has been shown, these are not (macroscopic) structures. Also inside such a crystal we see no macroscopic structure. There the crystal is macroscopically homogeneous.
From all this it is clear that the intrinsic symmetry of an ice crystal (or any other crystal, not belonging to the Asymmetrical Class of the Triclinic System for that matter) does not imply or demand that macroscopical morphological structures must be repeated by means of reflection or rotation, and thus, for the present case -- ice crystals -- be repeated six times around an axis and reflected in mirror planes. Even totally distorted ice crystals still have this intrinsic six-fold symmetry as long as their lattice is undisturbed. So what is demanded is that in uniform conditions the growth rate of crystallographically equivalent faces is equal, or, in other words, the intrinsic growth rate of crystallographically equivalent faces is always equal. They can become unequal (but still remaining intrinsically equal) when the supply of material is better at one growing face than at the other (crystallographically equivalent) face. The result then is, generally, a morphologically distorted crystal.
But in many snow crystals we nevertheless find a macroscopic morphological structure being repeated six times around an axis. All the branched snow crystals, that have grown and fallen more or less undisturbedly, show this. The morphology of the six arms is always the same, that is, in most cases a given morphology of an arm is repeated fairly accurately and often in great detail around an axis (which is then the main axis of the crystal). The snow crystal of the next Figure (taken from LIBBRECHT, The Little Book of Snowflakes, 2004) shows this convincingly. Even very minute details of the crystal or its etch figures [resulting from evaporation] are so repeated. To see it, click HERE (If necessary, click on image to see it in full size).
How can this be?
A branched crystal having shovels, sectored plates, or other flat structures, grows in a mixed mode, that is it grows by a mixture of branching and faceting (or in one mode after another). We could suppose that when a snow crystal develops in virtue of some determined (that is, some given) mixture or ratio of branching- and faceting- growth, a specific morphological type of crystal will be the result, while another mixture or ratio of branching- and faceting- growth results in another morphological type of crystal. And because there are so many possible ratios of branched and faceting mode of developing, we can expect an enormous diversity of resulting morphological types of snow crystals, which indeed there seems to be, that is to say, with each determined ratio of branching and faceting growth (determined by temperature and humidity) there is expected to exist one resulting corresponding morphological type of crystal, especially because the morphological development of a branched crystal (that is, a crystal developing under high levels of supersaturation) is very sensitive to changes of conditions.
However, against this supposition speaks the fact that the number of morphological types of snow crystals is relatively limited, albeit still large (See the Classification of snow crystal below ). It seems that when the conditions are such that there is a given determined ratio of branching and faceting growth (I mean just any definite ratio), the balance between (1) the resulting branching- or dendritic- aspect and (2) the faceting aspect, that is, the balance between resulting branches and facets, can be morphologically realized not in one, but in several ways, and so allowing for several different morphological types to result, determined by this one ratio, for example, sectored plates in one such case, and shovels in the other. We can imagine that a given 'density' of facial aspect and of dendritic aspect can still configure themselves in many ways without altering this ratio. So a definite condition of temperature and humidity, implying a corresponding ratio of branching and faceting, is not enough to fully determine the morphological type of snow crystal that will ensue. So to produce such a type there is, in addition to the mentioned conditions, another factor involved. And that factor clearly is a degree of randomness : The different morphologies of arms of different, but still morphologically very similar snow crystals must be the result of the presence of randomly distributed ice bumps on the structure of a developing snow crystal. And these random distributions must be different in different snow-crystal individuals. The fast growth of branched crystals lets these bumps increase in size rapidly. Side-arms and other side-structures come into being by this process. And on these new structures new random ice bumps appear, which also will increase rapidly, etc. In this way, and under conditions that correspond to some ratio between branching and faceting, a fully-fledged branched snow crystal will result . . . well, in fact, not a snow crystal, but only one arm and its morphology. That is, we have (roughly) explained the morpholgy of such an arm, that is, a single arm. But precisely the fact that randomness is supposed to be a very important factor in determining the resultant morphology of the arm, we would expect the other five arms of the same crystal to be different, at least in many details and also in grosser features. And this is definitely not so! As has been said and shown many times, the arms of a given snow crystal are very similar, if not, identical.
This means that the total set of features, as held by all six arms of a branched snow crystal cannot, insofar as they are repeated, be the result of randomness, and thus the total morphology of a branched snow crystal cannot (up to date) be explained by a combination of temperature and humidity conditions and a degree of randomness.
There must still be other factors involved, for example quantum mechanical factors like wave or vibration phenomena, resulting in the fact that there is communication throughout the crystal, for example : one arm 'knows' what the others (in the same crystal) are 'doing'. Therefore the crystal can adjust things (as we have seen in regeneration phenomena), and generate, restore and maintian a six-fold symmetry not only microscopically, and not only by showing six equal sides and six equal corners, but also (a six-fold symmetry) with respect to complicated macroscopical structures (such as arms) that are copied according to this symmetry ( Of course, it is not so that first one complete arm develops, which is then copied six times. The copying swings to and fro between the developing arms).
This brings (macroscopic) form or shape to the focus of our attention (where "form or shape" means : form in the sense of shape, or : macroscopic structure, such as the morphology of an arm of a branched snow crystal. In the present context we will often use just the single term "form" or the single term "shape").
Form or shape have their own share in determining things, in addition to that of thermodynamics. Said differently, it is not only thermodynamics that determines things : forms and shapes determine as well. It is generally the case that the matter and energy of which things are composed have the potential to be present in many different forms or shapes, and so these forms cannot be fully explained just in terms of their material constituents and the energy within them, because indeed different forms can be made from the same kind and amount of material and energy. The form seems to be something over and above the material components that make it up, but at the same time it can be expressed only through the organization of matter and energy.
A branched snow crystal is unstable, not immediately by virtue of its shape (or form), but only because its shape happens to be such that the surface area is large with respect to its volume (entailing a large amount of surface energy in the form of dangling [that is unsatisfied or distorted] chemical bonds). When conditions become more relaxed (low humidity, that is, a low level of supersaturation) the crystal will change its present branched light form or shape into a more compact form or shape, not because of this shape, but because such a compact and contracted form has a smaller surface area with respect to its volume and is thus more stable. So thermodynamically it is this relative surface area that counts (with respect to stability). A large relative surface area of a crystal carries a large energy cost so that such a crystal is thermodynamically unstable, regardless of the particular form or shape such a crystal possesses. So thermodynamic stability or instability is indifferent as to the particular form or shape of the crystal as this form is in itself : different forms or shapes can have the same ratio of surface area to volume. And this same ratio determines the thermodynamic stability or instability. So the energy household of the crystal only takes account of the relative surface area, and doesn't 'look' to the particular form that the crystal happens to possess. Another form could entail this same relative surface area.
Nevertheless a branched snow crystal turns out to take its form or shape 'seriously' : It strives to repeat this form six-fold around some axis, while from the viewpoint of its internal point symmetry, and also from the thermodynamic viewpoint, it need not do so, because an externally distorted crystal such that its arms are morphologically dissimilar (but with the same spatial extension and ratio of branching and faceting), still has intrinsic six-fold symmetry as long as its lattice is not disrupted, and still can be thermodynamically unchanged, as compared to the case when the crystal has morphologically similar arms.
So the form or shape, that is the macroscopic morphology of the snow crystal, indeed seems to be a 'quantity' or variable in its own right, independent of the thermodynamics of the crystal. And then we could imagine that, just like a large surface-area-to-volume ratio of a given crystal could make that crystal thermodynamically unstable, a form or shape that is such that it involves differently formed arms (as specified just above) of a single snow crystal, could make that crystal morphologically unstable. And to get stable in this respect is the crystal's intrinsic strife for 6mm symmetry as was mentioned in the previous document.
But how can such a strife be present in a crystal, and how can it be that (macroscopic) form or shape can be a 'quantity' in its own right, or even a determining agent? And what about the priority of the whole above its parts that seems to be implied by this view of form?
In order to deal with these (interesting) problems we must consider the metaphysics of crystals, that is, their way of being as substances (in the metaphysical sense), and the way of being of their intrinsic properties. This we have already done (to begin with) in First Part of Website, namely in the document Crystals and Metaphysics in the first Series of Documents (Non-Classical Series). A crystal is a substance in the metaphysical sense, which means that it is -- like an organism -- an intrinsic being, that is a being which is a unity and carries the cause of its what is it? , that is, its essence, within itself. Such a substance then is a continuum because it is absolutely and intrinsically one whole. A genuine continuum has no actual parts. Its parts are not totally non-existent but exist potentially (their way of being is that of potential being) : the continuum can be divided into parts. As soon as we've done that, the parts become actual. On the basis of this we would expect that a continuum is totally homogeneous, but this need not be so. When a physical continuum, say a molecule or a crystal, is formed from its elements, these elements -- which were initially present in an actual sense -- become now mere potential albeit still close to actuality. This particular kind of something having only a potential, but nevertheless still close to an actual, way of being, we have called virtual. So when the elements are taken up into the newly formed substance, and thus result in a continuum, they become virtual (and when the compound or crystal disintegrates they become actual again). What does it mean that the elements become virtual as soon as they form a genuine substance? It means that although initially they were more or less independent particles, they now have become, yes, qualities of the substance (not qualities of those particles). So the reticular structure of a crystal, that we see by means of modern high-resolution electron microscopy, is nothing else than the alteration of intensity of some one quality of the crystal, if we go from one region of it to another. And thus a crystal does not consist of a(n ordered) collection of particles, but of a qualitative pattern. While many so-called qualities can be reduced to quantity and configuration, and thus their alteration to be a reconfiguration of more or less independent particles, the alteration of a true quality does not involve such a reconfiguration. It is a genuinely variable quality, not reducible to quantity. So the 'parts' of a true substance are not (interacting) particles, but are a spatial (and/or temporal) distribution of qualities in that substance. Unity of substance, plurality of (its) qualities. And from this it is clear that, in addition to homogeneous continua, heterogeneous continua are possible, and actually observed. The (spatial) heterogeneity is the result of the preservation of some properties of the elements which were possessed by them when they were still free, and thus actually existing. These properties are, however, now properties of the one substance (mixtum).
All this had been considered earlier and the reader should, if necessary, consult, in addition to the just mentioned document, the following places of the website :
First Part of Website :
Status Quaestionis (second part of it, concerning P. HOENEN )
Classical Series of Documents :
In what way do the Elements exist in the Mixtum?
Fourth Part of Website ( = present Part of Website) :
Part XXIX Sequel-1 (second half : On the Transformation of the Organic into the Inorganic : The Inorganic as the result of a holistic simplification of the Organic).
Part XXIX Sequel-4 (about virtual existence of elements in wholes, but here in a still wider philosophical context).
Part XXIX Sequel-5 (about the demonstration of a variable genuine quality [Impetus Theory] ).
Part XXIX Sequel-6 (about the significance of snow crystals for ontological theory).
The holistic theories presented in the mentioned documents all try to cope with the clear indications of unity of substance and continuity within each substance. While these features were already acknowledged to be present in organisms, they are now found in crystals as well. Of course this finding strengthens the analogy between crystals and organisms.
The virtual existence of particles in crystals.
In the document In what way do the Elements exist in the Mixtum? (First Part of Website, Classical Series), we wrote about some (verbal) expressions that stated things about a mixtum [or, equivalently, a mixtum perfectum] (which here means, not a mixture, but a chemical compound or a crystal) and its elements (in a most general sense), and about the partial similarity of the mixtum on the one hand, and the elements from which it was formed on the other, in virtue of the conservation of some properties of these elements :
" The conservation of (some) properties of the elements in the mixtum"
Expressed in this way it is a low-level consideration. The corresponding high-level consideration is as follows :
In the mixtum perfectum, once formed, the conserved properties do not originate from a simultaneous presence of the qualities of the elements. The 'average' quality (i.e. how it behaves, and looks like) of the mixtum originates from the (one) Form [in the metaphysical sense] of the mixtum. Nevertheless it displays a similarity with some properties of the elements, in virtue of the 'genetic' kinship of the mixtum and its elements (After all, the mixtum originated physically from the elements). The elements themselves are present [in the mixtum] only in a virtual way (i.e. in a near potency to those elements), so also some of their properties. These properties have now become properties of the mixtum, they are generic propria (i.e. they are properties, typical for a particular genus).
Genuinely new properties of such a real mixtum can be considered as a Totality-resultant.
Precisely such a type of Totality must be demanded, if one assumes that every Substance [in the metaphysical sense] possesses only one substantial form.
End of quotation
How do we experience the virtuality of constituent particles (that is element-particles, or simply elements) in a mixtum when observing it? We will not experiencing it when physically examining a mixtum (Surely, we see the mixtum's element-particles when we let the mixtum disintegrate). This is because when element-particles enter the fabric of a mixtum, that is, form (in the case of molecules and crystals), or enlarge (in the case of crystals) the mixtum, they can undergo, it is true, some physical changes, especially with respect to their periphery, but they remain in such a condition that physically they can (still) be described as particles, bonded to each other in the mixtum. However, they can, at the same time also -- and equivalently so -- physically be described as a distribution of qualities-of-the-mixtum among the regions of that mixtum. This is so because although the element-particles are only virtually existing in the mixtum, they are, nevertheless, as qualities of the mixtum actually existing and thus observable.
If natural science rejects the existence of true qualities (by saying that they all can be reduced to quantity), then such a description (in terms of qualities) is not physical anymore. It is then a metaphysical description. And indeed,
metaphysically, the particles do change as soon as they enter the fabric of the mixtum, that is as soon as they form or expand the mixtum. And they do not do so only with regard to their periphery, they change totally, that is, their way of being changes : From initially being actual, they become virtual, that is, they get into a [metaphysical] state of near potency, 'near' with respect to freely existing, and therefore ontologically independent particles. Said slightly differently : From being ontologically independent particles, and thus each of them being a substance (in the metaphysical sense), they become incorporated into one and the same substance (mixtum) by becoming qualities of that substance.
When a mixtum is formed, we initially see separate particles entering into some definite configuration -- the mixtum. Precisely the transition from ontologically independent particles (substances) to ontologically dependent qualities of one substance (the qualities cannot exist on their own but must exist in a substance that has these qualities), is not observable, because it is a metaphysical transition (not concerning things, but the principles of things).
As a true holon (that is, a true whole) the substance or mixtum resides in the Implicate Order (and is separated there from other such holons only by a difference in specific content). And in virtue of being a holon its 'parts' project into the Explicate Order together : The specific holon, as it resides in the Implicate order, becomes individualized when it projects into the Explicate Order, in virtue of in-forming some physical substrate. And this can be repeated, resulting in a multitude of individuals in the Explicate Order.
Chemical molecules (and thus also crystals) involve chemical bonds. They therefore are subject to quantum conditions, which make them non-mechanical entities. Organisms consist of molecules (and also ions), but these molecules are generally not chemically bonded to each other. So organisms are holons in virtue of a different reason. This reason could be their categorical NOVUM as they possess it as compared with the inorganic beings, that is, their general categorical NOVUM.
All this was more extensively discussed in Summary and Extension of Ontological Theory in Part XXIX Sequel-4 .
In branched snow crystals we see form to be a determining agent, namely there where we see that the crystal takes into account the already developed local patches of morphology and ensures that this morphology will be symmetrically distributed over the crystal. The morphological influencing, or activity of determining, swings back and forth between the growing arms of the crystal. The latter ends up with six very similar arms each expressing a definite morphological type that is repeated six times (and because each arm is itself fairly symmetric according to a median mirror line, we in fact have a structure that is twelve times repeated according to the 6mm point symmetry).
Let us recapitulate some relevant discussions from Part XXIX Sequel-1, Sequel-2 and Sequel-4 in order to understand what precisely the holism is that we find in branched snow crystals. It has to do with the appearance of some categorical NOVUM. For this to understand we must depart from the (general) categorical NOVUM that is found in the Organic Layer of Being with respect to the Inorganic Layer of Being.
Many features in organisms suggest that the original transition from Inorganic to Organic takes place through the appearance of genuine and ontological novelty (and thus not only of some more or less fundamental ignorance of ours), i.e. through the appearance of a totally new category or principle, the categorical novum, as was proposed by Nicolai HARTMANN, in Der Aufbau der realen Welt, 1940. This implies that the Organic is neither epistemologically nor ontologically reducible to the Inorganic, or in other words, the Organic can in no sense (epistemologically or ontologically) be completely derived from the Inorganic, and such a position is called h o l i s m (as the opposite thesis with respect to reductionism mentioned above). This would mean that the Organic could not historically have evolved from the Inorganic. And when we (rightly so) refuse to assume that the Inorganic and the Organic have nothing to do with each other, i.e. when they are contingent with respect to each other, we must assume that the Inorganic has evolved from the Organic, because then we don't have the problem of the NOVUM (especially where it came from, i.e. the problem that it came out of the blue). However, we cannot assume this, because it is certain that the earlier stages of the Earth, and also of the universe as a whole, were entirely inorganic : In those early epochs temperatures were too high to sustain stable complex molecules (and according to recent cosmological theories, the very early stage of the universe could not even sustain stable atoms, let alone complex molecules). So physically, or, let us say, materially, and historically, the Inorganic has not evolved from the Organic. But however this may be, in some way the Inorganic must have been evolved from the Organic, if we are not willing to accept the appearance of a genuine NOVUM. Indeed, when the Inorganic evolves from the Organic, only certain typical aspects of the Organic need to be subtracted to result in the Inorganic. But, as has been just found out, this has not actually happened in the observable world.
And this is precisely where the Implicate Order comes in.
The theory of the Implicate (and the Explicate Order) was extensively discussed in Third Part of Website especially in the first document. So here we will be brief on it.
The Implicate Order, underlying the Explicate Order (which is the observable order within the framework of time and space), is timeless and spaceless. It is a so-called noëtic domain, that is, a purely logical domain in which an analogue of a thinking process is taking place, and from which structures are projected up into the Explicate Order and back again.
Well, the above assumed transition from Organic to Inorganic (such that the organic is always first), cannot, as established above, take place within the physical universe, which we now can translate as such a transition not being possible in the Explicate Order (which latter is -- it is important to realize -- just an aspect of the Whole). But it can take place in the Implicate Order, because a transition from Organic to Inorganic can now be seen as a (logical) d e r i v a t i o n , namely by just eliminating the NOVUM and, (automatically) with it, all that it entails. This we call Holistic Simplification from the Organic to the Inorganic, i.e. the Inorganic is a holistic simplification of the Organic (as was first proposed by MEYER-ABICH, A., in Naturphilosophie auf neuen Wegen, 1948). This simplification is thus a noëtic process, taking place in the Implicate Order in a space- and timeless fashion. The explicitation of this process, i.e. its appearance in the Explicate Order, must take place in r e v e r s e order : namely from Inorganic to Organic, because (as we now assume) the explicate Organic presupposes explicate Inorganic : To become explicate Organic, the implicate Organic needs an appropriate material substrate. This latter substrate must already be present in the Explicate Order and can now be over-formed by the implicate Organic, resulting in explicate Organic. So what we see in the Explicate Order (observable world) is the apparent emergence of the Organic from pre-existent Inorganic, while in fact the Inorganic was derived from the Organic in the Implicate Order by Holistic Simplification.
In this way we have circumvented the problem of the NOVUM, but, of course, at a price of introducing a hypothetical entity, the existence of which must be demonstrated. The hypothetical entity is the Implicate Order, that is, the Enfolded Order (expressing itself observationally by the Explicate Order, that is, the Unfolded Order). Indeed this seems to be a rather cavalier and ad hoc assumption, but in fact this is not so. The theory of the Implicate Order was first proposed by David BOHM in his Wholeness and the Implicate Order, 1980 (and expounded by me in the mentioned Third Part of Website ), and it was inspired by a certain interpretation (the so-called causal interpretation) of quantum mechanics (proposed by BOHM). So we can say that the assumption of an Implicate Order is, in its generality, at least not contradicting quantum mechanics, that is, not contradicting the most fundamental theory of matter.
In Part XXIX Sequel-1 we have exemplified all this with the structural relationships between the Inorganic and the Organic : As we go, in the Explicate Order, from Inorganic to Organic, we encounter the appearance of a categorical NOVUM. This NOVUM, then modifies all or at least many of the other categories that have entered the Organic Layer from the Inorganic. And in this way clearly lets stand out the Organic Layer with respect to the Inorganic Layer.
All this is based on the discovery of holistic features in organisms, to which we were led by the strong indication of the impossibility of a complete reduction of the Organic to the Inorganic.
It turns out, however, that such non-reducibility also crops up within the Inorganic itself. As an example we have come up with the generation of snow crystals. And what we had found for snow crystals probably holds for all solid crystals whatsoever. We have found that the point symmetry of snow crystals is not just an implication of their Space Group (just by eliminating from the latter all translational elements) -- as such it is crystallographic point symmetry. The point symmetry of these crystals is not just the symmetry of the translation-free chemical motif, but also morphological point symmetry like we see in organisms (Organisms do not have Space Group symmetry, nor crystallographic point symmetry, but only morphological point symmetry). The structure of an organism is not based on a periodic point lattice (at least not in the sense that an organism would simply be a crystal), and so its point symmetry is not the symmetry of the translation-free residue of its structure. It is morphological point symmetry, expressing itself by the presence of macroscopically defined antimers [ = counterparts] (i.e. antimers with genuine, macroscopically visible, boundaries which are not translationally repeated [as boundaries are in plain crystals, and as boundaries of metamers are in organisms] ).
While in plain crystals we do not encounter such antimers (there we can only recognize them in a more indirect way), branched snow crystals do have them, macroscopically indicated by the six main branches, which are as such only rotationally repeated. This indeed indicates that such crystals also possess genuine morphological symmetry. We could say that morphological symmetry is relevant to all crystals, but only expresses itself in crystals that possess a (macroscopic) morphology at all, that is, in branched crystals. And in the formation of such a branched crystal we clearly see a strife to reach and maintain a certain morphological equilibrium by keeping its six arms to be of the same morphological type. Where no macroscopic morphology is present, as in plain crystals, we see an analogue of it in their ability to regenerate after damage. Also in organisms we see such a strife to obtain and maintain some sort of morphological equilibrium, evidently by virtue of their heavily regulated individual development (morphogenesis) and their ability to regenerate.
It seems therefore that surely branched crystals (but also crystals in general) and organisms are somehow subjected to a certain holistic feature or determinant : a form-equilibrium. This form-equilibrium then is a NOVUM, meaning that the overall intrinsic structure of an organism or of a crystal (generally of an intrinsic being) is not completely derivable from the interactions of its components or elements. These components, i.e. the system of interacting components, is a holistic simplification of this overall structure, taking noëtically place in the Implicate Order, while what we s e e m to see in the Explicate Order is the reductionistic complexification, i.e. it looks as if the overall structure of the organism or of a crystal is the result of the interaction of its material parts (and nothing more). But what we a c t u a l l y see in the Explicate Order is the appearance of a NOVUM, when changing from material parts, or elements, to overall structure. But because of the underlying holistic simplification (as it occurs in the Implicate Order) this NOVUM is in fact not a novum. And whether we experience it as a novum or not, it is, in any case, some specific form-equilibrium, that dominates the development of the organism or crystal, in the form of a global controlling feature, a holistic factor. The kind of NOVUM that is, for instance, represented by the form-equilibrium of a snow crystal (here "form-equilibrium" is equivalent to the parts of such a crystal being correlated, guaranteeing a growth in unison of the crystal) differs from the kind of NOVUM that is involved at the (formal) transition from Inorganic to Organic : While the latter kind of NOVUM entails the modification of most other categories that pass over into the Organic while coming from the Inorganic (Space [inorganic] ===> Umwelt [organic], Increase of Size [inorganic] ===> Growth [organic], Inorganic intrinsic being ===> Organic Individual, etc.), the NOVUM involved in crystallization, and all other such NOVA, (because they are specific, i.e. less encompassing) do not entail modification of other categories, and so do not result in the appearance of a new Layer of Being. Generally, a NOVUM -- as is visible in the Explicate Order -- is correlated to a corresponding Holistic Simplification in the Implicate Order. Within the Organic Layer we see -- in the Explicate Order -- a transmutation (usually called "evolution", which term is deceptive in the present context) of lower (i.e. less complex) organisms, resulting in higher (i.e. more complex) organisms. And it is well-known that the actual derivation (as is attempted in science) of higher life-forms from lower ones proves to be difficult. In fact what we see, in every such case, is the appearance of a NOVUM, a NOVUM of the same type as we have found it in snow crystals, which means a NOVUM that does not entail modifications of other categories. And the appearance of such a NOVUM, in the evolution of higher life forms from lower such forms, corresponds directly to a holistic simplification noëtically taking place in the Implicate Order. Then, in the Explicate Order the existing lower life forms are over-formed, resulting in higher life forms.
It is to be expected that, in addition to the appearance of such NOVA, also instances of just (plain) Reductionistic Complexification take place (which is, according to strict reductionistic science, the only way transformations can take place at all). There we see an increase of complexity without the appearance of a NOVUM : The complex result is totally reducible to the simple initial structure from which it has emerged. And this reduction is just a simplification, not a holistic simplification. Thus when, in the present case, we watch the change from the initial simple structure to this complex result, we have to do with just a reductionistic complexification (i.e., ex hypothesi, not with the appearance of a NOVUM). One will see that Nature is replete with these cases of simple complexification (where thus no holistic factors are involved) :
All instances of the formation of aggregates belong to this type : such as the formation of natural deposits of materials (minerals, rock fragments, evaporation left-overs, etc.) resulting in sediment layers, as it takes place on the surface of the earth, in lakes and in oceans. Another example is the precipitation of a colloidal mass in some chemical environment. And yet another example is the formation of (most) clouds in the atmosphere. All these formations do not possess a specific, intrinsic form or shape. Very often their shapes differ strongly from case to case. Generally, all the solid amorphous substances (that is, chemical substances [now] being in a solid, but amorphous state) and all non-turbulent liquids (except liquid crystals) and gases are aggregates. The coming-together of their element-particles has extrinsic causes. More precisely : their 'what is it?' has extrinsic causes, meaning that they do not have a specific identity. Generally, their quantitative composition differs from case to case. They are not true substances (in the metaphysical sense), that is to say, they are not substances or beings that can (let) repeat themselves by means of individuals that are identical to each other as to their specific content. And their element-particles exist in an actual way (of being) in the aggregate, and the latter is nothing else than its element-particles. Every element-particle itself, either is also an aggregate, or a genuine substance. The aggregate is a contiguum, not a continuum. The element-particles of the aggregate are not logically (that is, noëtically) connected to each other in the Implicate Order (expressed by their state of actuality in the Explicate Order). They do not necessarily project together into the Explicate Order. The aggregate is a unity per accidens, it is not an intrinsic unity or being, that is, it is not a unity per se.
On the contrary, a totality or true substance (holon), such as an atom, a molecule, a crystal or an organism, is wholly one, that is, it is an intrinsic unity or being. It carries the cause of its 'what is it?' within itself. In the Implicate Order it is a non-local unity or, equivalently, a non-local continuum, which means that (1) in the connection and communication of its parts (among each other) no spatial distances are involved, (2) these parts are logically (noëtically) implying each other according to some noëtic network, that is, they form a coherent logical pattern or monad, different from other such patterns or monads, (3) there are no individuals, but only specifically defined unities. And such a true substance (holon) is, in the Explicate Order -- that is, the substance, now in its explicated or unfolded condition, and at the same time individualized --, also a unity, but now a local unity (local with respect to its virtual parts as they are locally placed in the substance), a local continuum, because now -- in virtue of its unfolding during projection -- spatial distances (within the substance) are involved in the connection and communication of its parts. Such a local continuum can be homogeneous or heterogeneous. If it is heterogeneous, then its different parts (separated by distances within the substance) -- element-particles -- exist only virtually in it, that is to say their way of being is that of near potency.
The following diagram illustrates the implicate and explicate state of a true substance (holon) :
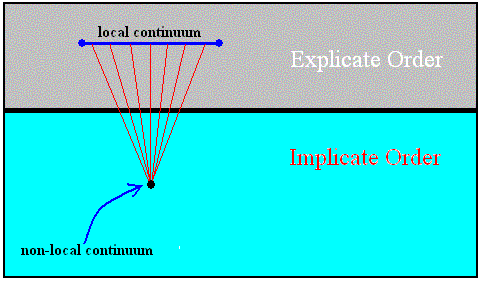
Diagram above : A true substance (holon) resides in the Implicate Order as a non-local continuum, that is a continuum in which there are no spatial distances involved in the (logical) interaction of its potential parts. When this (true) substance (holon) has been projected up into the Explicate Order, it resides there in the form of a local continuum, that is a continuum that is spatially extended, and thus having a natural size.
The diagram symbolizes the unfolding of the non-local continuum by projection into the Explicate Order.
All the ontological relations, discussed above, and meant to explain holism, the appearance of (special and general) NOVA, and the appearance of Layers of Being, can be integrated, summarized and generalized by a Diagram of the Holistic World which we already had given in earlier documents :
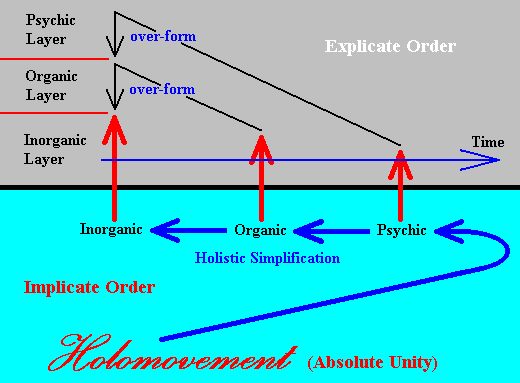
While holistic simplification is, in the case of organic beings versus inorganic beings, a matter of subtracting the general organic NOVUM, and also (subtracting) the changes it had entailed in the other categories of the Organic Layer, in the case of crystals holistic simplification is the following transformation :
Lowest-energy holistic configuration of molecules, atoms or ions ==>
Lowest-energy configuration of molecules, atoms or ions.
and in the case of snow crystals :
Lowest-energy holistic hexagonal configuration of water molecules ==>
Lowest-energy hexagonal configuration of water molecules.
And these latter holistic simplifications (that is, in the case of crystallization) do not entail a transition from one category Layer to another, because here we have a subtraction of a special NOVUM only.
To speak about holistic simplification, which takes place in the Implicate Order only, and saying that it subtracts a NOVUM, while all NOVA exclusively belong to the Explicate Order, could be confusing. So let me explain. To speak about holistic simplification is only possible in terms of its explicate counterpart, the categorical NOVUM, by considering the subtraction of that NOVUM. We must thereby realize that the appearance of this NOVUM takes place in Time, because it takes place in the Explicate Order, whereas holistic simplification does not take place in Time, because it takes place in the Implicate Order.
This special NOVUM, generally indicated above by adding "holistic", is in fact the morphological determinant, that is the determining nature of intrinsic form and shape. It determines things, alongside the determining activity of ordinary causality and dynamical laws (implying causality). It is a new nexus category (as explained further below). And holistic simplification (as it takes place in the Implicate Order) in the present case (crystallization) thus means the subtraction of this category, that is, the subtraction of this NOVUM. What is left then is a crystal which is just a lowest-energy configuration of its particles, which now exist actually in the crystal. The latter then is not a continuum anymore. And such a crystal is then the result of a mere reductionistic complexification and nothing else.
The NOVUM we just spoke about, appears in the Explicate Order (as the reverse counterpart of the mentioned holistic simplification). What happens there when the crystal is formed is the establisment of an all out communication throughout the crystal, that is, a communication over macroscopic distances (within the crystal). But this communication takes place via the Implicate Order. In this way one arm of a snow crystal 'knows' what the other is doing, and so the crystal can develop itself toward a morphological equilibrium.
In earlier documents ( Part XXIX Sequel-24 , Part XXIX Sequel-25 , Part XXIX Sequel-26 , and subsequent documents), we discussed HARTMANN's theory of Categories (which we can also call If / Then Constants) of the "Real World". This "Real World" was for HARTMANN the observable world. This world could -- as I speculate -- have originated by the complexification of an initially purely Mathematical World (or mathematical Layer [with its own gear of categories] ). All this we can now interpret as follows : The purely Mathematical World is the immaterial non-local noëtic world as we understand the Implicate Order to be, while the material world is the result of projection and unfolding of elements of the Implicate Order (up into the Explicate Order). In the Implicate Order holistic simplification takes place from complex to simple, and the results are then explicated in reverse order (but now in Time [and Space] ). In this way we see complexification to take place in the Explicate Order, partly by means of special and general categorical NOVA ( partly, because there also take place plain reductionistic complexifications, resulting in aggregates). The latter, that is, the general NOVA, cause the appearance of different Category Layers, that is layers each containing a special set of categories or principles. Many categories are commonly held by all Layers or by some, but other categories break off when we go from one Layer to the next higher one. And one or more new categories appear in each subsequent Layer (categorical NOVA). These new categories, or general NOVA, modify all other categories of their Layer, that is of the Layer in which such a NOVUM appears, while special NOVA do not do this.
But it is the general and broader metaphysical and ontological context, as outlined above, including the Implicate and Explicate Orders, into which we must place, and within which we must understand, the difficult concept of virtual existence of the elements in a mixtum (which [mixtum] is, in the inorganic world, either a free atom, or a free molecule, or a crystal). For snow crystals (being true substances [holons] ) this means the virtual existence of water molecules in such a crystal, guaranteeing it to be a true continuum. And although all (virtual) water molecules in the crystal are equal, they are definite entities (regions having a certain quality) that are arranged within the crystal according to the three-dimensional hexagonal point lattice itself having P6/m2/m2/m symmetry (After the formal insertion of the water molecules into this lattice the space group symmetry becomes P63/m 2/m 2/c). These regions alternate with their negations, and so form a heterogeneous continuum. And that is a(n internally) local continuum in the Explicate Order, while it is a non-local continuum in its enfolded state as it is so in the Implicate Order.
In the documents dealing with HARTMANN's categories we discussed the category of Causality. Causality is a nexus category (or at least lies at the foundation of nexus categories [as natural dynamical laws are] ), which means that it is a principle according to which (two) (system) states are being connected in time. And in the documents about Thermodynamics (Part XXIX Sequel-27 [from the Section "Energy" onwards], Part XXIX Sequel-28 , Part XXIX Sequel-29 , Part XXIX Sequel-30 and Part XXIX Sequel-31 ) we revisited the category of Causality and found out that in all probability the causal nexus contains an irreducible, albeit very small, statistical aspect (not only with respect to our possible knowledge of the course of dynamical systems, but also ontologically). Further, while studying branched snow crystals, we found out that thermodynamics, and thus also causality, does not exhaustively determine macroscopic morphological structure (form and shape), even if we take into account random events, such as randomly appearing ice bumps on the arms of these crystals, which (bumps) then become sites of preferential growth. Therefore we concluded that f o r m, in the sense of macroscopic structure, is itself a determinant, i.e. it at least co-determines subsequent states of some being or dynamical system (be it a crystal or an organism). And that means that we have, in all probability, found a new nexus category. This morphological determinant has a corresponding morphological potential (as an analogue of a thermodynamic potential) to which extreme the morphology of an intrinsic being strives : The form-equilibrium state of that (given) being. So a developed symmetrical branched snow crystal ( [point] symmetry : 6/m2/m2/m, and 6mm when looked down along its c-axis) has reached its form-equilibrium, and is thus morphologically stable, while it is still far from thermodynamic equilibrium ( = lowest Gibbs free energy), and is thus still thermodynamically unstable. When the branched crystal subsequently comes under milder conditions (low humidity, but still below-zero temperatures) it will gradually transform into a regular hexagonal tablet or prism. And also here the 6/m2/m2/m, respectively 6mm, form-equilibrium is held.
So indeed our long excursion into thermodynamics (finding there that it does not totally determine macroscopic morphology) and into the development of branched snow crystals, has yielded a new nexus category : the morphological determinant. Already present in crystals, this determinant will be seen to play an even greater role in the (individual) development of organisms, and of course this contributes to the power and value of the crystal analogy.
Implicate and Explicate Order, Natural Science, Metaphysics.
We have invoked the (theory of the) Implicate Order (and the Holistic Simplification taking place in it) in order to deal with the NOVA that appear when we observationally follow the generation of many things like snow crystals and organisms, and the generation of higher organisms from lower ones (as we see it in evolution as documented in fossils as well as in the constitution of recent organisms).
Having thus introduced this theory of the Implicate Order of Being, we can now (further) concentrate on the events as we see them in the observable world, that is, in the Explicate Order of Being (and thus [in the sequel] 'forgetting' about the Implicate Order [of which they are the observable manifestations] ). What we then in fact do is to just follow the investigations and results of natural science (like crystallography, mineralogy, thermodynamics, biology, etc.) and consider the principles of Being as all this is (manifested) in the Explicate Order, that is, we then just do ordinary natural science and metaphysics (of which that natural science is just a specification).
But we now know that this natural science and (ordinary) metaphysics are not fundamental in an ultimate way : Their results must be interpreted as expressions of the activities in and of the Implicate Order (and eventually and ultimately of the activity of the Holomovement within it). So all our science and metaphysics is only about the manifestation of (noëtic) processes and transformations (such as holistic simplifications) -- that is, of logical deductions -- taking place in the Implicate Order (while being well aware that the Implicate Order is also influenced by events taking place in the Explicate Order).
About the Implicate Order itself and its noëtic activities we can only speculate. And these speculations can only be derived by us from what happens in the Explicate Order. So we cannot directly investigate the Implicate Order, and so we do not have a science and metaphysics of this Order. Again, we have a science and metaphysics of the explicate condition of Being only ( But because the Implicate and Explicate Order together form one world [by reason of the fact that they influence each other], our theory of these two Orders of Being is itself a metaphysics. It is however a global metaphysics that purports to explain the metaphysics of the observable world).
Having said this, we continue our investigation of true substances like crystals and organisms (as we can actually observe them). Assuming it to be true that such (physically) composed bodies are (nevertheless) intrinsic wholes, not entirely reducible to constituent non-composed (or composed in a lesser degree) entities, such as element-particles (by reason of NOVA), we in fact assert the validity of some holistic metaphysics, in order to back up this non-reducibility, and which (metaphysics) is such that the relevant results of natural science can represent a specification of this more general metaphysics.
And indeed the best holistic metaphysics we can come up with is the Aristotelian-Thomistic Metaphysics (discussed and developed in First Part of Website ).
It is holistic (which here means that it acknowledges not only the existence of physically simple [that is, non-composed] elementary bodies, but also the existence of physically composed bodies that are [according to this metaphysic] nevertheless true wholes [just like the freely existing simple elementary bodies are], in addition to the existence of things that are also physically composed, but are at the same time just aggregates, and thus not intrinsic wholes), because it recognizes natures, forms and (genuine, non-reducible) qualities, not only as belonging to the smallest freely existing particles, but also to many entities (bodies) that appear to be built up by these particles. So although just-aggregates can, and often are, formed by the coming-together of such smallest particles, in many instances real wholes are formed by the coming-together of these same particles, (now) a coming-together in such a way that the resulting body has acquired a new identity, because, apart from a number of properties that are no more than additive resultants (as we see it all over in aggregates), this body has new properties, that are called totality-resultants. And these new properties point, according to the Aristotelian-Thomistic Metaphysics, to a new Form (in the metaphysical sense, as a nature or [formal] principle), as essence inhering in the new (individual) whole and giving it a new identity, with respect to the identity of either every single element-particle when freely existing on its own, or to the identity of the aggregate (which is almost the same as that of the freely existing element-particle). So -- again according to the Aristotelian-Thomistic Metaphysics -- the purely potential prime matter, which is the ultimate substrate (that is, ontological carrier), and which is a substrate only, has, in virtue of the process-of-the-coming-together-of-the-element-particles-resulting-in-a-new-whole, acquired a new nature or Form : The Form, as it initially in-formed the prime matter of each of the element-particles, is now replaced by a new Form. And because the Forms of the constituent element-particles are gone, these particles now exist only virtually, and in this way indeed letting the new whole to be a true continuum. And only a continuum is a true whole. And this true whole, although it originated from the mentioned element-particles, cannot be reduced to them. It is not just the sum of these element-particles. It is something new (but in many cases still more or less similar to the nature of these particles), having its own nature or Form.
Precisely by acknowledging natures and Forms, i.e. specific natures and Forms, to certain classes of things, that is, not only to the smallest 'most fundamental' particles, the Aristotelian-Thomistic Metaphysics conveys a holistic aspect to the natural world. And it does this more clearly than any other metaphysics.
Main features of the argument for substances (especially crystals) to be true continua.
Argument based on the constitution of a substance as is actually observed.
A continuum is an extensum (that is something having [spatial] extention) which is intrinsically one whole, that is, an all-out intrinsic unity. From this it follows that the parts of a continuum do not exist actually (that is, their way of being is not that of being [there] actually), but only potentially (because the appearance of actual parts would transform the intrinsic unity of the continuum into a plurality, that is, destroy the continuum).
So if a crystal (to stick to this particular example) is a true continuum, then all its parts (in fact their boundaries), and thus also all its element-particles exist only potentially (that is, are only potentially boundaries or particles), or at most they exist in a near potency (that is, close to being actually existing boundaries or particles). As has been said, we call this near potency "virtual" .
So we still have to demonstrate that the crystal is indeed a true continuum, that is, that it is an intrinsic unity in the strongest sense. Well, no doubt the crystal represents some sort of unity, by virtue of the chemical bonds, which connect all element-particles to each other.
But is this (already) an "all-out intrinsic unity"? Are the mentioned bonds and connections sufficient to make the crystal to be such an intrinsic unity?
We can say is that the quantum conditions that have to be imposed on the trajectories of electrons (and thus also on the chemical bond), make the atom, the molecule, and the crystal to be a non-mechanical entity. But is this sufficient for them to be all-out intrinsic unities (and thus continua)?
The non-mechanical nature of many things or beings is also expressed by the existence of variable quality (demonstrated in Part XXIX Sequel-5 ) : When such a quality changes (in fact the substance changes [accidentally or essentially] of which it is the quality) we have an instance of intrinsic change, that is a change not involving the movement or rearrangement of element-particles, and thus an instance of a non-mechanical event.
The unity of a crystal (and of a molecule, atom, etc.) is also expressed by its being based on the one particular dynamical law (physically interpreted, and thus including initial conditions -- these latter are such that they inhere this law) that produced the crystal. Whether this one dynamical law guarantees a holistic product or intrinsic unity is not certain beforehand, because this demands the appearance of a (special) categorical NOVUM (for example one that connects regions over macroscopic distances within the crystal).
We could say that the features that make the crystal to be an intrinsic unity are potentially present in its element-particles when still freely existing. But that is begging the question of course. When something can potentially be informed by a NOVUM, that is, when something is in potency with respect a state in which it possesses that NOVUM, this means nothing more than that the receptivity with respect to this NOVUM, is not a priori excluded.
Well, on the basis of what we see in snow crystals (communication within the crystal over macroscopic distances), we can say that the above features that convey some sort of intrinsic unity to the crystal turn out to be sufficient for this unity to be such that the crystal is a continuum. And the same can be said for all crystals, and also for all molecules and atoms. That is, all inorganic substances (in the metaphysical sense) are genuine continua. And then indeed, the way of being of the element-particles is to exist virtually.
Argument (demonstrating the existence of (internally) local continua) based on the necessity and intelligibility of the possibility of radical change.
The existence of local continua (as is demanded by the Aristotelian-Thomistic Metaphysics) can also be demonstrated (by arguing) from the Implicate Order :
Observation tells us about the existence of features that seem to demand a special holistic interpretation, for instance the often mentioned contacts of parts of a snow crystal, contacts spanning macroscopic distances within the crystal. Such contacts may only be possible within a non-local continuum, that is a continuum without distances within it. Such a non-local continuum can be provided by the Implicate Order : The immediate connection of parts of the crystal runs via the Implicate Order, that is via the enfolded 'aspect' or 'state' of the crystal. And of course such a non-local continuum, upon projection up into the Explicate Order, becomes (that is, expresses itself as) a local continuum (Q.E.D.).
Virtual existence of element-particles of crystals.
In order to further expound what is generally meant by the virtual existence of particles in a substance (compactly stated in the above quotation ), and in particular what it means in the case of crystals, we recapitulate and further extend the theory of the internal structure of crystals and its bearing on the mentioned virtual existence of their (constituent) particles, which (virtual existence) makes a crystal to be a true continuum. For this we will make use of the relevant discussions of P. HOENEN, in his Philosophie der Anorganische Natuur (in Dutch), 1947, p. 375-387. Thereby we will add some extra stuff and commentary, generally without indicating that we do so ( So what follows is not a quotation, we just paraphrase parts of the text, add things, omit things, etc. However, to remind the reader that we (still) are (sympathetically) following the lines set out by HOENEN insofar as the metaphysical interpretation of the crystalline state is concerned, we write in a different font).
Introduction
Properties of crystals
Crystals can look homogeneous and even under the microscope show no sign of heterogeneity, which, according to what follows, nevertheless must be there. If we consider only observable fragments, then they show, when they are taken from different regions of the crystal, no differences in their properties. Crystals, however, are not i s o t r o p i c, that is, if we consider properties that depend on direction : propagation of light and heat, cleavability, growth rate, etc., then these generally are different in different directions. Parallel directions, on the other hand, show the same properties.
These similarities and differences of properties are not the result of coincidence like it is in the case of amorphous substances (in the physical sense), if they have such differences at all. In crystalline materials these similarities and differences of properties are according to definite rules, characteristic for the species. What is especially important is that these rules describe different degrees of symmetry in different species of crystalline substances. The most important features of this symmetry, which co-determines the intrinsic structure -- the external shape is just the manifestation of the latter -- are : centers of symmetry [a point in a crystal with respect to which the crystal is symmetric], planes of symmetry [such as mirror planes and glide planes] and axes of symmetry such as [rotational axes and screw axes] which are combined with each other in different ways [If we consider only point symmetry, then we omit glide planes, screw axes and plain translations]. Not all forms of symmetric structure that are a priori possible in space [that is in spatial extension without qualification], are found in crystals. There would be an infinity of them. The number of forms of symmetric structures is even relatively small. The symmetrical forms that are found by experience in the world of crystals reduce to seven systems (or six, whether one considers the hexagonal and trigonal as two systems or as one system), and in the total of these systems one finds 32 classes of symmetric forms ( For a discussion of Crystal Systems and Crystal Classes, see the document The Morphology of Crystals (Special Series of documents) in First Part of Website ).
To give one example of this restriction of symmetry in crystals : A body has an axis of symmetry if it, when rotated (about that axis) by an angle measured as a part of 3600, coincides again with itself, that is, that every point outside the axis, is interchanged with another point which, in the body, had the same properties. The axis is of the second order if this only happens with a half-turn (1800), of the fourth order when this only happens with a quarter-turn ( 900) (and then, of course also with a half-turn), etc. (Of course every physical or mathematical body whatsoever has an axis of the first order ( 3600) (full turn)). Generally, the axis is of the n-th order, when the coincidence occurs at every turn of 360/n degrees. For bodies in general the magnitude of n is not fixed, so axes of every order are possible. For example the order of the axis of a homogeneous cylinder is infinitely high. This body coincides with itself after whatever degrees of turning about this axis.
But . . . in the world of crystals only symmetry axes of the 1st, 2nd, 3rd, 4th and 6th order are actually observed. Symmetry axes of the 5th order, so common among organismic bodies, are totally absent in the world of crystals [only an approximation to five-fold symmetry is seen in certain so-called quasi-crystals]. Also all higher than 6th-order axes do not occur in crystals. This is just a single example of the restriction of symmetry as it is the case in crystals. These restrictions are thus such that only the above mentioned Crystal Systems and Classes result.
Theory of the restriction of symmetry
Now as we know, one has developed a theory that can, in a detailed way, account for this. Its bottom line is as follows : One supposes that the crystal is, with respect to its smallest parts or particles, not homogeneous, but heterogeneous. In virtue of the apparent homogeneity the parts or particles having the same properties must be arranged periodically, separated by small regions which, again periodically aranged, have other (but equal among each other) properties. In different directions these regions, separating the mentioned particles, will generally have different sizes. After all, the crystal generally displays different properties in different directions.
We now consider an arbitrary point P in one of these particles and connect it by a line with the corresponding (the "homologous") point in the nearest particle (if there are more equidistant particles, we take one of them). Let the distance be a . If we extend this line we will (in virtue of the periodic heterogeneity, which displays itself as macroscopical homogeneity for the observer) meet again and again new homologous points at equal distances a . At smaller distances no homologous points occur. If we draw a line from P in another direction to the homologous point, that is nearest but one (i.e. that comes nearest after the first point of the first mentioned line), then also this new line carries a series of homologous points, lying at equal mutual distances, that generally differ from a , that is, larger. See next Figures : There the homologous points are represented by the intersections of auxiliary lines.
and for a more special case :
These two lines define a plane, and it is easy to prove that all points that are homologous to P are corners of a network of parallelograms [or their more special cases, such as rectangles], a network that can be constructed in that plane, and which occupies the whole plane [i.e. the network can be extended indefinitely over the plane].
Additional confirmation of the theory.
Nevertheless, at the end of the 19th century this theory shared the fate of all explicative theories : By reason of the attacks of the energetic interpretation of nature and by reason of the prevailing scepsis it was not accepted or was called in question, at least outside the arena of the crystallographers. But as, at the beginning of the 20st century, the kinetic molecular theory received its definitive confirmation, also the crystallographical theory received its definitive confirmation. It happened in 1912, by the initiative of Von LAUE. He considered the following : If indeed crystals have the structure as is described by the theory of point systems (three-dimensional networks), then they would exert the same influence on waves with very small wavelength as the long since known gratings of Rowland have on light-waves. By these gratings, light-waves, provided that the openings are sufficiently small and close enough to each other, are in such a way diffracted that in virtue of their interference the well-know grating spectra originate. Well, such a grating is in fact formed by any crystal according to the crystallographic theory. With two differences, however. The gratings of Rowland were linear. They consisted in a row parallel lines. There have been constructed two-dimensional ones, that carried a set of transversal lines, resulting in more complicated interference phenomena. Crystals then would represent three-dimensional gratings. But this only complicates the mathematical treatement. Another objection was more important. While openings of a grating that are too large neutralize the effect, openings that are too small also neutralize the effect. And if crystals are indeed gratings, then (learned by a simple calculation involving the number of atoms in a given slice of crystalline material) their openings are too small to result in diffraction phenomena of light-waves. But Von LAUE surmised that X-rays would have a wavelength small enough to revail the grating structure of crystals. The outcome of the relavant experiments has confirmed this surmise. Crystals indeed cause the interference phenomena of X-rays predicted by Von LAUE. Such experiments were again carried out, according to some other method, by W. H. and W. L. BRAGG, and again with another method by DEBIJE and SCHERRER.
Not only generally do the results confirm the theory, but also allow to measure the distances of the diffraction centers -- the centers of the atoms -- lying in different planes of the (3-dimensional) crystal network. At the same time they provide a measurement of the wavelength of the X-rays, which then has received a splendid confirmation by the results of the new atomic theory. For us is important : the particles occupying the nodes of the network turn out in many cases not to be molecules but atoms.
Again we can summarize the elements of the theory in a concise scheme : Suppose that crystals are point systems, and that the points are occupied by the centers of constituent atoms, then we must, by applying X-rays, expect certain well-determined interference phenomena. And the experiments confirm this expectation.
It is no wonder that these results were received with great approval. For our problem the great progress with respect to the results of the older crystallography consists of the following : First of all these methods let us know the distance and other features of the interior structure of crystals. But especially : the older theory still could do it by assuming complex molecules [that is, the assumption that the whole crystal was one giant -- and what is especially important -- single molecule, implying that the latter, and thus the whole crystal, does not necessarily need to be periodic as to its internal structrure]. And in that case there would be no proof whatsoever of the presence in the crystal of a c t u a l atoms [that is, of actually existing atoms in the crystal], provided it could be argued that molecules are continua. The new theory, on the other hand, assumes the actuality of atoms in the crystals, and this seems to be confirmed by experiments. So Prof. JAEGER says : " These atoms preserve, therefore, apparently their individuality as constituents of such crystalline substances." ( F.M. JAEGER, Lectures on the principle of Symmetry, 2nd edition, 1920 ).
Applying the Elimination Principle.
The Elimination Principle says that any unnecessary and superfluous elements of a given theory or argument must be eliminated from this theory, because, when they are retained, they might suggest that they also are demonstrated by that theory (while in fact they are not), that is, in addition to the things that the theory does demonstrate.
If the above opinion (actual existence of the constituent atoms in a crystal) is correct, then the problem of the chemical compound (i.e. the molecule) is solved. Then it is evident that a chemical compound in its crystalline state consists of actual atoms. Then the molecule is just an aggregate, not a totality or intrinsic unity. Nevertheless we must, as in all other such cases, carefully distinguish between the elements of the theory, and see whether there are superfluous elements among them. If all elements of the theory are necessary, then the above conclusion is correct. But if, on the other hand, the element that supposes the actuality of the atoms -- this element is explicitly mentioned -- turns out to be superfluous, then the conclusion is false.
To investigate this we set up, alongside the classical theory, another theory, in which precisely this element is replaced by another. It will be clear that the hypothesis of the reticular structure is not superfluous. With it the whole derivation of results stands or falls. If we suppose that the crystal is homogeneous all the way down including its smallest particles (meaning that there is then no reticular structure), or possessing another than reticular heterogeneity (that is, when although it is heterogeneous, the ensuing pattern is not periodic), then all results of the deduction are cancelled. However, this turns out not to happen if we (only) drop the hypothesis of the discontinuity (of the crystal interior). That is, if we drop the hypothesis of discontinuity, the deduced results of the theory still stand.
Indeed, suppose that a crystal is a continuum, optically (that is, referring to the behavior of light that is sent through the crystal), it is true, homogeneous [per direction], but with respect to its smallest parts heterogeneous in qualities, that is, a heterogeneous continuum. Suppose that in a crystalline substance this heterogeneity is p e r i o d i c. In this way : Parts or regions in the crystalline material with precisely the same qualities are separated from each other (and at the same time connected with each other) by parts or regions having the same properties among each other but different from those of the previous group.
To mention a particular property which surely is important here : The first group of regions may have a high density, the second group a low density (nothing forbids this latter density to be zero, but nothing demands it). If we draw a line through the center of one region belonging to the first set to another such center (for example the one that is closest), and then continue to extend the line in this way, then along this line the density will change : The density maxima along this line will lie -- and here we introduce the hypothesis, which is the foundation of the reticular structure -- at equal distances as measured along this line. Along another line (also going) through the original point, the distances of density maxima are generally different. So it is clear that also a continuum can possess a network structure with respect to the density of its smallest regions [
Philosophical analysis of the theory.
With this, of course, the advance in the atomic theory, insofar as it is achieved by the necessary and permanent elements of the crystallographic theory, is not eliminated. There is, first of all, the confirmation of the existence of minima and the magnitude of atomic weights that they entail. Further there is the important gain that it is now certain that crystals, despite their outward appearance, are not homogeneous in their smallest parts, that they possess a periodic spatial heterogeneity at least with respect to density, that is compatible with the reticular structure. And this periodic heterogeneity is a s p e c i f i c one : It is permanent, it is characteristic for each sort of crystal, it is connected to the properties of the elements from which the crystal is built and with whom the crystal stands in a genetic connection. That is then the further specification that this crystallographic theory adds to whatever general theory of matter. And this specification is necessary by reason of the results it gives. Now the g e n e r a l theory must be such that it allows itself to be specified in this way. So what is left is to investigate whether, and how, also in detail, this can be accomplished in the two systems -- Mechanicism and Aristotelian-Thomistic metaphysics -- that we investigate.
Because crystals generally are in fact a kind of chemical compound (they are the result of a regular repetition of certain atomic complexes, and involve chemical bonds throughout the crystal), we generally have to do with the problem of the unity of a molecule (which consists of a number of atoms chemically bonded to each other), and, in addition to this unity, we must investigate the difference in properties between (1) the molecule or crystal and (2) its elements, and also the similarity or identity of (other) properties between them.
Discontinuity hypothesis
Let us first consider the atomistic solution (that is, the solution according to the atomistic interpretation of nature -- atomism) of the problem of the molecule. First, in atomism the above mentioned problem of the similarity or identity of properties between the chemical compound (or crystal) and its elements is automatically solved. Atomism holds that upon chemically bonding to each other, atoms remain what they were before the bonding. And when, accordingly, we encounter correspondence of properties between the compound and its elements, then in atomism this does not ask for an explanation. The second question, namely as to the explanation of the d i f f e r e n c e in properties of compound and elements, was more alarming for atomism : these properties at first sight seemed to differ very much indeed. However, this problem is going to lose much of its disquieting face : because the way in which the different densities of (smallest) parts in the crystal correspond to the different atomic weights of the elements, proves that there are properties of elements that are at least in some way found again in the compound, that is, it points to some preservation of the elements.
With the problem of u n i t y, things are different. Its solution has become more difficult for atomism. Stronger demands are called for. Atomism, namely, can, in virtue of its essence, only accept an accidental unity, as an equilibrium, permanently resulting from forces (in the technical-physical sense) that the actual atoms exert on one another
[
Continuity hypothesis
For a solution of the problem of crystals as chemical compounds in the Aristotelian sense (that is, the crystal or molecule as a continuum) things are different. The unity of the molecule or crystal (mixtum perfectum) does not entail a new problem. The first principles of the theory (that is, the Aristotelian-Thomistic metaphysics) are already geared to account for the existence of such new unities. In contrast to atomism, for the Aristotelian-Thomistic metaphysical theory novelty of properties, that is the appearance of new properties when a mixtum is formed, only demands to look for an effective cause, an agent. And when it turns out that this newness is after all not so dramatic as appeared to be at first sight, this certainly lightens the task of the Aristotelian philosopher. Because he acknowledges the genetic kinship between the mixtum and its elements, this preservation of certain element-properties is to be expected. Exact observation should only decide in which degree and in what way this is the case.
Possessing now, thanks to crystallography, a specification of that "way", we only have to ask whether this way of preservation, as expressed by the reticular structure, can be explained.
General considerations had led us to see the principle of the heterogeneous virtual preservation of (some) element-properties (for short : the principle of heterogeneity) as derivable from, or at least compatible with, the Aristotelian principles of prime matter and substantial form. We learned that in the Aristotelian theory it is possible and, after the discovery of the relationship between elements and their compounds, even to be expected, that a mixtum will be heterogeneous in such a way that one part of it will show properties that are wholly or partially identical to the properties of one component (element), while other parts will have the same relation to the other components (elements).
Long Intermezzo on Specific Heterogeneity
At this stage (in following HOENEN's text, p.375-387) it is important to dwell a little longer on the problem of the specific heterogeneity of a molecule or a crystal.
A substance in the metaphysical sense is an individual intrinsic being (a being, thus, that carries its specific identity within itself). It consists of two principles, prime matter and substantial form, where prime matter is the ultimate substrate for all qualitative and quantitative content of a given being. The substantial form not only represents the substantial specification of such a being, in such a way that a specifically different substantial form results in another species, but its more fundamental and first 'task' is to transform potential being, prime matter, into a genuine being or "ens". Where then in prime matter there is already present a substantial form, not potentially, but actually, this particular prime matter has already become a genuine being or ens. And all this makes clear that a given substance can possess only one substantial form, because if there were more than one such form in one and the same prime matter, then we would automatically have to do with more than one substance. So if we consider a mixtum, say a molecule or a crystal, to represent one single substance (because it definitively differs from just a mixture of the same elements in the same proportions), then it has only one substantial form, which in turn means that the (several) substantial forms of the (different) elements of the mixtum (that is, the elements from which the mixtum was formed), as these elements had these forms when still existing independently, have somehow vanished, that is, as substantial forms they do not exist anymore in the mixtum. But they can exist in the mixtum in a different way, namely as its qualities (quantities, relations, etc.). This is possible because although a substance is an intrinsic unity it can possess a multitude of determinations -- 'accidents'. These determinations are determinations of the one substance or mixtum, and some of them stem from its elements.
Having all this in mind, let's now continue this intermezzo, and paraphrase HOENEN's text at page 333.
Unity of substantial form, and heterogeneity.
Specific heterogeneity possible. ( HOENEN, pp.336)
We saw that in one and the same substance, and thus also in one and the same mixtum, there is only one substantial form [but several forms representing the substance's determination, that are forms through which the substance manifests itself, that is, through which it is observable]. This one substantial form thus directly ' in-forms' the prime matter. Nevertheless prime matter is not d i r e c t l y a potency for all substantial forms whatsoever, but directly only for the elements, and only then for the mixta that originate from these elements (and even only from such mixta it is a potency for more complicated mixta). This g e n e t i c relationship points to a more fundamental and systematic n a t u r a l relationship (that is, a relationship according to natures), and this natural relationship expresses itself by the preservation of (certain) properties of the elements, alongside the new properties of the mixta. The unity of substantial form -- i.e. the presence of only one substantial form in one and the same mixtum -- does not mean that there is no gradation in the potentiality of prime matter. The 'realization' of prime matter (by getting itself informed by a substantial form, resulting in a genuine being or ens) demands a succession of s t e p s, as other potencies do [that's why all chemical (and all other) processes always proceed along certain definite lines or trajectories]. This p o s s i b i l i t y of gradation in the potency of prime matter could be derived a priori, that is by reflection alone. Its f a c t u a l i t y, on the other hand, could only be derived by experience (that is, by observation and experiment). This in contrast to geometric forms, in which we have a priori insight.
The oneness of substantial form (one form in one mixtum) has led other scholars to a different conclusion, that was as premature as the undertaking to derive from that oneness the equality of the potentiality of prime matter with respect to all substantial forms. That is to say, one held the opinion that the oneness of substantial form would imply : homogeneity with respect to properties of an extensum (that is, something that has spatial extension) when it is one substance. But from other considerations it was clear that oneness of substance does not exclude plurality of accidents [which are the above mentioned forms by which the substance is observable], and thus also of qualities. It was also evident that unity of e x t e n d e d substance does not prohibit a diversity of qualities with respect to the different parts of that substance. That is to say, heterogeneity in a given continuum is possible. Now, the oneness of substantial form is only demanded for the unity of the substance. Also this does not demand homogeneity of the (natural) body representing the substance. So the above mentioned conclusion indeed was premature.
The p o s s i b i l i t y of a heterogeneous substance, especially a mixtum, thus necessarily follows from these principles, the f a c t u a l i t y, however, not yet. For this we again need experience (observation and experiment). But the following is certain : If experience shows us an extensum that is heterogeneous, then this datum alone does not allow one to conclude that this extensum is not intrinsically one, not a continuum, because the possiblity of a heterogeneous continuum is already established. And this, it can be argued, holds for all sorts of heterogeneity, not only for temporary heterogeneity, but also for permanent heterogeneity, not only for smoothly running, but also for abrupt heterogeneity.
The fact that in mixta heterogeneity along the time dimension can exist is demonstrated by a very elementary experience [exchanging one everywhere-present-in-the-body property for another such property, that is, substitution of one property with respect to which the body is homogeneous, by another such property]. But this form of heterogeneity is not important in the present context, because such a property is not intrinsic and specific for the body that shows such heterogeneity. Also not all permanent heterogeneity is important here, for instance a scar on the body of a living being. What is relevant and important, however, is the following question : Does there exist in physical continua a permanent heterogeneity that is characteristic for the species, that is thus a p r o p e r t y in the strictest and truest sense? The possibility is certain, the actual occurrence must be revealed by experience.
This heterogeneity is important because it could have a connection with the preservation of properties of elements in a mixtum. It thus can provide a further specification of this preservation, and therefore of the relationships between elements and mixta. It will have to be called a "structure" according to the full meaning of this woord. The specific heterogeneity is a structure [. . .].
The correspondence or equality of properties between on the one hand the parts of a heterogeneous body (mixtum) and those (properties) of the components or elements of that mixtum as they were freely existing but correspond to those parts, originates in virtue of the preservation of qualities of the components or elements. Heterogeneity originates from the fact that the properties of the components or elements are not being amalgamated into a homogeneous quality. And this heterogeneity is, with respect to many qualities -- but not to all -- specific, and is thus present in all individuals of a given species. [. . . ]
Specific heterogeneity is, in line with scholastic principles, possible and even to be expected : The possibility of the existence of physical bodies that relate to each other as elements and mixtum can be derived from the principles of potency (prime matter) and its realizations (actualizations), because a potency admits steps of actualization. The prime matter of a mixtum is in near potency to its elements and only then to the mixtum. Experience then teaches us about the factuality of this relationship and the genetic connection between these bodies (elements as freely existing -- mixtum formed from these elements). The order, that becomes evident from this genetic connection is an order (a system) that originates from the degrees of correspondence or difference between the "natures" of these bodies. But, because the "nature" is origin of passive and active properties (properties in the strict sense), the relationships between bodies should also express themselves as correspondence and difference of these properties ( This is indeed what we directly observe. The "nature" is, as substance, not accessible to direct observation). An observed genetic connection will thus run parallel to an observable correspondence of properties (in the strict, and specific sense). A mixtum is thus expected to show (along with differences) correspondence of properties with its elements. So among the properties of the elements there must be some that must (in a certain degree, or completely) be "preserved" in the mixtum. Genetic connection demands this correspondence, this preservation : this necessarily follows, given the fact of the genetic connection, as this connection obtains between the mixtum and its elements.
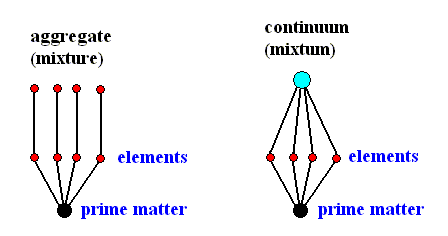
The aggregate is in fact nothing else than its elements. So apart from those properties of the aggregate that result from pure addition of element-properties (such as the weight of the aggregate), the properties of the aggregate and those of the corresponding, but freely existing 'elements', are identical.
In the case of a mixtum (perfectum), on the other hand (like a molecule or a crystal), the elements have, upon forming the mixtum, interacted with each other, resulting in a number of properties of the elements having been disappeared, but at the same time resulting in the appearance of a number of new properties, not present in the elements, and not the result of simple addition. But because the mixtum has been formed f r o m the elements, there definitely exists a genetic kinship between the mixtum and its elements, resulting in what could either be interpreted as "the preservation of a number of properties of the elements", or as "the correspondence, similarity or even identity of a number of properties of the mixtum with some properties of the elements".
During genesis of the mixtum from its elements the latter must, according to their active and passive properties, interact, until a "disposition" results that is intrinsic to the mixtum.
[
Principle of heterogeneity. (HOENEN, p.338)
We could then ask : Is it then a priori necessary that the result of the interaction is the same disposition in different elements that are going to connect to each other? There is no reason to assume this. The theoretical possibility of a heterogeneous disposition is certainly plausible. Indeed, heterogeneity is even to be expected. If this possibility will be realized, then the necessary preservation of (some) properties will necessarily be accompanied by heterogeneity. A heterogeneous mixtum (like a moleculeor crystal) will be the result of the genesis, heterogeneous in such a way that one particular part (region) of the mixtum has properties that recall, or are even identical to, the properties of some element, while other parts (regions) of the mixtum have properties that recall, or are identical to, other elements. There will be a heterogeneous s t r u c t u r e, corresponding to element-properties. And, where we have to do with properties in their strict sense, that is with specific properties, the resulting heterogeneity of the inorganic mixtum will be a specific one. And with this, the possibility of such heterogeneity is demonstrated on the basis of purely Aristotelian principles, that is, the possibility and even (after the specification of the virtual preservation of the elements in the mixtum, in which experience already plays a role) the probability of the expectation of this heterogeneity.
We do not yet assert that the molecule or the crystal is a genuine mixtum, one substance, but one thing is clear : If it is such a substance, then it can, and probably will, be specificly heterogeneous. So when we, on the basis of a more sophisticated experience, discover heterogeneity in a molecule or a crystal, corresponding to the different properties of the chemical elements, then this alone cannot be a reason to conclude that the compound is not a true mixtum, that is, a true substance in the metaphysical sense.
If the reader wants to know more about the nature of the chemical bond, he or she can consult the document The Chemical Bond in the first Series of Documents in First Part of Website .
]
We can call the above discussed specification of the Aristotelian principles of prime matter and one substantial form the "principle of the heterogeneous virtual preservation of properties", or, for short the "principle of heterogeneity" [
End of Intermezzo
(Continuing paraphrasing HOENEN's text pp.386, on the internal structure of crystals)
Intermezzo on Natural Minima
But before continuing, let us say something about the Aristotelian theory of natural minima in inorganic beings (later refined by the followers of Aristotle and accepted by St Thomas).
The continuum is infinitely divisible if we consider it as extensum only, that is as a geometric extensum (something that is spatially extended, and considered only insofar as it is so extended). Its analysis as ens, that is as a being, that has the ability to change (even radically) does not entail problems as soon as we have at our disposal the Aristotelian notion of real potency. But the continuum, when not exclusively considered geometrically or topologically, is not only ens, it is also something physical, that is, it is something specific with respect to content. That such a physical continuum must also be always divisible for us does not follow from its divisibility as pure extensum. Indeed our instruments and methods could be so imperfect that a limit is set as to a division in practise, just like our senses are imperfect such that they cannot observe the ever-smaller, while at the same time the intellect can grasp an unlimited division and thus can grasp the ever-smaller. So for our senses (or for equipment aiding them) there exist minima, but not for the intellect. But these limits of divisibility are not fundamental, they are extrinsic. Other limits can be imagined though that stem from the very nature of the physical continuum itself. This is so, because it is not a pure ens extensum. It is an extensum that possesses a specific nature.
Along these lines we arrive at a philosophy of these "physically indivisibles" and historically we find two of them : atoms [in the ancient Greek sense] and minima. The first one we encounter in the theory of DEMOCRITOS (460--371 B.C.), the second in that of Aristoteles (384/3--322/1 B.C.) and his follwers, the peripatetici.
With respect to Being or Ens, DEMOCRITOS had tried to 'save' its ability to change -- which was declared to be impossible by the Eleatic School, on the basis that a change of a being into another being would involve non-being, which does not, and cannot, exist. That is, change would be transition of being into non-being followed by the creation of being from non-being. To solve this problem, DEMOCRITOS assumed a special kind of non-being, empty space, in which unchangeable and indivisible atoms were flying around and could combine into different configurations which then represent other beings. ARISTOTLE, however, did not accept empty space as something actually existing. Nothingness does not exist. He, instead, assumed, in addition to real actual being, also a state of potential being, and could, by thus assuming two ways of being render real change intelligible : Something could be actually A, while at the same time it is potentially B. And under certain circumstances this potency could be actualized, resulting in the disappearance of the substantial form of A and the appearance of the substantial form of B while their (common) substrate remains. That which has potentiality, and is, in itself nothing else than pure potentiality, and is the mentioned common (and ultimate) substrate, ARISTOTLE called prime matter. The latter is then in potency to several forms, that, one or another, can be realized when certain conditions are met. Here, what appears and disappears are not things, not beings, but principles of being, which are themselves not beings.
Because he considered atoms as the ultimate beings, DEMOCRITOS denied unlimited divisibility. Dividing matter would necessarily halt when arrived at his atoms. But his atoms themselves possessed extension, they were not points. So as extended substances they could not be indivisible in an absolute sense. If they were so divisible we would, according to him (and to the Eleatic School), end up with an infinity of inextensa, that is, points. But these in turn cannot built up an extensum. This argument is, however, not correct, because continued division will only result in points when the division is actually carried out all the way to infinity. And this can't be done, also not conceptually. So unlimited division, in the sense of division that goes on and on, never results in points, and so never results in enforcing a continuum to be made up by points, creating the problem that it cannot be so made up (because a point has no extension, which means that addition of points never leads to something that has extension). So DEMOCRITOS' theory cannot assert absolute indivisibility of his atoms. At least geometrically they can be divided without end.
The solution can be found in the correction that Aristotle added to the Eleatic metaphysics. The same correction that could make Being changeable, also explains a form of becoming and perishing that consists in being partitioned and being united, namely the introduction of the notion of potential Being : because a continuum has potential parts (of all non-zero sizes), it can be divided into them. But this consideration does still not yield atoms, or something like it. If we consider a natural body as "ens extensum" only, then they are divisible without limit, that is, then no (natural) minima exist. Nevertheless Aristotle, and with him his later followers (the peripatetici), did justify the existence of natural minima.
But for this a natural body should not be considered as merely an ens extensum. And that broader view is possible because natural bodies indeed are not merely that. After all, the natural bodies are not exclusively ens and thus are not exclusively subject to the laws of metaphysics. They also are not exclusively extensum and thus not exclusively subject to the laws of geometry. They have, in addition to all this, a specific nature, which is the principle of activity and passivity, from which qualities and other determinations originate, which manifest that nature by rendering that body observable. So such natural bodies are also subject to the laws of their natures, and thus such a body is not only an "ens extensum" but also an "ens physicum". And these laws, that is, the laws of their natures, could modify the above derived unlimited divisibility (which certainly holds for an ens extensum).
Indeed, from observation of life forms Aristotle concludes that each species has, in addition to its own set of qualities, an intrinsic minimum (and maximum) with respect to size. Aristotle then concludes that also the constituent substances [in the chemical sense] of the organismic body must have their own minimum size, because if they were allowed to have every size whatsoever, then also an animal (of a given species) of any size could be built up by them, which contradicts experience. So the components of these living beings are not infinitely divisible. Although absolute divisibility of the smallest particles of these components is not ruled out by this argument, division of them, if it succeeds, will result in fragments having another nature. And precisely this is fully allowed and intelligible by the theory of actual and potential being. This line of thought, by the way, strongly recalls the results of modern chemistry. And so Aristotle concludes that, with respect to all natural bodies -- living or non-living -- possessing a specific nature, corresponding minima do exist. These are particles or parts that are indivisible, but not absolutely indivisible. They are relatively indivisible : namely such that continued division results in having them anatomized into specifically different substances. Aristotle further insists that the minima of specifically the same substance must be identical in size, which is no wonder, because the size of the minimum is determined by the specific nature.
The Aristotelian-Scholastic theory of natural minima automatically led to the question as to the actual size of these minima for each species of natural body. And this is already very close to the modern question about the atomic and molecular weights.
In contrast, the atomism of Democritos did not, and could not, ask this (fertile) question, because there all sizes, infinite in number, were assumed. Equal sizes (and shapes) of atoms present in some collection of them is, if it can be found at all, nothing more than a coincidence.
Here we strike at the heart of the difference between (1) (democritean) atomism in the sense of reductionism, and (2) (aristotelian) naturalism (that is, from a large range of entities we can find bodies that possess, each for themselves, a specific and intrinsic nature, a nature common -- and not coincidentally so -- to many other individual bodies, rendering this view [aristotelian naturalism] to be holistic).
Atomism, along the lines of Democritos' theory, reduces all beings, including living beings, chemical compounds and crystals, to ultimate and indivisible particles, the atoms. They move in a void and can aggregate into all kinds of configuration. Well, not into (all) KINDS (of configuration), that is, not into KINDS at all, but just into an infinity of configurations. In such atomism there are no KINDS, there is no specificity, there cannot be specificity, no common nature. In atomism, if we encounter a number of atoms that all have the same size and shape, this commoness is not the result of some common origin or common way of originating, but pure coincidence. There is, according to democritean atomism, an infinite number (or a number ever more 'approaching' infinity) of sizes and shapes. This means that not only every atom, but also every configuration of them is different from any other, not only as separated individuals, but also with respect to content. Such a theory can never lead to the modern atomic theory in which we have definite intrinsic KINDS or species of atoms and of molecules, (can never lead to modern atomic theory) despite the fact that this theory of Democritos assumes the existence of atoms. So this ancient atomic theory can never be the forerunner of the atomic theory of DALTON, which is verified by experiment and observation.
Indeed, it is the Aristotelian theory of natural minima which (qua content) automatically leads to modern atomic theory, because it does assume natures, and thus, in the end, specific atoms and specific molecules, the former as natural minima of chemical elements (as classified in the periodic system), and the latter as natural minima of molecules.
End of Intermezzo
(Continuing paraphrasing HOENEN's text pp.386, on the internal structure of crystals)
Principle of specific heterogeneity according to virtual preservation of atomic properties.
We must now unify these two specifications [as they have been expounded in the two intermezzo's].
From TOLEDO (immediately after the Middle Ages, 1579) we can hear in what way Aristotelian medievals already correctly imagined the generation of a mixtum (chemical compound or crystal) : the bulk elements are split up into their minima, these come to lie next to one another, then the minima of the one element interact with the minima of the other, and they change each other's qualities. The resulting properties will be specific for the chemical compound that emerges. We already saw during the derivation of the principle of heterogeneity that we can expect the following : Change of properties of the elements will not lead to a homogeneous property of the result, but to a specificly-heterogeneous one, indicated in the principle of heterogeneity. Well, according to the idea of the generation of a mixtum, as related by Toledo, the result will be this : There will be generated minima of the mixtum, which each for themselves comply with the demands of the principle of heterogeneity. Namely in this way : Properties of the periphery of the participating atoms will have changed, those of more central parts, and, still more probable, those of the nucleus, will have changed in a lesser degree, or, possibly not at all. And this heterogeneous complex then is, as expressed by the medievals, the "intrinsic", that is, the specific "disposition" of the minimum of the chemical compound, which disposition is preserved in that compound. The principle of heterogeneity thus will hold for the minima of the compound, the molecules. That is, each individual molecule of a chemical compound complies with the principle of heterogeneity. And this not only for the density, but also for other properties. Which properties, must be revealed by sophisticated experience, where the probability is high that the properties of the atomic nucleus will be totally preserved [implying that the corresponding natures are preserved. But in fact they are not preserved. They belong to the nature of the molecule. The properties that flow from it are properies of the molecule, and are identical to those of the atomic nuclei only with respect to their qualitative content. This identity qua content is to be expected on the basis of the genetic relationships obtaining between the compound and its atoms].
So we find a more detailed elaboration of the principle of heterogeneity. While it generally had teached us about the "heterogeneous virtual preservation [virtual, because it is not genuine preservation] of properties" of the elements, now we discover the heterogeneous virtual preservation of single atomic properties (namely those of the nuclei). In this way we arrive at the concept of "virtual atoms in the continuous molecule of the mixtum". This will have a heterogeneous structure according to virtual atoms. And if there does not emerge a single molecule (many of them together forming an aggregate -- the bulk compound) but an ordering of such molecules or their atoms into a macroscopic mass (still representing the compound), that is, a crystal, then this will, also when it is a continuum, carry a p e r i o d i c heterogeneity with virtual atoms. This is, accordingly, to be expected from the theory of the medievals. In what way this periodic aspect is precisely structured, experience must decide. Well, for crystals experience teaches us -- on the basis of the necessary elements that we found in the crystallographic theory (this is a theory that reveals the immediate causes of phenomena) -- the following : That periodic heterogeneous structure is in crystals a reticularly symmetric one.
And so we see that also this further specification of the atomic theory perfectly fits in the Aristotelian principles.
So now we have seen (while following HOENEN) how the general internal structure of crystals is fully compatible with the Aristotelian-Thomistic metaphysics. And (rightly) supposing that crystals are genuine continua (as we discussed above), we must conclude that its atomic constituents exist only virtually in the crystal, while all properties deducible from it and observed during investigation of it, are (actual) properties of that crystal.
The theory of the Implicate Order is expounded in Third Part of Website , and further elaborated (with respect to Holistic Simplification) in Part XXIX Sequel-4 of present Part of Website.
The Aristotelian-Thomistic Metaphysics is an ontology of the individual thing, rather than an ontology of Layers of Being. It is a general study of things in terms of their intrinsic natures. It is introduced and expounded in First Part of Website and it is much further elaborated in Fifth Part of Website on the basis of the theory of Being in Aristotle's Metaphysics as expounded by J. OWENS, The Doctrine of Being in the Aristotelian "Metaphysics", 1951, 1978, and on the basis of the expositions by P. HOENEN, Philosophie der Anorganische Natuur (in Dutch) (philosophy of the inorganic nature), 1947, A. van MELSEN, Van Atomos naar Atoom (in Dutch) (From atomos to atom, The history of the concept of Atom, 1949, A. van MELSEN, Natuurfilosofie (in Dutch) (philosophy of nature), 1955, and of other authors.
The next documents continue the study of ontological Layers, thereby further preparing for the Crystal Analogy (comparison of crystals and organisms).
The present document is concluded by a table displaying the classification of snow crystals.
Classification of Snow Crystals.
Despite their overwhelmingly morphological diversity, snow crystals can be classified, because certain definite key features can always be recognized in any collection of snow crystals, that is, they keep cropping up as we scrutinize any large harvest of snow crystals.
By clicking the next six 'buttons' one after another, the reader can inspect a proposed snow-crystal classification system. It is an extended version of NAKAYA's table. The extension is done by C. MAGANO and C. W. LEE. The resulting table is given in LIBBRECHT, K., The Snowflake, 2003, p.63. It consists of six columns :
First Column (click on image, to enlarge it, and scroll)
Second Column (click on image, to enlarge it, and scroll)
Third Column (click on image, to enlarge it, and scroll)
Fourth Column (click on image, to enlarge it, and scroll)
Fifth Column (click on image, to enlarge it, and scroll)
Sixth Column (click on image, to enlarge it, and scroll)
At the entry P6c I found a mismatch : In Libbrecht's reproduction of the table it there read : Stellar crystal with spatial dendrites. Here, obviously, "dendrites" must be replaced by "plates", as is done in our reproduction.
Summary
Apart from the Fundamental Categories, that pervade all Layers, including the Mathematical, the Inorganic category Layer contains many general categories : First of all those general categories that pervade all real-world Layers (Inorganic, Organic, Psychic and Super-psychic), such as Time (which is not analysed here, but taken for granted) and Process. Then we have the general category of physical Space (also not analysed here, but taken for granted), which is present in the Inorganic and Organic. Further the following general categories :
Process (already mentioned),
Causality (causal process),
Regular Causal Process (dynamical law),
Simultaneous Interdependency (Wechselwirkung), and
Intrinsic Being (dynamical system).
Apart from these general categories, the Inorganic also contains many special categories, like Regeneration, Growth, the Colloid State, the Crystalline State, Intrinsic Shape, Intrinsic Symmetry and Promorph (the latter five are extensively treated in earlier documents of the present Series).
The treatment was not, and cannot be, exhaustive, but we hope to have presented the main features of the Inorganic. They will play a role in comparing the Organic with the Inorganic.
Having discussed some important categories of the Inorganic Layer (present and previous documents), in the next document we will turn to a discussion of some important categories of the Organic Layer.
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-34.