

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Isosceles Trapezium (Bilateral Tetragon)
We will now investigate two-dimensional crystals with an intrinsic shape according to an isosceles trapezium (bilateral tetragon) as to their possible promorphs, but, as in the foregoing, limiting ourselves to holomorphic crystals, which means that we will only investigate crystals of which their intrinsic symmetry is the same as the symmetry of their intrinsic shape. In the present case this means that our bilaterally tetragonal (isoscelesly trapezoid) crystals will have D1 intrinsic symmetry (while in other cases -- meromorphic crystals -- this symmetry could be according to C1 (the Asymmetric Group), depending on the crystal's internal structure).
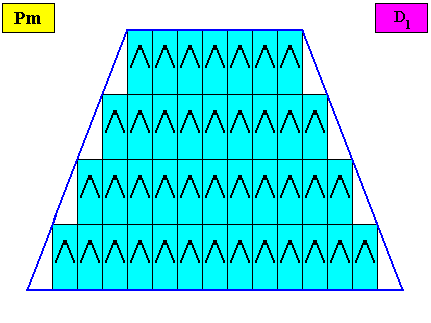
Figure above : Microscopic view of a two-dimensional isoscelesly trapezoid (bilaterally tetragonal) D1 crystal consisting of the periodic stacking of rectangular building blocks, provided with D1 motifs (black). These D1 motifs represent the translation-free residue of the crystal (all the same whether it belongs to the plane group Pm, Pg or Cm), and in this example the residue has two antimers. As drawn, the crystal belongs to the plane group Pm (primitive rectangular lattice, pattern of symmetry elements : mirror lines only, all of them of the same type). So the crystal of this example itself has two antimers and is thus non-eupromorphic (because the crystal's intrinsic shape suggests four antimers). Because the building blocks are in fact very small (i.e. in crystals they have microscopic dimensions), all the crystal faces are macroscopically smooth.
The intrinsic shape of our crystal is that of an isosceles trapezium or (equivalently) a bilateral tetragon. The grammatical adjective of the latter would be "bilaterally tetragonal" as in "bilaterally tetragonal crystal" (where "bilaterally" is an adverb). But because such a crystal itself is tetragonal as well as bilateral, we can legitimately use the expression "bilateral tetragonal crystal", which then, as a convenient term, we will use in what follows.
By removing the lattice connection lines (indicating the building blocks) and the motifs, we obtain a macroscopic view of this crystal :
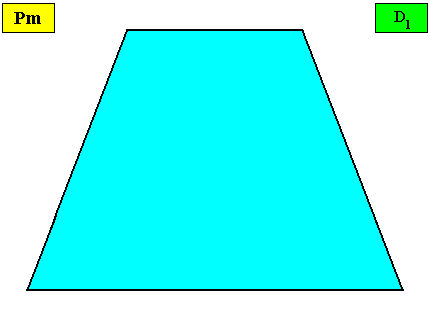
Figure above : Macroscopic view of the bilateral tetragonal crystal of the previous Figure.
The pattern of symmetry elements (with respect to the point symmetry) of our bilateral tetragonal D1 two-dimensional crystal is given in the next Figure.
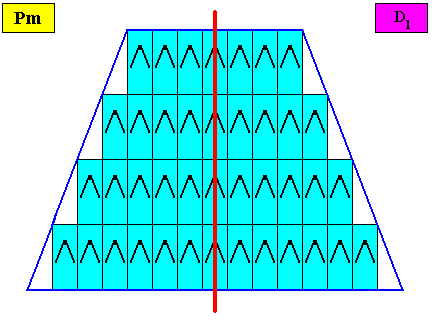
Figure above : Pattern of symmetry elements of the above given bilateral tetragonal D1 two-dimensional crystal. Its consists of one mirror line (red) only.
Three crystallographic Forms are needed to construct the outline of the bilateral tetragonal crystal, as the next Figure shows.
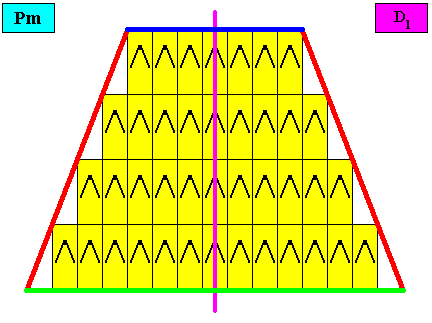
Figure above : Three crystallographic Forms (red, dark blue, green) are needed to construct the faces of our bilateral tetragonal D1 two-dimensional crystal : An initially given oblique face (red, not parallel, neither perpendicular to the mirror line) implies one more face in virtue of the mirror line, resulting in one open Form consisting of two faces (red). Then a second initially given face (dark blue) will not imply yet another face, so we then have a second Form consisting of one face only. Finally, in the same way a third initially given face (green) directly represents one Form. These three Forms combine to give our bilateral tetragonal crystal.
Possible a n t i m e r c o n f i g u r a t i o n s for holomorphic bilateral tetragonal two-dimensional crystals.
Two antimers.
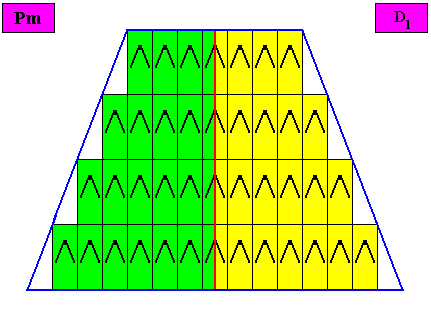
Figure above : A bilateral tetragonal D1 two-dimensional crystal. The case of t w o congruent (symmetric) antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D1 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that two antimers (related to each other by a reflection) can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests four antimers, while in fact there are only two.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :
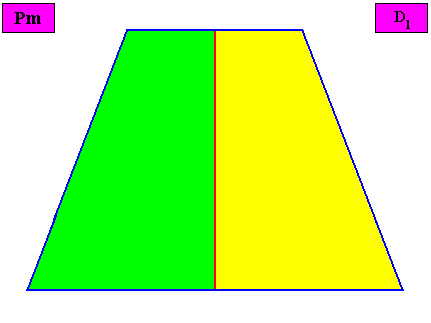
Figure above : Macroscopic view of the bilateral tetragonal D1 two-dimensional crystal of the previous figure, with two congruent (symmetric) antimers (green, yellow).
The promorph of the above bilateral tetragonal non-eupromorphic crystal is (as two-dimensional analogue) belonging to the Allopola Zygopleura eudipleura. This promorph is depicted in the next Figure.
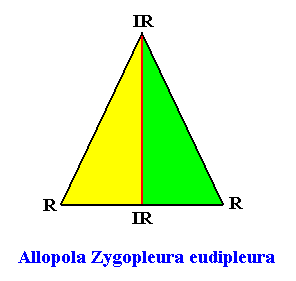
Figure above : The promorph of the bilateral tetragonal crystal with two antimers. It is an isosceles triangle (half a rhombus) and as such the two-dimensional analogue of the isosceles pyramid (half a rhombic pyramid), which represents the promorph of corresponding three-dimensional crystals or other objects. Note the difference in shape between this promorph (isosceles triangle ( = isosceles trigon) and that of the crystal (bilateral tetragon, or equivalently, isosceles trapezium) of which it is the promorph. Radial (R) and interradial (IR) directions are indicated.
Six antimers.
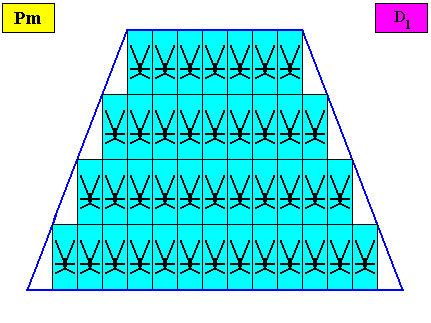
Figure above : A two-dimensional bilateral tetragonal crystal with intrinsic D1 symmetry. Its D1 motifs (black) have six antimers. Microscopic view.
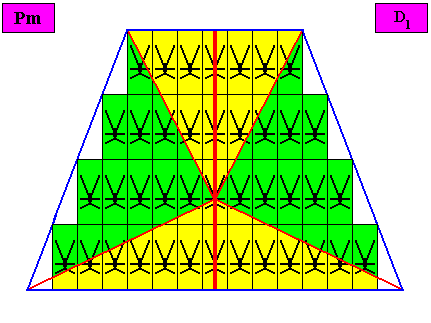
Figure above : The bilateral tetragonal D1 two-dimensional crystal of the previous Figure. The case of s i x similar antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue of the crystal) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers, is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D1 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that six antimers can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests four antimers, while in fact six are present. These six antimers are indicated by means of an alternative set of colors (green, yellow, blue) in the next Figure.
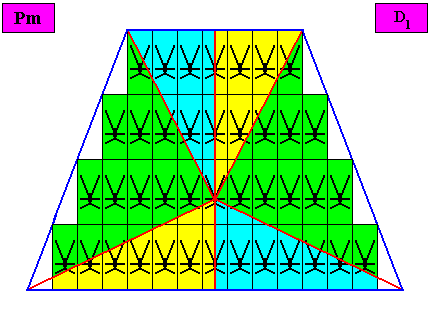
Figure above : Same as previous Figure. The six antimers are indicated by the colors green, yellow and blue.
The next Figure is the same as the previous Figure, but now with the lattice lines and motifs omitted and in this way presenting a macroscopic view of the crystal.
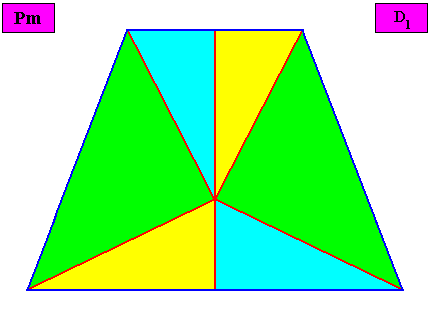
Figure above : Macroscopic view of the bilateral crystal under investigation. The non-congruity of the six antimers (green, yellow, blue) is clearly visible.
The promorph of the above bilateral tetragonal non-eupromorphic crystal with six antimers is (as two-dimensional analogue) belonging to the Allopola Amphipleura hexamphipleura (Allopola hexamphipleura). This promorph is depicted in the next Figure.
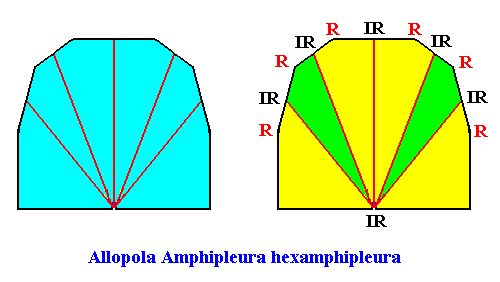
Figure above : The promorph (two images) of the bilateral hexagonal crystal with six antimers. It is half a 12-fold amphitect polygon and as such the two-dimensional analogue of half a 12-fold amphitect pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the (slight) difference in shape between this promorph (half a 12-fold amphitect polygon) and that of the crystal (bilateral hexagon) of which it is the promorph. Radial (R) and interradial (IR) directions are indicated.
Four antimers, radial configuration.

Figure above : A bilateral tetragonal two-dimensional D1 crystal. Its D1 motifs (black) have four radially arranged antimers. Microscopic view.
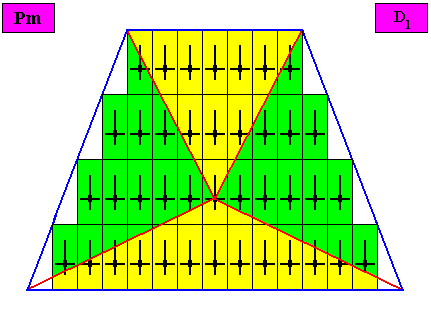
Figure above : The bilateral tetragonal D1 two-dimensional crystal of the previous Figure. The case of f o u r similar antimers (green, yellow) in radial configuration. Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue of the crystal) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers, is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D1 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that four radially arranged antimers can be distinguished in it. The crystal is eupromorphic because its intrinsic shape suggests four antimers, which are indeed present.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :
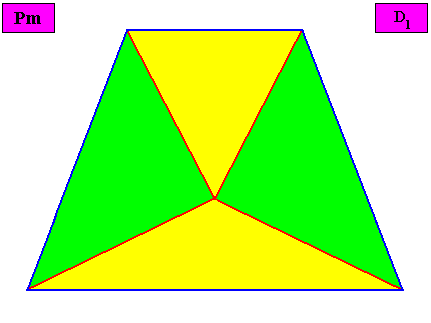
Figure above : Macroscopic view of the bilateral tetragonal D1 two-dimensional crystal of the previous Figure, with four radially arranged antimers (green, yellow).
The promorph of the bilateral tetragonal crystal is (as two-dimensional analogue) belonging to the Allopola Zygopleura Eutetrapleura radialia and is depicted in the next Figure.
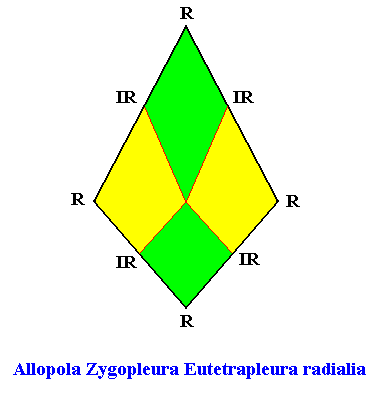
Figure above : The promorph of the bilateral hexagonal crystal with four radially arranged antimers (previous Figures). It is a bi-isosceles triangle and as such the two-dimensional analogue of the bi-isosceles pyramid which is the promorph of corresponding three-dimensional crystals or other objects.
Four antimers, interradial configuration.
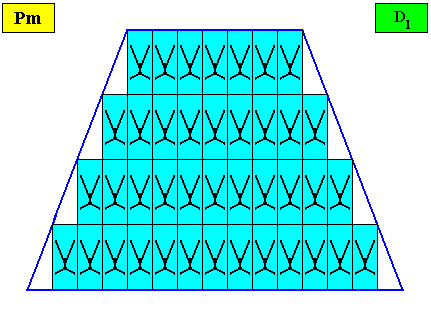
Figure above : A bilateral tetragonal two-dimensional D1 crystal. Its D1 motifs (black) have four interradially arranged antimers. Microscopic view.
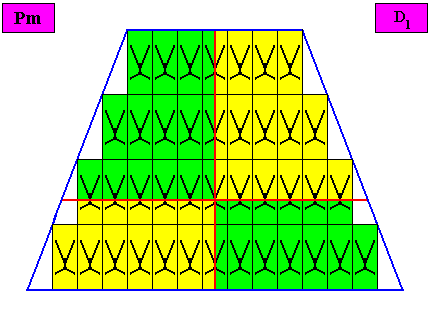
Figure above : The bilateral tetragonal D1 two-dimensional crystal of the previous Figure. The case of f o u r similar antimers (green, yellow) in interradial configuration. Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue of the crystal) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers, is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D1 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that four interradially arranged antimers can be distinguished in it. The crystal is eupromorphic because its intrinsic shape suggests four antimers, which are indeed present.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :
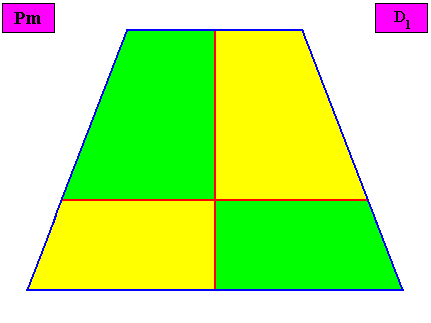
Figure above : Macroscopic view of the bilateral tetragonal D1 two-dimensional crystal of the previous Figure, with four interradially arranged antimers (green, yellow).
The promorph of the bilateral tetragonal crystal is (as two-dimensional analogue) belonging to the Allopola Zygopleura Eutetrapleura interradialia and is depicted in the next Figure.
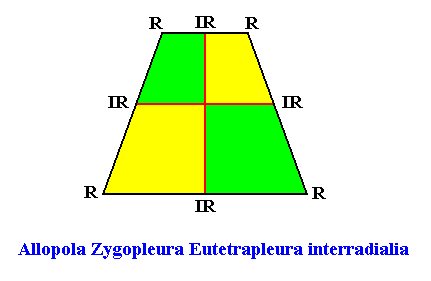
Figure above : The promorph of the bilateral tetragonal crystal with four interradially arranged antimers (previous Figures). It is an isosceles trapezium and as such the two-dimensional analogue of the isoscelesly trapezoid pyramid which is the promorph of corresponding three-dimensional crystals or other objects. Here the intrinsic shape of the crystal is the same as that of its promorph (both an isosceles trapezium, or equivalently, a bilateral tetragon).
Three antimers.
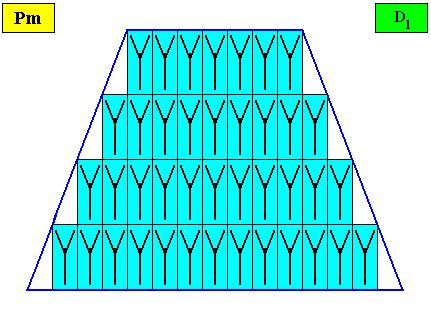
Figure above : A bilateral tetragonal two-dimensional D1 crystal. Its D1 motifs (black) have three symmetrically arranged antimers. Microscopic view.
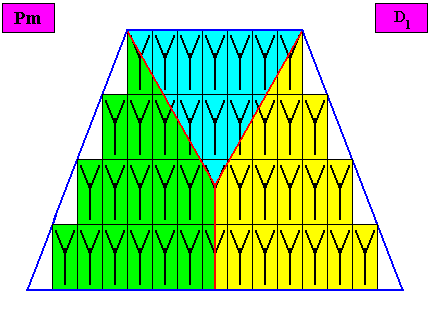
Figure above : The bilateral tetragonal D1 two-dimensional crystal of the previous Figure. The case of t h r e e similar antimers (green, yellow, blue). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue of the crystal) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers, is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D1 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that three similar antimers can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests four antimers, while in fact there are only three present.
The next Figure gives an alternative distribution of the three (macroscopical) antimers :
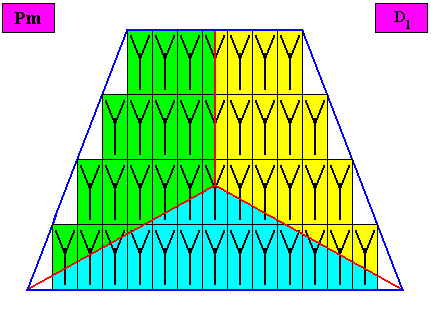
Figure above : The bilateral tetragonal D1 two-dimensional crystal under investigation. Alternative distribution of the three (macroscopic) antimers (green, yellow, blue).
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :
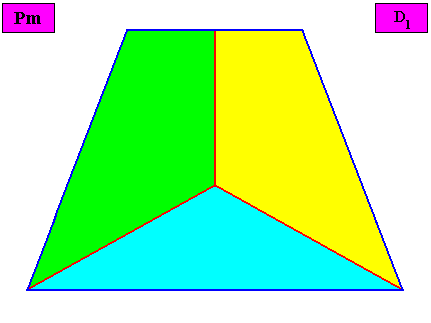
Figure above : Macroscopic view of the bilateral tetragonal D1 two-dimensional crystal of the previous Figure, with three symmetrically arranged antimers (green, yellow, blue).
The promorph of the bilateral tetragonal crystal is (as two-dimensional analogue) belonging to the Allopola Amphipleura triamphipleura (Allopola triamphipleura) and is depicted in the next Figure.
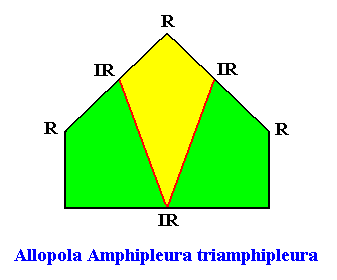
Figure above : The promorph of the bilateral tetragonal crystal with three similar antimers (previous Figures). It is half a six-fold amphitect polygon and as such the two-dimensional analogue of half a six-fold amphitect pyramid which is the promorph of corresponding three-dimensional crystals or other objects.
In the next document we will discuss the eighth crystal shape of our list (as given in Part XVI ) , viz. the isosceles triangle, with respect to intrinsic symmetry and promorph in holomorphic two-dimensional crystals having this shape intrinsically.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIII.