

e-mail :

Sequel-23 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-23) further elaborates on the analogy between crystals and organisms.
Sequel to the Preparations (XI) to the Repertoire of the Crystal Analogy
Solutions, Colloids and Surface Tension
In the crystal analogy to be systematically discussed (along the lines of PRZIBRAM, 1926) in the next document, crystallization from solutions is often mentioned. In addition to solutions also colloids are mentioned, because they are supposed to represent a more or less typical state of matter in organisms. Consequently, in the present document we will give some introductory facts concerning the states of solution and of colloids. These facts are largely taken from OUELLETTE, R., 1970, Introductory Chemistry, Chapter 8.
In chemistry we have mixta and mixtures.
A mixtum is a chemical compound. Its constuents (atoms or ions) are connected to each other by chemical bonds, of which there are several different types. The result is a molecule. The constituents of a molecule show definite proportions determined by the chemical valences of them. So a molecule is definitely not a mixture.
In a mixture the constituents are not chemically bonded, implying that their proportions can vary continuously between broad limits.
There are two main types of mixtures, viz., heterogeneous mixtures and homogeneous mixtures.
A true heterogeneous mixture is a dispersion of macroscopic entities, like a mixture of sand and salt.
A true homogeneous mixture is a dispersion of molecular elements (they can be atoms, ions or molecules). So it is homogeneous all the way down to the molecular level. Such mixtures are called solutions, like a solution of salt in water, or like the atmosphere, which is a solution of gases.
A colloid is an intermediate state of aggregation between a true heterogeneous mixture and a true solution. That is roughly to say that the size of the constituents is about intermediate between that of true solutions and that of true heterogeneous mixtures. Whereas true solutions are dispersions of atoms, ions or molecules, colloids are dispersions of aggregates of molecules. Among the commonly encountered colloids are whipped cream, mayonnaise, milk, aerosol sprays, glue and starch.
Solutions
The substance present in the largest quantity in a solution is referred to as the solvent. The substance dispersed in the solvent is called the solute. It is clear that these concepts do not have an absolute status, as we can see in the case of a solution where the quantities of the two substances are equal. Nevertheless they are convenient terms. In every conceivable case of a solution we have to do with a system of two components (in the simplest case) for which the composition is variable and continuous over the entire possible range of quantities.
There are many types of solute-solvent systems possible, because matter exists in three states.
Solutions of two gases (which are entirely equivalent to mixtures of two gases) have certain properties among which the partial pressures of the components.
There are no true solutions of a liquid in a gas or a solid in a gas. Such systems are colloids, which will be discussed later.
The most frequently encountered solutions are those of any of the three states of matter in a liquid solvent. Air (gas) dissolves in water (liquid solvent) the same as alcohol (liquid) and salt (solid).
While liquid solutions are more common, solid solutions involving all three states of matter as solutes are known :
There are many cases of solids dissolving in solids to form alloys. For example, a 16-carat gold piece consists of 16 parts of gold and 8 parts of copper by weight. Brass is a solution of copper and zinc, while bronze is a solution of copper and tin. Coinage metal always has been a solution of a precious metal and varying amounts of other metals to improve the durability of the coins.
The physical process that occurs when a solute is dissolved in a solvent can be pictured in terms of the kinetic molecular theory of matter. If a solid is placed in the proper solvent, it dissolves. This indicates that the forces maintaining the molecules in a crystal lattice are exceeded by a somewhat stronger interaction between them and the solvent molecules, causing the solute to be dispersed throughout the solvent (It is important always to realize that a solution is just a (homogeneous) mixture of components, one of which we call a solvent, although this does not attribute a special status to the latter. In a given solution the status of the 'solvent' and that of the 'solute' are the same.). If the quantity of solute relative to solvent is sufficiently large, the solid eventually ceases to dissolve. At this point the solution is said to be saturated. A solution is saturated when the concentration of dissolved solute is such that it can exist in equilibrium with excess undissolved solute.
While no further change is apparent in a saturated solution, two dynamic processes are continuing. Some of the solid is still dissolving in the solvent while some of the dissolved solute is returning to the solid lattice. The system is in a state of dynamic equilibrium, as can be demonstrated by placing an irregularly shaped crystal in the saturated solution and watching it change in shape. It retains its mass despite its obvious change. Some of the solid must be dissolving while a compensating precipitation of the solute is occurring (OUELLETTE, p.173). I would add, that this is an important phenomenon in the context of the crystal analogy : A fragmented crystal restores itself, i.e. it restores its intrinsic shape, even when there is no nutrient available (because the solution is not supersaturated but just saturated). This is a clear case of regeneration as we see it also in many organisms (especially lower organism). We will discuss this phenomenon further where it turns up in the ensuing systematic discussion of the crystal analogy along the lines of the mentioned book of PRZIBRAM.
The solubility of a solute in a solvent is its concentration in a saturated solution. This solubility can be shown experimentally to be a function of the nature of the solute, the nature of the solvent, the temperature, and the pressure. All of these factors must be considered in establishing a model for the dissolution process.
The separation of solute particles from each other requires energy. Likewise, the solvent molecules must be separated in order to provide for the introduction of the solute particles, a process that also requires energy. These two facts suggest that there must be a solute-solvent interaction in which energy is released (to balance the just mentioned energy requirements). If there were no net attraction (which corresponds to the energy release) between solvent and solute particles, energy would be required for the dissolution, and the substance would not be expected to dissolve spontaneously. However, since the tendency for a spontaneous change is controlled not only by energy release but by entropy changes as well, there are solution processes in which energy is not released. A solution is more disordered than either the pure solvent or solute and, therefore, the solution is a more probable state for the substances. Dissolution frequently occurs because of an entropy increase in spite of the fact that solvent-solute attractions are not sufficiently large to counteract the energy required to separate solute particles from each other and solvent molecules from each other.
There are several factors that have an effect on solubility, namely pressure, temperature, and solvent polarity. Here we only discuss the latter two.
Effect of temperature on solubility
The solubility of many gases in water decreases with increasing temperature. As water is warmed, the dissolved air can be seen to form bubbles and escape from the surface of the liquid. While the solubility in other solvents often exhibits the same behavior, there are cases known where the opposite effect is observed.
There is no general rule for the solubility changes of liquids (in liquids or in solids) and solids (in liquids or in solids) with temperature (Just as a solution of a gas in a liquid is itself a liquid -- i.e. the resulting solution is a liquid --, a solution of a solid in a liquid is a liquid, while a solution of a solid in a solid is a solid, and a solution of a liquid in a solid is a solid. If the latter case is actually possible I don't know).
Quite often solubility increases with increasing temperature.
The relationship between solubility and temperature can be predicted from the heat of solution of the substance in the solvent. The heat evolved or absorbed when the solute dissolves to produce a saturated solution is called the heat of solution. If heat is evolved when solution occurs, the heat of solution is a negative quantity :
solute + solvent = solution + heat ................. negative heat of solution.
heat + solute + solvent = solution ................. positive heat of solution.
When potassium chloride dissolves in water, the temperature of the solution decreases, indicating that heat is absorbed and that an endothermic process has occurred. Therefore the heat of solution of potassium chloride is positive. Thus, if heat is supplied to increase the temperature of the solution, Le Châtelier's principle predicts that the solubility of the potassium chloride should increase. The increased dissolution absorbs heat energy, thus decreasing the change imposed on the system. The heat of solution of cerium sulfate is negative, and its solubility decreases with increasing temperature, as would be expected from the proper application of Le Châtelier's principle.
Effect of solvent polarity on solubility
A maxim of the chemistry laboratory is that "likes dissolve likes" (OUELLETTE, p.177). This generalization is reasonable since molecules of solute that are similar to molecules of solvent are expected to be better able to coexist in the same phase. Water is classified as a polar solvent since it consists of a collection of polar molecules (i.e. molecules that are electrically positive at one side and negative at the other). It is a good solvent for polar solutes, ionic compounds, and substances that can produce ions in water. So salt (NaCl), which is an ionic compound, easily dissolves in water. Carbon tetrachloride (CCl4), which can be used to remove grease spots from clothes, is a poor solvent for salt. However, fats and waxes readily dissolve in this nonpolar solvent because they are relatively nonpolar substances themselves.
When water dissolves an ionic compound such as sodium chloride (salt, NaCl), the sodium and chloride ions are dislocated from their rigid crystal lattice structure in which strong electrostatic attractions exist between neighboring ions. In order to overcome these forces, water is postulated to be oriented about the ions in solution : A sodium ion, being positive, is surrounded by polar water molecules which point with their negative sides to these ions, while a chloride ion, being negative, is surrounded by water molecules that point their positive side to it. In the dissolution process, water weakens the interionic attractions and separates the ions from the crystal lattice by the development of attractions between the ions and the water dipole. The extant faces of a sodium chloride crystal -- the cubic faces -- are electrically neutral because their aspect as they present it to the growing environment contains both sodium and chloride ions. So their surface energy is small, they are the slowest growing faces and survive during development. On the other hand, the aspect of the potential octahedron faces of a sodium chloride crystal consists either entirely of chloride ions or entirely of sodium ions, so these potential faces are electrically charged, meaning that their surface energy is large, and they will attract ions of opposite sign from the solution, so they are fast growing faces that will eventually disappear during growth.
During dissolution the water will preferably 'attack' the octahedron faces when exposed, because their surface consists of ions with the same charge (of equal sign). These ions will be more easily separated from each other (because they already repel each other in virtue of their charge having the same sign) by the (bipolar) water molecules. See also next Figure.
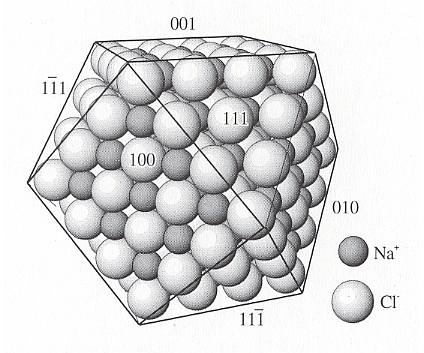
Figure above : Potential crystal faces on Halite (NaCl) (which as such is a natural found mineral and chemically identical to table salt) such as the octahedral faces (111), (11-1) and (111-), etc. (For these latter symbols see in First Part of Website, the Essay : The Morphology of Crystals ) are covered either with all Na+ or Cl- and have consequently a net charge and high surface energy. A very strong attraction for successive layers of Na+ and Cl- on the {111} faces (i.e. octahedral faces) produces high growth rates.
On the other hand, faces such as (100), (010) and (001) (i.e. the cubic faces) have equal numbers of Na+ and Cl-, are uncharged, and have low surface energy. Growth rates are slow.
(After NESSE, W., Introduction to Mineralogy, 2000.)
And apart from this we have the following : There is a dynamic of ions leaving the solid and returning to it anyway. But the water molecules will entrap the ions (as described above) that have entered the liquid as long as there are sufficient numbers of water molecules to do so. And I assume that the entrapped ions cannot easily return to the solid again.
Vapor pressure of solutions
The addition of salt or sugar to water decreases the vapor pressure of water. This can be seen in a direct comparison of the vapor pressures of water and sugar solution : We place two beakers under a bell-glass, a beaker of pure water and a beaker of a rather concentrated solution of sugar in water. Initially things are set such that the volumes of the contents of the beakers are the same. After a while we see the volume of pure water decrease, while the volume of the sugar solution increases. Eventually complete transfer of the liquid to the beaker containing the sugar solution takes place. The only possible interpretation for observed results is that the escaping tendency of water, its vapor pressure, has been reduced by the fraction of solute contained in the beaker. Therefore, the solution, which is in contact with the water molecules in the gaseous phase, eventually captures the water molecules escaping from the beaker of pure water. Of course water molecules are escaping and being captured in the liquid phase of each beaker. The net transfer results from the slower rate of escape from the solution as compared to the pure liquid. In the above experiment the bell-glass is needed to attain equilibrium between the liquid and gaseous states. The vapor pressure of water above the sugar solution is lower than that above the pure water surface, so a 'current' evolves that transports water vapor from the area above the beaker with pure water to the area above the beaker with the sugar solution. The actual water vapor pressure above the beaker with pure water will then be diminished resulting in extra evaporation of the water from that beaker. The actual water vapor pressure above the beaker with the sugar solution will have increased, resulting in more water molecules returning to the sugar solution. In the present case -- sugar solution -- we have to do with a covalent compound (sugar) that does not split into parts when dissolved. Further we have to do with a solute -- sugar -- that is itself nonvolatile, meaning that its vapor pressure (as a partial pressure above the solution) can be neglected. We thus have a mixture of two components, one of them being water, which is more or less volatile and creates a water vapor pressure, the other being sugar which does not create an extra vapor pressure.
The relationship between the vapor pressure of a solution (of a nonvolatile solute) and the vapor pressure of the pure solvent is expressed by Raoult's law :
Vapor pressure of solution = vapor pressure of pure solvent times mole fraction of solvent
where Xsolvent is the mole fraction of solvent.
The mole fraction of a substance A, XA , is the number of moles of substance A divided by the total number of moles.
When a solution contains volatile solutes both the solvent and solute exist in equilibrium with their vapors. Therefore the vapor pressure of such a solution cannot be predicted by Raoult's law as stated above. The individual vapor pressures or escaping tendencies of each component, however, should be proportional to the relative amount of that component in the system (Recall that one of these components is the solvent). It is observed often (OUELLETTE, p.179) that the total vapor pressure of a solution is equal to the sums of the individual partial pressures of the component substances as calculated by Raoult's law. The partial pressure of each substance is the product of the mole fraction of that component and the vapor pressure of the pure substance :
If a solution contains equimolar amounts of substances x and y (that is, mole fraction of x = Xx = 0.5 and mole fraction of y = Xy = 0.5, where one of these substances could be denoted as solvent), the vapor pressure can be calculated if the vapor pressures of x and y at the same temperature are known. If the vapor pressures of x and y are 80 and 20 mm mercury, respectively, the partial pressure of x will be 80 x 0.5 = 40 mm mercury, and that of y will be 20 x 0.5 = 10 mm mercury. The total vapor pressure of the solution can be predicted as 40 + 10 = 50 mm mercury.
The partial pressures of the components of a solution (again, including the solvent) are related to the vapor pressures of the pure substances and their relative amounts in solution. Since the concentration of substances in the gas phase are in the ratio of their partial pressures, and the latter depend not only on the concentration (mole fraction) of them in the solvent but also on their vapor pressure (which is -- as an intrinsic property -- the pressure that can be measured when there is equilibrium between the substance (in solution) and its gaseous phase at a specified temperature), the concentrations (in the gas phase) can be substantially different from those in the liquid solution. In the above example the mole fraction of x in the vapor phase is 0.8 (because the partial pressure was 40 for a total vapor pressure of the solution of 50 mm mercury). There is, consequently, an enrichment in the gaseous phase of the more volatile component ( The more volatile component has a higher vapor pressure : Substance x has a vapor pressure of 80 mm mercury, while substance y has a vapor pressure of 20 mm mercury). If the vapor were separated from the liquid and condensed, a partial separation of x from y would be effected. Repetition of the evaporation-condensation process would lead to a further increase in the mole fraction of x . Such a process is the basis for the distillation and separation of a volatile mixture into its components. The most volatile substance distills from the solution with the resultant residue having an increased concentration of the least volatile component.
Boiling point of solutions
The decreased vapor pressure of a solution of a nonvolatile solute means that the boiling point of the solvent must be elevated. It will require a higher temperature to raise the vapor pressure to atmospheric pressure (OUELLETTE, p.180). There is a direct relationship between the escaping tendency of the solvent molecules (vapor pressure) and the number of solute particles. Therefore, the increase in the boiling point of the solvent also is directly proportional to the concentration of solute. We can expect a higher increase of the boiling point of an aquous solution in the case where the solute is an ionic compound as compared with a non-ionic compound. That is because such an ionic compound dissociates into its corresponding ions resulting in the fact that the number of particles in the solution is higher than that of a non-ionic compound. A 1m (1 molal) aquous solution of sodium chloride (i.e. one mole of sodium chloride in 1000g of water) has twice as high a boiling point elevation as a 1m aquous sugar solution.
Freezing point of solutions
The escaping tendency of a solvent decreases upon addition of a solute both for the liquid-vapor (boiling) and liquid-solid (freezing) transformations. Therefore, the observed physical change in the case of freezing points is a decrease rather than the increase noted for boiling points. Indeed, when the escaping tendency of the particles of the liquid (the solvent) decreases, the liquid will 'try' to remain liquid toward both sides of the temperature range :
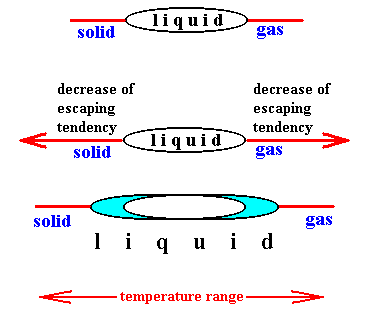
Figure above : Upon addition of a solute the escaping tendency of the particles of the solvent decreases in both transitions : boiling and melting. Therefore the temperature range for the liquid phase extends in both directions, meaning that the boiling point of the solution increases while its freezing point decreases. "Escaping" is here two-fold : (1) escaping from the liquid into the gaseous phase, and (2) escaping from the liquid into the solid state. In both cases -- and with nonvolatile solute -- we have to do with a demixing phenomenon, i.e. with the separation of solvent particles from solute particles.
The decrease in the freezing point can be qualitatively understood as follows : The solute particles are -- because we have to do with a solution, i.e. a homogeneous mixture -- uniformly dispersed between the solvent particles. Therefore, the latter particles are kept apart from each other preventing the solvent to gether its particles into a regular array, that is, preventing the solvent from freezing.
Osmotic pressure of solutions (OUELLETTE, p.183/4)
If a solution such as sugar in water is separated from pure water by a semipermeable membrane, a membrane through which water can pass but not other large molecules such as sugar (See next Figure), the height of the solution increases at the expense of the pure water.
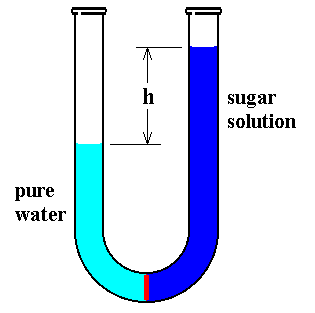
Figure above : Osmotic pressure of a sugar solution.
A U-formed tube, open at both ends, contains pure water in its left leg, separated by a semipermeable membrane (red) from a sugar solution in its right leg. Initially the volumes of both were equal. But a net water flow from left to right increases the volume of the solution at the expense of that of the pure water, until a balance is established.
The water remains pure because sugar molecules cannot pass through the membrane. The water molecules apparently can cross and do so up to a point by a process called osmosis. Eventually no further transfer occurs, and the level of the solution remains at a specific height above that of the water. The difference in the levels is a measure of the tendency of water to go through the membrane to dilute the solution. The height difference of the liquids exerts a pressure difference at the membrane that counterbalances the tendency of water molecules to continue to dilute the solution.
Colloids
While all solutions are homogeneous mixtures, a colloid (also being a mixture) is an intermediate state of aggregation between heterogeneous mixtures and true solutions. This state of matter can be regarded as a suspension whose lifetime is finite. Eventually most colloids separate into their component substances. Whereas a true solution is a molecular dispersion whose properties are uniform down to the molecular level, colloids consist of dispersions of aggregates of molecules.
Let us be more precise about the nature of colloids.
When water and sand are mixed, a suspension of the sand results that separates upon standing. Most samples of sand settle in seconds or minutes. However, in the case of very fine sand resulting from the grinding action of glaciers, a long-lived suspension called glacial milk is produced. The reason the particles remain suspended is that their sizes are comparable to atomic and molecular dimensions. The motion of the solvent molecules continually jostles the minute particles, counteracting the tendency of gravity to make them settle.
The size of atomic or molecular species is in the order of 10-7 cm in diameter. When aggregates of matter of 10-7 to approximately 10-5 cm in diameter are suspended in liquids, an intermediate state between heterogeneous mixtures and true solutions results. Substances in this state are referred to as colloids, colloidal solutions, or colloidal suspensions (OUELLETTE, p.185). Among the commonly encountered colloids are, as enumerated earlier, whipped cream, mayonaise, milk, aerosol sprays, glue, and starch. Some more examples are given in the next table.
| Dispersion Medium | Dispersed Phase | Example |
| gas | liquid | fog |
| gas | solid | smoke |
| liquid | gas | whipped cream |
| liquid | liquid | milk |
| liquid | solid | glue |
| solid | gas | foam rubber |
| solid | liquid | cheese |
| solid | solid | colored glass |
An important means to make colloidal solutions (colloidal suspensions) are surfactants.
We now come to the making of colloidal solutions (See BALL, Ibid, pp.227).
If the amount of surfactant in solution is increased, there comes a point at which it can no longer all accumulate at the surface. The surfactant molecules must then find other ways of shielding their hydrophobic tails from water. One such way is for the molecules to aggregate into clusters in which the tails point inwards, with the headgroups forming a water-soluble shell. These structures are called micelles, they form a colloidal suspension of surfactant in water. One such micelle is depicted in the next Figure.
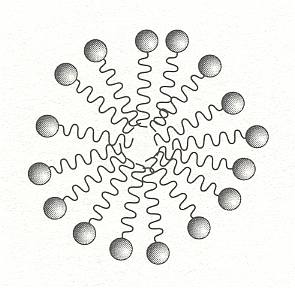
Figure above : Surfactants in water may shield their hydrophobic tails by forming micelles, clusters in which the tails are buried in the interior.
(After BALL, 1994.)
The formation of micelles, which occurs when the amount of surfactant exceeds the 'critical micelle concentration', can be detected by passing a beam of light through the solution, whereupon one can see the path of the beam clearly illuminated. This effect was discovered in the nineteenth century by the British physicist John Tyndall, and is due to the scattering of light by the micelles. Because they have dimensions similar to the wavelength of visible light, many colloidal systems scatter light strongly, and the Tyndall effect is a characteristic signature of their presence.
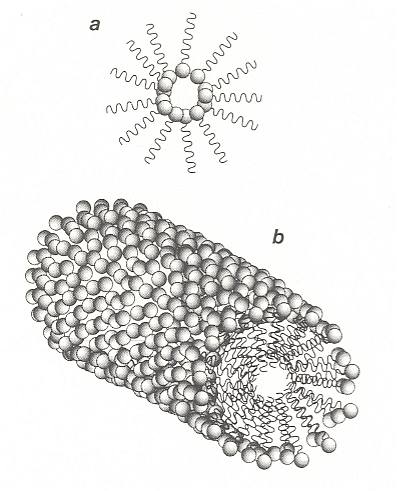
Figure above : (a) : A reverse micelle, formed by surfactant molecules in an oily solvent.
(b) : A cylindrical micelle.
(After BALL, 1994.)
When in close proximity, cylindrical micelles may line up like stacks of logs, forming structures similar to liquid crystals (which were discussed in Part XXIX Sequel-14 ).
This completes our exposition about colloids.
Surface Tension
Surface tension plays an important part in PRZIBRAM's crystal analogy (discussed in the next document), so we will expound it here to become well prepared.
For this we will use what D'Arcy Wentworth THOMPSON has written about it in his remarkable On Growth and Form, 1942 (first publication in 1917). An abridged edition of this work was published in 1961 and subsequently reprinted : On Growth and Form by D'Arcy Wentworth Thompson, an abridged edition edited by John Tyler Bonner.
It is mainly from page 49 onwards of this abridged edition that we will use D'Arcy Thompson's exposition about surface tension. We will follow his text (which is in English) very closely, coming very near to an extensive quote, but provided with extra Figures (in addition to his'), explanations and comments when necessary. We will also follow parts of D'Arcy Thompson's text in the 1942 edition not included in the abridged edition.
But before we will do so, we will first give our own understanding of surface tension (supplied with some considerations from the 1942 edition) and especially its bearing on crystal growth (not discussed by D'Arcy Thompson).
Surface-tension
An interface between two physical bodies, for example a drop of oil in water, always involves surface energy, because at such a boundary the forces, acting on each of the several molecules (or, generally, chemical motifs) do not cancel each other as they do in the interior of such a body. So a surface always has some energy cost. In addition to this, in, for example, crystals the surface generally contains dangling, i.e. unsatisfied, chemical valences, which is also an energy cost.
Now, in order to reduce this energy-cost of surfaces (i.e. to reduce the strain) the body tries to reduce the area of these surfaces (especially when there is no other way to reduce the system's potential energy), and this means the presence of a tendency towards shrinkage of such a surface, and this is surface tension.
We will see in due course that c r y s t a l s when they -- as crystals -- represent the stable state (with respect to the corresponding solution, melt, etc.) anyway, bring about a decrease in energy by g r o w i n g , despite the fact that in doing so their surface, and thus their surface energy, increases. This is because their free energy change ( DELTA Gv ), brought about by transforming from a melt, solution etc., into a crystalline configuration, if initially already negative (i.e. if conditions are such that less energy is involved in the crystalline state than in solution, melt etc.), proportionally decreases as the crystal's volume increases (because then more chemical motifs contribute to the total decrease of the free energy change of the crystal from a melt, solution etc.). While the surface energy of the crystal increases with (its) surface (involving a power of two with respect to the linear dimensions of the crystal), the absolute value of the free energy change increases with (its) volume (involving a power of three with respect to the linear dimensions of the crystal), meaning that the latter finally has the last word in determining the free energy of formation of a crystal, DELTA G (which should be negative for crystallization to continue, that is to say that the free energy of formation [from the elements] of the crystal should be, even when surface energy is accounted for, lower than the free energy of formation [from the elements] of the corresponding melt, solution etc.). The surface of the growing crystal increases steadily (and so does its surface energy), but faces with the highest surface energy grow fast, faster than those with lower surface energy, and will, when the latter grow closer and closer together, i.e. taper toward each other, grow themselves out of existence. So the crystal manages to get rid of most of its high-energy faces by just growing.
If the surface, undergoing such surface-tension that mainly expresses itself as a tendency for the surface to shrink, is c u r v e d , then it entails a pressure that is proportional to the degree of curvature. In this way a convex curvature causes a pressure inwards.
If, on the other hand, the surface is a p l a n e, then its surface tension does not bring about any pressure.
In isotropic bodies (i.e. bodies in which there are no preferred or special directions), such as water or oil droplets, the surface energy is equal with respect to all directions, and the smallest surface area enclosing a given volume (i.e. enclosing a given part or the whole of such an isotropic body) -- and thus the smallest surface energy -- is obtained when the enclosing boundary assumes the form of a sphere, if no external forces -- such as gravity -- biases the system of forces ( For a drop of fluid we can rule out the one-sided effects of gravity by letting this drop be suspended in a fluid medium of equal density, but a medium that does not mix with the droplet).
In a drop of liquid the potential energy of the system could be diminished (and so making the system more stable), and work manifested accordingly, in two ways.
First at the liquid surface, surface tension tends to set up an equilibrium of form , in which the surface is reduced or contracted either to the absolute minimum of the sphere, or at any rate to the least possible area, which is permitted by the various circumstances and conditions. And if the two bodies which comprise our system, namely the drop of liquid and its surrounding medium, be simple substances, and the system be uncomplicated by other distributions of force, then the energy of the system will have done its work when this equilibrium of form , this minimal area of surface, is once attained.
But the potential energy of the system can also be diminished (and its diminution will accordingly be manifested in work) if from any cause the specific surface energy be diminished, that is to say if it be brought more nearly to an equality with the specific energy of the molecules in the interior of the liquid mass (D'Arcy THOMPSON, 1942, p.445). Such a diminution of the specific surface-energy may be brought about in various ways (for example by the addition of surfactants, like soap, that diminish surface tension and therefore surface energy).
And yet another way to diminish surface energy is the following : Let us suppose that our liquid drop consists no longer of a single chemical substance, but contains other substances either in suspension or in solution. Suppose (as a very simple case) that it be a watery fluid, exposed to air, and containing droplets of oil : we know that the specific surface tension of oil in contact with air is much less than that of water, and it follows that, if the watery surface of our drop be replaced by an oily surface, the specific surface energy of the system will be notably diminished. Now under these circumstances it is found that (quite apart from gravity, which might cause it to float to the surface) the oil has a tendency to be drawn to the surface. And again this phenomenon of molecular attraction or adsorption represents work done, equivalent to the diminished potential energy of the system (i.e. this potential energy has been transformed into actual energy which can do work, here consisting of the accumulation of oil at the surface). In more general terms, if a liquid be a chemical mixture, some one constituent in which, if it entered into, or increased in amount, in the surface layer, would have the effect of diminishing its surface tension, then that constituent will have a tendency to accumulate or concentrate at the surface : the surface tension may be said, as it were, to exercise an attraction on this constituent substance, drawing it into the surface layer, and this tendency will proceed until at a certain 'surface concentration' equilibrium is reached, its opponent being that osmotic force which tends to keep the substance in uniform solution or diffusion. In other words, in any 'two-phase' system, a change of concentration at the boundary surface and a diminution of surface tension there, accompany one another of necessity. Positive adsorption means negative surface tension, and vice versa. Furthermore, the lowering of surface tension (as by soap) will permit, if other circumstances be the same, an extension of surface, manifesting itself in 'froth' (D'Arcy THOMPSON, 1942, p.444, 445 and 446).
In crystals on the other hand, which are anisotropic bodies, the surface energy is different in different directions (except when certain different directions are equivalent). Also here the crystal body will tend to reduce its surface area (in order to get rid of as much of its surface energy as possible). But because in some directions the surface energy is intrinsically higher than in other directions, the surface reduction will preferably take place for (crystal) faces corresponding to these higher-energy directions, i.e. for faces with higher surface energy, expressed in the fact that these faces will grow faster than others. The different surface energies of crystal faces translate in different surface tensions, But because the faces of sterro-crystals (solid crystals) are, generally, plane (i.e. not curved), surface tension there does not entail a corresponding (inward) pressure. And because faces are all there is in a sterro-crystal (because corners and edges belong to [i.e. are lost in] their adjacent faces) there are in sterro-crystals generally no curvatures at all and thus no surface-tension-caused pressures at all (Some sterro-crystals do, however, have curved faces, for example diamond crystals). Because actual shrinkage of a crystal face is hardly possible, the crystal body gets rid of the surface energy, first, and for the time being, by satisfying the dangling chemical valences (if there are any) of its faces, i.e. by letting material be deposited on the crystal faces which then chemically bonds with the material already there (In the case of ice crystals, which consist of water molecules we can say that the 'dangling hydrogen bonds' of the last layer are satisfied when a next layer of water molecules is deposited). But this results in new unsatisfied chemical valences. So eventually the only way to let the surface energy of the face disappear is to let the face itself disappear altogether. Well, indeed a crystal does the following (as we already know) : It tries to reduce the total surface energy by making the share of those crystal faces that intrinsically have the highest surface energy among all faces of the crystal as low as possible, as a result of the vanishing of all or a part of the high-energy faces.
While for isotropic bodies the result of total subjection to surface tension (shrinkage of surface) is the sphere, for anisotropic bodies such as crystals, it is the cube, prism, etc., depending on the crystal's intrinsic symmetry and its corresponding pattern of anisotropy, i.e. on the pattern of different surface tensions, or, more generally, on the pattern of surface energies. So crystals are not bodies that have "overcome" (i.e. superseded) surface tension, as is sometimes asserted. Surface tension in a crystal is just anisotropically distributed over its surface. Its value depends on direction. Therefore we will not expect that a sphere is the ultimate equilibrium form of whatever (sterro)crystal.
As has been said, in sterro-crystals surface tension cannot bring about a corresponding pressure because all faces are generally plane surfaces (but surface energy can cause some inward pressure resulting from the biased distribution of attractive forces that are experienced by chemical motifs of the crystal's surface layer as compared with the even distribution of these forces as experienced by all chemical motifs that lie in the crystal's interior (See Figure further down). PRZIBRAM (1926), in his crystal analogy, speaks about the surface-tension pressure in crystals, saying that the corners represent loci of high curvature and consequently of high inwardly directed pressures, while the faces would represent loci of low curvature and consequently of low inwardly directed pressures. But, according to me this is incorrect because, as has been said earlier, a crystal boundary (of a freely developed crystal) consists of faces only, and because they generally are plane, there can be no surface-tension pressure.
So in sterro-crystals it is the pattern of (different) surface energies in different directions (expressing the crystal's anisotropy), that causes a corresponding pattern of relative growth rates, and this in turn determines the final shape of the crystal (when the environment is uniform), or, equivalently it determines the crystal's intrinsic shape.
In isotropic bodies the surface energy, and therefore the surface tension, is uniform, i.e. not, in a constant and regular way, different in different directions (provided there are no (irregularly) localized chemical differences present), and the best ways of reducing it is either shrinkage of the surface, and in this way putting the surface tension to work, or the above described adsorption, that is to say to reduce the specific surface tension by (the effect of) the accumulation of appropriate substances in the surface layer, and in this way putting the surface energy to work. These two ways (shrinkage, resulting in some absolute or relative form-equilibrium, and adsorption, as a result of the accumulation of a certain substance in the surface layer) are, generally, better possible in liquids than in solids, although in the latter adsorption is possible (for example the occlusion of gases by charcoal).
If in an isotropic body shrinkage is allowed to proceed to completion, the shape of the body has become a sphere, and otherwise the shape approximates to it in several ways. All this results, in isotropic bodies, in more or less smoothly curved shapes or contours, unlike those in sterro-crystals. Because in organisms we have to do with watery or gell-like more or less isotropic materials, their shapes often show rounded contours. But of course this is not typically (and exclusively) organic : All kinds of non-living substances can assume rounded forms, like oil globules or water droplets. And even rheo-crystals (i.e. liquid crystals) are rounded precisely there where they are isotropic (mostly their projection along their main axis).
Summary of some findings with respect to surface tension in sterro-crystals.
In Part XXIX Sequel-14 we discussed the net decrease of potential energy ( DELTA G ) of a crystal with respect to its corresponding melt or solution, necessary for the crystal to be stable and crystallization to proceed further. This DELTA G consists of two terms,
(1) the so-called volume term ( DELTA Gv ) which is the free energy-difference between the free energy of formation of the crystal from the elements and that of the corresponding melt or solution, times the crystal volume (v), and
(2) the surface energy term ( DELTA Gs ) , which term (involving surface tension) was discussed above. In fact surface-energy is surface-strain, or, (surface-energy is) surface-tension times surface-area. Therefore, when the surface increases (or is subdivided), the surface-energy increases, not the surface-tension.
(these two terms) figuring in the following equation :
DELTA G = DELTA Gv + DELTA Gs
where DELTA G is the total change in potential energy involved in crystallization or its reverse.
The next diagram depicts the resulting balance (bold curve), at a certain temperature T1 , between the ever positive surface-energy term DELTA Gs , and the volume term DELTA Gv , as a function of embryo size (which as such refers to incipient crystallization, but can also refer to the size of a growing macroscopic crystal and the energetic effects of increasing this size).
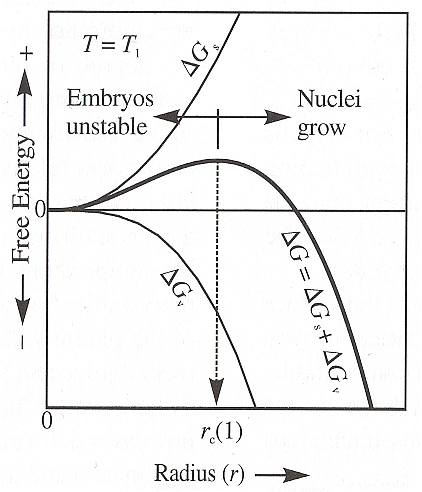
Figure above : The Gibbs free energy of formation DELTA G of crystal nuclei is the sum of the surface energy DELTA Gs and volume energy DELTA Gv (equation above). Only nuclei larger than the critical growth radius rc are stable with respect to the melt. Additional growth reduces the energy level. Crystal nuclei smaller than rc will spontaneously be resorbed by the melt because they represent a higher energy configuration than melt and additional growth involves an increase in energy. (After NESSE, 2000.)
Crystallization can only take place when DELTA G is negative, or quickly leads to it (meaning that the potential energy decreases when crystallization sets in and proceeds, and in which the surface energy is already accounted for in terms of its contribution to the total potential energy of the system).
The next two Figures are about the distribution of the forces of mutual attraction of chemical motifs in a crystal, exemplified in a two-dimensional crystal based on a hexagonal net.
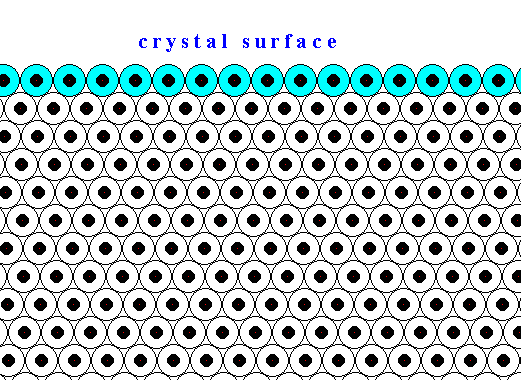
Figure above : Chemical motifs (black) arranged in an hexagonal array, and in this way forming a two-dimensional crystal.
The larger circles indicate half the radius of influence radiating from each chemical motif. In the Figure the exterior layer, representing a face of the crystal, is indicated (light blue).
Generally, each repeated chemical motif in a crystal is being symmetrically attracted by surrounding motifs. The range of the attraction forces could be approximately equal to one motif distance (just for the purpose of discussion, and as such indicated in the next Figure), or a few more. The pattern of attraction in surface motifs is different from, and especially, spatially biased as compared to, that in motifs lying under (i.e. beyond) the superficial layer. So the forces to which the motifs of the surface layer are subjected do not cancel out each other, like they do when they are subsurface motifs. This means that the surface layer of motifs bears energy. The surface motifs, and therefore the surface itself, experiences a downward force (in fact an inwardly directed force). And only the surface motifs, and no other motifs, are subjected to this force, which should, according to me, not be confused with the inward pressure as a result of surface tension of a curved surface. The next Figure shows the attraction forces experienced by subsurface and surface chemical motifs in a two-dimensional hexagonal crystal.
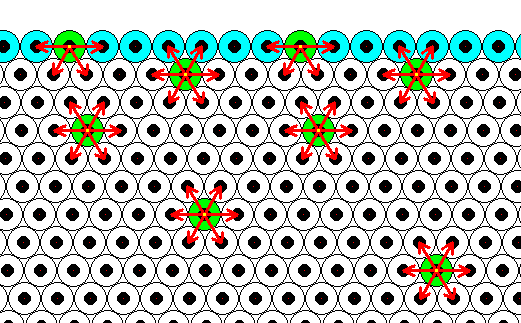
Figure above : Two-dimensional crystal of the previous Figure. Forces of attraction being exerted on a given chemical motif are reprented by red arrows. In the present Figure it is assumed that each chemical motif is attracted by those other chemical motifs that immediately surround it.
Chemical motifs lying in the interior of the crystal feel six forces, i.e. are attracted by six neighboring chemical motifs. Because these forces cancel each other (two by two), the net force felt by such a chemical motif is nil. On the other hand, a chemical motif that lies in the surface layer feels only four forces, of which the two forces parallel to the crystal face cancel each other, leaving a net force in the downward direction, i.e. perpendicular to the crystal face and pointing to the interior of the crystal. So these chemical motifs that lie in the surface layer possess energy as compared to those that lie within the crystal's interior. We can express this state of affairs in a different but equivalent way : The chemical motifs of the surface layer of a crystal have some of their chemical valences unsatisfied ('dangling'), which implies a higher energy configuration for these chemical motifs as compared with those that lie in the crystal's interior.
The forces to which the surface motifs are subjected will, I assume, result in a slight displacement of these surface motifs in the inward direction until equilibrium is reached by evoked elastic counter-forces. We could, perhaps compare all this with burls in a cushion. See next Figure.
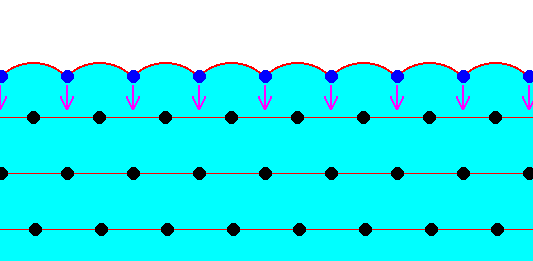
Figure above : The chemical motifs of the surface layer of a two-dimensional crystal are drawn into the direction indicated by the arrows. In the present Figure this is illustrated with the image of burls being pressed into a cushion.
In this way the surface is stressed somewhat, and diminishing of this stressed or strained surface is one way to be relieved from this stress, and, as has been said, this tendency to diminish the surface (surface shrinking) is surface tension. In fact we can say that the just described inward force experienced by the surface motifs is the direct result of unsatisfied ('dangling') chemical valences, as they are expected to be present on crystal faces.
All the above, about surface tension, represents my (not being an expert on the matter) understanding of the phenomenon and its relation to crystals. We will now consult D'Arcy THOMPSON for some more information about surface tension phenomena and thus for going a little deeper into the subject, which is very important for the inorganic-organic and crystal-organism analogies (while these in turn will tell us more about the ontological layering of Reality).
Roughly following (and annotating) D'Arcy THOMPSON from page 346 of the 1942 edition onwards, on the Forms of Cells :
Protoplasm is a fluid or a semi-fluid substance, and we need not try to describe the particular properties of the colloid or jelly-like substances to which it is allied, or rather the characteristics of the "colloid state" in which it and they exist. We should find it no easy matter. Nor need we appeal to precise theoretical definitions of fluidity, lest we come into a debatable land. It is in the most general sense that protoplasm is "fluid". When we can deal with protoplasm in sufficient quantity we see it f l o w. Particles move freely through it, air-bubbles and liquid droplets show (themselves as being) round and spherical within it. And we shall have much to say about other phenomena manifested by its own surface, which are those especially characteristic of liquids. Protoplasm may encompass and contain solid bodies, and it may "secrete" solid substances within or around itself. And it often happens in the complex living organism that these solid substances, such as shell or nail or horn or feather, remain when the protoplasm which formed them is dead and gone. But the protoplasm itself is fluid or semi-fluid, and permits of free (though not necessarily rapid) d i f f u s i o n and easy c o n v e c t i o n of particles within itself, which simple fact is of elementary importance in connection with form, throwing light on what seem to be common characteristics and pecularities of the forms of living things.
A crystal "grows" by deposition of new molecules, atoms or ions, one by one and layer by layer, each one superimposed on the solid substratum already formed. Each particle would seem to be influenced only by the particles in its immediate neighbourhood, and to be in a state of freedom and independence from the influence, either direct or indirect of its remoter neighbours So Lavoisier was the first to say [ We have, however, found, that it is highly probable that crystal growth -- as seen in snow crystals -- exhibits some h o l i s t i c aspects ]. And as Kelvin and others later on explained the formation and the resulting forms of crystals, so we believe that each added particle takes up its position in relation to its immediate neighbours already arranged, in the holes and corners that their (i.e. the neighbours already deposited) arrangement leaves (open to be filled), and in closest contact with the greatest number. Hence we may repeat or imitate this process of arrangement, with great or, apparently, even with precise accuracy (in the case of the simpler crystalline systems), by piling up spherical pills or grains of shot. In so doing, we must have regard to the fact that each particle must drop into the place where it can go most easily, or where no easier place offers. In more technical language, each particle is free to take up, and does take up, its position of least potential energy relative to those already there : in other words, for each particle motion is induced until the energy of the system is so distributed that no tendency or resultant force remains to move it more. This has been shown to lead to the production of p l a n e surfaces (in all cases where, by the limitation of material, surfaces m u s t occur [ If no material can be provided anymore -- for instance when a solution has, from a state of supersaturation, become (just) saturated, final facets develop, which are plane surfaces. ] ). Where we have planes, there straight edges and solid angles must obviously occur also, and, if equilibrium is to follow, must occur symmetrically. Our piling up of shot to make mimic crystals gives us visible demonstration that the result is : actually to obtain, as in the natural crystal, plane surfaces and sharp angles symmetrically disposed.
But the living cell grows in a totally different way, very much as a piece of glue swells up in water, by "imbibition" [ meaning "drinking-in" ], or, equivalently, by interpenetration into and throughout its entire substance. The semi-fluid colloid mass takes up water, partly to combine chemically with its individual molecules, partly by physical diffusion into the interstices between molecules or micellae, and partly, as it would seem, in other ways, so that the entire phenomenon is a complex and even an obscure one. But, so far as we are concerned, the net result is very simple. For the equilibrium, or tendency to equilibrium, of fluid pressure in all parts of its interior while the process of imbibition is going on, the constant rearrangement of its fluid mass, the contrast in short with the crystalline method of growth where each particle comes to rest to move (relatively to the whole) no more, lead the mass of jelly to swell up very much as a bladder into which we blow air, and so, by a g r a d e d and harmonious distribution of forces, to assume everywhere a rounded and more or less bubble-like external form. Here, in a non-crystalline or random arrangement of particles, symmetry ensures that the potential energy shall be the same per unit area of all surfaces. And it follows from geometrical considerations that the total surface energy will be least if the surface be spherical [ i.e. that the given volume of material is enclosed within a sphere, where its radius depends on that given volume. ].
Calling c y t o p l a s m the cell-protoplasm after subtraction of chloroplasts and other gross inclusions, we find it to contain fats, proteins, lecithin and some other substances combined with much water (up to 97 percent) to form a sort of watery g e l. The microscopic structures attributed to it, alveolar, granular or fibrillar, are inconstant or invalid. But it does appear to possess an invisible or submicroscopic structure, distinguishing it from an ordinary colloid gel, and forming a quasi-solid framework or reticulum. And we may speak of a "micellar framework" as representing in our cytoplasm the dispersed phase of an ordinary colloid. In short, as the cytoplasm is neither true fluid nor true solid, neither is it true colloid in the ordinary sense. Its micellar structure gives it a certain rigidity or tendency to retain its shape, a certain placticity and tensile strength, a certain ductility or capacity to be drawn out in threads, but yet leaves it with a permeability (or semi-permeability), a capacity to swell by imbibition, above all an ability to stream and flow, which justify our calling it "fluid or semi-fluid", and account for its exhibition of surface tension and other capillary phenomena.
The older naturalists, in discussing the differences between organic and inorganic bodies, laid stress upon the circumstance that the latter grow by "agglutination", and the former by what they termed "intussusception". The contrast is true, but it applies rather to solid or crystalline bodies as compared with colloids of all kinds, whether living or dead. But it so happens that the great majority of colloids are of organic origin, and out of them our bodies, and our food, and the very clothes we wear, are almost wholly made.
In a homogeneous crystalline arrangement, s y m m e t r y compels a locus of one property to be a plane or set of planes. The locus in this case being that of least surface potential energy [ slowest growing faces ]. Crystals "seem to be, as it were, the Elemental Figures, or the A B C of Nature's working, the reason [ i.e. the purpose ] of whose [ i.e. nature's or the crystal's ] curious Geometrical Forms (if I may so call them) is very easily explicable" (Robert Hooke, Posthumous Works, 1745, p.280).
So when the same school of older naturalists called attention to a new distinction or contrast of form between organic and inorganic objects, in that the contours of the former tended to roundness and curvature, and those of the latter to be bounded by straight lines, planes and sharp angles, we see that this contrast was not a new and different one, but only another aspect of their former statement, and an immediate consequence of the difference between the processes of aggutination and intussusception.
So far then as growth goes on undisturbed by pressure or other external force, the fluidity of the protoplasm, its mobility internal and external, and the way in which particles move freely hither and thither within, all manifestly tend to the production of swelling, rounded surfaces, and to their great predominance over plane surfaces in the contours of the organism. These rounded contours will tend to be preserved for a while, in the case of naked protoplasm by its viscosity, and in presence of a cell wall by its very lack of fluidity. In a general way, the presence of curved boundary surfaces will be especially obvious in the unicellular organisms, and generally in the external form of all organisms, and wherever mutual pressure between adjacent cells, or other adjacent parts, has not come into play to flatten the rounded surfaces into planes. But the rounded contours which are assumed and exhibited by a piece of hard glue when we throw it into water and see it expand as it sucks the water up, are not near so regular nor so beautiful as are those which appear when we blow a bubble, or form a drop, or even pour water into an elastic bag. For these curving contours depend upon the properties of the bag itself, of the film or membrane which contains the mobile gas, or which contains or bounds the mobile liquid mass. And hereby, in the case of the fluid or semifluid mass, we are introduced to the subject of s u r f a c e t e n s i o n.
REMARK : D'Arcy Thompson attributed much to surface tension when it comes to the generation of the shapes of organic cells (solitary or in a tissue framework). Perhaps we should, on the basis of evidence ( See comments of the editor of the abridged edition of D'Arcy Thompson's work, at p.49 ) downplay the importance of surface tension a bit, because it seems to be the complicated and sophisticated membranes that mainly do the job of cell-shaping. We must, however, realize that surface-tension phenomena in all probability must be considered as ontogenetically ( 'embryologically ' ), and if not, phylogenetically (i.e. evolutionarily), primary. They surely were the origin of the now sophisticated membranes with their regulating abilities and with a tension that is much higher than pure surface tension. Perhaps we can, in many cases, consider surface tension phenomena as having played the part of a scaffold, either an evolutionary scaffold or an ontogenetic one, i.e. an auxiliary structure that is later discarded. Seen in this way, surface tension remains important in all discussions involving inorganic-organic and crystal-organism analogies. In such discussions we could consider form-generation-as-we-see-it-happening-by-the-action-of-sophisticated-cell-membranes as the result of some sort of 'complexity jump' initiating from form-generation-by-pure-surface-tension-phenomena (and by these alone). Such a complexity jump, then, is among such features that mark the boundary between the inorganic and the organic.
Among the forces which determine the forms of cells, whether they be solitary or arranged in contact with one another, this force of surface tension is certainly of great, and is probably of paramount, importance. But while we shall try to separate out the phenomena which are directly due to it, we must not forget that, in each particular case, the actual conformation which we study may be, and usually is, the more or less complex resultant of surface tension acting together with gravity, mechanical pressure, osmosis, or other physical forces. The peculiar beauty of a soap bubble, solitary or in collocation, depends on the absence (to all intents and purposes) of these alien forces from the field. Hence Plateau spoke of the films which were the subject of his experiments as "lames fluides s a n s p e s a n t e u r." The resulting form is in such a case so pure and simple that we come to look on it as wellnigh a mathematical abstraction.
Surface tension, then, is that force by which we explain the form of a drop or of a bubble, of the surfaces external and internal of a "froth" or collocation of bubbles, and of many other things of like nature and in like circumstances. It is a property of liquids (in the sense at least with which our subject is concerned) [ But also solid bodies do have surface tension ], and it is manifested at or very near the surface, where the liquid comes into contact with another liquid, a solid or a gas. We note here that the term s u r f a c e is to be interpreted in a wide sense, for wherever we have solid particles embedded in a fluid, wherever we have a non-homogeneous fluid or semi-fluid, or a "two-phase colloid" such as a particle of protoplasm, wherever we have the presence of "impurities" as in a mass of molten metal, there we have always to bear in mind the existence of s u r f a c e s and of surface phenomena, not only on the exterior of the mass but also throughout its interstices, wherever like and unlike meet.
A liquid in the mass is devoid of structure. It is homogeneous, and without direction or polarity. But the very concept of surface tension forbids this to be true of the surface layer of a body of liquid, or of the "interphase" between two liquids, or of any film, bubble, drop, or capillary jet or stream. In all these cases, and more emphatically in the case of a "monolayer", even the liquid has a structure of its own. And we are reminded once again of how largely the living organism, whether high or low, is composed of colloid matter in precisely such forms and structural conditions.
In what comes next, we will continue following D'Arcy THOMPSON on surface tension, but now using the above mentioned abridged edition, pp.49, On Growth and Form by D'Arcy Wentworth Thompson, an abridged edition edited by John Tyler Bonner, published in 1961 (Reprinted at least up to 1975), which edition is perhaps more easily available than the original 1942 edition.
Surface tension is due to molecular force : to force, that is to say, arising from the action of one molecule upon another. And since we can only ascribe a small 'sphere of action' to each several molecule, this force is manifested only within a narrow range. Within the interior of the liquid mass we imagine that such molecular interactions negative one another. But at and near the free surface, within a layer or film approximately equal to the range of the molecular force -- or to the radius of the aforesaid 'sphere of action' -- there is a lack of equilibrium and a consequent manifestation of force.
The action of the molecular forces has been variously explained. But one simple explanation (or mode of statement) is that the molecules of the surface layer are being constantly attracted into the interior by such (other molecules) as are just a little more deeply situated. The surface shrinks as molecules keep quitting it for the interior, and this s u r f a c e - s h r i n k a g e exhibits itself as a s u r f a c e - t e n s i o n. The process continues till it can go no farther, that is to say until the surface itself becomes a 'minimal area'. This is a sufficient description of the phenomenon in cases where a portion of liquid is subject to no other than its own molecular forces, and (since the sphere has, of all solids, the least surface for a given volume) it accounts for the spherical form of the raindrop, of the grain of shot, or of the living cell in innumerable simple organisms. It accounts also, as we shall presently see, for many much more complicated forms, manifested under less simple conditions.
A physical or chemical system contains an amount of potential energy which we can qualitatively understand as representing the amount of stress under which the system finds itself to be (for example the stress experienced by a spring that is held stretched). Often this system's 'being in a state of stress' is masked for it by some energy barrier, but as soon as this barrier is somehow overcome (for example by a little push, or by igniting something), the system can, and will, get rid of its stress (which has now -- because of the removal of the mentioned energy barrier -- been actualized) for as much as possible, meaning that it gets rid of its potential energy for as much as possible as circumstances permit, implying the transition of the latter into actual energy, in short, the system delivers work. When the system has eventually arrived at a minimum of its potential energy, i.e. when it sits in an energy-well (and, because that is still a relative minimum, the well should be shielded by firm energy barriers, in order for the system to be stable), it is said to be in stable equilibrium ( When, no such barriers exist, and all forces cancel each other, like a needle that stands precisely vertically on a table top, there is also equilibrium, but it is an unstable equilibrium : however small a (relevant) perturbation will topple the system to a more stable equilibrium ).
The potential energy of the system (which it tries to reduce) can consist of several different energies, and one such energy (coexisting with the other potential energies of the system) is surface energy (which is the specific surface-tension multiplied by the area of the surface). At p.88 of the abridged edition D'Arcy Thompson explains what surface energy is :
Let us restate as follows, in terms of E n e r g y, the general principle which underlies the theory of surface-tension or capillarity.
When a fluid is in contact with another fluid [ where "fluid" means a substance that can flow, such as a gas or a liquid ] , or with a solid or with a gas, a portion of the total energy of the system (that, namely, which we call s u r f a c e - e n e r g y) is proportional to the area of the surface of contact. It is also proportional to a coefficient which is specific for each particular pair of substances and is constant for these, save only in so far as it may be modified by changes of temperature or of electrical charge. Equilibrium, which is the condition of m i n i m u m p o t e n t i a l e n e r g y in the system, will accordingly be obtained, caeteris paribus [ i.e. all other things being equal ], by the utmost possible reduction of the surfaces in contact.
Let us now make some enquiry into the forms which a fluid surface can assume under the mere influence of surface tension. In doing so we are limited to conditions under which other forces are relatively unimportant, that is to say where the surface energy is a considerable fraction of the whole energy of the system. And in general this will be the case when we are dealing with portions of liquid so small that their dimensions come within or near to what we have called the molecular range, or, more generally, in which the 'specific surface' is large. In other words it is the small or minute organisms, or small cellular elements of larger organisms, whose forms will be governed by surface tension, while the forms of the larger organisms are due to other and non-molecular forces. A large surface of water sets itself level because here gravity is predominant. But the surface of water in a narrow tube is curved, for the reason that we are here dealing with particles which lie within the range of each other's molecular forces. The like is the case with the cell-surfaces and cell-partitions, which we are about to study, and the effect of gravity will be especially counteracted and concealed when the object is immersed in a liquid of nearly its own density.
We have already learned, as a fundamental law of 'capillarity', that a liquid film i n e q u i l i b r i u m assumes a form which gives it a minimal area under the conditions to which it is subject. These conditions include (1) the form of the boundary, if such exist, and (2) the pressure, if any, to which the film is subject : which pressure is closely related to the volume of air, or of liquid, that the film (if it be a closed one) may have to contain. In the simplest of cases, as when we take up a soap-film on a plane wire ring, the film is exposed to equal atmospheric pressure on both sides, and it obviously has its minimal area in the form of a plane. So long as our wire ring lies in one plane (however irregular in outline), the film stretched across it will still be in a plane, but if we bend the ring so that it lies no longer in a plane, then our film will become curved into a surface which may be extremely complicated, but is still the smallest possible surface which can be drawn continuously across the uneven boundary.
The question of pressure involves not only external pressures acting on the film, but also that which the film is capable of exerting. For we have seen that the film is always contracting to the utmost, and when the film is curved, this leads to a pressure directed inwards -- perpendicular, that is to say, to the surface of the film. In the case of the soap-bubble, the uniform contraction of whose surface has led to its spherical form, this pressure is balanced by the pressure of the air within. And if an outlet is given for this air, then the bubble contracts with perceptible force until it stretches across the mouth of the tube, for instance across the mouth of the pipe through which we have blown the bubble. A precisely similar pressure, directed inwards, is exercised by the surface layer of a drop of water or a globule of mercury, or by the surface pellicle on a portion or 'drop' of protoplasm. Only we must always remember that in the soap-bubble, or the bubble which a glass-blower blows, there is a twofold pressure as compared with that which the surface-film exercises on the drop of liquid of which it is a part. For the bubble consists (unless it be so thin as to consist of a mere layer of molecules, or, more strictly : unless the thickness of the layer be less than twice the range of the molecular forces) of a liquid layer, with a free surface within and another without, and each of these two surfaces exercises its own independent and co-equal tension and its corresponding pressure (It follows that the tension of a bubble, depending only on the surface conditions, is independent of the thickness of the film).
If we stretch a tape upon a flat table [ now -- in this example -- using a stretching tension instead of a contraction tension ] , whatever be the tension of the tape, it obviously exercises no pressure upon the table below. But if we stretch it over a c u r v e d surface, a cylinder for instance, it does exercise a downward pressure. And the more curved the surface the greater is this pressure, that is to say the greater is this share of the entire force of tension which is resolved in the downward direction. In mathematical language, the pressure (p) varies directly as the tension (T), and inversely as the radius of curvature (R) : that is to say, p = T / R, per unit of surface [ 1 / R = (degree of) curvature. ].
If instead of a cylinder, whose curvature lies only in one direction, we take a case of curvature in two dimensions (as for instance a sphere), then the effects of these two curvatures must be added together to give the resulting pressure p : which becomes equal to T / R1 + T / R2 , or
[ In the 1942 as well as in the abridged edition of On Growth and Form the factor T in this equation is erroneously absent. ]
And if in addition to the pressure p, which is due to surface tension, we have to take into account other pressures, p', p'', etc., due to gravity or other forces, then we may say that the total pressure
This simple but immensely important formula is due to Laplace (1806).
We may have to take account of the extraneous pressures in some cases, for example when discussing the shape of a bird's egg, but in the present problem we are able for the most part to neglect them. So we stick to the first equation.
Our equation is an equation of equilibrium. The resistance to compression (this resistence is the pressure outwards) of our fluid mass is a constant quantity (p), standing at the left-hand side of the equation, while the pressure inwards, (1 / R1 + 1 / R2) T, is also constant, standing at the right-hand side of the equation. And if the surface (unlike that of the mobile amoeba) be homogeneous, so that T is everywhere equal, it follows that 1 / R1 + 1 / R2 = C (i.e. a constant), throughout the whole surface in question.
Now equilibrium is reached after the surface-contraction has done its utmost, that is to say when it has reduced the surface to the least possible area. So we arrive at the conclusion, from the physical side, that a surface such that 1 / R1 + 1 / R2 = C, in other words a surface which has the same m e a n c u r v a t u r e at all points [ i.e. whatever values R1 and (as representing a direction of curvature, perpendicular to it) R2 may have at a given point of the surface, their sum is the same as that at any other point of that surface ], is equivalent to a surface of m i n i m a l a r e a for the volume enclosed. And to the same conclusion we may also come by ways purely mathematical [ Intuitively : If 1 / R1 + 1 / R2 is a constant, no 'detours' are made by the surface, which implies that the surface is one of minimal area as far as the given volume enclosed by this surface permits. ]. The plane and the sphere are two obvious examples of such surfaces, for in both the radius of curvature is everywhere constant [ That the plane -- which does not enclose a volume -- is a surface of minimal area is immediately evident ].
From the fact that we may extend a soap-film across any ring of wire, however fantastically the wire be bent, we see that there is no end to the number of surfaces of minimal area which may be constructed or imagined. While some of these are very complicated indeed, others, such as a spiral or helical screw, are relatively simple. But if we limit ourselves to s u r f a c e s o f r e v o l u t i o n (that is to say, to surfaces symmetrical about an axis [ or, more precisely, M o n a x o n i a as described in the Promorphological System of Second Part of the present Website, Basic Forms ] ), we find, as Plateau was the first to show, that those which meet the case (i.e. which are surfaces of minimal area) are few in number. They are six in all, namely the plane, the sphere, the cylinder, the catenoid, the unduloid, and a curious surface which Plateau called the nodoid.
REMARK : A surface of revolution -- a monaxon form -- is obtained if we take a line, curved or straight, sharply bent or not, and rotate it about some axis. This results in a surface whose sections perpendicular to the axis of rotation are circles (and not polygons). Only six of such surfaces are surfaces of minimal area. From the vast set of possible surfaces of minimal area we have chosen to consider surfaces of revolution only, because they can be found in the shapes of many (unicellular) organisms, indicating that the shapes of these organisms are, for a large part at least, just a product of physical necessity, which means that they need not to be evolutionarily or ontogenetically engineered : they are obtainable 'for free'.
The effect of this surface tension will manifest itself in surfaces m i n i m a e a r e a e : where, as Plateau was always careful to point out, we must understand by this expression not an absolute but a relative minimum, an area, that is to say, which approximates to an absolute minimum as nearly as the circumstances and material exigencies of the case permit [ The a b s o l u t e surface of minimal area with respect to an enclosed volume is a sphere.].
On these (and all other) s u r f a c e s o f m i n i m a l a r e a D'Arcy Thompson, abridged edition, p.88, remarks further :
Continuing with p.53 of the abridged edition :
These several surfaces (the plane, the sphere, the cylinder, the unduloid, the catenoid, and the nodoid) are all closely related, and the passage from one to another is generally easy. Their mathematical interrelation is expressed by the fact (first shown by Delaunay, in 1841) that the plane curves by whose revolution they are generated are themselves generated as 'roulettes' of the conic sections [ A conic section is a curve that is obtained by cutting (sectioning) a cone (or apical bicone) with a plane : a section parallel to the base of the cone yields a circle, an inclined section yields an ellipse, a section parallel to a meridional line of the cone yields a parabola, a section perpendicular to the base of the cone (but, as all the previous ones, not going through its apex) yields a hyperbola (which consists of two curves, because in this case also the second cone of the apical bicone is hit by the section), and, finally, a section also perpendicular to the base but at the same time going through the apex of the cone yields a straight line (in fact two mutually intersecting straight lines). ].
Let us imagine a straight line, or axis, on which a circle, ellips or other conic section rolls. The focus of the conic section will describe a line in some relation to the fixed axis, and this line (or roulette), when we rotate it around the axis, will describe in space one or another of the six surfaces of revolution of which we are speaking.
If we imagine an ellipse so to roll on a base-line, either of its foci will describe a sinuous or wavy line (See next Figure, b) at a distance alternately maximal and minimal from the axis.
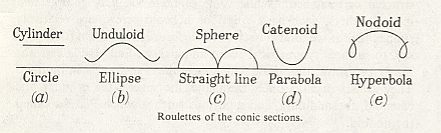
Figure above :
Generation of five of the six surfaces of minimal area that are surfaces of revolution.
Top row, consisting of names : Surfaces of revolution that are surfaces of minimal area.
Middle row, consisting of curves : Roulettes (and base-line).
Bottom row, consisting of names : Conic sections.
(After D'Arcy THOMPSON, 1942.)
This wavy line, by rotation about the axis, becomes the meridional line of the surface which we call the u n d u l o i d, and the more unequal the two axes are of our ellipse, the more pronounced will be the undulating sinuosity of the roulette. If the two axes be equal, then our ellipse becomes a circle. The path described by its rolling centre is a straight line parallel to the axis (Figure above (a)), and the solid (or surface) of revolution generated therefrom will be a c y l i n d e r : in other words, the cylinder is a 'limiting case' of the unduloid. If one axis of our ellipse vanish, while the other remains of finite length, then the ellipse is reduced to a straight line with its foci at the two ends, and its roulette will appear as a succession of semicircles touching one another upon the axis (See the above Figure (c), and next Figure). The solid of revolution will be a series of equal s p h e r e s.
Figure above : This diagram illustrates how a straight line can turn into a roulette having the form of a series of equal semicircles (which by rotation around the base-line results in a series of equal spheres). We can see this when we, while rolling the line XY along the base-line (starting left), follow the course of X (as one of the foci of the line [these foci are derived from the foci of the ellipse [itself having become a finite straight line by the vanishing of one of its two axes, namely the one not containing its two foci] ). This course of the point X clearly is a series of semicircles along the base-line.
If as before one axis of the ellipse vanish, but the other be infinitely long, then the roulette described by the focus of this 'ellipse' will be a circular arc at an infinite distance, i.e. it will be a straight line normal to the axis (not shown in the Figure showing roulettes), and the surface of revolution traced by this straight line turning about the axis will be a p l a n e. The next Figure illustrates the generation of the roulette, i.e. the line perpendicular to the base-line.
Figure above : Generation of a roulette (which will, when rotated about the base-line, generate a plane) from a horizontal straight infinite line (black). This line itself is generated from an ellipse by letting one focus move along the axis containing the foci, such that the distance of it from the other focus (held stationary) becomes infinite. If we now roll this line over the base-line (by interpreting the line's beginning as a hinge) we get an arc at infinite distance (i.e. the one focus at infinity describes an arc), which as such is identical to a straight line (purple) (because an arc with a radius infinitely long is identical to a straight line). This straight line is normal to the base-line.
If we imagine one focus of our ellipse to remain at a given distance from the axis, but the other to become infinitely remote [ while not, as in the previous case, letting one axis of the ellipse vanish ], that is tantamount to saying that the ellipse becomes transformed into a parabola. And by the rolling of this curve along the axis there is described a catenary (See (d) of the Figure above showing roulettes), whose solid of revolution is the c a t e n o i d.
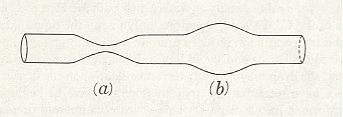
When, on the other hand, we stop the end and blow, we again convert the cylinder into an unduloid ((b) in the above Figure), but into one which is now positively, while the former was negatively, curved. The two figures are essentially the same, save that the two halves of the one, change places (in the vertical direction) in the other.
Before we go further in this enquiry we must consider, to some small extent at least, the c u r v a t u r e s of the six different surfaces, so far as to determine what modification is required, in each case, of the general equation which applies to them all. This equation was :
Where R1 is, with respect to a given point of the surface, its radius of curvature-in-one-direction, and R2 its radius of curvature-in-a-direction-perpendicular-to-the-first, with respect to the same point. And because curvature is inversely proportional to the radius of curvature, curvature is, when expressed most generally, equal to 1 / R. For a surface (which always has two dimensions) we can indicate the m e a n c u r v a t u r e in a given point of that surface by the expression 1 / R1 + 1 / R2 . This mean curvature can, generally, be different from point to point of the surface, but when the surface is one of minimal area, the mean curvature is constant from point to point.
We shall find that with this question is closely connected the question of the p r e s s u r e s exercised by or impinging on the film, and also the very important question of the limiting conditions which, from the nature of the case, set bounds to the extensions of certain of the figures. The whole subject is mathematical, and we shall only deal with it in the most elementary way.
We have seen that, in our general formula (which is a formula of equilibrium), the expression 1 / R1 + 1 / R2 is a constant. This constant we can call C, (Mean curvature is constant when going from point to point of the given surface (of minimal area)), and that this is, in all cases, the condition of our surface being one of minimal area. That is to say, it is always true for one and all of the six surfaces which we have to consider. But the constant C may have any value, positive, negative or nil.
In the case of the p l a n e, where R1 and R2 are both infinite (implying that both 1 / R1 and 1 / R2 are zero), 1 / R1 + 1 / R2 = 0. The expression (1 / R1 + 1 / R2)T therefore vanishes, and our dynamical equation of equilibrium becomes P = p [ This means that the internal pressure, insofar as it is caused by the tension of a c u r v e d surface, has become zero, and this in turn means that there exists no extra pressure at the inner side of the film, which is the same as saying that the pressure from outside on the film is equal to the pressure from its inside, so P = p . The fact that in the p l a n e the mean curvature is zero in every one of its points, is not because 1 / R1 and 1 / R2 , while different from each other, cancel each other, but because both are zero.
In the c a t e n o i d (discussed below) the expression 1 / R1 + 1 / R2 is also zero (mean curvature zero in every one of its points), but here this is so because 1 / R1 cancels 1 / R2 in everyone of its points ]. In short, we can only have a plane film, or we shall only find a plane surface in our (organic) cell, when on either side thereof we have equal pressures or no pressure at all. A simple case is the plane partition between two equal and similar cells, as in a filament of Spirogyra (Lower plants, Conjugatae).
In the s p h e r e the radii of curvature are all equal, R1 = R2. they are also positive, and (1 / R1 + 1 / R2)T, or 2T / R1 (or 2T / R2 for that matter), is a positive quantity, involving a constant positive pressure p, on the other side of the equation [ Within the film, enclosing a volume, the higher pressure is counteracted by the surface tension of the film, or, equivalently, the surface tension of the curved surface causes a pressure which is then counteracted upon by the compressed content of the volume enclosed by the surface ].
In the c y l i n d e r one radius of curvature has the finite and positive value R1, but the other (R2) is infinite. Our formula becomes T / R1 , to which corresponds a positive pressure p, supplied by the surface tension as in the case of the sphere, but evidently of just half the magnitude.
In plane, sphere and cylinder the two principal curvatures are constant, separately and together [ i.e. everywhere on the surface we find precisely the same situation with respect to the local curvature-configuration of the surface ]. But in the u n d u l o i d the curvatures change from one point to another. At the middle of one of the swollen 'beads' or bubbles, the curvatures are both positive. The expression (1 / R1 + 1 / R2) [ and thus also T(1 / R1 + 1 / R2) ] is therefore positive, and it is also finite. The film exercises (like the cylinder) a positive pressure inwards, to be compensated by an equivalent outward pressure from within. Between two adjacent beads, at the middle of one of the narrow necks, there is obviously a much stronger curvature in the transverse direction. But the total pressure is unchanged, and we now see that a negative curvature a l o n g the unduloid balances the increased curvature in the transverse direction. The sum of the two must remain positive as well as constant. Therefore the convex or positive curvature must always be greater than the concave or negative curvature at the same point, and this is plainly the case in the above Figure of the unduloid .
The c a t e n o i d, in this respect a limiting case of the unduloid, has its curvature in one direction equal and opposite to its curvature in the other [ like a saddle ], this property holding good for all points of the surface. R1 =
-
R2 .
The n o d o i d is, like the unduloid, a continuous curve which keeps altering its curvature as it alters its distance from the axis. But in this case the resultant pressure inwards is negative instead of positive. But this curve is a complicated one, and its full mathematical treatment is too hard for us.
And the expression becomes : (1 / R1 + 1 / R2) = (1 / R1
-
1 / R1) = 0
That is to say, the mean curvature is zero, and the catenoid, like the plane itself, has n o c u r v a t u r e, and exerts no pressure [ because now also (1 / R1 + 1 / R2)T (which is equal to p ) becomes zero ]. [ That it exerts no pressure, means, like in the case of the plane, that the film, while being in equilibrium, can be an o p e n structure, that is to say it needs not to be capped or closed ]. None of the other surfaces save these two share this remarkable property, and it follows that we may have at times the plane and the catenoid coexisting as parts of one and the same boundary system, just as the cylinder or the unduloid may be capped by portions of spheres [ For this to be so, the R of the sphere must be such that its 2T / R becomes equal to the T / R of the cylinder (and thus entailing equal pressures), or the R of the sphere must be such that its 2T / R is equal to the T(1 / R1 + 1 / R2) of the unduloid.]. It follows also that if we stretch a soap-film between two rings, and so form an annular surface open at both ends, that surface is a catenoid [ because the film, although curved, cannot exert pressure in virtue of the fact that the surface is open ] : the simplest case being when the rings are parallel, and normal to the axis of the figure.
In one of Plateau's experiments, a bubble of oil (protected from gravity by a fluid of equal density to its own) is balanced between annuli (rings). And by adjusting the distance apart of these, it may be brought to assume the form as displayed in the left image of the next Figure,
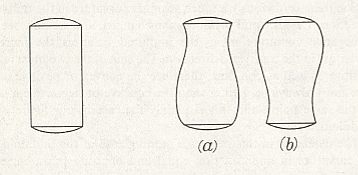
Figure above : Each image depicts a bubble of oil balanced between annuli. A cylindrical (left) and unduloid (a) and (b) main body is capped with spherical ends.
that is to say, of a cylinder with spherical ends. There is then everywhere a pressure inwards on the fluid contents of the bubble, a pressure due to the convexity of the surface film. This cylinder may be converted into an unduloid, either by drawing the rings farther apart or by abstracting some of the oil [ Because the rings remain at the same distance this time, the effect (of sucking out fluid) is the same as in the case of just drawing the rings apart : In both cases constriction of the fluid mass takes place ], until at length rupture ensues, and the cylinder breaks up into two spherical drops. Or again, if the surrounding liquid be made ever so little heavier or lighter than that which constitutes the drop, then gravity comes into play, the conditions of equilibrium are modified accordingly, and the cylinder becomes part of an unduloid, with its dilated portion above or below as the case may be (See Figure above, (a) and (b)).
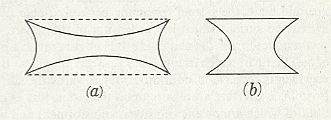
Figure above : Oil bubbles.
(a) : Portion of a nodoid (left-right) and concave portions of a sphere (top-bottom).
(b) : Catenoid capped by planes.
We may continue to withdraw more oil from our bubble, drop by drop, and now the upper and lower surfaces dimple down into concave portions of spheres, as the result of the n e g a t i v e internal pressure (See (a) in the Figure above). And thereupon the peripheral catenoid surface alters its form (perhaps, on this small scale, imperceptibly), and becomes a portion of a nodoid [ because the spherical surfaces cannot coexist with a catenoid in virtue of the fact that the sphere has overall positive (or negative, depending on which side of it is considered) curvature, while the overall curvature is nil in the catenoid.]. It represents, in fact, that portion of the nodoid which in the next Figure lies between such points as O, P.
While it is easy to draw the outline, or meridional section, of the nodoid, it is obvious that the solid of revolution to be derived from it can never be realised in its entirety : for one part of the solid figure would cut, or entangle with, another. All that we can ever do, accordingly, is to realise isolated portions of the nodoid.
If, in a sequel to the preceding experiment of Plateau's, we use solid discs instead of annuli, we may exert pressure on our oil-globule as we exerted traction before. We begin again by adjusting the pressure of these discs so that the oil assumes the form of a cylinder : our discs, that is to say, are adjusted to exercise a mechanical pressure just equal to what in the former case was supplied by the surface tension of the spherical caps or ends of the bubble. If we now increase the pressure slightly, the peripheral walls become convexly curved, exercising a precisely corresponding pressure. The form assumed by the sides of our figure is now that of a portion of an unduloid. If we increase the pressure, the peripheral surface of oil will bulge out more and more, and will presently constitute a portion of a sphere. But we may continue the process yet further, and find within certain limits the system remaining perfectly stable. What is this new curved surface which has arisen out of the sphere, as the latter was produced from the unduloid? It is no other than a portion of a nodoid, that part which in the above Figure lies between M and N. But this surface, which is concave in both directions ( 1 / R1 and 1 / R2 ) towards the suface of the oil within, is exerting a positive pressure upon the latter, just as did the sphere out of which a moment ago it was transformed. And we had just stated, in considering the previous experiment, that the pressure inwards exerted by the nodoid was a negative one. The explanation of this seeming discrepancy lies in the simple fact that, if we follow the outline of our nodoid curve in the above Figure , from OP -- the surface concerned in the former case -- to MN -- that concerned in the present --, we shall see that in the two experiments the suface of the liquid is not the same, but lies on the positive side of the curve in the one case, and on the negative side in the other.
Let me explain the latter closer as follows :
In the first experiment we had a portion of a nodoid capped above and below by portions of a sphere. The portion of the nodoid here is convex towards the surface of the oil within, as in (a) of the Figure given earlier .
In the second experiment we had a portion of a nodoid that was concave towards the surface of the oil within.
The next Figure shows to what side of the nodoid curve the oil in the two experiments belongs.
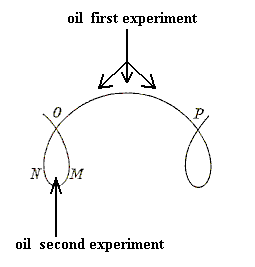
Figure above : Roulette of the nodoid. The Figure shows to what side of the curve the oil of the two above described experiments belongs. (Adapted from D'Arcy THOMPSON, 1942.)
These capillary surfaces of Plateau's form a beautiful example of the 'materialisation' of mathematical law. Theory leads to certain equations which determine the position of points in a system, and these points we may then plot as curves on a co-ordinate diagram. But a drop or a bubble may realise in an instant the whole result of our calculations, and materialise our whole apparatus of curves. Such a case is what Bacon calls a 'collective instance' (a collective case), bearing witness to the fact that one common law is obeyed by every point or particle of the system. Where the underlying equations are unknown to us, as happens in so many natural configurations, we may still rest assured that kindred mathematical laws are being automatically followed, and rigorously obeyed, and sometimes half-revealed.
Of all the surfaces which we have been describing, the sphere is the only one which can enclose space of itself. The others can only help to do so, in combination with one another or with the sphere. Moreover, the sphere is also, of all possible figures, that which encloses the greatest volume with the least area of surface. It is strictly and absolutely the surface of minimal area, and it is, ipso facto, the form which will be assumed by a unicellular organism (just as by a raindrop), if it be practically homogeneous and if, like Orbulina floating in the ocean, its surroundings be likewise homogeneous and its field of force symmetrical.
The essential conditions of homogeneity and symmetry are none too common, and a spherical organism is only to be looked for among simple things. The floating (or pelagic) eggs of fishes, the spores of red seaweeds, the oospheres of Fucus or Oedogonium, the plasma-masses escaping from the cells of Vaucheria, are among the instances which come to mind.
It is only relatively speaking that the rest of these configurations are surfaces minimae areae, for they are so under conditions which involve various pressures and restraints. Such restraints are imposed by the pipe or annulus which supports and confines our oil-globule or soap-bubble, and in the case of the organic cell, similar restraints are supplied by solidifications partial or complete, or other modifications local or general, of the cell-surface or cell-wall.
One thing we must not fail to bear in mind. In the case of the soap-bubble we look for stability or instability, equilibrium or non-equilibrium, in its several configurations. But the living cell is seldom in equilibrium. It is continually using or expending energy. And this ceaseless flow of energy gives rise to a 'steady state', taking the place of and simulating equilibrium. In like manner the hardly changing outline of a jet or waterfall is but in pseudo-equilibrium. It is in a steady state, dynamically speaking. Many puzzling and apparent paradoxes of physiology, such (to take a single instance) as the maintenance of a constant osmotic pressure on either side of a cell-membrane, are accounted for by the fact that energy is being spent and work done, and a steady state or pseudo-equilibrium maintained thereby.
Among the many theoretical discoveries which we owe to Plateau, one is of peculiar importance : namely that, with the exception of the sphere and the plane, the surfaces with which we have been dealing are only in complete equilibrium within certain dimensional limits, or in other words, have a certain definite limit of stability. Only the plane and the sphere, or any portion of a sphere, are perfectly stable, because they are perfectly symmetrical figures.
Perhaps it were better to say that their symmetry is such that any small disturbance will probably readjudge itself, and leave the plane or spherical surface as it was before, while in the other configurations the chances are that a disturbance once set up will travel in one direction or another, increasing as it goes. For equilibrium and probability (as Boltzmann told us) are nearly allied : so nearly that that state of a system which is most likely to occur, or most likely to endure, is precisely that which we call the state of equilibrium [ in fact only a s t a b l e equilibrium, because there are also unstable equilibria, for instance when a needle stands right up on the surface of a table. The slightest disturbance will topple it to a stable equilibrium, which is the case when it lies horizontally on the table. It is evident that such unstable equilibria will not endure for long in the natural world.].
For experimental demonstration of instabilities, the case of the cylinder is the simplest. If we construct a liquid cylinder, either by drawing out a bubble or by supporting a globule of oil between two rings, the experiment proceeds easily until the length of the cylinder becomes just about three times as great as its diameter. But soon afterwards instability begins, and the cylinder alters its form. It narrows at the waist, so passing into an unduloid, and the deformation progresses quickly until our cylinder breaks in two, and its two halves become portions of spheres. See next Figure.
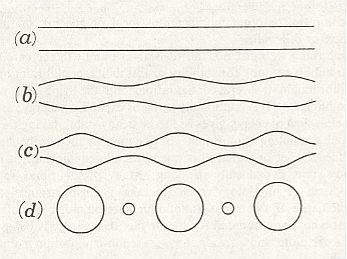
This physical change of one surface into another corresponds to what the mathematicians call a ' discontinuous solution' of a problem of minima. The theoretical limit of stability, according to Plateau, is when the length of the cylinder is equal to its circumference, that is to say, when L = 2(pi)r, or when the ratio of length to diameter is represented by pi.
We may take note here of a remarkable series of phenomena, which, though they seem at first sight to be of a very different order, are closely related to those which attend and which bring about the breaking-up of a liquid cylinder or thread.
In Mr. Worthington's beautiful experiments on splashes (A Study of Splashes, 1908, also various papers in Proc. Roy. Soc., 1876-82, and Phil. Trans., 1897 and 1900), it was found that the fall of a round pebble into water from a height first formed a dip or hollow in the surface, and then caused a filmy 'cup' of water to rise up all round, opening out trumpet-fashion or closing in like a bubble, according to the height from which the pebble fell. The cup or 'crater' tends to be fluted in alternate ridges and grooves, its edges get scolloped into corresponding lobes and notches, and the projecting lobes or prominences tend to break off or break up into drops or beads. See next Figure.
Figure above : An instantaneous photograph of a 'splash' of milk. From Harold E. Edgerton, Massachusetts Institute of Technology, and reproduced in D'Arcy Thompson, 1942.
A similar appearance is seen on a great scale in the edge of a breaking wave : for the smooth edge becomes notched or sinuous, and the surface near by becomes ribbed or fluted, owing to the internal flow being helped here and hindered there by a viscous shear. And then all of a sudden the uneven edge shoots out an array of tiny jets, which break up into the countless droplets which constitute 'spray'. The naturalist may be reminded also of the beautifully symmetrical notching of the calycles of many hydroid zoophytes, which little cups had begun their existence as liquid or semi-liquid films before they became stiff and rigid. The next phase of the splash (with which we are less directly concerned) is that the crater subsides, and where it stood a tall column rises up, which also tends, if it be tall enough, to break up into drops. Lastly the column sinks down in its turn, and a ripple runs out from where it stood.
From the simple fact that the sphere is of all configurations that whose surface-area for a given volume is an absolute minimum, we have seen it to be the one figure of equilibrium assumed by a drop or vesicle when no disturbing factor is at hand. But such freedom from counter-influences is likely to be rare, and neither does the raindrop nor the round world itself retain its primal sphericity. For one thing, gravity will always be at hand to drag and distort our drop or bubble, unless its dimensions be so minute that gravity becomes insignificant compared with capillarity. Even the soap-bubble will be flattened or elongated by gravity, according as we support it from below or from above. And the bubble which is thinned out almost to blackness will, from its small mass, be the one which remains most nearly spherical.
Innumerable new conditions will be introduced, in the shape of complicated tensions and pressures, when one drop or bubble becomes associated with another, and when a system of intermediate films or partition-walls is developed between them [ as can be seen in organic cell-aggregates or tissues ].
Meanwhile let us consider a few cases of the forms of cells, either solitary, or in such simple aggregates that their individual form is little disturbed thereby. Let us clearly understand that the cases we are about to consider are those where the perfect symmetry of the sphere is replaced by another symmetry, less complete, such as that of an ellipsoidal or cylindical cell. The cases of asymmetrical deformation or displacement, such as are illustrated in the production of a bud or the development of a lateral branch, are much simpler. For here we need only assume a slight and localised variation of surface-tension, such as may be brought about in various ways through the heterogeneous chemistry of the cell. But such diffused and graded asymmetry as brings about, for instance, the ellipsoidal shape of a yeast-cell is another matter.
If the sphere be the one surface of complete symmetry and therefore of independent equilibrium, it follows that in every cell which is otherwise conformed there must be some definite cause of its departure from sphericity. And if this cause be the obvious one of resistance offered by a solidified envelope, such as an eggshell or firm cell-wall, we must still seek for the deforming force which was in action to bring about the given shape prior to the assumption of rigidity. Such a cause may be either external to, or may lie within, the cell itself. On the one hand it may be due to external pressure or some form of mechanical restraint, as when we submit our bubble to the partial restraint of discs or rings or more complicated cages of wire. On the other hand it may be due to intrinsic causes, which must come under the head either of differences of internal pressure, or of lack of homogeneity or isotropy in the surface of its envelope.
Our formula of equilibrium, or equation to an elastic surface, is
where P is the internal pressure, pe any extraneous pressure normal to the surface, R1, R2 the radii of curvature at a point, and T1, T2 the corresponding tensions, normal to one another, of the envelope.
Now in any given form which we seek to account for, R1, R2 are known quantities. But all the other factors of the equation are subject to enquiry. And somehow or other, by this formula, we must account for the form of any solitary cell whatsoever (provided always that it be not formed by successive stages of solidification), the cylindrical cell of Spirogyra, the ellipsoidal yeast-cell, or, an even more obvious example, the egg of any bird. In using this formula hitherto we have taken it in a simplified form, that is to say we have made several limiting assumptions. We have assumed that P was the uniform hydrostatic pressure, equal in all directions, of a body of liquid. We have assumed likewise that the tension T was due to surface-tension in a homogeneous liquid film, and was therefore equal in all directions, so that T1 = T2 . And we have only dealt with surfaces, or parts of a surface, where extraneous pressure, pe , was non-existent. Now in the case of a bird's egg the external pressure pe , that is to say the pressure exercised by the walls of the oviduct, will be found to be a very important factor. But in the case of the yeast-cell or the Spirogyra, wholly immersed in water, no such external pressure comes into play. We are accordingly left in such cases as these last with two hypotheses, namely that the departure from a spherical form is due to inequalities in the internal pressure P, or else to inequalities in the tension T, that is to say to a difference between T1 and T2 . In other words, it is theoretically possible that the oval form of a yeast-cell is due to a greater internal pressure, a greater ' tendency to grow ' in the direction of the longer axis of the ellipse, or alternatively, that with equal and symmetrical tendencies to growth there is associated a difference of external resistance in respect of the tension, and implicitly the molecular structure, of the cell-wall. Now the former hypothesis is not impossible. Protoplasm is far from being a perfect fluid. It is the seat of various internal forces, sometimes manifestly polar, and it is quite possible that the forces, osmotic and other, which lead to an increase of the content of the cell and are manifested in pressure outwardly directed upon its wall may be unsymmetrical, and such as to deform what would otherwise be a simple sphere. But while this hypothesis is not impossible, it is not very easy of acceptance. The protoplasm, though not a perfect fluid, has yet on the whole the properties of a fluid. Within the small compass of the cell there is little room for the development of unsymmetrical pressures. And in such a case as Spirogyra, where most part of the cavity is filled by watery sap, the conditions are still more obviously, or more nearly, those under which a uniform hydrostatic pressure should be displayed. But in variations of T, that is to say of the specific surface-tension per unit area, we have an ample field for all the various deformations with which we shall have to deal. Our condition now is, that ( T1 / R1 + T2 / R2 ) = a constant [ because now we assume a uniform pressure ]. But it no longer follows, though it may still often be the case, that this will represent a surface of absolute minimal area. As soon as T1 and T2 become unequal, we are no longer dealing with a perfectly liquid surface film. But its departure from perfect fluidity may be of all degrees, from that of a slight non-isotropic viscosity to the state of a firm elastic membrane, and it matters little whether this viscosity or semi-rigidity be manifested in the self-same layer which is still a part of the protoplasm of the cell, or in a layer which is completely differentiated into a distinct and separate membrane. As soon as, by secretion or adsorption, the molecular constitution of the surface-layer is altered, it is clearly conceivable that the alteration, or the secondary chemical changes which follow it, may be such as to produce an anisotropy, and to render the molecular forces less capable in one direction than another of exerting that contractile force by which they are striving to reduce to a minimum the surface area of the cell. A slight inequality in two opposite directions will produce the ellipsoidal cell, and a great inequality will give rise to the cylindrical cell.
I take it therefore, that the cylindrical cell of Spirogyra, or any other cylindrical cell which grows in freedom from any manifest external restraint, has assumed that particular form simply by reason of the molecular constitution of its developing wall or membrane, and that this molecular constitution was anisotropous, in such a way as to render extension easier in one direction than another. Such a lack of homogeneity or of isotropy in the cell-wall is often rendered visible, especially in plant-cells, in the form of concentric lamellae, annular and spiral striations, and the like. But there exists yet another heterogeneity to help us account for the long threads, hairs, fibres, cylinders, which are so often formed. Carl Nägeli said many years ago that organised bodies, starch-grains, cellulose and protoplasm itself, consisted of invisible particles, each an aggregate of many molecules -- he called them micellae -- and these were isolated, or 'dispersed' as we should say, in a watery medium. This theory was, to begin with, an attempt to account for the colloid state, but at the same time, the particles were supposed to be so ordered and arranged as to render the substance anisotropic, to conver on it vectorial properties as we say nowadays, and so to account for the polarisation of light by a starch-grain or a hair. It was so criticised by Bütschli and von Ebner that it fell into disrepute, if not oblivion. But a great part of it was true. And the micellar structure of wool, cotton, silk and similar substances is now rendered clearly visible by the same X-ray methods as revealed the molecular orientation, or lattice-structure, of a crystal to von Laue.
This concludes the exposition of the phenomenon of surface tension and its bearing on the forms of organic cells, an exposition, largely based on D'Arcy Thompson. Biological examples of surface-tension forms will be given in our systematic crystal analogy.
All physical and chemical preparations being done now, in the next document we will discuss (eventually in two documents) the philosophical context (theory of ontological layers) of the crystal analogy, and after that (in new documents) we will actually begin with the systematic unfolding of the crystal analogy along the lines of PRZIBRAM's book Die anorganischen Grenzgebiete der Biologie (Insbesondere der Kristallvergleich) 1926.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-24.