

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Parallelogram / Rhombus (Promorphs)
We shall start with the Parallelogram
The Vector Rosette of Actual Growth of a parallelogrammatic crystal, i.e. of any two-dimensional crystal having as its intrinsic shape (when fully developed) the Parallelogram (which itself has C2 symmetry) and possessing whatever (possible) intrinsic (point) symmetry, is as follows (blue lines) :
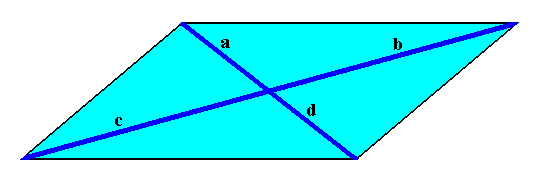
This Vector Rosette, viz. a vector rosette of a parallelogrammatic two-dimensional crystal, in fact consists of four vectors, a, b, c, d, each originating in the center of the crystal and ending up at a corner. As such it encodes the crystal's shape.
Only two plane groups, viz. P1 and P2 support crystals with the parallelogram as their intrinsic shape. See the table given in the previous document , where also the corresponding point groups are given (with the crystallographic notation between brackets), and the number of crystallographic Forms needed to construct a parallelogram in each case (of point group).
We will now consider several possible cases of the given example of a parallelogrammatic two-dimensional crystal as depicted just above, with respect to possible promorphs.
C2 symmetry.
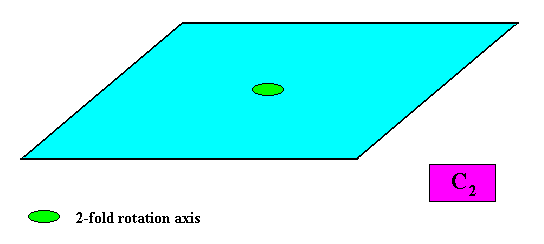
Two crystallographic Forms are needed to conceptually construct a crystal having as its intrinsic shape the Parallelogram and having an intrinsic point symmetry according to the Cyclic Group C2 . See next Figure.
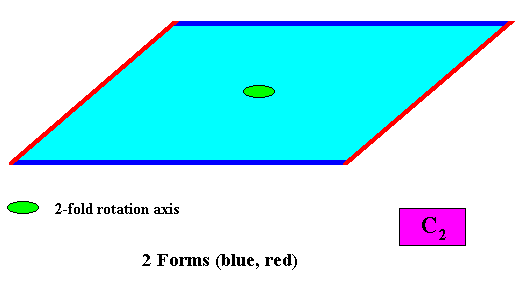
Figure above : Two Forms are needed to construct a parallelogram on the basis of intrinsic C2 symmetry : An initially given crystal face (blue) implies a second face (blue) parallel to it, in virtue of the 2-fold rotation axis. The result is an open Form consisting of two parallel faces (blue). As such this Form cannot represent a crystal, so a second Form is needed : Another initially given crystal face (red), not parallel to the first one, implies a second face (red) parallel to it, in virtue of that same 2-fold rotation axis. The two Forms together constitute a parallelogram.
Crystals with intrinsic C2 symmetry allow for several different promorphs depending on the number of antimers :
C2 symmetry and four antimers.
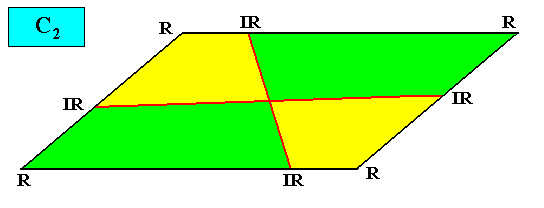
Figure above : A parallelogrammatic two-dimensional crystal with intrinsic C2 symmetry and four antimers (green, yellow).
And with the Vector Rosette of Actual growth added :
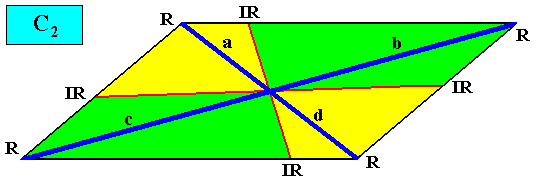
Figure above : A parallelogrammatic two-dimensional crystal with intrinsic C2 symmetry and four antimers (green, yellow). Vector Rosette of Actual Growth (blue lines) added. The vectors are two by two equivalent : a with d and b with c .
The next Figure gives the promorph (and its name) of the above (parallelogrammatic) crystal (C2 , four antimers). It is a two-dimensional analogue of the four-fold amphitect gyroid pyramid (i.e. it is its base). The four antimers are indicated (yellow, green).
Its three-dimensional counterpart (i.e. the corresponding pyramid) is given in the next Figure (slightly oblique top-view) :
C2 symmetry and two antimers.
And with the Vector Rosette of Actual Growth added :
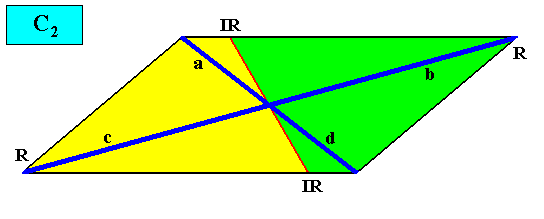
Figure above : Vector Rosette of Actual Growth of the above crystal (C2 , two antimers). The vectors are two by two equivalent : a with d and b with c .
The next Figure gives the promorph (and its name) of the above depicted parallelogrammatic two-dimensional crystal (C2 , two antimers). It is a two-fold amphitect gyroid polygon, and as such a two-dimensional analogue of the corresponding three-dimensional two-fold amphitect gyroid pyramid.
Its three-dimensional analogue -- the pyramid -- is depicted in the next Figure (slightly oblique top-view) :
There can in principle be any even number of antimers, dependent on the geometry of the translation-free chemical motif. The next Figures show the case of eight antimers (green, yellow).
C2 symmetry and eight antimers.
And with the Vector Rosette of Actual Growth added :
The next Figure gives the promorph (and its name) of the above parallelogrammatic crystal (C2 , eight antimers). It is an 8-fold amphitect gyroid polygon and as such the two-dimensional analogue of an 8-fold amphitect gyroid pyramid (i.e. it is its base). The eight antimers (green, yellow) are indicated.
The next Figure gives this same promorph, but now with the median lines of the antimers omitted, in order to let the latter stand out more clearly.
C1 symmetry and no antimers.

Figure above : A parallelogrammatic two-dimensional crystal with intrinsic C1 symmetry. There are no symmetry elements.
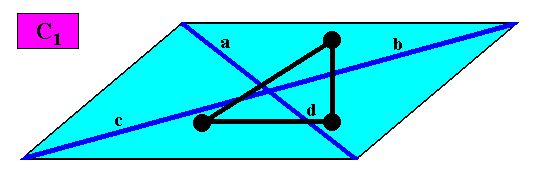
Figure above : A parallelogrammatic two-dimensional crystal with intrinsic C1 symmetry. There are no symmetry elements. The inserted asymmetric motif (black) is meant to express the intrinsic C1 symmetry of the crystal (despite its intrinsic parallelogrammatic shape), and shows that the four vectors a, b, c, d, are all non-equivalent, because there is no symmetry transformation that transforms one (vector) into another. There are no genuine antimers.
Four crystallographic Forms are needed to conceptually construct a parallelogrammatic crystal with C1 symmetry :
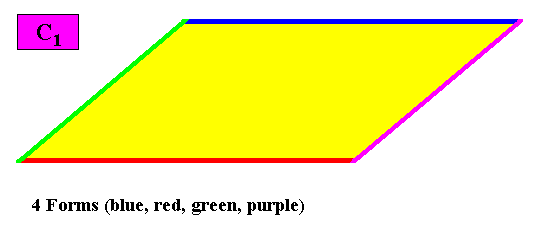
Figure above : Any initially given crystal face will not imply other faces, because there are no symmetry transformations that generate new faces. Consequently any such initially given crystal face is a Form. So to construct a parallelogrammatic (two-dimensional) crystal, four Forms are needed (blue, red, green, purple).
The next Figure (two images) gives the possible promorphs (and their names) of this parallelogrammatic crystal. The promorph is either (left image) half an isosceles triangle (and, equivalently, a quarter of a rhombus), and is as such the two-dimensional analogue of a quarter of a rhombic pyramid, or (right image) an irregular triangle, indicating two unequal antimers (yellow, green), and is as such the two-dimensional analogue of an irregular pyramid (or, equivalently, a 1-fold pyramid).
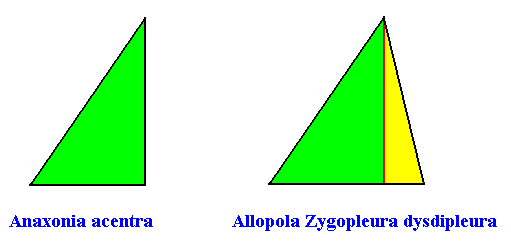
This concludes our investigation concerning the relation of intrinsic parallelogrammatic (2-dimensional) crystal shape to intrinsic point symmetry and to promorph.
Next we consider the Rhombus
The Vector Rosette of Actual Growth of a rhombus-shaped crystal, i.e. of any two-dimensional crystal having as its intrinsic shape (when fully developed) the Rhombus (which itself has D2 symmetry) and possessing whatever (possible) intrinsic (point) symmetry, is as follows (blue lines) :
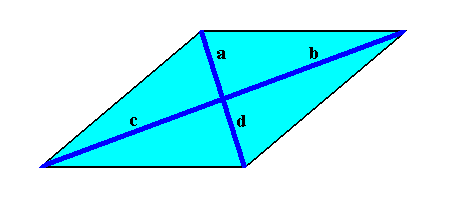
This Vector Rosette, viz. a vector rosette of a rhombic two-dimensional crystal, in fact consists of four vectors, a, b, c, d, each originating in the center of the crystal and ending up at a corner. As such it encodes the crystal's shape.
The following plane groups support a rhombus as the intrinsic shape of a two-dimensional crystal :
P1, P2, Pm, Cm, Pg, P2mm, C2mm, P2mg and P2gg.
See also the table in the previous document indicating these plane groups, the implied point groups (with the crystallographic notation between brackets) and the number of crystallographic Forms needed to construct the rhombus-shaped crystal in each case of point symmetry. In the table we can see that a rhomb-shaped crystal can have either an intrinsic symmetry equal to that of a rhombus, or a lower symmetry, down to no symmetry at all.
We will now consider several possible cases of the given example of a rhombus-shaped two-dimensional crystal as depicted just above.
D2 symmetry.
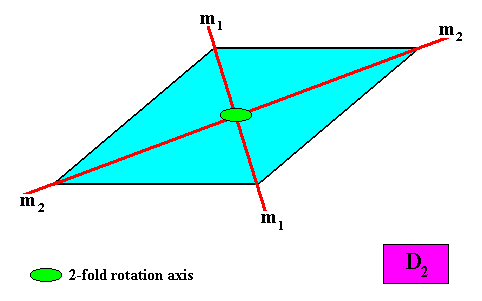
Figure above : Symmetry elements of an intrinsically rhomb-shape two-dimensional crystal with intrinsic D2 symmetry : Two mirror lines (m1, m2), perpendicular to each other, and connecting opposite corners. One two-fold rotation axis at the intersection point of the mirror lines.
If we take an initially given crystal face to be such that it is not perpendicular to one of the mirror lines, only one crystallographic Form is needed to construct the whole rhomb-shaped D2 crystal. See next Figure.
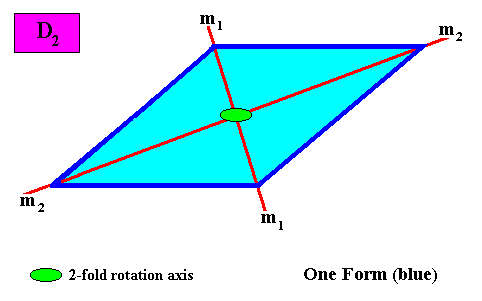
Figure above : One Form (blue) is needed to conceptually construct a rhomb-shaped D2 crystal : An initially given crystal face not parallel to one of the mirror lines implies three more faces, together making up a closed Form having the shape of a rhombus : The initial face is reflected in one of the mirror lines resulting in two faces. This set of two faces is then reflected in the other mirror line resulting in a rhombus.
Crystals having intrinsic D2 symmetry can have several different promorphs depending on the geometry of the chemical motif. Let's consider the several possibilities.
D2 symmetry and four antimers.
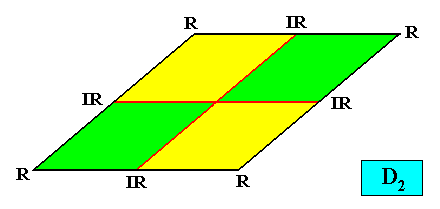
Figure above : A two-dimensional rhomb-shaped D2 crystal with four antimers (green, yellow). Radial (R) and interradial (IR) directions indicated.
And with the Vector Rosette of Actual Growth added :
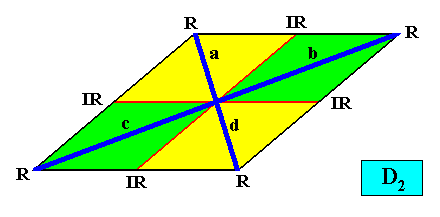
Figure above : A two-dimensional rhomb-shaped D2 crystal with four antimers (green, yellow). Vector Rosette of Actual Growth added (blue lines). The vectors of the rosette are two by two equivalent : a with d and b with c .
Depending on the motif (translation-free residue) the four antimers can be configured differently, as the next Figures illustrate.
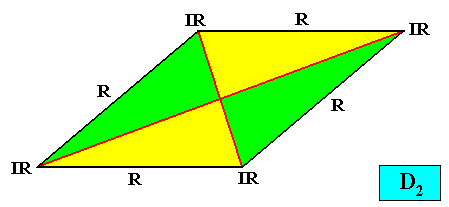
Figure above : Alternative configuration of four antimers (green, yellow) in a two-dimensional rhomb-shaped D2 crystal.
And with the Vector Rosette of Actual Growth added :
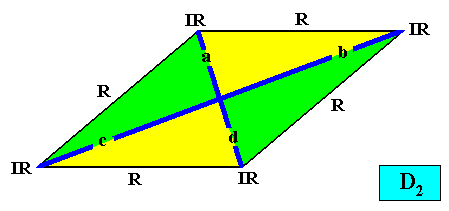
Figure above : The two-dimensional rhomb-shaped D2 crystal with four antimers (green, yellow) of the previous Figure. Vector Rosette of Actual Growth added (blue lines).
The two types of configuration of the four antimers as shown above imply two slightly different promorphs :
The first configuration corresponds to the following promorph :
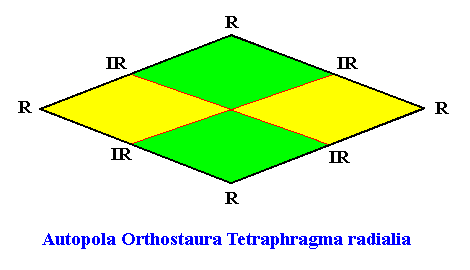
Figure above : Promorph of a two-dimensional (rhomb-shaped) D2 crystal with four antimers arranged according to the first configuration. It is a rhombus, and as such the two-dimensional analogue of the rhombic pyramid. The directional axes (see next Figure), i.e. those cross axes that are perpendicular to each other, run through the antimers, and are therefore radial directional axes.
The next Figure indicates the directional axes (strong red lines) of the just given promorph.
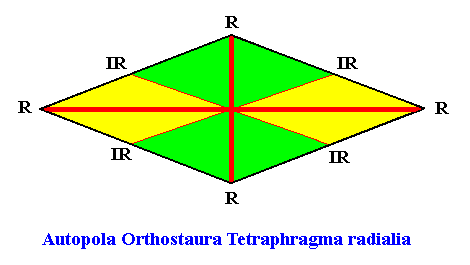
The second configuration corresponds to the following promorph :
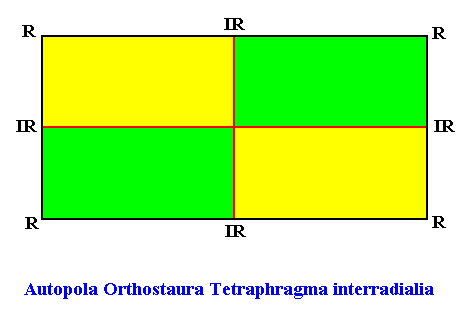
Figure above : Promorph of a two-dimensional (rhomb-shaped) D2 crystal with four antimers arranged according to the second configuration. It is a rectangle, and as such the two-dimensional analogue of the rectangular pyramid. The directional axes (red lines), i.e. those cross axes that are perpendicular to each other, run between the antimers, and are therefore interradial directional axes.
D2 symmetry with two antimers.
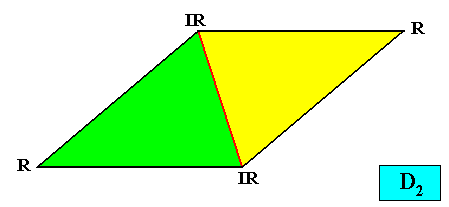
Figure above : A two-dimensional rhomb-shaped crystal with intrinsic D2 symmetry and two antimers (green, yellow).
And with the Vector Rosette of Actual growth added :
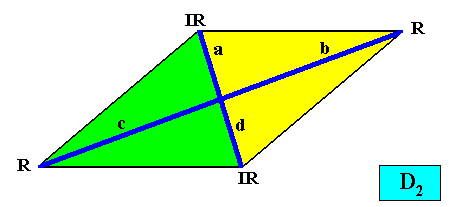
Figure above : A two-dimensional rhomb-shaped crystal with intrinsic D2 symmetry and two antimers (green, yellow). Vector Rosette of Actual growth added. The vectors are two by two equivalent : a with d and b with c .
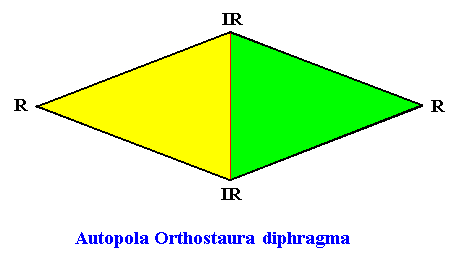
The next Figure gives the promorph of our rhomb-shaped D2 crystal with two antimers. It is a rhombus, and as such the two-dimensional analogue of a rhombic pyramid.
D2 symmetry and six antimers.
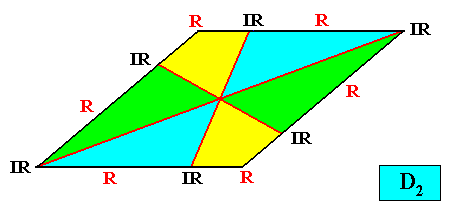
Figure above : A two-dimensional rhomb-shaped crystal with intrinsic D2 symmetry and six antimers (green, yellow, blue).
And with the Vector Rosette of Actual growth added :
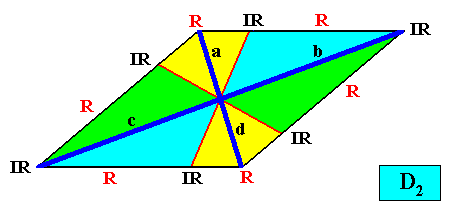
Figure above : A two-dimensional rhomb-shaped crystal with intrinsic D2 symmetry and six antimers (green, yellow, blue). Vector Rosette of Actual growth added. The vectors are two by two equivalent : a with d and b with c .
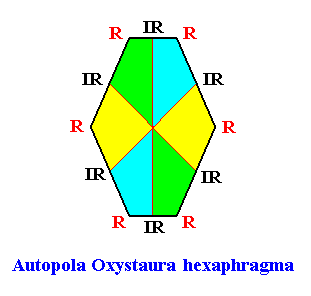
The next Figure gives the promorph of our rhomb-shaped D2 crystal with six antimers. It is a six-fold amphitect polygon, and as such the two-dimensional analogue of a six-fold amphitect pyramid.
D2 symmetry and eight antimers.
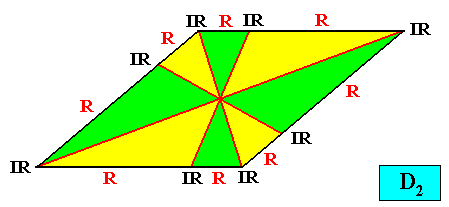
Figure above : A two-dimensional rhomb-shaped crystal with intrinsic D2 symmetry and eight antimers (green, yellow).
And with the Vector Rosette of Actual growth added :
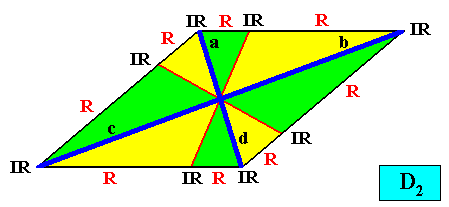
Figure above : A two-dimensional rhomb-shaped crystal with intrinsic D2 symmetry and eight antimers (green, yellow). Vector Rosette of Actual growth added. The vectors are two by two equivalent : a with d and b with c .
The next Figure gives the promorph of our rhomb-shaped D2 crystal with eight antimers. It is an eight-fold amphitect polygon, and as such the two-dimensional analogue of an eight-fold amphitect pyramid.
D1 symmetry.
The next Figure gives the pattern of symmetry elements of such a crystal, a pattern which consists of just one mirror line.
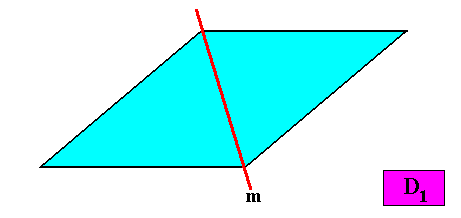
Figure above : A mirror line (m) as the only symmetry element of a two-dimensional rhomb-shaped crystal with intrinsic D1 symmetry.
Two crystallographic Forms are needed to conceptually construct a rhomb-shape crystal with intrinsic D1 symmetry : An initially given crystal face, not parallel, and also not perpendicular to the mirror line, implies one more face. The result is an open Form consisting of two faces. A second initially given face, parallel to the first, implies a second face, resulting in a second Form. The two Forms together constitute the rhombus, and thus the rhomb-shaped crystal. See next Figure.
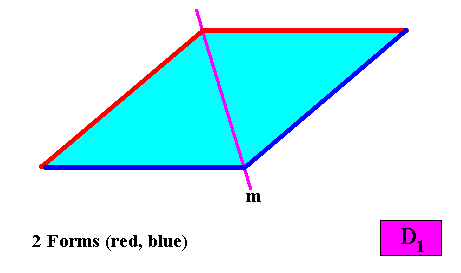
Figure above : Two crystallographic Forms (red, dark blue) are needed to construct a rhomb-shaped D1 two-dimensional crystal.
D1 crystals allow for different numbers of antimers to be present. We give some examples.
D1 symmetry and four antimers.
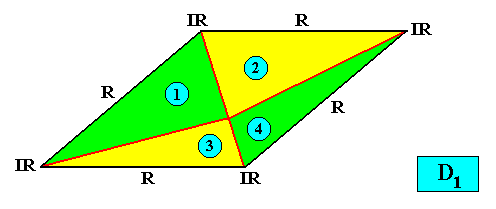
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with four antimers (green, yellow, indicated by numerals). Interradial configuration of antimers.
And with the Vector Rosette of Actual Growth added :
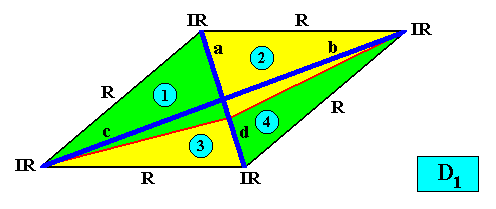
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with four antimers (green, yellow, indicated by numerals). Interradial configuration of antimers. Vector Rosette of Actual Growth added. The vector b is equivalent with the vector c .
We have just depicted the interradial configuration. One should not, however, think that this is directly based on the image of the crystal with its antimers. See next Figure.
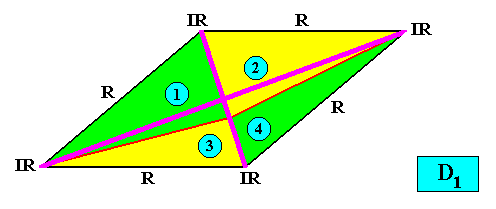
Figure above : One would be tempted to interpret the purple axes (which are perpendicular to each other) as directional axes, which would then imply that one of them runs between antimers while the other runs through two antimers, so that we cannot decide whether the directional axes taken together (as a pair) are radial or interradial. The directional axes of which we assess whether together they are radial or interradial -- and which assessment in turn determines whether the promorph is radial or interradial -- must be the directional axes of the promorph. The purple lines in the present Figure are the directional axes of the rhombus, which here is the (intrinsic) shape of the crystal. The geometric figure representing the promorph of this crystal (i.e. the D1 crystal with four antimers, arranged as in the above illustration : two at one side of the mirror line and two at the other) is not a rhombus, but an isosceles trapezium (See the promorph below ). And in such a trapezium both directional axes run between antimers. They are therefore definitely interradial.
The next Figures illustrate the radial configuration of antimers.
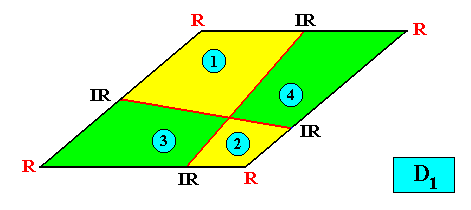
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with four antimers (green, yellow, indicated by numerals). Radial configuration of antimers.
And with the Vector Rosette of Actual Growth added :
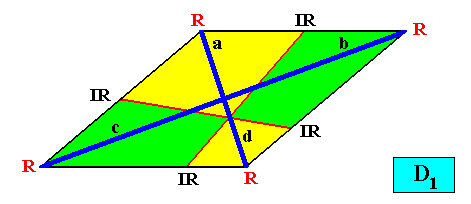
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with four antimers (green, yellow). Radial configuration of antimers. Vector Rosette of Actual Growth added. The vector b is equivalent with the vector c .
The promorph of our two-dimensional rhomb-shaped D1 crystal with four antimers arranged according to the interradial configuration (two at one side of the mirror line, two at the other) is depicted in the next Figure. It is an isosceles trapezium and as such the two-dimensional analogue of a trapezoid pyramid (and thus -- as promorph -- in turn the two-dimensional analogue of an instance of the Allopola Zygopleura Eutetrapleura interradialia.
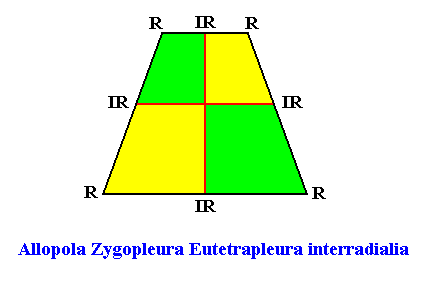
The promorph of our two-dimensional rhomb-shaped D1 crystal with four antimers arranged according the radial configuration (one at each side of the mirror line, and two on the mirror line) is depicted in the next Figure. It is a bi-isosceles triangle and as such the two-dimensional analogue of the bi-isosceles pyramid, and thus -- as promorph -- in turn the two-dimensional analogue of an instance of the Allopola Zygopleura Eutetrapleura radialia.
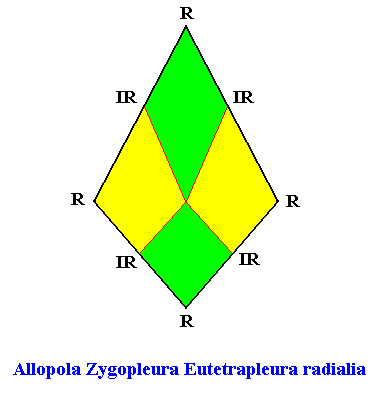
D1 symmetry and two antimers.

Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with two antimers (green, yellow). A motif (black) is inserted in order to express the D1 symmetry of the crystal, i.e. to express the fact that there is only one mirror line present.
And with the Vector Rosette of Actual Growth added :
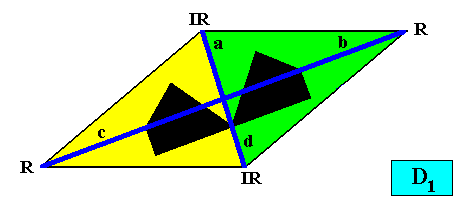
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with two antimers (green, yellow). Vector Rosette of Actual Growth added. The vector b is equivalent with the vector c .
The promorph of our two-dimensional intrinsically rhomb-shaped D1 crystal with two antimers is depicted in the next Figure. It is an isosceles triangle and as such the two-dimensional analogue of half a rhombic pyramid, and -- as promorph -- in turn the two-dimensional analogue of an instance of the Allopola Zygopleura eudipleura.
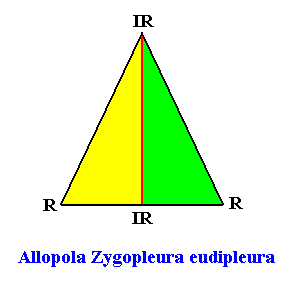
D1 symmetry and three antimers.
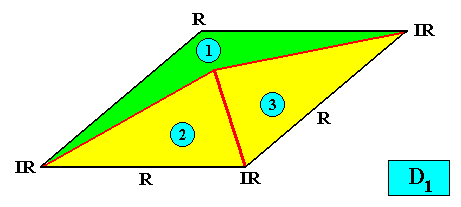
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with three antimers (green, yellow, and indicated by numerals).
And with the Vector Rosette of Actual Growth added :
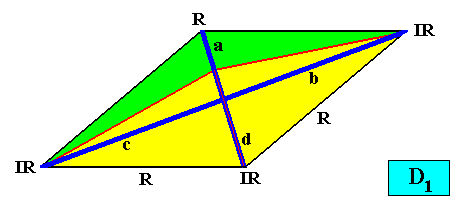
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with three antimers (green, yellow). Vector Rosette of Actual Growth added. The vector b is equivalent with the vector c .
The promorph of our two-dimensional intrinsically rhomb-shaped D1 crystal with three antimers is depicted in the next Figure. It is half a six-fold amphitect polygon and as such the two-dimensional analogue of half a six-fold amphitect pyramid, and -- as promorph -- in turn the two-dimensional analogue of an instance of the Allopola Amphipleura triamphipleura.
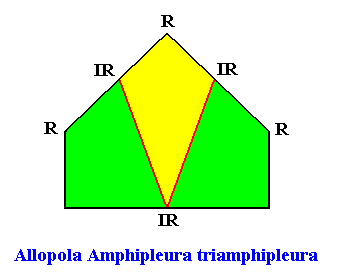
D1 symmetry and five antimers.

Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with five antimers (green, yellow, and indicated by numerals).
And with the Vector Rosette of Actual Growth added :
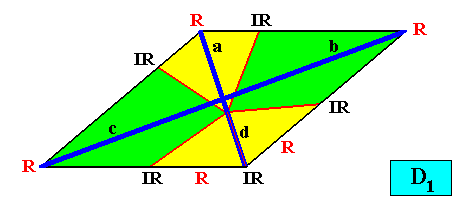
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with five antimers (green, yellow). Vector Rosette of Actual Growth added. The vector b is equivalent with the vector c .
The promorph of our two-dimensional intrinsically rhomb-shaped D1 crystal with five antimers is depicted in the next Figure. It is half a ten-fold amphitect polygon and as such the two-dimensional analogue of half a ten-fold amphitect pyramid, and -- as promorph -- in turn the two-dimensional analogue of an instance of the Allopola Amphipleura pentamphipleura.
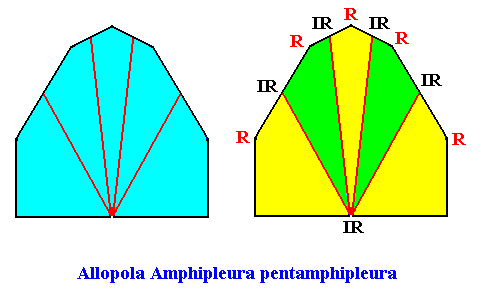
D1 symmetry with six antimers.
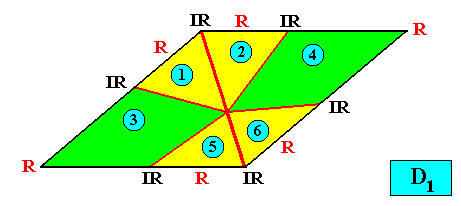
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with six antimers (green, yellow, and indicated by numerals).
And with the Vector Rosette of Actual Growth added :
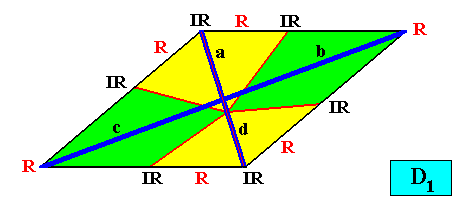
Figure above : A two-dimensional intrinsically rhomb-shaped D1 crystal with six antimers (green, yellow). Vector Rosette of Actual Growth added. The vector b is equivalent with the vector c .
The promorph of our two-dimensional intrinsically rhomb-shaped D1 crystal with six antimers is depicted in the next Figure. It is half a twelve-fold amphitect polygon and as such the two-dimensional analogue of half a twelve-fold amphitect pyramid, and -- as promorph -- in turn the two-dimensional analogue of an instance of the Allopola Amphipleura hexamphipleura.
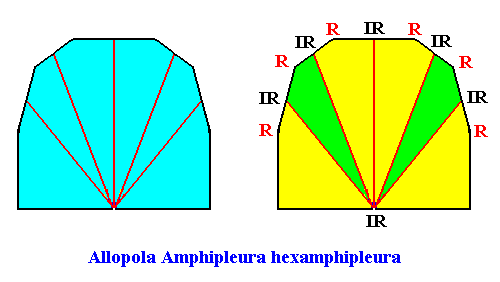
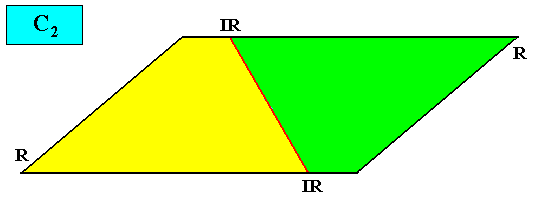
C2 symmetry.
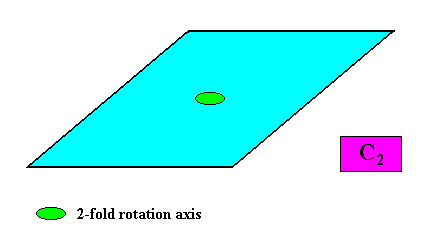
Figure above : The only symmetry element of a two-dimensional (intrinsically rhomb-shaped) crystal with intrinsic C2 symmetry is a two-fold rotation axis (green).
Two crystallographic Forms are needed to conceptually construct an intrinsically rhomb-shaped C2 crystal. See next Figure.
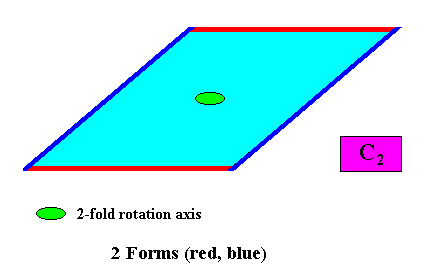
Figure above : Two crystallographic Forms are needed to construct a rhomb-shaped C2 two-dimensional crystal : An initially given crystal face (red) implies (in virtue of the 2-fold rotation axis) one more face parallel to it, resulting in an open Form consisting of two faces (red). A second initially given face (blue), not parallel to the first, implies a second face, in virtue of the same rotation axis, also resulting in an open Form consisting of two faces (blue). The two Forms together (red, blue) constitute a rhombus, and therefore constitute the whole rhomb-shaped crystal.
C2 symmetry and two antimers.

Figure above : A two-dimensional intrinsically rhomb-shaped C2 crystal with two antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
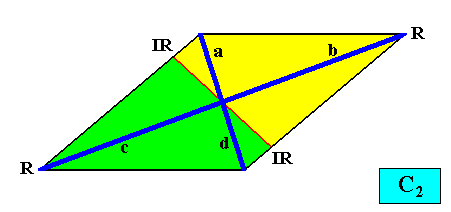
Figure above : A two-dimensional intrinsically rhomb-shaped C2 crystal with two antimers (green, yellow). Vector Rosette of Actual Growth added.
a is equivalent to d , and b to c .
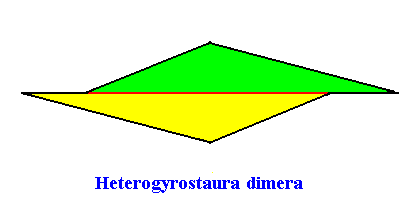
The promorph of our two-dimensional intrinsically rhomb-shaped C2 crystal with two antimers is depicted in the next Figure. It is a two-fold amphitect gyroid polygon and as such the two-dimensional analogue of a two-fold amphitect gyroid pyramid, and -- as promorph -- in turn the two-dimensional analogue of an instance of the Heterogyrostaura dimera.

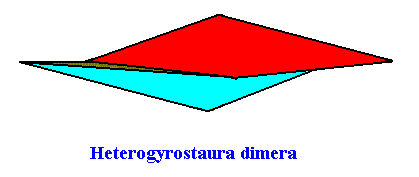
The next Figure gives the three-dimensional analogue of the just given (two-dimensional) promorph. It is a two-fold amphitect gyroid pyramid.

C2 symmetry with four antimers.
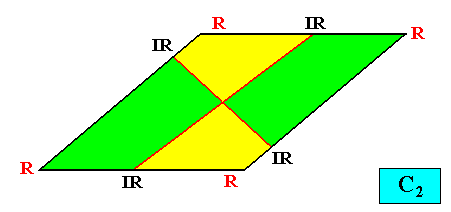
Figure above : Two-dimensional rhomb-shaped C2 crystal with four antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
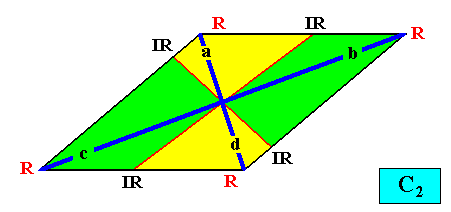
Figure above : Two-dimensional rhomb-shaped C2 crystal with four antimers (green, yellow). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
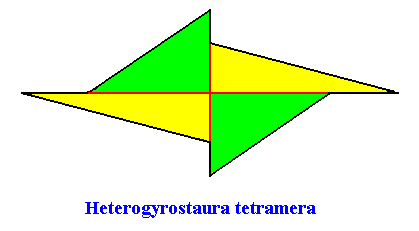
The next Figure depicts and names the promorph of our intrinsically rhomb-shaped two-dimensional crystal with intrinsic C2 symmetry and with four antimers. It is a four-fold amphitect gyroid polygon, and as such the two-dimensional analogue of a four-fold amphitect gyroid pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Heterogyrostaura tetramera .

Figure above : Promorph of the above discussed two-dimensional rhomb-shaped C2 crystal. The four antimers are indicated (green, yellow).
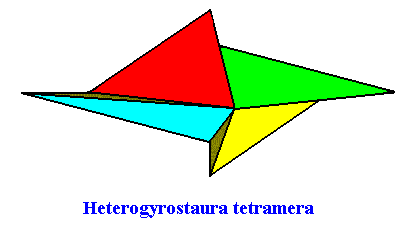
The next Figure depicts the three-dimensional analogue of our just established (two-dimensional) promorph.

Figure above : Slightly oblique top view of a four-fold amphitect gyroid pyramid, as the basic form of the Heterogyrostaura tetramera . The four antimers are indicated by colors.
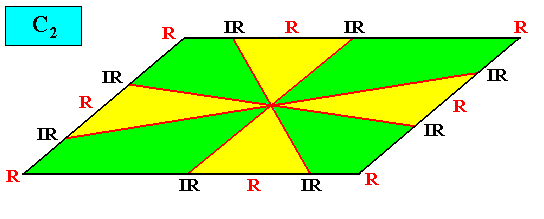
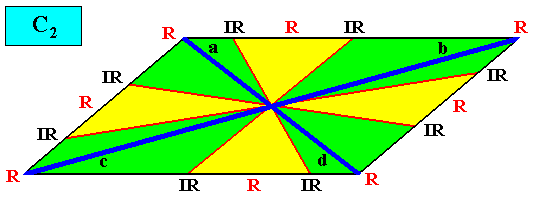
C2 symmetry and eight antimers.
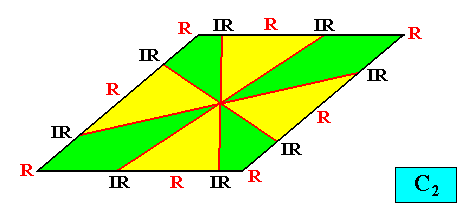
Figure above : A two-dimensional intrinsically rhomb-shaped C2 crystal with eight antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
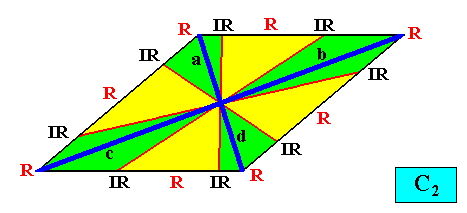
Figure above : A two-dimensional intrinsically rhomb-shaped C2 crystal with eight antimers (green, yellow). Vector Rosette of Actual Growth added.
a is equivalent to d , and b to c .
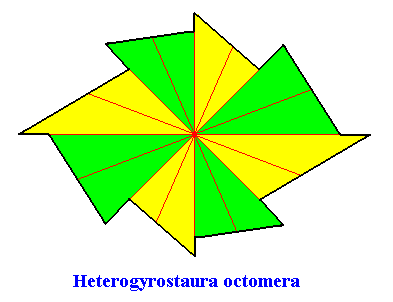
The promorph of our two-dimensional intrinsically rhomb-shaped C2 crystal with eight antimers is depicted in the next Figure. It is an eight-fold amphitect gyroid polygon and as such the two-dimensional analogue of an eight-fold amphitect gyroid pyramid, and -- as promorph -- in turn the two-dimensional analogue of an instance of the Heterogyrostaura octomera.

The promorphs of C2 crystals were represented here by polygons (pyramids) with receding angles. They can equally be represented by polygons (pyramids) not involving such angles, as is the case in all single crystals. But because in organisms receding angles are allowed, and because they more clearly indicate the gyroid nature of those promorphs, we prefer such angles to figure in the geometric structures representing such promorphs.
C1 symmetry and no antimers.
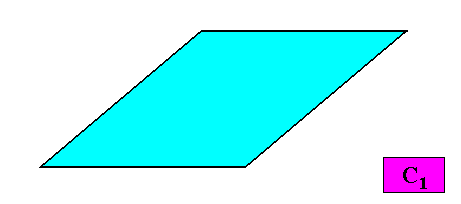
Figure above : A (two-dimensional) C1 crystal does not have any symmetry elements (with respect to point symmetry).
Four crystallographic Forms are needed to conceptually construct a two-dimensional rhomb-shaped crystal with intrinsic C1 symmetry. See next Figure.
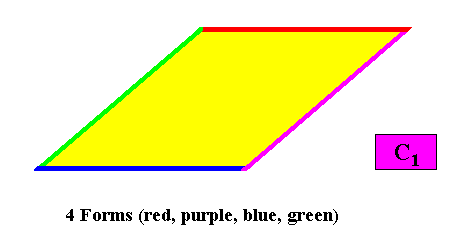
Figure above : Four crystallographic Forms are needed to construct a rhomb-shaped two-dimensional C1 crystal : Any intially given crystal face does not imply other faces. So each face is itself already a crystallographic Form. Evidently four such Forms are needed to construct a rhombus, and thus the whole rhomb-shaped C1 crystal.
C1 crystals cannot have genuine antimers. See next Figures.
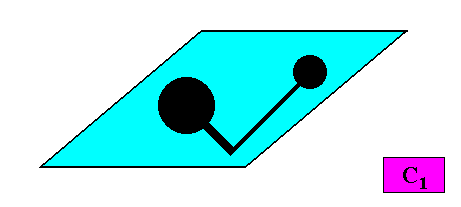
Figure above : A two-dimensional intrinsically rhomb-shaped C1 crystal.
A motif (black) is inserted to express the crystal's C1 symmetry.
And with the Vector Rosette of Actual Growth added :
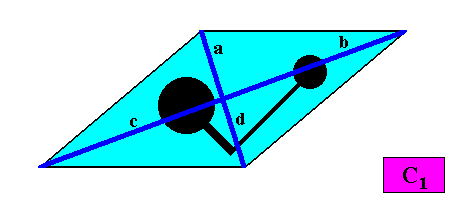
Figure above : A two-dimensional intrinsically rhomb-shaped C1 crystal. A motif (black) is inserted to express the crystal's C1 symmetry. Vector Rosette of Actual Growth added. All vectors a, b, c, d, are unique (i.e. non-equivalent).
The next Figure (two images) gives the possible promorphs (and their names) of our rhomb-shaped C1 crystal. The promorph is either (left image) half an isosceles triangle (and, equivalently, a quarter of a rhombus), and is as such the two-dimensional analogue of a quarter of a rhombic pyramid, or (right image) an irregular triangle, indicating two unequal antimers (yellow, green), and is as such the two-dimensional analogue of an irregular pyramid (or, equivalently, a 1-fold pyramid).

This concludes our investigation concerning the relation of intrinsic rhombic (2-dimensional) crystal shape to intrinsic point symmetry and to promorph.
In the next document we will investigate the fifth shape from our above given list : rectangle, square, parallelogram, rhombus, equilateral triangle, regular hexagon.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XI.
e-mail : 