

e-mail :

Introduction
This document is, first of all, a continuation and implication of the philosophical ideas put forward in the
First Part of Website concerning the ontology or metaphysical constitution of the m a t e r i a l i n d i v i d u u m like a (single) crystal or an organism (whether the latter is a human person, an individual starfish, an individual bacterium, or whatever), and, secondly, it is a continuation of the vistas laid down in the document (within the Group Theory Series) on the ontology of mathematical structures. In the latter document it was argued that there are two different s p h e r e s o f e x i s t e n c e (in addition to an intermediate one, connecting the two) : The Ideal Sphere of Existence and the Real Sphere of existence. They differ in the way of being-there of their inhabitants.
In the Ideal Sphere we can find non-physical, general, coherent and consistent objects : mathematical and logical objects and structures. In this Sphere there is no physical space and no time, implying that no genuine processes are going on there.
In the Real Shpere we find all material objects and structures, and all determining relations inhering in them. This implies that genuine processes can and do occur within this Sphere.
The intermediate sphere or layer consists of physically interpreted mathematical laws and structures which are, however, not completely physically interpreted, implying them to be still general, and thus closely related to the corresponding structures in the Ideal Sphere.
In order to easily pick up matters that will be the concern of what follows we reproduce the s u m m a r y of the last mentioned document :
In all the foregoing [of the mentioned document] we have spoken about several "Spheres of existence", differing in the way-of-being-there of their inhabitants, namely the Ideal and Real Spheres in the sense of Nicolai HARTMANN. We found out that mathematical and logical structures have an independent existence in the Ideal Sphere of Being, and that they are indifferent as to their possible 'realization' within the Real Sphere. Only when those structures are each for themselves coherent and consistent can they be genuine beings in the Ideal Sphere.
With respect to the Real Sphere, we found out that it is ontologically homogeneous, in the sense that its different inhabitants do not effect or represent different ontological layers within that Sphere. There can, however, be some sort of ontological layering, but only in such a way that the same whole system of layering cuts across every being of that Sphere (so that every being remains ontologically equivalent to any other being in that Sphere). This layering could consist of metaphysical levels or layers, going from the fully abstract (i.e. no qualitative content, or, perhaps equivalently, bare relations without (specified) relata), via intermediate levels, down to the fully determined concrete individual real being. And this stratigraphy is the same for every such being. In this way we go from the Ideal Sphere, via intermediate levels, down to the Real Sphere.
The system of layering just mentioned, is metaphysical (ontological) in character. Let's explain.
It consists of an ordered set or stack of general conditions that are absolutely necessary for something to be a real being at all (implying that these conditions are not beings themselves). This set of conditions is the same for every real being, and the conditions themselves are not specific with respect to one or another qualitative content.
For something whatsoever to be a genuine being in the first place (real or ideal), it must be coherent and consistent (logical or otherwise), which (also) makes it independent of thought (Ansichsein).
For something whatsoever to be moreover a real genuine being ("real" in the sense of HARTMANN), it must be, in addition to the just mentioned conditions, fully determined as to its qualitative content, and moreover resting on a formless substrate effecting it to be in principle repeatable, i.e. it must be an individuum, which in turn means that it stands under specific here-and-now conditions, which ultimately make it physical and dynamic. As such it is the product of one or another here-and-now dynamical system. And this product remains dynamical in character, continually interacting with other such products.
The full qualitative determinedness of such a real being consists of a complete stack of partial whatnesses, like symmetry and promorph (which exist -- in the Real -- realiter, but are not beings themselves, while they are so in the Ideal Sphere), together making up the full intrinsic content, which is the full and phenotypically manifest what-is-it of a given real being. While these partial whatnesses just statically constitute the overall whatness, the latter -- and also the former -- is generated and sustained by the fully physically interpreted dynamical law of the corresponding dynamical system, and this dynamical law is the genotypical or ultimate whatness of the given real being, effecting the phenotypical manifestation of its properties. Further, as has been said, all this qualitative content rests on a formless substate, which makes it repeatable over several instances. And as such it is, moreover, constantly subjected and perturbed by extrinsic agents, resulting in accidental features falling to it, that mask the intrinsic content (the what-is-it) of that real being.
Indeed, it is this being embedded within a dynamical context, externally and internally, which makes it a true real being, and distinguishes it from it to be merely an ideal being (in HARTMANN's sense).
So all these general conditions together make up the metaphysical layering, a layering that as such pervades every genuine real being in the same general way, and which has been expounded in more detail in all the forgoing of the present document [i.e. the document to which this summary belongs].
Each non-concrete layer of a real being exists realiter in the Real and idealiter in the Ideal. So the same what-is-it aspect can have two different ways-of-being-there, realiter and idealiter.
But of course there are many coherent structures or patterns in the Ideal Sphere that are not materialized in the Real at all, because its overall dependency web does not admit such structures to pervade the whole of the Real. Some of them could, however, occur in remote or more or less hidden and isolated corners of the Real, and could be discovered by Natural Science.
Above we referred to another type of layering of the Real, namely a layering that expresses a more or less discrete increase in material complexity. This layering is not of a metaphysical character, and does not, as a whole system of layers, cut across every individual being of the Real, because some inhabitants of the Real are much more complex than others in that Sphere.
Today, there is much speculation about the so-called emergent properties resulting from complex dynamical systems. The 'emergent' status of these properties is not, however, ontological in character. They do not come out of the blue. They are merely unexpected and unpredicted, so their 'emergence' is of an epistemological nature. They were already contained in the relevant dynamical system, albeit implicitly so. They are the unfoldings of (previous enfoldings in) its physically determined dynamical law. Such unfoldings often manifest themselves as more or less abrupt increases in material complexity and as such show the way how something like the human mind can emerge from a complex dynamical system. But all this addresses the problem (or question) whether dynamical systems, and indeed evolution itself, actually do represent an increase in complexity (or in fact do not), because as has been said, this complexity was already, in a sense, present in the system anyway. It demands special investigations about the nature of the mentioned implicitness, and thus of the nature of emergence. The theory of David BOHM's Implicate Order answers this question : All the complexities are already present, but initially enfolded within the Implicate Order. And there is a constant process of unfolding and enfolding going on, from the Implicate Order to the Explicate Order and back again, a dynamics in, so to say, the vertical direction, while the resulting horizontal sequence, visible in the Explicate Order, suggests a physical horizontal process. Describing and explaining the latter process, as Natural Science does, is, however, according to BOHM, only an approximation to the real process that takes place.
As has been related earlier, this theory is expounded in the Third Part of my website, and according to me is interesting (especially because its doctrinal ties with the metaphysics of PLOTINUS ), but speculative.
For the time being we could stick to the current scientific paradigm that complexity is truly increasing during the course of dynamical systems, and evolution in general, and that the degree of implicitness of those subsequently emerging structures and properties within the physically interpreted dynamical law is very high indeed, and that, moreover, this implicitness and the subsequent explicitness is of a purely physical nature, without different Orders being involved within the Real Sphere of being. The transition from being implicit in the physical dynamical law to being explicit should then be considered as a causal process, i.e. a physical generation. But, the degree being high or low, the implicitness, as being something physical, strongly underlines the ontological homogeneity of the Real Sphere.
So with all this we have set the symmetry groups into a general ontological context, clarifying their existential status, and increasing our understanding of the most significant aspect of STRUCTURE : SYMMETRY.
In addition to that we have introduced the PROMORPH, which constitutes a further specification (and reference) toward the Real Sphere of existence. It goes beyond symmetry down into further domains of the STRUCTURE of material objects.
In the Real Sphere symmetry is not actually generated by the symmetry group, which is only its what-is-it, but by certain dynamical systems. The same goes for the promorph.
In the Ideal Sphere there is no generation at all. The symmetry groups just exist there idealiter as coherent timeless structures (when interpreted mathematically), and their status is intermediate between the Ideal and the Real when interpreted physically but still being general. The corresponding abstract group as such exists in the very Ideal Sphere of being. Finally, the promorphs as promorphs are intermediate between the Ideal and the Real, while the corresponding geometric solids, as just geometric solids, exist in the Ideal Sphere of being.
General Ontology
O n t o l o g y is the science of the fundamental constitution of b e i n g s.
Beings are entities that are independent of thought, i.e. their very existence is independent of their being thought of. Their w a y o f e x i s t i n g (their way of being), however, is not yet determined by their being independent of thought. This way of being, or, better, this way of being-there, could be ideal or real, in the sense defined above.
So Ontology is the metaphysics of being or beingness.
Ontology assesses (i.e. makes explicit) and analyses all conditions that must prevail for something to be a b e i n g at all, and further, more particularly, assesses the conditions for it to be merely an ideal being, and the conditions for it to be a real being. Such conditions can be seen as entities, somehow existing, but entities which are themselves n o t beings (ideal or real, things or processes).
So ontology differs from natural science in that it investigates all which lies beneath b e i n g n e s s, while natural science limits itself to beings, and more particularly to real beings (things and processes). Thus ontology investigates all what leads (up) to beingness (real or ideal). One of the types of entities it so finds are natural laws. It does not find what laws do actually obtain, but finds the in the form of determinants insofar as determinants. These laws are -- as they objectively are in the real world, and thus our supposing the 'laws' as they are presented by natural scientists to be correct, and so rightly representing the fundamental relations as they obtain in the real world (Real Sphere of Existence) -- o n t o l o g i c a l c o m p o n e n t s of the real world, as has been explained in the above mentioned document.
But, one could counter, natural science also investigates the 'laws of nature'. However, it actually does not. It investigates the material world, as it is revealed by observation, and tries to explain its phenomena by discovering natural laws. It has found out that the material world is reigned by laws and it tries to assess what these laws are, in the sense that it can give a law for every category of process. So not these laws themselves, but the natural phenomena are the very subject of natural science, while the corresponding laws insofar as determinants are one of the subjects of ontology (metaphysics of being or beingness), where it investigates their way of being, and their relation to more general or more special laws. And, in addition to laws, which are dynamic determinants, ontology investigates static determinants. The latter are w h a t n e s s e s of either material objects and their properties, or ideal objects. A whatness, or what-is-it of a real being or of one of its properties, is the intrinsic qualitative content of it. It normally differs from its total qualitative content actually present, as a result of perturbations that continually take place in the Real Sphere of Existence and so adding extrinsic elements to that qualitative content. In the Ideal Sphere of Existence there is no such difference between intrinsic and extrinsic, because in that Sphere there are no processes.
So ontology investigates (1) dynamically determining entities, like laws, prevailing in the Real Sphere, and (2) statically determining entities, like whatnesses, in the Real as well as in the Ideal. The latter entities are static determinants because the only difference between a whatness as definitively assessed (for example the "symmetry group D5" indicated by its group table) and the whatness as initially observed or conceived and named (for example the "five-fold symmetry of a pentagon or of a starfish"), is that the former is fully a n a l y s e d (as a dihedral symmetry group with ten specified group elements), while the latter is not.
The Determined and the Determining
In what follows one could detect certain mild inconsistencies when compared to the findings in the mentioned document of which the present one is the continuation. I deliberately do not adapt either text, because the whole (ontological) theory is still in an 'experimental' state. If I would rigorously enforce consistency, then some valuable ideas could be lost.
Afterall, the texts are meant to trigger creative thinking about the subject of ontology, and the mentioned (slight) inconsistencies will help to do so. And, in any case, on this website we are not actually p r e s e n t i n g a (full-fledged) theory, but d e v e l o p i n g such a theory.
In the Real Sphere we can ontologically discriminate between two absolute main 'layers', domains or systems :
In the Ideal Sphere we can also ontologically distinguish two such layers, but they have only a relative status with respect to each other.
The Determined and the Determining in the Real Sphere of Being (Cosmos and Nomos)
In what follows we will stick to the Real Sphere of Being (Real Sphere of Existence), and assess more closely the domain of the Determined and that of the Determining.
First of all the Real Sphere is a m a n i f o l d , viz. on the one hand a spatial manifold of different things, and of things in different states, and, further, within those things : (a manifold) of different properties, and, on the other hand, (the Real Sphere is) a temporal manifold of states of things and properties.
It means that things themselves, and things among each other, and, further, states of things (some state of thing X here, and some state of thing Y there), and (of) properties, are actually spatially patterned (and thus e x t e n s i v e), and/or actually temporally patterned (and thus s u c c e s s i v e), and so there are manifolds within manifolds.
Secondly, in many cases these spatial and temporal manifolds turn out to be o r d e r e d , in the sense that their spatial and temporal patternedness is regular, i.e. somehow compulsory.
For intrinsic things or systems this means that a given species (class) of them turns out always to display some specific and repeatable behavior (including the reflection and absorbtion of light resulting in color, resistence against pressure, etc.), i.e. it interacts with other things in a way typical for it. It also displays a typical internal spatial pattern expressing how its material components are organised. And in these two ways it displays its properties (in the braoder sense). And all this is its typical and unequivocal being-so-and-so (being-thus). We call it material or static ordered connectedness with respect to a given being or system : A certain behavior and internal spatial pattern is definitively connected with the given (class of) intrinsic thing.
The manifolds to be ordered means further that some things, or some properties, or some states, follow upon another within Time (one thing is followed by another, one property is followed by another, etc.) in a necessary and repeatable way. We call it causal or dynamic ordered connectedness : The necessary connection of things, etc. in time.
Both types of order (material or causal) can be understood as an expression or function of d e t e r m i n i n g l y a p p l y i n g (or, equivalently, obtaining) s p e c i f i c c o n s t a n t s (i.e. constants in their 'act' of applying, or, in their 'act' of being valid). The ceaseless obtaining (i.e. the validity, as it is under way) of these constants results in the mentioned types of order. What are these constants in their generality? They are n o t the constants that occur (as numbers) in physical and mathematical formulations, i.e. they are not constant magnitudes. They are also n o t conditions for one or another particular order (because for one particular order to be realised, many different conditions will do equally well). They are conditions PLUS the resulting order. And we can express them by means of the general scheme :
which we could simplify as :
or for short :
Although this relation can signify a logical implication (as it does in the Ideal Sphere of Existence), here, i.e. in the Real Sphere, it means an ontological implication (dynamic or static).
The If component in itself is not necessarily constant, nor is the Then component. But the whole relation If / Then is constant for every particular instance of it. That is an expression of the thoroughgoing deterministic network of the Real Sphere.
The only exception could be the events in the quantum domain. But quantum entities are -- according to me -- just because of this exception not really genuine beings at all, but deficient beings.
And apart from this there could be discovered hidden variables in the subquantum domain responsible for the alleged statistical behavior of quantum particles.
The relation If / Then is moreover not in space nor in time. Each If / Then is a determining constant. It determines, and results in the determined. So the domain of the determined consists of the determinable and the determining. As such these relations have the character of the categories of HARTMANN (See the above mentioned document).
In all cases of If / Then relations, the degree of generality of the Then component is the same as that of the If component.
Another type of ordering (in addition to the material and the causal orders) consists in the fact that there are classes of things, properties, states and events. Some things, some properties, some states and some events, are more similar to each other than to respectively other things, properties, states and events. This means that in addition to an individual here-and-now If . . . , implying a particular Then . . . , there can also be g e n e r a l If / Then relations, ultimately resulting in natural laws. A c l a s s as such is immaterial and atemporal. Only its individual here-and-now cases are material, and extensive, also in time. It is rooted in its here-and-now cases and is therefore from case to case realiter, while as a whole it is idealiter, residing beyond the Real Sphere of Existence.
A conditio sine qua non is a necessary condition for a feature X, i.e. without that condition X cannot be. However, such a condition could not be sufficient for X to be.
But if the complete set of all such necessary conditions (i.e. all conditiones sine qua non) are actually present (are actually satisfied), then (at last) we have sufficient ground, having as its necessary effect the being-there of X.
As essential parts or aspects of s u f f i c i e n t g r o u n d , as we can collectively call the If / Then constants, we experience (and seek for) two roots of it, namely
In fact the ratio (sic) essendi, the ground of being-thus in a broader sense, is the supreme concept, because it refers to the being-thus as a result of generation, as well as to the being-thus not as a result of generation.
Dynamic If / Then constants.
A causal chain can always be considered as (part of) a trajectory of some dynamical system [not necessarily a totality-generating dynamical system, i.e. not necessarily a system that produces (new) genuine beings]. Let's take the following simple example :
The dynamical law effecting this trajectory is :
which says that the value of the (n+1)th state is five times that of the (n)th state, which means that every (next) state has a value five times as big as that of the previous state.
The variable X should be interpreted physically, but here we just consider a numerical simulation (of some physical process).
This law describes the general and binding relation between the states of a dynamical system (and not only the actual first this, then that as an observed sequence).
In the above sequence we can see that for example state E (which has the value 75) is generated from state D (which has the value 15).
S p e c i a l If / Then constants are here for example :
If D, then E
If C, then D
If E, then F
The g e n e r a l If / Then constant is :
If X, then 5X will follow (which is the above dynamical law, expressed as an If / Then constant).
Such dynamical constants always refer to a complete state of a dynamical system.
They are not genuine beings (that ARE), but apply. We could perhaps say : The If / Then constants ARE not, but ARE VALID, i.e. do (always) apply.
As a concrete example we consider the generation of an ice crystal, and thus of an intrinsic genuine being, from a particular volume of liquid water. This volume of water can then be considered to be a dynamical system generating -- under appropriate conditions -- an ice crystal (Normally there will be formed many crystals simultaneously that lock into each other, forming a crystalline aggregate, but we here concentrate on one single ice crystal only).
So when we have a particular volume of liquid H2O -- water -- , under normal atmospheric pressure, and when we lower the temperature of this volume a little below 00 centigrade, then ice crystals will eventually be formed (generated), and we -- as has been said -- concentrate on the fate of one of them (its formation and growth). The water molecules will then arrange themselves into a hexagonal array, resulting in the mentioned individual crystal.
Also when -- because normally many ice crystals will be formed simultaneously -- the faces of the crystal have no chance to become expressed, we can still speak of a single here-and-now crystal, because the generated crystal lattice contains already all the properties of an ice crystal, albeit that some of them are only more or less implicitly, i.e. only potentially, present : For example the possible crystal faces are already determined by the generated crystal lattice.
And this means that -- with respect to the intrinsic symmetry of the crystal -- the corresponding Space Group (which is a three-dimensional symmetry group containing in addition to rotations and reflections also translational elements), representing the total symmetry of the ice crystal, is implied, and this Space Group implicitly contains the corresponding Point Group symmetry (i.e. the translation-free residue of that Space Group) of the ice crystal, which is D6xC2 (which is a so-called product group). When the crystal has grown unimpededly, i.e. freely, also its point group symmetry will be expressed.
The development of the mentioned ice crystal will proceed in stages, amounting to the growing of the crystal from an incipient very small seed which is spontaneously formed in the liquid. These stages or states of the corresponding dynamical system (including the mentioned water volume and the developing crystal), are linked to each other linearly and causally, they form a trajectory in the phase space of the dynamical system, and the latter operates according to its corresponding dynamical law (which here is a certain crystallization law).
If we call the stages A, B, C, D, etc., then we can say that some special If / Then constants, which are dynamical constants, are :
If A, then B
If B, then C
If C, then D
etc.
The general If / Then constant is equivalent to the operating dynamical law (i.e. the crystallization law, ruling the freezing of water under normal atmospheric pressure). Also this general constant is a dynamic constant.
Static If / Then constants.
There are three types of static If / Then constants :
All three are If / Then constants, and as such ARE not, but APPLY. Their being consists in being valid.
Implication of properties of a given intrinsic being (entitative constants).
As an example we take a non-twinned, and thus single, ice crystal (generated under normal thermodynamic conditions).
A twinned crystal is a regular growing together (i.e. a growing together according to definite rules) of two or more crystal individuals, resulting in identical but mutually differently oriented lattices.
Although such an ice crystal is indeed generated by some dynamical system, we here do not look at it as representing a state of such a dynamical system (and then considering the next state), but concentrate on all its potential behaviors, and thus all its properties (and thus seeing the ice crystal as it is also outside the context of the dynamical system that has generated it).
The material of such a crystal is the (chemical) substance H2O (i.e. each molecule consists of two Hydrogen atoms chemically bonded to one Oxygen atom) ( The viewpoint from the material will be discussed below).
An ice crystal -- and thus a being -- consists of H2O molecules that are arranged in a regular hexagonal three-dimensional array, implying the point symmetry of such a crystal to be that of the Crystal Class 6/m 2/m 2/m, and thus having the symmetry group D6xC2.
So the property of having symmetry group D6xC2 with respect to an ice crystal, can be expressed as the following If / Then constant :
If we have an ice crystal, grown under normal conditions (that need to be specified), then an intrinsic symmetry according to the symmetry group D6xC2 will be present in such a crystal (The intrinsic symmetry can always be perturbed, often resulting in a lower actual (extrinsic) symmetry).
As will be clear, this symmetry is not generated by the ice crystal (but is co-generated by the dynamical system that has generated this crystal in the first place), but implicated by it. Consequently this constant is a static constant. The same goes for other properties such as density, degree of hardness, etc. But also all typical dynamical interactions in which the crystal can engage can be expressed as static If / Then constants, and are as such properties of such a crystal.
Material Constants (constants of given bulk matter).
Material If / Then constants refer to intrinsic properties of bulk matter. The latter is a macroscopic arbitrarily shaped volume of some chemical substance.
Bulk H2O (as an example) generally is not a single being, but an aggregate of beings. And the latter are either H2O molecules (i.e. each molecule is a genuine intrinsic being), or H2O crystals (i.e. each non-twinned ice crystal is a genuine intrinsic being). Both (i.e. molecules or crystals) can be considered as being generated by a corresponding dynamical system or subsystem.
Generally a m a t e r i a l is not (considered to be) a state of a dynamical system, because we can take any arbitrary piece or fragment of it, and as such it is still that same material. A material is bulk matter of a given chemical substance. So a material either consists of a large collection of more or less freely existing molecules (or atoms), and as such appears as amorphous solid, a liquid or a gas, or as a crystalline aggregate, i.e. an aggregate consisting of many individual crystals (of the same substance) positioned in random orientations and displaying a range of sizes.
To continue with our example -- bulk H2O -- we can say the following :
When we have s o l i d bulk H2O, we have a particular case of being-thus. The latter is determined by an If / Then constant as follows :
If bulk H2O is subjected to a certain pressure and temperature (of which there is a whole range of possible relevant combinations, and this range is here supposed to be specified), then we get s o l i d H2O (ice).
This If / Then constant is in fact a property of bulk H2O. It is i m p l i e d, (not generated) by the w h a t n e s s of bulk H2O.
The w h a t n e s s of bulk H2O is a g e n e r a l If / Then constant, general with respect to bulk H2O. It is the total of all special If / Then constants with respect to it, i.e. the total of potentially being-thuses of bulk H2O. To become solid under certain conditions is one of them.
The being-thus, actually present, namely s o l i d H2O, is as such determined by the just given If / Then constant. But in fact we must express this differently : The being-thus, actually present, namely the s o l i d i t y of bulk H2O, is as such generally, i.e. in every individual case, determined by the mentioned If / Then constant. And solidity cannot be generated, but only co-generated, namely when ice crystals are generated in the first place (within the context of the present example). The If / Then constant only then is in the 'process' of determining, when the If component is satisfied.
Summarizing with respect to H2O : What is generated is an ice crystal or (many) ice crystals. What is just implied (and not generated) is, for example, D6xC2 symmetry (of the single ice crystal [for example a snow crystal], i.e. of every individual ice crystal, and as such corresponding to a property, not of a material, but of an intrinsic genuine being), and (to mention the above example of just being implied :) the solidity (of the single ice crystal and of the (aggregate of) ice crystals). So the constants determining the symmetry and the solidity are static constants. But in many cases in the Real Sphere of Existence, even static If / Then constants must be expressed dynamically [And when we say, for example, that reflections (as symmetry transformations) are implied by the D6xC2 symmetry, we are (dealing with things) in the Ideal Sphere of Existence, where no generation takes place, and where the implication is just a logical relation].
A being-thus, associated with a property is not a thing, not a being, because its appropriate substrate does not belong to it. Therefore, a being-thus cannot be truly generated, but only co-generated. It is as such just an implication of the whatness (what-is-it) of a given concrete being or system of beings. So indeed the If / Then constants determining such being-thuses are static constants. When it is determining an intrinsic being-thus of bulk matter of a given chemical substance, it is a material constant. When it is determining an intrinsic being-thus of a given genuine being, we will call it an entitative constant.
But when a being-thus is not associated with a property, when it is, for example associated with a state of a given dynamical system, it is generated, namely from the previous state on the basis of the prevailing dynamical law, which is itself a general If / Then constant. And this constant is a dynamical constant, as we saw above.
Determining intrinsic whatness of things, materials and their properties (whatness categories, or, equivalently, eidetical constants).
Conventionally the whatness of something is expressed as a definition. In it the meaning of some concept is given. As such a definition is a logical or gnoseological entity, not an ontological entity, and thus not a category or If / Then constant, because the reference is to concepts, not to things, materials or their properties. The direction of 'movement' is from unanalysed (not understood) to analysed (and therefore understood), for instance in
Man is a featherless biped.
In a whatness category, on the other hand, the direction is from analysed to unanalysed. And here we have, moreover not to do with concepts and their meaning, but with beings (which can be either physical or mathematical), materials and properties .
The whatness category (eidetical constant) can first of all determine the intrinsic whatness of a genuine being (When this being is mathematical there is no difference between intrinsic and extrinsic whatness). In the physical case such a whatness category or eidetical constant is the dynamical law of the physical dynamical system that generated that being ( This dynamical law is at the same time a nexus category, connecting states of the dynamical system).
The whatness category can also determine the intrinsic whatness of some given material, and, finally it can determine the whatness of some property of a given being or of a given material.
In the case of a whatness category, the "unanalysed" does not refer to something-not-understood, but to something-being-just-there. And the latter is necessarily what it intrinsically is, i.e. it is determined as to what it intrinsically is by the "analysed", where the latter does not mean analysed by us. It means the ontological 'machinery' that determines something as to what it is in itself.
This theory of If / Then constants is further developed in the Section Preliminary investigation of the domain of NOMOS of the present document.
The Real is the Ideal
In the First Part of my Website I studied the E s s e n c e of intrinsic genuine individual b e i n g s , like organisms and (single) crystals. Every such intrinsic being is considered there as the product of some dynamical system, and the dynamical law of that system was equated with the Essence of that generated intrinsic being. During the genesis of that being the fully physically interpreted dynamical law (implying as such definite (physical) initial conditions) is the dynamic determinant of that being as a whole, while at the same time it is its intrinsic whatness or essence. So what is generated is that particular b e i n g , while its p r o p e r t i e s are co-generated, which in fact means that they are (only) i m p l i e d by the Essence (in the form of special If / Then constants, which here are just implications). For example, a c r y s t a l is generated, while its intrinsic symmetry is directly implied. This is because symmetry as such is not a genuine being or thing, so it cannot be physically generated.
In simple beings, like molecules or crystals, all their properties are d i r e c t l y implied by their essence or whatness, which means that the Then component of the corresponding If / Then constant is d i r e c t l y connected with the Essence (which is the If component).
In higher beings, which means much more complex beings, the Then component of the determinants of many of their properties (including typical behavior) is only m e d i a t e l y connected with the Essence. Between such a Then component and the Essence a whole stack of l e v e l s is inserted (See for this, First Part of Website, the document on Structural Levels). And this means that the what-is-it of such a property seems to have nothing to do anymore with that Essence (i.e. the Essence of the particular being that has this property). We can only trace it back to some next lower (but still very high) complexity level. This is, for instance, the case with at least much of human behavior. The latter floats as it were on a huge stack of complexity levels (structural and dynamical levels). It is far away from the ultimate physical lowest levels, so that even its causal nature is not apparent anymore. It (i.e. human behavior) is in fact such an e m e r g e n t phenomenon referred to above (in the reproduced summary close to the beginning of the present document). The next drawing illustrates such an emergence in a symbolic way :
The above Figure symbolically indicates that although a human brain, at the level of its neurons, acts strictly causally, and logically for that matter, it can, at its highest levels, at times act irrationally or illogically. So the latter illogical behavior is, curiously enough, based on logical interactions.
At the lower levels elementary units interact with each other, causing some higher units (composed of them) to appear, which in turn interact (and involving feed-back loops) with each other (while their constituent elementary units cooperate). All this results in still higher more inclusive units to be formed that enjoy a certain degree of independence and act as if they were elementary units themselves (This state of affairs is described by HOFSTADTER, in his wonderful book GÖDEL, ESCHER, BACH (1979, 1999). When we now contemplate what happens at the highest levels, we cannot explicitly and clearly link this high-level behavior to the interaction of constituent elementary units at the lowest level. There seems to be no evident and necessary connection between these levels. This has lured many philosophers into the trap of the dualism of mind and body (with respect to humans), in the sense that, in addition to physical reality, a quite new order of reality appears in human beings, where no natural physical laws are operating. The latter are "super-formed" or "superseded" and make place for 'free will', for moral values as determinants, for immaterial psychological processes, according to (fundamental) psychological laws, etc. (Free Will has been discussed on the First Part of Website in the document Organisms IV ).
It seems, however, much more reasonable to suppose that such emergent phenomena are the results of very complex physical dynamical systems or subsystems, originated and functionally fine-tuned during organic evolution. But those systems are so massive with respect to the number of participating elements (think of the millions of neurons in a brain), and, in addition to that, so subtle, that we are unable to trace human thinking or behavior all the way back to the interactions of neurons (which themselves are fed with sensory or internal data) and ultimately of molecules and atoms.
Not dualism, which is the easy way out, but the diligent study of such systems (with the aid of computer simulations) will offer the prospect of some more understanding of such high-level phenomena.
But, be this as it may, we cannot deny that with higher organisms, and especially with human beings, we do find these new behaviors, which we can collectively call the Psyche. We at least experience it as something novel with respect to the low-level physiological processes, which are themselves wholly chemical or electro-chemical. Indeed we experience Life as such already to be a novel feature with repect to inorganic beings like crystals or gravitational systems ( The latter are, despite their often awsome magnitude, also low-level phenomena, not displaying Life or Psyche at all ). And again, as we descend from crystals and molecules into the quantum domain of elementary particles, we enter into yet another range of phenomena, such that we can consider the behavior of ordinary (bulk) matter as a high-level phenomenon with respect to that quantum level [ The latter displays, for instance, the weird particle-wave duality and other strange phenomena, not encountered (in an observable degree) at the macroscopical level ]. It seems that quantum particles, because of their indeterminateness (according to the famous Heisenberg uncertainty relations), are not truly beings at all, they seem d e f i c i e n t beings, or, 'not-yet-beings'. We find such particles at magnitudes of about 10-17 cm. Presently we cannot yet descend further down, but it is assumed that qualitative detailedness, i.e. structure, continues to reach all the way down to magnitudes of around 10-33 cm, i.e. all the way down into the subquantum domain, beyond which, so it seems, space and time as we know it, become totally undefinable ( BOHM, 1980/1988, Wholeness and the Implicate Order, p. 190 of the 1988 edition). So below this magnitude of 10-33 cm space and time (as we know it) vanish all together. This could mean that the very p h y s i c a l itself vanishes below that magnitude. And we should realize that the range extending from 10-33 cm to 10-17 cm is about the same as the range from quantum particles to everyday objects. When the physical nature vanishes, what is left? Well, we could speculate that what is left is the p u r e l y m a t h e m a t i c a l , a world of mathematical points (or numbers for that matter) standing in certain complex relations to one another, without any genuine physical interaction or process taking place at all [All mathematical (geometrical) figures and shapes, and also all mathematical 'spaces', can be expressed numerically or, more generally, algebraically (for example as equations), so there is no actual (geometric) space needed]. But this in turn would mean that we have landed in the I d e a l S p h e r e o f E x i s t e n c e !
Because, however, the only thing that we have conceptually done is descending along the (scale of) magnitudes of our Real Sphere of Existence down to the lowest levels, we haven't truly left the Real Sphere, which in turn could mean that our 'Real Sphere' is in fact just the Ideal Sphere !
The 'Real Sphere' with its matter, energy, and processes, is then just a high-level phenomenon (i.e. an epiphenomenon) of an Ideal Sphere (analogous to the assumed fact that the mind is just an epiphenomenon of the physical brain), meaning that in fact the Real Sphere is ultimately Ideal, and that there, consequently, is only ONE Sphere of Existence, namely the Ideal Sphere.
If this is correct, then all of Reality is ultimately mathematical in character, it is ultimately immaterial, and all the connections between entities are ultimately not of a causal, but of a l o g i c a l nature.
Our ordinary material processes are thus (relatively) high-level phenomena and emerge from lowest-level l o g i c a l d e r i v a t i o n s , and the latter can, so it seems, be reproduced and explored by the human mind, when it is doing mathematics. In fact it is precisely because the world is wholly mathematical (including mathematical structures that have not participated in complexification resulting in physical matter) that we can do mathematics at all ! And the whole world, as it is just a vast logical structure, becomes, in a sense, mind-like.
When we suppose that the real world is ultimately wholly mathematical, we must assume that its physical manifestation originates by a logical 'process' of complexification (including its further development), a complexification of mathematical entities, leading up to particles, waves, matter and energy, liquids and crystals, all the way up to starfishes and humans.
But there are also mathematical structures that seem not to have participated in this logical complexification, and remain what they are.
So our 'Real World' is just an epiphenomenon within the much vaster Ideal Sphere as a whole. This is expressed in the following diagram :
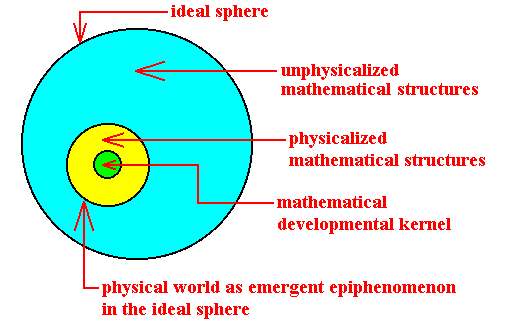
Figure 2. The one Ideal World, containing the physical world as its epiphenomenon.
The mathematical kernel (green) lies at the base of the logical derivations and complexifications, leading up to the physical, biological and psychical worlds, together forming the 'Real Sphere'.
The upshot of all this is that there is only ONE world after all (not two worlds or spheres, the Real and the Ideal), and this appears very plausible indeed.
Of course we cannot in any way imagine how mathematical entities can, by prolonged complexification, ever become such that we experience them as material entities or processes. But the same is the case with respect to the Psyche. How do chemical substances and their interaction, leading to complexification, manage -- all by themselves -- to become psychical, and how does the complexification of inorganic matter lead to Life? Obviously it cannot be just any complexification : Toffee molecules, for example, are just as complex as DNA molecules, but they totally lack the subtle functions of the latter. So the genesis must consist in functional complexification, at least in the case of organisms ultimately originating (emerging) from inorganic matter. An instructive very simple case of emergence is heat, that emerges from kinetic energy of molecules present in large numbers.
As irrational and illogical thoughts and behavior ultimately is rooted somehow in the rational and logical behavior of neurological circuits, and these in turn in the rational and logical behavior of chemical molecules (and the same goes for so-called free decisions ultimately emerging from deterministic 'decisions' taking place in neurological circuits), so is physical matter, energy and time ultimately rooted in, and emerging from, non-physical purely mathematical entities that more and more complexify (not in time, but logically). Also in this latter case we cannot imagine how this is supposed to have taken place.
Nevertheless, mathematical complexification all by itself is imaginable, as we can see for example in certain recursive mathematical systems, like the logistic equation (Here expressed as a mathematical dynamical law) :
Starting with an initial value of X (say, 0.1), and a fixed value for r (from the range 1.9 -- 3.0), we can find a next value of X. And with respect to that obtained value, we do the same, i.e. we determine the next value of X, and so on. We continue to do so [which means we iterate the function F(X) = X + rX(1 - X)], till the system settles at a certain value (steady state), or till it enters into a cycle. If we do this for a large number of values of r (from the range 1.9 -- 3.0), then we will see that the total set of values representing steady states, cycles, or infinite cycles, has a very complex structure indeed, including self-replication, as is well known. It consists of a series of point attractors, cyclic attractors and chaotic attractors inherent (i.e. potentially present) in the system. So iteration of a simple mathematical function can lead to baffling complexity. But in this given example the generated complexity is still of a purely mathematical nature. So much more is needed to let physical matter emerge, and in turn, to let Life emerge from (complexification of) inorganic matter, and, finally, to let Consciousness emerge from (complexification of) organic matter. But all this being far from understood may not let us capitulate in our effort to grasp the world as it presents itself to us (including our own being).
Until now we can only detect some major structural and functional levels of complexity, leading from purely mathematical structures all the way up to human subjects. And because such a theory offers ONE monistic world, it is, I think, very plausible indeed, despite our lack of understanding the mentioned emergence of higher levels.
All this means that the nature of all If / Then constants, referred to earlier, is ultimately logical, i.e. all the necessary and repeatable connections are in fact l o g i c a l d e r i v a t i o n s (like the derivation of the above mentioned set of attractors from the logistic equation), and that there are ultimately no physical processes and causal connections at all. The world is wholly mathematical.
Of course, for the time being, we must work with physical, biological and psychical determinants ( If / Then constants), in order to provisionally understand the physical level, the organic level and the psychical level. And as long as we do not absolutize and hypostatize our findings (saying for instance that the psychic determinants, or even 'free' causes, are fundamental, underivable and underived), we are not in error when doing so.
But we can make a beginning to place all these levels and phenomena into a broader and unifying context, the context of the mathematical, within the one and only Sphere of Being, namely the Ideal Sphere, as our one and only world.
And all this does not in any way degrade human dignity, because truth (assuming the hypothesis to be correct) never degrades anything.
And the world, now being utterly mathematical and logical, is then -- as has been said -- mind-like, i.e. it is a sort of mind. Maybe this mind is the God that is sought for in many cultures and nations.
And, as has been referred to earlier, in our Ideal World (which we could now just as well call our (one) World, or Real World for that matter) we have detected several c o m p l e x i t y l e v e l s. And if we go from the bottom to the top we see an increase in (functional) complexity. But this increase is -- as it seems to us -- more or less discrete. That's why we can detect complexity levels in the first place. As complexity levels they are not ontological, i.e. they are not fundamentally (which in turn means underivably) different and novel with respect to lower levels, but differ only in degree (of complexity). The discontinuities
are nevertheless remarkable. They seem to have to do with certain critical thresholds that apparently occur within the sequence of increasing complexification (as we can see in the iteration of the logistic equation, referred to above, where at a certain definite value of the parameter r highly complex 'chaos' sets in). The most spectacular discontinuities are the mathematical--quantum discontinuity (if this really is a discontinuity) and the organic--psychic discontinuity. The latter has vexed and baffled philosophers for centuries, and, as has been said, they sought a way out by supposing the appearance of a fundamentally and thus ontologically different domain of being (not necessarily transcendent). The ensuing mind-body debate is still going on at present.
The most important feature with respect to complexification is dynamic and static s t r u c t u r e. An aspect of the latter is s y m m e t r y, and I have devoted much of my website (Second Part) to the latter phenomenon and extended it with a study of p r o m o r p h s (stereometric basic forms, also Second Part of Website) that sink a little deeper (than symmetry alone) in the phenomenon of structure. The latter should be further studied with the aid of general topology, which discusses continuity and possible (mathematical) spaces, and throws some light on the phenomenon of spatial distance (metric topology) and spatial neighborhood. All this could become a science of e x a c t o n t o l o g y, giving us some preliminary understanding of the fundamental structure of Reality. Apart from such very general studies, the most important point of departure is the study of complexity-generating dynamical physical systems, especially with the aid of computer simulations, which is a hot topic today, but which is still in its infancy.
In the First Part of my Website much attention is addressed to an elementary introduction to such systems and their computer simulations (Cellular Automata, Boolean Networks, L-systems, real and simulated dissipative systems), that generate (or can generate) definite p a t t e r n s. As has been said, patterns are further extensively studied as we find them in two- and three-dimensional crystals (Second Part of Website).
Our symmetry groups (describing symmetry) can already show a modest increase in complexity when we go from subgroup to group to supergroup (Of course the above mentioned iteration of a non-linear equation shows much more (mathematical) complexification). However, the ultimate elements of symmetry and promorph are asymmetric units, that cannot be further studied by Group Theory or Promorphology. They must be studied in the light of the mentioned dynamical systems or subsystems that generate such asymmetric units.
So if we indeed suppose that there is only one world, i.e. only one world that is moreover ultimately mathematical, then all the If / Then constants discussed above are ultimately l o g i c a l (i.e. not physical, and thus not causal). 'Physical' If / Then constants are constants as they appear on higher (but still low) complexity levels, they are higher-level constants penultimately determining physical states of affairs, but resulting from lower-level constants that logically determine mathematical states of affairs. And because the latter are until yet unreachable for science (its laws are already physically interpreted) we must -- while doing natural science -- stick to its physically interpreted natural laws, symmetry groups, etc., where the "physically interpreted" will mean the emergent physical matter and energy, emergent from an ultimate mathematical ground. One must realize that a non-physically interpreted natural law, although it then is indeed a purely mathematical structure, is as such not relevant on the physical complexity level, because as such it has not materialized in the sense that its own complexity would directly imply the material physical aspect. When we interpret the law physically, we have supposed this complexification (from the mathematical to the physical) already to have taken place. So we still don't know how precisely such a law or symmetry becomes 'physically interpreted', i.e. how their elements become physical, for instance how an abstract group -- like the two-element abstract group -- becomes, say, the symmetry group D1 , where the reflection m is physically interpreted, i.e. has physical meaning, or, even better is physical (See for them the mentioned document of which the present document is the continuation).
So when we speak of physical determinants, i.e. physical If / Then constants, and also of physical beings or processes, we express the fact that we are working within the p h y s i c a l l e v e l, without reference to the underlying ultimate mathematical level. And although we can say that the what-is-it of some symmetry is some symmetry group, and thus a mathematical (algebraic) structure, it is still a physically interpreted group, and thus not purely mathematical. Only when we know what precisely "physically interpreted" (or being in a physically state) should mean, we can get to the bare mathematical bones. As yet this is not achievable. After all, our theory is no more than a speculative account of the world. And there are other such accounts, like for instance the mentioned Theory of the Implicate Order by David BOHM (click the link to see how I have discussed this theory), the Theory of Morphogenetic Fields by Rupert SHELDRAKE (1981, 1988), or the more conventional accounts.
As has been said, the complexity levels are not metaphysical levels. What is metaphysical (ontological) is the division of the world into the system of the determined (Cosmos), and the system of the determining (Nomos). These systems can initially be understood as ontological layers, especially if we distinguish them as the determinable and the determining. As such they both ARE not : The latter just applies, and the former is just a potential. But eventually we must realize that they wholly interpenetrate each other (and are then not layers in the strict sense). Only the determinable being determined by the determining results in existence, i.e. results in something-there.
Let us, finally, succinctly repeat the most compelling arguments in favor of the above hypothesis :
Ontology of Nicolai Hartmann
One of the best ontology texts we have, is surely that of the philosopher Nicolai Hartmann, having worked in the first half of the 20th century. HARTMANN demonstrated the independent existence (i.e. independent of thought) of the world of temporal entities (physical, organic, psychic and superpsychic structures) as well as of the world of mathematical structures and other timeless structures, and established two Spheres of being (existence), the Real and the Ideal Spheres, that differ in the way of being-there of their inhabitants. These Spheres were not considered as totally separate, but as interpenetrating each other. And each Sphere has its own set of determinants (categories), although they have many of them in common. In the above mentioned document (within the Group Theory Series) of which the present document is a continuation, we discussed these two Spheres of existence (In the present document we speculated that they ultimately refer to ONE sphere of existence only). Further we discussed the problem of how to understand HARTMANN's "categories" as to what they really should represent (In the present document we found out that they are in fact certain If / Then constants (of which HARTMANN gives only the Then-component). These constants ARE not, but determine (like HARTMANN's categories do).
In a work called Der Aufbau der realen Welt [ The (fundamental) structure of the real world], 1940, pp. 230, HARTMANN considers the categories of his Real World or Sphere, i.e. the world in which the category of Time reigns throughout : The world of inorganic and organic (including human) beings, properties, relations and processes, in general, i.e. categories generally applying to the Real Sphere as a whole. In that work (pp. 188) he discriminates four ontological layers within the Real, viz. the physical, organic, psychic (subjective spirit) and the super-psychic (objective spirit). He discusses the applying categories in each of these layers, establishing several categorical laws that relate categories to each other and to their respective layers in a definite way. Although these layers are erected as a result of the presence of certain types of beings, like crystals, organisms and human beings, they cut across every individual being, although some higher layers are absent in lower beings. While a human being is a four-fold layered being, a crystal represents only one layer. Because HARTMANN sees each new layer as being characterized by the appearance of fundamentally new categories (in addition to some old categories inherited from the lower layer), he considers each layer as being ontological, i.e. as a whole underivable and underived from the lower layers (Although he -- rightfully -- maintains that any higher layer cannot exist in the absense of all the lower layers that 'went before'. So when entering a new (higher) layer (within the Real), some categories of the previous (lower) layer break down and are 'over-formed' or superseded, or totally replaced by wholly new categories. If we allow such categories to be valid for all four layers (as the category of Time indeed is), then we, according to HARTMANN, make the error of either materialism, biologism or psychologism.
In the light of our present hypothesis of mathematical wholeness we cannot accept such a doctrine, because we think that, for example, organisms have evolved ultimately from inorganic matter, without anything being added from outside the physical world. The same applies to the emergence of humans and their psyche and consciousness.
I think there is good evidence to suppose that Life and Consciousness are the result of increased functional complexity of physical matter, where certain physical dynamical systems play a crucial role. So his over-formed or new categories are not fundamental determinants, but emergent determinants that appear as a result of material complexification. They are so to say 'after the fact determinants', ultimately based on more fundamental determinants of the lower levels, or causes that are unrecognizably scattered within those lower levels. In fact we can say that a certain high-level phenomenon emerges from a multitude of low-level phenomena as a result of their complicated interactions, which themselves are determined by the determinants of that same low level.
The studies of HARTMANN concerning the categories of the Real, and of its layers, are interesting and important, and we can safely study them, as long as we consider HARTMANN's layers of the Real as just c o m p l e x i t y l a y e r s and nothing more. The determinants of the higher layers are such that they are relatively independent and thus more or less sealed off from those of the lower layers. This condition of being more or less sealed off from lower layers is itself a result of the mentioned complexification, and justifies to initially study them in isolation, which in fact has occurred in the development and differentiation of the sciences.
As has been established earlier, all Hartmannian categories are to be understood as If / Then constants, where the Then-component is HARTMANN's concretum (which is the set of all entities that are so-and-so determined by the category (the If / Then constant), while the If-component indicates the range of relevance of the category ( The way a category is formulated, namely as an If / Then constant, lets this category be valid everywhere. However, its range of relevance, generally is limited. And the degree of generality of the Then-component should exactly match that of the If-component, which means, for example, that a Hartmannian category, applying to the Real Sphere as a whole, i.e. to the whole temporal set of layers that at least includes the macroscopic inorganic, the organic, the psychic and the 'super-psychic' layers, has as its If-component this whole set of layers (ultimately derived and emerging from the non-physicalized mathematical layer), and consequently its Then-component (the so-and-so-determined, i.e. the concretum) has the same degree of generality as this whole set of layers taken together (range of relevance).
HARTMANN presents his general categories of the Real-as-a-whole as oppositional pairs, for example the pair :
This pair now must be represented by the corresponding If / Then constant. The If-component is the Real Sphere, i.e. the mentioned set of layers, which together form the range of relevance of the category. The Then-component is the concretum of the category, namely being permeated by Form-Matter relations of all beings and processes of the Real Sphere.
The If / Then constant (i.e. the Hartmannian category as analysed) will then read :
If we are considering the Real (i.e. if the Real as such is (considered to be) there), then we find the relation Form ---Matter permeating all of the Real.
In the same way we should consider the other general categories. And when we discuss more special categories (having a more limited range of relevance), e.g. categories obtaining only within the macroscopic inorganic level, then the If- and Then-components have the corresponding degree of (lower) generality.
We shall normally indicate categories by their (single) name, as HARTMANN does, but nevertheless always understand them as If / Then constants.
As has been said, HARTMANN's ontological layers must be re-interpreted as complexity levels, and the Theory of Levels is presented in the First Part of my Website, namely in the document Structural Levels. It is extensively discussed in the book "GÖDEL, ESCHER, BACH" of HOFSTADTER, D. (1979/1999), and also in the book "The Cosmic Blueprint" of DAVIES, P. (1987/1989).
A higher-level phenomenon, like a certain behavior or structure, depends, first of all on determinants in that same level. But, according to our hypothesis, the higher-level phenomenon + same-level cause secondly depends wholly on features of the previous level (According to HARTMANN this is only partially the case, because he assumes that novel features are being added when we ascend from a lower layer to a typical high-layer feature), that in turn and ultimately depends on features of the lowest level. These downward dependencies are, however seldom straight forward, but often of a very i n d i r e c t nature. It can be so indirect that the higher-level determinants appear to be self-sustained, i.e. independent of lower-level entities. The higher level is, in a sense, more or less sealed off from the previous levels. The relevant determinings trickle through the intervening levels and sublevels all the way up to that higher level. And because of this prolonged trickling-up (i.e. traversing a long 'distance', during which 'much happens') the lower-level features, ultimately responsible for the higher-level features, become as such unrecognizable to the investigator. Especially when we ascend from the physical level to the organic, but also from the organic to the psychic, the lower-level laws are in a way harnessed by the higher-level structures, in the same way as we harness some natural laws for our purposes with respect to, for instance, the construction of devices or buildings.
The phenomenon of being more or less sealed off of a higher level from lower levels is the result of a discrete 'jump' to higher functional complexity as we ascend from a lower to a higher level, e.g. from the physical to the organic. And even within one and the same layer, for example the organic, we find -- in evolution -- sudden jumps to new organic types. For the time being such jumps remain little understood, but they have occurred many times.
If we would assume that the rules, obtaining in each level of the set of dependency levels, as described above, can, in principle be changed, then this set of levels always demands the existence of one (ultimate) inviolable level, the rules of which can never be changed.
Based on the above considerations we can summarize the l a y e r e d w o r l d in the following diagram :
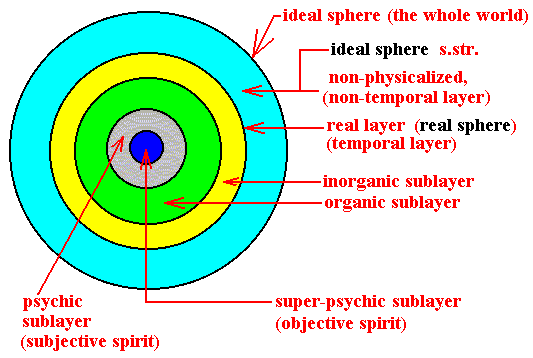
Figure 3. The Total World and its complexity layers and sublayers.
Because the 'Real Sphere' as such, i.e. as temporal, is just an epiphenomenon emerging in virtue of complexification of mathematical structures, this 'Real Sphere' is still ideal, i.e. it consists of certain hypercomplex mathematical structures, determining it still to belong to the Ideal Sphere of Existence (which is the whole objective world anyway).
While the non-physicalized layer is atemporal, the real sphere is temporal, which implies that all its sublayers (physical [inorganic], organic, psychic, super-psychic) are temporal (and in this particular sense physicalized).
The discrimination and interpretation of complexity levels
In order to understand the complexity levels, and with it an attempt to grasp how HARTMANN himself understands them (in his case as ontological layers), we must consider a level X as it is in itself, i.e. we must take it only insofar as it is in itself. How do we do this?
Every level, except the lowest one, is dependent on the previous level. This previous level should be seen as a relatively inviolable level or substrate (The lowest level, viz. the non-physicalized mathematical level, is the absolutely inviolable level). When we now consider one particular level, let us call it X, we deliberately ignore the next lower level (i.e. the inviolable level on which X is dependent -- and the inviolableness expresses this dependence), and this is equivalent to consider X only insofar as it is X.
For example, the psychic (level) is surely based on the individual organism having such a psychic level. So the psychic is dependent on an o r g a n i c structure (which in turn depends on a physical-chemical structure, etc.), and in this sense the psychic is spatio-temporal. But the psychic AS psychic (i.e. only insofar as it is psychic) is not spatial (while it is still temporal), because the phenomenon of experiencing itself and (discriminating itself from) its not-itself in a conscious way, is not spatial. In this sense, and only in this sense, the category of s p a c e breaks off when we enter from the organic into the psychic. The non-spatial aspect is, however, dependent on the s p a t i o-temporal aspect of the substrate of the psychic, the organism. The non-spatial aspect is an epiphenomenon, emerging from the s p a t i o-temporal by a discrete increase of functional complexity.
When we say -- following, for the time being, an for the sake of argument, HARTMANN -- that the psychic (layer) is not spatial, by ignoring the next lower level (which is s p a t i a l-temporal), it could sound like throwing away the baby together with the bath water : when we (conceptually) remove the spatial then what is left is (of course) non-spatial. However, we do not actually remove the spatial at all, because we have said that the non-spatiality of the psychic layer is d e p e n d e n t on the s p a t i a l-temporal substrate, i.e. on the next lower level which is s p a t i a l-temporal.
According to HARTMANN each layer is characterized by the appearance in it of -- what he calls -- a c a t e g o r i c a l n o v u m , i.e. some quite new category or set of categories, new with respect to the categorical content of previous levels. Such a novum determines the 'new face' of such a layer and influences the categories that come in from lower layers. It places these categories in a new setting and partially transforms them into variants (new versions of the old lower-layer categories). He does, however not indicate where such a novum comes from, which is of course consistent with its being a genuine novum after all. But although the latter is new, with respect to the set of categories of the previous level, it must somehow emerge from what went before. I think it is reasonable -- especially in the context of our hypothesis of mathematical wholeness -- to interpret such a categorical novum, as we see it, for example in the psychic layer, as implied by emergent material structures which appear as a result of a discrete ('jump-like') increase of functional complexity. These emergent structures -- still in the case of the psychic -- as material structures, as such still belong to the organic level, but bring with them the psychic, which means that within the psychic itself they are not material structures anymore, but immaterial structures, dependent, however, upon the corresponding material structures of the organic (layer). Indeed, the psychic layer cannot -- also according to HARTMANN -- exist without the organic layer on which it rests. We should realize that this transition from the organic to the psychic is less dramatic than the transition from the mathematical to the physical, because in the mathematical even the time category is absent, so that complexification of it, resulting first of all in the physical, is hard to visualize.
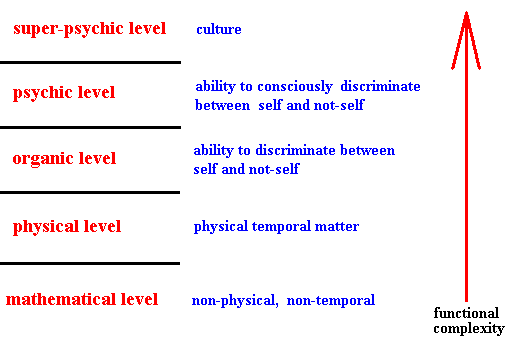
Figure 4. The Mathematical Level (Atemporal Level) and the four (sub)levels of the Real Sphere (Temporal Level).
A jump in complexity somewhere within the mathematical level results in the physical level.
A jump in complexity somewhere within the physical level results in the organic level.
A jump in complexity somewhere within the organic level results in the psychic level.
A jump in complexity somewhere within the psychic level results in the super-psychic level.
As the above diagram indicates, the complexification, responsible for emergent phenomena, refers to the jump-like increase of complexity within a certain layer (representing a complexity level) resulting in a new layer on top of it. The higher layers are always carried by (i.e. are dependent on) their previous layer. They enjoy, however, a certain independence of them in the sense that having acquired its higher-level features, it continues its business wholly within the context of these features. The latter consist of new behavior and structure, not present in the previous layer.
All this means -- as already concluded earlier -- that HARTMANN's layers are not ontologically new, i.e. they are not fundamentally different from each other, which means that the dependence of higher layers on all the previous layers (which also HARTMANN admits) is t o t a l. This in turn implies that the world is categorically homogeneous, i.e. one set of (fundamental, i.e. ultimate) categories or determinants reigns throughout the world, implying that there are no ontological layers at all, but only levels of complexity. The transformed and new categories prevailing in a particular layer are then derived categories. But because the above mentioned entanglement, intervening between the old and the 'new', cannot be analysed (i.e. the 'new' categories and corresponding features are underivable), we have no choice than to work with these 'new' categories. And as long as the intervening entanglement (or knot) is not understood (i.e. not wholly disentangled), the possibility of an ontological status of the layers cannot be excluded.
Preparation and motivation to study Hartmann's theory of layers
In what follows we will try to get as close as we can to HARTMANN's theory of the ontology of the Temporal World, i.e. of the whole system of layers above the mathematical. This system of layers is his 'Real Sphere of Existence'. In this we will not follow in all rigor the above expositions about the derived and the cognitive non-derivability, and with it about the 'definition' of the "new" (the novum). Our demand of consistency of the whole exposition, i.e. consistency between what follows and what went before, will be somewhat mitigated. This will give us room for d e v e l o p i n g a theory about the existence and content of the layers instead of just p r e s e n t i n g it fully-fledged (which is, after all, not even possible). However, we will in a stronger fashion emphasize the dependence of the higher upon the lower, i.e. stronger than HARTMANN already does, implying that the higher categories ( If / Then constants) are not absolutely fundamental, but only relatively so, resulting in the fact that the whole set of layers, including the mathematical one, is ontologically homogeneous.
The whole theory of layers (or levels) is meant to give some preliminary understanding of the ever increasing wealth of structures and subtleties as we ascend from the purely physical (ultimately from the purely mathematical) via the organic and psychic (subjective spirit) to the super-psychic ( The latter is the supra-individual layer of human culture and institutions -- the objective spirit).
It cannot be expected that the above given inherent problems of such an investigation will be solved, certainly not by one writer all by himself. The only intention is to trigger further thought and discussion with respect to those problems.
The NOVUM (i.e. the genuinely new feature), appearing in a higher layer (and representing this layer) consists in a very special complexification. The latter results not only in a highly complex structural unit, but also complexifies its relevant surroundings in such a way that that unit obtains a specific m e a n i n g, like we see in DNA molecules. Just for themselves these molecules are just complex chemical structures, and as such belong to the physical layer. But their having acquired a specific meaning elevates the whole system (DNA + its chemical environment) onto a higher structural and functional level. The mentioned meaning consists of certain definite r u l e s, determining from now on the whole structure. This is the NOVUM and leads to Life, provided this kind of meaning-generating complexification is such that the whole structure is not only determined by the new rules, but only by these new rules, i.e. when it can now go its business all on its own (which means for example that it also takes care for the selective import of matter and energy, and the selected export of matter and entropy, and thus guaranteeing its own continuation as a process).
The dependency of the higher upon the lower is a consequence of the higher having emerged after, and in virtue of, the entanglement of jumpy (i.e. more or less abrupt) complexification of (domains of) the lower layer. So without that lower layer there will not be any entanglement of complexification and consequently no emergence of a higher layer. Thus the (presence of the) (next) lower layer is in any case a conditio sine qua non (i.e. a condition that must, in all cases be satisfied [there could be more such conditions that should be satisfied, and only when all such conditions are satisfied we have sufficient ground, and the consequent will then necessarily follow.] ) for the higher layer to exist at all. And, what is important, the lower layer determines the higher layer ONLY as a conditio sine qua non, and certainly we here have not to do with a determination by a category of its concretum (but with a concretum--concretum determination [which itself stands under a certain category] ).
The lower layers, determining -- as we now know -- only as a conditio sine qua non, are i n d i f f e r e n t as to what higher layer can emerge after the entanglement of complexification, i.e. whether it be Life, Consciousness, or whatever. A layer all by itself does not have a tendency to complexify, i.e. self-organize into a higher layer, it only has the ability, the potential, to do so.
Something comparable (with that what was exemplified for the case of the emerging of the organic layer) is the case with respect to the emergence of the psychic and the super-psychic layers from their respective lower layers. They go their business according to special rules, however, not contradicting the lower-level rules.
The fundamental (and thus most general) laws of Nature (not necessarily as they are described by science, but as they really are) have room for such high-level special rules. The same goes for the case of more special natural laws, like crystallization laws or laws of other types of dynamical systems : Also they leave room for high-level special rules. Those low-level dynamical systems are then selectively fed with certain ingredients, which deflect their course, and become moreover included into a larger (i.e. high-level) dynamical system, while those same special low-level laws are at the same time constraining those high-level rules, but only as a conditio sine qua non for them.
The indifference of a layer with respect to the content of higher layers and also to their appearance at all, also implies a certain independence of the higher layer with respect to the lower, because the latter does not determine the specific content of the higher layer, apart from it being a conditio sine qua non. The only dependency of a particularly structured higher layer upon the next lower layer is the p l a y that is allowed by the lower layer. The lower elements, in the sense of lower-level laws or rules, cannot be trans-formed, but only be o v e r - f o r m e d.
HARTMANN, discusses also the possiblity -- as it is supposed to occur at the transition from the organic to the psychic -- of becoming o v e r - b u i l t, in which case the lower layer remains only in its function of being the carrier of the higher. The latter is then only dependent on the capacity (of carrying) of the lower layer. But because we here entertain just a mitigated version of the NOVUM in general, we, for the time being, do not consider a layer to be over-built).
Life as a definitively n e w phenomenon is affirmed not only by philosophers but also by many natural scientists, so for example DAVIES, P., The Cosmic Blueprint, 1987/9, p. 101 (1989 edition) :
"Biology will never be reconciled with physics until it is recognized that each new level in the hierarchical organization of matter brings into existence new qualities that are simply irrelevant at the atomistic level."Every lower layer co-determines, it is true, the next higher layer, but at most only as its matter (i.e. its substrate), matter that becomes in-formed. The independence of higher layers (and ultimately the independence of their corresponding categories -- their nomos) is only a partial independence, generally because of the mentioned conditio sine qua non o n l y, that the lower features are for the higher, and, more specifically, because of the dependence of their content on the degree of available play o n l y, (a play) that is allowed by the lower categories (which in most cases are laws). And this only partial independence (and thus not complete independence) causes the higher categories not to be absolutely fundamental. The only categories that are truly fundamental are those of the lowest layer, namely the mathematical. So insofar as absolute fundamental categories are concerned, the whole layered system of the World is ontologically homogeneous, as found out earlier.
An instructive example is the o v e r - f o r m a t i o n (not trans-formation) of the c a u s a l n e x u s, i.e. the repeatable connection between states (of dynamical systems). The causal nexus as such is not a whole series of states, but just the generation of one state (effect) out of another (cause). In itself the causal nexus is not directed to predetermined end states : If the cause changes, for example when it is perturbed, a different effect will ensue, while the original effect will not take place. So causality does not lack direction, but lacks direction to a specific target. This indifference of the causal nexus as to the final result makes it susceptible to be harnessed, i.e. to be over-formed, which means that a definite influence can be applied to the cause resulting in a corresponding effect, i.e. a definite specific target.
In an organism we have causality, and this causality, in itself -- as we saw -- not being directed to a specific end result, is susceptible to noise (perturbations) coming from outside the organism. The latter, however, blocks this noise and posits its own causal factors, resulting in a specific outcome. In this way a specific structure- (or behavior-) generating law appears, which is, however, fully compatible with causality. The latter is just over-formed (not trans-formed). Of course here the ability of the organism to discriminate between factors that are relevant to it or irrelevant or even noxious, is already presupposed. But this ability can initially be in a very primitive state, i.e. just a physical function, and not yet (requiring) an organic function. In a later stage of organic constitution this ability will become more subtle and effective. It is best to assume that both phenomena (over-forming of causality, and the mentioned ability of discriminating between the self and the not-self) go hand in hand, and represent in fact one and the same event of jumpy complexification.
In this way we get systems in which the elements seem to 'cooperate' in such a way that causality is, in a sense, masked, and that a specific goal is being realized by the dynamics of such systems. Such goal-oriented directiveness (as if teleology came into play), although compatible with all physical laws (Again, the laws how they really are in themselves, not insofar as we suppose to know them), is irrelevant to physics, but relevant to biology.
What is needed is a comprehensive theory of organization, a theory that investigates and explains emerging structures and laws, already apparent in the crystallization process and in some other inorganic dynamical systems, and that goes all the way up to investigate the staggering organizational processes that take place in living beings.
The recent dynamical systems approach has entered this line of research, but is still a long way from explaining fully even the crystallization process, let alone those of organisms. And, the investigations of Nicolai HARTMANN (in the 1930's and 1940's), which are conducted at a very fundamental and general level, already are, despite the mentioned inherent difficulties, very providential in this respect and should be studied by at least all philosophically minded biologists and physicists who want to place their subject into a broader context. And, above all, it should be studied by philosophers, which has -- as far as my knowledge goes -- hardly taken place.
Let's now return to our main concern with respect to HARTMANN's ontological layers (which we will interpret -- for the time being -- as complexity levels), namely the vexed problem of the NOVUM (i.e. the "new"). We again try to illustrate it -- but now in some more detail -- in the case of the o r g a n i c, in which we do not present a reconstruction of its actual origin but of its constitution. Some aspects of the foregoing discussion will be more or less repeated, while others are added.
In the physical layer the mode of determination is causality [where "determination" does not mean a category--concretum determination, but a concretum--concretum determination (in the present case standing under the category of causality) ]. In the complexification that will eventually lead to the organic layer to emerge, complex molecules will be formed by the above described harnessing (over-formation) of causality, and the physical laws based on it. These molecules encode blueprints for the synthesis of proteins, in definite amounts and temporal order. These proteins assist in the realization of biochemical reaction chains, etc. By means of feedback loops the whole system is then controlled. All this results in the fact that the organism grows and maintains itself (under import of matter and energy and export of matter and entropy) according to certain intrinsic rules that are only relevant (i.e. geared to) large organic units that play the role of system elements and that interact according to these rules, which are consequently high-level rules or laws, only as such appearing at high structural levels, and not present at lower levels. And such a rule is not just the result of a simple summation of lower level rules, they are of a different nature all together, i.e. their qualitative content is different.
High-level rules can also be observed in inorganic systems, but in organisms they imply dynamical (sub)systems [A rule implies a dynamical system, because a rule or law of such a system is, in a dispersed fashion, immanent in the elements of the system.] that show a resistance against perturbations, i.e. those systems are not allowed to be fed by alien elements. As has been said, this can initially be just some purely physical function, but should further be sophisticated, hand in hand with the origin of the higher-level rules themselves, into the ability to discriminate between Self and not-Self (which is, by the way, the essence of Life). And in this way there is just a selected set of causal factors admitted, while others are neutralized. And only in this way we have a self-contained set of rules (and with it a self-contained dynamical system) that connect certain specific high-level states to subsequent states and, finally, to certain special high-level end states. Organisms are therefore called autopoietic systems, i.e. systems that 'produce themselves' (that do themselves, in contrast to them being done [by something else] ). Such self-contained sets of high-level rules (or laws) and the corresponding dynamical systems do not occur in the inorganic world, where dynamical systems can and will accept in principle any alien factor coming in its way. Under circumstances such factors can be damped by such an inorganic system, it is true, but when the system is unstable it will alter its course in virtue of such an incoming factor. Such inorganic systems are, because of this, in many cases not precisely repeatable in the
'wild'. One of the exceptions are presented by the formation of crystals, which, however, involve relatively simple equilibrium systems.
So the above discussed (strongly) self-contained high-level dynamical laws, though not occurring in the inorganic world, are completely compatible with causality and with the fundamental physical laws based on it : When we examine the e l e m e n t a r y state transitions (of which the high-level state transitions are composed of), we will see that they represent each for themselves purely causal connections. The NOVUM thus consists of the fact that these elementary causal connections stem from a highly selective, i.e. choosy environment (within the system itself), resulting in the organization of particular causal connections, in turn resulting in a particular and stable succession of complex high-level states, leading to some specific end state or cycle.
With all this we have, in a crude and more or less vague way, described the o v e r - f o r m i n g (not trans-forming) or h a r n e s s i n g of causality. The latter is, as it were, the 'matter' for the former, which then is its 'form'. And so, with the presence of such high-level laws -- which, taken all by themselves, represent a qualitatively different type of NEXUS, different from that of causality -- pure causality still exists at the lower level, while at the higher level it is over-formed. And, as has been said, in the same way physical laws presupposing causality, can be over-formed. And because the resulting law is of a different type (namely a different type of nexus, and, moreover, self-contained and high-level), we call it a n e w c a t e g o r y (i.e. a new determinant in HARTMANN's sense), a c a t e g o r i c a l n o v u m, as such responsible for the appearance of the organic layer -- which has taken up many categories from the inorganic layer, but more or less being modified by the novum -- on top of the inorganic (physical) layer.
One must realize that the "organic layer" does not as such consist of individual organisms : In each individual organism (including humans) we find both layers, the inorganic and the organic. And in some higher organisms yet another layer appears in addition to these two.
And, as is clear from the above, the appearance (emergence) of the NOVUM, and with it of the new layer, is accomplished by a leap-like increase in functional complexity of physical matter ( This increase of complexity follows a very long and highly entangled path compressed into a very small 'reaction-container').
The foregoing complicated and more or less unclear discussion that tries to explain the phenomenon of over-forming, is no more than an attempt to get rid of the awkward notion of the NOVUM as something not being produced somehow but coming out of the blue.
About the h a r n e s s i n g or over-forming of existing physical laws, see also DAVIES, 1989, The Cosmic Blueprint, p. 143 and p. 149.
So in the foregoing we have 'explained' the appearance of the NOVUM, namely as the result of over-forming. HARTMANN, however, postulates the appearance of the NOVUM as something totally new without antecedents. And this NOVUM is responsible for the modification of many categories of the lower layer reappearing in the next higher layer, i.e. is responsible for their over-forming.
Maybe this is true, and we keep it in mind (i.e. we accept it for the time being). But it implies the NOVUM coming out of the blue, which assumption causes the theory to come close to those that assume some non-physical directive that is responsible for the organization of many -- in themselves -- physico-chemical units into functional high-level 'routines' as we find them in organisms. But, as hinted at already, maybe we should try to assimulate with the idea of the appearance of something totally new, of a totally new principle or set of principles.
Turning our attention for a while to the m a t h e m a t i c a l non-physicalized l a y e r, we see something similar to harnessing. For example, we begin with considering a most primitive starting point, the topological space. This is a collection of points endowed with only very basic properties such as connectedness and dimensionality. Such a space can be seen to be gradually enriched with new properties, eventually resulting in a metric space, where the concepts of distance and angle have full meaning. So we have then ascended from the primitive topological level to the higher level represented by metric space. The latter is not reducible to topological space, because new features have appeared in metric space, but it is fully compatible to the former. We have witnessed a (modest but genuine) increase in complexity with respect to mathematical entities. If we now deduce the relevant theorems, then we make explicit the complete content of the newly added features.
Something similar can be done with primitive arithmetic.
Concerning b i o l o g y, we can read about all these level phenomena, lower levels and higher levels, in for example The Cosmic Blueprint of the physicist Paul DAVIES, and many other works laid down in the second half of the 20th century. But, as has been said, these issues were already laid down, and moreover in a much more precise fashion, in the works of Nicolai HARTMANN in the first half of that century. Concerning authors of the second half of the century, in PEACOCKE, A., 1986, God and the New Biology we can read the following (as cited by DAVIES) :
"It is possible for higher level concepts and theories . . . to be non-reducible to lower level concepts and theories, that is, they can be autonomous. At the same time one has to recognize the applicability of the lower level concepts and theories (for example those of physics and chemistry) to the component units of more complex entities and their validity when referred to that lower level. That is, with reference to biology, it is possible to be anti-reductionist without being a vitalist."All this is already laid down in a rigorous ontological context (and not confusing the epistemological -- concerning knowledge -- with the ontological -- concerning being, as we unfortunately see it in almost all english writing authors) in the chapters on Categorical Laws of HARTMANN's Der Aufbau der realen Welt of 1940.
As DAVIES (1987/9) reports, "Similar views have been developed by the physicist Walter ELSASSER" (1966), who writes the following (cited by DAVIES) :
"We shall say at once that we accept basic physics as completely valid in its application to the dynamics of organisms . . . Still, we must be clearly prepared to find that general laws of biology which are not deducible from physics will have a logical structure quite different from what we are accustomed to in physical science.We should understand that the higher-level laws, as they occur in biology, must have been in some way actually o r i g i n a t e d from lower-level physical laws (in the way tentatively described). But because the latter offer play for several different possible high-level laws, the particular high-level law, that had actually originated from a lower-level law, is not as such deducible from the latter (as is claimed). But of course if we take the originating process, that actually happened -- and that has lead to these higher-level laws -- into account, which in fact means, that if we take the whole Sphere of Being into account, then it is more difficult to claim the mentioned irreducibility (in an ontological sense, not concerning our ability to actually derive). So we have to be careful in this respect. We should come to know what exactly happens during a 'complexification leap' creating a new and higher layer of existence.To be specific, then, we assume that there exist regularities in the realm of organisms whose existence cannot be logico-mathematically derived from the laws of physics, nor can a logico-mathematical contradiction be construed between these regularities and the laws of physics."
New behaviors, that can be precursors to the creation of a new layer of existence, can already consist in so-called entrainments, where different oscillators, materially connected with each other, are going to tick in unison. Cooperative vibration modes occur, for example, in crystal lattices, where each atom acts as a tiny oscillator. So the system has in this respect self-organized spontaneously, and the propagation of light waves through crystals depends crucially on this organized collective motion. It is a small step towards complexification within the physical layer. The discussed harnessing of physical laws is a stronger form of complexification, but, as has been said, not wholly understood.
Preliminary investigation of the domain of NOMOS
( The domain of determinants, determining the determinable, resulting in the domain of COSMOS )
The dimensions of determining. Static and dynamic categories.
REMARK : The following is a preliminary and preparatory investigation into the types of general and special categories ( If / Then constants). It should be emphasized that this investigation is -- and will for the time being remain -- still in an 'experimental state', which means that the relevant expositions are continually being updated, revised, etc. (or maybe even abandoned, if they turn out to be wholly inadequate). The reader is invited to participate in this ongoing investigation, and to criticise it where deemed necessary. He or she can put remarks in the GUESTBOOK (where other readers can see them too), or e-mail me personally.
Only when such a preliminary investigation meets with some success, we can begin with a SYSTEMATIC CATEGORICAL ANALYSIS, along the lines HARTMANN has set out, especially his Intercategorical Laws.
We will now say some more about static and dynamic determination, and of general and special categories. As has been established above (See from the Section The Determined and the Determining onwards), each c a t e g o r y, in the sense of HARTMANN, is in fact an If / Then constant [as first -- independently of HARTMANN -- proposed by WOLTERECK, R., 1932, Grundzüge einer allgemeinen Biologie, and explained above], where "Then" stands for "being so-and-so". The latter can thus signify any quality, state, property, thing, being-individual, being-in-time, being-extended, and so also being-green, being-symmetric, being-3-fold-cyclic-symmetric, being-periodic, etc. etc. Thereby we should realize that the degree of generality of the Then-component is the same as that of the corresponding If-component.
So the category is the full If / Then constant, while its concretum (which is that what is determined by the category) loosely is the complete set of beings that are so-and-so, or being in such and such a state, or having such and such properties, as is indicated by the Then-component. So the concretum consists of all individual cases that fall under the Then-component. The If-component, on the other hand, indicates the sufficient ground for the Then-component to appear, and with it, indicates the range or domain of relevance of the category. The category actually determines in virtue of it containing the If-component, which indicates the sufficient ground for the category's concretum to be so-and-so, and as soon as the category is in its range of relevance, i.e. when it is there where the sufficient ground is satisfied, the concretum will necessarily be so-and-so as specified by the Then-component. The sufficient ground itself is the total of all necessary conditions for the concretum to be so-and-so as indicated by the Then-component.
Above we distinguished between dynamic categories (dynamic If / Then constants) and static categories (static If / Then constants), and among static categories, between constants referring to implied properties of a given intrinsic being (entitative constants) and constants referring to implied properties of given bulk matter (material constants).
We can say that the s t a t i c categories determine only 'vertically', from principle to concretum, and determine w h a t n e s s e s and necessary i m p l i c a t i o n s, while d y n a m i c categories determine first of all also 'vertically' (from principle to concretum), and so also determine a whatness, but, moreover, and most important, bring about a n e x u s, which is a 'horizontal' determination, i.e. a concretum--concretum determination.
It should be emphasized that all the categories are ontological in nature, despite the epistemological elements appearing here and there in their exposition.
To understand the 'action' of a c a t e g o r y , which we express as an If / Then constant, we presuppose its THEN-component (i.e. its concretum), and then assess the IF-component as the sufficient ground for the THEN-component :
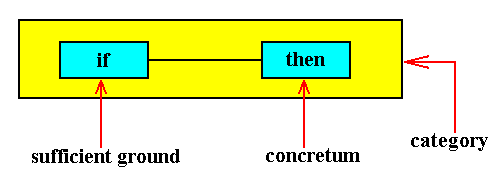
The category determines its concretum by invoking the sufficient ground. The category includes its concretum as well as the sufficient ground for the latter.
Indeed, because the category includes its concretum it is intrinsically connected with it and has no existence without it. In the same way the concretum has no existence without the category.
We shall discuss the following types of categories :
In expounding these types of categories we have in mind those of the Physical Layer. They are basic with respect to the categorical constitution of the higher Layers (In the Mathematical Layer this constitution is quite simple and straightforward. All determinations there are of a logical nature).
When we speak of a category "presupposing" something, it is meant in an ontological sense.
Whatness Category
Recall that the whatness or what-is-it of an entity X is the latter's intrinsic content. This content comes from within X and is constant (like intrinsic behavior, properties, etc.). Its extrinsic content comes from without X and is variable (while this variability is not strictly-and-only dependent on X, but is dependent on external agents). Extrinsic content is excluded from the whatness of X.
A whatness, implicitly presupposes a substrate, i.e. that of which it is the whatness. When X is a property, then the latter already implicitly presupposes a substrate, which is that of which it is a property, and this substrate is then at the same time the ultimate substrate of the whatness of the given property.
The next diagram illustrates a whatness category.
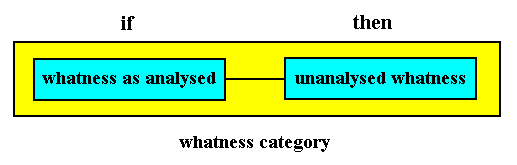
A whatness category analyses a whatness, i.e. it makes it explicit.
No existence is presupposed, i.e. no object or bulk matter. Only a substrate is presupposed (because whatness is intrinsic), however, only implicitly so. This substrate is irrelevant to the category, because the category is not about that substrate. What the category explicitly presupposes is the unanalysed whatness (and this does not explicitly presuppose existence of something).
The determination of the category brings about an EXPLICITATION (unfoldment) of the whatness.
Whatness categories are stated in the form of definitions. As such they seem to be only logical. About their ontological status, see Part II of the present series of documents.
Entitative and Material Constants
A material (i.e. given bulk matter), and also any intrinsic object (which is an individualization of a material), have, first of all an overall whatness which consists of a complete set of constant properties ( The latter are therefore intrinsic properties). And so each one of such properties is necessarily implied by that overall whatness and thus at the same time by that particular material or that particular intrinsic object.
As examples we can give :
The freezing point of a certain material, its specific density, etc. (material constants).
The intrinsic symmetry of a species of crystal, for example alpha-quartz, ice, common salt, etc., optical properties of a species of crystal, chemical properties, etc. (entitative constants).
Entitative Constant
The next diagram illustrates an entitative category.
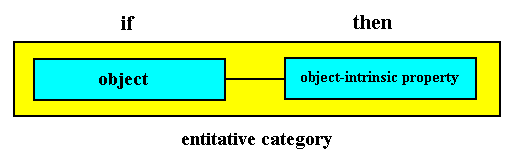
An entitative constant or entitative category determines the necessary implication of an intrinsic property of an intrinsic object by that object.
Presupposed is the pre-existence of an intrinsic object (i.e. an object which is a unified integrated whole, generated by a specific dynamical system), and also (presupposed is) the analysed whatness of that property.
The determination of the category brings about an IMPLICATION (derivation) of a property. It is not a generation, because only objects are truly generated (produced), and they are already presupposed.
Material Constant
The next diagram illustrates a material category.
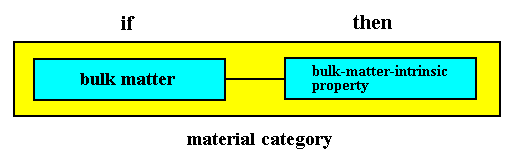
A material constant or material category determines the necessary implication of an intrinsic property of given bulk matter by that bulk matter.
Presupposed is the pre-existence of given bulk matter, and also the analysed whatness of that property.
The determination of the category brings about an IMPLICATION (derivation) of a property. It is not a generation, because only objects (here constituents of the bulk matter, and with them the bulk matter itself) are truly generated, and they are already presupposed.
Nexus Category
The most significant constants are the nexus categories.
A nexus constant or nexus category determines the successive, generative and necessary connection between states of a dynamical system, either of only two states (as cause and effect), which embodies causality (which is the general nexus category of the physical layer), or between a multitude of states, which embodies a dynamical law (implying causality between every two states).
The next diagram illustrates a nexus category.
The determination of the category brings about a (physical) NEXUS between system states.
These are the main types of categories or constants. They can occur in several degrees of generality.
Let us give some elementary examples.
But before we proceed, we give a few notes on s y m m e t r y :
A c o v e r o p e r a t i o n (or superposition operation) is whatever operation (rotation, reflection, etc.) performed on some object, such that after having been accomplished, the object occupies the same patch of space as it did before the operation was performed. The trivial cover operation is : doing nothing at all, i.e. a rotation of 00, or, equivalently, of 3600, about any axis. Other cover operations are, for example rotation of an equilateral triangle by 1200 about its center, reflection of such a triangle in one of its bisectors, etc. Each cover operation with respect to some object is a symmetry transformation, and the total set of all possible symmetry transformations allowed by that object defines the symmetry of that object, and forms a g r o u p, which is a self-contained algebraic structure (in the present case a symmetry group). The elements of this structure -- the group elements -- are those same symmetry transformations (cover operations). They can be combined with each other, which here means that they can be performed one after the other (the former being applied to the result of the latter). When we do so combine (and here this way of combining them is called the group operation) no new group elements are generated, so the set of symmetry transformations is closed under the group operation.
Generally a group is a set of elements associated with one operation (the group operation) which is such that this operation -- let us call it * -- is associative, i.e. for every three elements a, b, c of the group the relation (a*b)*c = a*(b*c) holds. Further there must be one identity element, i.e. an element which has no effect whatsoever when combined with any other element of the group. Finally, every element must have its inverse, i.e. for every element of the group there must be another element of the group that, when combined with the former neutralizes its effect.
There are many types of groups, and also of symmetry groups, denoted by symbols like Cn (cyclic groups), Dn (dihedral groups), Dn x Cm (product groups), etc.
For an exposition of Group Theory, and especially of symmetry groups, see Second Part of Website.
Static categories.
Category of Symmetry (a whatness category) :
If all cover operations of something, together form a group (in the above given mathematical sense) other than the group C1 (which, as the trivial group, describes total asymmetry), then that something is symmetric.
This is indeed the category of symmetry. It determines (statically) the what-is-it of a property of something, namely symmetry, by analysing it.
The concretum of this category is the total set of symmetric beings, but more strictly it is symmetry as unanalysed.
[ The (trivial) group C1 is a group, consisting of the identity element only. Therefore the only 'symmetry transformation' it can contain is a rotation (about any axis) of the object by 3600, or, equivalently, by 00.
An object having just this group has no true symmetry at all.]
A more special category could then be the
Category of 3-fold Cyclic Symmetry (whatness category) :
If all cover-operations (let us call them) 1, p, p2 of something, together form the group (as given by a group table) :All possible combinations of the group elements 1, p, and p2 are given in the interior of the table.
then that something has 3-fold cyclic symmetry.
The category determines 3-fold cyclic symmetry by analysing it.
The concretum of this category is the total set of beings having this symmetry, or more strictly, it is 3-fold cyclic symmetry as unanalysed.
The property of crystallinity.
Another more or less specific static category determines the what-is-it of crystallinity.
Category of Crystallinity (whatness category) :
If something has a periodic internal intrinsic structure, then it is crystalline.The concretum of this category is all beings (objects) that are crystalline, but more strictly it is crystallinity as unanalysed.
In addition to determine a whatness of a property by its definition, static constants can also refer to the implication of certain properties of a given entity, be it a given genuine being or given bulk matter, as we saw earlier :
Category of Intrinsic D6xC2 symmetry (entitative constant) :
If we have an Ice crystal (say a snow flake), grown under normal conditions (that need to be specified), then an intrinsic symmetry according to the symmetry group D6xC2 will be present in such a crystal ( The intrinsic symmetry can always be perturbed, often resulting in a lower actual (extrinsic) symmetry).
The concretum of this category is the set of all beings having an intrinsic symmetry according to the group D6xC2 , but more strictly it is object-intrinsic D6xC2 symmetry.
The category presupposes the pre-existence of a certain intrinsic object, and also the analysed whatness of dihexagonal-bipyramidal symmetry ( This analysis results in the group D6xC2 , which should then be displayed by its group table). See below.
An ice crystal, grown under normal conditions (that need to be specified) embodies sufficient ground and is the domain of relevance for the constant to apply.
But in fact it is only one of the many equally valid domains of relevance for an intrinsic D6xC2 symmetry to appear, because many other crystal species and even some organisms possess intrinsic D6xC2 symmetry. (See for an elaboration of this, further down).
Category of Dihexagonal-bipyramidal Symmetry (whatness category) :
Dihexagonal-bipyramidal symmetry is the symmetry of, for example, a regular 6-fold bipyramid, or of a hexagonal prism, and can be given -- i.e. analysed -- as a group by a group table indicating the possible combinations of its 24 group elements. So this table represents the fully analysed whatness of Dihexagonal-bipyramidal symmetry, and as such it can figure in the Category of Dihexagonal-bipyramidal Symmetry (expressed as an If / Then constant), while the previously discussed category was the Category of i n t r i n s i c D6xC2 symmetry, i.e. the symmetry as necessarily implied by some object and given as analysed (by mentioning the corresponding group, which should then be presented by its group table, or by its generator set and defining relations).
The category of Dihexagonal-bipyramidal Symmetry does not explicitly presuppose the pre-existence of an object or substrate, but only implicitly so. It is irrelevant for the category, which isn't about such an object or substrate. The category only presupposes the unanalysed whatness, which is dihexagonal-bipyramidal symmetry.
Category of Bilateral Symmetry (whatness category) :
If all cover-operations (let us call them) 1 and m of something, together form the group (as given by a group table) :The category determines bilateral symmetry by analysing it.
then that something has bilateral symmetry.
Categories of Promorphology (Static Categories).
Intrinsic symmetry is one of the aspects of the structure of a being. The promorph is also such an aspect. It presupposes intrinsic point symmetry, and is in many cases equivalent to it (apart from the fact that it involves exclusively geometric and dimensional aspects of structure), while in other cases the promorph goes beyond symmetry, especially in all cases where the number of antimers (counterparts of a body) is not fixed by symmetry alone. So like symmetry the promorph is an intrinsic property which is implied by the Essence of the given being and is as such part of that being's whatness.
We can say that an object (where we always mean an intrinsic being) has or has not symmetry. And only when we consider the trivial group C1 to be a symmetry as well, we can say that every object has (a certain) symmetry, or, equivalently, is symmetric.
In the same way we can say that an object has or has not a promorph. And only if we consider completely irregular bodies, namely bodies that do not possess a definite geometric body center, nor repeating parts, nor similar or homologous parts, as having a promorph as well, i.e. if we consider the Anaxonia acentra of our Promorphological System to represent a promorph as well, then we can say that every object has a promorph, or, equivalently, is promorphic. If, on the other hand, we do not so consider, then all promorphic bodies, and only promorphic bodies, show a definite pattern of polarities with respect to their axes, as well as to all other parts of their overall structure.
A body axis can be either homopolar, which means that both ends of that axis represent (or are embedded within) equal or similar body parts, or heteropolar, which means that one end of that axis represents a body part unequal to the body part represented by the other end of that axis ( Think of head---tail as representing a heteropolar axis of the body of many an animal). As with axes, these polarity features can also be present in other structural elements of a body. It is possible to express these polarities in a geometric way, and this is what Promorphology is doing, it finds the simplest geometric bodies or figures that fully express these polarities geometrically, which is equivalent to geometrically express the intrinsic point symmetry of the object and the number and arrangement of its antimers (See for Promorphology, Second Part of Website , Main Section Basic Forms (Promorphological System)).
So in line with the Category of Symmetry, we can establish the Category of Promorphology and the corresponding more special promorphological categories (Recall that categories are If / Then constants, and are, consequently, expressed in an ontological fashion, i.e. as determinants, and not as logical definitions) :
Category of Promorphology (whatness category) :
If an object possesses at least a geometric body center, or allows for certain definite body axes, then it is promorphic.The concretum of this category is all beings (objects) that are promorphic, but more strictly it is promorphic as unanalysed.
[If we consider the Anaxonia acentra to be a promorph as well, then all beings are promorphic.]
The corresponding logical definition would run as follows :
An object is called promorphic if it contains at least a geometric body center, or allows for certain definite body axes.
The logical and ontological expressions are logically equivalent, but the logical definition is not a category.
General Category of Promorph (whatness category) :
If a given being (object) is promorphic, then its body possesses a definite pattern of polarities, not only of its body axes, but of all parts of its overall structure. This pattern is its promorph.The concretum of this category is all beings (objects) that have a promorph, but more strictly it is promorph as unanalysed.
Although these two categories, viz. the Category of Promorphology and the General Category of Promorph, are more or less equivalent, it is contributing to clarity if we present them separately.
A promorph, or, equivalently, a stereometric basic form (for 3-D space) or planimetric basic form (for 2-D space), implies and contains the corresponding symmetry group, while the latter in turn implies and contains the corresponding abstract group.
See for symmetry group and abstract group The Intermezzo of Part XIII of the Series Subpatterns and Subgroups in
Second Part of Website .
Click H E R E to see this Intermezzo in a separate window (To leave it again, close the window).
To actually go there, click the just given Second Part of Website link, then scroll the left frame through the Series on Group Theory, then click on "SEQUEL TO GROUP THEORY two-dimensional patterns", and then, finally, click on Part XIII of the Series on Subpatterns and Subgroups and scroll down to INTERMEZZO.
So the structure of the General Category of Promorph can be visualized as follows :
The following is a statement that is wholly equivalent to that of the General Category of Promorph , but is as such not ontologically meant, but methodologically :
A promorph is the simplest geometric solid expressing the intrinsic point symmetry of a given being and the number and arrangement of that being's bodily counterparts (antimers). This simple geometric solid directly depicts the polarity pattern of that given being.
In the exposition of the special categories of promorphs we will use this methodological definition, while nevertheless interpreting it o n t o l o g i c a l l y, i.e. m e a n i n g it according to the content of the above General Category of Promorph .
So let us then give a special promorphology category :
Category of Allopolar Pentamphipleural Promorph [or just, Category of Allopola pentamphipleura] (whatness category) :
If we have a promorphic being (object) of which the pattern of polarities can be expressed as half a ten-sided amphitect pyramid (and in a 2-D case : as half a ten-sided polygon), then the promorph of this being is that of the Allopola pentamphipleura.The mentioned pyramid, viz. half a ten-sided amphitect pyramid must then be explicitly indicated :
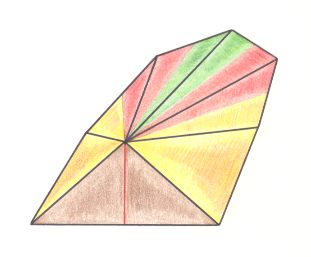
Figure 5. Oblique top view of the promorph of the bodies of, say, irregular sea urchins (Besides sea-urchins, also many flowers have this promorph). It is half a 10-fold amphitect pyramid with the five antimers (corresponding to five body parts in the animal) indicated by colors. It therefore belongs to the Pentamphipleura (Allopola amphipleura). The brown plane facing the beholder is the bisection face associated with the bisection of the 10-fold amphitect pyramid.
The concretum of this category is all beings (objects) that have this promorph, but more strictly it is this promorph as (partly) unanalysed, namely as (just) belonging to the "Allopola pentamphipleura", or just "Pentamphipleura".
The Category of Allopola pentamphipleura implies and contains the Symmetry Group D1 , and the latter in turn implies the Abstract Two-element Group.
The Abstract Two-element Group can be given by the following group table. Its elements are not in any way interpreted. They are what they are in virtue of their relations as defined in that group table :
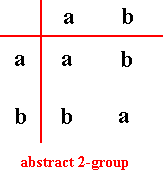
From the table it is clear that the element a is the group's identity element.
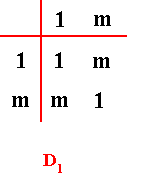
( This group D1 can itself be a whatness category, namely the Category of Bilateral Symmetry, as we defined it above ).
So the structure of the Category of Allopola pentamphipleura , as such a special promorph, can be visualized as follows :
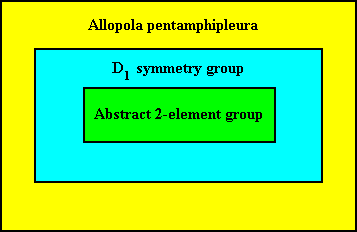
This promorph, viz. that of the Allopola pentamphipleura, which as such is just a geometric figure, involving just 3-D metric space (and not physical space), and so still being a purely mathematical entity, can now be physically interpreted, viz. inorganically or organically. We will often find it interpreted organically, as in irregular sea-urchins and in flowers of at least many Scrophulariaceae. However, this organic interpretation of the promorph does not mean just its materialization (i.e. transition of the involved space from mathematical to physical space) of the promorph : We generally don't find organisms appearing as pyramids or other such polyhedral solids.
This concludes our examples of promorphological categories.
Category of Freezing Points, under different pressures, of bulk matter (whatness category) :
If a given bulk matter is subjected to a certain pressure and temperature (of which there is a whole range of possible relevant combinations, and this range is here supposed to be specified, for example by a temperature-pressure diagram), then we get s o l i d bulk matter, or, more precisely, solid bulk matter is (then) the stable state.The category only presupposes the unanalysed whatness of freezing point
Category of Intrinsic Freezing Points, under different pressures, of bulk H2O (material constant) :
If we have bulk H2O, then it implies definite freezing points at definite pressures (which should be specified by a temperature-pressure diagram, see next Figure).
Phase diagram of H2O (water), after LIBBRECHT, www.snowcrystals.com.
According to LIBBRECHT the triple point pressure of water is 6.1 mbar, and the triple point temperature is 0.00980C. (1 mbar = 0.75 mm mercury = 0.001 Atm) (1 mm mercury = 1 torr). Each point of the surface of the diagram represents a possible state in which the substance H2O can find itself. The almost vertical line starting from the triple point (lower black dot) and running upwards, represents all the pressure-temperature combinations such that solid water becomes the stable state when we cross it, coming from the right.
These "definite freezing points" are necessarily implied by : being-bulk-H2O.
In addition to such special static categories as discussed above, there are static categories that are general with respect to one whole layer, for example
Category of (physical) Level Hierarchy (mentioned by HARTMANN, 1950, second edition 1980, Philosophie der Natur, Abriss der speziellen Kategorienlehre, p. 258 ) :
If we consider the physical (i.e. the inorganic) layer to be there, Then we can observe that it is structured according to a hierarchy of levels (within that layer).The concretum is here "The being structured according to a hierarchy of levels of all of the material and objective content of the physical layer".
This is not an entitative constant, and also not a material constant, nor a whatness category, but a layer state category.
Another static category applying to all of the physical (inorganic) layer determines the spatiality of all what is in this layer.
Category of physical Space :
If we consider the physical (i.e. the inorganic) layer to be there, Then we can observe that it is spatial.This is a dimensional substrate category of the physical (inorganic) layer ( Another such category is Time, but Time is valid not only for the physical layer, but for the organic, psychic and super-psychic layers as well ). It does not reign in the mathematical layer, i.e. that layer has no physical space. Genuine physical space implies physical objects.
An example of a fully general, and thus f u n d a m e n t a l, static category, concerns a category that consists in a pair of opposites :
Category of E l e m e n t -- S y s t e m (Fundamental Category) :
If we consider the whole World to be there (i.e. the complete system of layers : the Mathematical, the Inorganic, the Organic, the Psychic, and the Super-psychic), then we can observe objective systems (not necessarily dynamic) and their corresponding elements, among beings (objects) and among properties, on all scales of magnitude.An example of a s y s t e m that can be found in the inorganic layer, and which is not a dynamical system, is the Periodic System of Chemical Elements.
So this feature permeates the whole World, i.e. the whole domain of Being.
Slightly more special static categories are the following :
Category of Dynamical System (whatness category) :
If a system is a system that (actively or logically) organizes its elements into a pattern, or, reversely, disorganizes them into chaos (in its technical sense), or, finally, creates them in one way or another, then it is a dynamical system.Such a dynamical system can be physical or just mathematical, and goes about its business according to some dynamical law, which in the physical case is inherent in the elements of the system, in such a way that the law is as it were 'smeared out' (spread out) over the collection of elements. The unfolding of such a physical dynamical system, i.e. the unfolding of its physical dynamical law, takes place according to a causal nexus between every two successive states of the system, together forming the special nexus of the given physical dynamical law.
"Logical" here (and also earlier and later), should be understood in a broad sense : immaterial, non-physical. There can be defined, or there indeed are, mathematical systems, such as the arithmetized "MIU-system", or, also, the supposed arithmetic formal system of noëtic strategy-strings in the Implicate Order, that are mathematical but not strictly logical. Strictly logical are, for instance, the Propositional Calculus and formalized number theory (TNT) of Mathematical Logic. There the rules ( ' laws' ) are logical principles of inference.
See for all this our noëtic theory of organic evolution, as it is developed in Fifth Part of Website, Evolution, part LXa, and earlier parts . There, organismic species are considered to be strategies to exist in the Explicate Order, while being present in the Implicate Order (the "mathematical layer", we may say) as a formal, ultimately arithmetical, system of noëtic strategies, -- strategy-strings.
Although a dynamical system is, dynamic, in the mathematical case as well as -- and here more concretely -- in the physical case, the category itself is static, determining the whatness of a dynamical system.
Category of Totality-generating Dynamical System (whatness category) :
If a dynamical system generates a coherent pattern or object (or several such objects), which we call a totality, expressing its wholeness and coherence, then it is a totality-generating dynamical system.When we take the term "generating" loosely, then such a system can be either purely mathematical or physical. In the mathematical case the "generating" is of a logical nature only.
Dynamic categories.
To begin with, all s t a t i c categories determining or implying (part of) the what-is-it of beings (objects), materials, properties and nexus, have their d y n a m i c counterparts. They determine how those whatnesses are actually co-generated ["co-generated", because only beings are generated. Their whatnesses and properties are then implied, and thus (only) co-generated].
So for "being symmetric" we have the following dynamic category (which is a nexus and thus brings about a 'horizontal' determination, a concretum--concretum determination) :
If * * * * , then an object is generated that is intrinsically symmetric, i.e. the what-is-it of symmetry is co-generated.or, more analysed (i.e. explicitly stating that what-is-it) :
If * * * * , then an object is generated of which the set of all its cover operations forms a group (in the mathematical sense) other than the group C1 .In this case we must -- after If -- state all the sets of conditions that each for themselves brings about a being that is symmetric. Of course this is a huge superset of sets of conditions, and that is so because of the very high degree of generality of this being-thus, which is "having symmetry".
The recursive dynamical law Xn+1 = 2Xn is as such a nexus category :
Category of Continued Doubling :
If X, then 2X will follow.The concretum of this category is the set of all cases of continued doubling, i.e. all (cases of) 2X-will-follow. As such it still determines statically (and thus 'vertically', from principle to concretum), determining the what-is-it of continued doubling.
Because the doubling law, as given above, is determining and still general (it applies to all cases of doubling whatsoever), it is indeed a category.
The general recursive multiplication law is a general version of the above doubling law :
where r is some numerical constant.
Category of Continued (recursive) Multiplication :
If X, then rX will follow.The concretum of this category is the set of all cases of continued multiplication by the number r, i.e. all (cases of) rX-will-follow. As such it still determines statically (and thus 'vertically', from principle to concretum), determining the what-is-it of continued multiplication by the number r.
Category of Organizing Law
When we have a given totality-generating dynamical system (of which its whatness is (vertically) determined by the Category of Totality-generating Dynamical Systems, as given above), the dynamical law, according to which it unfolds, and that organizes the system's elements, is as such a nexus, and represents a special nexus category. Such a law can, in the continuous case, be represented by a differential equation (or set thereof), or, in the discrete case, by a difference equation. The law is first of all a dynamical category. It can be purely mathematical, namely when not physically interpreted, resulting in a coherent mathematical pattern, as we see it for example in some Cellular Automata (especially their simulations on a computer). In this (mathematical) case there is in fact no genuine generation taking place, but just a logical derivation. Or it can be physical (s.l.), namely when the law is in a physically realized condition (or, we can say, when it is physically interpreted), as such involving a complexity leap (or, we can say, a jump), resulting in the transition from the purely mathematical to the physical (s.l). The action of the law then results in some intrinsic, inorganic or organic, object, i.e. in some higher-level pattern, as discussed above. In the latter case (viz., the generation of an organic object) again a complexity leap is involved (transition from inorganic to organic). ( The same applies to psychical and super-psychical events that result in a corresponding high-level pattern, that is to say, also here we have to do with at least analogues of totality-generating dynamical systems).
But at the same time such a dynamical law (of a totality-generating dynamical system) forms (that is to say, represents) the ESSENCE of the generated object, i.e. the total, and thus complex, whatness of that object-as-a-whole ( This is expounded in
First Part of Website). So it is also a whatness category, but still, in a sense, dynamic in nature, because that whatness (representing the object as it intrinsically is) is, in the physical layer at least, not just defined, but, as whatness, actually generated, i.e. produced within the context of a process which involves time (which is absent in the mathematical layer).
In fact only the object (totality) is truly generated, and in this generation -- a generation according to the dynamical law -- this law itself becomes the Essence or whatness of that object.
So generally the dynamical law of such a system can be categorically assessed two-fold :
Category of organizing nexus :
If a nexus is such that its corresponding dynamical system (the states of which are connected with each other linearly by this nexus) ultimately generates a coherent pattern (in the case of the mathematical), or a coherent object (in the case of the physical), then it is an organizing nexus.As such this is a static whatness category, determining vertically (i.e. it is a principle--concretum determination), but it brings about a connection of system states, leading up to the formation of a coherent pattern or object. As such it is horizontally determining (i.e. it is a concretum--concretum determination), and thus a nexus category (and consequently a dynamic category).
Insofar as such a dynamical law is the ESSENCE of the generated object ( That is to say, when we, in the case of the generation of a coherent object, only consider the law's aspect of "it constituting the ESSENCE of such an object"), it is a dynamic whatness category :
Category of Essence of an object :
If we have an object that is generated by a (totality-generating) dynamical system, then the dynamical law of that dynamical system is the ESSENCE (or total -- and thus complex whatness) of that object.And as we now know, the intrinsic properties of such an object are co-generated, i.e. they are just implied by the ESSENCE or whatness of that object (Again, because we consider that only objects -- genuine beings -- can be truly generated, not their intrinsic properties).
With the above we have given some examples of different sorts of categories, indicated as If / Then constants.
Let us now give a preliminary scheme of all these sorts of categories :
These determine all things and phenomena in the whole non-mathematical COSMOS (which is HARTMANN's reale Welt). They appear in the Physical Layer, and reappear in every Layer above it (but are then modified according to the corresponding NOVUM of every such Layer).
Maybe we will find still more types of categories, resulting in a more extensive scheme. Such a scheme displays a sort of systematics or classification (of the determinative entities) of the World's NOMOS.
The Threads of Determination
Let us now more closely analyse some categories in order to exactly see how they determine.
We'll take as an example the Category of Intrinsic D6xC2 symmetry, which is an entitative constant. The category is about the necessary implication of intrinsic D6xC2 symmetry. It is not about the co-generation of that symmetry, so the pre-existence of the object implying that symmetry, can be presupposed. Also the whatness of this symmetry is already presupposed (it is the corresponding group table, or, equivalently, the set of generators and defining relations).
The Category reads :
If we have an ice crystal, grown under normal conditions (that need to be specified), then an intrinsic symmetry according to the symmetry group D6xC2 will be present in such a crystal ( The intrinsic symmetry can always be perturbed, often resulting in a lower actual (extrinsic) symmetry).
As always, the If-component indicates the s u f f i c i e n t g r o u n d, i.e. the set of all conditiones sine qua non, where a conditio sine qua non is an absolutely indispensible condition, such that when it is absent, the relevant result will not appear. Such a condition, although indispensable, need not be enough : The result will only appear when the totality of all such conditions is there, and only then we have sufficient ground, and the corresponding result will now appear with necessity.
In the case of the present example the If-component indicates the sufficient ground for intrinsic D6xC2 symmetry-to-be-implied.
In an individual Ice crystal (for example a snow crystal) all those conditions sine qua non are evidently present (together making up sufficient ground), which we can know for sure, because the crystal's intrinsic symmetry is indeed according to the group D6xC2 . (While an Ice crystal is sufficient ground for D6xC2 symmetry to be implied, the If-component is most comprehensibly expressed by the total disjunctive set of all objects implying this symmetry. This is explained in what comes next).
But, when we consider a crystal of the mineral Beryl, Be3Al2Si6O18 , we see that its intrinsic symmetry is also that of D6xC2 , and we must therefore conclude that also here the complete set of conditions sine qua non, and thus sufficient ground, for intrinsic D6xC2symmetry-to-be-implied, is satisfied.
The same applies for a crystal of the mineral Molybdenite, MoS2 , and also for a crystal of the mineral Nicolite, NiAs.
So in any (single) crystal of H2O we find sufficient ground for intrinsic D6xC2 symmetry to be implied. But because we find this sufficient ground also in any crystal of Beryl, Molybdenite, or Nicolite -- and these are qualitatively different entities -- it seems that, say, a crystal of H2O contains, in addition to the mentioned sufficient ground, also other features totally irrelevant to (the implication of) intrinsic D6xC2 symmetry. The same applies to the crystals of the three mentioned (other) minerals.
So the sufficient ground for intrinsic D6xC2 symmetry-to-be-implied is something that is commonly possessed by these crystals, and probably by much more others as well. And in addition to such crystals we also have all the organisms that have intrinsic D6xC2 symmetry. So, to sum up, this sufficient ground is present in all entities, organic or inorganic, that belong to the Polypleura dodecapleura (Stauraxonia homopola isostaura) of the Promorphological System of Stereometric Basic Forms, as expounded in Second Part of Website.
In Promorphology the intrinsic symmetry of some object (for example an organism) is expressed not algebraically, i.e. not as a group, but as the simplest geometric solid geometrically representing fully that symmetry.
The D6xC2 symmetry is accordingly expressed there as a regular 6-fold bipyramid as the basic form of the form class Polypleura dodecapleura.
Many of the features (intrinsic or extrinsic) of these objects (the relevant crystals and organisms) therefore are totally irrelevant in this respect, i.e. do not enter the sufficient ground for the implication of D6xC2 symmetry.
So if we conceptually place "D6xC2 symmetry-being-implied" (which is a being-thus) in the center of our field of contemplation, then we see t h r e a d s radiating out from it, and leading to all relevant objects. Each such object in itself contains the sufficient ground, and can as such figure as the If-component of the If / Then constant representing the category. It is, however, more instructive to place all these objects disjunctively together into the If-component, thus in the sense of : an Ice crystal, or a Beryl crystal, or a Molybdenite crystal, or a Nicolite crystal, or some indicated pollen grain (having this symmetry), or, . . . , etc., where each one of them already fully satisfies the condition for this symmetry to be implied. So the phenomenon of continually implying D6xC2 symmetry is connected to all these objects by d e t e r m i n a t i v e t h r e a d s in a disjunctive (not conjunctive) fashion. All this is symbolized in the following diagram :
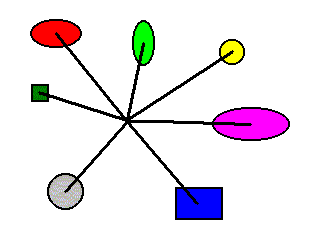
Figure 6. Diagram symbolizing the Category of Implication of D6xC2 symmetry by an object. Several equivalent objects (discs, ellipses, etc.) are indicated (as such representing all relevant objects). As in the example, the several objects depicted refer to different s p e c i e s of (intrinsic) objects, that are equivalent with respect to the category. The determinative threads, going from the objects to the D6xC2 symmetry feature (center), represent the implication of the latter feature by these objects. The disjunctive totality of these objects form the If-component of the category, while the center, in which the threads converge, forms the Then-component (intrinsic D6xC2 symmetry as intrinsic). The whole pattern (objects plus threads plus point of convergence) represents the category ( If / Then constant).
A whatness category on the other hand, determines the whatness or what-is-it (i.e. the intrinsic content) of something (an object, property or nexus), not as intrinsic, but as such. It does not presuppose that something which has this whatness (Apart from this intrinsic content, an object also has extrinsic content, i.e. a set of features not coming from within, but from without, as effects of external agents.). Only the whatness itself is presupposed. It is presupposed however as non-analysed. The category only analyses it, i.e. it shows all its necessary apects and how they integrate, resulting in the given whatness.
If the object in question, of which the whatness is determined, is an object residing in the Mathematical Layer it does not have extrinsic features, because in the Mathematical Layer there are no perturbations that mask the intrinsic content.
How things are with respect to the whatness of a property or of a nexus is straightforward.
With respect to things (objects) it needs some explanation :
With "objects" we here refer to coherent things generated by some dynamical system. In the First Part of Website we have established that the ESSENCE of such an object is the dynamical law of the dynamical system that generated this object. This ESSENCE is not as such visible. It expresses itself by the total of all intrinsic properties of the given object. This total we can call the 'phenotypical' whatness of that given object.
As we have seen, an intrinsic property can be stated in the form of an entitative constant. And indeed the total of entitative constants of a given object can be interpreted as the phenotypical expression of the ESSENCE of that object, and because (1) the set of constants is unfolded as to its individual constants, and moreover (2) in each entitative constant the analysed whatness of the corresponding property is presupposed, we can call the total of entitative constants the whatness of the object as analysed. The next diagram symbolizes this analysed whatness of an object.
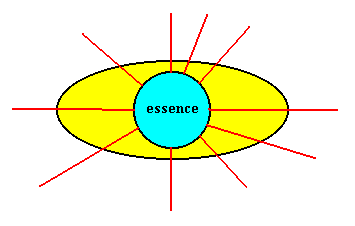
Figure 7. Diagram symbolizing an intrinsic object.
The ontological core consists of the object's ESSENCE. The ontological periphery consists of the intrinsic properties, the total of which is the phenotypical expression of the ESSENCE, it is the total of entitative constants (indicated by lines radiating from the ESSENCE) of the object.
In the next document, representing Part II of the present series, we will elaborate further on this.
The relation of a whatness category concerning a property (of some given object) with the corresponding entitative category will be explained by an example concerning (the intrinsic property of)
Ditrigonal Pyramidal Symmetry. The bare structure of this symmetry can be given by the abstract dihedral group D3 :

Figure 8. Abstract D3 group ( The symbol O in the upper left corner signifies the group operation, i.e. the binary operation that combines group elements).
If we interpret the elements of the group geometrically we get :
| 1 | p | p2 | a | b | c | period | |
| 1 | 1 | p | p2 | a | b | c | 1 |
| p | p | p2 | 1 | c | a | b | 3 |
| p2 | p2 | 1 | p | b | c | a | 3 |
| a | a | b | c | 1 | p | p2 | 2 |
| b | b | c | a | p2 | 1 | p | 2 |
| c | c | a | b | p | p2 | 1 | 2 |
Figure 9. Table of D3
Geometrically interpreted D3 group ( Symmetry Group D3 ).
In this representation of the group table the p e r i o d s of the six group elements are indicated. If x is a group element, and k is the smallest number such that xk = 1 (identity element) holds, then the period of the element x is k. The period distribution is typical, and as such diagnostic, for groups of which the number of elements is below 27.
Here (in the above group table, Figure 9) the element p is a rotation of 1200, while the element p2 is a rotation of 2400. The elements a, b, c are reflections in respectively three differently oriented reflection planes, and 1 is the identity element (rotation by 00, or, equivalently, by 3600). This D3 group table represents the whatness of ditrigonal pyramidal symmetry. We can visualize the group elements in a trigonal pyramid :
Figure 10. Trigonal Pyramid.
(A possible) explicit geometric interpretation of the abstract D3 group.
The rotation axis of the pyramid of Figure 10 coincides with the pyramid's main axis, while the reflection planes (mirror planes) contain this main axis ( The crystallographic symbol indicating the symmetry is 3m ). This pyramid, as stereometric basic form, belongs to the promorphological form class Triactinota (Stauraxonia heteropola homostaura). As such the pyramid represents unanalysed D3 symmetry, while the D3 group table (Figure 7) represents the analysed D3 symmetry.
The six group elements are symmetry transformations, but they can be geometrically (and also physically) represented by areas or solids, which we illustrate with the base of a trigonal pyramid ( This base is a 2-dimensional figure, it is true, which, however, also has D3 symmetry. The six indicated areas can represent the corresponding six irregular pyramids that together make up the whole trigonal pyramid, and that (also) can represent the six group elements). See next Figure.
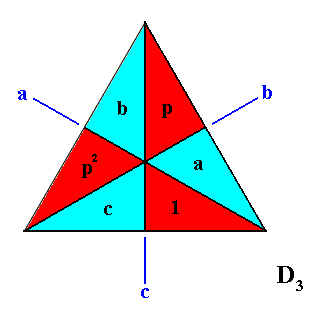
Figure 11. Equilateral triangle representing a trigonal pyramid. The triangle as wel as the pyramid possesses D3 symmetry. The six areas represent group elements as indicated, and at the same time represent the corresponding six irregular pyramids (representing the same group elements) together making up the whole trigonal pyramid. The latter's three mirror planes, a, b, and c are indicated. The center of the triangle represents the 3-fold rotation axis.
All the entities given above (Figure 8, 9, 10 and 11) belong to the Mathematical Layer. The space involved in the latter is purely geometric space (In the present case three-dimensional metric geometric space). As soon as the elements of the abstract D3 group (Figure 8 ) are i n t e r p r e t e d as physical symmetry transformations, i.e. involving physical space (which implies physical objects), we enter the Physical Layer. The mentioned physical interpretation must ontologically be seen as a discrete complexity leap, as explained earlier in this document.
Such a physically interpreted (abstract group, and with it the corresponding) symmetry group is presupposed in the Category of Intrinsic D3 Symmetry, because that category presupposes a physical object. The relation between the whatness category, consisting of D3 table (analysed symmetry) and trigonal pyramid (unanalysed symmetry), on the one hand, and the corresponding entitative category (entitative constant, consisting of the disjunctive set of objects and object-intrinsic D3 symmetry) on the other, is illustrated in the following diagram (where the D3 group table is represented by the symbol D3 ).
Figure 12. Whatness category and Entitative constant. Mathematical Layer and Physical Layer ( With the term "Physical Layer" is here meant the Inorganic plus Organic Layer of Being ). The vertical connection line (blue) represents the presupposition of the analysed D3 symmetry by the entitative constant. The other lines represent the connection between the IF-component and the THEN-component of the respective categories (whatness category and entitative constant), and are determinative threads. See next Figure.
Figure 13. As previous Figure. Entitative constant and whatness category.
If- and Then-components indicated.
The disjunctive set of objects implies intrinsic analysed D3 symmetry, together (as disjunctive If--Thens) constituting the entitative category of intrinsic D3 symmetry, which presupposes (vertical green line) analysed D3 symmetry, and as such -- i.e. as a category -- determining the mentioned implication.
The whatness category, consisting of the D3 group table ( If-component ) and unanalysed "Ditrigonal Pyramidal Symmetry" ( Then-component ), determines Ditrigonal Pyramidal Symmetry as to be the group consisting of three rotations and three reflections as given in the D3 group table (Figure 9).
Finally, the objects in the Physical Layer are dynamically connected with each other by 'horizontal' threads (concretum--concretum determinations), representing nexus categories :
Causality is a general (but not totally so) nexus category, but only with regard to two entities, viz. the cause and its effect :
General Ontology only considers the generalities of this determinative web, while Natural Science tries to unravel those threads and assess them as to their specific content.
The general ontology as presented on this website puts much emphasis on the aspect of determination. And this comes out clearly even in the 'individual being'-approach (pursued in the First and Second Parts of the website) : There we consider a genuine being as a complete unity, i.e. it is one, and only one thing. But what about the material parts of such a being, which often clearly stand out? Isn't such a being a multitude of beings after all? We could answer this question as follows :
An intrinsic being as it shows itself to an observer, is one thing, while its intrinsic parts and features are a distribution of d e t e r m i n a t i o n s of that one thing. Even moving parts should be so considered. All these parts and features of a given genuine being are a changing pattern of determinations, which can -- as we saw -- be formulated as If / Then constants.
So it is the NOMOS that is actually there : The COSMOS is the NOMOS.
In the next document we will elaborate further on categories.
To continue click HERE for further study of the Theory of Layers, Part II
e-mail :
