

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Regular Ditetragon
We will now investigate two-dimensional crystals with an intrinsic shape according to a regular ditetragon as to their possible promorphs, but, as in the foregoing, limiting ourselves to holomorphic crystals, which means that we will only investigate crystals of which their intrinsic symmetry is the same as the symmetry of their intrinsic shape. In the present case this means that our regular ditetragonal crystals will have D4 intrinsic symmetry (while in other cases -- meromorphic crystals -- this symmetry could be according to C4 (Cyclic Group of order 4), D2 (Dihedral Group of order 4), D1 (Dihedral Group of order 2), or C2 (Cyclic Group of order 2), or according to C1 (the Asymmetric Group), depending on the crystal's internal structure).
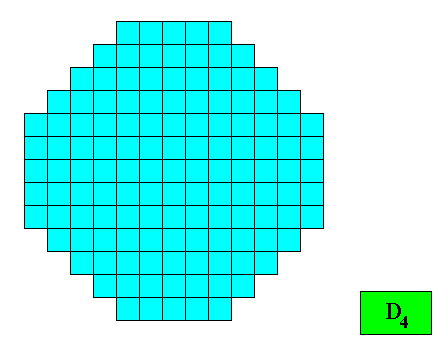
Figure above : Two-dimensional crystal (microscopic view) built up from a stacking of quadratic building blocks, resulting in a regular ditetragon (and not in a regular octagon). If the motifs (not drawn) in the building blocks have D4 symmetry (or are such that their translation-free residue has this symmetry), then the intrinsic point symmetry of the crystal is according to the group D4 . As one can see, the depicted crystal shape is an octagon, but not a regular octagon (it lacks the equality of all its sides). According to the four-fold symmetry the number of antimers must be four, or a multiple of it.
Either the crystal as drawn here, i.e. with empty building blocks, which by themselves already have D4 symmetry, implying the intrinsic point symmetry of the crystal to be that of D4 ,
or it having those building blocks provided with explicit D4 motifs, is, although being holomorphic (symmetry of shape is equal to intrinsic symmetry of crystal -- both D4 ), not eupromorphic if it has four equal antimers, (because the intrinsic shape suggests eight similar antimers). If it has eight (2x4) similar antimers, then it is eupromorphic.
The next Figure indicates the 'faces' of this crystal.
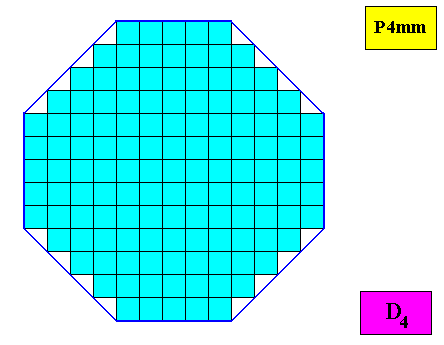
Figure above : The regular ditetragonal D4 crystal of the previous Figure. Crystal 'faces' indicated (dark blue lines).
In order to emphasize the D4 intrinsic symmetry of the crystal, we provide the square building blocks explictitly with D4 motifs :
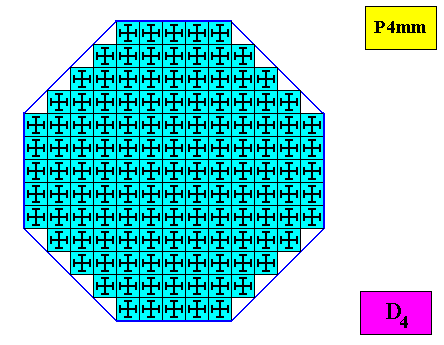
Figure above : A regular ditetragonal D4 crystal. Its D4 motifs (black) consist of four equal antimers. Moreover each antimer is mirror symmetric. One can see that the shape of the crystal is not that of a regular octagon, but indeed of a regular ditetragon : If we set the length of a side of the square building block (the stacking of which results in the crystal) as being 1 , then its diagonal has a length of square root(2). The length of an oblique side of the octagon is then 4{square root(2)}. The length of a horizontal or vertical side of the octagon is, however, equal to 5 . So the octagon has no equal sides and is therefore irregular. In fact the figure's sides of lenght 5 alternate with those of length 4{square root(2)}, so its shape is that of a regular ditetragon.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :
Figure above : Macroscopic view of the regular ditetragonal D4 two-dimensional crystal of the previous Figure.
The next Figure gives the pattern of symmetry elements of our regular ditetragonal D4 two-dimensional crystal.
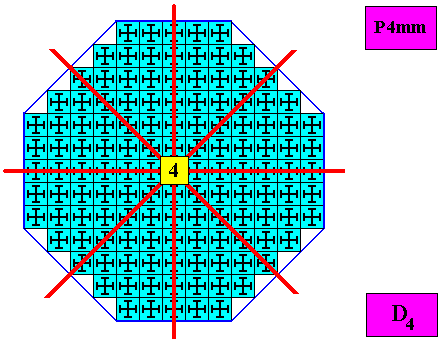
Figure above : Pattern of symmetry elements of the regular ditetragonal crystal of the above Figures. It consists of a 4-fold rotation axis at the intersection point of four mirror lines. The latter comprise two sets : One set consists of a horizontal and vertical mirror line, while the second set consists of two diagonal mirror lines. So in all we have four mirror lines and one 4-fold rotation axis as the symmetry elements of the crystal.
Two (crystallographic) Forms are needed to conceptually construct the outline of our two-dimensional regular ditetragonal crystal :
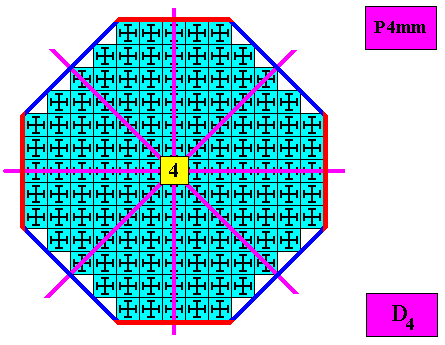
Figure above : Two crystallographic Forms are needed to construct the (eight) faces of a regular ditetragonal two-dimensional crystal. An initially given face (dark blue) implies three more faces in virtue of the 4-fold rotation axis. The result is a closed Form -- a square -- consisting of four faces. A second initially given face (red), not parallel nor perpendicular to the first one, also implies three more faces, also resulting in a quadratic closed Form consisting of four faces. Combining these two Forms yields our regular ditetragonal crystal.
Possible a n t i m e r c o n f i g u r a t i o n s for holomorphic regular ditetragonal two-dimensional crystals.
Four antimers.
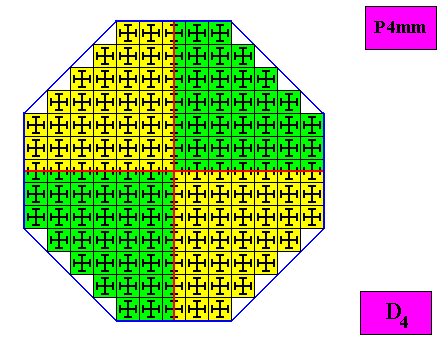
Figure above : A regular ditetragonal D4 two-dimensional crystal. The case of f o u r equal (and in themselves mirror symmetric) antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D4 motif (black) inside each quadratic building block. It is -- or represents -- an atomic configuration such that four equal, and in themselves mirror symmetric, antimers (as such related to each other by a 4-fold rotation axis) can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests eight similar antimers, while in fact there are four equal antimers.
Another possible configuration of four equal antimers is the following :
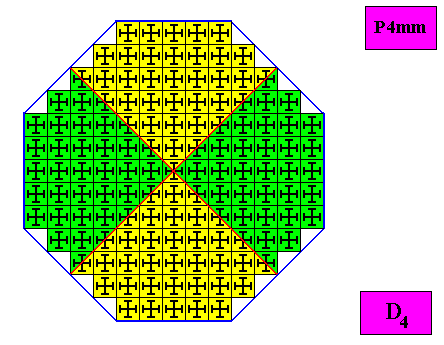
Figure above : Alternative configuration of four equal antimers in a regular ditetragonal D4 crystal .
Removing the lattice connection lines and the motifs in the above Figure, results in a macroscopic view of the crystal :
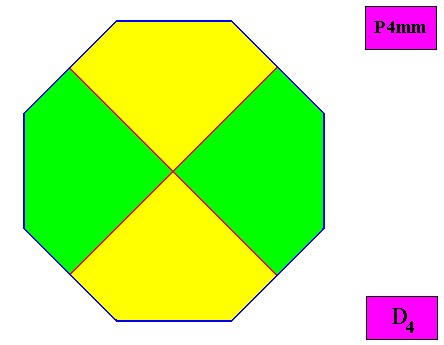
Figure above : Macroscopic view of the regular ditetragonal D4 two-dimensional crystal of the previous figure, with four equal antimers (green, yellow).
The promorph of the above non-eupromorphic crystal is (as two-dimensional analogue) belonging to the Homostaura Isopola tetractinota. This promorph is depicted in the next Figure.

Figure above : The promorph of the regular ditetragonal D4 crystal with four antimers. It is a regular 4-fold polygon -- a square -- and as such the two-dimensional analogue of the quadratic pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the difference in shape of the promorph (square, regular tetragon) and the crystal (regular ditetragon). Radial (R) and interradial (IR) directions are indicated.
We have just found out that the promorph of our regular ditetragonal D4 crystal belongs to the Homostaura Isopola tetractinota. We must realize that here "Isopola" means that the poles of each c r o s s a x i s (whether radial or interradial) of the crystal (or any other object having this promorph) are mirror symmetric with respect to each other. These poles refer to body parts. But what are the cross axis of our regular ditetragonal crystal? They are not simply the lines connecting opposite corners (these lines together form -- in crystals -- the Vector Rosette of Actual Growth). Indeed we can see that in our present case these lines do not possess poles that are mirror symmetric with respect to each other :
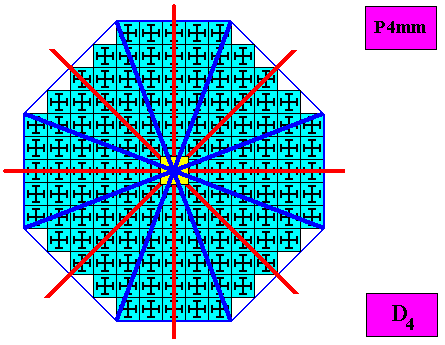
Figure above : The regular ditetragonal D4 crystal under investigation. Its four mirror lines are indicated (red). The dark blue lines do not possess mirror symmetric poles. In fact these lines do not represent cross axes of the ditetragon.
If we want to find the cross axes of the ditetragonal crystal we should consider the fact that the crystal has D4 symmetry and four antimers. This means that the promorph must be a square. And the cross axes of this square can easily be located :
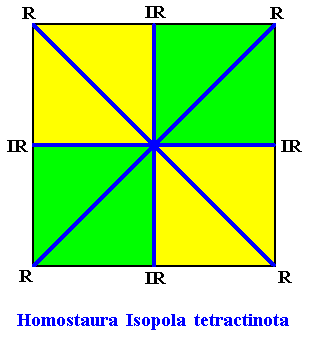
Figure above : The promorph of the regular ditetragonal D4 crystal under investigation. It has four cross axes (dark blue lines). Two of them are radial, and the other two are interradial. For each cross axis its two poles are mirror symmetric, which means that these axes are equipolar.
So now we know the cross axes of the ditetragonal crystal :
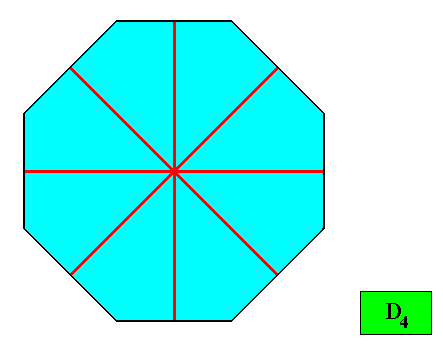
Figure above : The cross axes of the regular ditetragon : one horizontal, one vertical, two diagonal. All of them are equipolar (expressed in the term "Isopola" figuring in the name of the promorph).
The next Figure shows yet another configuration of four antimers of the regular ditetragonal crystal under investigation. This configuration, however, is not consistent with the intrinsic symmetry of the crystal which is supposed to be according to the group D4 . And this symmetry demands (4n equal) antimers, each one of which is mirror symmetric, while in the present drawing the antimers are not mirror symmetric.
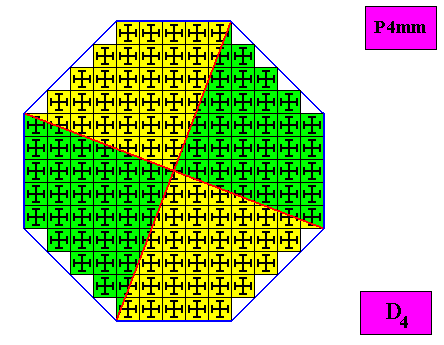
Figure above : Incorrect delineation of the four antimers of the regular ditetragonal crystal under investigation. Although the antimers are equal, they are not (each for themselves) mirror symmetric.
Eight antimers.
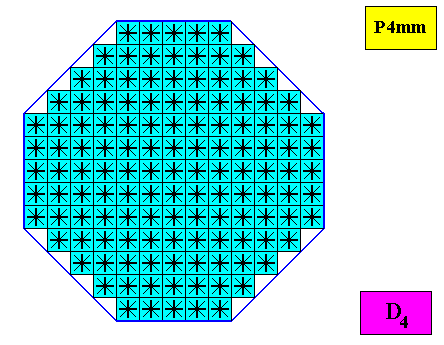
Figure above : Microscopic view of a regular ditetragonal D4 crystal. Its D4 motifs have eight similar antimers. Two types of antimer alternate with each other.
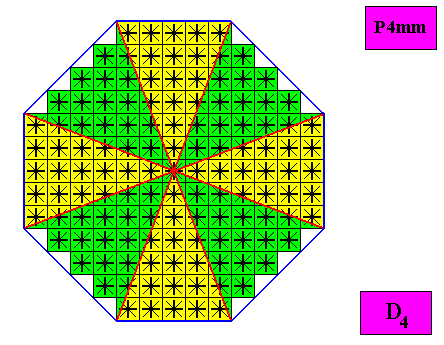
Figure above : The regular ditetragonal D4 two-dimensional crystal of the previous Figure. The case of e i g h t similar (and in themselves mirror symmetric) antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D4 motif (black) inside each quadratic building block. It is -- or represents -- an atomic configuration such that eight similar (and four by four equal), and in themselves mirror symmetric, antimers, forming pairs that relate to each other by a 4-fold rotation axis), can be distinguished in it. The crystal is eupromorphic because its intrinsic shape suggests eight similar (and in themselves mirror symmetric) antimers, which are indeed present.
Removing the lattice connection lines and the motifs in the above Figure, results in a macroscopic view of the crystal :
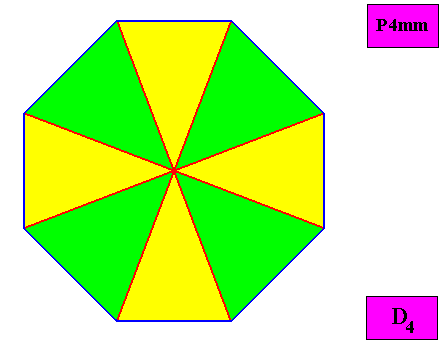
Figure above : Macroscopic view of the regular ditetragonal D4 two-dimensional crystal of the previous figure, with eight similar (and in themselves mirror symmetric) antimers (green, yellow).
The promorph of the above eupromorphic crystal is (as two-dimensional analogue) belonging to the Dihomostaura Isopola tetractinota. This promorph is depicted in the next Figure.
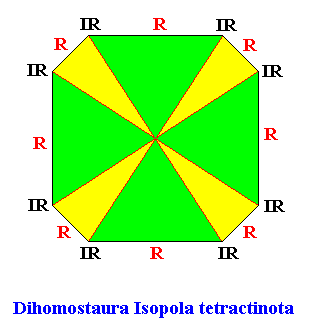
Figure above : The promorph of the regular ditetragonal D4 crystal with eight similar antimers. It is a regular ditetragon and as such the two-dimensional analogue of the ditetragonal pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the identical shapes of the promorph (regular ditetragon) and the crystal (regular ditetragon). Radial (R) and interradial (IR) directions are indicated.
It is important to realize that not only ditetragonal, but also q u a d r a t i c D4 crystals, i.e. D4 crystals having as their intrinsic s h a p e not a ditetragon, but that of a square, have this same promorph, if they possess eight similar antimers, configured such that they display alternation. See next Figure, and some more explanation further down.
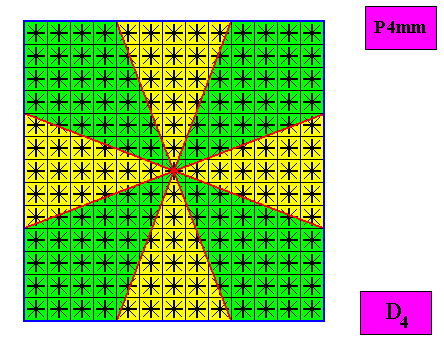
Figure above : A regular tetragonal (i.e. quadratic) D4 two-dimensional crystal. The case of e i g h t similar (and in themselves mirror symmetric) antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D4 motif (black) inside each quadratic building block. It is -- or represents -- an atomic configuration such that eight similar (and four by four equal), and in themselves mirror symmetric, antimers, forming pairs that relate to each other by a 4-fold rotation axis), can be distinguished in it. The crystal is (like the other crystals discussed here) holomorphic ( The symmetry of its shape is the same as the intrinsic symmetry of the crystal (both D4 )). It is non-eupromorphic because its intrinsic shape suggests four equal and in themselves mirror symmetric antimers, while eight similar antimers are actually present.
Removing the lattice connection lines and the motifs in the above Figure, results in a macroscopic view of the crystal :
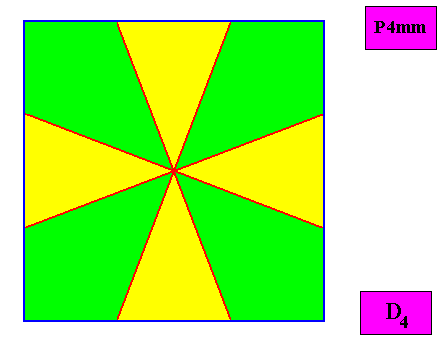
Figure above : Macroscopic view of the regular tetragonal (i.e. quadratic) D4 two-dimensional crystal of the previous figure, with eight similar (and in themselves mirror symmetric) antimers (green, yellow). The promorph of this crystal (like the ditetragonal crystal discussed earlier) belongs to the Dihomostaura Isopola tetractinota and was depicted above . Note, with respect to the present case, the difference in shape obtaining between that of the promorph (ditetragon) and that of the present crystal (square) of which it is the promorph.
Let's return to the d i t e t r a g o n a l D4 crystal that we were discussing earlier .
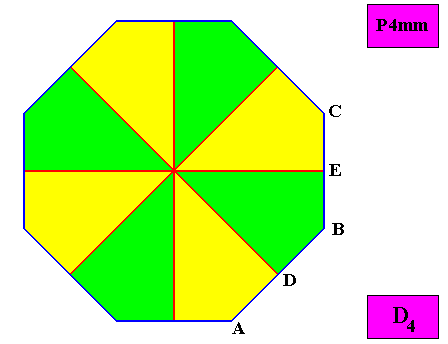
Figure above : Macroscopic view of the regular ditetragonal D4 two-dimensional crystal (again) under investigation, with eight supposedly similar antimers (green, yellow). The delineation of the eight antimers is incorrect because -- as depicted -- they are not each for themselves mirror symmetric (with respect to a mirror line passing through the crystal's center) : The length of the line segment AB is to that of BC as 4{square root(2)} to 5, implying that DB is not equal to BE. Moreover, the antimers as depicted here (green, yellow) are congruent (not just similar), which they shouldn't be according to the morphology of the translation-free residue (motif) (See Figure above ). In fact the 'antimers' as depicted here are not really antimers. Only when we consider pairs consisting of two 'antimers' (the latter) related to each other by a reflection, we have genuine antimers. And then we get the regular ditetragonal crystal with four antimers that was discussed earlier . And the promorph of that crystal is, consequently, belonging to the Homostaura Isopola tetractinota which promorph was depicted above .
Above we have established that the promorph of our two-dimensional ditetragonal D4 crystal with eight similar antimers (See Figure above ) belongs to the Dihomostaura Isopola tetractinota. Let us explain this promorph (and its name).
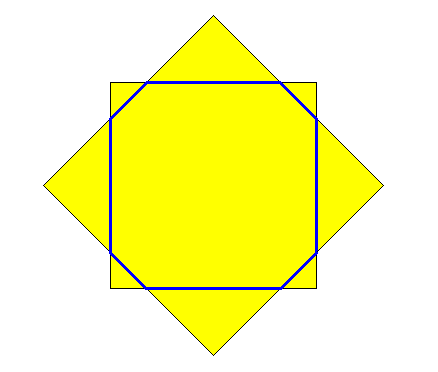
Figure above : A d i t e t r a g o n is formed when two unequal squares, with their centers coinciding, but differing in orientation by 450, cut off each other's corners. In two-dimensional crystals these two squares represent two crystallographic Forms (See Figure above ).
So the promorph of our ditetragonal D4 crystal with eight similar antimers (See Figure above ), or of the above discussed quadratic crystal (also with eight similar antimers) for that matter, which (promorph) is itself a regular ditetragon (as depicted above), can be seen as being composed out of two squares. Well, a promorph that has the shape of a square (regular tetragon) belongs to the Homostaura Isopola tetractinota. So a promorph consisting of the superimposition of t w o (different) Homostaura Isopola tetractinota (i.e. of two different squares) can conveniently be called "Dihomostaura Isopola tetractinota". The prefix "Di" in combination with "tetractinota" indicates that the number of antimers is 2x4 = 8, and that they are not equal (In the case of 8 equal antimers we would have to do with a promorph belonging to the Homostaura Isopola octactinota, which is discussed further below ).
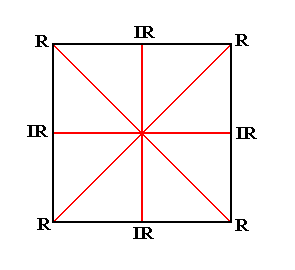
Figure above : A square ( = regular tetragon) has four cross axes (red), two radial (R-R) and two interradial (IR-IR). Each cross axis is equipolar (which feature is expressed by the term "isopola" in the name of the promorph that the square can represent (Homostaura Isopola tetractinota)).
Wheras a regular ditetragon (which is in fact a special octagon) can be constructed from two non-equal squares, a regular octagon can be constructed from two equal squares :
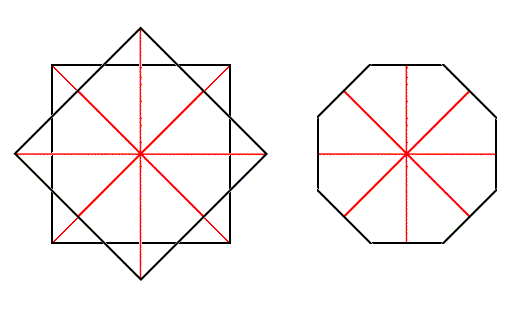
Figure above : Superimposing two equal squares results in a regular octagon.
A regular octagon possesses eight mirror lines (and an 8-fold rotation axis at their intersection point). These mirror lines show two types. One type connects the centers of opposite sides of the octagon, the other type connects opposite corners. See next Figures.
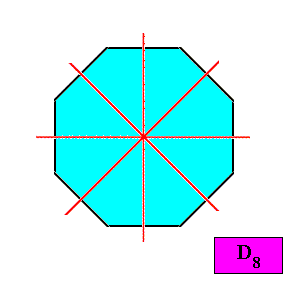
Figure above : Regular octagon. One type of mirror line connects opposite sides.
Figure above : Regular octagon. A second type of mirror line connects opposite corners. One example shown.
Figure above : Regular octagon. The second type of mirror line connects opposite corners.
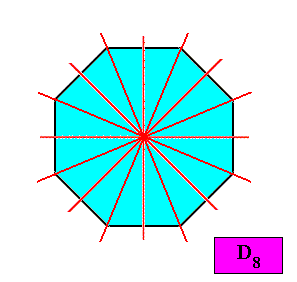
Figure above : Regular octagon. The total set of its mirror lines, consisting of the two types considered above.
A regular octagon cannot occur in crystals, because it cannot be constructed from identical building blocks that repeat themselves periodically. This implies that an 8-fold rotation axis cannot occur in crystals. So the symmetry of the regular octagon being according to the group D8 , there are no crystals with intrinsic symmetry according to this group. On the other hand, in organisms this symmetry can occur (because organisms are not built by the periodic stacking of identical building blocks). Some Coelenterates (polyps, corals) seem to have this symmetry (D8 ). A structure (some object, some organism) having D8 intrinsic symmetry, can have 8n antimers (either eight equal antimers, or 8n (n > 1) similar antimers). When there are eight (equal) antimers present in such a D8 object, its promorph is belonging to the Homostaura Isopola octactinota. The next Figure illustrates a regular octagon with eight equal (and in themselves mirror symmetric) antimers.
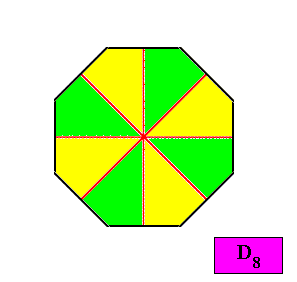
Figure above : A regular octagon with eight equal antimers (green, yellow).
The promorph of such a regular octagon with eight equal antimers, i.e. of something that has an intrinsic shape according to a regular octagon, while its internal structure admits of eight equal antimers to be distinguished, is itself just a regular octagon partitioned into eight similar sectors, and as such belonging to the Homostaura Isopola octactinota :
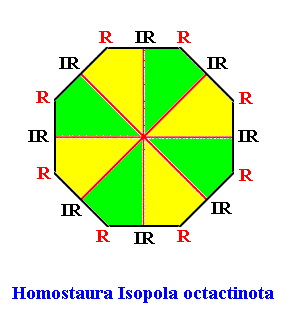
Figure above : The planimetric figure (regular octagon) representing the promorph of two-dimensional objects having eight equal, and in themselves mirror symmetric, antimers. If these objects are three-dimensional, then the figure representing their promorph is a stereometric figure, in the present case a regular octagonal pyramid. Radial (R) and interradial (IR) directions indicated. The antimers of the object are represented in the promorph as green and yellow areas.
The next Figure gives an object having the above promorph, a promorph belonging to the Homostaura Isopola octactinota.
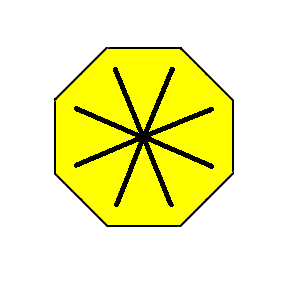
Figure above : An object having eight equal, and in themselves mirror symmetric, antimers.
The next object also has eight equal and symmetric antimers.
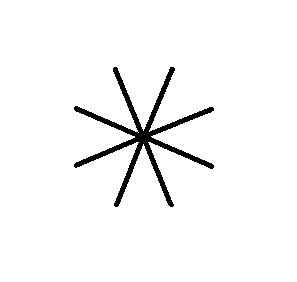
Figure above : An object having eight equal, and in themselves mirror symmetric, antimers.
Of course both objects just depicted have the same promorph (Homostaura Isopola octactinota), and this promorph is a regular octagon.
Without destroying the initial D8 symmetry, the number of antimers can be doubled.
If this doubling were such that the new antimers were exact copies of the original ones, and were inserted such that they bisect the angles between the original antimers (into two equal angles), then the symmetry of this object would have changed to D16 (in which D8 symmetry is still comntained as a subgroup), and the object's promorph would then have been transformed from the Homostaura Isopola octactinota to the Homostaura Isopola hexakaidecactinota ( The latter is a regular 16-gon, or sixteen-fold regular polygon).
If, on the other hand, the extra 'antimers' are totally different from the original antimers, we cannot consider them as additional antimers, but as a morphological extention of the original antimers, meaning that the number of antimers does not change, it remains eight.
If, finally, the extra antimers resemble the original antimers very closely (but are not identical to them), then the number of antimers is doubled : we end up with 16 similar antimers (eight by eight equal) that alternate between two types. An object that satisfies this condition is depicted in the next Figure.
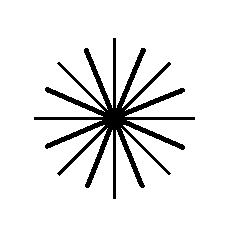
Figure above : An object having 16 similar (in themselves mirror symmetric) antimers. The symmetry of this object is still according to the group D8 .
The promorph of this object can be conceived as a combination of two non-equal (but) regular octagons, i.e. two Homostaura Isopola octactinota. Therefore the promorph of this object belongs to the Dihomostaura Isopola octactinota, and is depicted in the next Figure.
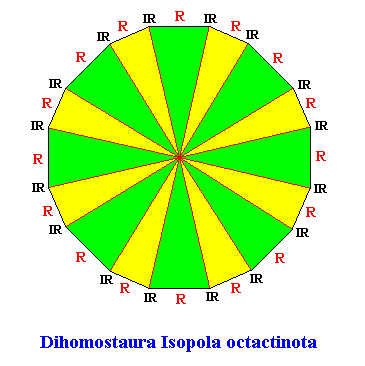
Figure above : Promorph of the just described and depicted object (not a crystal) having 16 similar (in themselves mirror symmetric) antimers. The symmetry of this object is still according to the group D8 . The promorph is a regular dioctagon (not a regular 16-gon). It is the two-dimensional analogue of the regular dioctogonal pyramid, which represents the promorph of corresponding three-dimensional objects (not crystals). This (two-dimensional) promorph possesses eight mirror lines and an 8-fold rotation axis through their point of intersection. So the symmetry is according to the group D8 (and not D16 ). Radial (R) and interradial (IR) directions indicated. The 16 similar antimers of the object are represented in the promorph by non-congruent (and thus just similar) areas (green, yellow). The antimers are eight by eight equal.
The next Figure again depicts the dioctagon of the just given promorph, but with an incorrect delineation of the 16 antimers.
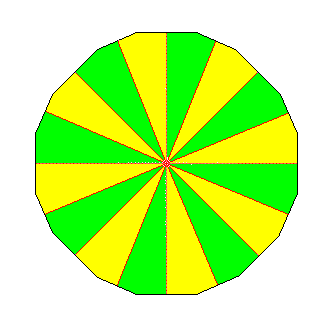
Figure above : Incorrect delineation of the sixteen antimers in the figure supposed to represent the promorph of the object depicted above . The antimers of this object are not congruent, and this feature should be expressed in the figure representing its promorph. However, in the present Figure the areas representing antimers are congruent. Moreover, the antimers, as depicted here, are not in themselves mirror symmetric, what they should be (because Homostaura, and by implication also Dihomostaura, have symmetric antimers). In fact the figure represents a different promorph, and the antimers as presented here (green, yellow) are not antimers. See next Figure.
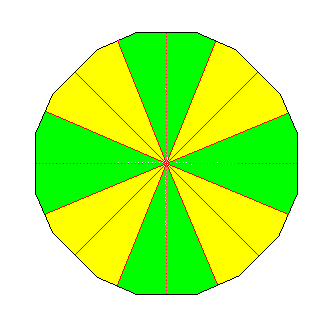
Figure above : The previous Figure actually does not represent the Dihomostaura Isopola octactinota, but the Homostaura Isopola octactinota, because it expresses in fact eight equal antimers (which are in themselves mirror symmetric). These eight equal and symmetric antimers are shown in the present Figure, and derived from the previous one. Each such an antimer itself consists of two congruent, namely mirror symmetric, 'antimers' (second order antimers), which we could call "paramers". Because, in the present case, every two paramers are mirror symmetric, they can be considered as belonging to each other, constituting an antimer ( This in contrast to considering the object, represented by this promorph, as possessing 16 congruent asymmetric antimers).
In the next document we will discuss the twelfth crystal shape of our list (as given in Part XVI ) , viz. the regular gyroid ditrigon, with respect to intrinsic symmetry and promorph in holomorphic two-dimensional crystals having this shape intrinsically.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXVII.