e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to Introduction to Other Crystal Shapes
In the foregoing documents we have studied and summarized some simple two-dimensional crystal shapes, viz. the Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon, with respect to intrinsic symmetry and promorph. After that (in the previous two documents) we started an introduction to some other, more complex shapes, which will be studied also with respect to symmetry and promorph, and in the present document we will still occupy ourselves with this introduction. The complex shapes to be discussed had (earlier) been chosen as :
As indicated earlier, we will (in this introduction and in the systematic Parts that follow) only discuss holomorphic crystals having these shapes, i.e. only those cases where the intrinsic symmetry of the crystal is fully expressed by its intrinsic shape (At some occasions also meromorphic crystals are being considered, but only to highlight the difference between holomorphic and meromorphic crystals). And such a holomorphic crystal comes in two 'species' namely eupromorphic and non-eupromorphic. If it is eupromorphic, then -- as has been explained earlier -- its intrinsic shape not only precisely reflects its intrinsic symmetry, but also (precisely reflects) its promorph.
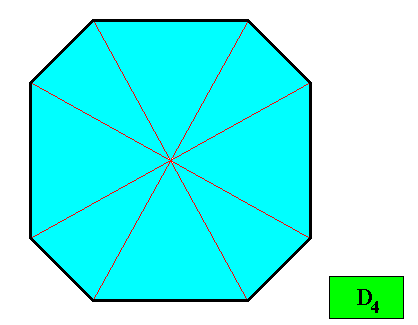
Next we consider the persistence of faces of a two-dimensional crystal having as its intrinsic shape that of the regular ditetragon.

Figure above : A two-dimensional crystal having as its intrinsic shape that of a regular ditetragon, and supposed to possess an intrinsic symmetry according to the group D4 (i.e. while in the present case -- because we consider only holomorphic crystals [symmetry of shape = intrinsic symmetry of crystal] -- we have set the intrinsic symmetry to be that of D4 , while a crystal having this shape could -- in other cases -- have an intrinsic symmetry according to D2 or C2 or a symmetry according to some other subgroup of D4 ). The vectors of the Vector Rosette of Actual Growth (here indicated by thin red lines) precisely bisect the angles between adjacent crystal faces into two equal angles, guaranteeing that the macroscopic growth layers (next Figure) are all of equal width (equality not only with respect to successive layers but also with respect to layers in different directions), and so expressing the fact of equal growth rates of all the eight faces, which in turn guarantees that these faces will persist during prolonged crystal growth. See also next Figure.
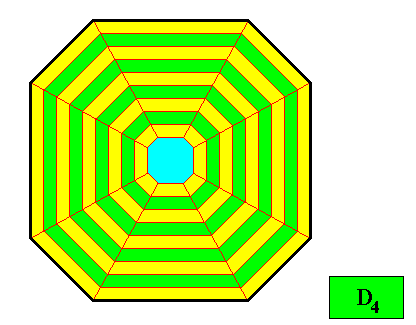
Figure above : The two-dimensional crystal of the previous Figure, namely the crystal having as its intrinsic shape that of a regular ditetragon, and supposed to possess an intrinsic symmetry according to the group D4 . The equal macroscopic growth layers or increments (green, yellow) express equal growth rates of all the eight faces, guaranteeing the persistence of these faces.
And without auxiliary lines :
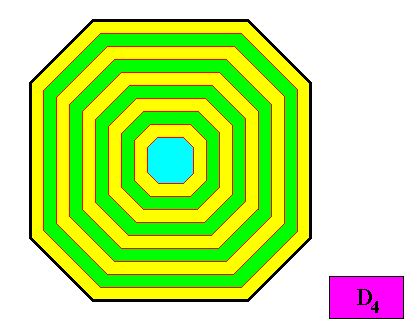
Figure above : Same as previous Figure. Auxiliary lines removed.
The next Figure indicates a possible antimer configuration : eight similar antimers (two types alternating with each other).
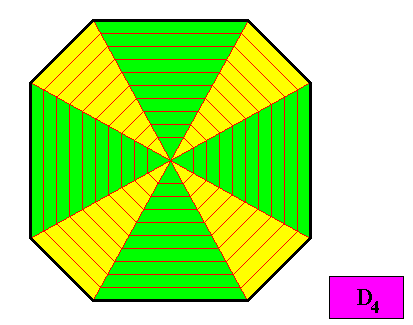
Figure above : A possible configuration of antimers in the D4 ditetragonal two-dimensional crystal presently under investigation (previous three Figures). As such the crystal is holomorphic and eupromorphic.
Another possible antimer configuration is as follows :
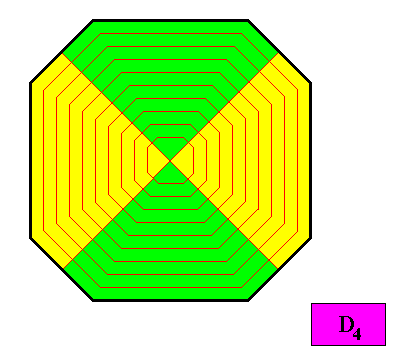
Figure above : Another possible configuration of antimers in the D4 ditetragonal two-dimensional crystal presently under investigation. As such the crystal is holomorphic and non-eupromorphic.
The next Figure depicts another possible antimer configuration for our present ditetragonal crystal, namely when this crystal has an intrinsic symmetry according to the group C4 (instead of D4 ). The crystal is then meromorphic.
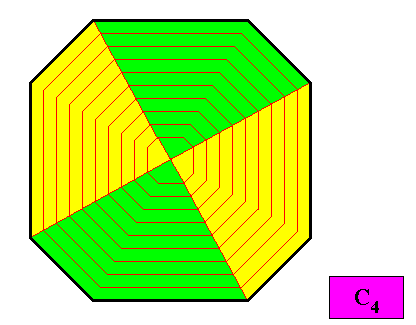
Figure above : A possible configuration of antimers in a C4 ditetragonal two-dimensional crystal. The crystal now has four equal, but in themselves asymmetric antimers, and loosing therefore all its mirror lines (that were present in the above D4 crystal).
The next Figures depict and discuss a two-dimensional crystal with intrinsic symmetry according to the group C2 and with an amphitect gyroid octagon as its intrinsic shape.

Figure above : A two-dimensional crystal with C2 intrinsic symmetry and with an intrinsic shape according to an amphitect gyroid octagon. The thick blue lines bisect the angles between adjacent faces exactly into two equal angles (as indicated by marks in the Figure), guaranteeing that the macroscopic growth layers (drawn in the next Figure) have equal width with respect to different directions, expressing in this way the equal growth rates of all the eight faces (as we want them to be so). This equal growth in turn guarantees that the eight faces will persist during prolonged growth of the crystal.
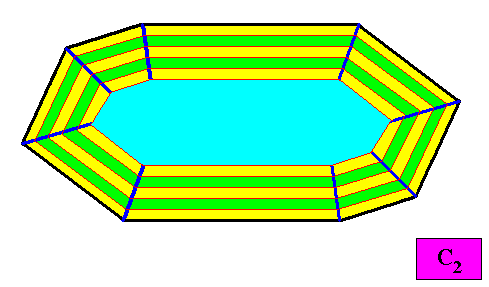
Figure above : Macroscopic growth layers or increments (green, yellow) of the above two-dimensional crystal with C2 intrinsic symmetry and with an intrinsic shape according to an amphitect gyroid octagon. The macroscopic growth layers (increments) are equal in all (different) directions, expressing equal growth of all the eight faces of the crystal, guaranteeing that they do not vanish during prolonged crystal growth.
And with auxiliary lines removed :
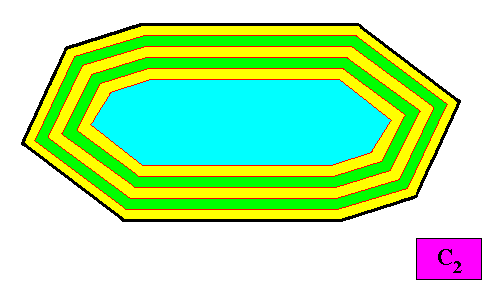
Figure above : Macroscopic growth layers or increments (green, yellow) of the above two-dimensional crystal with C2 intrinsic symmetry and with an intrinsic shape according to an amphitect gyroid octagon. Auxiliary lines removed.
Antimer configurations.
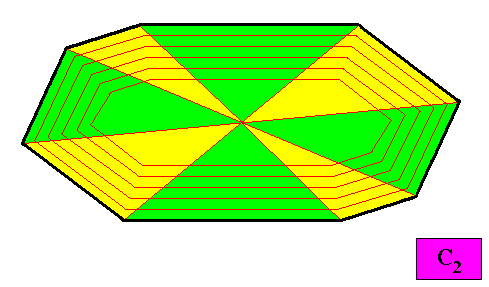
Figure above : The eight antimers (green, yellow) of the above two-dimensional holomorphic crystal with C2 intrinsic symmetry and with an intrinsic shape according to an amphitect gyroid octagon. As such the crystal is eupromorphic.
The next two Figures give two other possible antimer configurations for our C2 amphitect gyroid octogonal crystal.
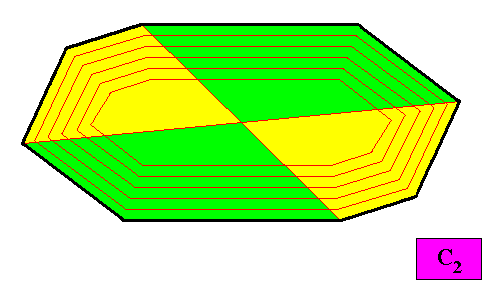
Figure above : A configuration of four antimers (green, yellow) of the above two-dimensional holomorphic crystal with C2 intrinsic symmetry and with an intrinsic shape according to an amphitect gyroid octagon. As such the crystal is non-eupromorphic.
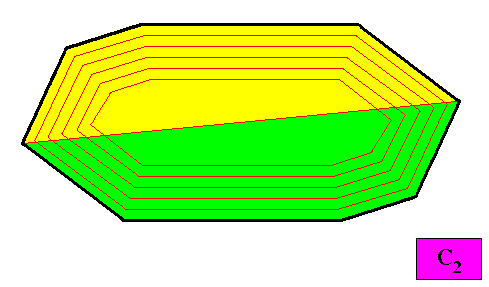
Figure above : A configuration of two antimers (green, yellow) of the above two-dimensional holomorphic crystal with C2 intrinsic symmetry and with an intrinsic shape according to an amphitect gyroid octagon. As such the crystal is non-eupromorphic.
Next we will discuss a two-dimensional crystal having as its intrinsic shape that of an amphitect octagon.
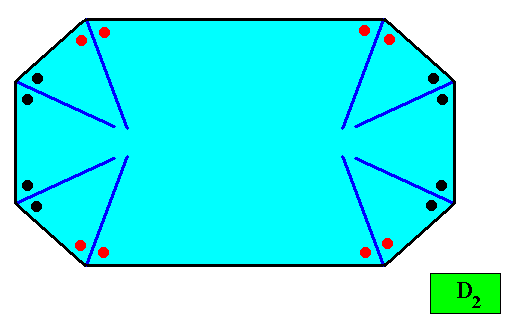
Figure above : A two-dimensional crystal with D2 intrinsic symmetry and with an intrinsic shape according to an amphitect octagon. The thick blue lines bisect the angles between adjacent faces exactly into two equal angles (as indicated by marks in the Figure), guaranteeing that the macroscopic growth layers (drawn in the next Figure) have equal width with respect to different directions, expressing in this way the equal growth rates of all the eight faces (as we want them to be so). This equal growth in turn guarantees that the eight faces will persist during prolonged growth of the crystal. As in the foregoing cases of crystal shapes and supposed equal growth of faces, we consider only holomorphic crystals, which for the present crystal implies that its intrinsic symmetry is according to the group D2 .
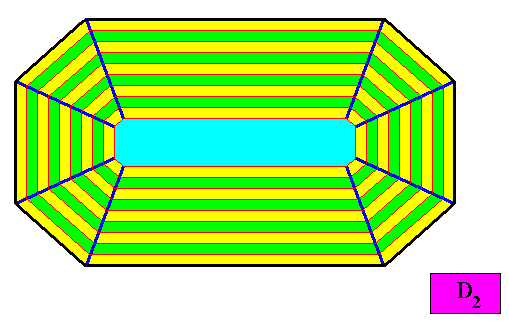
Figure above : Macroscopic growth layers or increments (green, yellow) of the above two-dimensional crystal with D2 intrinsic symmetry and with an intrinsic shape according to an amphitect octagon. The macroscopic growth layers (increments) are equal in all (different) directions, expressing equal growth of all the eight faces of the crystal, guaranteeing that they do not vanish during prolonged crystal growth.
And with the auxiliary lines removed :
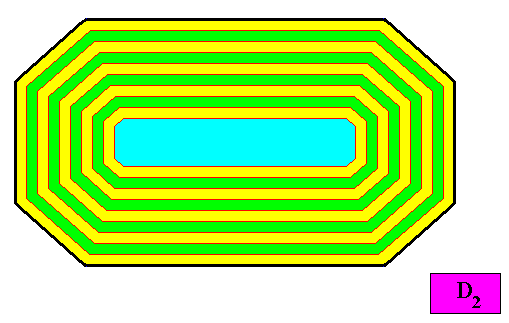
Figure above : Same as previous Figure : Macroscopic growth layers or increments (green, yellow) of the two-dimensional crystal with D2 intrinsic symmetry and with an intrinsic shape according to an amphitect octagon. Auxiliary lines removed.
A possible antimer configuration is given in the next Figure.
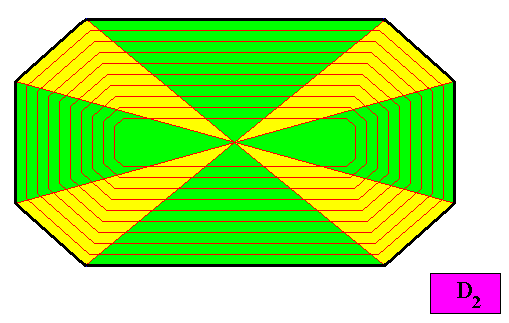
Figure above : A possible antimer configuration of the crystal presently under investigation : Eight similar antimers. With such a configuration the crystal is eupromorphic.
The next three Figures give three ways for a configuration of f o u r antimers.
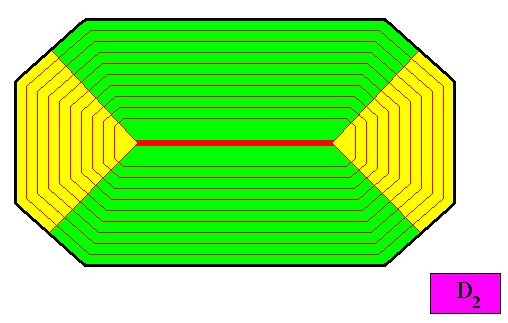
Figure above : A possible configuration of four antimers of the D2 crystal presently under investigation. The center of the (2-dimensional) crystal is here supposed to be a line, instead of a point. The latter is, however, more natural : The diagonals of the amphitect octagon meet in a point. With this antimer configuration the crystal is non-eupromorphic.
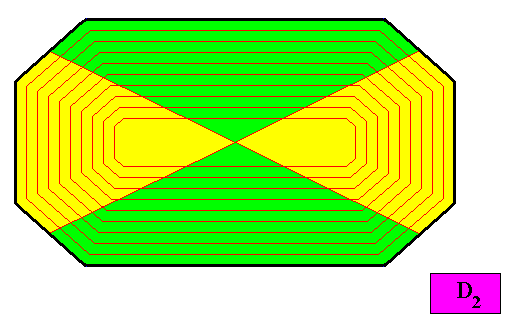
Figure above : Another possible configuration of four antimers of the D2 crystal presently under investigation. The center of the (2-dimensional) crystal is now the point just mentioned when discussing the previous Figure, namely the intersection point of the amphitect octagon's diagonals. Also in this case the crystal is non-eupromorphic.
The most natural configuration of four antimers is, however, the following :

Figure above : A configuration of four antimers (opposite antimers equal, adjacent aantimers symmetric). This configuration is naturally expected. Also here the crystal is non-eupromorphic.
The next five Figures illustrate (in a step by step construction) the case in which the four oblique crystal faces (of the crystal presently under investigation) have a higher growth rate than that of the adjacent faces. And because the latter are tapering in the direction of growth, the mentioned four oblique faces will grow themselves out of existence, resulting in a rectangular shape of the crystal.
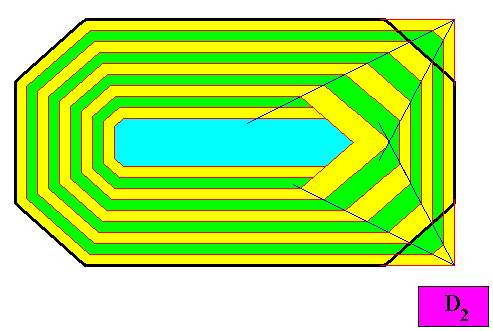
Figure above : First step in the transformation of the above amphitect octogonal two-dimensional crystal into one where the oblique faces grow faster than their adjacent faces. This faster growth is expressed by the greater width of the macroscopic oblique growth layers (Here shown for the right side of the crystal only).
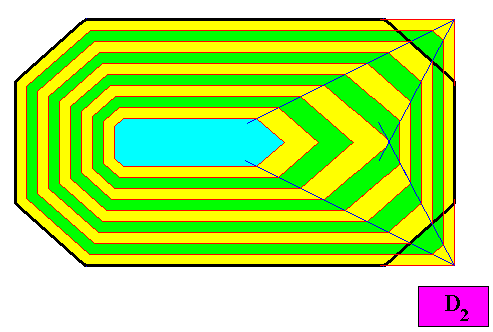
Figure above : Second step in the transformation begun in the previous Figure.
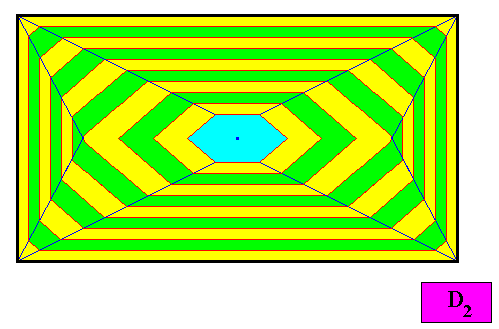
Figure above : Final step in the transformation.
One can see that the dividing lines (blue, oblique) do not bisect the angles between a horizontal or vertical face and an oblique (initially) possible face into exactly two equal angles, resulting in the fact that the width of the macroscopical growth layers changes when they change direction. The oblique layers become thicker than the other layers, expressing the fact of faster growth of the former. And because of this, together with the tapering of the adjacent faces, the oblique faces will finally disappear when growth is continued.
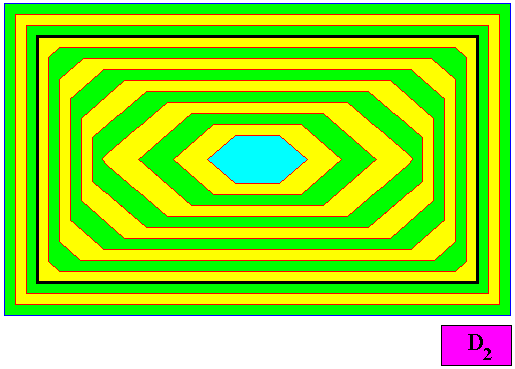
Figure above : Same as previous Figure. Auxiliary lines removed. Three next (macroscopical) growth layers are added, which consist of only two directions, horizontal and vertical. The crystal shape has become rectangular and will remain so when growth is prolonged. So the intrinsic shape of the crystal is now that of a rectangle.
The next Figure emphasizes the fact that the intrinsically rectangular crystal, as depicted in the previous Figures, goes -- while it grows -- through a series of different morphological stages.
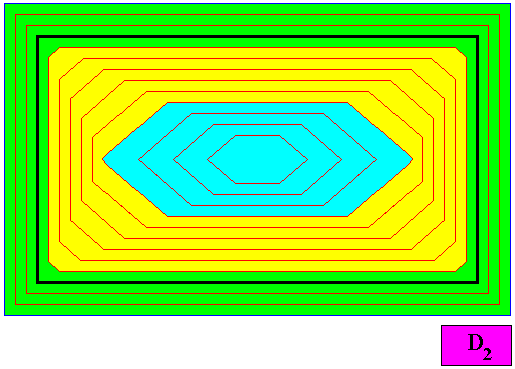
Figure above : The rectangular crystal of the above Figures in fact goes through a series of different morphological stages (indicated by colors) while it grows larger : The amphitect hexagonal crystal seed (intial crystal, blue), after having grown for a while, first becomes an amphitect octogonal crystal (yellow) and then a rectangular (amphitect tetragonal) crystal (green), which is its definitive shape.
The next Figures depict and discuss a two-dimensional crystal having as its intrinsic shape the bi-isosceles trapezium (bilateral hexagon).
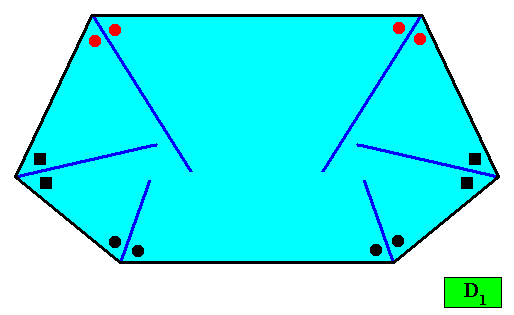
Figure above : A two-dimensional crystal with D1 intrinsic symmetry and with an intrinsic shape according to a bi-isosceles trapezium (bilateral hexagon). The thick blue lines bisect the angles between adjacent faces exactly into two equal angles (as indicated by marks in the Figure), guaranteeing that the macroscopic growth layers (drawn in the next Figure) have equal width with respect to different directions, expressing in this way the equal growth rates of all the six faces (as we want them to be so). This equal growth in turn guarantees that the six faces will persist during prolonged growth of the crystal. As in the foregoing cases of crystal shapes and supposed equal growth of faces, we consider only holomorphic crystals, which for the present crystal implies that its intrinsic symmetry is according to the group D1 (A crystal with this shape could -- in other cases -- have a C1 intrinsic symmetry. It is then a meromorphic crystal.).
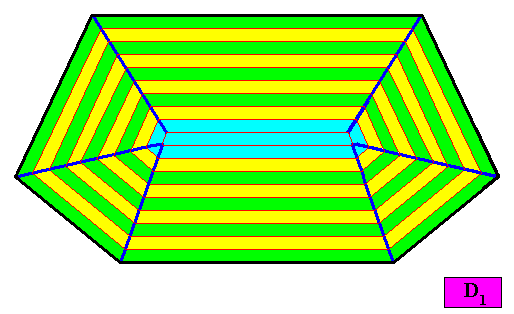
Figure above : Macroscopic growth layers (increments, green, yellow) of the two-dimensional crystal, with D1 intrinsic symmetry and with an intrinsic shape according to a bi-isosceles trapezium (bilateral hexagon), of the above Figure. The Figure shows equal growth of the six faces, guaranteeing their persistence during prolonged crystal growth.
And with the auxiliary lines removed :
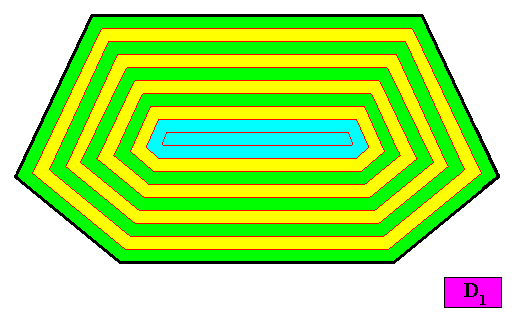
Figure above : Macroscopic growth layers (increments, green, yellow) of the two-dimensional crystal, with D1 intrinsic symmetry and with an intrinsic shape according to a bi-isosceles trapezium (bilateral hexagon), of the above Figures. Auxiliary lines removed.
The next two Figures show two possible antimer configurations of the crystal presently under investigation.
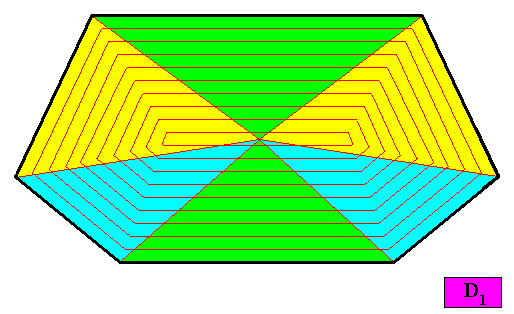
Figure above : A configuration of six antimers in the two-dimensional crystal with D1 intrinsic symmetry and with an intrinsic shape according to a bi-isosceles trapezium (bilateral hexagon) of the above Figures. With this configuration the crystal is eupromorphic.
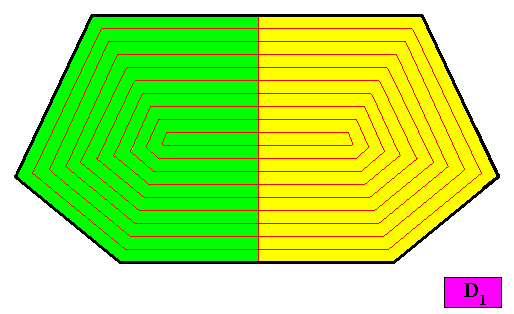
Figure above : A configuration of two antimers in the two-dimensional D1 crystal presently under investigation. With this configuration the crystal is non-eupromorphic.
The next Figures depict and discuss a two-dimensional crystal with intrinsic shape according to a bilateral pentagon.
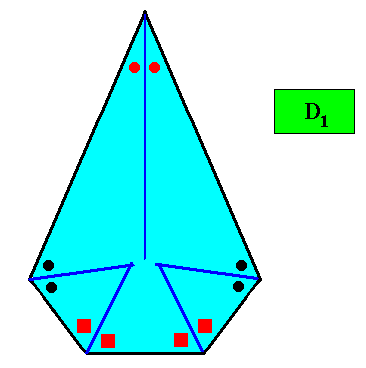
Figure above : A two-dimensional crystal with D1 intrinsic symmetry and with an intrinsic shape according to a bilateral pentagon. The blue lines bisect the angles between adjacent faces exactly into two equal angles (as indicated by marks in the Figure), guaranteeing that the macroscopic growth layers (drawn in the next Figure) have equal width with respect to different directions, expressing in this way the equal growth rates of all the five faces (as we want them to be so). This equal growth in turn guarantees that the five faces will persist during prolonged growth of the crystal. As in the foregoing cases of crystal shapes and supposed equal growth of faces, we consider only holomorphic crystals, which for the present crystal implies that its intrinsic symmetry is according to the group D1 (A crystal with this shape could -- in other cases -- have a C1 intrinsic symmetry. It is then a meromorphic crystal.).
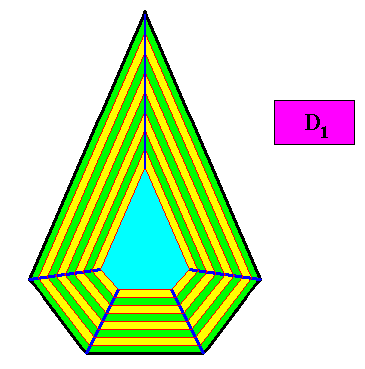
Figure above : Macroscopic growth layers (increments, green, yellow) of the two-dimensional crystal, with D1 intrinsic symmetry and with an intrinsic shape according to a bilateral pentagon, of the above Figure. The Figure shows equal growth of the five faces, guaranteeing their persistence during prolonged crystal growth.
And with the auxiliary lines removed :
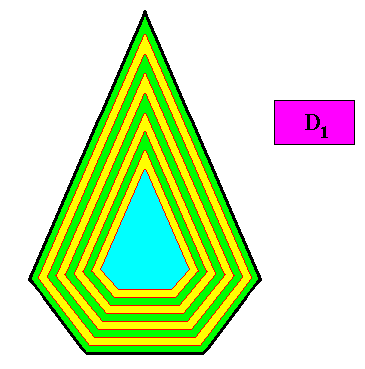
Figure above : Macroscopic growth layers (increments, green, yellow) of the two-dimensional crystal, with D1 intrinsic symmetry and with an intrinsic shape according to a bilateral pentagon, of the above Figures. Auxiliary lines removed.
The next three figures give some possible antimer configurations in the crystal presently under investigation.
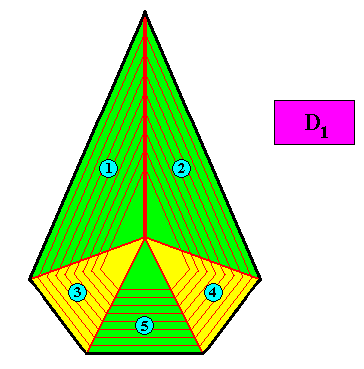
Figure above : Possible arrangement of five antimers in the D1 bilateral pentagonal crystal of the above Figures. With this configuration of five antimers the crystal is eupromorphic.
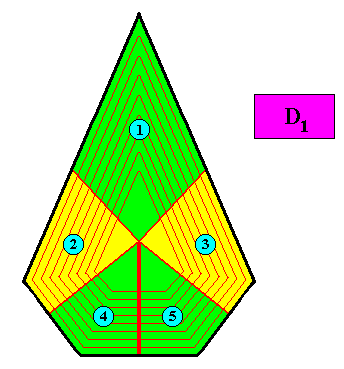
Figure above : Another possible arrangement of five antimers in the D1 bilateral pentagonal crystal of the above Figures. Also with this configuration of five antimers the crystal is eupromorphic.
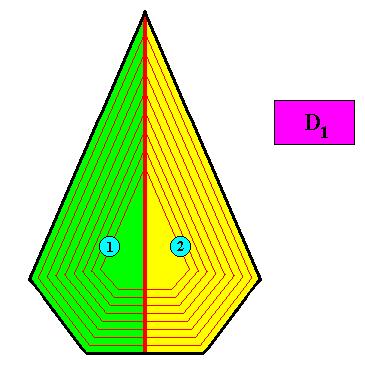
Figure above : The case of two antimers in the D1 bilateral pentagonal crystal of the above Figures. The crystal is now non-eupromorphic.
The next Figures, depict and discuss a two-dimensional crystal having as its intrinsic shape that of a regular gyroid ditrigon.
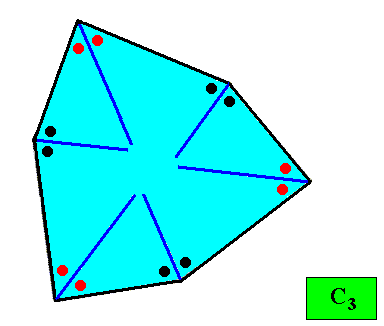
Figure above : A two-dimensional crystal with C3 intrinsic symmetry and with an intrinsic shape according to a regular gyroid ditrigon. The thick blue lines bisect the angles between adjacent faces exactly into two equal angles (as indicated by marks in the Figure), guaranteeing that the macroscopic growth layers (drawn in the next Figure) have equal width with respect to different directions, expressing in this way the equal growth rates of all the six faces (as we want them to be so). This equal growth in turn guarantees that the six faces will persist during prolonged growth of the crystal. As in the foregoing cases of crystal shapes and supposed equal growth of faces, we consider only holomorphic crystals, which for the present crystal implies that its intrinsic symmetry is according to the group C3 .
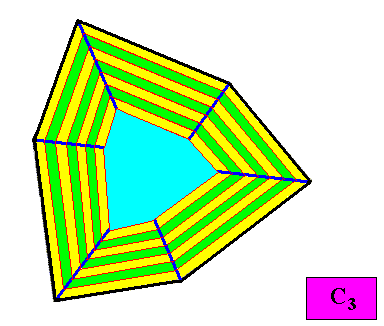
Figure above : Macroscopic growth layers (increments, green, yellow) of the two-dimensional crystal, with C3 intrinsic symmetry and with an intrinsic shape according to a regular gyroid ditrigon, of the above Figure. The Figure shows equal growth of the six faces, guaranteeing their persistence during prolonged crystal growth.
And with the auxiliary lines removed :
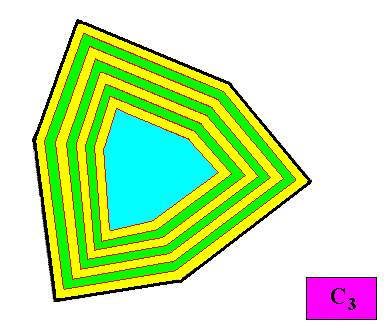
Figure above : Macroscopic growth layers (increments, green, yellow) of the two-dimensional crystal, with C3 intrinsic symmetry and with an intrinsic shape according to a regular gyroid ditrigon, of the above Figures. Auxiliary lines removed.
The next two Figures give two possible positions of the three antimers of the above C3 regular gyroid ditrigonal crystal.
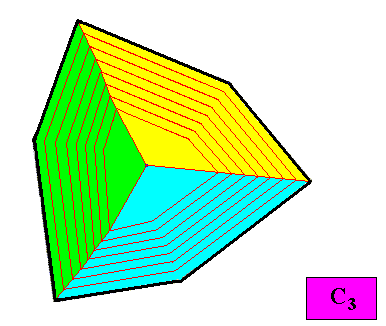
Figure above : Possible position of the three equal antimers (green, yellow, blue) of the C3 regular gyroid ditrigonal two-dimensional crystal presently under investigation. The promorph of this crystal belongs to the Homogyrostaura trimera.
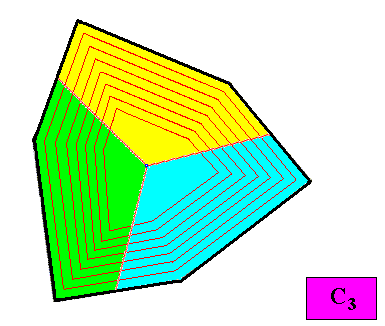
Figure above : Another possible position of the three equal antimers (green, yellow, blue) of the C3 regular gyroid ditrigonal two-dimensional crystal presently under investigation. The promorph of this crystal also belongs to the Homogyrostaura trimera.
The next two Figures show a configuration of six antimers for our C3 regular gyroid ditrigonal crystal presently under investigation.
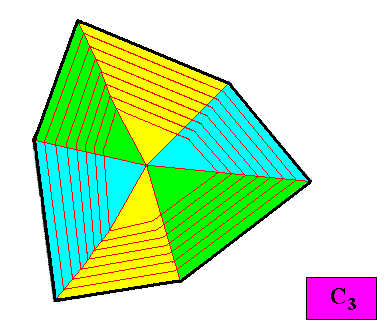
Figure above : A possible configuration of six similar antimers (green, yellow, blue) of the C3 regular gyroid ditrigonal two-dimensional crystal presently under investigation. With this antimer configuration the crystal is eupromorphic. The six antimers are alternatively different, i.e. two types alternate with each other. Therefore the promorph of such a crystal is assessed as beloning to the Homogyrostaura ditrimera (two sets of three antimers). Below we will see an example of the Homogyrostaura hexamera (i.e. also involving six antimers, but this time six e q u a l antimers).
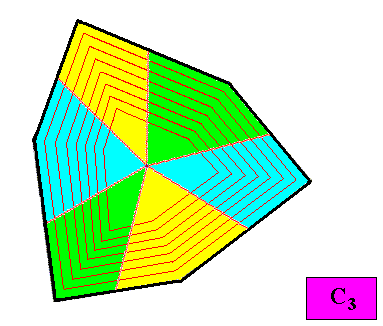
Figure above : Another possible configuration of six similar antimers (green, yellow, blue) of the crystal presently under investigation. Also with this antimer configuration the crystal is eupromorphic. And the promorph of this crystal is also belonging to the Homogyrostaura ditrimera.
The next Figures (several construction steps) show the case when the above C3 crystal is such that the three smaller faces grow faster than the other faces, which, together with the fact that the adjacent faces taper in the direction of growth, causes these three smaller faces to disappear during continued growth of the crystal.
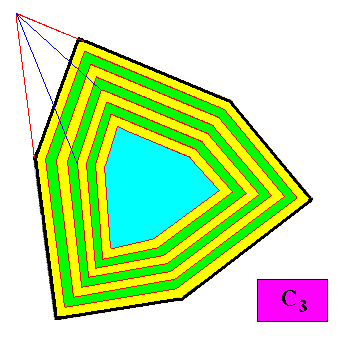
Figure above : First step in the transformation of the above discussed C3 crystal into one where the three smaller faces grow faster than the other faces of the same crystal.
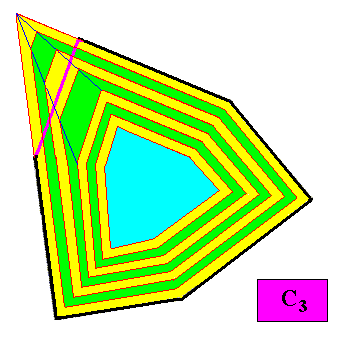
Figure above : Second step in the transformation of the above discussed C3 crystal into one where the three smaller faces grow faster than the other faces of the same crystal.

Figure above : Third step in the transformation of the above discussed C3 crystal into one where the three smaller faces grow faster than the other faces of the same crystal. The initially regular gyroid hexagonal crystal becomes triangular (equilateral triangle, regular trigon).
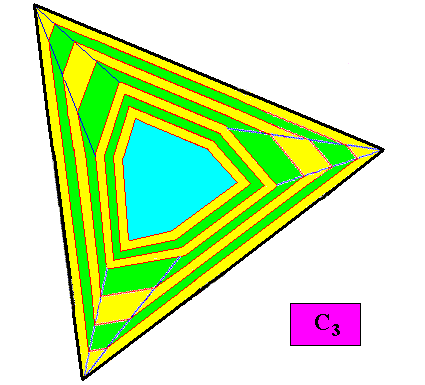
Figure above : Final step in the transformation of the above discussed C3 crystal into one where the three smaller faces grow faster than the other faces of the same crystal. The initially regular gyroid hexagonal crystal becomes triangular (equilateral triangle, regular trigon).
With all auxiliary lines removed, and three (macroscopic) growth layers added :
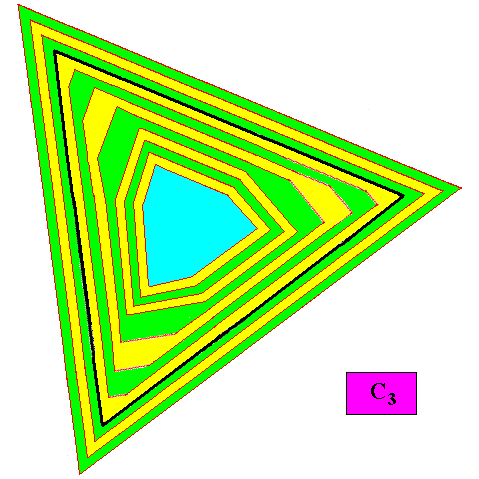
Figure above : Same as previous Figure. Auxiliary lines removed. Three (macroscopic) growth layers added. One can clearly see that the crystal will remain triangular when growth is continued. The intrinsic shape is therefore that of a (regular) triangle.
The variant of the C3 crystal presently under investigation (previous Figures) passes through a series of two morphological stages (indicated by colors) : From a regular gyroid ditrigonal seed stage (blue), it transforms, after some growth, into an equilateral triangle (yellow).
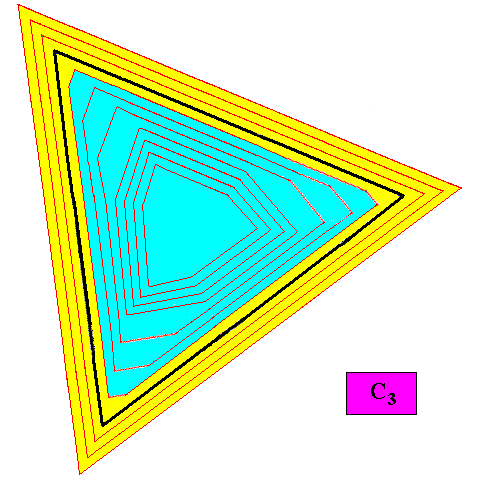
Figure above : Two growth stages (blue, yellow) of the C3 two-dimensional crystal under investigation (previous Figures).
The next Figures, depict and discuss a two-dimensional crystal having as its intrinsic shape that of a regular gyroid dihexagon.
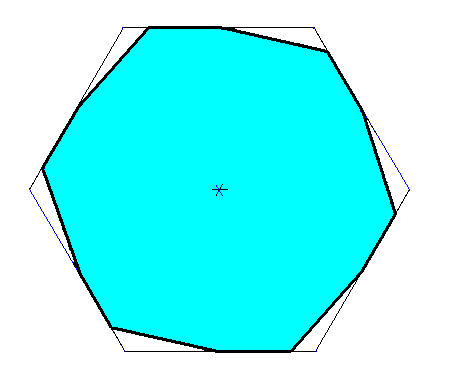
Figure above : Construction of a regular gyroid dihexagon from a regular hexagon.
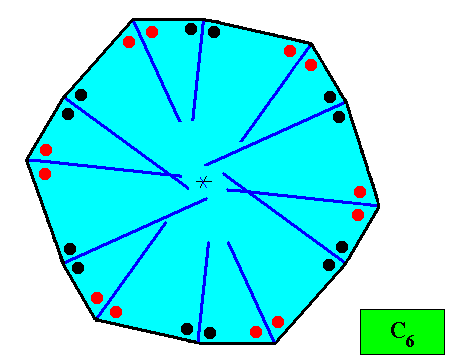
Figure above : A two-dimensional crystal with supposed C6 intrinsic symmetry and with an intrinsic shape according to a regular gyroid dihexagon (12-gon). The thick blue lines bisect the angles between adjacent faces exactly into two equal angles (as indicated by marks in the Figure), guaranteeing that the macroscopic growth layers (drawn in the next Figure) have equal width with respect to different directions, expressing in this way the equal growth rates of all the 12 faces (as we want them to be so). This equal growth in turn guarantees that the twelve faces will persist during prolonged growth of the crystal. As in the foregoing cases of crystal shapes and supposed equal growth of faces, we consider only holomorphic crystals, which for the present crystal implies that its intrinsic symmetry is according to the group C6 . (In other cases the crystal, with its shape according to a regular gyroid dihexagon, could have only C3 symmetry, or C2 symmetry, causing the crystal to be meromorphic).
The next two Figures depict the macroscopic growth layers of the above crystal.
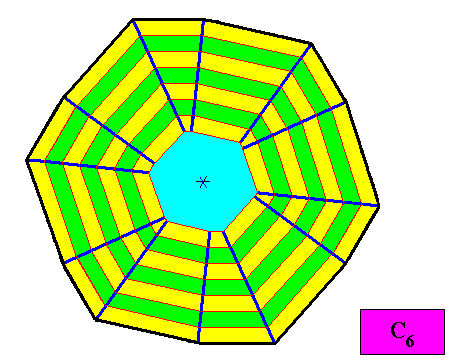
Figure above : Macroscopic growth layers (green, yellow) of the C6 regular gyroid dihexagonal two-dimensional crystal of the previous Figure. As one can see, all the twelve faces will remain, i.e. they will not vanish during prolonged crystal growth.
And without auxiliary lines :
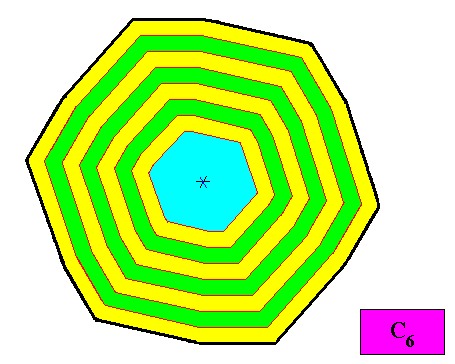
Figure above : Macroscopic growth layers (green, yellow) of the C6 regular gyroid dihexagonal two-dimensional crystal of the previous Figures. Auxiliary lines removed.
The next four Figures give some possible antimer configurations :
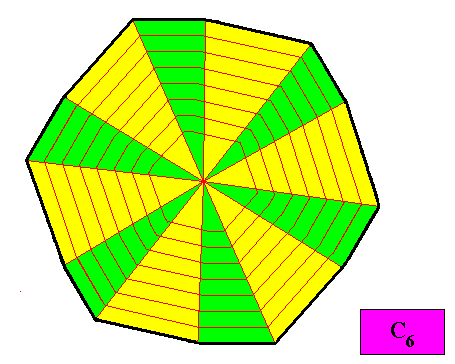
Figure above : A configuration of twelve similar (and alternating) antimers (green, yellow) of the C6 regular gyroid dihexagonal two-dimensional crystal of the previous Figures. The crystal is eupromorphic. Its promorph belongs to the Homogyrostaura dihexamera.
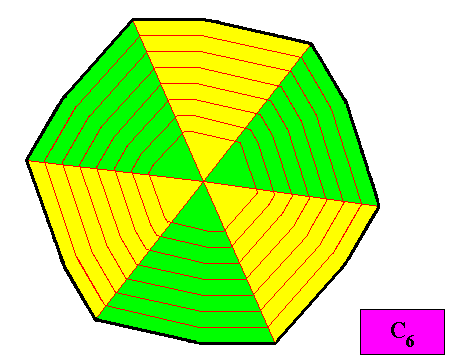
Figure above : A configuration of six equal antimers (green, yellow) of the C6 regular gyroid dihexagonal two-dimensional crystal under investigation. The crystal is non-eupromorphic. Its promorph belongs to the Homogyrostaura hexamera. Compare with the above discussed C3 crystal belonging to the Homogyrostaura ditrimera.
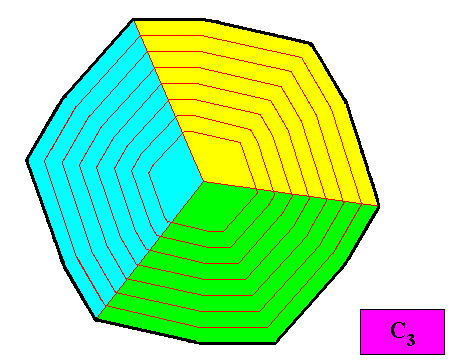
Figure above : A configuration of three equal antimers (green, yellow, blue) of the regular gyroid dihexagonal two-dimensional crystal under investigation. Because of the three equal antimers the 6-fold rotation axis is lost. The intrinsic symmetry of the crystal is now according to the group C3 , and therefore the crystal is meromorphic. It is non-eupromorphic. Its promorph belongs to the Homogyrostaura trimera. Compare with the above discussed C3 crystal also belonging to the Homogyrostaura trimera.
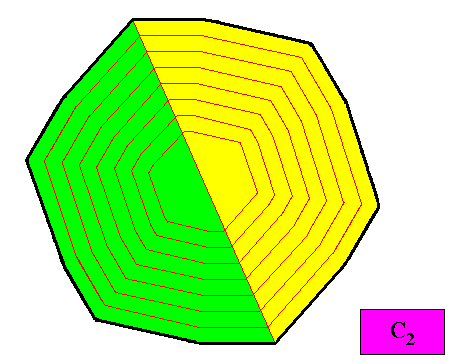
Figure above : A configuration of two equal antimers (green, yellow) of the regular gyroid dihexagonal two-dimensional crystal under investigation. Because of the two equal antimers (as the only antimers being present) the 6-fold rotation axis is lost. Only a rotation of 1800 superimposes the crystal upon itself. There are no other symmetries. The intrinsic symmetry of the crystal is therefore according to the group C2 , and therefore the crystal is meromorphic. It is non-eupromorphic. Its promorph belongs to the Homogyrostaura dimera.
Generally, a crystal with intrinsic shape X can have an intrinsic symmetry that is either the same as the symmetry of that shape (in that case the crystal is holomorphic), or is lower than the symmetry of the shape. But in the latter case the intrinsic symmetry of the crystal is not just lower without qualification. The internal structure of such a crystal ruins some symmetry of the shape, which means that the resulting symmetry group -- expressing the intrinsic symmetry of the crystal -- is a genuine s u b g r o u p of the group expressing the symmetry of the crystal's intrinsic shape. And such a crystal is then meromorphic.
Let's give the group tables of the group C6 and of its three subgroups C1 , C2 and C3 . Before doing so we must consider the following : The group C6 consists of six group elements, viz. six rotations (about the center of some object) :
We will now then give the group tables of the group C6 and its subgroups ( The elements of the latter are indicated by blue coloring).
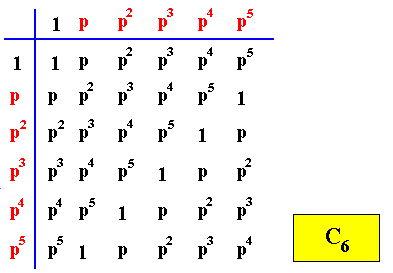
Figure above : Group table of the Cyclic Group of order six, C6 .
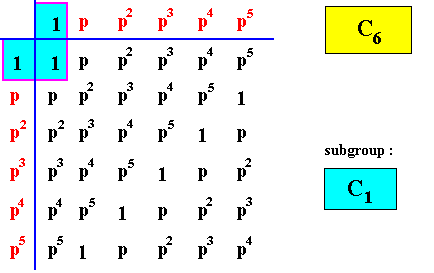
Figure above : Group table of a subgroup of C6 : The Cyclic Group of order one, C1 (the Asymmetric Group).
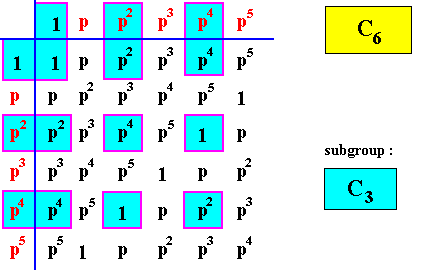
Figure above : Group table of a subgroup of C6 : The Cyclic Group of order three, C3 .
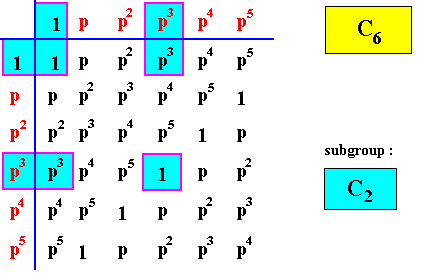
Figure above : Group table of a subgroup of C6 : The Cyclic Group of order two, C2 .
The fact that the intrinsic symmetry of a crystal is either equal to the symmetry of its intrinsic shape or to a symmetry represented by a (genuine) subgroup of the group representing the symmetry of that intrinsic shape, is also made clear by the intrinic symmetries (crystallographic symmetries) that are possible for a quadratic (two-dimensional) crystal, i.e. a crystal with intrinsic shape according to a square, which itself has D4 symmetry. In the next Figure we indicate the possible asymmetries for such a quadratic crystal by arrows. The subgroups of the group D4 (representing the symmetry of the intrinsic shape) are then : C4 , C2 , D2 , D1 and C1 .
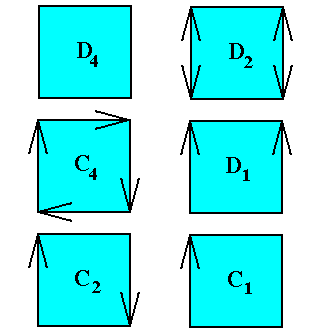
Figure above : Intrinsic symmetries (crystallographic symmetries) possible for a quadratic crystal. Such intrinsic symmetry is either according to D4 , or to one of its subgroups. Asymmetries (lowering the crystal's symmetry with respect to the symmetry of its shape) are indicated by arrows. In real (i.e. three-dimensional) crystals we can see such asymmetries in the form of the direction and distribution of striae on their faces, or in the form of the shapes and symmetries of etch figures on the several faces, or in the form of some other physical or chemical properties of the faces.
This concludes our introduction to the above enumerated complex shapes of two-dimensional crystals, of which in the next documents we're going to investigate more explicitly the promorphs of their holomorphic versions.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XVI.
e-mail : 