

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
While in previous documents (Part V -- XV) we investigated simple (intrinsic) two-dimensional crystal shapes (Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon), an introduction to more complex shapes was given (Part XV Sequel-1, Sequel-2, Sequel-3), and in the next series of Documents we will investigate these more complex (intrinsic) two-dimensional crystal shapes more closely with respect to the plane groups supporting these shapes, the intrinsic point symmetry and the promorph. The complex shapes choosen for study were the following :
Amphitect Gyroid Hexagon
The next two Figures give a holomorphic two-dimensional crystal having as its intrinsic shape that of an amphitect gyroid hexagon. It is holomorphic because the symmetry of its intrinsic shape is the same as the intrinsic (crystallographic) point symmetry of the crystal ( The intrinsic symmetry of an amphitect gyroid hexagonal crystal can be different, namely according to the group C1 , but, because we now only consider holomorphic crystals, we have set the intrinsic symmetry to be that of C2 , i.e. we have set this symmetry to be the same as the symmetry of the intrinsic shape). This point symmetry, as set according to the group C2 , is as such implied by the crystal's plane group symmetry, which is according to the group P2 : the crystal consists of a periodic stacking of parallelogrammatic building blocks each containing in its center a motif with C2 symmetry (In the present case empty building blocks can already represent all by themselves a C2 motif. Nevertheless, a C2 motif is explicitly inserted for reasons of clarity.).

Figure above : Microscopic view of a two-dimensional C2 crystal (plane group P2) with the intrinsic shape of an amphitect gyroid hexagon. Each parallelogrammatic building block contains in its center a C2 motif (black, consisting of two motif units, related to each other by a half-turn about the center of the building block).

Figure above : Same as previous Figure. The six crystal 'faces' are indicated (dark blue lines). Recall that the building blocks are actually very small indeed, resulting in all the crystal faces being perfectly smooth.
Microscopic and Macroscopic View of a (two-dimensional) crystal.
The above two Figures depict a two-dimensional amphitect gyroid hexagonal crystal. And because they also depict as visible entities its building blocks and the motifs they carry, these Figures are meant to give a m i c r o s c o p i c v i e w of the crystal, where "microscopic" here means the atomic or molecular scale. And although a crystal, as the one of the above Figures, with still only so small a number building blocks -- i.e. such a 'young' crystal -- cannot be considered to already have grown into its final shape (i.e. where all faces that can grow themselves out of existence have already done so), the Figure nevertheless is supposed to refer to a fully grown crystal. We must imagine that the Figure is actually (drawn) much more extended, so that it consists of a vastly greater number of building blocks than actually drawn. And if we now -- while contemplating this very large drawing -- recede backwards and look to the depicted crystal from a great distance, we as it were reduce the large image to a normal size again, and in this way now obtain a m a c r o s c o p i c v i e w of the crystal. In this macroscopic view the faces (exterior lines in two-dimensional crystals) are perfectly smooth, and the building blocks and their motifs are not visible anymore. The next Figure gives such a macroscopic view of the crystal depicted above.
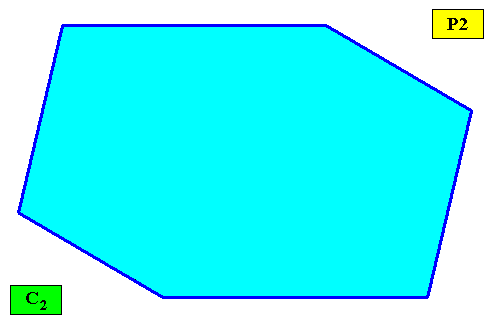
Figure above : Macroscopic view of the above depicted two-dimensional C2 crystal (plane group P2) with the intrinsic shape of an amphitect gyroid hexagon. Building blocks and motifs are not visible. Crystal faces look smooth.
In the following we will, in addition to the microscopic view, also give the macroscopic view of the crystal under investigation.
The next Figure gives the pattern of symmetry elements (with respect to the point symmetry) of the above C2 crystal [Recall that a symmetry element is a geometric entity -- a point, line, axis or plane -- to which a symmetry (a rotation, reflection, etc.) refers]. In the present case this pattern consists of only one two-fold rotation axis.
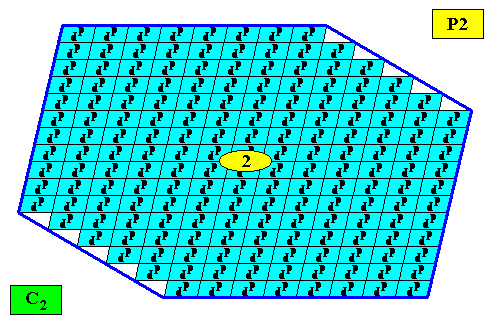
Figure above : Symmetry elements (one 2-fold rotation axis, perpendicular to the plane of the drawing, and indicated by a small yellow ellipse) of the above amphitect gyroid hexagonal C2 crystal.
Three crystallographic Forms are needed to construct the (outline of the) crystal :
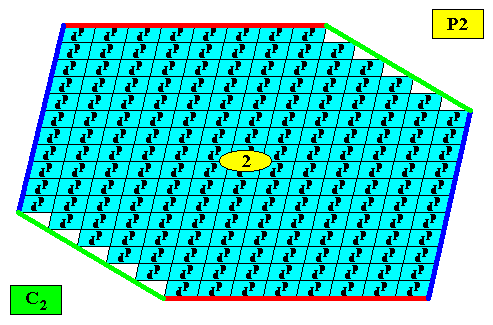
Figure above : Three (crystallographic) Forms are needed to conceptually construct the amphitect gyroid crystal : An initially given face (red) implies another face (red) in virtue of the 2-fold rotation axis. The result is a Form consisting of two faces. It is an open Form and cannot therefore represent a crystal. A second initially given face (dark blue) implies another face (dark blue), resulting in a second Form. A third initially given face (green), finally, implies another face (green) resulting in a third Form. These three Forms together combine to yield the whole crystal.
Possible a n t i m e r c o n f i g u r a t i o n s of the above discussed amphitect gyroid hexagonal crystal with intrinsic symmetry according to the group C2 .
The number and arrangement of a n t i m e r s in a crystal depend on the geometry of its translation-free residue. This residue is the motif as it remains after having everything 'telescoped in', i.e. after elimination of all translational elements in the crystal.
In the above Figures that would mean that the translation-free residue is the following :  . And here we clearly have to do with two antimers. However, in the present document (concerning C2 crystals) we will interpret motifs, as they are drawn in the ensuing Figures, not as motifs just like that, but as only r e p r e s e n t i n g the existence of a C2 motif w i t h a n y p o s s i b l e n u m b e r o f a n t i m e r s .
. And here we clearly have to do with two antimers. However, in the present document (concerning C2 crystals) we will interpret motifs, as they are drawn in the ensuing Figures, not as motifs just like that, but as only r e p r e s e n t i n g the existence of a C2 motif w i t h a n y p o s s i b l e n u m b e r o f a n t i m e r s .
The precise relation of antimers and the internal structure of the crystal will be studied in later Parts.
The next Figure depicts the case of our amphitect gyroid hexagonal C2 crystal having six antimers.

Figure above : A two-dimensional amphitect gyroid hexagonal C2 crystal with six similar antimers (green, yellow, blue) ( The inserted C2 motifs have -- as they are drawn here -- only two antimers (represented by two motif units related to each other by a half-turn), but are, in the present case, meant to represent C2 motifs with six antimers). The Vector Rosette of Actual Growth is here supposed to coincide with the boundary lines of the antimers, letting the crystal be eupromorphic (But also when the vectors of the mentioned Rosette coincide with the median lines of the antimers, or correspond in some other way with the antimers, the crystal is eupromorphic).
As was already discussed earlier, the lines, connecting the crystal's center with its corners together with the colors green, yellow and blue, are supposed to indicate the a n t i m e r s of the crystal. But in fact the only (slight and, as it seems, indirect) macroscopic indications of the presence of antimers (and thus the presence of a definite promorph) in a crystal is the (constancy and definiteness of its) intrinsic shape. There we generally see plane faces (3-D) or straight lines (2-D), and always encounter definite and constant angles between them. Every single crystal, grown in a uniform medium, is a definite polyhedron (3-D) or polygon (2-D), and thus allows for the existence of genuine and definite symmetry and promorph.

Figure above : The two-dimensional amphitect gyroid hexagonal C2 crystal of the above Figures, which, in the present case, is supposed to consist of six similar antimers (green, yellow, blue). The line b is supposed to separate two antimers (blue, green), but many more lines, parallel to it, as for instance, the lines a and c , are totally equivalent to it, except for the fact that line b ends up in a corner, while the others do not. So line b only differs from the many other lines parallel to it by an external feature of the crystal. See also next Figures.
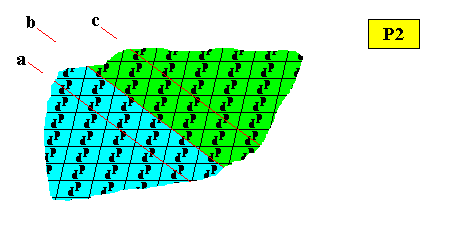
Figure above : Part of the interior of the crystal of the previous Figure containing (parts of) the lines a, b and c .
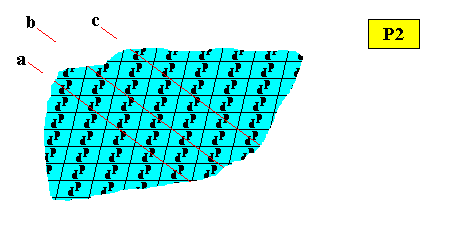
Figure above : Same as previous Figure. Color difference removed.
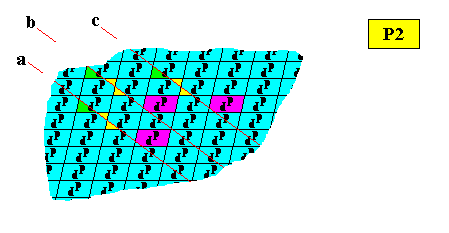
Figure above : Same as previous Figure. One can clearly see that the lines a, b and c are wholly equivalent.
The only straightforward evidence of antimers (and with them of a definite promorph) in crystals, is the symmetry and morphology of the (microscopic) translation-free residue of the crystal, that can be obtained by eliminating all translational features of the crystal. If we do so, while considering only intrinsic symmetry, we in fact go from the crystal's Space Group (3-D) or Plane Group (2-D), describing its total symmetry (including translations), to its Point Group, describing all the non-translational symmetries of the crystal (A non-translational symmetry is a superimposition operation of some object, where at least one point remains where it was, before the operation was applied to that object). The translation-free residue so obtained is a certain configuration of atoms (or, sometimes just one single atom), and as such not only has a certain definite (point) symmetry (representing a crystal class), but also has a definite promorph in so far as antimers can be unequivocally distinguished in this residue. So a promorph of a crystal turns out to be only present microscopically, and if it were not for some macroscopic indications of it (as mentioned above), we would never have devoted so much attention to promorphs of crystals, and not have indicated them macroscopically in our drawings as we have indeed done.
The next Figure again depicts the crystal under investigation (Figure above ) but now with the building blocks and motifs omitted, which in fact means that it now gives a macroscopic view of the crystal (as explained above).
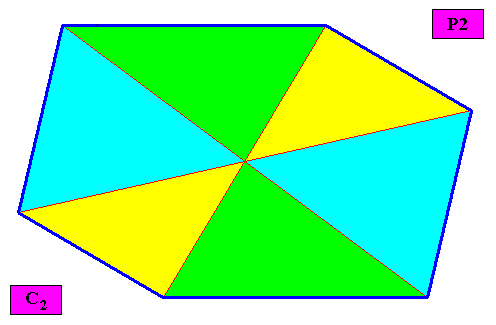
Figure above : Macroscopic view of the above discussed two-dimensional amphitect gyroid hexagonal C2 crystal with six similar antimers (green, yellow, blue).
The promorph of this crystal, viz. the two-dimensional C2 crystal with an intrinsic shape according to an amphitect gyroid hexagon and with s i x antimers, belongs to the (2-dimensional analogue of the) Heterogyrostaura hexamera. This promorph, i.e. the geometric figure fully (and geometrically) representing this promorph, is depicted in the next Figure.
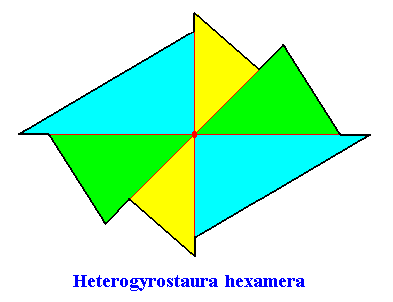
Figure above : Possible representation of the promorph of the above discussed two-dimensional amphitect gyroid hexagonal C2 crystal with six antimers. It is an amphitect gyroid six-fold polygon (six antimers, green, yellow, blue), and as such the two-dimensional analogue of the amphitect gyroid six-fold pyramid, which is the promorph of corresponding three-dimensional crystals or other objects.
To represent this promorph geometrically, we could have chosen a somewhat simpler figure : In fact we can use a drawing of the crystal itself, namely that which gave a macroscopic view of it and its antimers, as was done in the above Figure . We have nevertheless chosen to use the present Figure because it emphasizes very clearly the gyroid nature of the polygon.
The just discussed crystal with six antimers is eupromorphic, because its intrinsic shape indeed suggests the existence of six antimers. If, in other cases, such a crystal has a different number of antimers (but with still the same shape and intrinsic symmetry), then the crystal is non-eupromorphic. The next Figures give examples.
Amphitect gyroid hexagonal C2 crystal with f o u r antimers :

Figure above : A two-dimensional amphitect gyroid hexagonal C2 crystal with four similar antimers (yellow, blue) ( The inserted C2 motifs have -- as they are drawn here -- only two antimers, but are, in the present case, meant to represent C2 motifs with four antimers). The crystal is non-eupromorphic because its intrinsic shape suggests six antimers while in fact there are only four.
Omitting the lattice lines (delineating building blocks) and motifs results in a macroscopic view of this crystal :
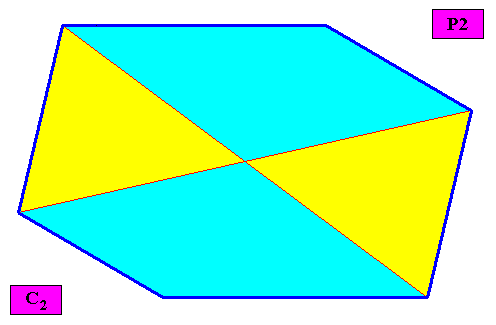
Figure above : Macroscopic view of the two-dimensional amphitect gyroid hexagonal crystal with four antimers (yellow, blue) of the previous Figure.
The promorph of the crystal of the previous Figures is belonging to the (2-D analogue of the) Heterogyrostaura tetramera. This promorph is depicted in the next Figure.
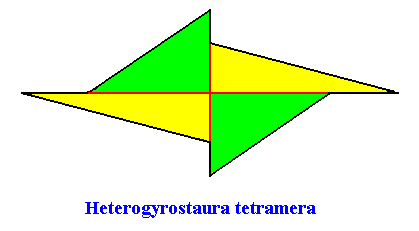
Figure above : The promorph of a two-dimensional amphitect gyroid hexagonal C2 crystal with four similar antimers. It is a 4-fold amphitect gyroid polygon, and as such the 2-D analogue of a 4-fold amphitect gyroid pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects.
Amphitect gyroid hexagonal C2 crystal with t w o antimers :

Figure above : A two-dimensional amphitect gyroid hexagonal C2 crystal with two equal antimers (yellow, blue, related to each other by a half-turn) ( The inserted C2 motifs have -- as they are drawn here -- two antimers, and are, in the present case, also meant to represent C2 motifs with two antimers). The crystal is non-eupromorphic because its intrinsic shape suggests six antimers while in fact there are only two.
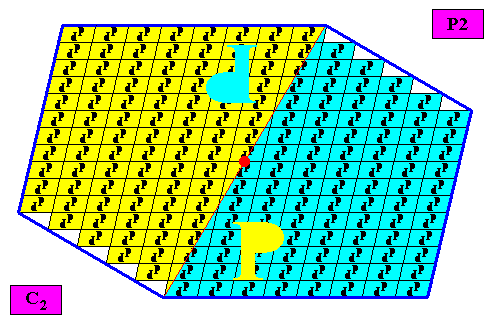
Figure above : Same as previous Figure. Here we let the motifs (consisting of two motif units, related to each other by a half-turn) macroscopically represent the two antimers of the crystal. The axis of the half-turn, relating the two macroscopic motif units, is indicated by a red dot in the center of the crystal. The next Figure depicts the same in a slightly different way.
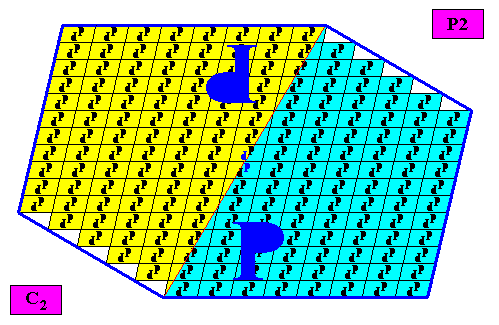
Figure above : Same as previous Figure. In the center of the crystal we can see the microscopic motif (two motif units) as it is represented by the inserted macroscopic motif (two motif units).
The next Figure gives a macroscopic view of the crystal under investigation, by omitting the lattice connection lines (delineating building blocks) and the motifs.
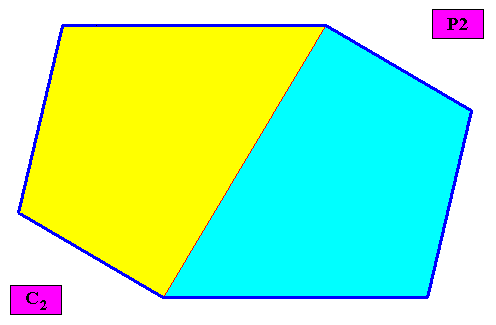
Figure above : Macroscopic view of the two-dimensional amphitect gyroid hexagonal C2 crystal with two equal antimers (yellow, blue, related to each other by a half-turn) of the previous Figures.
The promorph of the crystal of the previous Figures is belonging to the (2-D analogue of the) Heterogyrostaura dimera. This promorph is depicted in the next Figure.
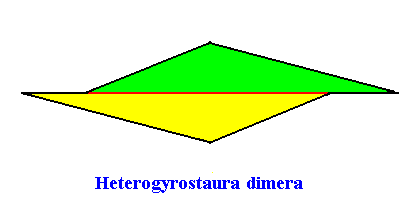
Figure above : The promorph of a two-dimensional amphitect gyroid hexagonal C2 crystal with two equal antimers. It is a 2-fold amphitect gyroid polygon (i.e. an amphitect polygon meant to represent two antimers), and as such the 2-D analogue of a 2-fold amphitect gyroid pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects.
In the next document we will discuss the second crystal shape of our list (given above) , the amphitect gyroid octagon , with respect to intrinsic symmetry (crystallographic symmetry, discussing only holomorphic versions) and promorph.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XVII.
e-mail : 