e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to Introduction to Other Crystal Shapes
In the foregoing documents we have studied and summarized some simple two-dimensional crystal shapes, viz. the Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon, with respect to intrinsic symmetry and promorph. Further (in the previous document) we started an introduction to some other, more complex shapes, which will be studied also with respect to symmetry and promorph, and in the present document we'll continue this introduction. These complex shapes to be discussed are, as has been enumerated earlier, the following :
Holomorphic crystals and Antimers
P r o m o r p h o l o g y is about symmetry and general structure, first of all of natural three-dimensional bodies, like real crystals and organisms. To understand three-dimensional crystals in these respects we study imaginary two-dimensional crystals, which are easier to grasp and to figure, and still reveal most of the structural principles pertaining to three-dimensional crystals. And this brings us in the domain of purely mathematical figures (in fact purely geometrical figures).
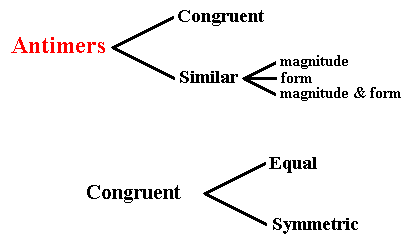
The p r o m o r p h of a natural body, or of some two-dimensional analogue of it, not only expresses its intrinsic symmetry, but also the number and arrangement (configuration) of congruent, or similar structural units (which could be seen as next-lower-level individuals, or subindividuals -- See the Section on Tectology in Second Part of Website ), that are arranged about either the central point, or the central axis, or the central plane of such a body (depending on what kind of body it is), and these structural units are called antimers or counterparts. The antimers of a particular given body can be either congruent, or (just) similar, and when they are congruent they (1) either are totally equal, which means that they can be transformed into each other by a mechanical operation like a translation (shift) or a rotation (In the case of antimers this operation is always a rotation), or (2) they are reflectional symmetric (i.e. they can be transformed into each other only by a reflection which as such is not a mechanical operation). When, on the other hand, they are (only) similar, this means that, although they are not congruent, they (as antimers) are nevertheless not entirely different (dissimilar) from each other with respect to their own shape, symmetry and structure. And this means that they either differ in magnitude only, or differ slightly with respect to morphology (form), or (differ) with respect to both. See next diagram.

Let us illustrate this with holomorphic or meromorphic two-dimensional crystals, having -- to begin with -- the square and some of its derivatives (viz. the ditetragon and the regular gyroid octagon), and the regular octagon, as their intrinsic shape. As we by now know well, the promorph of a natural body expresses intrinsic symmetry and antimers. The latter can be seen as represented by structural elements which we can call m o t i f s. In crystals the latter are parts of the translation-free residue, which itself is some chemical configuration of atoms (or just single atoms). In organisms the motifs representing antimers are macroscopic structural units positioned around the body center.
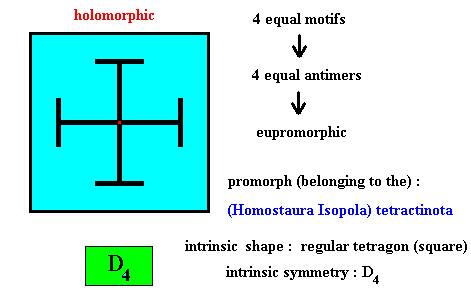
Figure above : Four equal m o t i f s (black) of the translation-free residue of a quadratic two-dimensional crystal with intrinsic symmetry according to the group D4 .
The crystal is holomorphic because the symmetry of its intrinsic shape is the same (D4 ) as its intrinsic symmetry.
It is eupromorphic because its intrinsic shape fully expresses its promorph.
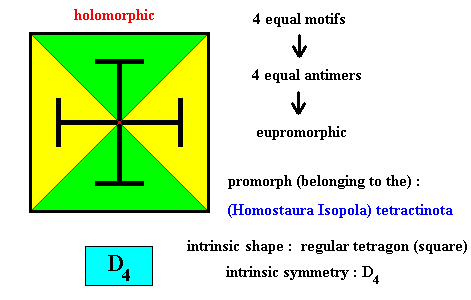
Figure above : Four equal a n t i m e r s (green, yellow) of the translation-free residue of a quadratic two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group D4 .
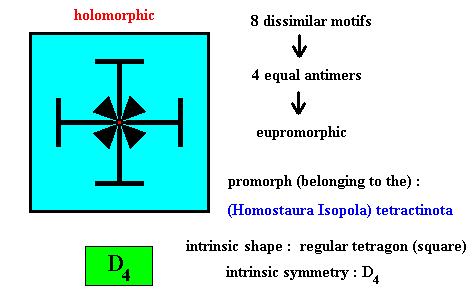
Figure above : Eight dissimilar m o t i f s (black) of the translation-free residue of a quadratic two-dimensional crystal with intrinsic symmetry according to the group D4 .
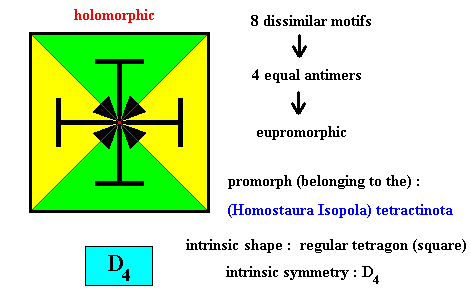
Figure above : Four equal a n t i m e r s (green, yellow) of the translation-free residue of the quadratic two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group D4 .
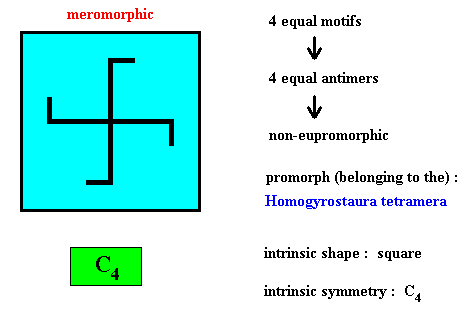
Figure above : Four equal m o t i f s (black) of the translation-free residue of a quadratic two-dimensional crystal with intrinsic symmetry according to the group C4 . The crystal is meromorphic because the intrinsic symmetry (C4 ) is lower than the symmetry (D4 ) of its shape.
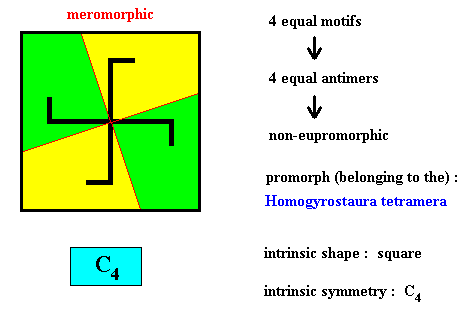
Figure above : Four equal a n t i m e r s (green, yellow) of the translation-free residue of the quadratic two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C4 .
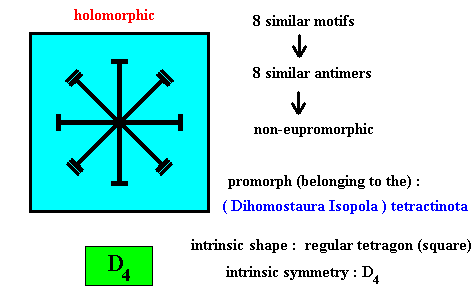
Figure above : Eight similar m o t i f s (black) of the translation-free residue of a quadratic two-dimensional crystal with intrinsic symmetry according to the group D4 . The crystal is non-eupromorphic because its intrinsic shape suggests four equal antimers, while in fact the crystal has eight similar antimers.
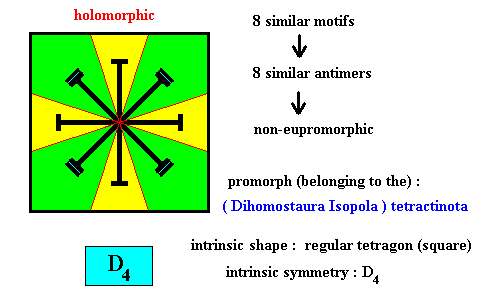
Figure above : Eight similar a n t i m e r s (green, yellow) of the translation-free residue of the quadratic two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group D4 .
The eight motifs of the translation-free residue are each for themselves mirror symmetric. This feature must be reflected (i.e. must be expressed) by the (macroscopically conceived) antimers. And this has been rightly done so in the Figure above.
The next Figure shows an incorrect delineation of the eight antimers :
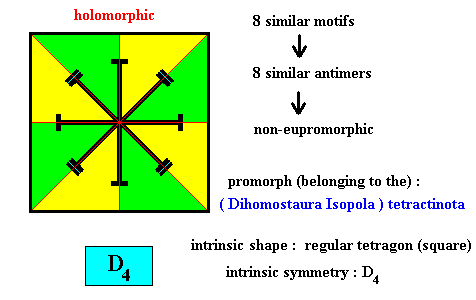
Figure above : Incorrect delineation of the eight similar a n t i m e r s (green, yellow) of the translation-free residue of the quadratic two-dimensional crystal of the previous Figures, with intrinsic symmetry according to the group D4 . The (macroscopically conceived) antimers, as depicted here (green, yellow), are not each for themselves mirror symmetric (with the mirror line passing through the crystal's center), and so do not rightly reflect the morphology of the translation-free residue. Moreover the antimers, as depicted here, are congruent, while the motifs of the translation-free residue are not. They are just similar.
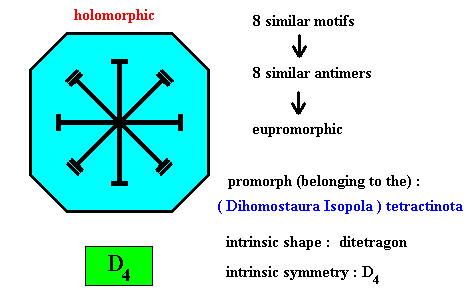
Figure above : Eight similar m o t i f s (black) of the translation-free residue of a ditetragonal two-dimensional crystal with intrinsic symmetry according to the group D4 .
We here encounter a promorph belonging to the Dihomostaura Isopola tetractinota. This name expresses the fact that this particular promorph consists of two Homostaura Isopola tetractinota, i.e. it is a composition of two different (with respect to size) squares, where the D4 symmetry is retained. So the prefix "Di" refers to (all of) homostaura isopola tetractinota, which means that then -- because of Di . . . . . . tetractinota -- 2x4 = 8 antimers are present (expressed by the name of the promorph). This type of promorph has not yet been included in our System of Basic Forms (Promorphological System) in Second Part of Website.
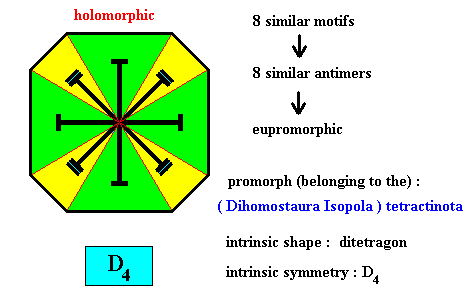
Figure above : Eight similar a n t i m e r s (green, yellow) of the translation-free residue of the ditetragonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group D4 . The areas (green, yellow) of the crystal, which are the antimers, rightly reflect the a l t e r n a t i o n of the m o t i f s : The morphological alternation of the motifs is expressed by the morphological alternation of the areas that are antimers.
The next Figure gives a delineation of the eight antimers (of the crystal of the previous two Figures) that does not reflect or express the alternation of the motifs (except for an alternation of reflected area, rotated area, reflected area, etc.).
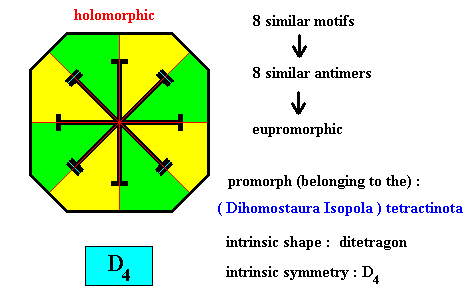
Figure above : Incorrect delineation of the eight antimers of the crystal of the previous two Figures. The (slightly) different morphologies of the motifs is not reflected by (slightly) different morphologies of the areas supposed to be the antimers of the crystal.
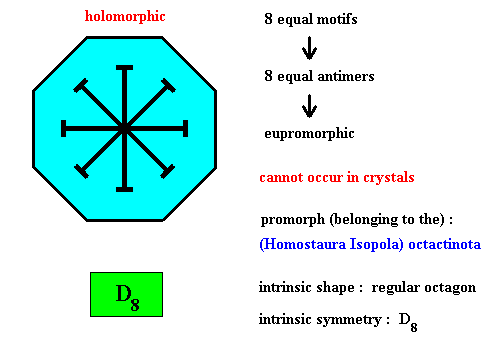
Figure above : Eight equal m o t i f s (black) of a regularly octogonal two-dimensional intrinsic object (not a crystal) with intrinsic symmetry according to the group D8 . The eight equal and regularly radially positioned motifs imply an eight-fold rotation axis to be present. Such an axis cannot occur in crystals (because it cannot occur in any periodic pattern, which crystals are). It can, however, in principle occur in organisms.
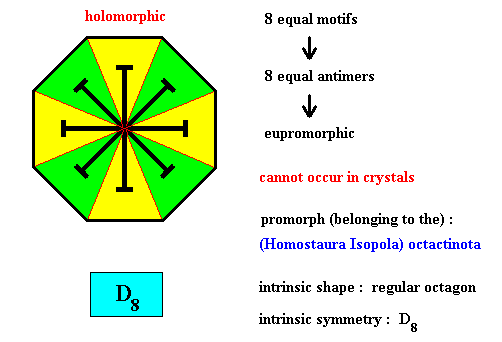
Figure above : Eight equal a n t i m e r s (green, yellow) of the regularly octogonal two-dimensional object (not a crystal) of the previous Figure, with intrinsic symmetry according to the group D8 .
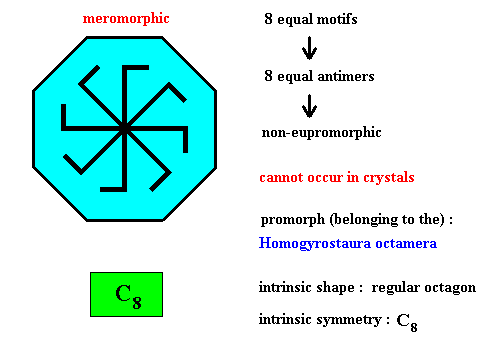
Figure above : Eight equal m o t i f s (black) of a regularly octogonal two-dimensional intrinsic object (not a crystal) with intrinsic symmetry according to the group C8 . The eight equal and regularly radially positioned motifs imply an eight-fold rotation axis to be present. Such an axis cannot occur in crystals. It can, however, in principle occur in organisms.
The object is meromorphic because its intrinsic symmetry (C8) is lower than the symmetry (D8) of its intrinsic shape.
It is non-eupromorphic because its shape suggests eight symmetric antimers, implying the promorph to belong to the Homostaura Isopola octactinata, while in fact the antimers are asymmetric, implying the promorph to belong to the Homogyrostaura octamera .
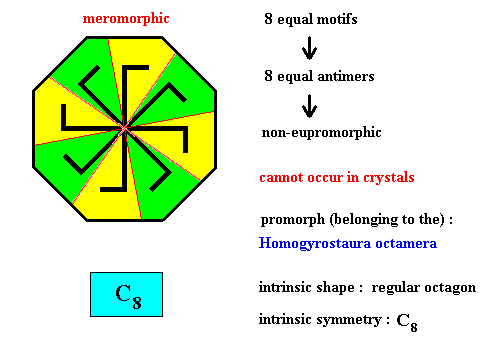
Figure above : Eight equal a n t i m e r s (green, yellow) of the regularly octogonal two-dimensional object (not a crystal) of the previous Figure, with intrinsic symmetry according to the group C8 .
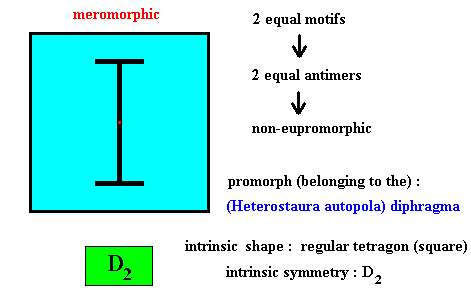
Figure above : Two equal m o t i f s (black) of the translation-free residue of a quadratic two-dimensional crystal with intrinsic symmetry according to the group D2 .
The crystal is meromorphic because its intrinsic symmetry (D2) is lower than the symmetry of its shape (D4 ).
It is non-eupromorphic because its intrinsic shape suggests four equal antimers to be present, while it in fact has only two equal antimers.
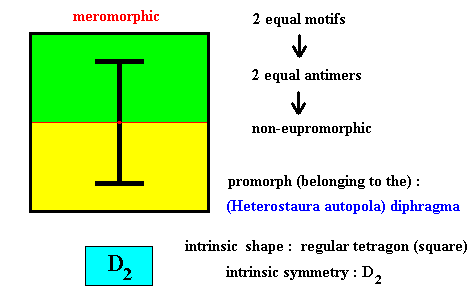
Figure above : Two equal a n t i m e r s (green, yellow) of the translation-free residue of the quadratic two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group D2 .
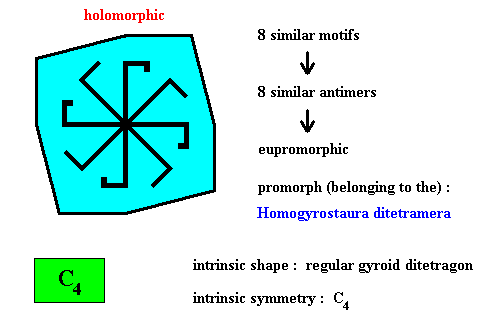
Figure above : Eight similar m o t i f s (black) of the translation-free residue of a four-fold gyroid octogonal two-dimensional crystal with intrinsic symmetry according to the group C4 . The crystal is holomorphic because its intrinsic symmetry (C4) is the same as the symmetry of its shape (C4 ).
Here we encounter a promorph belonging to the Homogyrostaura ditetramera. Let's say something about this name. One might be tempted (when thinking of the Dihomostaura (Isopola) tetractinota considered earlier ) to use the name "Dihomogyrostaura tetramera". But this would be incorrect, because the present promorph does not consist of two homogyrostaura tetramera but of two homostaura tetractinota (namely two squares superimposed upon each other in such a way that all mirror lines disappear). However, the name Dihomostaura tetractinota does, as such, not yet express the absence of any mirror line. This is expressed by the syllable "gyro" in "homogyrostaura". So we transfer the prefix "di" to tetramera and obtain the name Homogyrostaura ditetramera, where "ditetramera" expresses the number of antimers (2x4 = 8) in Homogyrostaura.
This promorph has not yet been included into our System of Basic Forms (Promorphological System) in Second Part of Website.
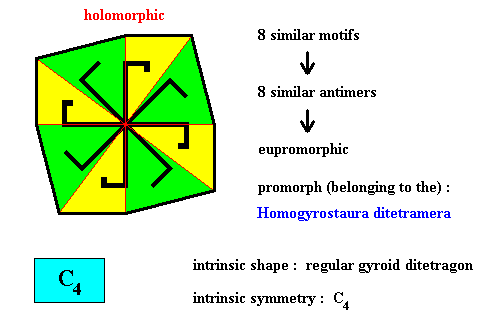
Figure above : Eight similar a n t i m e r s (green, yellow) of the translation-free residue of the four-fold gyroid octogonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C4 .
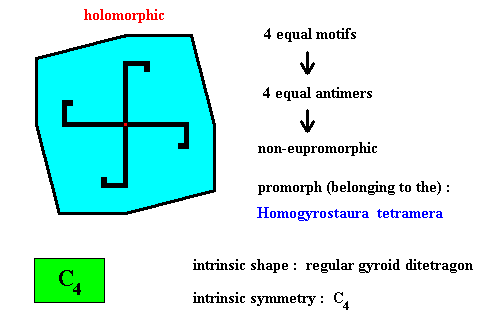
Figure above : Four equal m o t i f s (black) of the translation-free residue of a four-fold gyroid octogonal two-dimensional crystal with intrinsic symmetry according to the group C4 . The crystal is holomorphic because its intrinsic symmetry (C4) is the same as the symmetry of its shape (C4 ). It is not eupromorphic because the shape suggests eight alternating antimers, while in fact there are four equal antimers.
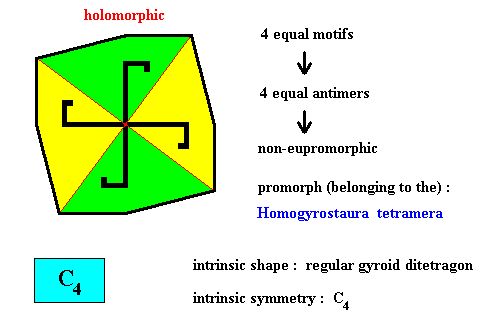
Figure above : Four equal a n t i m e r s (green, yellow) of the translation-free residue of the four-fold gyroid octogonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C4 .
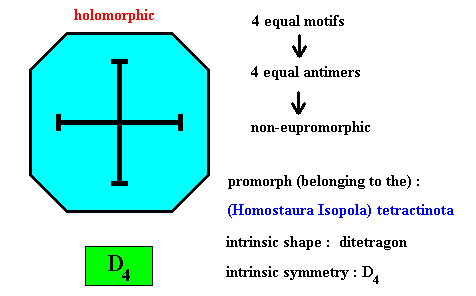
Figure above : Four equal m o t i f s (black) of the translation-free residue of a ditetragonal two-dimensional crystal with intrinsic symmetry according to the group D4 . The crystal is holomorphic because its intrinsic symmetry (D4) is the same as the symmetry of its shape (D4 ). It is not eupromorphic because the shape suggests eight alternating antimers, while in fact there are four equal antimers.
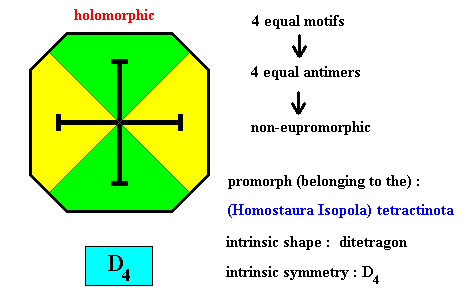
Figure above : Four equal a n t i m e r s (green, yellow) of the translation-free residue of the ditetragonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group D4 .
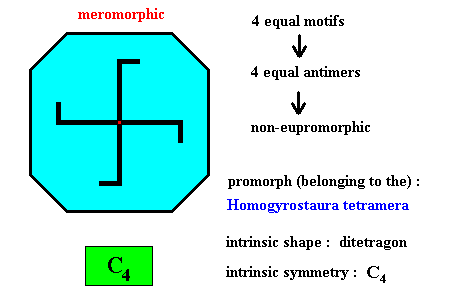
Figure above : Four equal m o t i f s (black) of the translation-free residue of a ditetragonal two-dimensional crystal with intrinsic symmetry according to the group C4 . The crystal is meromorphic because its intrinsic symmetry (C4) is lower than the symmetry of its shape (D4 ).
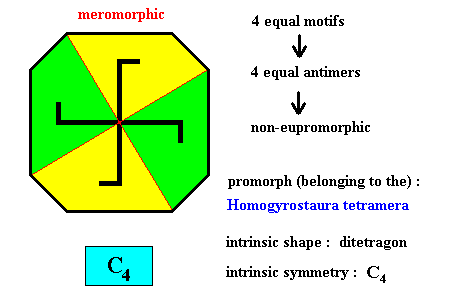
Figure above : Four equal a n t i m e r s (green, yellow) of the translation-free residue of the ditetragonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C4 .
The relation of the antimers being congruent or similar, equal or dissimilar, to the promorph is further illustrated by flattened figures, namely by some derivatives of the rectangle which have -- as shapes -- C2 symmetry. Because of the flattened shape of such (two-dimensional) crystals, the motifs are expected generally not to be equal to each other : Only where no more than two motifs are present, (can we say that) all the motifs are necessarily equal, they relate to each other by a half-turn (and are therefore equal) and as such represent equal antimers. Where more than two motifs are present (their number must be even), these motifs are only equal within pairs, while these pairs can differ among themselves (i.e. from one pair to another) considerably. So it is clear that we, when considering differences in size of the motifs of such (C2) crystals, we must, when evaluating their state of difference, take into account the differences of available space in which these motif reside, and assess the corresponding antimers accordingly.
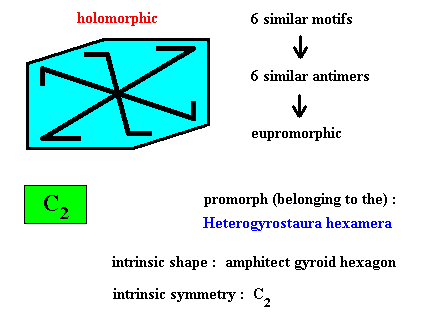
Figure above : Six similar m o t i f s (black) of the translation-free residue of an amphitect gyroid hexagonal two-dimensional crystal with intrinsic symmetry according to the group C2 . The crystal is holomorphic because its intrinsic symmetry (C2) is the same as the symmetry of its shape (C2 ).
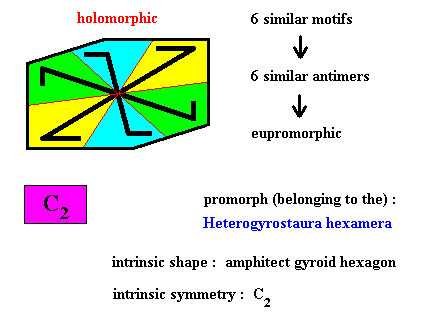
Figure above : Six similar a n t i m e r s (green, yellow, blue) of the translation-free residue of the amphitect gyroid hexagonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C2 .
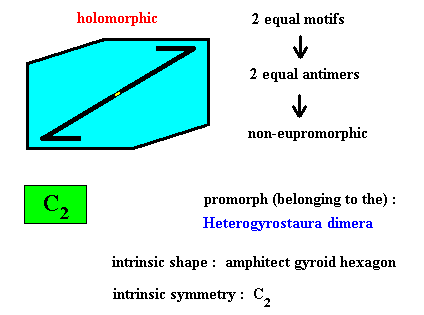
Figure above : Two equal m o t i f s (black) of the translation-free residue of an amphitect gyroid hexagonal two-dimensional crystal with intrinsic symmetry according to the group C2 . The crystal is holomorphic because its intrinsic symmetry (C2) is the same as the symmetry of its shape (C2 ). The crystal is non-eupromorphic because the shape suggests six antimers, while in fact there are only two.
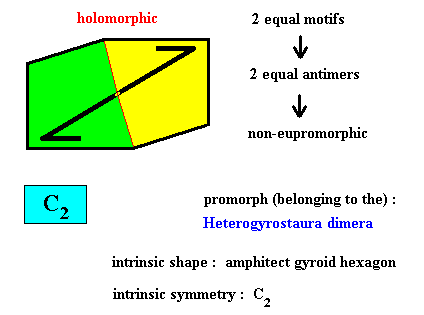
Figure above : Two equal a n t i m e r s (green, yellow) of the translation-free residue of the amphitect gyroid hexagonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C2 .
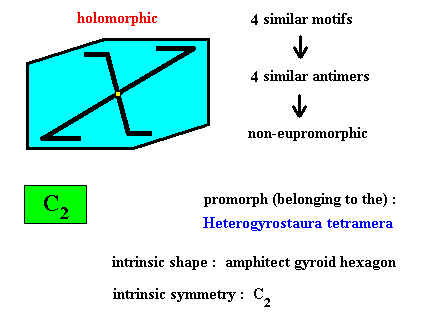
Figure above : Four similar m o t i f s (black) of the translation-free residue of an amphitect gyroid hexagonal two-dimensional crystal with intrinsic symmetry according to the group C2 . The crystal is holomorphic because its intrinsic symmetry (C2) is the same as the symmetry of its shape (C2 ). The crystal is non-eupromorphic because the shape suggests six antimers, while in fact there are only four.
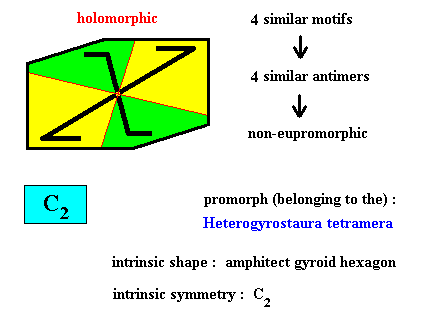
Figure above : Four similar a n t i m e r s (green, yellow) of the translation-free residue of the amphitect gyroid hexagonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C2 .
Precisely the same as has just been established for the above depicted flattened crystal, can be said about a more general amphitect gyroid hexagonal crystal, namely one lacking right angles, as the next two Figures show.
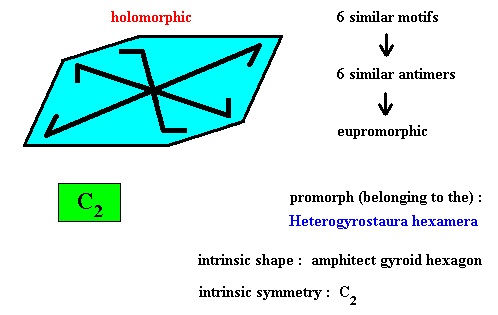
Figure above : Six similar m o t i f s (black) of the translation-free residue of an amphitect gyroid hexagonal two-dimensional crystal with intrinsic symmetry according to the group C2 . The crystal is holomorphic because its intrinsic symmetry (C2) is the same as the symmetry of its shape (C2 ).
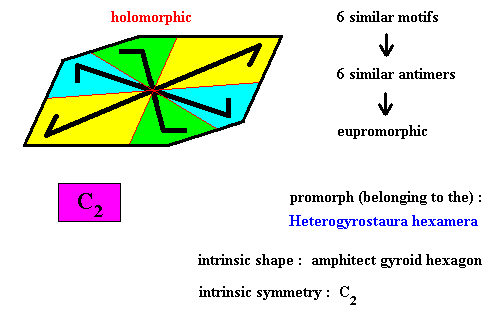
Figure above : Six similar a n t i m e r s (green, yellow, blue) of the translation-free residue of the amphitect gyroid hexagonal two-dimensional crystal of the previous Figure, with intrinsic symmetry according to the group C2 .
This concludes our consideration about the relation between the congruency, equality, similarity and dissimilarity of the antimers in a natural body (a crystal or an organism) and the promorph.
The next Figures are going to illustrate that the above enumerated shapes are indeed p o s s i b l e in two-dimensional crystals, even when growth of them is prolonged indefinitely, i.e. that the faces involved in these shapes will not grow out of existence. The latter depends on certain intrinsic conditions involving the relative growth rates and direction of the faces making up these shapes.
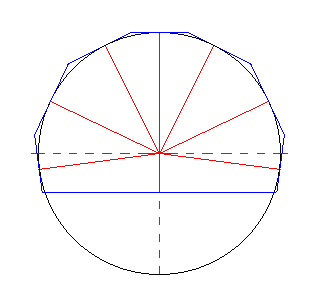
Figure above : A case of a two-dimensional crystal with relative growth rate vectors, (solid red lines radiating from a center) of faces (blue). These relative growth rate vectors are perpendicular to the faces of which they indicate their growth. Seven of these are equal (indicated by the circle) but in different directions. One of them is short, indicating a lower growth rate as compared to that of the other faces. The vectors are symmetrically arranged with respect to a mirror line.
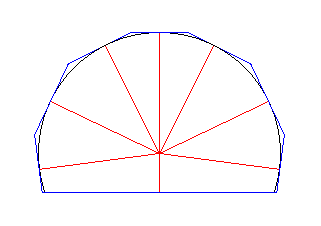
Figure above : The pattern of the eight faces as a result of the relative growth rate vectors as indicated in the present and previous Figure.
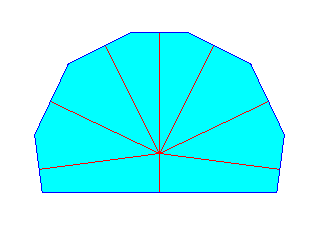
Figure above : Resulting (initial) crystal and its shape in virtue of the above given relative growth rate vectors. The shape is that of a bilateral octagon as one of the crystal shapes to be discussed.
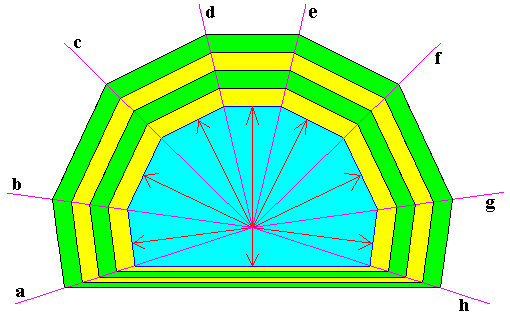
Figure above : A two-dimensional crystal, intrinsically shaped as a bilateral octagon. The eight arrows are the vectors of relative growth rate. Prolonged growth (phases) of the initially present crystal (blue) is indicated by newly appearing layers (indicated as yellow, green, yellow, green) onto the crystal. As one can see, especially by inspecting the lines a, b, c, d, e, f, g and h , the possible faces that are drawn will persist, no matter how far growth will proceed.
We have constructed the crystal such that the growth rates of seven of its faces (viz. one upper horizontal face and six oblique faces) are equal. We have done this by drawing equal growth rate vectors (red lines with arrow heads). The corresponding faces are then perpendicular to these vectors. So with respect to the equal growth rates we can indicate several bi-triangles (i.e. areas consisting of two triangles) indicated by yellow coloring. Each of such a bi-triangle in fact consists of two right-angled triangles. And because of the common hypotenusae and the equality of two other sides (the equal growth rate vectors) the two right-angled triangles making up one bi-triangle are congruent. And from this it follows that the marked (i.e. marked in the Figure) acute angles must be equal. This equality of angles then holds for every bi-triangle associated with equal growth vectors. An it is this equality of the mentioned angles that guarantees that the layers of the crystal do not change width when they pass from one direction to the other. And this indeed neatly expresses the equal growth rate of the relevant faces of the crystal.
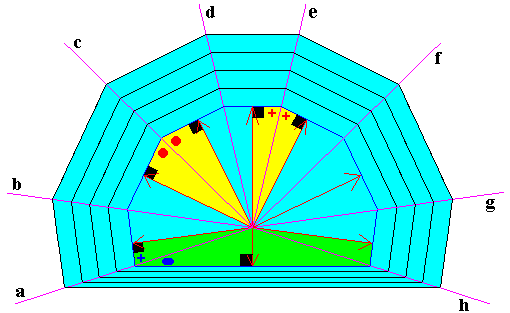
Figure above : Growth layers of equal width, in virtue of the equality of angles (marked). And because the relevant angles in the bottom section (green colored bi-triangles) of the crystal are not equal, the layers do change width, indicating a different growth rate of the bottom face (which is lower than that of the other faces).
The next Figure indicates the eight antimers of the above crystal, which is supposed to be an eupromorphic crystal.
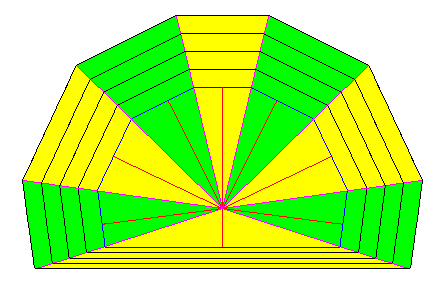
Figure above : The eight antimers (green, yellow) of the crystal of the previous Figure. Here we assume that the boundaries of the antimers go through the corners of the crystal, which means that these boundaries coincide with the Vector Rosette of Actual Growth of the crystal. In the present case we have eight faces with growth rates such that they balance each other (despite some difference between them), resulting in the prolonged coexistence of these eight faces. In this way they point to the existence of a corresponding number of a n t i m e r s, in the present case eight.
The pattern of relative growth rates of the possible faces of a given crystal determines the crystal's intrinsic shape. It is therefore important to ruminate for a while about the phenomenon of crystal growth.

Figure above : Besides the chemical composition (chemical aspect presented to the environment) the growth rate of a face is inversely proportional to the number of lattice nodes that are encountered by that face.
The figure shows a primitive rectangular point net (The argument to come also applies to a 3-D point lattice). The intersections of the lines making up the rectangular cells (meshes) are lattice nodes (These nodes represent the locations of chemical units).
Four possible faces are indicated by a, b, c and d. The arrows indicate their respective directions of growth (At the same time there is also a corresponding growth in the opposite directions of the arrows). Generally the slowest growing faces become the most prominent faces on the crystal. The fastest growing faces quickly grow themselves out of existence.
This Figure -- which concerns the growth rates of faces -- only pays attention to one feature of the atomic aspect (The atomic aspect determines the growth rate of a face), namely the density of nodes encountered by the crystal face in question (The other feature refers to the chemical composition of the crystal).
The slowest growing face (on the basis of the feature mentioned) is face b , because here the density of nodes (encountered by that face) is highest.
Next comes face c, and then a.
The fastest growing face is d.
So the faces b and c will become the most prominent faces. The other faces will eventually grow themselves out of existence.
Because the faces b and c are perpendicular to each other the faster growing face of these two, namely c, will not grow itself out of existence. It keeps on growing, and keeps on growing faster than b, so the crystal will finally adopt a rectangular shape with its longest dimension oriented vertically.
Of course a crystal grows faster when there is a greater supply of material. And when this greater supply comes from one particular direction the crystal shape will be distorted, resulting in an extrinsic shape of the crystal. However, in the present discussion we only refer to relative growth rates when comparing the faces of a single individual crystal, growing in a uniform environment, resulting in the crystal's intrinsic shape.
In the Figure above we have set the growth rates of all faces (but one) equal. They do not therefore grow themselves out of existence when growth is prolonged. Also the lower horizontal face will not disappear because its growth rate is lower than that of the other faces.
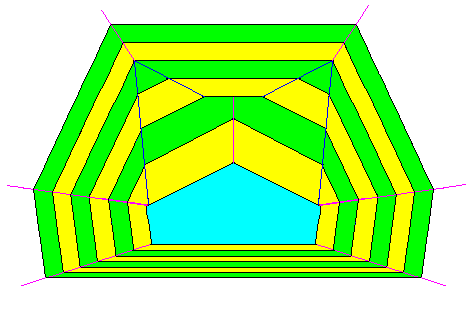
Figure above : Two faces of the above depicted octogonal (D1) crystal grow much faster than all the other faces. They will finally disappear. The blue area is supposed to represent an initially present crystal seed from which growth proceeds. The next Figure is the same, but without auxiliary lines.

Figure above : Same as previous Figure. A two-dimensional crystal of which two possible faces grow much faster than all its other faces. They will finally disappear, resulting in a hexagonal D1 crystal (bilateral hexagon) instead of an octogonal D1 crystal (bilateral octagon).
Remark : One should not take this drawing too seriously, because I am not entirely sure about its correctness. It only serves to illustrate the disappearance of the two fast growing faces.
In the following we study some other and, generally, more simple cases of two-dimensional crystals and the retention or disappearance of certain faces.
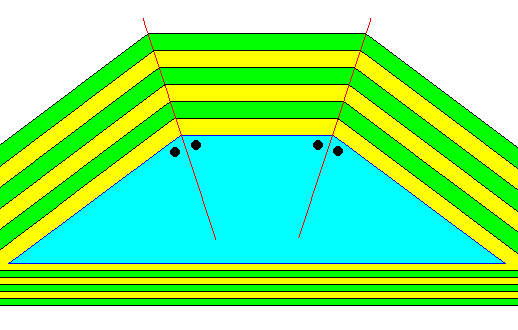
Figure above : Growth of a two-dimensional crystal having as its intrinsic and persistent shape that of the isosceles trapezium. Oblique layers (green, yellow) change to horizontal layers (green, yellow) which again change to oblique layers. If the lines (red), connecting the points of these directional changes of all the layers involved, bisect the top angles of the trapezium (indicated by black dots), the layers will not change their width as they go from the oblique direction to the horizontal direction and then to the oblique direction again. This means that we have depicted e q u a l g r o w t h r a t e s of the two oblique faces and the top horizontal face. And this implies that the top horizontal face will not disappear when growth is prolonged. In addition to this it is clear from the drawing that the bottom horizontal face, to which we have assigned a lower growth rate, will also not disappear when growth is prolonged (See also next Figure). And this means that the crystal's shape, as being an isosceles trapezium, will persist throughout growth, and will then represent the intrinsic shape of the crystal.
The next Figure depicts the complete right half of the crystal of the previous Figure, to show that also the other faces (oblique and bottom horizontal face) do not vanish during prolonged growth of the crystal.
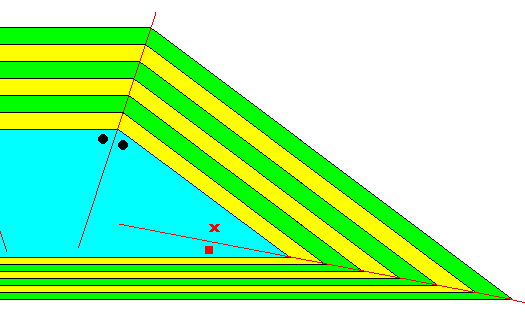
Figure above : Same crystal as in previous Figure. Complete right half revealed. All four faces are persistent during further growth of the crystal.
The next Figures illustrate the case where the growth rate of the upper horizontal crystal face of our (initially) trapezoid crystal is significantly higher than that of its adjacent faces. We have constructed this by not letting the lines (red), connecting the points of the directional changes of all the involved layers, bisect the upper two angles of the trapezium. This unequality of the angles is indicated by marks in the Figure. The effect of the higher growth rate of the top face with respect to that of its adjacent faces, together with the fact that the latter are tapering, is that the top face grows out of existence, i.e. when growth is prolonged it will eventually disappear, and this process necessarily results in a crystal having as its intrinsic shape, not an isosceles trapezium, but an isosceles triangle.
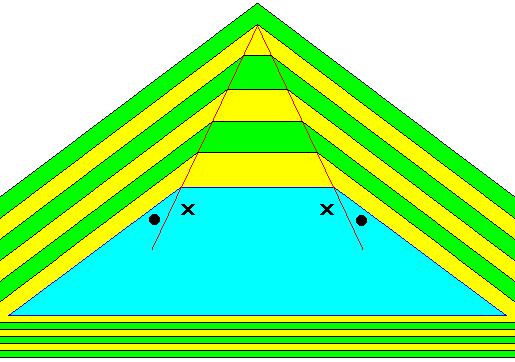
Figure above : Growth of a two-dimensional initially trapezoid crystal (blue), though having as its intrinsic and persistent shape that of the isosceles triangle. Oblique layers (green, yellow) change to horizontal layers (green, yellow) which again change to oblique layers (green, yellow). The lines (red), connecting the points of these directional changes of all the layers involved, do, in the present case not bisect the top angles of the trapezium (indicated by black marks). The layers will therefore change their width as they go from the oblique direction to the horizontal direction (they get wider) and then to the oblique direction again (they get thinner again). This means that we have depicted u n e q u a l g r o w t h r a t e of the top horizontal face as compared to the two adjacent oblique faces. In fact the top face grows faster. And, together with the fact that the two adjacent faces taper, this implies that the top horizontal face will eventually disappear when growth is prolonged. In addition to this it is clear from the drawing that the bottom horizontal face, to which we have assigned a lower growth rate, will not disappear when growth is prolonged. And all this means that the crystal's shape becomes an isosceles triangle, and this new shape will then persist throughout growth, and represents the intrinsic shape of the crystal.
The next Figure depicts the same crystal, but now without auxiliary features.

Figure above : Same as previous Figure ( Two-dimensional triangular crystal, partially depicted). Auxiliary features omitted.
In the next Figure we follow the accomplished growth further back towards the crystal's center, meaning that we consider its growth stages from a still smaller initial crystal (blue in the Figure).
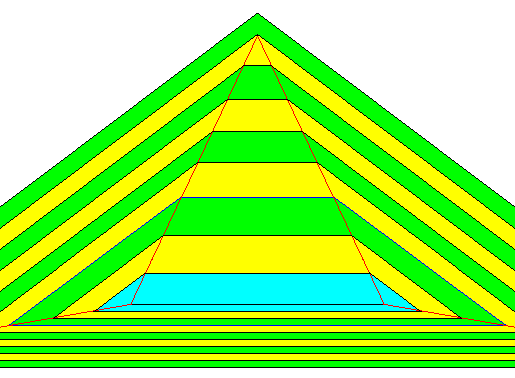
Figure above : Same as previous Figure ( Two-dimensional triangular crystal, partially depicted). Earlier growth stages (also) indicated. Initial crystal indicated by blue coloring.
The next Figure is the same as the previous one, but now with the auxiliary lines omitted.

Figure above : Same as previous Figure : Two-dimensional triangular crystal (partially depicted). Growth stadia indicated, auxiliary lines omitted.
The intrinsic shape of the present two-domensional crystal is that of an isosceles triangle. There are three persistent faces. In an eupromorphic crystal this could indicate the presence of t h r e e antimers. But because a triangle is the simplest possible figure bounded by straight lines in two-domensional space, the so-called symplex figure of 2-D space, a third side, in addition to two, is always necessary in two-dimensional space to obtain a polygon. So the number of antimers based on the number of balanced (i.e. persistent) crystal faces can be three or two. The next Figure depicts the case of three antimers ( This number, i.e. either two or three) is dependent on the morphology of the translation-free residue) of our present triangular crystal.
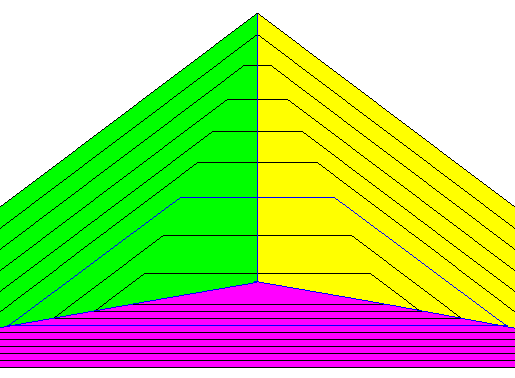
Figure above : Three antimers (green, yellow, purple) of the present triangular two-dimensional crystal (partially depicted).
The case of two antimers is depicted in the next Figure :
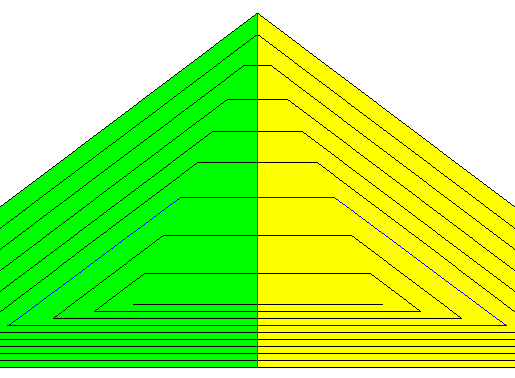
Figure above : Two antimers (green, yellow) of the present triangular two-dimensional crystal (partially depicted).
Having investigated the bilateral octagon, the isosceles trapezium and the isosceles triangle as to their possible and persistent existence as two-dimensional crystals, we now consider the six-fold amphitect polygon in the same respect.
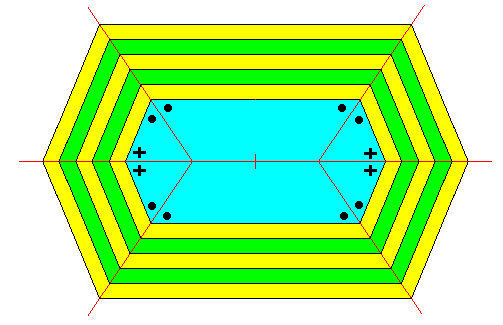
Figure above : A two-dimensional crystal having as its intrinsic shape that of the 6-fold amphitect polygon (amphitect hexagon). It is assumed that the growth rates of all six faces is the same, resulting in a succession of layers (yellow, green, yellow, etc.) with the same width (geometrically guaranteed by the equality of the angles as indicated).
The next Figure omits all auxiliary features.
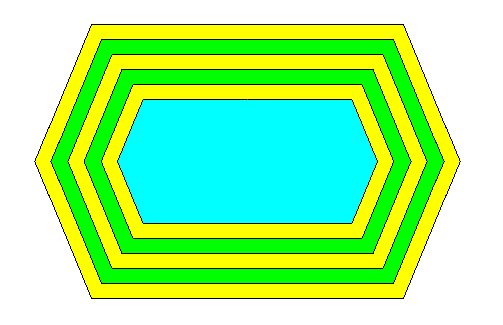
Figure above : Same as previous Figure. Two-dimensional crystal with the 6-fold amphitect polygon as its intrinsic shape. Growth rate of all six faces is set equal.
If the crystal is an eupromorphic crystal, then the six antimers could be conceived as follows :
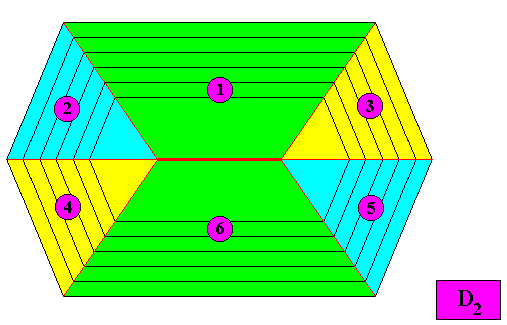
Figure above : Suggestive configuration of the six antimers of the eupromorphic crystal considered just above.
The just depicted configuration of the six antimers is not, however, compelling, nor evident, because the boundary lines, each connecting points where the layers change direction (red lines in the above Figure) only relate to the development of f a c e s , i.e. they only refer to external features, not to internal structure as the next two Figures show.
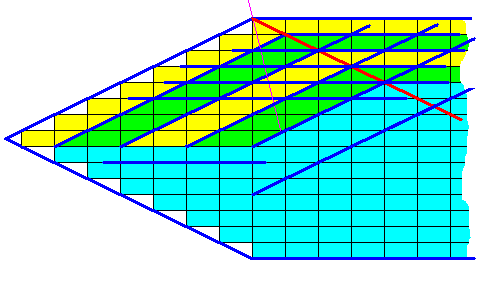
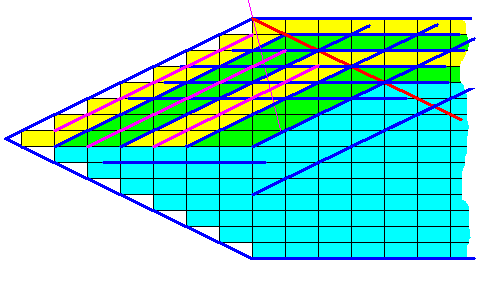
Figure above : Part of a 2-dimensional crystal. Four actual (crystal) faces shown (exterior blue lines). The drawing shows that potential faces (blue lines within the crystal body) can be anywhere in the crystal, they are not restricted to certain areas of the crystal [In the present drawing the width of the oblique layers (yellow, green, yellow) is different from that of the horizontal layers (yellow, green, yellow), but for this we can still imagine equal growth : the thicker layer can be supposed to deposit slower (i.e. deposit at a lower rate), precisely neutralizing the extra gain in growth rate obtained from its being thicker than the other layer. And so the two faces could still have the same net growth rate (in terms of increase of distance from the center of growth). And because in the present drawing the layers change their width when changing direction, the dividing line (thick red line) connecting the points where these directional changes take place, does not bisect (i.e. divide into two equal angles) the angle between the oblique and horizontal faces (it would be the thin purple line if it did), but implies different angles]. So the horizontal potential faces exist at both sides of the dividing line (thick red line), and also the oblique potential faces exist at both sides of this line, which indeed means that this dividing line is not an internal structural feature of the crystal, and is therefore not necessarily representing a boundary between antimers.
The l a y e r s of the crystal depicted in the previous Figure, especially the oblique layers, can also be indicated -- as layers -- differently. Let's think of it for a while : In the Figure mentioned the oblique layers, as they were interpreted as layers, at least contained w h o l e building blocks, just like the horizontal layers, and this looks as a perfectly natural state. However the oblique layers, so conceived, do not as such express successive incrementive increase of distance of the oblique actual face from the growth center, because they o v e r l a p (the rectangular building blocks neatly lock onto each other), as the next Figure shows (strong purple lines).
The successive increase by genuine increments of distance is, as it seems, better expressed by the area between two consecutive possible faces (or between the actual face and the immediately backwards following possible face). The next two Figures show this alternative interpretation of a layer (of growth).
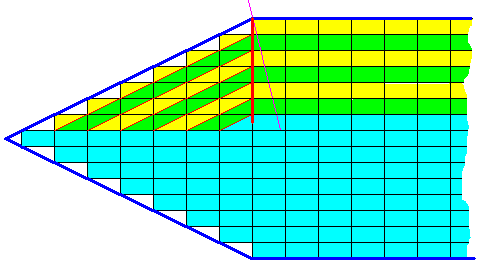
Figure above : Same crystal fragment as in previous Figure. Alternative interpretation of growth layers. The strong red line connects the points where the layers change direction. This line does not bisect (into two equal halves) the angle between the oblique and horizontal faces (it would be the thin purple line if it did) causing the layers on both sides of it to be of slightly different width. And, as in the above case, we could imagine the thicker layer to be deposited at a slightly lower rate precisely neutralizing the surplus of growth rate in virtue of its being somewhat thicker. Or, equivalently, we could imagine the thinner layer (which is the oblique layer) to deposit slightly faster precisely compensating (in the net average result) for the deficiency of distance growth due to its smaller width. But the latter consideration exposes some problem inherent in this alternative interpretation : The thinner 'layer' of the two, viz. the oblique layer, is thus seen as possessing a definite physical or chemical property. And this exposes the unnaturalness of the oblique layer so conceived, because such a 'layer' only consists of half building blocks instead of whole ones. So if we start from the assumption that the crystal grows by adding more and more of the depicted rectangular building blocks, the present interpretation of a g r o w t h l a y e r is more or less unnatural, leaving the original interpretation to be preferred.
The next Figure demonstrates that also the alternative interpretation of layers just discussed shows that the dividing line (strong red line in the Figure) is not an internal structural feature of the crystal, because the same possible crystal face extends on both sides of it. So also in this interpretation of a growth layer the dividing line does not necessarily represent the boundary between antimers.
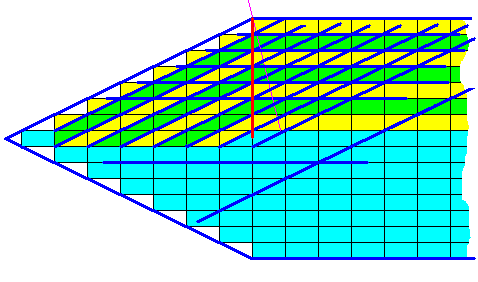
Figure above : Directions (strong dark blue lines) of actual and possible crystal faces and the alternative interpretation of growth layers (green, yellow, green, etc.).
The next Figure shows a case where the angle of the boundary or dividing line (red), separating directions of actually developing faces, neatly guarantees that the oblique and horizontal layers as they have been deposited onto the crystal have equal width, and so reflecting equal growth of the corresponding faces, resulting in their persistence. Nevertheless the oblique and horizontal potential faces (blue) could be anywhere in the crystal. They are not restricted to separated areas (one face direction in one area -- at one side of the dividing line -- and the other face direction in another area -- at the other side of the dividing line).
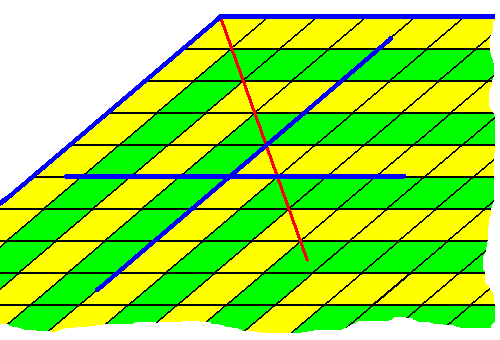
Figure above : Growth of a two-dimensional crystal by successive deposition of layers (yellow, green, yellow, ...) of equal width. A red line indicates the boundary between different directions of faces, and exactly bisects the angle between the facial directions into two equal angles. Nevertheless potential faces having one and the same direction can be anywhere in the crystal, i.e. on both sides of the boundary line, meaning that this boundary line is not an internal structural feature of the crystal, and can therefore not be considered as necessarily representing a boundary between antimers.
The next Figure gives a possible configuration of the six antimers of the six-fold amphitect D2 crystal, discussed earlier , such that they all meet in one point (viz. the center of the crystal).
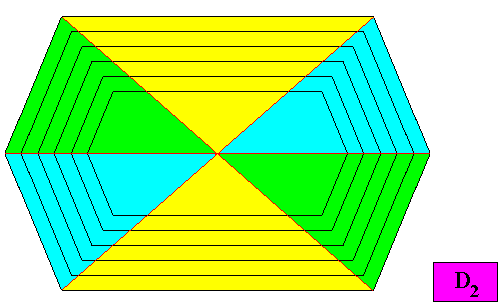
Figure above : The six antimers (green, yellow, blue) of the two-dimensional crystal with an intrinsic shape according to a six-fold amphitect polygon discussed earlier.
With a crystal like this, namely a D2 crystal, there is something remarkable with respect to the boundaries of the antimers as just drawn in the above Figure :
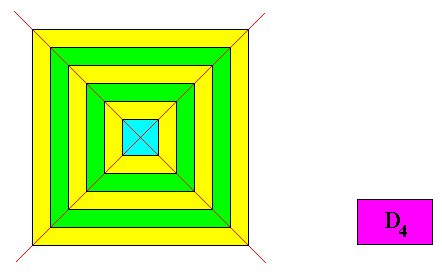
While in C3 , D3 , C4 , D4 , C6 and D6 crystals the direction of the vectors of the Vector Rosette of Actual(ly accomplished) Growth, represented by lines originating at the center of the crystal and going through its corners, remains constant during growth, as the next Figure shows for a D4 two-dimensional crystal,
in intrinsically elongated crystals, like our 6-fold amphitect polygon discussed above, some vectors of the Vector Rosette of Actual Growth gradually change direction as growth proceeds. See next Figure.
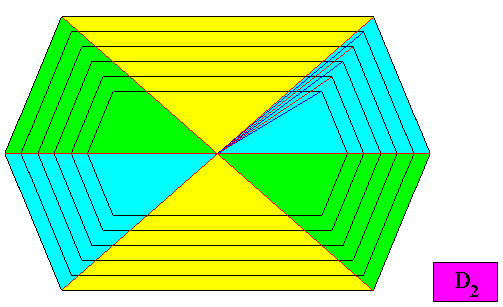
At each growth stage of such a crystal we must take the line originating at the center of the crystal and passing through a corner of the crystal as it is at that particular growth stage, as indicating maximally accomplished local growth, where the elongated shape of the crystal causes this vector to gradually change direction as growth proceeds, as soon as this particular vector does not lie in the direction of the elongation or perpendicular to it.
Now we will discuss another crystal shape of our list , namely that of a two-dimensional C2 crystal with six faces. Its intrinsic shape is that of a six-fold amphitect gyroid polygon (amphitect gyroid hexagon).
The next Figure shows a C2 crystal as specified above. It indicates the successive 'rings' or zones (green, yellow, blue, yellow, green) of (microscopic) building blocks being added during growth, finally resulting in a crystal having the mentioned shape.
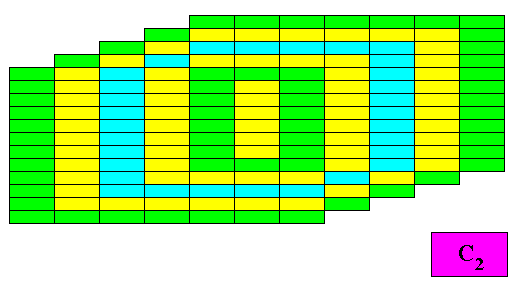
Figure above : A crystal having as its intrinsic shape the six-fold amphitect gyroid polygon grows by adding rectangular building blocks.
The general outline of the present crystal in terms of actual crystal faces is shown in the next Figure.
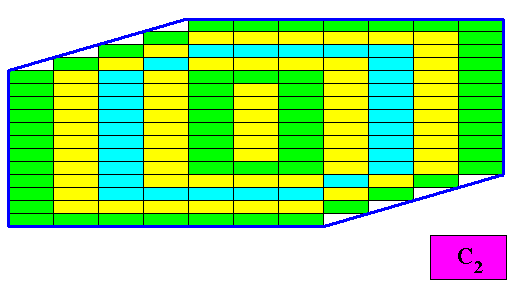
Figure above : General outline (blue lines) in terms of crystal faces of a crystal having as its intrinsic shape the six-fold amphitect gyroid polygon.
The next Figure indicates some actual (exterior boundary of crystal so far developed) and possible crystal faces of our C2 crystal.
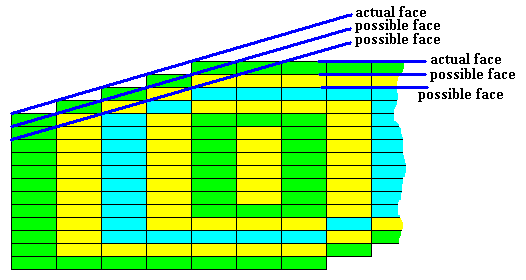
Figure above : Some actual and possible f a c e s of a crystal (presently under investigation) having as its intrinsic shape the six-fold amphitect gyroid polygon, while possessing an intrinsic symmetry according to the group C2 . Crystal only partially displayed.
The next Figure indicates that, with respect to the oblique faces of our C2 crystal, the area between two consecutive actual/possible faces does not represent a concrete material l a y e r of crystal growth (i.e. not a natural layer, as theorized above) : A genuine layer (in this -- oblique -- direction) includes three actual/possible faces.
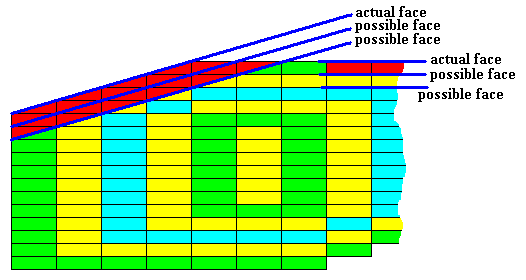
Figure above : Two-dimensional C2 crystal presently under investigation : Some genuine l a y e r s of crystal growth indicated (red).
The next Figure shows that the l a y e r s, so conceived, consist of (or at least contain) w h o l e building blocks.
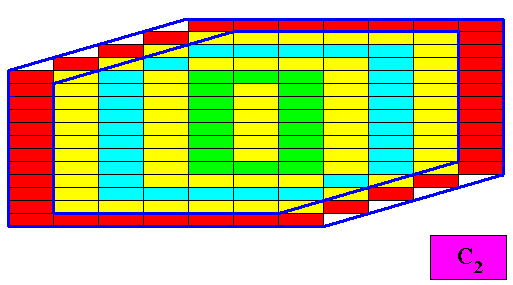
Figure above : Two-dimensional C2 crystal presently under investigation : True layers (one such layer highlighted by red coloring) consist of -- or at least contain -- whole building blocks (red).
The crystal presently under investigation will retain its six faces during prolonged growth, provided their growth rates (in terms of distance increase) are identical. We assume the condition for this identity to be present : The surplus growth rate in the oblique direction due to the layers being thicker than those of growth in the vertical direction (resulting in horizontal faces) is neutralized by a slower rate of deposition of the material for these (oblique) layers. And at the same time the deposition in the horizontal direction (resulting in vertical faces) is slow, precisely neutralizing the surplus growth obtained from the layers being thicker in this direction. And because such a condition is reasonable, we can assume that crystals having the 6-fold amphitect gyroid polygon as their intrinsic shape can indeed exist in the sense that the six faces will persist during prolonged growth.
Above we discussed two possible interpretations of growth layers in two-dimensional crystals. And they both referred to the continued addition of m i c r o s c o p i c building blocks. Both interpretations are not entirely satisfactory, because in both cases (also) half building blocks are involved. But for our subject, which is whether their can be conditions for the persistence of all faces of certain crystals having certain shapes, this is not so important. A crystal face situated between two tapering adjacent faces will persist if its growth rate is equal to that of its adjacent faces, or at least such that, as an effect, the two dividing lines (separating the directions of the relevant faces) are parallel to each other or are widening their distance as growth proceeds. And this in fact is a m a c r o s c o p i c a l state of affairs. Faces are macroscopic features of crystals. The demanded growth rates can just be set in a macroscopical context : We can geometrically measure the increase in volume of the growing crystal every five or so minutes, and with it measure the increase of the distance of faces from the growing center (which ultimately is the initial microscopic crystal seed). The increase of volume during every five minutes we can call g r o w t h l a y e r s , and we can depict growth layers so conceived m a c r o s c o p i c a l l y in all our drawings to come, which relate to demonstrating that certain crystal shapes (in terms of symmetry, and number and orientation of faces) can persist during prolonged growth. And so we do, i.e. in all relevant drawings of crystals we will depict macroscopical growth layers. And these layers are nothing but successive increments of volume or distance.
The next two Figures (two construction stages) depict the growth of our C2 crystal under investigation in terms of equal and macroscopic increments of distance (equal with respect to successive increments as well as to those of different faces).
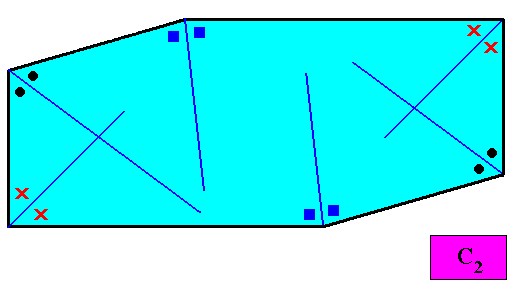
Figure above : Two-dimensional C2 crystal presently under investigation : First stage in the construction of growth stages in terms of equal and macroscopic distance increments (equality not only of successive distance increments, but also of those corresponding to different directions of growth), expressing equal growth (in terms of distance) of all the six faces of the crystal. The mentioned increments are given by 'layers' of equal width, (this equal width) guaranteed by dividing lines (separating directions of faces) that exactly divide the angle between two relevant faces into two equal angles as indicated in the Figure. On the basis of these dividing lines the 'layers', signifying distance growth (i.e. increase of distance from a growing center), will be drawn in the next two Figures.
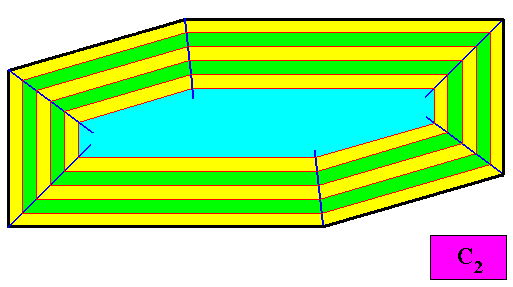
Figure above : Two-dimensional C2 crystal presently under investigation : Second and last stage in the construction of growth stages in terms of equal and macroscopic distance increments (equality not only of successive distance increments, but also of those corresponding to different directions of growth), expressing equal growth (in terms of distance) of all the six faces of the crystal, guaranteeing that these faces will be preserved during prolonged growth. The mentioned increments are given by macroscopic 'layers' of equal width (yellow, green, yellow, etc.) extending from an initial crystal (blue). The just mentioned equal width of layers of different directions is guaranteed by dividing lines (separating directions of faces) that exactly divide the angle between two relevant faces into two equal angles.
And with the auxiliary lines removed :

Figure above : Same as previous Figure (2-dimensional crystal having as its intrinsic shape that of an amphitect gyroid hexagon). Auxiliary lines omitted.
The next Figure indicates the six antimers of our eupromorphic C2 crystal with six (permanent) faces.
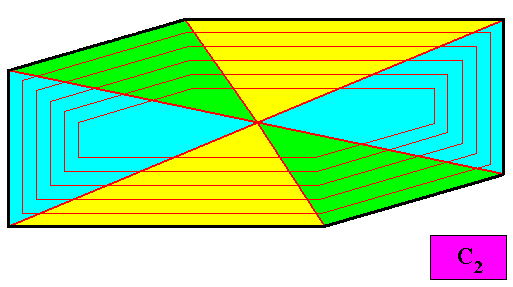
Figure above : The six antimers (green, yellow, blue) of the presently discussed two-dimensional crystal having as its intrinsic shape that of an amphitect gyroid hexagon.
Next we consider the persistence of faces of a two-dimensional crystal having as its intrinsic shape that of the regular gyroid ditetragon.
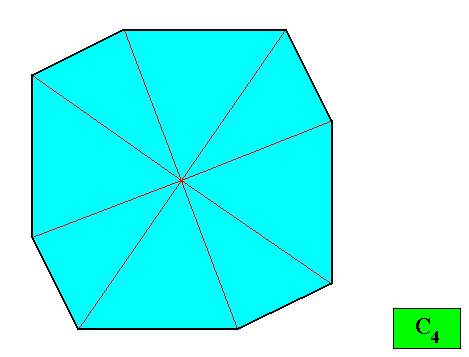
Figure above : A two-dimensional crystal having as its intrinsic shape that of a regular gyroid ditetragon, and supposed to possess an intrinsic symmetry according to the group C4 (i.e. while in the present case -- because we consider only holomorphic crystals [symmetry of shape = intrinsic symmetry of crystal] -- we have set the intrinsic symmetry to be that of C4 , while a crystal having this shape could -- in other cases -- have an intrinsic symmetry according to C2 ). The vectors of the Vector Rosette of Actual Growth (here indicated by thin red lines) precisely bisect the angles between adjacent crystal faces into two equal angles, guaranteeing that the macroscopic growth layers (next Figure) are all of equal width (equality not only with respect to successive layers but also with respect to layers in different directions), and so expressing the fact of equal growth rates of all the eight faces, which in turn guarantees that these faces will persist during prolonged crystal growth. See also next Figure.
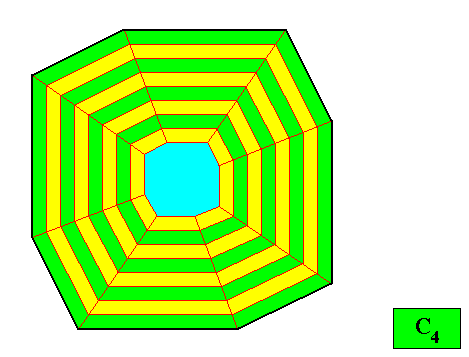
Figure above : Equal growth layers (green, yellow) of the crystal of the previous Figure. The dividing lines (radially positioned red lines), coinciding with the vectors of the Vector Rosette of Actual Growth of this crystal, exactly bisect the angles between adjacent faces. They clearly show that the eight faces will not disappear during prolonged growth of the crystal.
And without auxiliary lines :
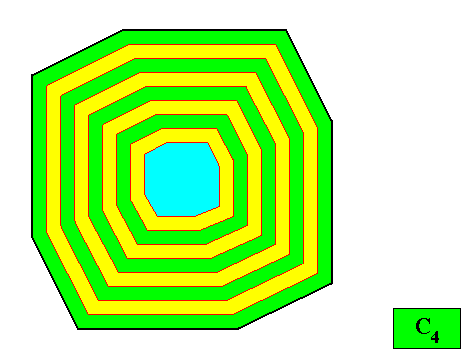
Figure above : Same as previous Figure. Two-dimensional C4 crystal with intrinsic shape according to a regular gyroid ditetragon. Auxiliary lines removed.
The next Figure indicates the case of eight antimers to be present in the two-dimensional crystal presently under investigation.
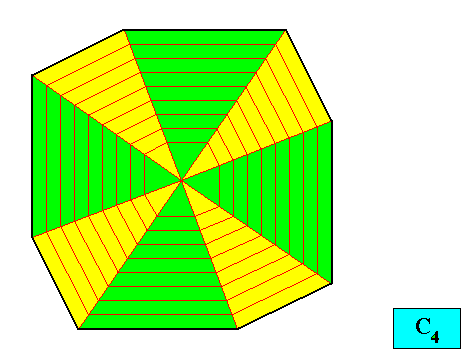
Figure above : The case of eight similar antimers (green, yellow) of the two-dimensional crystal with intrinsic shape according to a regular gyroid ditetragon and with intrinsic symmetry according to the group C4 . There are e i g h t s i m i l a r antimers present if the translation-free residue consists of eight similar motifs. The crystal is then eupromorphic.
Another possible configuration of antimers of the crystal presently under investigation (C4 , regular gyroid ditetragon) is depicted in the next Figure.
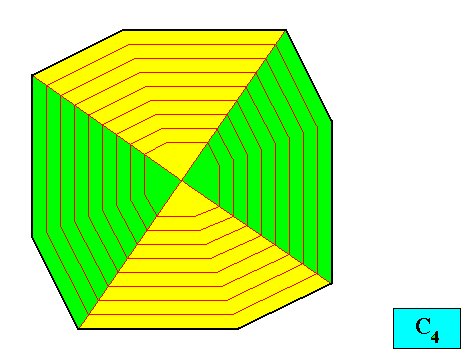
Figure above : The case of four equal antimers (green, yellow) of the two-dimensional crystal with intrinsic shape according to a regular gyroid ditetragon and with intrinsic symmetry according to the group C4 . There are f o u r e q u a l antimers present if the translation-free residue consists of four equal motifs. The crystal is then non-eupromorphic, although still holomorphic.
In the next document we will consider the rest of the above enumerated shapes with respect to their possible existence as (two-dimensional) crystals, i.e. with respect to the persistence of their faces as given with the enumerated shapes.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XV (3rd Sequel).
e-mail : 