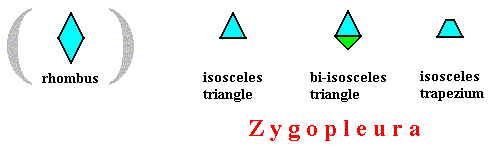General Ontology
Cosmos and Nomos
(Takes a little while to load the images)
Theory of Ontological Layers and Complexity Layers
Part XV
Crystals and Organisms
Theory of intrinsic Shape, intrinsic Symmetry and Promorph
e-mail : 
Back to Homepage
This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Summaries and some theorizing
Further down a table will be given that summarizes all the results obtained so far, for each of the (until now selected) six intrinsic shapes, viz. Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon. We give the intrinsic point symmetry, the general promorph, i.e. the higher promorphological category, or 'family' to which the ultimate promorph belongs, and the ultimate promorph itself, that can be possesed by a two-dimensional crystal having that particular intrinsic shape.
But before we proceed, some explanations of promorphological names used in the table and elsewhere (and which were already given earlier) are presented (but for full details see Second Part of Website (and there) at : BASIC FORMS ) :
Axonia :
In three dimensions : Bodies with one or more fixed axes.
In two dimensions : Figures with one or more fixed axes.
Stauraxonia :
In three dimensions : Pyramidal forms (pyramids and bipyramids, regular or irregular). Cylinders, Cones, and the like, do not belong to the Stauraxonia.
In two dimensions : Polygons (regular or irregular). Circles do not belong to the Stauraxonia.
Stauraxonia homostaura :
In three dimensions : Regular single pyramids (Stauraxonia Heteropola homostaura).
In two dimensions : Regular polygons (Stauraxonia homostaura).
Homostaura anisopola :
Homostaura with unequipolar cross axes.
Homostaura isopola :
Homostaura with equipolar cross axes.
Homostaura (anisopola) triactinota :
Homostaura with three antimers :
In three dimensions : regular 3-fold single pyramids.
In two dimensions : Equilateral triangles.
Homostaura (isopola) tetractinota :
Homostaura with four antimers :
In three dimensions : regular 4-fold single pyramids, i.e. quadratic single pyramids.
In two dimensions : Squares.
Homostaura (anisopola) pentactinota :
Homostaura with five antimers :
In three dimensions : regular 5-fold single pyramids.
In two dimensions : Regular pentagons.
Homostaura (isopola) hexactinota :
Homostaura with six antimers :
In three dimensions : regular 6-fold single pyramids.
In two dimensions : Regular hexagons.
Stauraxonia heterostaura :
In three dimensions : Irregular single pyramids, either whole flattened pyramids (amphitect pyramids), or one half of such a pyramid, or one quarter of such a pyramid.
In two dimensions : Irregular polygons, either whole flattened polygons (amphitect polygons), or one half of such a polygon, or one quarter of such a polygon.
Heterostaura autopola :
In three dimensions : whole amphitect pyramids.
In two dimensions : whole amphitect polygons.
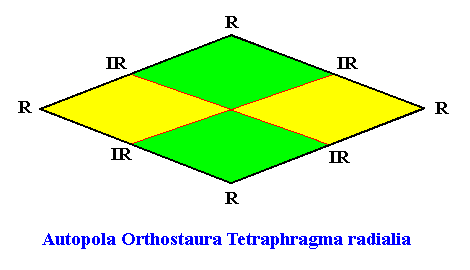
Autopola orthostaura :
Autopola with two or four antimers, implying that the number of radial cross axes is maximally two, and these are then intersecting at right angles. If, however, in Autopola with four antimers, viz. the Autopola tetraphragma, the four antimers are arranged such that the directional axes (i.e. the two cross axes that intersect at right angles) are interradial (i.e. not coinciding with the median lines of the antimers), as in the Autopola tetraphragma interradialia, the two radial cross axes intersect at acute angles. This is the case with rectangular pyramids (three dimensions) and rectangles (two dimensions) with four antimers. And because the symmetry of such a rectangular pyramid or rectangle is the same as a rhombic pyramid or rhombus with four antimers, where indeed the radial cross axes meet at right angles, implying them to be true Autopola orthostaura, and because the rhombus is a more simpler figure then a rectangle, we still consider the latter, viz. rectangular pyramid an rectangle, to be orthostaura as well. In the case of Autopola with only two antimers, there are only two cross axes, one radial, one interradial, and these meet at right angles (Autopola Orthostaura diphragma). In the drawings of the geometric figures representing the Autopola (Autopola Tetraphragma radialia, Autopola Tetraphragma interradialia, Autopola diphragma, Autopola hexaphragma, etc.) this all will become clear.
Autopola oxystaura :
Autopola with 6, 8, 10, 12, . . . antimers, implying that the number of radial cross axes is minimally three, and these are then generally intersecting at acute angles.
Autopola (orthostaura) diphragma :
Autopola with two antimers.
Autopola (orthostaura) tetraphragma :
Autopola with four antimers.
Autopola (oxystaura) hexaphragma :
Autopola with six antimers.
Autopola (oxystaura) octophragma :
Autopola with eight antimers.
Heterostaura allopola :
In three dimensions : half- or quarter-amphitect pyramids (bilateral forms s.l.).
In two dimensions : half-or quarter-amphitect polygons (bilateral forms s.l.).
Allopola zygopleura :
Allopola with two or four antimers.
Zygopleura eutetrapleura :
Symmetric Zygopleura with four antimers.
Zygopleura eudipleura :
Symmetric Zygopleura with two antimers (bilateral forms s.str.).
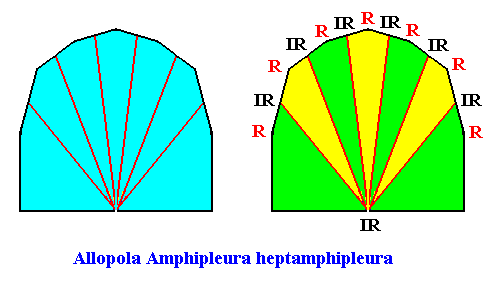
Allopola amphipleura :
Allopola with 3, 5, 6, 7, 8, . . . antimers.
Stauraxonia (listed already earlier) :
In three dimensions : Pyramidal forms (pyramids and bipyramids, regular or irregular).
In two dimensions : Polygons (regular or irregular).
Stauraxonia gyrostaura :
In three dimensions : Twisted single pyramids (flattened or not) (Stauraxonia heteropola gyrostaura).
In two dimensions : Twisted polygons (flattened or not) (Stauraxonia gyrostaura).
Gyrostaura homogyrostaura :
In three dimensions : Regular twisted single pyramids.
In two dimensions : Regular twisted polygons.
Homogyrostaura trimera :
In three dimensions : Regular twisted single pyramids with three antimers.
In two dimensions : Regular twisted polygons with three antimers.
Homogyrostaura tetramera :
In three dimensions : Regular twisted single pyramids with four antimers.
In two dimensions : Regular twisted polygons with four antimers.
Homogyrostaura pentamera :
In three dimensions : Regular twisted single pyramids with five antimers.
In two dimensions : Regular twisted polygons with five antimers.
Homogyrostaura hexamera :
In three dimensions : Regular twisted single pyramids with six antimers.
In two dimensions : Regular twisted polygons with six antimers.
Homogyrostaura heptamera :
In three dimensions : Regular twisted single pyramids with seven antimers.
In two dimensions : Regular twisted polygons with seven antimers.
Homogyrostaura octomera :
In three dimensions : Regular twisted single pyramids with eight antimers.
In two dimensions : Regular twisted polygons with eight antimers.
Gyrostaura heterogyrostaura :
In three dimensions : Amphitect twisted single pyramids.
In two dimensions : Amphitect twisted polygons.
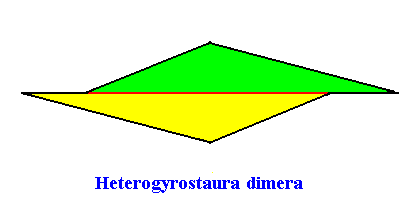
Heterogyrostaura dimera :
In three dimensions : Amphitect twisted single pyramids with two antimers.
In two dimensions : Amphitect twisted polygons with two antimers.
Heterogyrostaura tetramera :
In three dimensions : Amphitect twisted single pyramids with four antimers.
In two dimensions : Amphitect twisted polygons with four antimers.
Heterogyrostaura hexamera :
In three dimensions : Amphitect twisted single pyramids with six antimers.
In two dimensions : Amphitect twisted polygons with six antimers.
Heterogyrostaura octomera :
In three dimensions : Amphitect twisted single pyramids with eight antimers.
In two dimensions : Amphitect twisted polygons with eight antimers.
Anaxonia :
In three dimensions : Bodies without fixed axes.
In two dimensions : Figures without fixed axes.
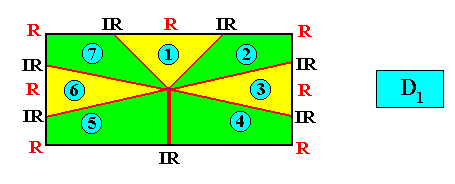
Because in crystals (2-dimensional and 3-dimensional) the only rotation axes that can occur are 1-fold, 2-fold, 3-fold, 4-fold and 6-fold rotation axes, the following promorphs in the above list cannot occur in crystals (but can occur in organisms) :
Homostaura (anisopola) pentactinota, Homogyrostaura pentamera, Homogyrostaura heptamera and Homogyrostaura octomera.
Well, now then the table summarizing our results obtained so far :
| Symmetry |
Family of Promorphs |
Promorph |
| D2 |
Heterostaura autopola (orthostaura) |
Diphragma |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma interradialia |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma radialia |
| D2 |
Heterostaura autopola (oxystaura) |
Hexaphragma |
| D2 |
Heterostaura autopola (oxystaura) |
Octophragma |
| D1 |
Allopola zygopleura |
Eudipleura |
| D1 |
Allopola zygopleura |
Eutetrapleura interradialia |
| D1 |
Allopola zygopleura |
Eutetrapleura radialia |
| D1 |
Allpola amphipleura |
Triamphipleura |
| D1 |
Allpola amphipleura |
Pentamphipleura |
| D1 |
Allpola amphipleura |
Hexamphipleura |
| D1 |
Allpola amphipleura |
Heptamphipleura |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura dimera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura tetramera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura hexamera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura octomera |
| C1 |
Anaxonia |
Anaxonia acentra * |
| C1 |
Stauraxonia heterostaura |
Allopola heteropleura ** |
* For three dimensions the Anaxonia (forms without definite and constant axes) can be divided into the Anaxonia acentra and the Anaxonia centrostigma. In the former there is no definite body center, while in the latter there is, namely a center of symmetry. For two dimensions such a center of symmetry is identical to a 2-fold rotation axis, which implies that the three-dimensional Anaxonia centrostigma do not have a two-dimensional counterpart (because there we then have an axis, viz. the mentioned 2-fold rotation axis, which makes them Axonia [i.e. figures with one or more axes] ). A two-dimensional figure possessing only a 2-fold rotation axis promorphologically belongs to the Heterogyrostaura, which are twisted amphitect [i.e. flattened] polygons. And when we see such a polygon as the base of a pyramid, we then have its three-dimensional counterpart, namely the three-dimensional Heterogyrostaura, which are twisted amphitect pyramids.
** Allopola heteropleura : These are all bilateral forms, where also the poles of the right-left axis are differentiated (like in flat-fishes). They divide into Amphipleura heteropleura (asymmetric Amphipleura) and Zygopleura heteropleura (asymmetric Zygopleura). In the Zygopleura Dipleura heteropleura (Zygopleura dysdipleura), as also in their homopleural counterparts the Zygopleura homopleura (Zygopleura eudipleura), one can distinguish only two definite and constant axes, one radial and one interradial (three axes with respect to 3-dimensional forms), and these axes are moreover perpendicular to each other. So all Allopola Zygopleura dipleura, whether homopleural or heteropleural, can also be called Diaxonia (Triaxonia for 3-dimensional forms). And the least symmetric of them, viz. the Zygopleura dysdipleura, come closest to those forms that have no axes at all, namely the Anaxonia.
| Symmetry |
Family of Promorphs |
Promorph |
| D4 |
Stauraxonia homostaura |
Isopola tetractinota |
| C4 |
Stauraxonia Gyrostaura |
Homogyrostaura tetramera |
| D2 |
Heterostaura autopola (orthostaura) |
Diphragma |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma interradialia |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma radialia |
| D2 |
Heterostaura autopola (oxystaura) |
Hexaphragma |
| D2 |
Heterostaura autopola (oxystaura) |
Octophragma |
| D1 |
Allopola zygopleura |
Eudipleura |
| D1 |
Allopola zygopleura |
Eutetrapleura interradialia |
| D1 |
Allopola zygopleura |
Eutetrapleura radialia |
| D1 |
Allpola amphipleura |
Triamphipleura |
| D1 |
Allpola amphipleura |
Pentamphipleura |
| D1 |
Allpola amphipleura |
Hexamphipleura |
| D1 |
Allpola amphipleura |
Heptamphipleura |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura dimera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura tetramera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura hexamera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura octomera |
| C1 |
Anaxonia |
Anaxonia acentra |
| C1 |
Stauraxonia heterostaura |
Allopola heteropleura |
| Symmetry |
Family of Promorphs |
Promorph |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura dimera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura tetramera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura hexamera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura octomera |
| C1 |
Anaxonia |
Anaxonia acentra |
| C1 |
Stauraxonia heterostaura |
Allopola heteropleura |
| Symmetry |
Family of Promorphs |
Promorph |
| D2 |
Heterostaura autopola (orthostaura) |
Diphragma |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma interradialia |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma radialia |
| D2 |
Heterostaura autopola (oxystaura) |
Hexaphragma |
| D2 |
Heterostaura autopola (oxystaura) |
Octophragma |
| D1 |
Allopola zygopleura |
Eudipleura |
| D1 |
Allopola zygopleura |
Eutetrapleura interradialia |
| D1 |
Allopola zygopleura |
Eutetrapleura radialia |
| D1 |
Allpola amphipleura |
Triamphipleura |
| D1 |
Allpola amphipleura |
Pentamphipleura |
| D1 |
Allpola amphipleura |
Hexamphipleura |
| D1 |
Allpola amphipleura |
Heptamphipleura |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura dimera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura tetramera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura hexamera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura octomera |
| C1 |
Anaxonia |
Anaxonia acentra |
| C1 |
Stauraxonia heterostaura |
Allopola heteropleura |
| Symmetry |
Family of Promorphs |
Promorph |
| D3 |
Stauraxonia homostaura |
Anisopola triactinota |
| C3 |
Stauraxonia gyrostaura |
Homogyrostaura trimera |
| D1 |
Allopola zygopleura |
Eudipleura |
| D1 |
Allopola zygopleura |
Eutetrapleura interradialia |
| D1 |
Allopola zygopleura |
Eutetrapleura radialia |
| D1 |
Allpola amphipleura |
Triamphipleura |
| D1 |
Allpola amphipleura |
Pentamphipleura |
| D1 |
Allpola amphipleura |
Hexamphipleura |
| D1 |
Allpola amphipleura |
Heptamphipleura |
| C1 |
Anaxonia |
Anaxonia acentra |
| C1 |
Stauraxonia heterostaura |
Allopola heteropleura |
| Symmetry |
Family of Promorphs |
Promorph |
| D6 |
Stauraxonia homostaura |
Isopola hexactinota |
| C6 |
Stauraxonia gyrostaura |
Homogyrostaura hexamera |
| D3 |
Stauraxonia homostaura |
Anisopola triactinota |
| C3 |
Stauraxonia gyrostaura |
Homogyrostaura trimera |
| D2 |
Heterostaura autopola (orthostaura) |
Diphragma |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma interradialia |
| D2 |
Heterostaura autopola (orthostaura) |
Tetraphragma radialia |
| D2 |
Heterostaura autopola (oxystaura) |
Hexaphragma |
| D2 |
Heterostaura autopola (oxystaura) |
Octophragma |
| D1 |
Allopola zygopleura |
Eudipleura |
| D1 |
Allopola zygopleura |
Eutetrapleura interradialia |
| D1 |
Allopola zygopleura |
Eutetrapleura radialia |
| D1 |
Allpola amphipleura |
Triamphipleura |
| D1 |
Allpola amphipleura |
Pentamphipleura |
| D1 |
Allpola amphipleura |
Hexamphipleura |
| D1 |
Allpola amphipleura |
Heptamphipleura |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura dimera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura tetramera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura hexamera |
| C2 |
Stauraxonia gyrostaura |
Heterogyrostaura octomera |
| C1 |
Anaxonia |
Anaxonia acentra |
| C1 |
Stauraxonia heterostaura |
Allopola heteropleura |
Below we will present a second summary of the investigation of the above (intrinsic) shapes (Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon) of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
The enumeration of the crystals with the mentioned intrinsic shapes will, in this summary, be done from the viewpoint of Promorphology. Things allow that, in the present cases, the names of the given two-dimensional promorphs -- planimetric basic forms -- can be the same as those of their three-dimensional counterparts. The complete System of three-dimensional promorphs -- stereometric basic forms -- (and their systematic derivation) can be found on Second Part of Website (and there) at : BASIC FORMS.
It is with promorphs, but only those based on i n t r i n s i c symmetry and geometrical structure, that crystals (here exemplified by their imaginary two-dimensional counterparts) connect with organisms.
While also individual molecules of chemical substances do have intrinsic symmetry and promorph, they are still microscopic, as are atoms. Crystals, on the other hand, although, in a way, being just molecules, are macroscopic and do as such fall into the size-range of organisms. In this way we have three types of intrinsic dynamical systems (or their immediate products) representing intrinsic things (beings), viz. molecules, crystals and organisms. And crystals clearly are intermediate between molecules and organisms. That's why it was so important for us to find out that crystals do have, like molecules and organisms, definite promorphs, so that there is a certain continuity of basic structure as we go from the microscopic molecules to the macroscopic organisms via the (macroscopic) crystals. It must be admitted, however, that crystals, in a way, resist to being promorphologically interpreted because of their periodic nature. This nature lets them to be homogeneous in the sense that the same surroundings, and with the same orientation, are found with respect to points that are very close together and which are regularly arranged throughout the crystal. So no macroscopic boundaries seem to be present in the interior of a (single, i.e. not twinned) crystal, as we do find such boundaries in organisms, such as in regular sea-urchins, where we find ten radially spaced areas alternately of the same nature, resulting in the fact that such a sea-urchin consists of five identical counterparts (antimers) arranged around its main body axis. Indeed we can distinguish between ambulacral and interambulacral areas within the sea-urchin's body. And although something like this seems not to be present in (single) crystals, we have found (Last Series of documents of Second Part of Website : Basic Forms of Crystals) that (single) crystals nevertheless do have promorphs ( Radially twinned crystals do have promorphs anyway), but in a more or less concealed way, based on the structure of the translation-free residue of the crystal. The symmetry of that residue is macroscopically visible as the intrinsic point symmetry of the crystal, and this latter (macroscopic) symmetry reveals part of the promorph (i.e. generally this point symmetry reveals only one aspect of the promorph, and sometimes it reveals the whole promorph, which boils down to revealing the number and arrangement of the antimers). And in addition to this we found -- in the present series of documents -- that the intrinsic s h a p e of a (single) crystal could be related in some way to the number of antimers, but, as the foregoing documents have shown, only very loosely so. The crystal has a definite and (for the particular species) constant pattern of corners, which expresses definite accomplished growth in certain well-defined directions. And these somehow co-express the crystal's promorph. But, compared to organisms this expression is weak. On the other hand, the main aspect of the promorph, viz. the particular intrinsic point symmetry, is clearly and directly expressed in (single) crystals, while in organisms it is not. All organisms are, strictly speaking, asymmetric. Their true symmetry is more or less hidden, and has to be derived from (the evaluation of) certain constant structural main features of the given organism. So in this way also in organisms their promorph is more or less hidden, i.e. not directly visible.
In the present series of documents we will concentrate on the promorphs of crystals (illustrated in imaginary two-dimensional crystals), and later compare them with those of organisms.
Intrinsic shape, translational symmmetry (i.e. total symmetry, or symmetry including all translational features -- plane group symmetry), intrinsic non-translational symmetry (i.e. point group symmetry) and promorph are structural features of natural (intrinsic) bodies, such as crystals and organisms. Taken in themselves they are whatness categories or entitative If / Then constants, determining their c o n c r e t a within the Mathematical, Inorganic and Organic Layers of Being. And their study here only serves to create an insight into the workings of If / Then constants in general, which will help to set up a general ontology as indicated in the first documents (especially Part I of the present series).
Well, let's now go ahead with our summary of promorphs as they can occur in two-dimensional crystals having the above mentioned intrinsic shapes. Recall that the promorph of some natural body (here exemplified by two-dimensional crystals) is (expressed by) the simplest geometric figure geometrically expressing the intrinsic point symmetry and the number and arrangement of antimers in that natural body. So one must not confuse the shape of the promorph and that of the relevant natural body. Where necessary, we have, into the drawing of the crystal, inserted a motif to express the intrinsic point symmetry of that crystal.
Let's now consider things about the above mentioned second summary of our results (given below), a summary, relating things from the promorphological viewpoint.
The presented promorphs relate to crystals, discussed in the forgoing, and having the above mentioned intrinsic shapes. We list these (crystal) shapes together with their own point symmetries :
- Rectangle, D2
- Square, D4
- Parallelogramm C2
- Rhombus, D2
- Equilateral Triangle, D3
- Regular Hexagon, D6
The promorphs, encountered among these shapes, are now, together with the corresponding two-dimensional crystals themselves, arranged in the same spirit as was done in our Promorphological System of Basic Forms (Second Part of Website, see LINK above), namely according to decreasing symmetry (i.e. increasing differentiation). In the resulting presentation each (large) heading indicates the promorphological Section to which the relevant crystals promorphologically belong.
Holomorphic and Meromorphic crystals
Let's say something more about the relationship between the symmetry of the crystal's intrinsic shape and that of the crystal itself, i.e. that between the geometric and crystallographic symmetry.
We call a crystal h o l o m o r p h i c when the point symmetry of its intrinsic shape is the same as the intrinsic point symmetry of the crystal. If the crystal's point symmetry is l o w e r than that of its intrinsic shape we call the crystal m e r o m o r p h i c.
So in holomorphic crystals their whole shape reflects the intrinsic symmetry of the crystal, while in meromorphic crystals only a part of their shape reflects the intrinsic symmetry of the crystal.
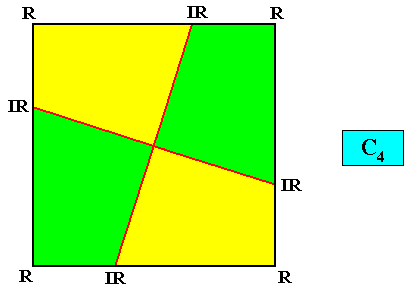
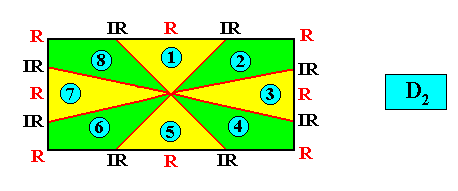
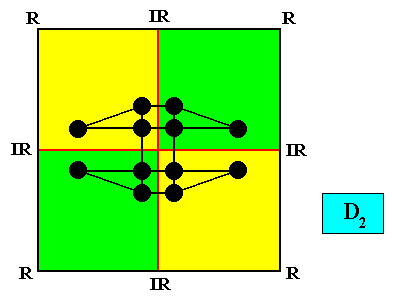
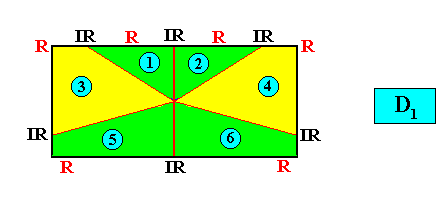
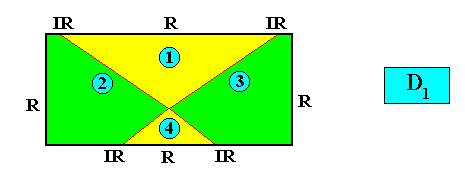
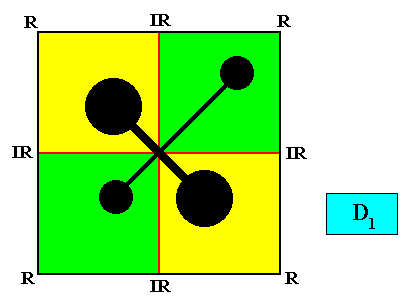
If we have, for example, a (two-dimensional) crystal with intrinsic C2 symmetry, and possessing as its intrinsic shape that of a rectangle, then only a part of this rectangle indicates the true symmetry of the crystal, namely the 2-fold rotation axis of the rectangle. In different but equivalent words : The symmetry of the rectangle is according to the group D2 , while the true symmetry of the crystal is according to the group C2 , and the group C2 is a subgroup of the group D2 what we denote as follows : C2 < D2 , and which is shown in the next diagram (group table) :
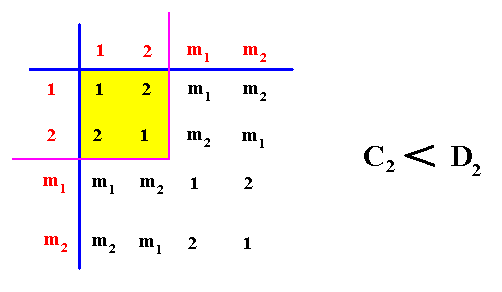
Diagram above : The Cyclic Group C2 (yellow) is a subgroup of the Dihedral Group D2 (whole table).
So in general meromorphic crystals have an intrinsic (point) symmetry that is represented by a subgroup of the group representing the symmetry of their intrinsic shape, while in holomorphic crystals their intrinsic symmetry is the same as the symmetry of their intrinsic shape.
For an introduction to Group Theory see Second Part of Website (and there) at : GROUP THEORY .
Summary of the Promorphs of some two-dimensional crystals
Homostaura (regular polygons) :
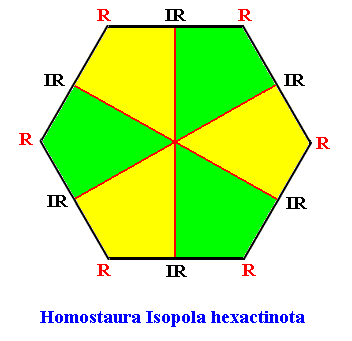
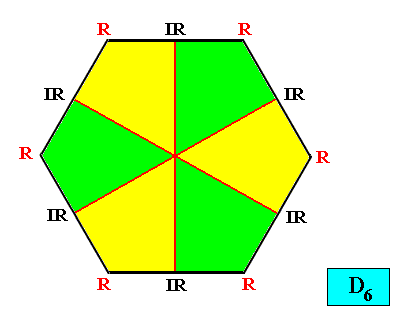
Homostaura Isopola hexactinota
(Regular polygons with equipolar cross axes and six antimers)
Planimetric Basic Form, representing this promorph :
Example of crystal :
Holomorphic crystal
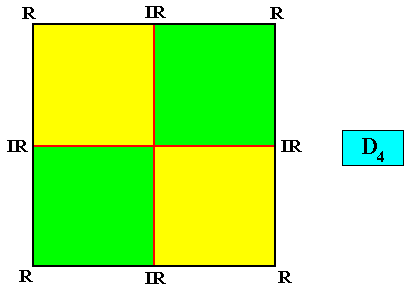
Homostaura Isopola tetractinota
(Regular polygons with equipolar cross axes and four antimers)
Planimetric Basic Form, representing this promorph :
Example of crystal :
Holomorphic crystal
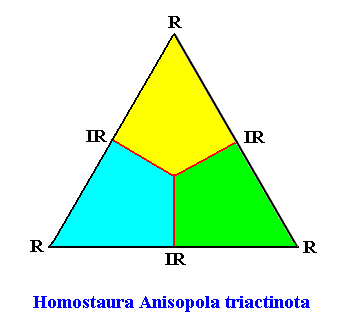
Homostaura Anisopola triactinota
(Regular polygons with unequipolar cross axes and three antimers)
Planimetric Basic Form, representing this promorph :
Examples of crystals :
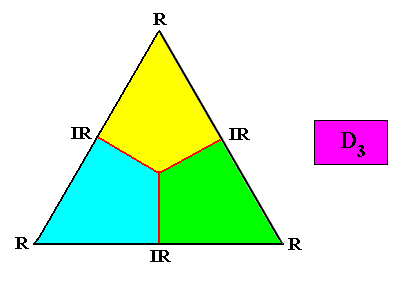Holomorphic crystal
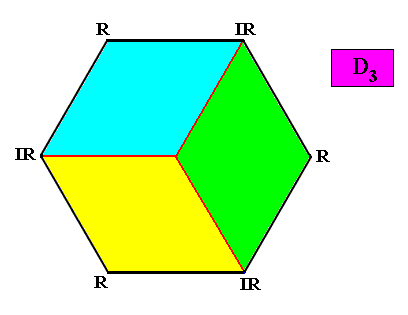Meromorphic crystal D3 < D6
Gyrostaura (gyroid, i.e. twisted, polygons) homogyrostaura (regular gyroid polygons) :
Homogyrostaura hexamera
(Regular gyroid polygons with six antimers)
Planimetric Basic Form, representing this promorph :
Example of crystal :
Meromorphic crystal C6 < D6
Homogyrostaura tetramera
(Regular gyroid polygons with four antimers)
Planimetric Basic Form, representing this promorph :
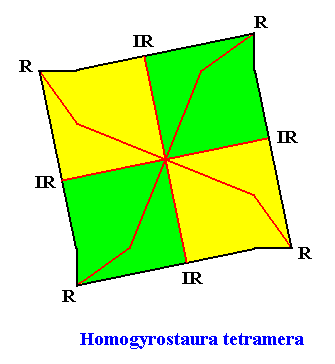
The next two Figures illustrate this basic form still further by giving equivalent geometric figures all representing and expressing the same promorph :
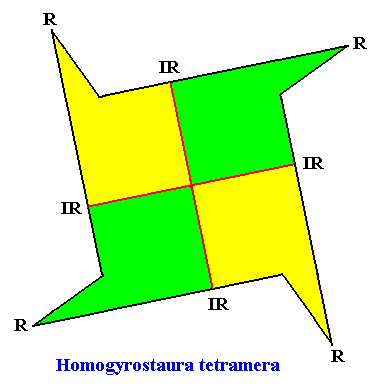
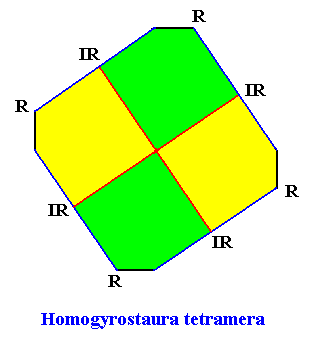
Example of crystal :
Meromorphic crystal C4 < D4
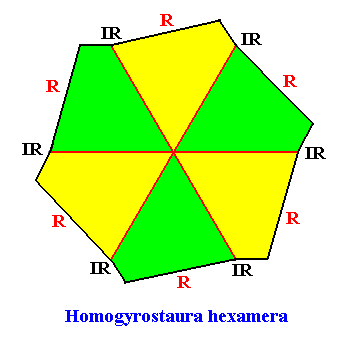
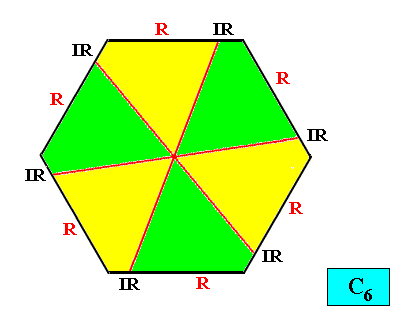
Homogyrostaura trimera
(Regular gyroid polygons with three antimers)
Planimetric Basic Form, representing this promorph :
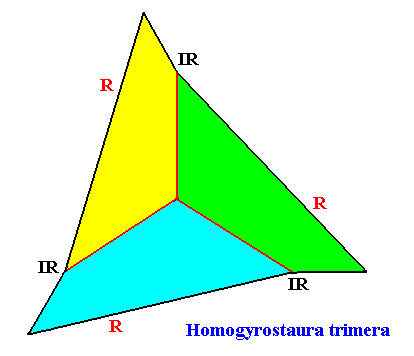
Examples of crystals :
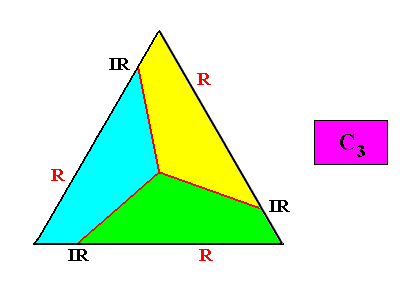Meromorphic crystal C3 < D3
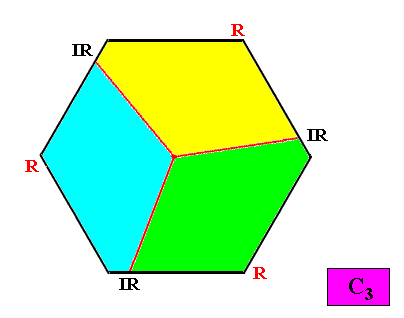Meromorphic crystal C3 < D6
Gyrostaura (gyroid, i.e. twisted, polygons) heterogyrostaura (amphitect, i.e. flattened, gyroid polygons) :
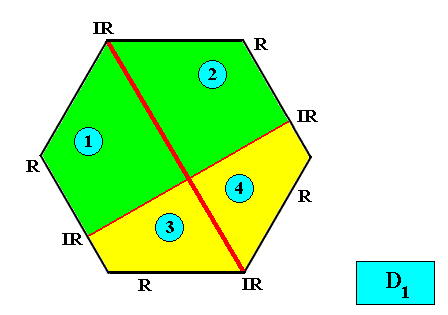
Heterogyrostaura octomera
(amphitect gyroid polygons with eight antimers)
Planimetric Basic Form, representing this promorph :
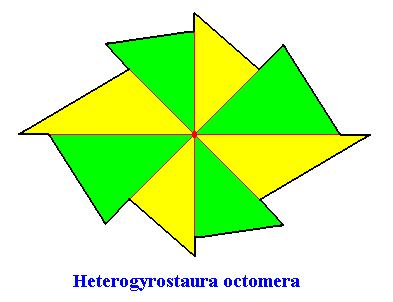
Examples of crystals :
Meromorphic crystal C2 < D2
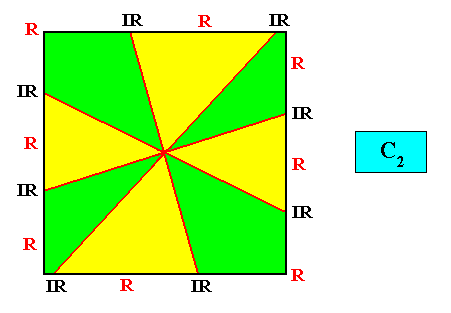Meromorphic crystal C2 < D4
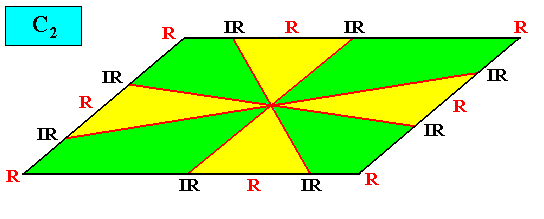Holomorphic crystal
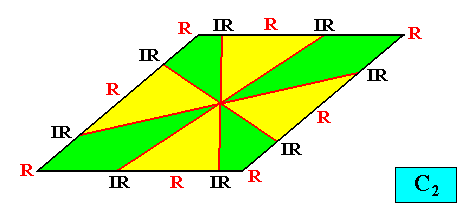Meromorphic crystal C2 < D2
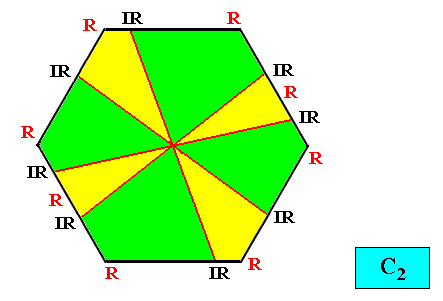Meromorphic crystal C2 < D6
Heterogyrostaura tetramera
(amphitect gyroid polygons with four antimers)
Planimetric Basic Form, representing this promorph :
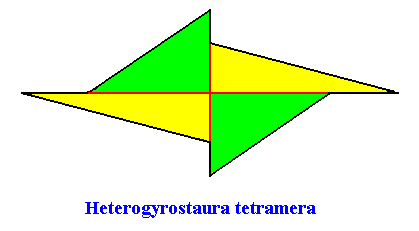
Examples of crystals :
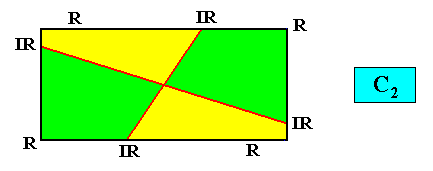Meromorphic crystal C2 < D2
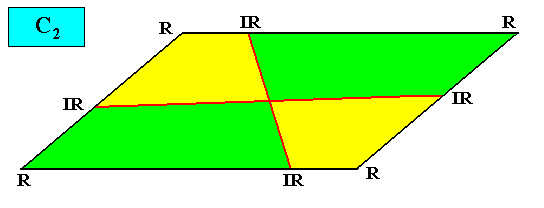Holomorphic crystal
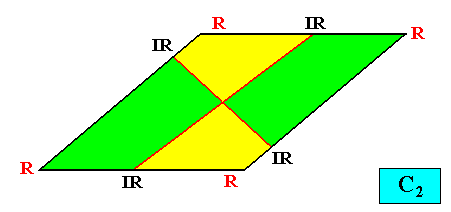Meromorphic crystal C2 < D2
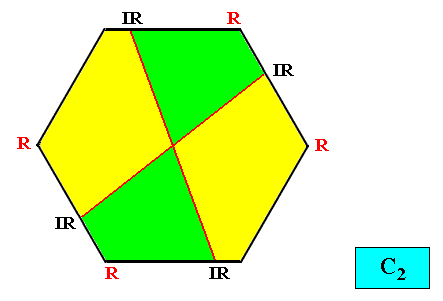Meromorphic crystal C2 < D6
Heterogyrostaura dimera
(amphitect gyroid polygons with two antimers)
Planimetric Basic Form, representing this promorph :
Examples of crystals :
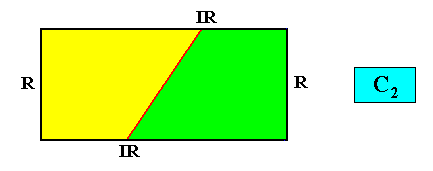Meromorphic crystal C2 < D2
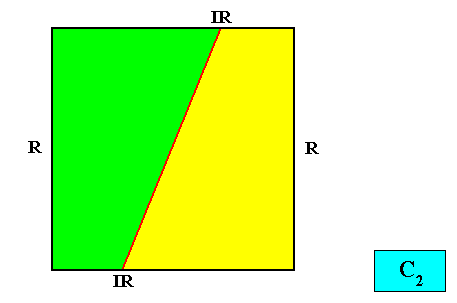Meromorphic crystal C2 < D4
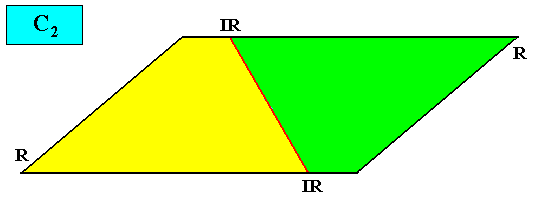Holomorphic crystal
Meromorphic crystal C2 < D2
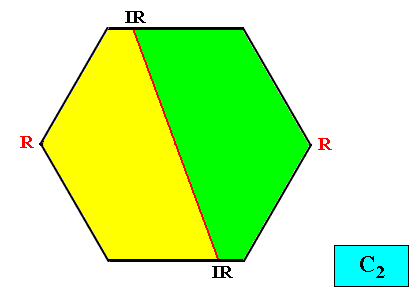Meromorphic crystal C2 < D6
Heterostaura Autopola (amphitect polygons),
Autopola oxystaura (autopola with 6, 8, 10, ..., antimers, therefore at least three radial cross axes present, that must, consequently intersect at a c u t e angles) :
Autopola Oxystaura octophragma
(amphitect polygons with eight antimers)
Planimetric Basic Form, representing this promorph :
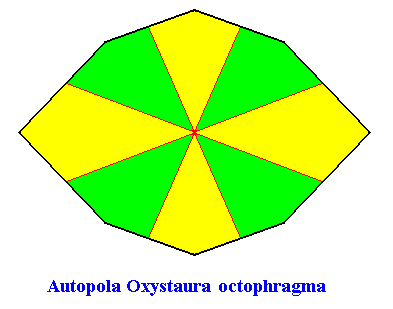
Examples of crystals :
Holomorphic crystal
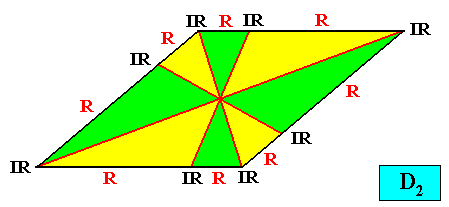Holomorphic crystal
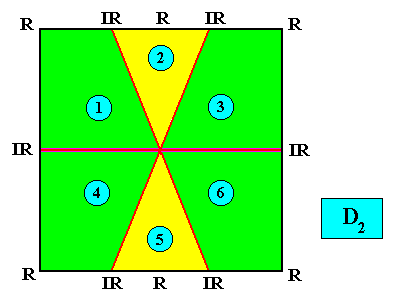
Autopola Oxystaura hexaphragma
(amphitect polygons with six antimers)
Planimetric Basic Form, representing this promorph :
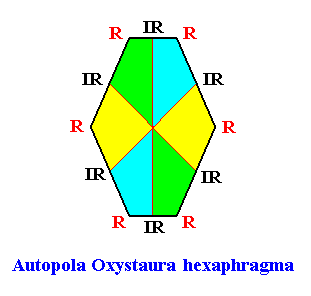
Examples of crystals :
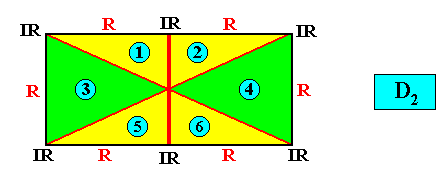Holomorphic crystal
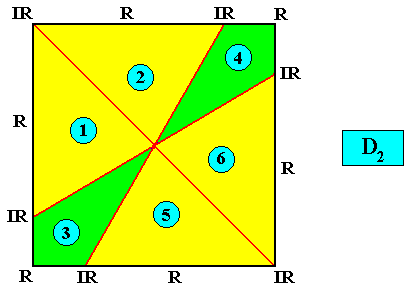Meromorphic crystal D2 < D4
Meromorphic crystal D2 < D4
Holomorphic crystal
Meromorphic crystal D2 < D6
Heterostaura Autopola (amphitect polygons),
Autopola orthostaura (autopola with 4 or 2 antimers, i.e. tetraphragma or diphragma : therefore there is either only one radial cross axis present, or two radial cross axes, coinciding with respectively with one or two directional axes. In the latter case these radial cross axes are p e r p e n d i c u l a r to each other, i.e. they intersect at right angles),
Orthostaura tetraphragma (orthostaura with four antimers) :
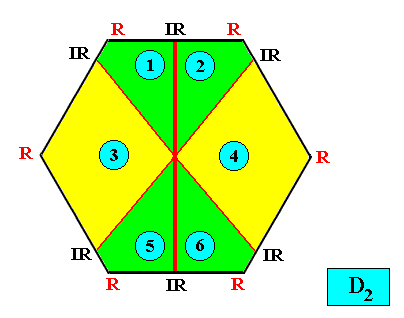
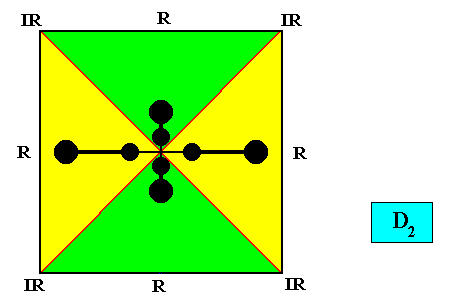
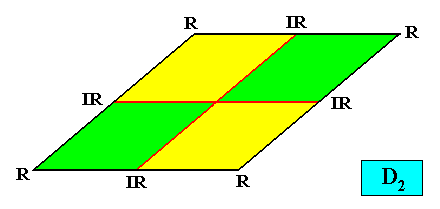
Autopola Orthostaura Tetraphragma radialia
(amphitect polygons, here rhombi, with four antimers and with radial directional axes)
Planimetric Basic Form, representing this promorph :
Examples of crystals :
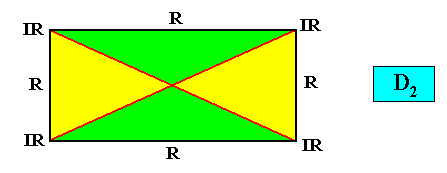Holomorphic crystal
Meromorphic crystal D2 < D4
Meromorphic crystal D2 < D4
Holomorphic crystal
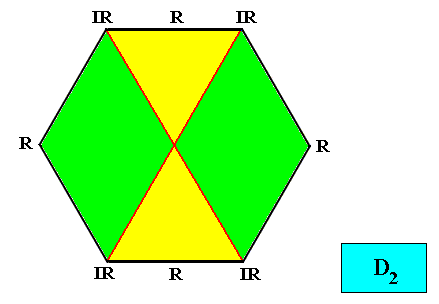Meromorphic crystal D2 < D6
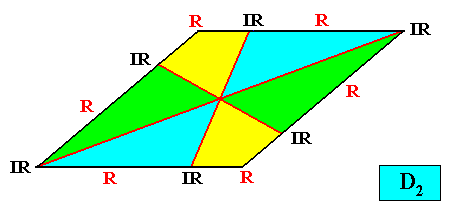
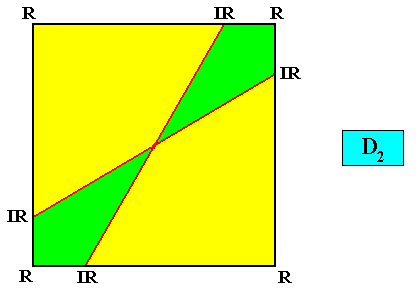
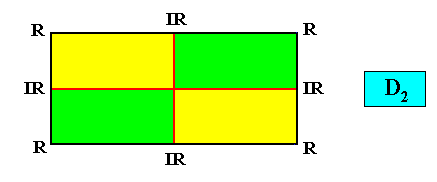
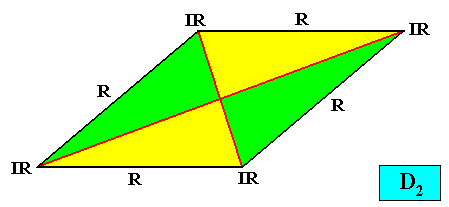
Autopola Orthostaura Tetraphragma interradialia
(amphitect polygons, here rectangles (or rhombi), with four antimers and with interradial directional axes)
Planimetric Basic Form, representing this promorph :
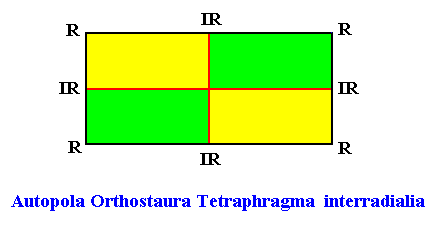
In fact the Autopola Orthostaura Tetraphragma interradialia can be represented by a still more general geometric Figure. See next Figure.
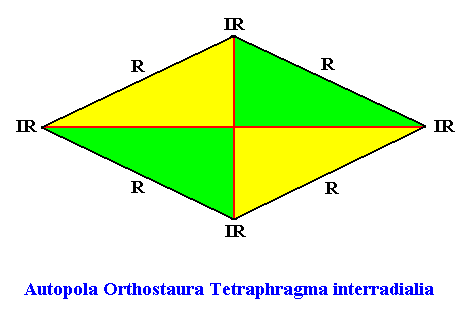
Examples of crystals :
Holomorphic crystal
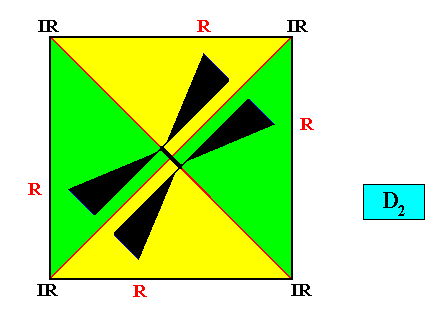Meromorphic crystal D2 < D4
Meromorphic crystal D2 < D4
Holomorphic crystal
Meromorphic crystal D2 < D6
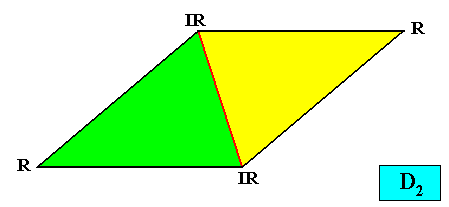
Autopola Orthostaura Diphragma
(amphitect polygons, here rhombi, with two antimers)
Planimetric Basic Form, representing this promorph :
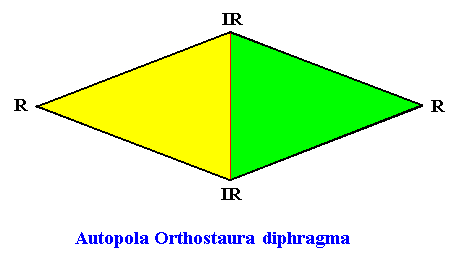
Examples of crystals :
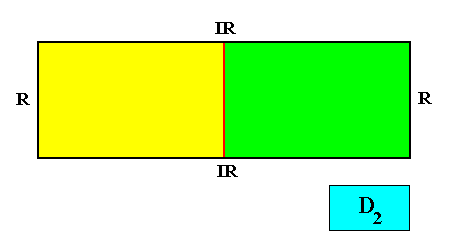Holomorphic crystal
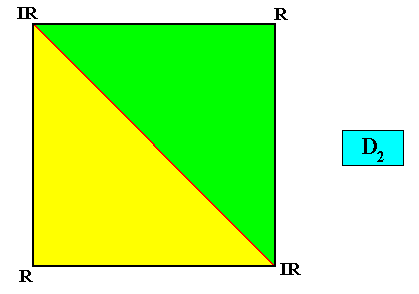Meromorphic crystal D2 < D4
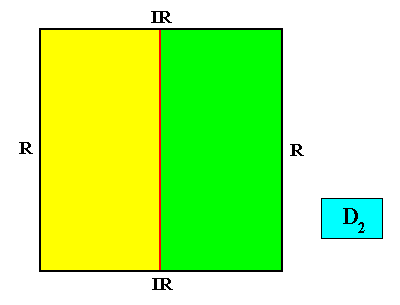Meromorphic crystal D2 < D4
Holomorphic crystal
Meromorphic crystal D2 < D6
Heterostaura Allopola (half amphitect polygons, bilateral forms),
Allopola amphipleura (bilateral forms with 3, 5, 6, 7, 8, ... antimers) :
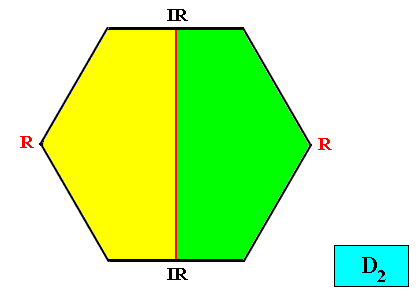
Allopola heptamphipleura
(half amphitect polygons, with seven antimers)
Planimetric Basic Form, representing this promorph :
Example of crystal :
Meromorphic crystal D1 < D2
Allopola hexamphipleura
(half amphitect polygons, with six antimers)
Planimetric Basic Form, representing this promorph :
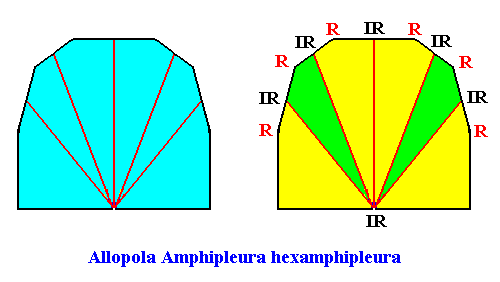
Examples of crystals :
Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D4
Meromorphic crystal D1 < D4
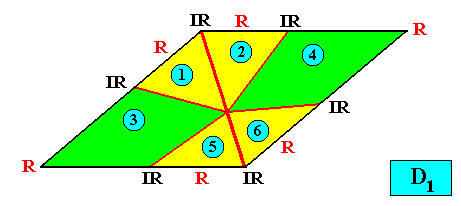Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D3
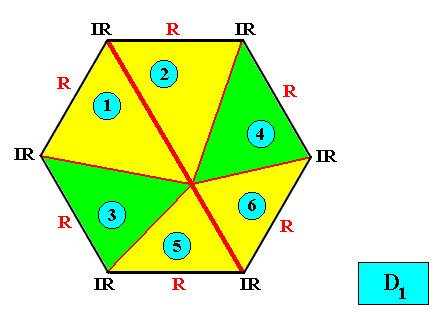Meromorphic crystal D1 < D6
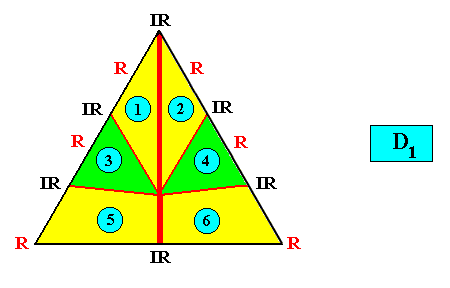
Allopola pentamphipleura
(half amphitect polygons, with five antimers)
Planimetric Basic Form, representing this promorph :
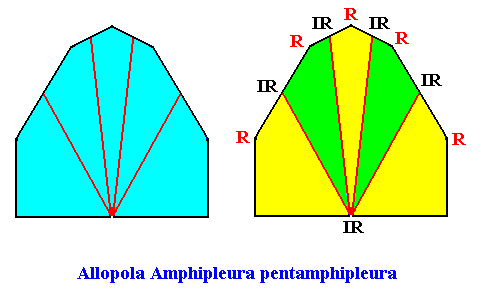
Examples of crystals :
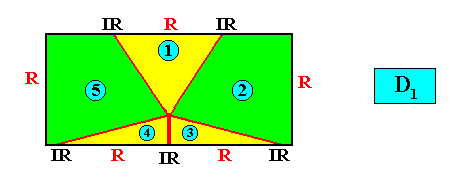Meromorphic crystal D1 < D2
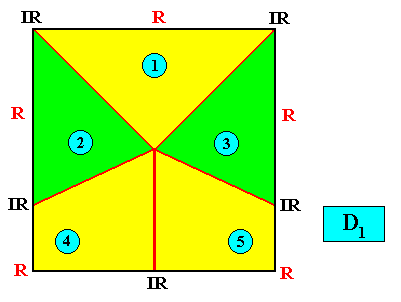Meromorphic crystal D1 < D4
Meromorphic crystal D1 < D2
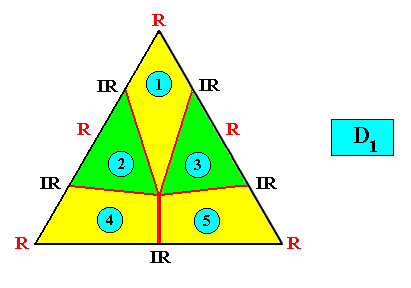Meromorphic crystal D1 < D3
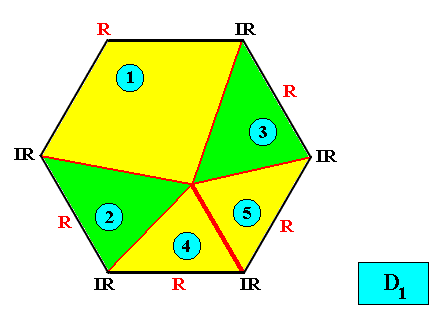Meromorphic crystal D1 < D6
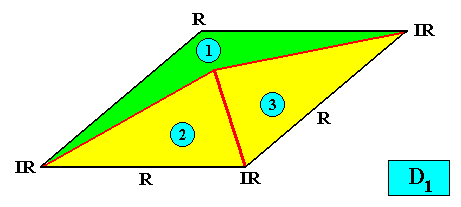
Allopola triamphipleura
(half amphitect polygons, with three antimers)
Planimetric Basic Form, representing this promorph :
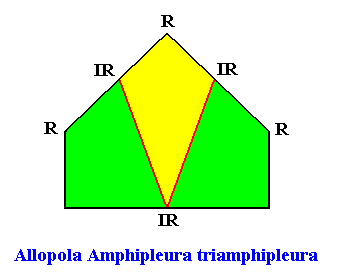
Examples of crystals :
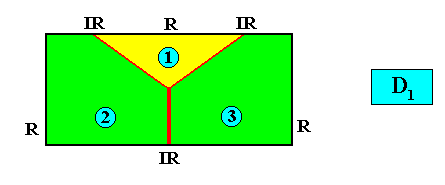Meromorphic crystal D1 < D2
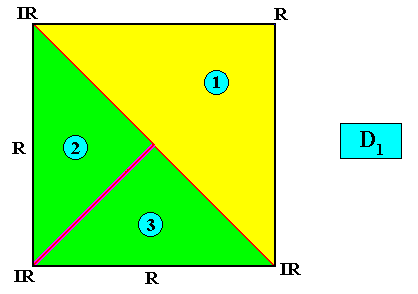Meromorphic crystal D1 < D4
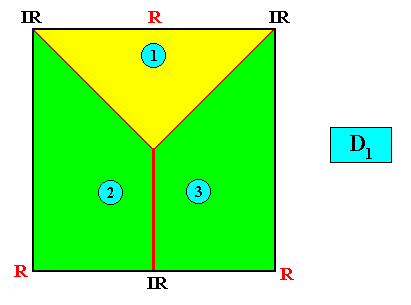Meromorphic crystal D1 < D4
Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D3
Meromorphic crystal D1 < D6
Heterostaura Allopola (half amphitect polygons, bilateral forms),
Allopola zygopleura (half rhombic polygons [i.e. isosceles triangles], or isosceles trapezia [i.e. bilateral tetragons] ; bilateral forms with four or two antimers),
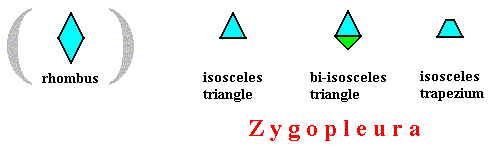
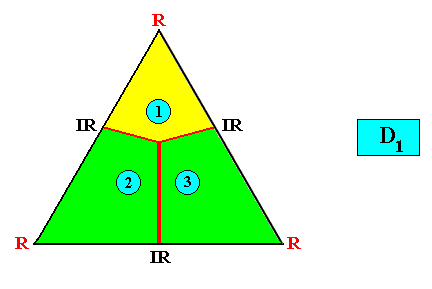
Zygopleura Eutetrapleura (symmetric zygopleura with four antimers) :
Eutetrapleura radialia
(zygopleura with four antimers and radial directional axes, bi-isosceles triangles)
Planimetric Basic Form, representing this promorph :
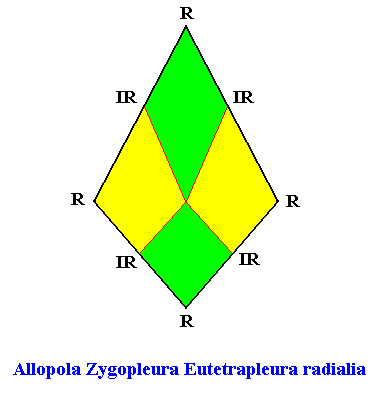
or, another, but equivalent representation (with straight interradial cross axes) :
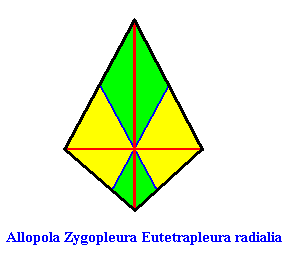
As one can see, the geometric figure representing this promorph consists of two isosceles triangles connected base to base.
Examples of crystals :
Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D4
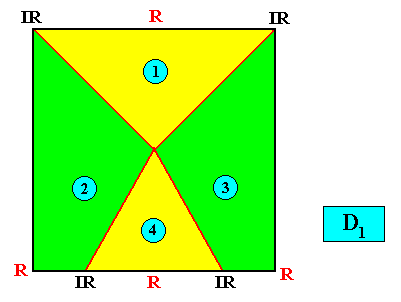Meromorphic crystal D1 < D4
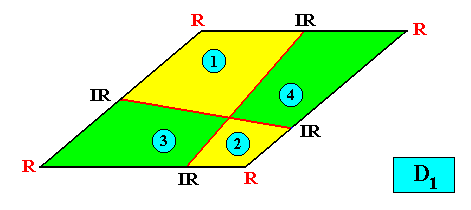Meromorphic crystal D1 < D2
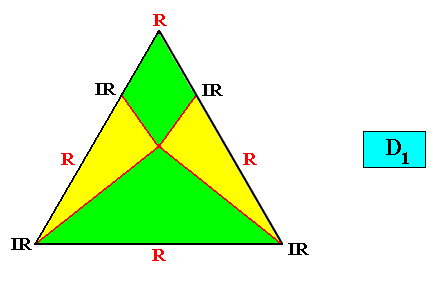Meromorphic crystal D1 < D3
Meromorphic crystal D1 < D6
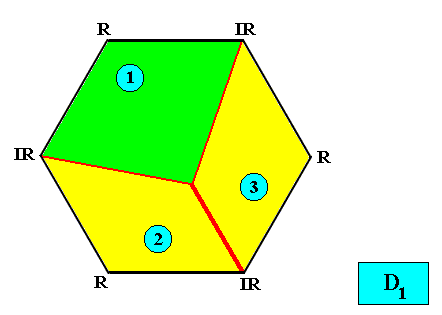
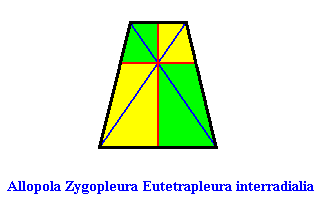
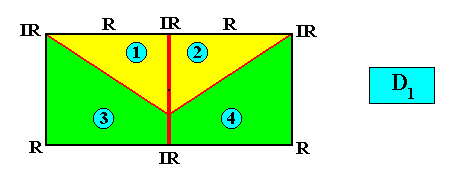
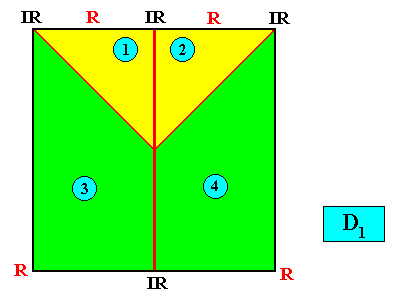
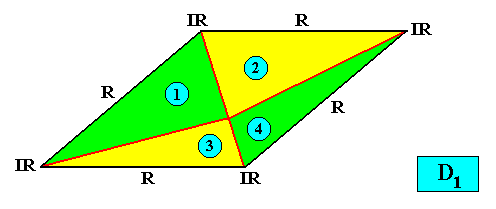
Eutetrapleura interradialia
(zygopleura with four antimers and interradial directional axes, isosceles trapezia)
Planimetric Basic Form, representing this promorph :
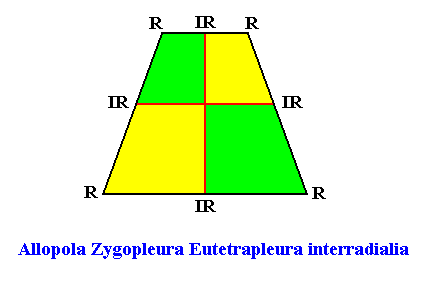
or, another, but equivalent representation (with straight radial cross axes) :
Examples of crystals :
Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D4
Meromorphic crystal D1 < D4
Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D3
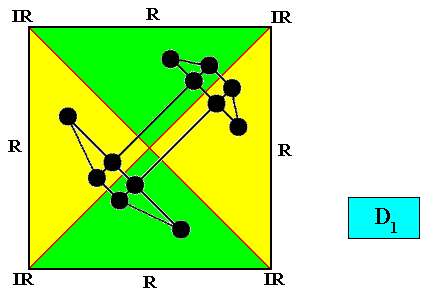Meromorphic crystal D1 < D6
Heterostaura Allopola (half amphitect polygons, bilateral forms),
Allopola zygopleura (half rhombic polygons [i.e. isosceles triangles], or isosceles trapezia [i.e. bilateral tetragons] ; bilateral forms with four or two antimers),
Zygopleura dipleura (symmetric or asymmetric zygopleura with two antimers : eudipleura or dysdipleura) :
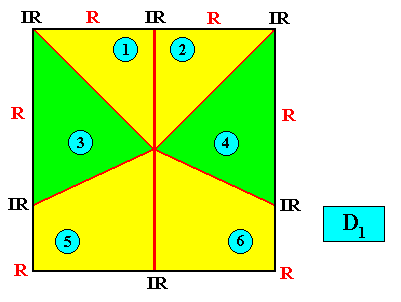
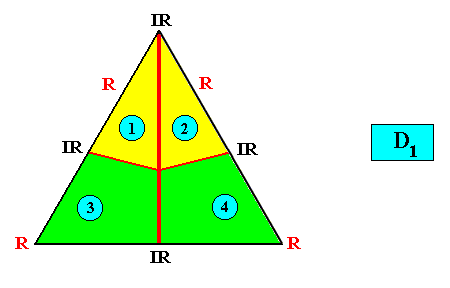
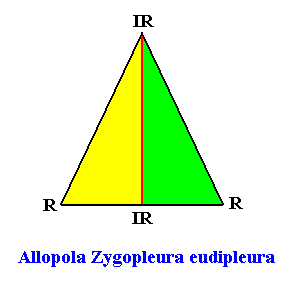
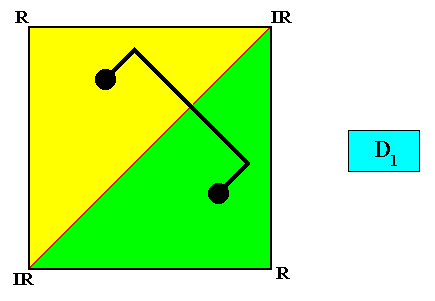
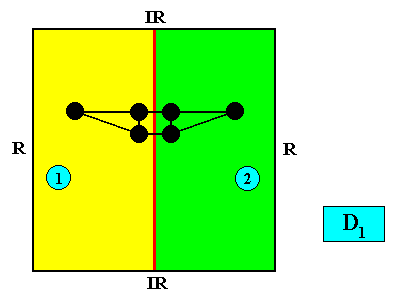
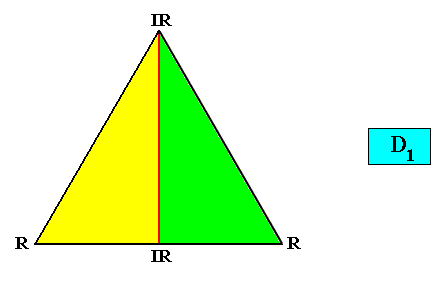
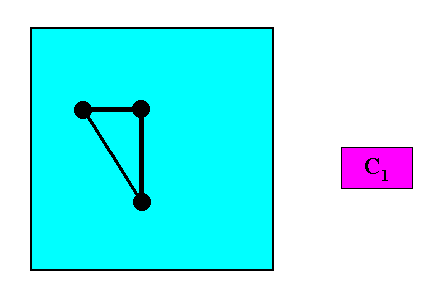
Zygopleura eudipleura
(isosceles triangles, symmetric zygopleura with two antimers, bilateral forms s.str.)
Planimetric Basic Form, representing this promorph :
Examples of crystals :
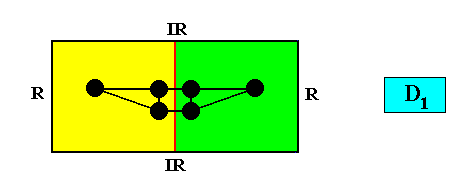Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D4
Meromorphic crystal D1 < D4
Meromorphic crystal D1 < D2
Meromorphic crystal D1 < D3
Meromorphic crystal D1 < D6
Asymmetric forms : Either forms without axes (apart from the trivial 1-fold rotation axis) and without antimers, or asymmetric Allopola with antimers.
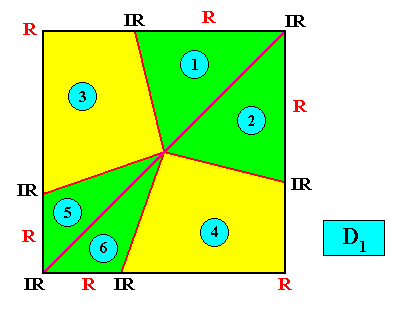
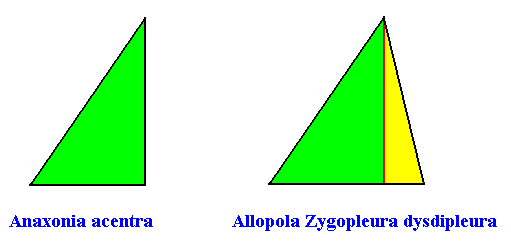
Asymmetric Allopola : either heteropleural, i.e. asymmetric, Amphipleura, or heteropleural Zygopleura [ In what follows we only display the Anaxonia acentra (no axes, no antimers, and promorphologically represented by a right-angled triangle), and the Zygopleura dysdipleura (heteropleural Zygopleura with two (unequal) antimers, promorphologically represented by an irregular triangle) ] :
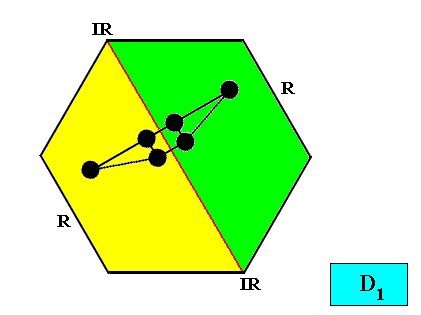
Anaxonia acentra / Zygopleura dysdipleura
(quarter-rhombi, i.e. right-angled triangles, or asymmetric zygopleura with two (unequal) antimers, irregular triangles)
Planimetric Basic Forms, representing these two promorphs :
Examples of crystals :
Meromorphic crystal C1 < D2
Meromorphic crystal C1 < D4
Meromorphic crystal C1 < C2
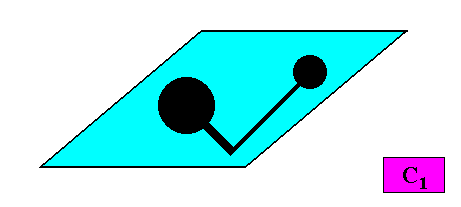Meromorphic crystal C1 < D2
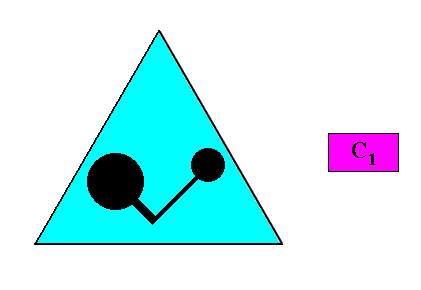Meromorphic crystal C1 < D3
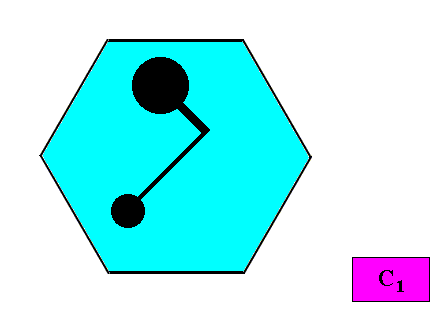Meromorphic crystal C1 < D6
This concludes our (second) summary, a summary of promorphs that can be possessed by two-dimensional crystals having the respective intrinsic shapes : Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon.
And in order to facilitate the overview of this summary we present it succinctly in the form of a table . One should realize, however, that the above (second) symmary and its corresponding overview table give the several promorphs together with some examples of crystal shapes, which means that the absence (in the summary and its table) of a particular potential example in addition to other examples already presented (in that summary and its table), has no theoretical significance . For instance for the Oxystaura octophragma two crystal examples were presented in the summary and in its corresponding overview table, viz. rectangular and rhomb-shaped crystals. And although, with respect to this promorph, which implies D2 intrinsic symmetry of the relevant crystal, the latter cannot have, among others, an intrinsic regularly triangular shape (because the 2-fold rotation axis of the D2 symmetry does not occur in a regular triangle, i.e. in an equilateral triangle), crystals having the shape of, say, a regular hexagon (as one of our six simple shapes) are possible (because a regular hexagon possesses at least all the D2 symmetries, viz. two mirror lines meeting at right angles, and a 2-fold rotation axis at their point of intersection). So, again, the following table only summarizes examples, examples that were given above (in the second summary). In it we state (1) the general promorph, (2) the ultimate promorph and its implied symmetry (which is the intrinsic point symmetry of the given crystal) and (3) the given examples of crystal shape (And after having presented this table, we give an overview (third summary) which shows which of our six simple shapes can be supported by the intrinsic crystal symmetries involved).
| Family of Promorphs |
Promorph
(and Symmetry) |
Shape |
| Stauraxonia homostaura |
Isopola hexactinota ( D6 ) |
Regular Hexagon |
| Stauraxonia homostaura |
Isopola tetractinota ( D4 ) |
Square |
| Stauraxonia homostaura |
Anisopola triactinota ( D3 ) |
Equilateral Triangle |
| Stauraxonia homostaura |
Anisopola triactinota ( D3 ) |
Regular Hexagon |
| Stauraxonia Gyrostaura homogyrostaura |
Homogyrostaura hexamera ( C6 ) |
Regular Hexagon |
| Stauraxonia Gyrostaura homogyrostaura |
Homogyrostaura tetramera ( C4 ) |
Square |
| Stauraxonia Gyrostaura homogyrostaura |
Homogyrostaura trimera ( C3 ) |
Equilateral Triangle |
| Stauraxonia Gyrostaura homogyrostaura |
Homogyrostaura trimera ( C3 ) |
Regular Hexagon |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura octomera ( C2 ) |
Rectangle |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura octomera ( C2 ) |
Square |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura octomera ( C2 ) |
Parallelogram |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura octomera ( C2 ) |
Rhombus |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura octomera ( C2 ) |
Regular Hexagon |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura tetramera ( C2 ) |
Rectangle |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura tetramera ( C2 ) |
Parallelogram |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura tetramera ( C2 ) |
Rhombus |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura tetramera ( C2 ) |
Regular Hexagon |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura dimera ( C2 ) |
Rectangle |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura dimera ( C2 ) |
Square |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura dimera ( C2 ) |
Parallelogram |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura dimera ( C2 ) |
Rhombus |
| Stauraxonia Gyrostaura heterogyrostaura |
Heterogyrostaura dimera ( C2 ) |
Regular Hexagon |
| Stauraxonia Heterostaura autopola |
Oxystaura octophragma ( D2 ) |
Rectangle |
| Stauraxonia Heterostaura autopola |
Oxystaura octophragma ( D2 ) |
Rhombus |
| Stauraxonia Heterostaura autopola |
Oxystaura hexaphragma ( D2 ) |
Rectangle |
| Stauraxonia Heterostaura autopola |
Oxystaura hexaphragma ( D2 ) |
Square |
| Stauraxonia Heterostaura autopola |
Oxystaura hexaphragma ( D2 ) |
Rhombus |
| Stauraxonia Heterostaura autopola |
Oxystaura hexaphragma ( D2 ) |
Regular Hexagon |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma radialia ( D2 ) |
Rectangle |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma radialia ( D2 ) |
Square |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma radialia ( D2 ) |
Rhombus |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma radialia ( D2 ) |
Regular Hexagon |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma interradialia ( D2 ) |
Rectangle |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma interradialia ( D2 ) |
Square |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma interradialia ( D2 ) |
Rhombus |
| Stauraxonia Heterostaura autopola |
Orthostaura Tetraphragma interradialia ( D2 ) |
Regular Hexagon |
| Stauraxonia Heterostaura autopola |
Orthostaura diphragma ( D2 ) |
Rectangle |
| Stauraxonia Heterostaura autopola |
Orthostaura diphragma ( D2 ) |
Square |
| Stauraxonia Heterostaura autopola |
Orthostaura diphragma ( D2 ) |
Rhombus |
| Stauraxonia Heterostaura autopola |
Orthostaura diphragma ( D2 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Amphipleura heptamphipleura ( D1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Amphipleura heptamphipleura ( D1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Amphipleura heptamphipleura ( D1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Amphipleura heptamphipleura ( D1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Amphipleura heptamphipleura ( D1 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Amphipleura hexamphipleura ( D1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Amphipleura hexamphipleura ( D1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Amphipleura hexamphipleura ( D1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Amphipleura hexamphipleura ( D1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Amphipleura hexamphipleura ( D1 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Amphipleura pentamphipleura ( D1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Amphipleura pentamphipleura ( D1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Amphipleura pentamphipleura ( D1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Amphipleura pentamphipleura ( D1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Amphipleura pentamphipleura ( D1 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Amphipleura triamphipleura ( D1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Amphipleura triamphipleura ( D1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Amphipleura triamphipleura ( D1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Amphipleura triamphipleura ( D1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Amphipleura triamphipleura ( D1 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura radialia ( D1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura radialia ( D1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura radialia ( D1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura radialia ( D1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura radialia ( D1 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura interradialia ( D1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura interradialia ( D1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura interradialia ( D1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura interradialia ( D1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Zygopleura Eutetrapleura interradialia ( D1 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Zygopleura eudipleura ( D1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Zygopleura eudipleura ( D1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Zygopleura eudipleura ( D1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Zygopleura eudipleura ( D1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Zygopleura eudipleura ( D1 ) |
Regular Hexagon |
| Anaxonia |
Anaxonia acentra ( C1 ) |
Rectangle |
| Anaxonia |
Anaxonia acentra ( C1 ) |
Square |
| Anaxonia |
Anaxonia acentra ( C1 ) |
Parallelogram |
| Anaxonia |
Anaxonia acentra ( C1 ) |
Rhombus |
| Anaxonia |
Anaxonia acentra ( C1 ) |
Equilateral Triangle |
| Anaxonia |
Anaxonia acentra ( C1 ) |
Regular Hexagon |
| Stauraxonia Heterostaura allopola |
Zygopleura dysdipleura ( C1 ) |
Rectangle |
| Stauraxonia Heterostaura allopola |
Zygopleura dysdipleura ( C1 ) |
Square |
| Stauraxonia Heterostaura allopola |
Zygopleura dysdipleura ( C1 ) |
Parallelogram |
| Stauraxonia Heterostaura allopola |
Zygopleura dysdipleura ( C1 ) |
Rhombus |
| Stauraxonia Heterostaura allopola |
Zygopleura dysdipleura ( C1 ) |
Equilateral Triangle |
| Stauraxonia Heterostaura allopola |
Zygopleura dysdipleura ( C1 ) |
Regular Hexagon |
The third summary consists of a table having as its first entries the point symmetries of the relevant two-dimensional crystals, while for each of these symmetries we list the intrinsic crystal shapes that can be supported by these symmetries.
A certain intrinsic crystal shape can only be supported if at least all the intrinsic symmetries (rotations, mirror reflections) of the crystal are also present in the overall symmetry of that particular shape. For example, a regular hexagon as intrinsic crystal shape can be supported by, among others, C2 intrinsic symmetry, because the half-turn (i.e. 1800 rotation, that already totally makes up C2 symmetry) is also present in a regular hexagon. Further, an equilateral triangle as intrinsic crystal shape cannot be supported by intrinsic D2 symmetry, because the half-turn of the latter is absent in an equilateral triangle. (In the table below we have written for "Equilateral Triangle" : "Regular Trigon").
| Crystal Symmetry and Supported Crystal Shape |
| D3 |
Regular Trigon |
Regular Hexagon |
| C3 |
Regular Trigon |
Regular Hexagon |
| D2 |
Regular Hexagon |
Rhombus |
Square |
Rectangle |
| D1 |
Regular Hexagon |
Regular Trigon |
Rhombus |
Square |
Rectangle |
| C2 |
Regular Hexagon |
Parallelogram |
Rhombus |
Square |
Rectangle |
| C1 |
Regular Hexagon |
Regular Trigon |
Parallelogram |
Rhombus |
Square |
Rectangle |
As a fourth summary, finally, we consider a shape, one after the other from the collection of intrinsic crystal shapes, considered in all the foregoing, and list their own point symmetry and the point symmetries that can support the given intrinsic shape.
| Shape |
Symmetry of Shape |
Supporting Symmetry |
| Rectangle |
D2 |
D2 D1 C2 C1 |
| Square |
D4 |
D4 C4 D2 D1 C2 C1 |
| Parallelogram |
C2 |
C2 C1 |
| Rhombus |
D2 |
D2 D1 C2 C1 |
| Equilateral Triangle |
D3 |
D3 C3 D1 C1 |
| Regular Hexagon |
D6 |
D6 C6 D3 C3 D2 D1 C2 C1 |
This concludes our four summaries concerning Intrinsic Shape, Intrinsic Point Symmetry and Promorph of two-dimensional crystals, where the intrinsic shapes considered were : Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon.
In the next document we continue theorizing about the mentioned crystal shapes and their relation to intrinsic point symmetry and promorph.
e-mail :
To continue click HERE for further study of the Theory of Layers, Part XV (Sequel-1).
e-mail :
Back to Homepage
Back to Contents
Back to Part I
Back to Part II
Back to Part III
Back to Part IV
Back to Part V
Back to Part VI
Back to Part VII
Back to Part VIII
Back to Part IX
Back to Part X
Back to Part XI
Back to Part XII
Back to Part XIII
Back to Part XIV