

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Regular Hexagon
REMARK : In this document (and also the next) the terms "hexagonal" and "hexagon" always refer to respectively "regularly-hexagonal" and "regular hexagon" .
Let us consider a fully developed two-dimensional crystal having an intrinsically hexagonal shape :
Any intrinsically hexagonal crystal can be conceived as being built up by a periodic stacking of microscopic rhombic units, where the rhombi possess angles of 60 and 120 degrees. See next Figure.
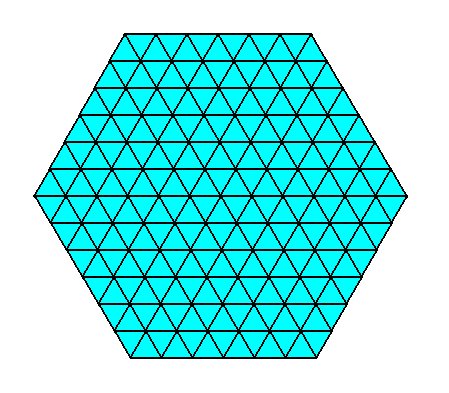
Figure above : Two-dimensional crystal consisting of the periodic stacking of rhombi with 60 and 120 degrees angles. These rhombi are thus unit meshes. In the drawing these rhombi are provided with lines dividing each one of them into two equilateral triangles. These triangles are repeated, but not periodically, because they show two different orientations. So they do not represent unit meshes. They represent a triangular non-periodic tiling of the two-dimensional plane. Six such triangles form a hexagon, which is, like the rhombus, a genuine unit mesh but not the smallest possible (which is the rhombus as drawn). The next Figures illustrate all this.
In the previous Figure a few half-rhombi are involved to smooth out some edges of the hexagon which should otherwise be jagged. The next Figure shows how things are if we strictly adhere to the crystal as consisting of whole rhombic building blocks only. (One should realize that these features, like the mentioned jaggednes, or the involvement of half-rhombi, are macroscopically not visible at all : The crystal consists of an astronomical number of microscopic rhombic building blocks, i.e. building blocks of very small size, causing the edges (crystal 'faces') to be smoothed out).
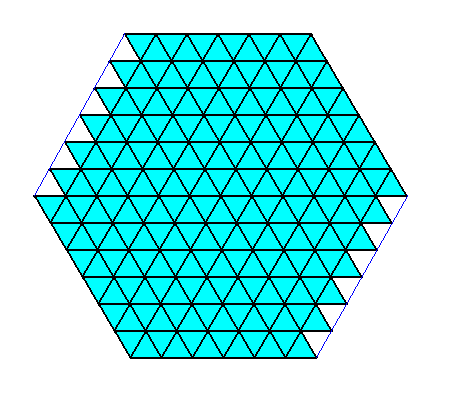
Figure above : Two-dimensional crystal consisting of the periodic stacking of rhombi with 60 and 120 degrees angles. These rhombi are thus unit meshes. As has been said, the triangles are not building blocks of the crystal in the sense of unit meshes, because their repetition is not periodic. Two edges are jagged, because of the strict adherence to periodic building blocks, in the present case rhombi with 60 and 120 degrees angles.
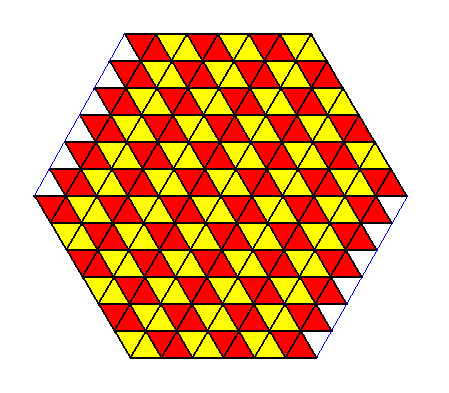
Figure above : This Figure clearly shows, by means of coloration, that the stacking of the rhombi (with 60 and 120 degrees angles) is periodic : their orientation (and size and shape) is the same throughout the pattern.
The next Figure shows the hexagonal symmetry of (also) the internal structure of our hexagonal crystal. Because the meshes are not provided with a motif lowering the symmetry (for instance 3-fold motifs), the symmetry of the pattern, as hexagonal net, is maximal, which means that the pattern (now imagined to be extended indefinitely over the plane) has a symmetry according to the plane group P6mm . The point symmetry of the hexagonal crystal, as drawn, is according to the Dihedral Group D6 . See also next Figure.
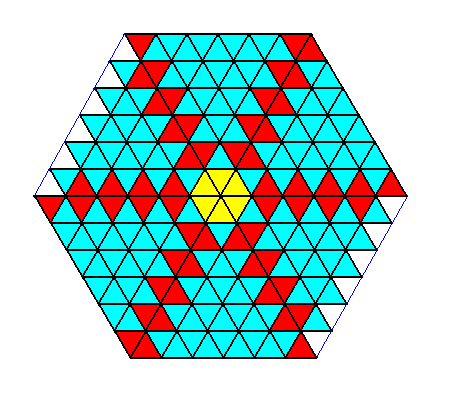
Figure above : This Figure indicates the hexagonal point symmetry (D6) of the two-dimensional crystal of the above Figures.
As has been said, a larger building block (larger than the above discussed rhombi) for our hexagonal crystal is possible : regularly-hexagonal building blocks. The next Figure indicates these building blocks by coloring.
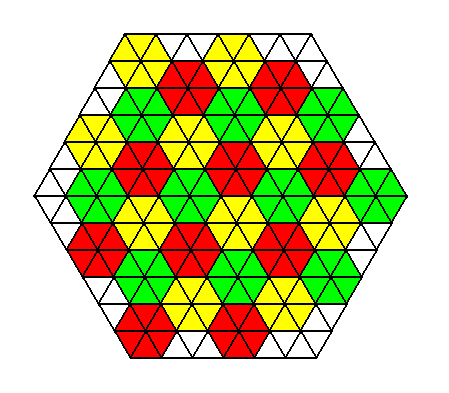
Figure above : Two-dimensional crystal of the above Figures. Hexagonal building blocks.
The next Figure indicates the symmetry elements of the two-dimensional hexagonal crystal consisting of empty rhombic building blocks.
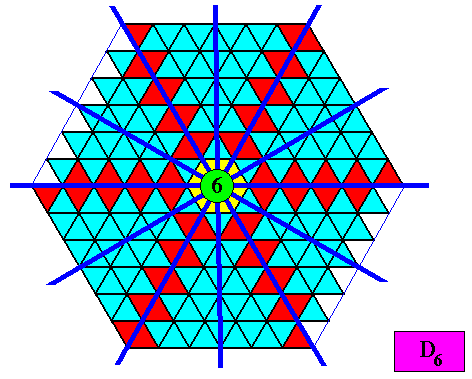
Figure above : Symmetry elements of the two-dimensional crystal of the above Figures. Rhombic (60/1200) building blocks. Six mirror lines and one 6-fold rotation axis at their point of intersection.
As was the case in the previous two documents, the hexagonal lattice, i.e. a lattice consisting of the periodic stacking of 60/1200 rhombi, is equivalent to a lattice consisting of the stacking of special rectangles, namely such that their diagonals involve angles of 600. See next Figures.
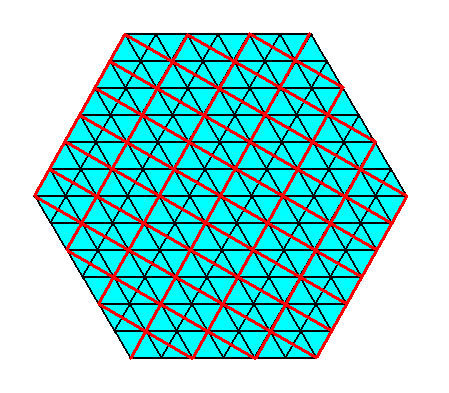
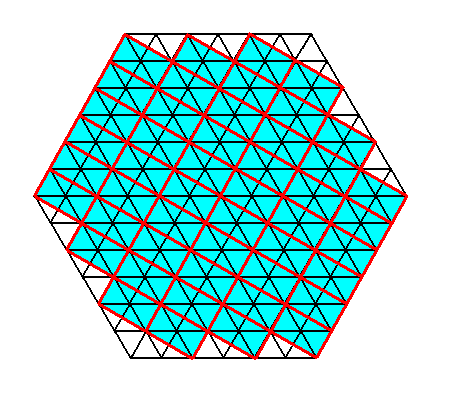
Figure above : Two-dimensional hexagonal crystal consisting of the stacking of special rectangles (red lines), of which the diagonals involve 600 angles. Recall that the lines delineating small triangles or rhombi do not, strictly speaking, belong to the pattern presently under discussion. The 'motifs' of this pattern are the (empty) hexagonal contents of unit hexagons (each divisible into six equilateral triangles, see Figure above ). Such a motif has D6 symmetry, letting the pattern have the maximal plane group symmetry that a hexagonal net can support. As has been said, this symmetry is according to the group P6mm. Other motifs, but of the same point group symmetry (D6), do not change this maximal plane group symmetry. If, however, instead of such motifs, lower symmetric motifs are inserted in the hexagonal net, then the plane group symmetry (and by definition also the point group symmetry) will be lower (with "motif" here is meant : translation-free residue).
In the Figures to come, concerning hexagonal crystals based on one or another plane group, we will use the 60/1200 rhombi as meshes for our hexagonal lattice, because these rhombi are smaller than the corresponding rectangles. However, with respect to the plane groups Pm, Pg, P2mm, P2mg, and P2gg, we will use the mentioned special rectangles, to express the primitive rectangular net associated with these plane groups.
We will now give some general preliminaries concerning the ensuing discussion and exemplifications of the several possible types of two-dimensional crystals which have an intrinsically hexagonal shape.
The true, i.e. intrinsic, point symmetry of such a crystal is either the same as the symmetry of its intrinsic shape, the regular hexagon, and thus according to the Dihedral Group D6 (crystallographically denoted as 6mm), or this (intrinsic) symmetry is lower. It is then either according to the Cyclic Group C6 (crystallographically denoted as 6), or to the Dihedral Group D3 (crystallographically denoted as 3m), or according to the Cyclic Group C3 (crystallographically denoted as 3), or to the Dihedral Group D2 (crystallographically denoted as 2mm), or to the Dihedral Group D1 (crystallographically denoted as m), or to the Cyclic Group C2 (crystallographically denoted as 2), or, finally, according to the Asymmetric Group C1 (crystallographically denoted as 1), all depending on the crystal's internal structure.
That a hexagonal crystal can have these intrinsic symmetries can be explained succinctly as follows (and will be further evident in the sequel) :
A regular hexagon as such has the following symmetries, i.e. it will be superposed upon itself by the following transformations (which are then for that reason symmetry transformations) (See also Figure below ) :

| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 6 |
| P2 | C2 ( 2 ) | 3 |
| Pm Cm Pg |
D1 ( m ) | 3 |
| P2mm C2mm P2mg P2gg |
D2 ( 2mm ) | 2 |
| P3 | C3 ( 3 ) | 2 |
| P3m1 P31m |
D3 ( 3m ) | 1 |
| P6 | C6 ( 6 ) | 1 |
| P6mm | D6 ( 6mm ) | 1 |
For each of these plane groups we will show how it supports a hexagonal crystal shape. The intrinsic shape of the crystal, i.e. the shape a crystal adopts when fully grown (i.e. fully developed) under uniform conditions, in the present case its hexagonal shape, depends on the Growth Rate Vector Rosette, which in turn depends on the atomic aspects (chemical nature of motifs and geometry of lattice) presented to the growing environment by the possible crystal faces. The hexagonal crystal can be formed by the periodic stacking of 60/1200 rhomb-shaped building blocks (unit meshes) or special rectangles of which the diagonals involve angles of 600, building blocks containing a motif s.str. compatible with the point symmetry implied by the given plane group. The point symmetry is indicated in each case. Recall that the point symmetry of a crystal is the translation-free residue of its plane group symmetry.
A regular hexagon, which has a point symmetry according to the group D6 , will be supported by those plane groups of which all the implied point symmetries (i.e. implied by the plane group) are also symmetries of the Regular Hexagon. This does not necessarily hold the other way around : A crystal can have an intrinsic shape that is a regular hexagon, but nevertheless some, or even all, symmetries of this hexagon can be absent in the crystal, resulting in the fact that the intrinsic symmetry of the crystal is lower than that of its intrinsic shape.
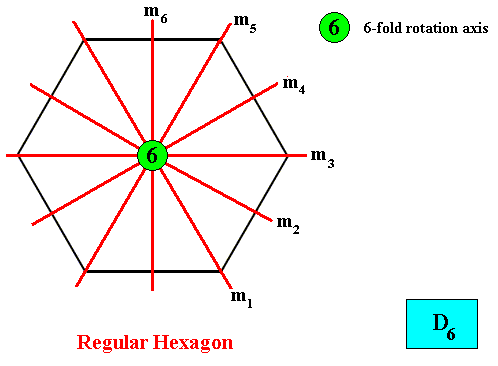
Figure above : The symmetries (indicated by symmetry elements) of the Regular Hexagon : Six mirror lines and a six-fold rotation axis at their point of intersection.
Plane Group P6mm.
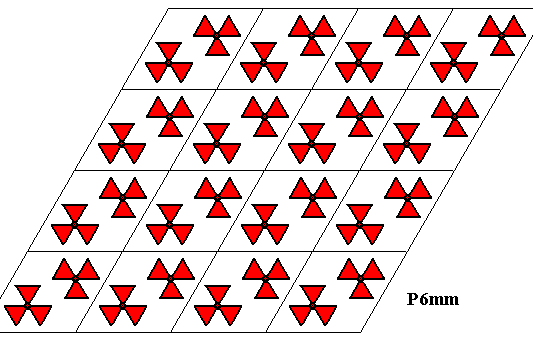
Figure above : A pattern according to the plane group P6mm .
Each rhombic lattice mesh contains two D3 motifs s.str. that are rotated 600 with respect to each other. The pattern must be imagined to be extended indefinitely over the plane.
On the periodic pattern of the above Figure a hexagonal crystal can be based as follows :
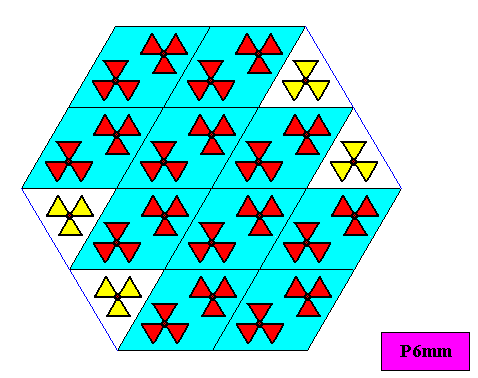
Figure above : A two-dimensional hexagonal crystal with point symmetry D6 based on a hexagonal lattice, i.e. on a periodic stacking of 60/1200 rhombi. At the jagged sides the motif pattern is extended a little bit by adding some motif units (yellow) at appropriate locations, in order to make evident the crystal's point symmetry.
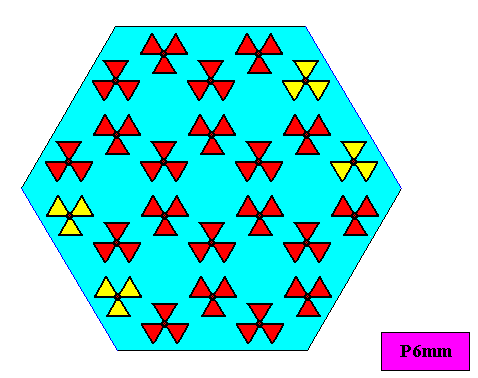
Figure above : Same as previous Figure. Lattice connection lines (which do not belong to the pattern) erased.
The next Figure shows the D6 symmetry of the hexagonal crystal of the previous Figures.
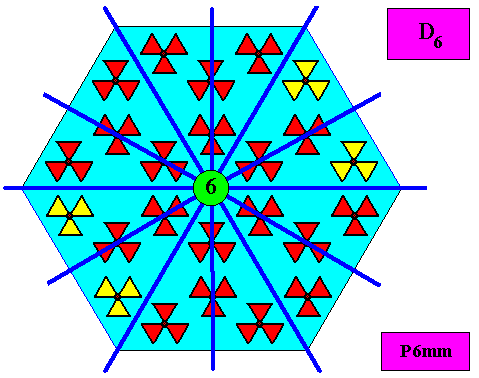
Figure above : Symmetry elements of the hexagonal crystal of the previous Figures : Six mirror lines and one 6-fold rotation axis at their point of intersection. And this pattern of symmetry elements is the fingerprint of D6 symmetry. In the present case the intrinsic point symmetry of the crystal is the same as that of its intrinsic shape (regular hexagon).
Plane Group P6.
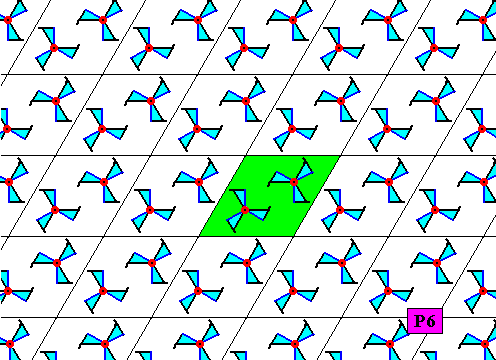
Figure above : A pattern representing the plane group P6 . It has its three-fold motifs s.str. at the mid-points of the equilateral triangles that make up the rhombic unit meshes of the hexagonal point lattice. A lattice mesh is indicated (green).
Hexagonal crystals can be supported by this (P6) pattern, as the next Figure shows.
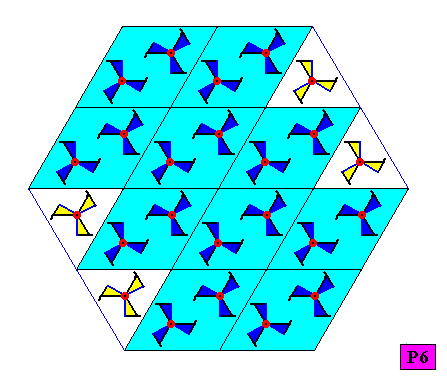
Figure above : A two dimensional hexagonal crystal, supported by a P6 pattern. It can be conceived as consisting of a periodic stacking of 60/1200 rhombic building blocks. The intrinsic point symmetry of the crystal is according to the group C6 . This is shown in the next two Figures, where the first one depicts, to begin with, the pattern proper, i.e. without the lattice connection lines.
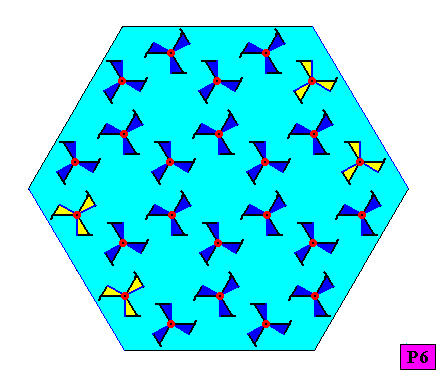
Figure above : The above two-dimensional C6 crystal with hexagonal shape. Lattice connection lines omitted (they do not belong to the pattern).
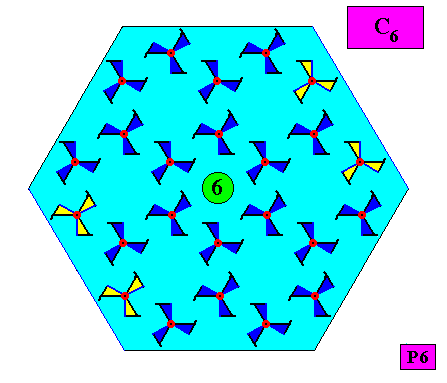
Figure above : A 6-fold rotation axis as the only symmetry element of the above two-dimensional C6 crystal with hexagonal shape. Its point symmetry is therefore C6 . As also all the crystals below, the present crystal (thus) has a lower intrinsic symmetry than that of its (intrinsic) shape (which is a regular hexagon and has D6 symmetry).
Plane Group P3m1.
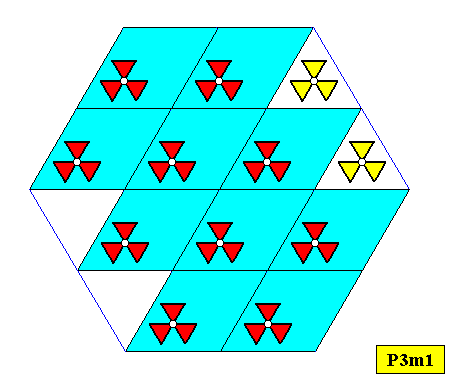
Figure above : A two-dimensional hexagonal crystal supported by a P3m1 pattern. The point symmetry of this crystal is D3 . The crystal results from a periodic stacking of 60/1200 rhombic building blocks according to a hexagonal net.
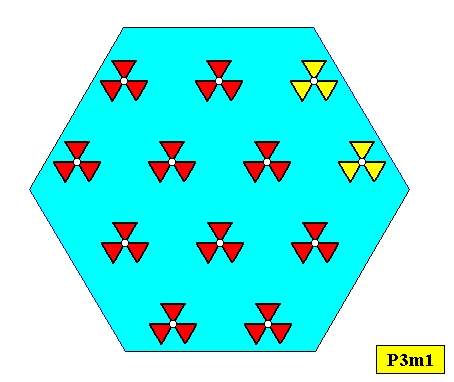
Figure above : Same as previous Figure. Lattice connection lines removed.
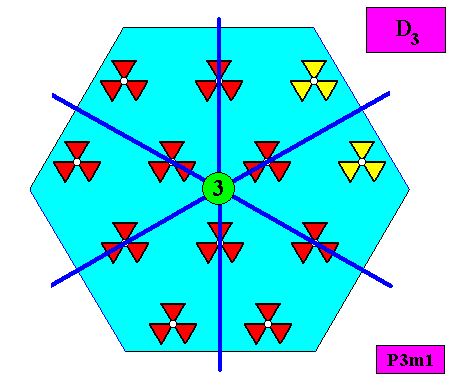
Figure above : Symmetry elements (three mirror lines and one 3-fold rotation axis at their point of intersection) of the above depicted two-dimensional hexagonal crystal based on a P3m1 pattern. The point symmetry of the crystal is accordingly D3 .
Plane Group P31m.
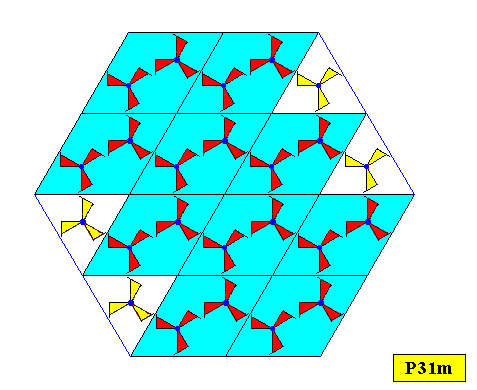
Figure above : A two-dimensional hexagonal crystal supported by a P31m pattern. The point symmetry of this crystal is D3 . The crystal results from a periodic stacking of 60/1200 rhombic building blocks according to a hexagonal net.
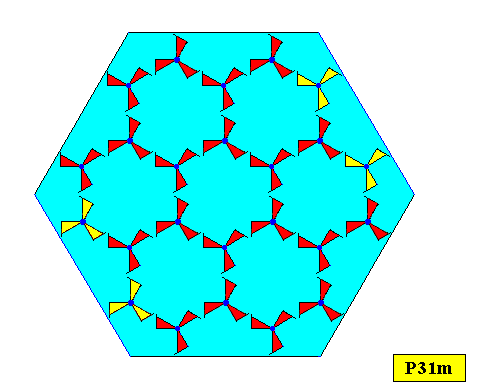
Figure above : Same as previous Figure. Lattice connection lines removed.
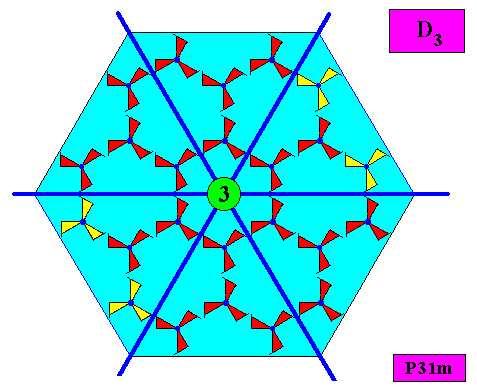
Figure above : Symmetry elements (three mirror lines and one 3-fold rotation axis at their point of intersection) of the above depicted two-dimensional hexagonal crystal based on a P31m pattern. The point symmetry of the crystal is accordingly D3 .
Plane Group P3.
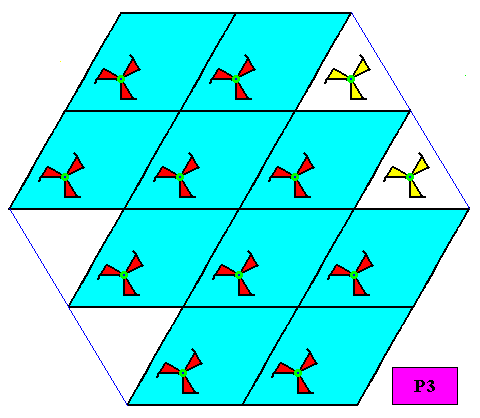
Figure above : A two-dimensional hexagonal crystal supported by a P3 pattern. The point symmetry of this crystal is C3 . The crystal results from a periodic stacking of 60/1200 rhombic building blocks according to a hexagonal net.
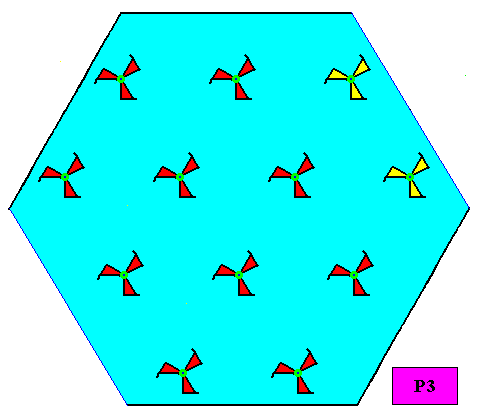
Figure above : Same as previous Figure. Lattice connection lines removed.
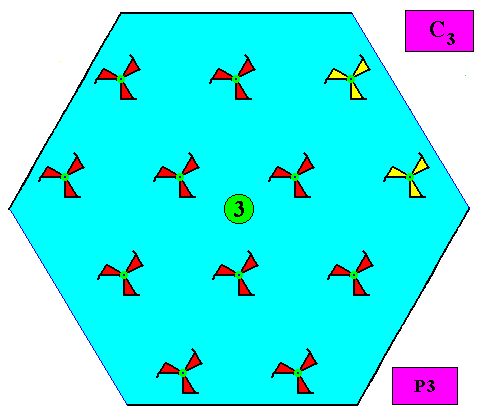
Figure above : Symmetry elements (one 3-fold rotation axis only) of the above depicted two-dimensional hexagonal crystal based on a P3 pattern. The point symmetry of the crystal is accordingly C3 .
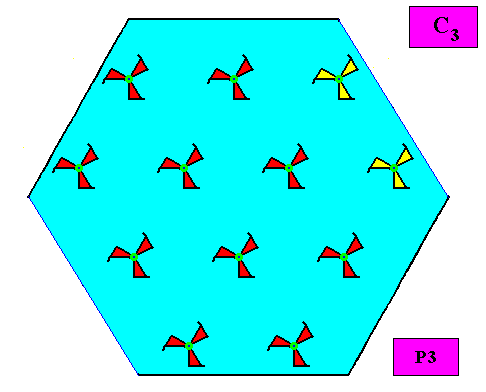
Figure above : Slightly smaller version of the above crystal (hexagonal, C3), for convenient overview of its hexagonal shape.
Plane Group P2mm.
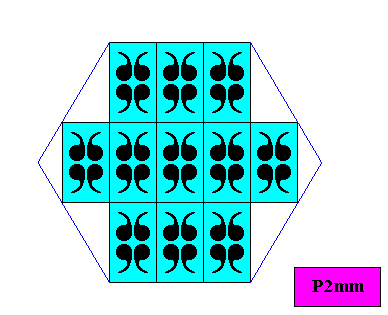
Figure above : Two-dimensional hexagonal crystal, i.e. a crystal having as its intrinsic shape a regular hexagon, consisting of a stacking of special rectangles, viz. rectangles such that their diagonals involve angles of 600. The lattice plus D2 motifs is a periodic pattern with a symmetry according to the plane group P2mm. The crystal therefore, despite its regularly-hexagonal intrinsic shape, has D2 (point) symmetry (and not D6 symmetry). That the crystal shape, so obtained, is indeed a regular hexagon is partially proven in the next Figure. There we found three corners of the six-sided polygon to be 1200. The other three corners are then also 1200 by reason of the reflectional symmetry of the pattern.
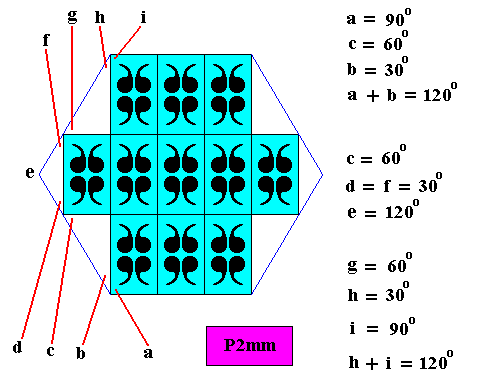
Figure above : The crystal's six-sided shape obtained by periodic stacking of special rectangles (having diagonals involving 600 angles) has corners of 1200. The next Figure shows that also the six sides are equal in length.
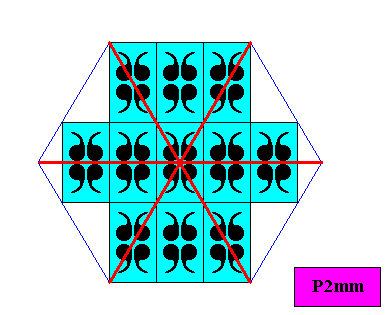
Figure above : Because of the fact that the relevant angles are all 600, the polygon (with corners of 1200) consists of six congruent equilateral triangles, proving it to be a regular hexagon.
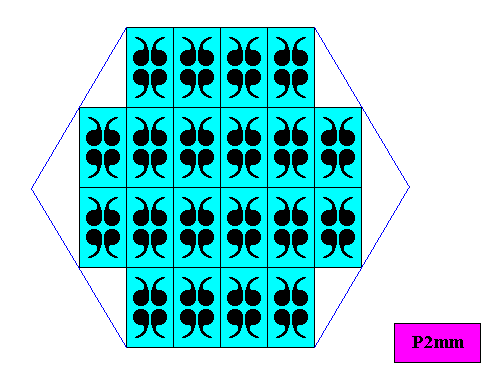
Figure above : As in the three previous Figures. A two-dimensional crystal, having a regular hexagon as its intrinsic shape, obtained by periodic stacking of special rectangles (having diagonals involving 600 angles). Larger version.
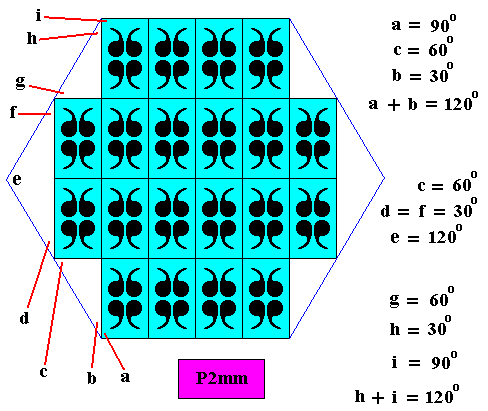
Figure above : Same as previous Figure. Also here the corners are 1200 each.
Also this larger version (with corners of 1200) consists of six congruent equilateral triangles, proving the six-sided polygon to be a regular hexagon.
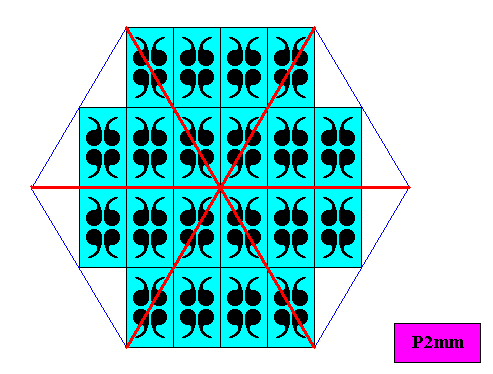
Figure above : Same as previous Figure. Also here the six-sided polygon is a regular hexagon.
The next Figures show the symmetry elements of the above two-dimensional intrinsically hexagonal crystal (both size versions) based on the plane group P2mm. It shows that the intrinsic point symmetry of this crystal is according to the group D2 .
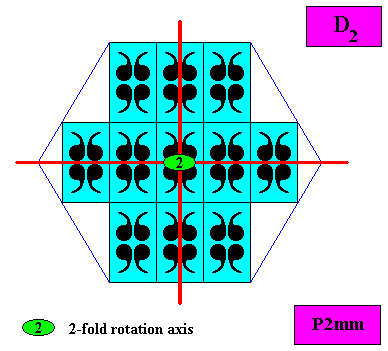
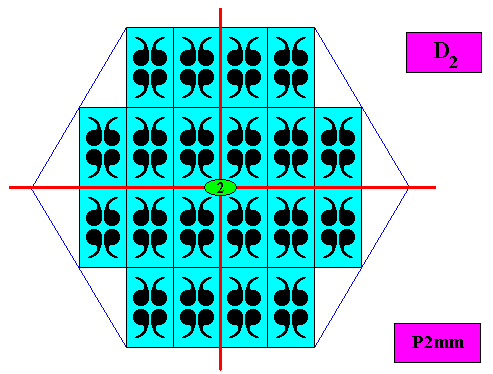
Plane Group P2mg.
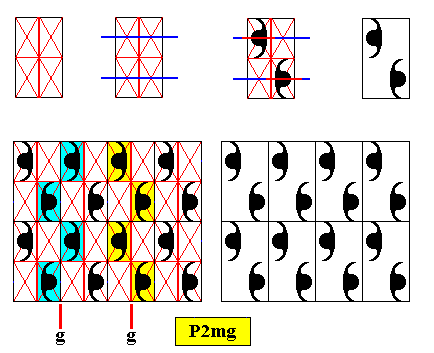
Figure above : Construction of a P2mg pattern based on special rectangles, namely rectangles such that their diagonals involve angles of 600 . Some glide lines ( g ) indicated. See also next Figure.

Figure above : Result of the construction of a P2mg pattern based on special rectangles, namely rectangles such that their diagonals involve angles of 600 (As always, the lattice connection lines -- here the lines delineating the rectangles -- do not belong to the pattern).
The next Figure demonstrates the P2mg nature of the pattern. Some glide lines ( g ), some mirror lines ( m ) and some 2-fold rotation axes are indicated.
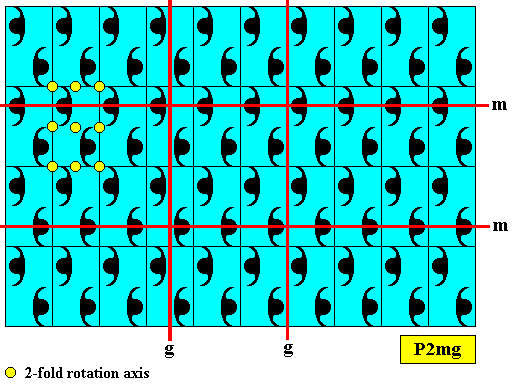
From the just constructed P2mg pattern we derive a two-dimensional crystal with point symmetry D2 and having an intrinsic hexagonal shape (regular hexagon) :
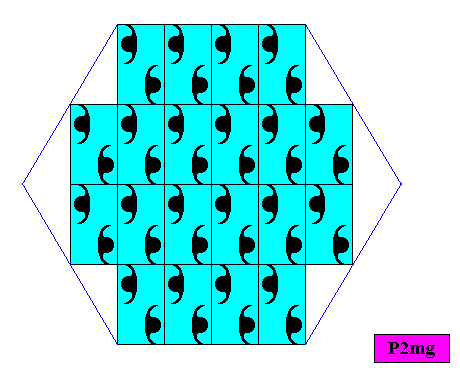
Figure above : A two-dimensional intrinsically hexagonal crystal based on a P2mg pattern. The lattice consists of special rectangles, viz. rectangles such that their diagonals involve angles of 600.
The next two Figures indicate the symmetry elements (with respect to point symmetry) of our hexagonal crystal (two size versions).
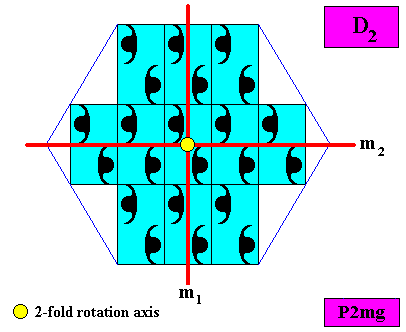
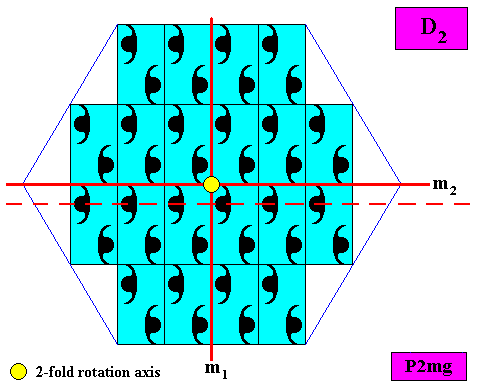
The two Figures above : Symmetry elements -- two mirror lines ( m1, m2 ) and a two-fold rotation axis -- of the just discussed two-dimensional intrinsically hexagonal crystal, based on a P2mg pattern. The set of these symmetry elements determines the point symmetry of the crystal to be according to the group D2 . In both Figures one can see that the lines m1 and m2 do not in fact present themselves as mirror lines : The vertical line is in fact a glide line, but macroscopically this becomes a mirror line. The horizontal line is a little diplaced from the position where it should be (indicated by a dashed line in the Figure directly above), but this displacement is macroscopically invisible because of its utter smallness.
Plane Group P2gg.
The next two Figures show the construction of a P2gg pattern based on a stacking of special rectangles, viz. rectangles such that their diagonals involve angles of 600 .
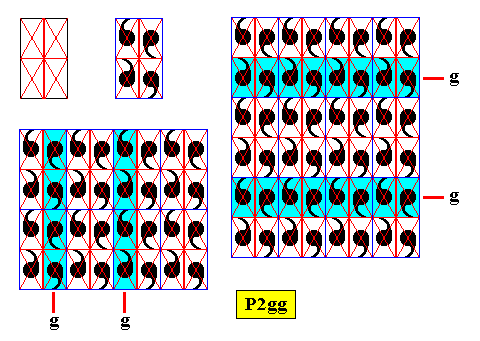

The two Figures above : Construction and its result of a P2gg pattern consisting of a stacking of (filled-in) special rectangles, viz. rectangles of which the diagonals involve angles of 600 . Some glide lines ( g ) indicated. See also next Figure.
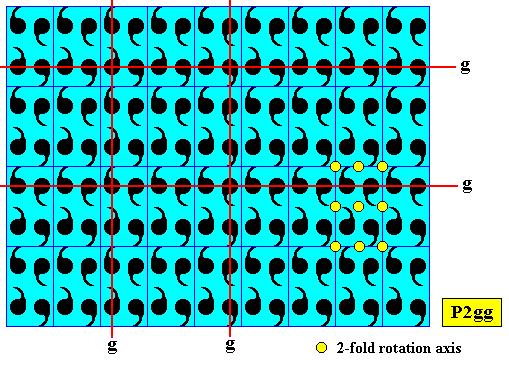
Figure above : The pattern is clearly a P2gg pattern : Some glide lines and some 2-fold rotation axes are indicated (Recall that a periodic pattern, as depicted here, must always be imagined to extend indefinitely over the plane).
From the just constructed P2gg pattern we will derive hexagonal crystals, i.e. crystals based on the periodic stacking of special rectangles filled in with motifs (as described above), resulting in P2gg plane group symmetry and D2 point group symmetry, while the intrinsic shape of such a crystal is that of a regular hexagon. See next Figures.
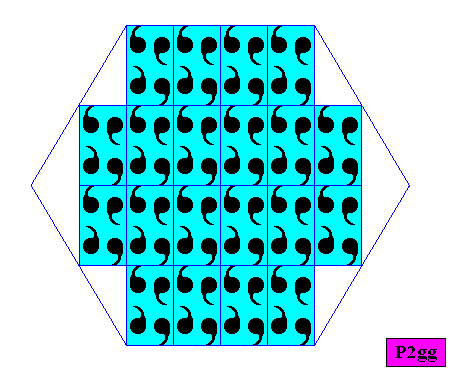
Figure above : Intrinsically hexagonal two-dimensional crystal based on a P2gg pattern. Its point symmetry is according to the group D2 .
The next Figures are about the symmetry elements (regarding point symmetry) of such hexagonal crystals.
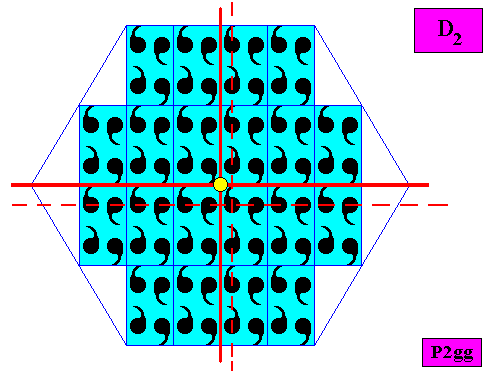
Figure above : Intrinsically hexagonal two-dimensional crystal based on a P2gg pattern. Its symmetry elements are indicated : Two mirror lines (red) perpendicular to each other, and a two-fold rotation axis (indicated by a small yellow circle) at the intersection point of the mirror lines. The point symmetry of the crystal is therefore according to the group D2 . In fact the solid lines fail to express mirror lines of the crystal. But this is only seemingly so : First of all they must be seen as the translation-free residues of glide reflections, because the translations (shifts) involved in the glide reflections are macroscopically undetectable, changing in this way the glide line into a mirror line at the macroscopical level. Second, the relevant glide lines (indicated by dashed lines) are somewhat displaced with respect to the relevant crystal corners, but this displacement also is not detectable macroscopically [Realize that -- as in real (3-dimensional) crystals -- the number of building blocks making up our crystal must conceived to be huge].
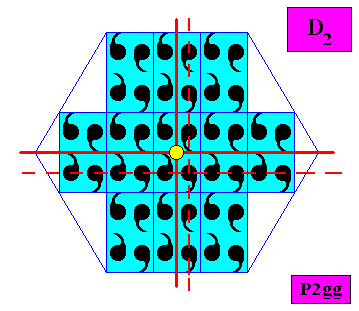
Figure above : Same as previous Figure. Smaller version of crystal. Also here the displacements of the glide lines (dashed lines) -- which macroscopically will present themselves as mirror lines -- are macroscopically undetectable.
Plane Group C2mm.
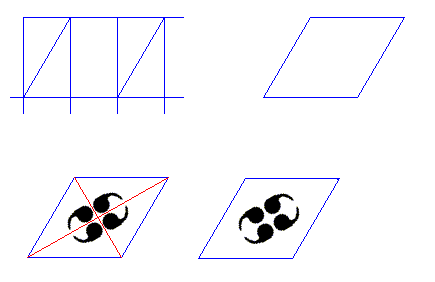
Figure above : Construction of a 60/1200 rhombic unit mesh (with compatible motif) from the rectangle used in the Figures above, viz. a rectangle the diagonals of which involve angles of 600. This unit mesh can be the building block for an intrinsically hexagon-shaped crystal based on the plane group C2mm. See next Figures.
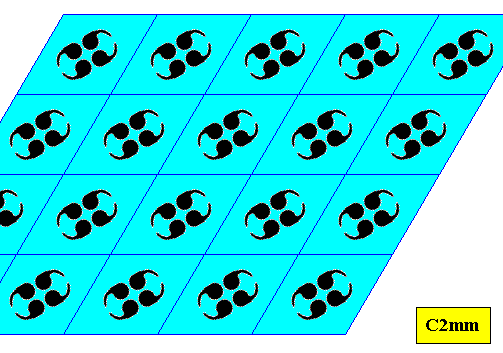
Figure above : C2mm pattern based on 60/1200 rhombic building blocks as constructed in the previous Figure.
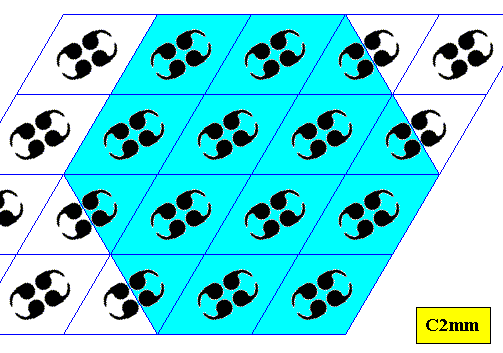
Figure above : Construction of a hexagon-shaped crystal based on the C2mm pattern of the previous Figure.
The next three Figures show the result of this construction.
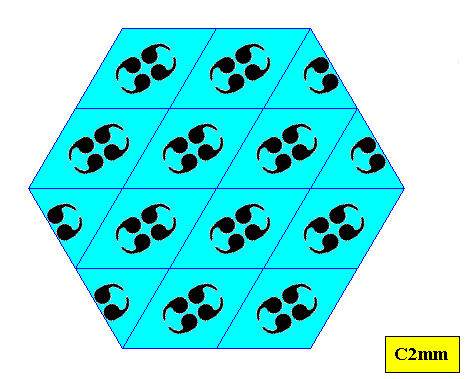
Figure above : Result of the construction of a hexagon-shaped crystal based on the C2mm pattern as given above. In fact, two edges are not smooth. See next two Figures.
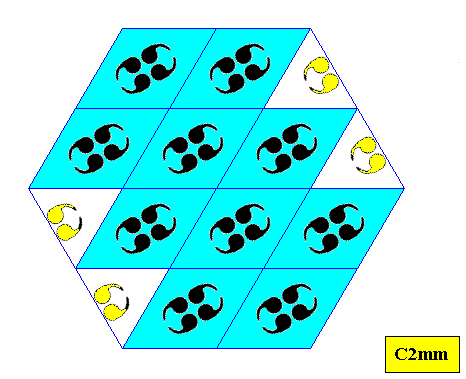
Figure above : A hexagon-shaped crystal based on the C2mm pattern as given above, and formed by the periodic stacking of (whole) 60/1200 rhombic building blocks (as constructed above). Two edges are not smooth.
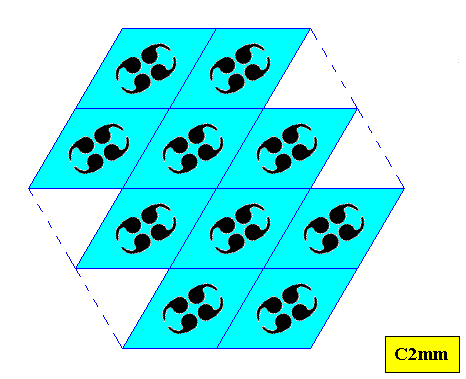
Figure above : A hexagon-shaped crystal based on the C2mm pattern as given above. Two edges are not smooth.
Including half building blocks, in order to let the hexagonal shape stand out clearly, as in the Figure above , and removing the lattice connection lines, gives the following :
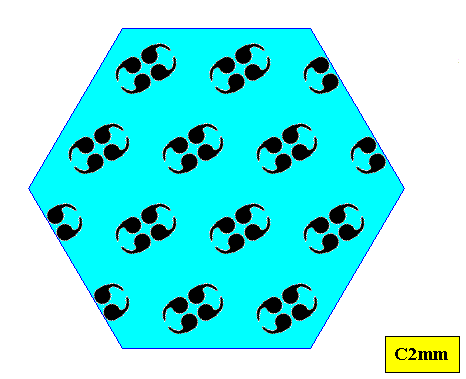
Figure above : A hexagon-shaped crystal based on the C2mm pattern as given above. Lattice connection lines removed (they do not belong to the pattern).
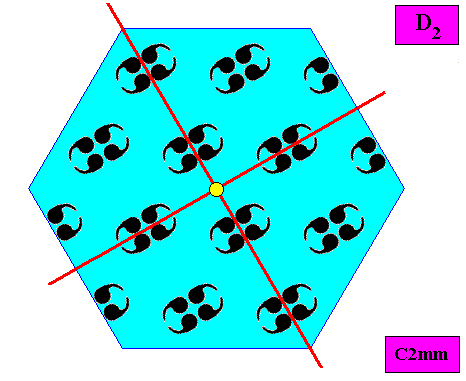
Figure above : Symmetry elements (with respect to point symmetry : two perpendicular mirror lines and a 2-fold rotation axis -- yellow circle -- at their point of intersection) of a hexagon-shaped crystal based on the C2mm pattern as given above. The point symmetry of the crystal is clearly according to the group D2 .
Plane Group Pm.
On the basis of the plane group Pm a hexagon-shaped crystal can be formed by the periodic stacking of special rectangular building blocks (provided with a compatible motif) : The rectangles are such that their diagonals involve angles of 600. See next Figure.
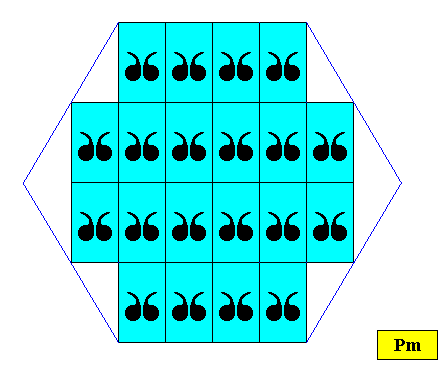
Figure above : Intrinsically hexagon-shaped two-dimensional crystal, based on a Pm pattern with special rectangular building blocks, and D1 motifs.
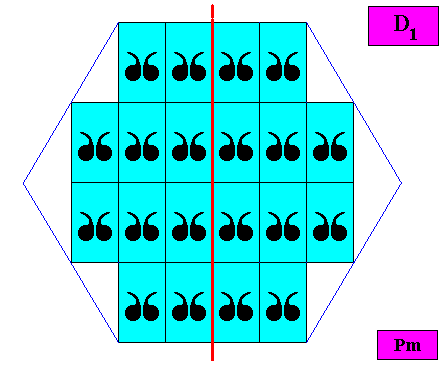
Figure above : Symmetry elements (with respect to point symmetry : a mirror line (red) only) of the above given intrinsically hexagon-shaped two-dimensional crystal. The point symmetry of the latter is indeed clearly according to the group D1 .
Plane Group Pg.
On the basis of the plane group Pg a hexagon-shaped crystal can be formed by the periodic stacking of special rectangular building blocks (provided with a compatible motif) : The rectangles are such that their diagonals involve angles of 600. See next Figure.
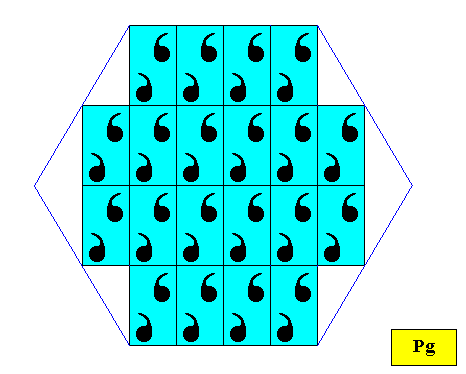
Figure above : Intrinsically hexagon-shaped two-dimensional crystal, based on a Pg pattern with special rectangular building blocks, and D1 motifs as translation-free residues (i.e. after elimination of the translational component of the glide reflection -- which is equivalent to looking at the crystal from a macroscopic perspective -- we end up with a mirror line).
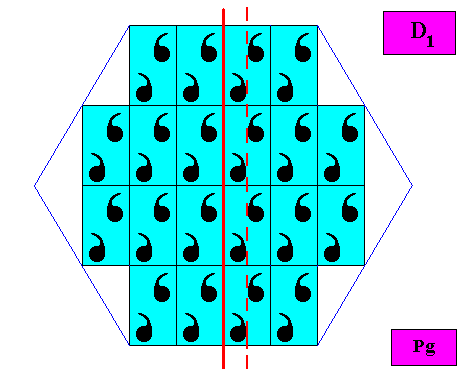
Figure above : Symmetry elements (with respect to point symmetry : a mirror line (red) only) of the above given intrinsically hexagon-shaped two-dimensional crystal. In fact, the glide line, which macroscopically expresses itself as a mirror line, and in this way representing the mentioned symmetry element of the crystal, is a little displaced (dashed line) with respect to the corners of the crystal, but this displacement is macroscopically undetectable. So the point symmetry of the latter is indeed clearly according to the group D1 .
Plane Group Cm.
On the basis of the plane group Cm a hexagon-shaped crystal can be formed by the periodic stacking of special rhombic building blocks (provided with a compatible motif) : The rhombi have angles of 60 and 1200. The stacking of these rhombi results in a hexagonal lattice. See next Figure.
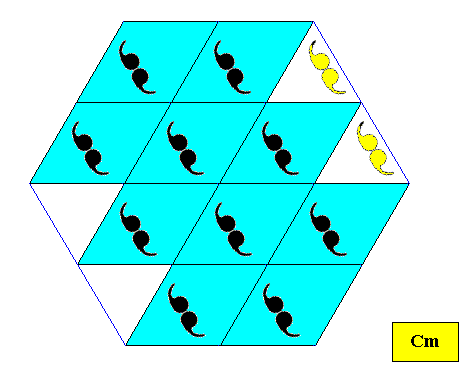
Figure above : Intrinsically hexagon-shaped two-dimensional crystal, based on a Cm pattern with 60/1200 rhombic building blocks, and D1 motifs.
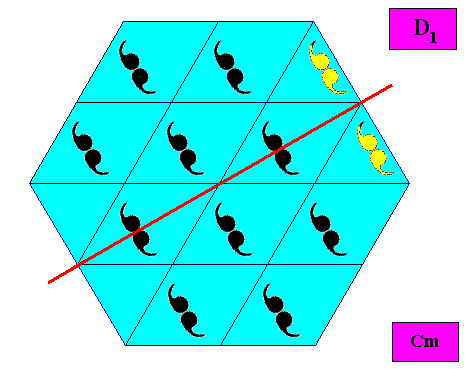
Figure above : Symmetry elements (with respect to point symmetry : a mirror line (red) only) of the above given intrinsically hexagon-shaped two-dimensional crystal. The point symmetry of the latter is indeed clearly according to the group D1 .
Plane Group P2.
An intrinsic hexagon-shaped crystal can be derived from a P2 pattern, based on an oblique lattice, where the two independent translations happen to be perpendicular to each other, with lengths such that the diagonals of the resulting rectangular meshes involve angles of 600 . See next Figure.
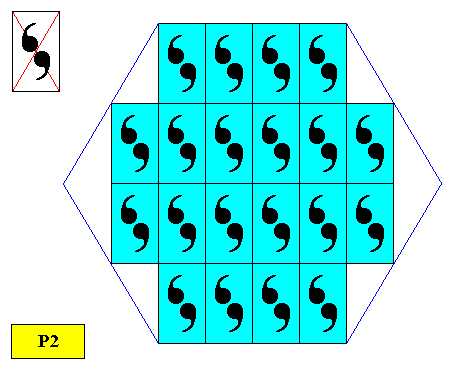
Figure above : Intrinsically hexagon-shaped two-dimensional crystal based on a P2 pattern with oblique lattice, where the meshes happen to be rectangles with diagonals involving angles of 600 .
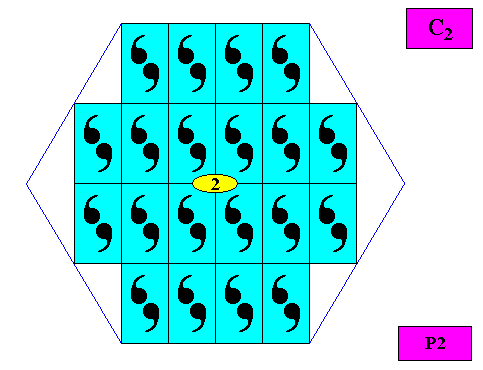
Figure above : Symmetry elements (with respect to point symmetry : a 2-fold rotation axis [yellow ellipse] only) of the hexagonal crystal of the previous Figure. The point symmetry of this crystal is clearly according to the group C2 .
Plane Group P1.
An intrinsic hexagon-shaped crystal can be derived from a P1 pattern, based on an oblique lattice, where the two independent translations happen to be perpendicular to each other, with lengths such that the diagonals of the resulting rectangular meshes involve angles of 600 . See next Figure.
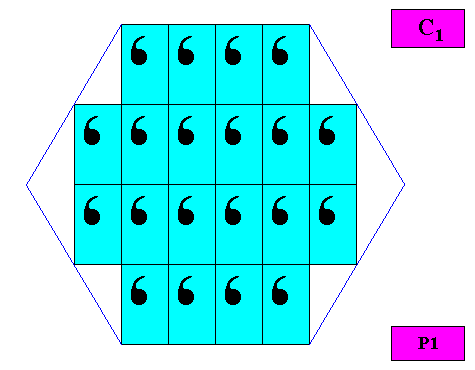
Figure above : Intrinsically hexagon-shaped two-dimensional crystal based on a P1 pattern with oblique lattice, where the meshes happen to be rectangles with diagonals involving angles of 600 . The crystal has no symmetry elements (with respect to point symmetry), so its point symmetry is according to the Asymmetric Group C1 .
This concludes an overview of how and when intrinsically hexagon-shaped two-dimensional crystals are supported.
In the next document we will investigate the possible promorphs of these two-dimensional regularly-hexagonal crystals.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XIV.
e-mail : 