General Ontology XXIXc

General Ontology Cosmos and Nomos

Theory of Ontological Layers and Complexity Layers

Part XXIX (Sequel-3)

Crystals and Organisms

Theory of intrinsic Shape, intrinsic Symmetry and Promorph

e-mail :

Back to Homepage

Sequel-3 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).

This document (Part XXIX Sequel-3) appends a preliminary investigation into the 'phyllotaxis', symmetry, promorphology and ontology of snow crystals, as
i n o r g a n i c w h o r l e d s t r u c t u r e s.

When a crystal starts growing from a solution or melt, the conditions have apparently become such that this initial solution or melt have become unstable. And because there are always perturbations going on, the system -- solution or melt -- will spontaneously slide off to a lowest-energy configuration. Which configuration (of atoms) this is, is determined by the relevant quantum mechanical properties of the system elements. But the question is how do the elements in the solution or melt actually manage to organize themselves into this lowest-energy configuration. The answer to this question could run as follows :
There are enough opportunities for the solution or melt to perform an enormous number of random 'trials' -- element configuration trials -- finally resulting in a lowest-energy configuration of sufficient size, and thus resulting in a crystal seed. This is eased by the fact that atoms or atomic groups cannot just combine in any way whatsoever, but only according to definite chemical affinities. Further growth from the crystal seed is then guided by the seed itself, which functions as template. In this way a definite materially filled-in crystal lattice will emerge and grow, with (a set of) growth rates corresponding to the (set of) atomic aspects presented to the growing environment in several directions by this (materially filled-in) lattice. So it seems that a reductionistic explanation is possible for the emergence of crystalline structures from a melt or solution (or from a vapor for that matter).
However, we know that a same chemical substance can take up different possible structures when crystallizing, depending on the prevailing thermodynamic conditions. Even such a simple chemical compound like Aluminum silicate, Al₂SiO₅ , can crystallize as three different minerals, depending on the thermodynamic condition :

Mineral	Chemical Formula	Crystal Class (Point Group)	Space Group
Andalusite	Al₂SiO₅	2/m 2/m 2/m	P 2₁/n 2₁/n 2/m
Sillimanite	Al₂SiO₅	2/m 2/m 2/m	P 2₁/n 2₁/m 2₁/a
Disthene (= Kyanite)	Al₂SiO₅	1*	P 1*

(See STRÜBEL, G., Mineralogie, 1977, p. 217)

Here 2/m2/m2/m means the Rhombic-Dipyramidal Class of the Orthorhombic Crystal System, and 1* means the Pinacoidal Class of the Triclinic Crystal System.
The three minerals belong to different Space Groups (i.e. three-dimensional symmetry groups including translational elements, and thus representing the total symmetry), which implies that their symmetry is different, which in turn means that their respective crystal structures are different. And this shows that specific chemical affinities are not enough to fully determine (crystal) structure.
Moreover -- still discussing how a set of chemical entities, initially present in a solution or as melt, actually manages to aggregate such that a lowest-energy configuration is obtained -- the trajectory of the system of chemical entities often meets, on the way to the lowest-energy configuration, a certain number of small energy barriers, that must be overcome. One could, however, assume that, given sufficient time and nudges of energy from the environment (which is called annealing) the lowest-energy state will eventually be reached by the system of chemical entities. The problem is, however, that it is very well possible that, especially complex chemical substances do not have just one unique lowest-energy configuration with respect to a particular range of thermodynamic conditions, but several such configurations, which have the same lowest energy, or differ only slightly in this respect. So when it is about to crystallize, such a substance has several alternative pathways at its disposal, each one of which leading to a more or less structurally different lowest-energy configuration. We can in fact speak of an energy landscape which is more or less tilted. A ball, running down this landscape -- consisting of valleys, hills, slopes, etc. -- represents the system of chemical entities seeking its lowest-energy configuration, i.e. trying to end up at the lowest site of the landscape. See next Figure.

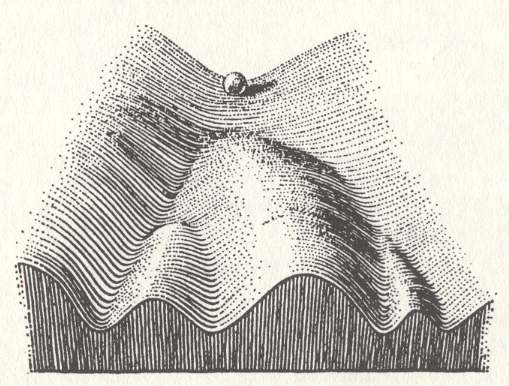
Figure above : Possible energy landscape of a system of chemical entities (represented by a ball) seeking a lowest-energy configuration. For such a configuration there are several alternative possibilities, each corresponding to a different crystal structure. The ball rolls down the valleys toward lowest altitudes. We must further imagine (not shown in the Figure) that small barriers are present at several locations in the valleys, which must be taken by the system in order to reach the lowest-energy state.
(After WADDINGTON, C., The Strategy of Genes, 1957)

It is known, however, that within a particular range of thermodynamic conditions, the system always takes up one particular and unique configuration, always resulting in the same crystal structure (while there are several equally possible alternative structures for that particular range of thermodynamic conditions). So it seems that, apart from being assisted to find any one lowest-energy configuration, there is some guiding of the system of chemical entities towards a particular configuration (crystal structure), despite the fact that some other configurations are, from an energetic point of view equivalent. This assistance and guiding is based on global features, not on local interactions. And they seem necessary, because just a piecewise partially (because of the specific chemical affinities obtaining between the elements of the system) random search for the most stable crystalline structure (configuration) could be inefficient, unpredictable, and time-consuming. By contrast, the processes of Nature often tend to be smooth, and fairly reproducible (repeatable). So indeed we could be forced to assume that the system of chemical entities is actually directed, or informed about the whole energy landscape during its path 'downhill'. In such cases fields of information, or an implicate order, could be involved : While the actual driving force is still the quantum mechanical desire to minimize energy by moving to the lowest valley, the actual process is given form by information in the fields themselves or in aspects of the Implicate Order (See PEAT, F., Synchronicity, The Bridge Between Matter and Mind., 1987, p. 163).
But, in addition to all this, there is another indication of this h o l i s t i c state of affairs in crystallization, an indication provided by snow crystals. Moreover, snow crystals (snowflakes) are excellent examples of inorganic whorled structures, that come about by the presence of macroscopic antimers. So it is certainly worthwhile to consider snow crystals in more detail.

Before we begin, we quote something from the introduction to the book Snow Crystals by W.A. BENTLEY and W. J. HUMPHREYS, 1931 / 1962, which depicts over 2000 microphotographs of snow crystals (from which a few are reproduced below) :

Snow, the beautiful snow, as the raptured poet sang, winter's spotless downy blanket for forest and field, has ever challenged pen to describe, and brush to paint, its marvelous mass effects. Nor is the aestetic urge of its very tiniest flake or smallest crystal that gently floats from heaven to earth any less compelling. It is even more insistent -- doubly more -- for it not only quickens that response to the dainty and the exquisite that makes us human, but equally arouses our desire to understand, our curiosity to know, the how and the why of this purest gem of surpassing beauty and of a myriad myriad forms. But it is so tiny, so fragile, and so evanescent save in the coldest of weather, that few, very few indeed, have come to know the snow crystal at first hand. All the rest of us must get our knowledge of this endless gallery of Nature's delicate tracery and jewel design through the careful drawings and faithful photographs, microphotographs, by that devoted few whose enthusiasm never wanes and whose patience never tires.

Water ( H₂O ), that most remarkable of chemical substances, crystallizes in the Dihexagonal-Dipyramidal Class (6/m 2/m 2/m) of the Hexagonal Crystal System (NESSE, W., Introduction to Mineralogy, 2000). A snowflake generally is a plate-like hexagonal prism. When we project this prism onto its base, we are left with a regular hexagon, and the symmetry of such a hexagon is according to the group D₆ , which implies that there are six mirror lines (divided over two types : connecting opposite corners, connecting centers of opposite sides) and a six-fold rotation axis, hence the crystallographic symbol -- referring to 2-dimensional crystals -- 6mm, which denotes the Crystal Class.

These seven symmetry elements are also present (in their 3-dimensional versions) in the mentioned snowflake prisms, but the latter have in addition to these, also a mirror plane half way up, and perpendicular to, the 6-fold rotation axis, i.e. a mirror plane coinciding with the equatorial plane of the prism, and within this plane there are six 2-fold rotation axes. So all in all a snowflake prism -- which often is a flat prism -- has one 6-fold rotation axis, one equatorial mirror plane, two types of 2-fold rotation axis lying in that plane, and two types of mirror plane perpendicular to the corresponding 2-fold axes, hence the crystallographic symbol 6/m 2/m 2/m, denoting the (3-dimensional) Crystal Class. The corresponding bipyramid (two regular hexagonal pyramids joined base to base), expressing the promorph of the snowflake, has this same symmetry (6/m2/m2/m).

There are other types of snow crystals, but for our present discussion the mentioned plate-like hexagonal prisms are the most important. So we will stick to these. And, as has been said, we can represent them conveniently by regular hexagons. To be more precise, of the snow crystals that, for the present, interest us most, the flat hexagonal prism is the core of a class of snow crystals that consist of this hexagonal core plus six highly similar outgrowths (extensions) from the corners of that core, resulting in star-shaped snow crystals. These more complex crystals, especially those with branching extensions, occur at higher temperatures, and, consequently, when the absolute humidity is relatively great. They are the result of rapid growth. Hence they are most abundant in the front portion of the snowstorm, where the snow is heaviest and the clouds are lowest.
Let us first, in more general terms, point out how these outgrowths on a crystal -- generally referred to as hopper growth -- come into being. For this purpose we consider, as an example, crystallization from a solution, and then apply the findings to the case of snow crystals (In fact, the formation of snow is also crystallization from a solution, but this time a gaseous solution [of water vapor in the air] ). See next Figure.

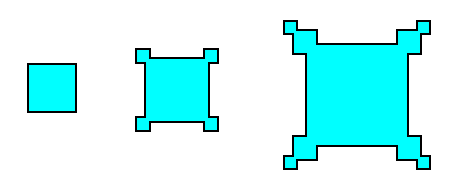
Figure above : Idealization of hopper growth in crystals. Faster growth at corners and edges than on faces can be self-perpetuating when it partly shields the center of the face from a fresh supply of solution.

The hopper growth is a result of a variation of growing conditions over the parts of a crystal face. The variation in degree of supersaturation of a solution (liquid or gaseous) over a growing crystal often urges its edges to grow faster than the centers of its faces. An edge can draw upon more solution than a similar area on a face because the edge looks outward in more directions. If it succeeds in racing ahead of its surrounding faces, some little faces will grow out from it, and they will tend to shield the original face from fresh solution and so will further exaggerate the difference in supersaturation between the face and the edge.
Analysis of the shapes of snow flakes, such as will be shown below, often suggests that a similar succession of especially fast growths has occurred at the corners of a hexagonal plate. But the symmetry of the pattern of these growths on a snow flake remains extraordinary. Whatever one corner does, the others do too, at the same time, to the same extent and and to the same m o r p h o l o g y. Several explanations have been offered for this unanimity in the detailed behavior of a snow flake in the six directions, but none has yet been generally accepted. (See HOLDEN, A. & MORRISON, P., Crystals and Crystal Growing, 1960 / 1982, p.130 / 131).
The next nine Figures depict some snow crystals (enlarged), reproduced from the above cited book (BENTLEY & HUMPHREYS) on snow crystals. We have numbered each depicted crystal for easy reference.

Figure above : Snow crystal 1. Hexagonal plate without extensions, but with inner features (air or water inclusions, ice ridges or grooves) symmetrically arranged.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 26.)

Figure above : Snow crystal 2. Small hexagonal plate with six similar broad extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 51.)

Figure above : Snow crystal 3. Small hexagonal plate with six similar broad extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 51.)

Figure above : Snow crystal 4. Small hexagonal plate with six similar branched extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 183.)

Figure above : Snow crystal 5. (Presumably) very small hexagonal central plate with six similar branched extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 183.)

Figure above : Snow crystal 6. (Presumably) very small hexagonal central plate with six similar branched extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 183.)

Figure above : Snow crystal 7. (Presumably) very small hexagonal central plate with six similar branched extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 183.)

Figure above : Snow crystal 8. Small hexagonal central plate with six similar branched extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 183.)

Figure above : Snow crystal 9. Small hexagonal central plate with six similar branched extensions at its corners.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962, p. 183.)

There are organisms that are very reminiscent of snow crystals, especially some members of the Acantharia, which are a certain class of Radialaria (planktonic marine unicellular organisms, often possessing very regular mineral skeletons). They are, however, four-fold instead of six-fold. The next Figure depicts such an Acantharian.

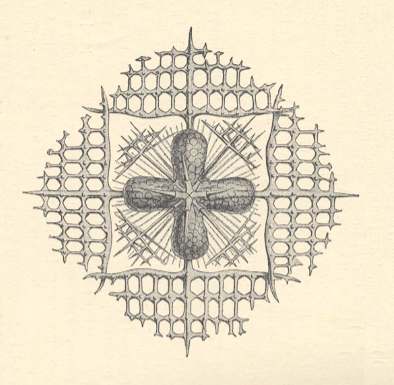
Figure above : Lithoptera dodecaptera (Acantharia, Radiolaria). A unicellular organism with a snowflake-like mineral skeleton (which consists of Strontium sulphate). This skeleton could be called a biocrystal.
(After HAECKEL, E., Kristallseelen, Studien über das anorganische Leben, 1917)

The above depicted snow crystals are viewed along the 6-fold axis, which is the crystal's main axis. They are thin plates. As one can see, it is possible, when discussing symmetry features, to consider them as two-dimensional entities (two-dimensional crystals) possessing D₆ symmetry, crystallographically denoted by the symbol 6mm (while the symmetry of the corresponding three-dimensional crystals -- whether tabular, columnar or pyramidal -- is crystallographically denoted by the symbol 6/m 2/m 2/m ).

The remarkable feature that is displayed by the above depicted snow crystals 2--9, are the outgrowths or extensions. They probably are expressions of the hopper growth referred to above. In such a crystal they are morphological features (in the form of plumes, sectors, etc.) that are repeated six times according to the point symmetry of the crystal, resulting in the presence of six macroscopic antimers (i.e. antimers based on the presence of macroscopical features). The remarkable thing is that the entire morphology of such an extension is copied six times around the crystal's 6-fold rotation axis. If, on another snow crystal, an extension with a different morphology, different from the originally considered crystal, is present, then this particular morphology is repeated six times around the 6-fold axis of this crystal. It turns out that this morphology varies endlessly among different crystal individuals where such extensions occur. But in each individual snow crystal we see : Whatever the morphology of an extension is, this morphology is repeated six times around the 6-fold axis (Sometimes we see snow crystals with only three extensions, and they need special crystallographic studies in order to understand them [which is done in Part XXIX Sequel-19, Sequel-20, Sequel-21, and Sequel-22]. Perhaps H₂O is crystallographically polymorphic, even with respect to just snow).
Because naturally grown crystals never experience a perfectly uniform growing environment, they always show irregularities with respect to their intrinsic symmetry. That's why the six outgrowths are seldom precisely identical. Instead they are similar, but very similar indeed. So intrinsically these six outgrowths are precisely identical.
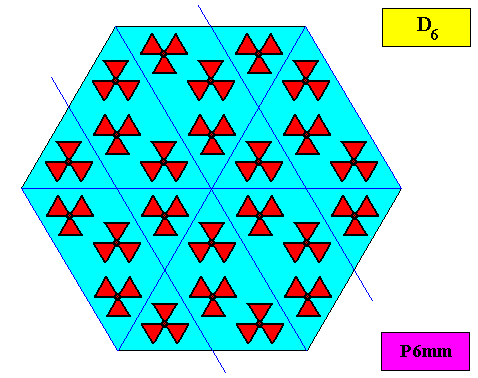
The next Figure depicts a hexagonal two-dimensional crystal (itself not necessarily a [ 2-dimensional projection of a] snow crystal), which is in certain respects well comparable with our two-dimensional version of a snow crystal (or, we can say, with a projection onto the equatorial plane of a three-dimensional snow crystal). The crystal is provided with fictitious atomic motifs that have the symmetry and distribution compatible with the plane group P6mm and with the point group 6mm ( = D₆ ). Of course as such this crystal has an extremely small size, but this is immaterial for the present discussion. These motifs should not be confused with inclusions of all kinds as seen in snow crystals, because these inclusions are macroscopical. The motifs and their distribution express the (two-dimensional) crystal's internal symmetry (P6mm) and also its point symmetry (6mm).

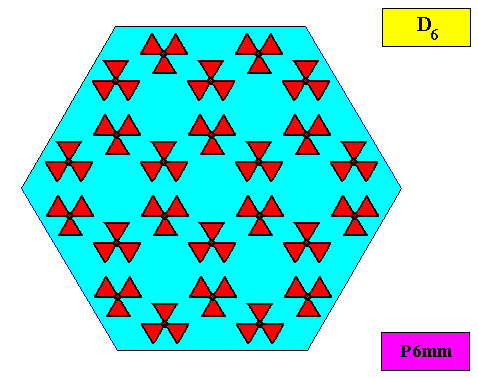
Figure above : Two-dimensional hexagonal crystal belonging to the plane group P6mm and to the point group 6mm (or, equivalently, to the D₆ symmetry group). The motifs (having themselves D₃ symmetry) and their distribution express the crystal's internal symmetry and also its point symmetry. As such this crystal is comparable with a projection onto the equatorial plane of a tabular snow crystal.

The next Figure depicts the hexagonal point lattice -- indicated by lattice connection lines -- of the just depicted two-dimensional crystal.

Figure above : A pattern according to the plane group P6mm , from which the just depicted two-dimensional crystal can be constructed, by deriving one crystallographic closed Form consisting of six (equivalent) faces, each representing an equivalent atomic aspect. Point lattice indicated by connection lines. Each rhombic lattice mesh contains two D₃ motifs s.str. that are rotated 60⁰ with respect to each other. The pattern must be imagined to be extended indefinitely over the plane.

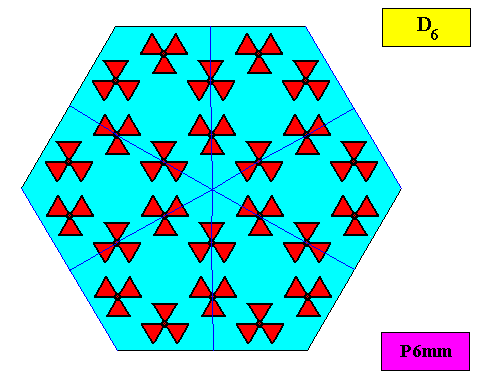
The next Figure gives the set of symmetry elements of the above depicted two-dimensional crystal.

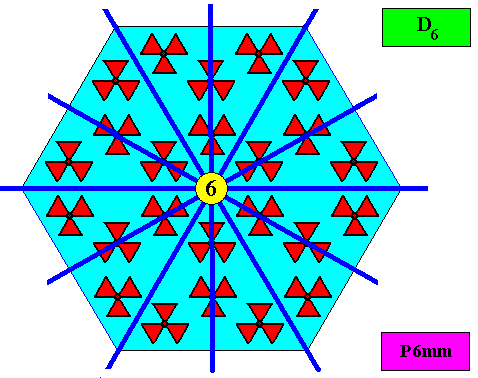
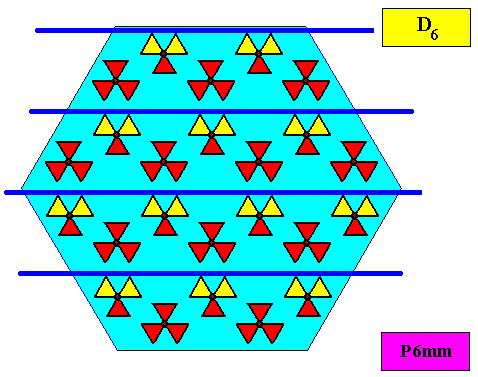
Figure above : Symmetry elements of the two-dimensional hexagonal crystal of the Figure above belonging to the plane group P6mm and to the point group 6mm (or, equivalently, to the D₆ symmetry group). It has six mirror lines and one 6-fold rotation axis at their point of intersection.

Figure above : Each atomic aspect, that can as such be presented to the growing environment of the crystal, and which represents a possible crystal face, is translationally being repeated throughout the crystal, i.e. given some particular atomic aspect, we see copies of it parallel to it. This holds for all possible atomic aspects of the crystal. One such atomic aspect is highlighted (yellow coloring of relevant parts of the motifs, dark blue lines).

As we compare our two-dimensional crystal (previous Figures) with a tabular snow crystal with six similar outgrowths, we see that it does not possess real and unique macroscopical boundaries of (or intermediate regions between) some equivalents of the outgrowths. This is illustrated by the next three Figures.

Figure above : Two-dimensional crystal of the previous Figures. It doesn't show genuine boundaries or intermediate areas between radially repeated structures, as we do see them in many snow crystals that have outgrowths.

Figure above : Also in alternative positions there are no genuine boundaries in the two-dimensional crystal of the previous Figures that could suggest the radial repetition of six similar or equal parts. This, despite the fact that the suggested boundaries do not cut through motifs, as the next Figure shows.

Figure above : Same as previous Figure. The suggested boundaries are not unique boundaries, because each of the six boundaries is repeated by parallel copies, as is shown for one such boundary.

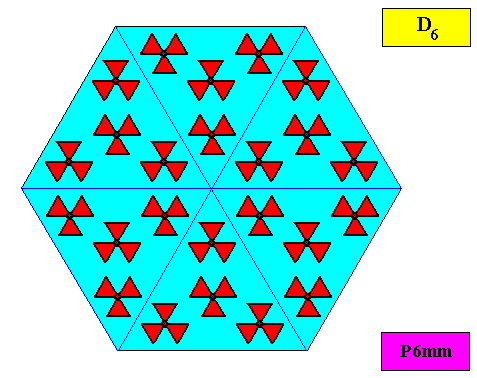
The next Figure depicts snow crystal 5, and shows that the morphology of an outgrowth is not translationally repeated, and is thus not comparable with an atomic aspect.

Figure above : Snow crystal 5 (from the series of snow crystals depicted earlier).
The morphology of the outgrouwths is not translationally repeated, i.e. the crystal does not contain parallel copies of its outgrowths.

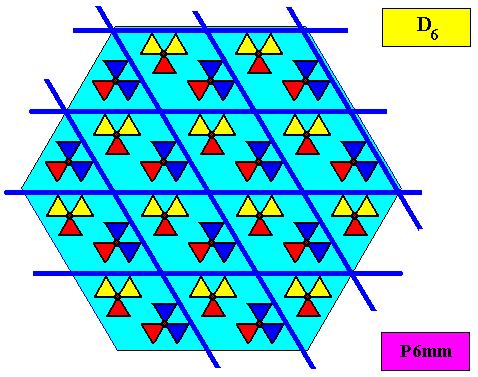
Above we depicted the hexagonal point lattice on which the two-dimensional hexagonal crystal was based. The plane group symmetry was according to the group P6mm. This symmetry was accomplished by placing two D₃ motifs into each rhombic lattice mesh, motifs that are rotated with respect to each other by 60⁰. But precisely the same plane group symmetry can also be obtained, by placing a D₆ motif at each lattice node of that same hexagonal point lattice :

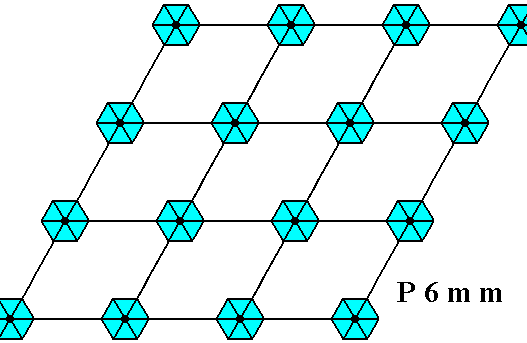
Figure above : Pattern representing the plane group P6mm . The motifs s.str. (blue) are interpreted as D₆ structures placed at the lattice points, i.e. having their centers coincide with the lattice points. The pattern must be imagined to extend indefinitely over the plane.

Let us analyse all the above, concerning the status of the six similar and symmetrically arranged outgrowths in the above depicted snow crystals, more closely.

The structure of a crystal is : Point lattice plus chemical filling-in. This in fact means that certain chemical units are arranged according to a certain lattice (which itself does not belong to the actual crystal structure, but indicates the arrangement of the mentioned chemical units, resulting in the possibilitiy of distinguishing a unit cell that is periodically repeated). The chemical motifs have a certain morphology and a certain symmetry.

The Space Group (3-dimensional) or Plane Group (2-dimensional) is : Point lattice plus chemical filling-in with motifs-only-considered-with-respect-to-their-symmetry. When we eliminate all translational elements from the Space Group (or Plane Group) symmetry, we obtain the corresponding point group symmetry. So the different features of crystals, relevant to our discussion, are related to each other in the following ways :

The Point Group is the translation-free residue of the Space Group (or Plane Group) symmetry. But also objects without periodic internal structure, and thus not belonging to whatever Space Group or Plane Group, can have a symmetry according to a Point Group, which in fact means that the object's symmetry operations (reflection, rotation, etc.) are such that at least one point remains in place, i.e. it remains where it was before any such operation is applied to the object.
The intrinsic shape of a crystal is determined by the pattern of growth rates, which in turn are determined by the possible atomic aspects of the crystal that can be presented to the growing environment. An atomic aspect can be symmetric or asymmetric, but this does not influence the intrinsic shape of the crystal. When it is asymmetric it influences the point symmetry by eleminating a mirror reflection.
The geometric symmetry of a crystal is the symmetry of its intrinsic shape.
The crystallographic point group symmetry of a crystal is either the same as its geometric symmetry, or lower, and in that case it is according to a genuine subgroup of the group describing the geometric symmetry of the crystal.
This crystallographic point group symmetry (point symmetry) of the crystal is in fact the symmetry of the pattern of the crystal's possible atomic aspects presented to the growing environment, in combination with the symmetry of each of these aspects themselves. These aspects represent possible crystal faces. Same aspects imply same growth rates under uniform growing conditions (concentration of nutrient material, temperature, pressure etc). So the crystallographic point symmetry of the crystal is determined by its atomic aspects (which in turn are determined by the crystal's internal structure). But these aspects are in fact not morphological units, but some chemical state of affairs connected with certain directions within the crystal. That's why any particular atomic aspect is repeated translationally within the crystal, i.e. it has many parallel copies within the crystal, and is thus not a unique (or only radially repeated) morphological unit (See Figure above ). So the crystallographic point symmetry of a crystal is not a morphological symmetry, as we see it (morphological symmetry) in o r g a n i s m s or their parts, for instance flower whorls, Radiolarian skeletons, jelly-fishes, star-fishes, etc.
A particular morphological point symmetry of a crystal, say it is a D₆ symmetry, is always the same as its crystallographic point symmetry (and consequently also D₆ symmetry), because the relevant morphological units, expressing morphological point symmetry, are repeated wholly in accordance with the crystal's crystallographic point symmetry. However, these morphological units are macroscopical substructures of the crystal, and are only repeated r a d i a l l y, and in this way expressing morphological point symmetry (i.e. they are in any case not translationally repeated).
As an example of the mentioned morphological macroscopic unit, determining the point symmetry of the object also to be morphological point symmetry, we can mention outgrowths (as in hopper growth) in crystals that underwent rapid growth under uniform conditions. We could then be tempted to visualize a crystallographic Form of a crystal, i.e. a set of equivalent faces, also as such a morphological unit. But this would be incorrect, because the crystal face is in fact a certain atomic aspect (that could as such be presented to the growing environment), and we know that this aspect is not only radially repeated (for instance as the six sides of a regular hexagonal prism) but also translationally so. One such individual atomic aspect is part of a whole set of parallel aspects within the crystal, while another individual version of this same aspect (in the same crystal), but now making an angle with the former, also is part of a whole parallel set of aspects, i.e. of another set making an angle with the first set. But these sets completely interpenetrate each other, resulting them not to be independent structures, and thus not representing independent macroscopical morphological units. See next Figure.

Figure above : Interpenetration of atomic equivalent aspects, shown for two of them.
Each atomic aspect, that can as such be presented to the growing environment of the crystal, and which represents a possible crystal face, is translationally being repeated throughout the crystal, i.e. given some particular atomic aspect, we see copies of it parallel to it. The Figure shows two (out of six) equivalent atomic aspects of the crystal interpenetrating. One such individual atomic aspect is highlighted by yellow coloring of relevant parts of the motifs and dark blue lines, while the other equivalent aspect is highlighted by dark blue coloring of the relevant parts of the motifs and dark blue lines.

Well, such a morphological point symmetry is clearly expressed in the complex (in contrast to simple) snow crystals, i.e. in snow crystals possessing large similar outgrowths or extensions from some central region. We have depicted such crystals above (crystal 2--9). They show 'hexastichous phyllotaxis' although having only one whorl. Clearly they have six antimers, based on macroscopic structures, like it is the case in all organisms that have antimers.

As has been said, the crystallographic point symmetry is the symmetry of the pattern of atomic aspects plus their symmetries. Above we considered a two-dimensional hexagonal crystal having D₆ point symmetry ( = 6mm) and P6mm plane group symmetry. The atomic aspects, as represented by the faces, were, each for themselves mirror symmetric. The crystal, in terms of its set of faces, can be seen as constructed by such a symmetric atomic aspect that is radially repeated six times. Hence the crystallographic point symmetry is D₆ (six mirror lines, one 6-fold rotation axis).
Let us now consider the case of a two-dimensional crystal that also has an intrinsic shape according to a regular hexagon, and thus also consists of six equal atomic aspects related to each other by a 6-fold rotation axis, but which (atomic aspects) are not mirror symmetric. We then see that this entails that the crystallographic point symmetry of the crystal is not D₆ but C₆ . See next two Figures.

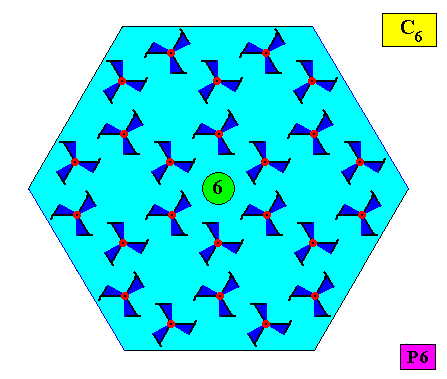
Figure above : A two-dimensional hexagonal crystal having a crystallographic point symmetry according to the group C₆ (crystallographically denoted by 6), and a plane group symmetry according to the group P6. The (fictitious) motifs each have a symmetry according to the group C₃ . Their arrangement, however, ensures that the point symmetry of the crystal is C₆ . The 6-fold rotation axis (as the crystal's only symmetry element with respect to its point symmetry) is indicated.

The next Figure indicates the atomic aspects representing the faces of the just depicted crystal. These aspects are not mirror symmetric, causing mirror lines to be absent.

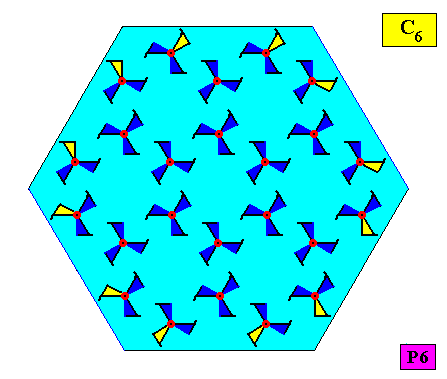
Figure above : The six asymmetric atomic aspects (highlighted by yellow coloring of parts of motifs) of the above depicted two-dimensional hexagonal crystal (point symmetry C₆ , plane group symmetry P6). Because of the asymmetry of the atomic aspects, the crystal does not possess mirror lines.

So now we have clearly seen that the crystallographic point symmetry of a crystal depends on the pattern of atomic aspects of which their own symmetry must also be taken into account. The nature of the atomic aspects, as presented to the growing environment, determines the relative growth rates of the corresponding crystal faces. So in a hexagonal D₆ crystal (six equal atomic aspects), as well in a hexagonal C₆ crystal (also six equal atomic aspects), we have to do with a regular pattern of six equal growth rates. These are growth rates that are perpendicular to the corresponding crystal faces that have actually developed. In addition to the mentioned six atomic aspects there are also other atomic aspects present. They regularly alternate with the atomic aspects mentioned earlier. But these atomic aspects represent faces that grow faster than the faces we've just discussed, which implies that these faster growing faces quickly grow themselves out of existence, and are not present anymore in the fully-grown crystal. However, these alternating atomic aspects still represent six equal growth vectors (originating from the center of the crystal to its corners). And when hopper growth takes place (See Figure above , illustrating a four-fold case), which occurs when the absolute growth rate of the crystal is very high), the outgrowths that start from the corners of the hexagon (or from the six edges of the hexagonal prism) will grow with the same speed, i.e. every outgrowth increases with a certain speed, which is the same for all six of them.
So what we expect to see in a very fast growing snow crystal is the emergence of six outgrowths (because there are six corners, and it is at corners where outgrowths will emerge in such a fast growing crystal). And, especially we will expect that these outgrowths, when the growing medium is uniform, have the same spatial extensions. But what we cannot expect is a same m o r p h o l o g y of them, i.e. a repetition of six extensions (outgrowths) that are also equal morphologically. Instead we would expect that snow crystals like the following can occur :

Figure above : A fictitious snow crystal, that could be expected to occur, if the outgrowths solely depended on (equal) growth rates. We see (six) outgrowths that have about the same spatial extension, but which show different morphologies. In fact we see three different morphological types of outgrowth, destroying the crystal's morphological point symmetry.

But in nature we do not encounter such snow crystals. We only see crystals where not only the spatial extension of the outgrowths is equal, but also their entire morphology. So this degree of equality of the outgrowths does not solely depend on (equal) growth rates, and thus not solely on a pattern of atomic aspects, which in turn means that the complete equality of the outgrowths does not solely depend on the crystallographic point symmetry (as defined above) of the crystal. What then is the extra factor that co-determines this morphological equality of the outgrowths? Well, this factor seems to be of a g l o b a l nature (with respect to the space that the crystal finally occupies), and thus not of a local nature. It must be some 'restoring force' that begins to operate when some fixed form-equilibrium is broken by the appearance of an outgrowth on one of the corners. Or, differently expressed, the six outgrowths emerge simultaneously while constantly 'keeping in touch with each other' as to their morphology, in such a way that a same morphology develops in all six of them.

What we see in such snow crystals, we also see in organic forms : Consider, for example, your right and left hands. They are different from everyone else's, in both the pattern of lines on the palms and the pattern of ridges on the finger-tips. Yet they are very similar to each other (i.e. the right and left hands of one person), just like the outgrowths of an individual snowflake are similar to each other. This suggests that within the developing organism or a growing crystal some 'morphic resonance' takes place between similar structures, i.e. there is some sort of correlation between their development (See SHELDRAKE, R., The Present of the Past, 1988, p.132). It is as though this correlation guarantees the symmetrical development of structures, or, in other words, it ensures the maintenance of some form-equilibrium. Concerning snow crystals, there seems to be some long-range connection between the developing outgrowths. And this connection is not just some sort of connection, but a very subtle one, because it involves not just some quantitative feature to be repeated, but a complex morphology, i.e. the complex morphology of an outgrowth of a snow crystal. We could surmise that a given particular morpholgy of such an outgrowth depends on some specific initial condition at the site of the crystal where the outgrowth starts to grow, and that such a specific condition is symmetrically present at all six corners of the initial hexgonal plate of the (growing) snow crystal, in virtue of the intrinsic point symmetry of that hexagonal plate. But, as we will show below, there is an almost infinite number of different outgrowth morphologies to be seen in different snow crystals. So when such different morphologies of outgrowths only depended on different intial conditions at the sites of their origin, these morphologies should then be utterly sensitive to such initial conditions, i.e. already very small differences of such conditions must result in different morphologies. They do not relate to gross meteorological differences, because the star-shaped snow crystals all occur in the front portion of the snowstorm, i.e. they are not scattered all over it and so over many different meteorological conditions (temperature, saturation, etc.). But the condition within such a portion of snowstorm, within which the growing snow crystals tumble about, is likely to be very uniform, at least on average. Moreover, infinitesimal differences in the mentioned initial conditions are already morphologically accounted for, because the six outgrowths on a single snow crystal are seldom exactly alike. So within the front part of a particular snowstorm we could expect that all the snowflakes bear similar outgrowths if we go from snowflake to snowflake, because of the mentioned uniform conditions, with minor differences due to corresponding minor differences in conditions. But this is not observed. As far as my knowledge goes, wherever looked for, no two star-shaped snowflakes are found to be semi-identical. All are significantly different as to the morphology of their outgrowths. The morpholgy of an outgrowth cannot be sensitive to already very small differences of conditions, because these -- very small -- differences must already be present at the six corners of the hexagonal plate, which are, in the case of rapid growth, expected to contain several crystallographic defects, while the outgrowths of any particular snow crystal are still very similar. In fact we should maintain that the appearance of one or another morphology of outgrowth does nevertheless depend on very small differences in conditions (crystallographical and meteorological), which is why there occur so many different morphologies, but that the determining influence of these differences of conditions are, within any particular individual snow crystal, o v e r r u l e d by a h o l i s t i c f a c t o r that safeguards some form-equilibrium. So although very small differences of local conditions determine a particular outgrowth morphology, the mentioned holistic factor guarantees that that particular morphology will be present in all six outgrowths of that crystal. At the site of another crystal individual, slightly different conditions prevail, resulting in a different outgrowth morphology, but again form-equilibrium is maintained by distributing this same morpholgy to all other outgrowths of that crystal.
As far as I know, no such factor is found in physical or chemical investigations. We must take into account that this is a genuine holistic factor (which will undoubtedly also play a role in the individual development of organisms). Such a factor, which is global in character, not local, connects the parts of the crystal, i.e. it keeps all the parts more or less informed about each other. And, in terms of the Theory of the Implicate Order, such a holistic connection cannot take place in the Explicate Order : The parts of the crystal, including its remote parts, are connected to each other via the Implicate Order. Why this is so, we cannot tell, but some facts point to it. In fact, any discovery of a holistic aspect in nature, points to the existence of some irrational element in Nature, which means that there are certain absolute limits as to how far Natural Science can proceed and succeed to uncover the structure of Reality.

It is now time to discuss the snowflake not only in terms of some analogous two-dimensional crystals, that, while possessing the symmetry of a projection of the snowflake (D₆ ), have fictitious microscopic motifs, but in terms of the real structure of solid H₂O (under normal conditions).
To begin with, an ice crystal (and thus also a snow crystal) consists not of a periodic arrangement of ions (in the usual chemical sense of electrically charged atoms or atomic complexes) or of (neutral) atoms, but of (periodic arrangements of) molecules. Such a water molecule consists of three atoms, viz., one oxygen and two hydrogen atoms. Almost, if not all, anomalies of water (especially its high boiling point and the fact that ice is less dense than liquid water) are caused by the fact that the two hydrogens are not neatly placed at either side of the (much larger) oxygen, but making an angle with each other of 104.5⁰. Why this is so is explained by Quantum Mechanics. Without loosing anything important, let us paraphrase this explanation (See BALL, P., H₂O, A Biography of Water, 1999). The true shape of water is not a ' V ', but (approximately) a tetrahedron (A (regular) tetrahedron is a mathematical regular solid consisting of four faces that have the shape of an equilateral triangle). The water molecule looks kinked because we are seeing (in a diagram of the molecule) only two of the (four) corners of the tetrahedron. The other two are occupied not by atoms but by pairs of electrons, called lone pairs. These are electrons from the oxygen atom's complement, which don't partake in the bonding between the molecule's atoms but which nevertheless have to go somewhere. They pair up, as electrons in atoms are wont to do, and take up residence about as far from each other and from the hydrogen atoms as they can get. The tetrahedral arrangement affords the greatest distance between each of these four entities -- the two hydrogen atoms and the two lone pairs. If it was a perfect tetrahedral arrangement, the angle of the kink, i.e. the angle between the two hydrogen atoms, would be 109.5⁰. The difference between that and 104.5⁰, which is actually observed, is the consequence of the slightly stronger aversion of the lone pairs for each other than for the hydrogen atoms, so that the latter are pinched together (BALL, 1999, Ibid., p.155/156). Well, generally, some atoms hold on more tightly to the bonding electrons than others. In its greed for electrons, oxygen is surpassed only by fluorine. So in the water molecule, oxygen hogs the electrons. As a result the oxygen atom in a water molecule acquires a negative charge, and the hydrogens are left positively charged. It has been proposed that these charges in the water molecule give rise to an electrical force of attraction between neighboring molecules, in which the hydrogen atoms of one molecule point towards the oxygen atom of another. This attraction can be regarded as a kind of chemical bond, about ten times stronger than the van der Waals forces that hold 'regular' liquids together -- but ten times weaker than the bonds that link hydrogen and oxygen atoms into discrete molecules. This is called a hydrogen bond (BALL, 1999, Ibid., p.157). The hydrogen bond is really a bond between a hydrogen atom and a lone pair (of electrons). This means that a water molecule can form four hydrogen bonds : the molecule's two hydrogens form two bonds with neighboring oxygens, while the molecule's two lone pairs interact with neighboring hydrogens. In fact there is in this bond, in addition to the electrostatical element, also an element of electron sharing (as the latter is the case in covalent bonds).
So water molecules attract each other more strongly than in most other liquids. And this hydrogen bond also links the water molecules together in ice crystals, formed when temperatures are low. There these molecules form a regular hexagonal network, i.e. they form the crystal lattice of snowflakes and other forms of ice. For all this, see next Figures.

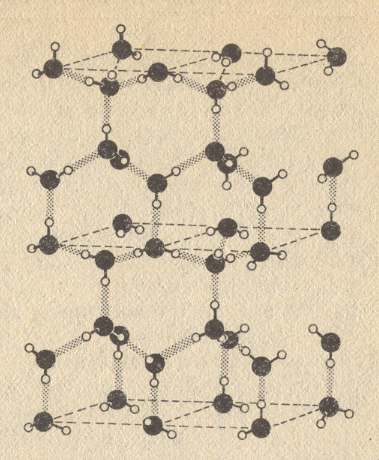
Figure above : Water molecules have an affinity for one another through the hydrogen bond (dotted). A positively charged hydrogen nucleus which 'belongs' to one oxygen atom can still be attracted to the negatively charged electron cloud of a nearby oxygen atom in another water molecule. In ice this attraction causes the molecules to form a crystalline array similar to the structure of diamond, but not as strong. This very open structure gives ice its low density, and explains why ice floats on water.
(After GRIBBIN, J., In Search of the Double Helix, 1985/1987.)

REMARK :
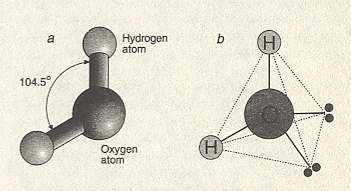
Above we stated that the (crystallographical) point symmetry of ice or snow crystals is 6/m 2/m 2/m (i.e. the most symmetric Class of the Hexagonal Crystal System) as it is given by NESSE, W., Introduction to Mineralogy, 2000.
I am not sure how well established this is, because there are snow crystals with only three-fold symmetry, suggesting a lower-symmetry Class of the Hexagonal System. In x-ray studies only the oxygen atoms seem to count (BENTLY & HUMPHREYS, Snow Crystals, 1931). But because oxygen atoms are much larger than hydrogen atoms, the latter may be disregarded, which means that only the arrangement of oxygen atoms creates the symmetry of the ice or snow crystal.

Figure above :
Left image (a) : The water molecule is bent, with the two bonds between oxygen and hydrogen splayed at an angle of 104.5⁰. These bonds are normal chemical bonds. Relative sizes of atoms of atoms are in reality different than displayed here : The oxygen atom is much larger than the hydrogen atom.
Right image (b) : In fact a water molecule forms approximately a tetrahedron, the four corners of which can form bonds (hydrogen bonds) with other tetrahedra, i.e. with other water molecules. The four corners consist of two hydrogen atoms (H) at one side of the oxygen atom (large sphere), and two lone pairs of electrons at the other side. At the molecular scale, the structure of water is imprinted with this tetrahedral geometry.
(After BALL, P., H₂O , 1999.)

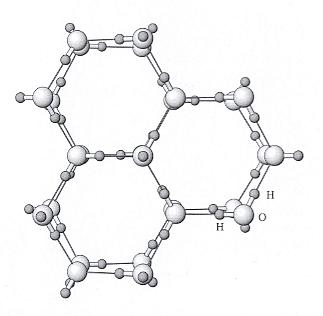
Figure above : Ice structure viewed down the c axis (i.e. down the 6-fold rotation axis of a single crystal). Water molecules consisting of one oxygen (large sphere) and two hydrogens (small spheres) are arranged in a hexagonal array. Hydrogen bonds between water molecules are shown with thinner lines. The positions of the H (hydrogen) and O (oxygen) are shown accurately, but the sizes of the atoms are not. (See next Figure).
(After NESSE, W., Introduction to Mineralogy, 2000.)

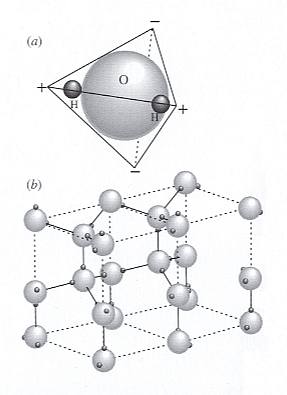
Figure above : Hydrogen bonding in ice.
Image (a) : A polar H₂O molecule is formed by covalent / ionic bonds between H and O using 2p orbitals on O (See for the covalent bond and the ionic bond, our essay The Chemical Bond in First Part of Website . The different types of chemical bond can be mixed up in a single such type).
The O has greater claim on the electrons, so the H consists of little more than its positively charged nucleus, a single proton. Charge is tetrahedrally distributed -- positive at the H atoms and negative at nodes on the opposite side of the O.
Image (b) : Each negative node on the molecule attracts a positive node (an H atom) on an adjacent H₂O molecule to form hydrogen bonds that hold the water molecules together (partially and changeably in liquid water, totally and constant in ice). Two (crystallographic) unit cells are outlined in the ice structure with dashed lines.
The top face (and also the bottom face) of the unit cell has the shape, not of a square, but of a rhombus with angles of 60⁰ and 120⁰. The crystallographic c-axis runs parallel to the vertical edges of the unit cell.
(After NESSE, W., Introduction to Mineralogy, 2000.)

Above we have spoken about snow crystals that possess six virtually equal outgrowths. Although sometimes these outgrowths are a bit dissimilar, their strong similarities in most other cases stand out. We have indicated that it could be hard to provide a local explanation for this phenomenon, i.e. an explanation solely based on local interactions of crystal constituents. Instead we probably have to admit a global factor at work, ensuring the symmetry of the whole crystal, especially its morphological symmetry (which is its crystallographic symmetry, but now also expressed in all macroscopic details of the crystal). We have spoken about the fact that in snow we encounter an almost unlimited number of different morphologies of these outgrowths on different crystals (but almost always the same morphology within a single crystal). The next Figure, shows some of these different morphologies actually found in snow.

Figure above : A selection from the huge set of actually occurring different outgrowth morphologies in snowflakes (Each image shows only one of the six outgrowths).
For a larger version of this Figure (showing more details) click HERE .
(Taken from microphotographs of whole snow crystals in W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962.)

We have discussed the high degree of similarity of the morphology of the six outgrowths of a snow crystal, as something not fully understood by natural science. I can, however, imagine that the reader cannot believe this, because it looks so much to be just a trivial problem, while moreover I am not a professional chemist or physicist. So let me quote the natural scientist Philip BALL in his book H₂O , A biography of water, of the year 1999, p.177--178, when discussing branched snowflakes (comments between square brackets [ ] ) :

A continuing mystery about dendritic snowflakes is why all six of their branches seem to be more or less identical. The theory of dendritic growth explains why the side branches will develop at certain angles, but it contains no guarantee that they will all appear at equivalent places on different branches [i.e. at corresponding locations on the different outgrowths of the crystal, causing their s h a p e -- their morphology -- to be the same], or [the theory of dendritic growth contains no guarantee that the side branches] will grow to the same dimensions [The sameness of these dimensions of at least the main branches is more or less guaranteed by the equal growth rates implied by equal atomic aspects]. Indeed, these branching events are expected to happen at random. Yet snowflakes can present astonishing examples of coordination, as if each branch knows what the other is doing. One hypothesis is that vibrations of the crystal lattice bounce back and forth through the crystal like standing waves in an organ pipe, providing a degree of coordination and communication in the growth process. Another is that the apparent similarity of the arms is illusory, a result of the spatial constraints imposed because all the branches grow close together at more or less the same rate. But for the present, the secret of the snowflakes endures.

We can elaborate a little further on the appearance of outgrowths on a snow crystal, i.e. as to their general structure that they all (in all star-shaped snow crystals) have in common. One such general feature is the fact that the side branches, that shoot off from the main axis of an outgrowth, do this by making an angle of 60⁰ with this main axis. The next two Figures try to give more insight into this phenomenon.

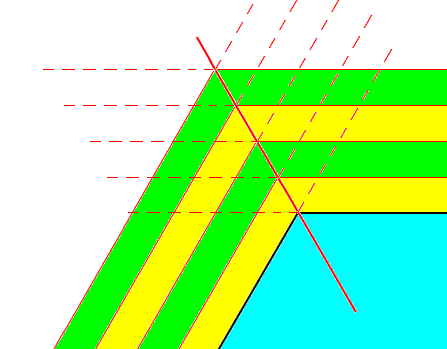
Figure above : Growth of a hexagonal crystalline plate (blue, only a part of it shown) by increments (yellow, green).

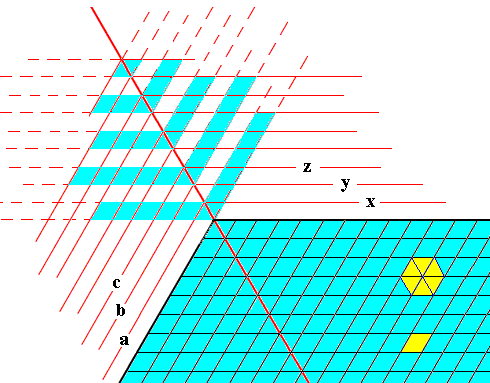
Figure above : Formation of an outgrowth (blue) at a corner of a hexagonal crystalline plate (blue) in the context of crystal growth by increments, like in the previous Figure, but smaller. These increments, as representing possible crystal faces, are indicated by x, y, z, etc., and a, b, c, etc. The Figure is not meant to present a full explanation of the appearance and general morphology of an outgrowth, but is only meant to give some indications that could stimulate further pondering. It probably gives some hint why the angles that the side-branches make with the outgrowth's main axis are all 60 degrees.

Liquid H₂O
Snow crystals are made of water. The water molecules are held together by hydrogen bonds. The resulting crystalline structure is rather open. When ice melts the structure is allowed to telescope inwards, because the net of hydrogen bonds becomes partly broken up, (becomes) more or less random and dynamic. And because of this telescoping, liquid water is more dense than ice.
The precise situation in liquid water is only partially understood. Computer models indicate that most water molecules (in liquid water) have two or three hydrogen bonds, and a relatively small proportion has four or none. Clearly there is a significant rearrangement of hydrogen bonds when ice melts. In particular, whereas hydrogen bonding in ice links each water molecule into rings of six, the most common ring structure in liquid water contains five molecules, not six. And while each vertex of the ice network is tetrahedral : the confluence of two hydrogen bonds, departing from two hydrogens, themselves covalently / ionically bonded to an oxygen atom, and two hydrogen bonds in which the lone pairs of electrons of that same oxygen atom participate, in liquid water some molecules are left dangling -- broken struts on a mangled frame. And a few of the molecules appear to break the rules of the 'dance' by forming five hydrogen bonds instead of four. The picture of water structure that emerges from computer simulations, therefore, is neither ice-like nor like a fully random vapor. The molecules form a continuous, disordered and dynamic network of hydrogen bonds in which each molecule is linked with up to four (or very rarely, five) others. Because the hydrogen-bonded network is floppier, more distorted and more defective than that in ice, the molecules are, when the ice is melting, able to occupy some of ice's interstitial space, making the liquid denser than the solid. The degree of distortion becomes greater as the temperature is raised from the melting point of 0⁰C, and so the liquid goes on getting denser until it reaches a maximum of 4⁰C. Above this temperature, enough hydrogen bonds have been broken that the liquid starts to behave normally (or at least, more normally), becoming less dense with increasing temperature because the thermal jiggling of the molecules tends to keep their neighbors at an increasing distance. (BALL, P., H₂O , 1999, p.166--167). See next Figure, which gives a computer model of liquid water.

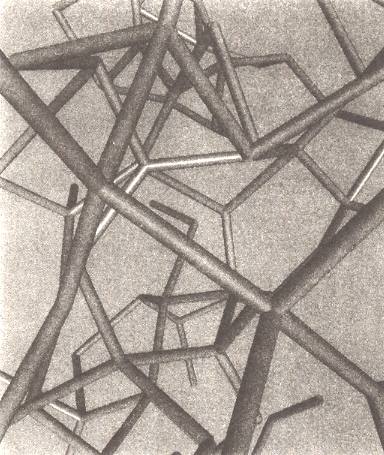
Figure above : Computer models of liquid water indicate that its hydrogen-bonded network is random and disorderly, and extends throughout the entire collection of molecules like a crazy climbing frame. Here the network is depicted as a lattice of struts representing the hydrogen bonds between molecules. The oxygen atoms of the molecules are located at the junctions of struts.
(Figure and subscript after BALL, P., H₂O, 1999.)

General physical context of dendritic crystals.

The formation of outgrowths in dendritic (i.e. star-shaped) snow crystals is probably a special case of a much more general phenomenon, which can be characterized as the effect of some sudden impact where energy or material rapidly expands from the point of impact, like we see in (1) a splash, caused by (say) a falling drop into a liquid, resulting in a crown-shaped morphology at the site of impact, in (2) the impact of a not to fast moving projectile on a glass plate, resulting in a star-shaped crack figure, or in (3) star-shaped electric discharge figures, etc. In branched snow crystals we then must think of very rapid crystal growth around some small initial nucleus (which triggers crystallization, under appropriate circumstances). Apposition of particles then goes so fast that supply of fresh particles cannot catch up.
The characterization of this more general physical phenomenon, resulting in star-shaped or radiate forms, is well expressed in, for example, PRZIBRAM, H., Die anorganischen Grenzgebiete der Biologie, 1926, pp.91, there in the context of a comparison of crystals and organisms, as to their morphology, energetics, dynamics and microstructure.
The next paragraph is in its essence taken from p.91 / 92 (and part of p.93). While reading this paragraph one must of course be aware of the date (1926) in which this (little) book was written, but as far as I know the bottom line of the argument, presented on the mentioned two pages, and to be paraphrased next, still holds :

In physical expansion phenomena the influence that the antagonism of reception and supply has on emerging shapes, is particularly remarkable. Whether it concerns the expansion of the effects of forces or the accumulation of material particles, the resulting figures all obey the same natural laws. The common regularity of the resulting forms or figures properly belong to an area of general morphology.
When an effect of force expands, leaving behind visible traces, it depends on whether there is sufficient energy available, to still leave (behind) these traces, during the force's passage through increasing space, at all the points of the latter, or not.
If the amount of available energy is large enough to leave behind its visible traces at all points during passage, then, in an ideal homogeneous isotropous medium (i.e. a medium that is uniform and without preferred directions) one can expect the boundary front of the affected area to progress in the form of a spherical shell, while its interior is fully filled up with the mentioned traces.
If, while the amount of energy still being the same, the medium is not homogenous or not isotropous, there will, it is true, appear differences in the boundary contour, but the 'packing' of traces will still remain more or less dense.
If, however, the amount of energy available at any one time during passage of the force through the expansion space having a certain radius, is too small to leave visible traces at every point, then, in an ideal homogeneous and isotropous medium, it is to be expected that the visible effect ever more decreases, resulting in the disappearance of any definite figure, i.e. the spherical contour of the visible expansion fades away. But because in real media there are always minor irregularities to be found, the locations at equal radial distances from the center of the expansion phenomenon do not receive equal amounts of energy, and instead of a spherical expansion figure we now get a radiate expansion figure. And when once such a difference has appeared, an ever sparser figure is obtained, because an ever increasing number of locations do not receive enough supply. Although secondary and tertiary branches will, again because of irregularities of the medium, appear, they will not be sufficient for completely and visibly filling up the expansion space. The rate of the expansion will determine whether, at the points successively 'visited' by the effecting force, there will, per unit of time, be left a sufficient amount of energy.
When the expansion rate is low, all locations are sufficiently supplied, resulting in a complete space-filling that is bounded by smallest possible faces, (a space-filling) attained by the emerging expansion figure. If, on the other hand, the expansion rate increases beyond a certain degree, then the described sparsening and formation of rays will express themselves in ever stronger ways, because the time of the passage of force is not enough for sufficient energy effects to be manifested at all locations of the expansion space. But only up to a certain limit of the rate of expansion the branching will increase. And increasing above this limit the deliverance per unit of time is not sufficient anymore for prolonged emergence of new branches or rays. The number of the latter decreases, and they shorten. And at highest expansion rates, finally, they altogether disappear.
In the latter case the visible figure looks similar again to the one that was obtained at a low expansion rate that was sufficient for a complete filling up of the expansion space, namely stocky or even a round figure. But now we do not have to do anymore with an expansion figure, but a figure that was instantaneously produced. If, for example, a bullet penetrates a glass pane with very high velocity, then the pane shows a circular hole with a diameter equal to that of the bullet. So no expansion phenomenon took place. Because of the high speed of the process there was no transmission of force accross the glass, not even to locations adjacent to the rim of the bullet hole. When, on the other hand, one hits a pane, without smashing it, with a piece of rock having the same shape as the bullet, then one sees a radiate figure of cracks. Here the velocity was not high enough to prevent the transmission of kinetic energy (energy of motion) to adjacents parts of the glass, but too high to effect a homogeneous deformation all along the rim of the hole.

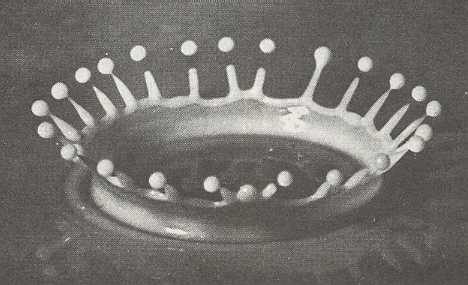
Precisely the same, as just described, we see in the case of a splash caused by a liquid drop falling into a bowl filled with the same liquid. See next Figure.

Figure above : An instantaneous photograph of a splash of milk.
After a drop of milk has fallen into a bowl also containing milk, a crown-shaped expansion figure is formed.
(From D'Arcy THOMPSON, On Growth and Form, 1942.)

In a plash, from the point of impact rises a smooth, circular ring, surprisingly thin-walled, curving gracefully outwards as it rises. But such a ring does not remain circular, because as such it becomes unstable. It breaks up into 24 spikes. The spikes come to a sharp point. Most have just thrown off a tiny rounded droplet of milk -- because, again, a pointed spike is as such unstable -- and the rest of the spikes are about to. The result is a crown of 24 spikes plus a droplet thrown off. The initial symmetry of the system -- bowl of milk plus falling drop -- is circular, while the effect has a lower symmetry (In the ideal case the 24 spikes are regularly arranged, resulting in D₂₄ symmetry). Here, clearly we have a case of symmetry-breaking. But seen from a broader perspective, the symmetry is not broken at all, because every rotation of the crown, i.e. every rotated (about its vertical axis) version of it is physically equally possible. That is to say that the total collection of all possible versions of the crown, obtained by rotating it, has (still) circular symmetry. The particular (rotational) orientation that the emerging crown actually takes up is determined by some small irregularity of the system.
The relation of the instability of the initial circular ring and the above mentioned expansion figures probably must be sought in some rapid expansion by widening and hightening of the ring, such that it cannot be supplied by enough liquid to remain a smooth ring or cone and now expands by sending out rays or spikes. Obviously we are here in the domain of fluid dynamics, which is a very specialized and difficult branch of physics. And we are not in a position to speculate further about the exact causes of the successive shapes of a splash.
The case of the appearance of a branched crystal, like we saw it in snow crystals, can roughly be seen as the presence of an instability of a medium containing water. The instability consists in that medium being strongly supersaturated, and when an appropriate seed happens to come in rapid crystallization will follow. In such a case many chemical particles will rapidly flow together onto the seed. But because not enough particles can be transferred to the crystallization site at any one time and to any one site of the growing crystal, the latter will only grow in certain directions, resulting in a branched or dendritic crystal.
So all this, albeit roughly, explains how branches (outgrowths) appear in rapidly growing crystals. It does not explain why the detailed morphology of the branches repeats itself in one and the same crystal. As has been said, it seems that some holistic factor must be assumed that guarantees the establisment and preservation of a form equilibrium.

As we have remarked earlier, it is probably not fully certain that the intrinsic symmetry of snow crystals is 6/m2/m2/m. The occurrence of triangular snow crystals seems to point to a lower symmetry class that has a 3-fold rotation axis in place of a 6-fold rotation axis. The next Figure depicts such a triangular snow crystal.

Figure above : A trangular snowflake ( The shape is that of an equilateral triangle). It shows 3-fold symmetry.
(After W.A. BENTLEY and W. J. HUMPHREYS, Snow Crystals, 1931 / 1962 in which more such crystals are depicted)

Whether it consists of two interpenetrating unequal equilateral triangles, or of only one such triangle, the symmetry of such a crystal seems to be three-fold instead of six-fold. But these crystals could represent another rare case of the habitus of a crystal suggesting a lower symmetry than its actual intrinsic point symmetry. Although the inverse case is well understood, nobody seems to know why some intrinsic crystal shapes suggest a lower symmetry than its true symmetry. An example is Potassium Chloride, known to mineralogists as Sylvine (or Sylvite). Repeated observation of habit (intrinsic shape under certain conditions) led early chrystallographers to assign Potassium Chloride to a cubic Class (i.e. to one of the Classes of the Isometric Crystal System) having no plane of symmetry. But X-ray investigations have shown it to have the structure of Sodium Chloride, and have thus placed it in the Class that has the full symmetry of a cube. (HOLDEN & MORRISON, Crystals and Crystal Growing, 1960 / 1982, p.257, NESSE, Introduction to Mineralogy, 2000, p.376).

Promorphology of snow crystals.

If we assume that the intrinsic crystallographic point symmetry of all snowflakes is 6/m2/m2/m, then we can say that they all have six antimers. And we can say this without looking to the morphology of the translation-free (chemical) microscopic motif, because the occurrence, among snowflakes, of the described star-shaped (single, i.e. non-twinned) snow crystals, directly and macroscopically, establishes the presence, in all of them, of these six antimers. The promorph of these crystals (i.e. of all snow crystals) is then also directly macroscopically evident. And we give this way of determining the promorph priority, overruling the assessment based on microscopic features ( This same priority of macroscopical assessment of the promorph is given in the case of certain twinned crystals).
Snow crystals have as their main body axis a 6-fold rotation axis, which is at the same time the line of intersection of six equally spaced mirror planes. Further their equatorial plane is also a mirror plane. So the main body axis is equipolar. And because the equatorial plane is a polygon (not a circle), and thus having cross axes (stauri) the promorph belongs to the Stauraxonia homopola, bipyramids (base to base). And because the cross axes of any one (and the same) type (radial, interradial, semiradial) are equal, the promorph can be further assessed as to belong to the (Stauraxonia) Homopola isostaura, regular bipyramids. And because such a pyramid has twelve sides, the promorph can be ultimately determined as to belong to the Homopola Isostaura dodecapleura. See next Figure.

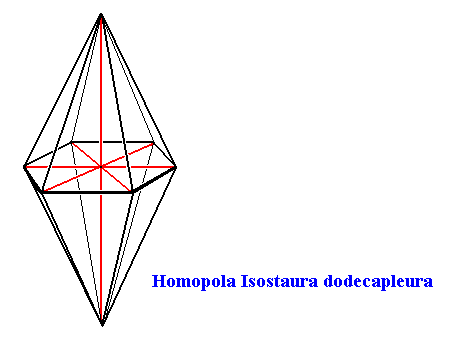
Figure above : The Hexagonal Bipyramid (twelve-sided bipyramid) representing the promorphs belonging to the Homopola Isostaura dodecapleura. The equatorial section of the bipyramid is a regular hexagon.
Main axis and radial cross axes are indicated in red.

So this promoph (i.e. the regular hexagonal bipyramid) is common to all snow crystals.

The two-dimensional analogue of the snow crystal, i.e. the projection of a snow crystal onto its equatorial plane, is geometrically a regular hexagon. The promorph of such a two-dimensional snow crystal is then belonging to the (two-dimensional analogue of the) (Stauraxonia)Homostaura Isopola hexactinota, regular hexagons with six antimers. See next Figure.

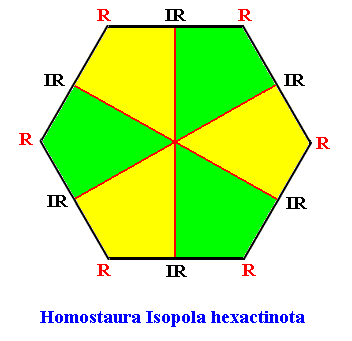
Figure above : The Regular Hexagon with six antimers (green, yellow), representing the promorphs belonging to the Homostaura Isopola hexactinota (It is "Isopola" because all cross axes are equipolar). It is the promorph of the two-dimensional analogue of all snow crystals.

This concludes our main investigation of snow crystals as to their intrinsic shape, morphology, symmetry, promorphology and metaphysics. In the next document we present a pictorial appendix to this investigation, which depicts many more microphotographs of snowflakes, all from the book of BENTLEY and HUMPHREYS (1931), Snow Crystals, which (pictorial appendix) is then followed by a discussion that summarizes our ontological theory so far developed, and extends it a little further.

e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-4.