

(Takes a little while loading the images)
e-mail :

Sequel-14 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-14) further elaborates on the analogy between crystals and organisms.
Sequel to the Preparations (II) to the Repertoire of the Crystal Analogy
The thermodynamics involved in the first stages of the generation of crystals
The ensuing discussions are largely based on NESSE, W., Introduction to Mineralogy, 2000, Chapter 5, Crystal Growth, pp.74.
To understand the conditions of crystallization-to-get-started, we must again turn to the Gibbs free energy, which can (as explained above) be considered as a thermodynamic potential, in the same way that the gravitational potential (potential gravitational energy) determines the stable position (in space) of a gravitational body. And like in this case we must compare the gravitational potentials of different spatial positions, and know that of these positions the position with the lowest gravitational potential (the lowest gravitational potential energy) is the stablest position, so we must, in the case of changes of phases and of chemical changes, compare the thermodynamic potentials or Gibbs free energies of the initial states (or of the reactants) with the final states (or with the products) in order to judge the stability of them.
For comparing the Gibbs free energy, the common basis of comparison is adopted in chemistry to compare Gibbs free energy levels based on the free energy of formation from the (chemical) elements DELTA Gf . This can also be used in all cases where no genuine chemical reaction takes place as in simple crystallization (formation of the melt from the chemical elements, and formation of the corresponding crystal from the elements).
For crystallization in a system to take place, it is not enough to have the system in the appropriate temperature-pressure conditions. When these are realized, crystallization can still be delayed. The atoms/ions/molecules must arrange themselves into the lowest-energy configuration, but they, as it were, do not 'know' exactly how to do that. Apart from the cases of very high degrees of supersaturation or supercooling, i.e. cases of a high degree of instablity (where the smallest disturbance directly leads to crystallization), they need a template of some kind, that guides them into such an arrangement. This can be accomplished by nucleation. Two types of nucleation can be distinguished, viz., homogeneous nucleation and heterogeneous nucleation.
In the first type, homogeneous nucleation, we have to do with the presence of very small crystalline fragments that already represent (parts of) the very crystals to be formed. Particles from the solution, melt or vapor are deposited on such a fragment, and the microscopic structure of the latter guarantees that these particles are deposited in the right way and in the right orientation. The fragment then grows into a full-fledged crystal.
In the second type of nucleation, heterogeneous nucleation, we have to do with nuclei that are chemically different from the crystals to be formed, but having an interior structure that is similar to that of the crystals to be formed, or having exterior morphological features that resemble those of the crystals to be formed. Such nuclei can be dust grains as they occur in the atmosphere (where they also can serve as nuclei for condensation) or any other (extraneous) grains with the appropriate structural or morphological properties. Particles from the solution, melt or vapor then precipitate onto the surface of these grains, resulting in the growth of the crystals (In the case of minerals in rocks, certain minerals grow on the surface of other minerals which form a template).
While in homogeneous nucleation certain energetic problems must be overcome for the nuclei to persist (discussed below), these are avoided in heterogeneous nucleation. The mentioned dust grains, that can serve as crystallization nuclei, are normally stable, independent of their size, while this is not a priori the case in homogeneous nucleation. So in our thermodynamic discussions, concerning the first stages of crystallization, we will concentrate on homogeneous nucleation.
Homogeneous nucleation.
With homogeneous nucleation the growth of a crystal (be it a mineral grain in a rock, a crystal from a solution or a snow crystal from a droplet of water (in a snow cloud) requires that the appropriate atoms, ions or molecules must find each other and then chemically bond (in the case of snow crystals we have to do with H2O molecules bonding to each other by hydrogen bonds) to form what will become the nucleus of a crystal. Th enucleus must then grow by progressively adding additional atoms/ions/molecules to its surface. In any chemical system, such as a melt, a solution or vapor, the atoms/ions/molecules are constantly moving about, bumping into neighbors, and forming a variety of chemical combinations. Some of these combinations, called embryos, will, by chance, have the composition and structure of substance that could crystallize from the melt. (NESSE, 2000, p.77). Most of the embryos will be small, consisting of only a few atoms/ions/molecules, but some will be larger. In general the size distribution of embryos decreases exponentially with size, as the next Figure shows.
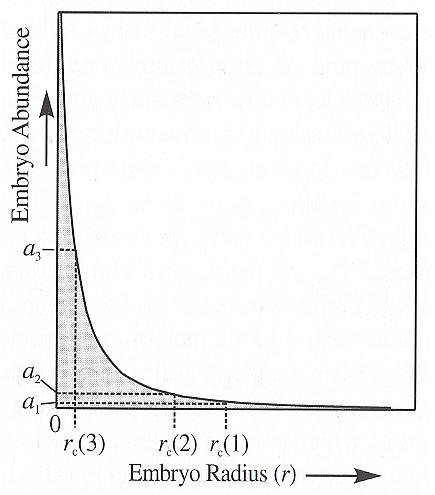
Whether these embryos will ultimately grow to form full-fledged crystals depends on both the stability of such a crystal and the size of the embryos.
The first term is the free energy change represented by changing from a melt to a crystalline configuration whose volume is v :
DELTA Gv = ( DELTA Gf (xl) - DELTA Gf (melt) )v ............................................. (1)
where DELTA Gf (xl) and DELTA Gf (melt) are the free energy of formation of the crystal and the melt, respectively, expressed in units of calories or joules per unit volume of crystal. The volume v of the crystal represents the number of units of material that obtains a lower energy, and so contributing to a total amount of decrease of G.
If DELTA Gv < 0, the chemically bonded crystalline solid represents a lower energy configuration than the same atoms/ions/molecules in a melt.
If DELTA Gv = 0, the melt and the crystalline configurations have the same energy levels. They are in equilibrium.
If DELTA Gv > 0, the melt is the lower energy configuration.
The second term included in the energy change involved in forming a crystal nucleus from a melt is the surface energy :
DELTA Gs = GAMMA . a ................................................................................. (2)
where GAMMA is the surface energy per unit area, and a is the surface area of the crystal or nucleus. ( GAMMA . a is the surface energy that manifests itself from a = 0, i.e. as soon as there is surface area, so GAMMA . a is the increase in surface energy, and thus DELTA Gs ).
The surface energy in crystallization in fact represents the energy barrier (or, equivalently, the activation energy), that stands in the way in the transition from a higher energy state (melt) to a lower enegy state, i.e. it represents a positive energy 'bump' (as a kind of threshold) in the energy-transition curve between the (higher) energy of the melt and the (lower) energy of the crystal. This barrier gets effectively lower as a result of more intensive undercooling (See next Figure). Surface energy we encounter where surfaces strive to be as small as possible, because they have a surplus of energy. In liquids we see this as their tendency to form drops, while in crystals we see it in their tendency to eliminate those crystal faces with the highest energy.
Figure above : Energy differences in different conditions :
no undercooling [melting point] (left), small degree of undercooling (middle), stronger undercooling (right), relating to the stability of crystal embryos in a melt.
Energy level of melt : upper edge of yellow rectangle.
Energy level of crystal (embryo) : upper edge of blue rectangle.
Level of surface energy : upper edge of red rectangle.
Even when conditions (temperature, pressure) are such that the Gibbs free energy of formation of the crystal ( DELTA Gf (xl) ) is lower than the Gibbs free energy of formation of the melt ( DELTA Gf (melt) ), i.e. (even when) DELTA Gv is negative, as in the middle image, the surface energy is a barrier for crystallization to get started. Crystallization can only proceed if the volume v (and thus the radius r) of the nuclei are large (enough), effecting a compensating contribution of material units of lower energy, and thus increasing the absolute value of DELTA Gv (See equation (1)).
When, as a result of changed conditions (stronger undercooling, right image) the difference between the mentioned energies of formation has become greater to such an extent that it more than compensates for the surface energy, the embryo is stable and further crystallization can proceed, because now not only DELTA Gv is negative, but also DELTA G.
If we, with respect to surface energy, assume a cubic crystal whose edges are length c, the area is 6c2 and the volume is c3 . The (ultimate) free energy of formation of such a crystal is therefore
DELTA G = DELTA Gv + DELTA Gs =
( DELTA Gf (xl) - DELTA Gf (melt) )c3 + GAMMA . 6c2 ........................................ (3)
The next Figure shows the balance between the surface energy ( DELTA Gs ) term, which is (always) positive, and the volume term ( DELTA Gv ), which in this case is negative because the temperature ( T1 ) is slightly below the equilibrium temperature. If the temperature selected is above the equilibrium temperature, DELTA Gv will be positive and the net free energy DELTA G must be positive for all sizes of embryos (NESSE, 2000, p.78), so embryos cannot persist.
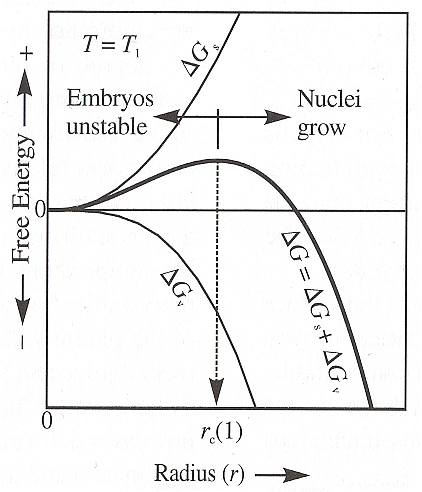
Figure above : The Gibbs free energy of formation DELTA G of crystal nuclei is the sum of the surface energy DELTA Gs and volume energy DELTA Gv (equation (3)). Only nuclei larger than the critical growth radius rc are stable with respect to the melt. Additional growth reduces the energy level. Crystal nuclei smaller than rc will spontaneously be resorbed by the melt because they represent a higher energy configuration than melt and additional growth involves an increase in energy.
The next Figure schematically shows the free energy of formation of crystal nuclei as a function of the embryo size for different degrees of undercooling below the equilibrium temperature, T0 , T1 (as in the previous Figure), T2 and T3 .
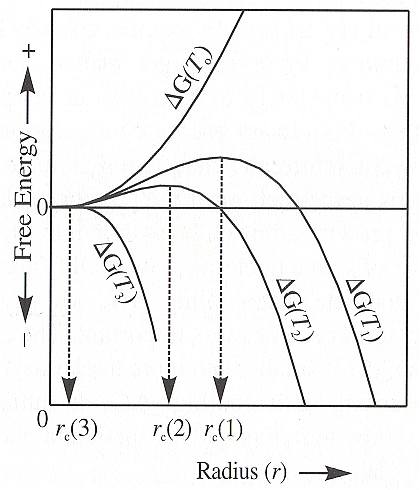
Let us discuss all the cases depicted in the above Figure :
The above temperatures, T0 , T1 , T2 and T3 can be set in the context of the triple point diagram. In the next Figure we do this for water :
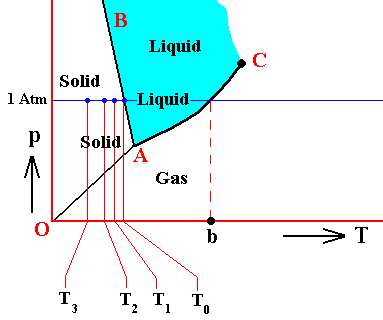
Figure above : (Approximate) Phase diagram of H2O (water) as a one-component system (C = 1). The phases are Ice, Water and Water vapor. A = triple point, AB = melting curve, AC = vapor-pressure curve of liquid water, OA = vapor pressure curve of solid water (ice), C = critical point, T0 = melting point (2730K = 00C) at 1 Atm, b = boiling point (3730K = 1000C) at 1 Atm. T1 -- T3 are temperatures of undercooling (discussed above). Although the system having these temperatures (T1 -- T3 ) finds itself in all those three cases within the 'solid' area of the triple-point diagram, its condition of aggregation is supposed to be still that of a liquid : undercooled liquid. As such the system is unstable.
The fact that crystals do not begin forming as soon as the temperature drops slightly below the equilibrium temperature, indicates that melt is remaining metastable with respect to crystals. To get crystals growing, it is necessary to supercool the melt to provide the activation energy (equivalent to the energy nudge that must be applied to a system in order to overcome the energy barrier that separates it from a lower-energy state) to overcome the difficulties related to surface energy. The magnitude of the required supercooling, and therefore the activation energy, is time dependent. For conditions in which cooling is slow and lots of time are available, the activation energy is small (more time, more chance for the appearance of large nuclei). Where cooling is rapid, the activation energy is larger (NESSE, 2000, p.78).
Heterogeneous nucleation
With heterogeneous nucleation, new crystal species nucleate by taking advantage of the structure of an existing crystal (fragment) of a different species. Some of the energetic problems associated with homogeneous nucleation are avoided. If an existing potential material substrate has a surface or structure that is similar to the new crystal, it can serve as the nucleus for growth. Such a nucleus then forms a template for the new crystal. The need to actually form (stable) embryos is largely eliminated (In the case of the formation of snowflakes, heterogeneous nucleation takes place by dust grains that are already in the atmosphere, and are, moreover, relatively stable entities).
This concludes our discussion of the thermodynamics of crystal growth as was laid down in the present document and in the previous document.
Because of their fluid, but still anisotropic state, liquid crystals (rheo-crystals) suggest to represent some sort of formal intermediate between solid crystals (sterro-crystals) on the one hand, and organisms (which are more or less semi-liquid) on the other : Rheo-crystals share with sterro-crystals their anisotropy (different properties in different directions within one and the same individual crystal), and with organisms their fluidity. And, of course, sterro-crystals, rheo-crystals and organisms all share the property of individuality, which is one of the main characteristics that have inspired, and legitimated, the crystal analogy.
In 1888 a botanist had synthesized cholesteryl benzoate, a compound derived from the cholesterol molecule. He crystallized the benzoate and discovered that it apparently had two melting points. At 145.50C the crystals turned into a cloudy liquid, which turned clear at 178.50C.
In perplexity the botanist sent a sample of his compound to LEHMANN, who was known to be an expert in microscopic studies of crystallization. LEHMANN observed that the cloudy form of the liquid exhibited a property called birefringence, which is a characteristic of many crystals that display double refraction. Double refraction occurs when the effective speed of light in a material differs in different directions. In such materials the plane of polarized light may become rotated as the light passes through the material -- this is birefringence (BALL, Ph., Designing the Molecular World, 1994, p.249).
LEHMANN was astonished to find that the first liquid state of cholesteryl benzoate is birefringent. In crystals this property derives from the ordered structure, which means that the properties may differ in different directions. In a normal liquid, on the other hand, the molecules drift about at random, so that on average one direction should look like any other. The only possible explanation for the behavior of the botanist's compound seemed to be that it possessed some degree of nonrandom, orderly structure. Here, apparently was a new, fourth state of matter : neither gas, liquid nor solid, but a 'soft' or 'liquid' crystal. Under a polarizing microscope, in which polarized light is used to illuminate the sample, the birefringence of liquid crystals gives rise to a variety of beautiful colored patterns (BALL, Ibid., p.249). Many other such substances were subsequently discovered.
In the beginning there was some controversy about these substances. Were they crystals or just anisotropic liquids? It was found out that they were (liquid) crystals, which means that such a crystal is not only anisotropic, but is also one single individual structure, and not just a patch of (anisotropic) liquid.
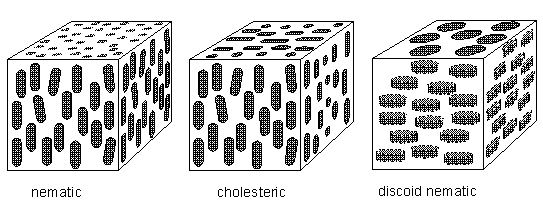
In 1924 VORLÄNDER showed that liquid crystalline materials are comprised of molecules with long, rod-like shapes. The realization soon followed that the molecular order in liquid crystals resides in the orientation of these rods. Materials comprised of spherical particles can possess only one kind of order : a regularity in the positions of the particles. But for assemblies of rods, order can also be present in the form of a regularity in the rods' orientations. Regularity in position and in orientation are independent, in that one does not necessarily imply the other. In a crystal formed from rod-like molecules, the simplest kind of periodic array has them packed side by side and all lined up in the same direction -- there will be order of both position and orientation (BALL, Ibid., p.249). See next Figure.
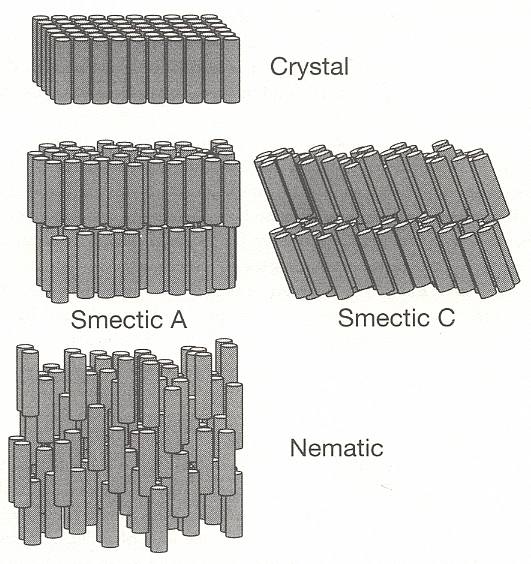
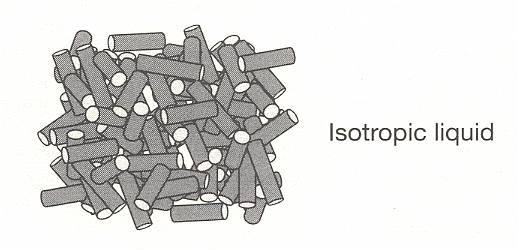
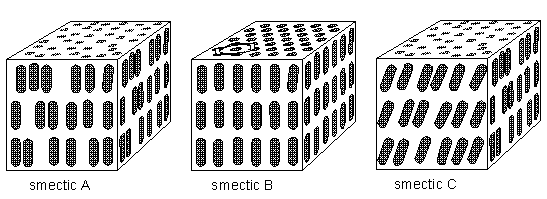
Figure above : The structure of solid, liquid crystal, and liquid phases, formed from rod-like molecules :
Sterro-crystal (i.e. solid ordinary crystal),
Rheo-crystal (i.e. liquid crystal), smectic A,
Rheo-crystal, smectic C,
Rheo-crystal, nematic, and
Isotropic liquid (i.e. ordinary liquid).
Note that, for simplicity, all of the molecules in the liquid-crystal phases are depicted here as having identical tilts, whereas in reality there are appreciable variations around a well-defined average tilt angle.
(After BALL, 1994.)
Above the melting point, the rods can jostle around so as to lose positional order but may retain some degree of orientational order, remaining pointed in the same direction on average. The proximity of a molecule's neighbors prevents it from tilting too far out of alignment. This is a liquid crystal phase, in which there is no regularity in the positions of their molecules (In smectic liquid crystals there is a vestige of positional order, evident by their layered structure.), but there is, on average, a well-defined orientational preference (BALL, Ibid., p.249) [ There exist, however, also polyhedric liquid crystals, as we will see later on ]. So apart from possible polyhedric forms, liquid crystals possess at most (namely the smectic forms) a lattice in the vertical direction only, and that is why their sections perpendicular to their main axis are circular, i.e. in these transverse sections these crystals are isotropic (no preferred directions within the section).
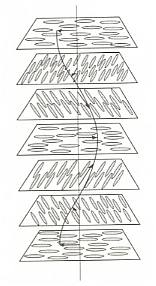
Figure above : The cholesteric phase, in which the direction of molecular orientation rotates in a helical fashion. Because they scatter light strongly, cholesteric phases give rise to iridescent colors such as those observed in butterfly wings and insect cuticles. For a larger version of this Figure click HERE (to return to text, close window).
The pitch of the helix in cholesteric phases is generally of the same order of magnitude as the wavelengths of visible light, so that these phases reflect light much as crystals scatter X-rays. This wavelength-dependent reflection gives rise to iridescent colors. The iridescence of some beetle cuticles and butterfly markings stems from the formation of cholesteric phases by the molecules that comprise the tissues (BALL, Ibid., p.251).
Rod-like molecules are not alone in their ability to form orientationally ordered liquid crystalline phases. Indeed, any molecules that are not essentially spherical should in principle be able to show orientational ordering, and in (solid) crystals many molecules do. In the fluid state, however, only those that have a pronounced degree of nonsphericity can retain some of this order. For example, the opposite extreme to a molecule that is stretched out into a rod is one that is flattened into a disc. Orientationally ordered arrangements of discs are very familiar -- just think of a stack of dinner plates or gramophone records (BALL, Ibid., p.252). In 1977 such 'discotic' liquid crystalline phases have indeed been discovered. See next Figure.
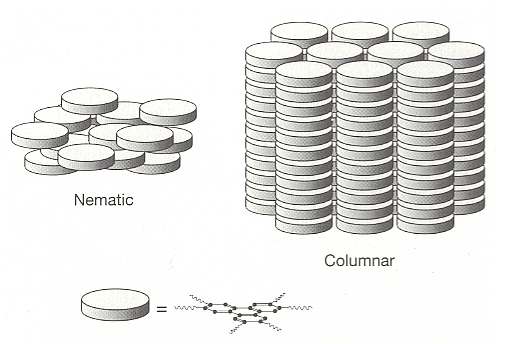
Figure above : Discotic liquid crystals. In the liquid crystalline columnar phase the disc-like molecules are stacked like dinner plates, while in the nematic phase they have approximately the same orientation but no positional order.
(After BALL, 1994)
Additional information from websites on liquid crystals : http://liqcryst.chemie.uni-hamburg.de and http://www.tu-berlin.de
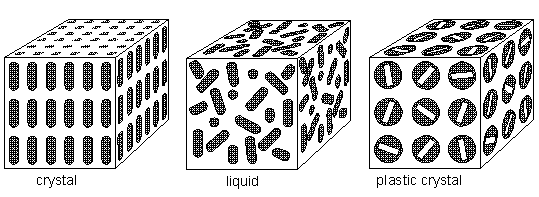
Mesophases (liquid crystals and plastic crystals) are a state of order between true crystals (sterrocrystals) and true liquids. They have imperfect long range orders of orientation and/or position. Thus they can be fluid like a liquid and they can have anisotropic properties like crystals. Whereas plastic crystals (see Figure below) have a predominating positional order (predominating over orientational order), the liquid crystals have predominating orientational order (predominating over positional order). In solid crystals (sterrocrystals) there is both positional and orientational order, resulting in strict three-dimensional periodicity, i.e exact repetition of some unit in three independent (crystallographic) directions. In true liquids there is neither positional, nor orientational order.
The molecules of liquid crystals (or, as we can say more generally, anisotropic liquids) are typically rod-shaped (chemically) organic entities about 25 Angstroms in length (1 Angstrom = 10-8 cm) and their ordering is a function of temperature. As stated above there are several types of anisotropic liquids (nematic, smectic, cholesteric, etc.). The nematic phase , for example, is characterized by the orientational order of the constituent molecules (and no positional order). The molecular orientation (and hence the material's optical properties) can be controlled by applied electric fields. The smectic phases , which are found at lower temperatures than the nematic, form well-defined layers that can slide over one another like soap. The smectics are thus positionally ordered along one direction (which can be seen to be an axis). In the smectic A phase, the molecules are oriented along the layer normal (i.e. they are oriented perpendicular to the plane of the layers), while in the smectic C phase they are tilted away from the layer normal. These phases (smectic A and smectic C) are liquid-like within the layers
The smectic B phase (see Figure below) seems particularly interesting because here there is still, it seems, a great deal of positional order within the layers (together with orientational order). Although the positions (and also the orientations), as drawn for smectic B in the Figure below, are, I think, only averages, the structure appears to approach a genuine space lattice, like in sterrocrystals. It is a "crystalline smectic".
As discussed above, also disc-like molecules can form liquid-crystalline phases, for example a discoid nematic phase.
If there is no orientational order, but nevertheless full positional order, we have a plastic crystal phase, which is, like the liquid crystal phase, also a mesophase.
The next Figures illustrate all these phases schematically. They are borrowed from one of the above mentioned websites on liquid crystals :
http://liqcryst.chemie.uni-hamburg.de .
The main factors involved in the formation of liquid crystalline phases are :
Typical chemical structures (chemical compounds, recent nomenclature) that form liquid crystalline phases are (according to the above mentioned website) :
There are many more substances that can form liquid crystalline phases, like for example DNA, Lecitine and Ammonium oleate.
So organic substances (i.e. more or less complex compounds containing carbon), some of them occurring in living organisms, can form liquid crystalline phases. And although they do not form true lattices (except perhaps the smectic B phase), such substances could form some sort of spatial reference system within an organism, a system that at least defines a definite direction within its body. So liquid crystalline textures must not be excluded from our consideration of 'organic lattices' in so far as a basic spatial reference system, present in organisms, is meant.
The next exposition of liquid crystals (rheo-crystals) is taken from Handwörterbuch der Naturwissenschaften, 1912--1915, Volume V, Article "Flüssige Kristalle" written by R. BRAUNS, p.1074-1088. It is evidently a rather old text (not too long after the discovery of liquid crystals), so we only consider those features given in this text that are not too liable to become obsolete (Apart from the above discussion, that was based on a 1994 text, I hope to find some more recent texts). Anyway, the Handwörterbuch der Naturwissenschaften perfectly represents the scientific background of PRZIBRAM, whose book on the crystal analogy (1926) we are about to discuss and update (next document).
Rheocrystals share with sterro-crystals (solid, ordinary crystals) the property of double refraction of light (Crystals of the Isometric System do not show this property). This property shows them to have some ordered internal structure. All rheo-crystals and sterro-crystals share the general property of anisotropy, which means that with respect to many features certain directions within an individual crystal are not equivalent to others. But in contrast to sterro-crystals, rheo-crystals are in a true liquid state. The substances that can form a crystalline-liquid phase happen to be all (or almost all) organic compounds. We will mention some of them in due course.
Every substance, that can form a crystalline-liquid phase, possesses at least two melting points. At the first melting point the crystalline-solid substance transforms into the cloudy crystalline-liquid version, while at the second melting point the substance becomes clear and isotrop (all directions equivalent). This second point therefore is called the clearing point. It is not uncommon that such a substance shows, in its solid form, polymorphy and is enantiotropic.
In substances, occurring in two variants (polymorphs) one distinguishes between e n a n t i o t r o p i c (not to be confused with anisotropic) and m o n o t r o p i c substances. In the latter (for instance, phosphorus) one can prepare a form (i.e. a variety) (for instance, yellow phosphorus), which is always metastable with respect to the other, and automatically, or by the help of a catalyst, transforms into the stable form. In enantiotropic substances, on the other hand, each form (i.e. each polymorphic variant) is represented by an area in the pressure-temperature diagram, in which it is stable ( Handwörterbuch der Naturwissenschaften, Volume VII, p.682 / 3 ).
Also in their liquid state substances can be considered as polymorphic, enantiotropic or monotropic. As a given modification of a polymorphic solid substance is stable within a definite temperature range, so also the crystalline-liquid modification. The lower limit represents the melting point, at which the transformation of the solid state into the cloudy liquid anisotropic state takes place, while the upper limit represents the clearing point, at which the liquid becomes clear and isotropic. For some substances these points are the following :
| Substance | Melting Point | Clearing Point |
| Cholesterylbenzoate | 145.50C | 178.50C |
| Cholesterylpropionate | 980C | 1140C |
| p-Azoxyanisol | 1160C | 1340C |
| p-Azoxyphenetol | 137.50C | 1680C |
| p-Azoxyanisolphenetol | 93.50C | 149.60C |
| Anisaldazine | 1600C | 1800C |
| p-Azoxybenzoeacidethylester | 113.50C | 120.50C |
If the melt, after the clearing point was overstepped, is cooled again, then it first passes through the crystalline-liquid state again, before it becomes crystalline-solid. There is, accordingly, a complete analogy with enantiotropic substances. Cholesterylacetate behaves differently in this respect, expressed by the fact that there is no definite stability range for its crystalline-liquid form, so its forms behave like monotropic entities.
| Substance | Viscosity of Anisotropic Phase |
Viscosity of Isotropic Phase at clearing point |
| Cholesterylbenzoate | 893--621 | 420 |
| p-Azoxybenzoeacidethylester | 856--472 | 357 |
| p-Diacetoxylstilbenchloride | 327--309 | 449 |
| p-Azoxyanisolphenetol | 171--111 | 167 |
| p-Azoxyanisol | 141--128 | 174 |
| p-Methoxycinnamonacid | 106--91 | 159 |
| p-Azoxyphenetol | 79--66 | 95 |
The first two substances have about the consistency of olive oil, the remaining substances (apart from the last one) that of the higher alcohols, while the last one is more fluid than water. In the majority of investigated substances the anisotropic liquid turned out to be significant more fluid than the isotropic ones. The viscosity increases abruptly (but not discontinuous) to the higher value at the clearing point. Only in the case of the two most viscous substances the anisotropic phase possesses the higher viscosity. The transition of the viscosities turned out to be smooth, but the smooth change of viscosity at the transition from crystalline-fluid to the amorphous melt is typical for the phenomenon of viscosity only. Already smoothness is not typical anymore for density. For Anisaldazine it was determined that at the clearing point the change in density is discontinuous : The value 2.034 of the isotropic melt, as it is at at 183.720C, jumps to 1.315 of the anisotropic melt as it is at 182.330C, where the clearing point is at 182.750C.
The cloudy melts, which are as such aggregates of rheocrystals, and which are therefore best called crystalline liquids (in contradistinction to any single rheocrystal), turn out, when investigated in polarized light, to show lively double refraction, in a, with their movements, constantly changing way. If we only want to show that these substances are liquids and at the same time are double refractive, we only have to put the sample under a suitable (polarization) microscope, hold it under the clearing temperature and see whether it flows when tilted, and see whether it shows double refraction. But in order to investigate the shape that is taken up by the free-floating rheocrystals, the substance must be subdivided into small parts, which can be accomplished by the addition of very small amounts of solvent (Brominenaphtaline, Colophonium, oil, etc.).
While the crystalline liquids (which are thus aggregates of rheocrystals) appear cloudy as a result of refraction, reflection and bending of light taking place at the boundaries of the individual crystals, the latter are, when isolated, clear and transparent. LEHMANN rejects the term "double refractive liquids" for such individual crystals, because liquid crystals distinguish themselves in an essential way from liquids that have become doubly refractive by severe mechanical disturbances, in that the new layers, deposited during their growth, show the same anisotropy, and that the structure is preserved during the most diverse and far-reaching disturbances. From this LEHMANN concludes that the rheocrystals possess "molecular directing force" , something that ordinary liquids do not have (How to interpret this force -- from a modern standpoint -- is not easy. We could surmise that the molecular directing force is a resultant of the forces of many (interacting) individual atoms/molecules, and, in the form of such a resultant, is the 'form-generating force' of the given substance, which is then equivalent to the spatial patterning of surface energy, i.e. different surface energies in different directions, where the sites with the highest surface energy tend to reduce themselves as much as possible (resulting in a relaxation of the relevant system), and in this way resulting in s h a p e, or, maybe better, in this way c r e a t i n g shape.).
As to the shaping of individual rheocrystals we can distinguish between those that, when freely floating, adopt only a spherical shape, others that are bicones (two cones connected by their (circular) bases), and, finally those that have a polyhedric shape (where "polyhedric" means that the shape of the crystal individual involves facets, (straight) edges and corners). In rheocrystals that form just spheres, their shape is formed exclusively by surface tension. They are called liquid crystals in the narrow sense. In the others the shape is, in addition to the surface tension, co-determined by their substance, i.e. by the form-generating forces of the substance, which means that the surface tension is partly or wholly overruled by these form-generating forces of the substance. Such rheocrystals are called flowing crystals.
Rheocrystals having spherical shape can be obtained from p-Azoxyphenetol, or from a mixture of this substance with Azoxyanisol.
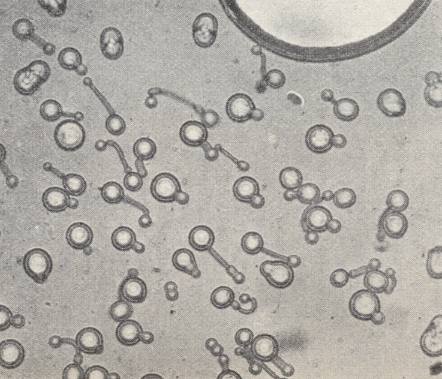
Azoxyphenetol, which, in its crystalline-liquid state is more mobile (i.e. has a lower viscosity) than water (See table above ), adopts a spherical shape of its crystals when free-floating. See next Figure.
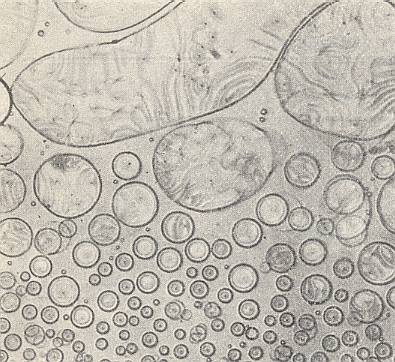
The spheres possess a regular interior structure, expressed -- in unpolarized light and sufficient magnification -- in such a way that a sphere seems to possess, depending on its orientation, either a dark nucleus in its center surrounded by a grey 'court' (Crystal droplet in First Main Orientation), or (seems to possess) a biconvex lens (Crystal droplet in Second Main Orientation). These are structures that do not actually exist, but only appear as a result of light refraction caused by the crystals' interior structure (which must be some atomic or molecular regular pattern, i.e. a certain patterned arrangement of atoms/molecules).
We nowadays know that the organic phenomenon is much more complicated than it is in rheocrystals : While in the latter we have to do with only one or a few substances, in organisms many substances are involved, orchestrated into a complicated functional system, in which much regulation takes place. We could say that in such organisms the phenomenon is an 'elevated ' version of the corresponding phenomenon in rheocrystals, in this way on the one hand emphasizing the analogy between crystals and organisms, but, on the other, stressing the fact that it is only an analogy. The relative simple laws that govern the merging of crystal droplets are in the organism ' harnessed ' in some way, in order to make it robust, controlled and repeatable.
If, in the case of merging crystal droplets, the mixing substances are significantly different, then characteristic structural disturbances take place. See next Figure.
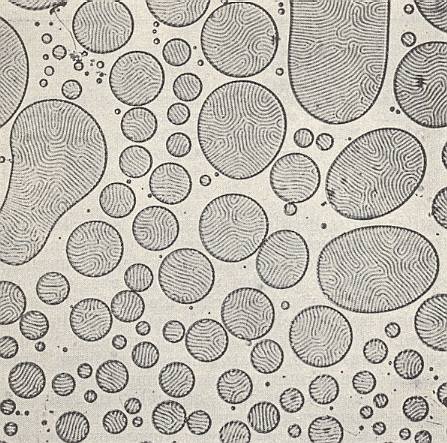
In such mixtures we see, for example, droplets that consist of a layering of lamina, which can be so fine that very strong magnification is required to see them. Their structure could be compared to the microperthite structure of alkali feldspars (which is a result of demixing into components) (Alkali feldspars are certain silicate minerals occurring in certain rocks).
With these phenomena we again encounter analogies with organisms. They express the i n d i v i d u a l i t y of (rheo)crystals, a property strongly expressed by organisms.
On the surface of an air bubble, present in the crystal growing environment, the rheocrystals expand into a pseudo-isotropic layer, i.e. empty sphero-crystals appear.
Investigations concerning interference phenomena in polarized convergent light are carried out especially by VORLÄNDER. According to these investigations the "pseudo-isotropic" crystalline liquids produce, after they have become clear and transparent as a result of the erection of the crystals between object glass and cover glass, an, also during rotation unchanged, sharp interference pattern of u n i a x i a l crystals, which (interference pattern), cannot be distinguished from that of a solid (optical) uniaxial crystal slice, cut perpendicular to its optical axis. The double refraction of alpha-methylized and alpha- ethylized Cinnamonacidethylester is more than two times as strong as that of calcite.
In rheocrystals, according to LEHMANN, the arrangement of atoms/molecules -- in rheocrystals probably always molecules -- only in rare cases corresponds to the space lattice structure of the sterrocrystals (solid crystals). In most cases only the axis, about which (according to LEHMANN) the molecules especially easily turn, is parallel in most molecules (i.e. there is one specific -- but average -- direction to which most molecules of a sample point with their axis), while the subsidiary axes normal to that axis are oriented in all possible constantly changing directions (This is not to be understood that such crystals rotate about their main axis, neither that the molecules (as a whole) orbit the axis, but that, although they go around the axis, they do so irregularly and individually, resulting in the absence of a definite figure of subsidiary axes, which is equivalent to no (subsidiary) axes being present at all.). This half- or pseudo-isotropic structure seems to represent an intermediate between that of homogeneous sterrocrystals and that of homogeneous non-crystalline liquids.
(Because of the absence of subsidiary axes, the promorph -- the ideal stereometric basic form -- of such a crystal is that of the Monaxonia haplopola (spheroids, bicones, cylinders), despite its spherical shape (because such a crystal has a main axis as its only axis, while the axiality of a sphere (Homaxonia) can either be interpreted as having an infinity of equivalent axes, without any additional axes present that are different from them, or (equivalently) as having no axes at all (but being regular nontheless).)
Rheocrystals with polyhedric shape, flowing crystals.
Many rheocrystals take up a more or less perfect polyhedric form when free-floating. The form-generating force of the substance is in these cases stronger than the surface tension. Such crystals are therefore distinguished from liquid crystals in the strict sense by calling them flowing crystals.
A note on form generation in crystals.
The relationship between the surface tension of a given substance and the "form-generating force of that substance" is not easy to establish, because the latter is more or less ill-defined. But let us give it a try.
The overall surface tension of a quantity of solid or liquid substance is present at its boundaries, i.e. at its surface. The molecules of the substance which are at its surface "cannot experience as many attractive, stabilizing interactions with neighbors as do molecules in the bulk of the liquid, and so the surface molecules have a high energy relative to the bulk. Therefore, the presence of the surface carries an energy cost. The larger the surface area, the greater the energy cost. We generally speak of this surface 'excess energy' as the surface tension, since its effect is to 'pull' the liquid into a compact form, keeping the surface area as small as possible." (BALL, 1994, p.227). The smallest area for a given volume of substance is a sphere, so the surface tension tries to compact the substance into a sphere, and because in a sense, a sphere is no (specific) form or shape at all (because all its body axes -- axes that go through its center -- are the same), we can say that the overall surface tension tries to eliminate shape.
Antagonistically to this tendency to reduce shape (surface tension) there can be other factors that tend to create (definite) shape. One such factor is the tendency to realize a lowest-energy structure, i.e. an arrangement of constituents (particles) of the substance that represents a lowest-energy configuration, like we see in the lattice structure of sterrocrystals, i.e. a lattice provided with chemical motifs. This lowest-energy internal (periodic) structure makes possible several faces, i.e. boundary facets that point (with their normals) in several definite directions. Because they are surfaces, these facets have higher energy than is present in the interior of the body of the given substance. But generally this energy surplus is not the same for all such facets. Some of them have a higher energy than others. So the system, in its effort to get rid of all forms of strain or tension, i.e. in its effort to relax, will try to eliminate those facets with higher energy, as far as it is possible to do so. And this results in a definite s h a p e of the body of the given substance.
So if the surface tension is not very strong, it will, in the case of many substances, be counteracted by the selective elimination of high-energy facets, or in other words, if the surface tension is not totally dominant, a definite shape will appear, and if its relative strength is still great enough the overall surface tension will tend to round off corners and edges, if it is not, then we have a genuinely polyhedric crystal with sharp edges and corners.
The polyhedric r h e o crystals, that are about to be discussed, could be the just described polyhedric bodies of which the edges and corners are more or less rounded off by the overall surface tension.
True representatives of the polyhedric rheocrystals are Ammoniumoleate (next Figure), Paraazoxybenzoeacidethylester and Paraazoxybrominecinnamonacidethylester (Figure thereafter).
Ammoniumoleate is stirred with alcohol while heated, an the solution is investigated on an object glass with a plane cover glass. In order for the appearing crystals to be well recognized, it is recommended to use the direct light of some intensive lamp. In natural (i.e. unpolarized) light these crystals only weakly contrast with their background, because their light refraction differs only slightly from that of the solution. They are more clearly recognized in polarized light, but also in this case they do not contrast strongly with their background. See next Figure.

The form (shape) of these crystals (i.e. of rheocrystals of Ammoniumoleate) is that of an acute quadratic bipyramid, i.e. two congruent acute pyramids fused together with their quadratic bases (In the text, Handwörterbuch der Naturwissenschaften, 1912--1915, Volume V, p.1084, it reads "quadratic pyramid", but, judging from the photograph, but also by the fact that this form is, a little bit further down, referred to as "acute octahedron", it is certain that it is a bipyramid).
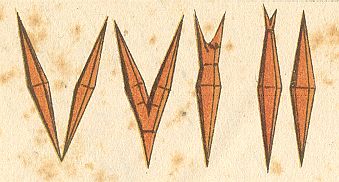
Liquid crystals of Ammonium oleate can also adopt a monaxon form :

Figure above : A soft spool crystal of Ammonium oleate. Cylindric, conically pointed at both poles of the axis. The edges and corners (except the apices) of the bipyramid are rounded off by the action of surface tension. (In HAECKEL, E., Krystallseelen, 1917, after a drawing by LEHMANN)
Lecithine, when dissolved in alcohol, produces rheocrystals which behave perfectly analogous to Ammoniumoleate. The formation of polyhedric forms, the double refraction of the crystals and their dichroism (white and yellow colors when seen over one nicol -- of a polarization microscope, i.e. seen in polarized light), are properties that contradict the assumption that we would have to do here with emulsions. During the flowing circulation of the growing environment around obstacles, rheocrystals that freely float in that growing environment, can, because of their very low inner friction, deform while their directions of (light) extinction are constinuously changing, deform that is, corresponding to the curvatures of the streamlines, and behave as if they were just parts of the liquid, parts provided with double refraction. When the effected curvature (deformation) of a crystal is strong, a kink can appear, causing the molecules on either side of it to be placed in twin position.
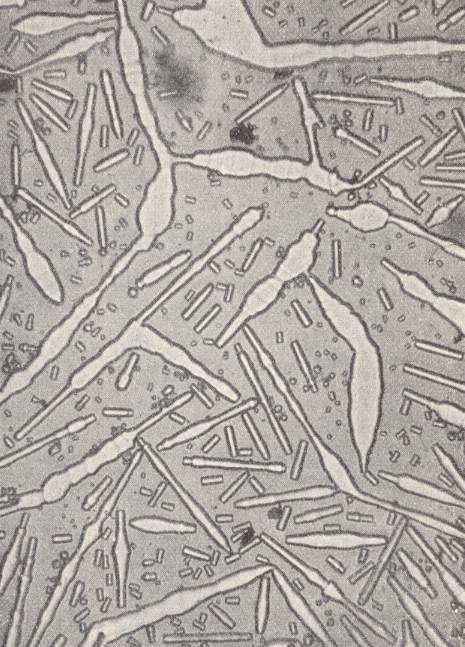
When a free-floating crystal is arbitrarily deformed, it, when left alone, returns again to the polyhedric shape.
The most remarkable phenomena are exhibited by the flowing crystals of Paraazoxycinnamonacidethylester , that had been prepared by VORLÄNDER, the "pseudo-living crystals" of LEHMANN. According to his observations they have the property to copulate, to divide, to grow by intussusception (i.e. grow by taking up particles into their interior) and to move like bacteria. The substance is flowing-crystalline between the temperatures 139.50C and 2980C. To obtain the mobile crystals one must heat the substance, with addition of a trace of solvent (Monobrominenaphthaline), close to melting. On cooling at first polyhedric crystals appear with rounded-off edges and corners with a basic form of that of a quadratic hemimorphic pyramid (i.e. a single quadratic pyramid (a pyramid whose base is a square)). See next Figure.
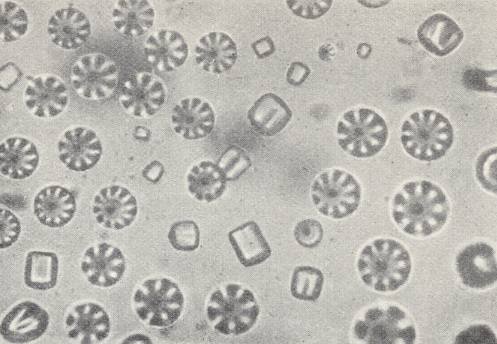
When two such crystals make contact with each other, they directly flow together into one, having uniform structure, provided that their orientation was more or less the same. If not, then they can unite into twins according to their bases (i.e. they will unite with their bases). So far they are like the crystals just described. They are, like all next forms, doubly refractive and dichroitic with symmetric extinction like other quadratic crystals (i.e. like crystals of the Quadratic System). If the temperature decreases further, then, because of intake of solvent, crystals, that become more and more soft, appear, which finally cannot counteract the pressure of the surface tension anymore, resulting in their contraction into droplets, which, at one side are weakly flattened. On contact with another droplet or a pyramid they both flow together. In the case of many of them uniting, a facetted spherical object can be formed, that with respect to its structure is a unification of many pyramids whose apices point to the center (See Figure above ).
Immediately after this, the bud develops into a long 'hose' (See next Figure), which coils and curves like a worm while executing vigorous swinging movements.
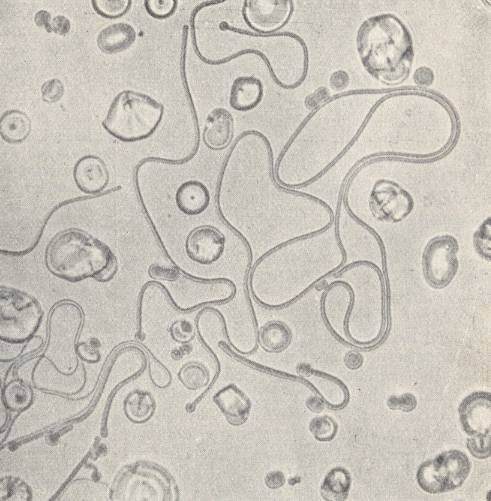
Often they lie together in dense entanglements and fill out the entire field of vision. Suddenly they have disappeared, they have contracted into spheres. After this, the phenomenon can repeat itself if the temperature is kept unchanged. Another droplet simply draws itself out into its length direction, and in this way forms a small rod with hemispherical ends. It moves along between other such entities and crawls forwards and backwards like bacteria. Sometimes such a rod suddenly bends itself into a ring which directly transforms into a droplet. Because the forms grow in longitudinal direction despite the fact that their material is taken up laterally, their growth is by way of intussusception (like it is in organisms). Often one of the forms divides into two of equal form and structure, which LEHMANN compares with cell division in organisms. Or, out of one 'hose' a thinner one shoots forward, and from this a yet thinner one, etc.
In my considerations I am still making use of the above mentioned article in the Handwörterbuch der Naturwissenschaften (1912-1915, Volume V, p.1074--1088). It is part of the background of PRZIBRAM's book (1926) on the crystal analogy, in which rheocrystals play an important role.
Certainly in those days, but in fact also today, it is hard to correctly reduce the properties and shapes of rheocrystals to the properties of their constituent molecules, if they are so reducible (in principle) at all. In the mentioned article (1914) several theories are proposed, none of them seems acceptable to me. And matters are worse, because the shapes of rheocrystals could receive only a limited attention in this article (in virtue of observational difficulties). Nevertheless it is instructive to briefly discuss these theories (as they are presented in the article) in order to understand the difficulty of such attempts, and of the problem of the generation of macroscopic patterns in general. So here we go.
As a result of his investigations concerning rheocrystals LEHMANN abandoned certain well-established theories. So he now (1914) maintains that polymorphism and amorphism do not exist in the sense of current theories : It is not the way of aggregation of molecules (or atoms for that matter) that determines the properties of a substance, but their constitution, implying that we should state : No substance can be in several polymorphic modifications. No substance possesses a crystalline and an amorphic modification. No substance has three conditions of aggregation -- gaseous, liqiud and solid. All these so-called modifications rather are materially different, i.e. they differ by virtue of the nature of their molecules. Also to the current notion of a crystal and to the theories about the space-lattice structure, rheocrystals -- still according to LEHMANN -- do oppose. Not the regular ordering or arrangement of molecules (or single atoms) into a regular system of points represents the essence of a crystal, but the anisotropy of the molecule itself, which only indirectly results in the regular structure of the given body. So LEHMANN defines a crystal generally as follows : "A crystal is an anisotropic body possessing molecular directing force", which, in virtue of these properties, has the ability to grow.
VORLÄNDER agrees with this position : From the linear form (rod-like shape) of the molecules the parallel directedness of them follows, implying the anisotropy of the liquid. "The anisotropy of the molecule is, up to a point, made evident by the structural formulas of the crystalline-liquid substances".
R. SCHENCK agrees with LEHMANN in that the molecules possess a directing force of their own (meaning that the directing force of a substance is not something that only comes into existence as a collective result) and that the linear form of the molecules certainly is an essential factor for the stability of rheocrystals, which (factor) supports the action of the form-generating force. But he opposes LEHMANN's view where it holds that in polymorphic modifications the molecules themselves are differently constituted, but assumes that the differences between polymorphic forms are caused by some quantitative (incontradistinction to qualitative) differences within the molecules (without changing the type of molecule).
G. LINCK, in his elements of crystallography, assumes that a rheocrystal (here a liquid crystal s.str. as opposed to a flowing crystal) possesses so low a viscosity that its molecular net is not able to counteract the surface tension. In that case the molecules must, following the law of surface tension, together form a sphere. If the molecules possess a predominant longitudinal extension (i.e. if they are rod-like), then they must orient themselves radially to this extension and form a spherocrystal of which the optical properties become very similar to those of optically uniaxial crystals (tetragonal or hexagonal system). The movements of the pseudo-living crystals he explains also by the temperature fall in the sample, as did the writer of the presently discussed article (in the Handwörterbuch der Naturwissenschaften) on an earlier occasion.
V. GOLDSCHMIDT prefers to interpret the liquid crystals not as crystals, but as "oriented liquids". However, this interpretation cannot apply to those rheocrystals that are able to adopt a polyhedric shape of their own. Further GOLDSCHMIDT defines : "Oriented liquid is a spoolically gliding system of particles", where, with "gliding system" he means a system, such that every point does not change its average distance from the totality of neighbors, so that every system point moves glidingly on its neighbor. The particles would find themselves in a condition of uniaxial bonding. In the direction of this axis they only perform oscillation, while rotating about this axis. The surface of oscillation (depicting the extent of oscillation) would then be that of a rotational body having the shape of a spool.
These kinetic-theoretic views come more or less close to the molecular-theoretical views of VORLÄNDER which seem well-founded (according to te writer of the mentioned article).
G. WULFF assumed, based on his observations, that the doubly refracting droplets are in fact vesicles filled with isotropic liquid, vesicles of which the wall is doubly refractive. The "liquid crystals" of Paraazoxyphenetol would therefore be foam-cells. However, the physical properties of liquid crystals, contradict this assumption.
FRIEDEL and GRANDJEAN think that the state of liquid crystals represents a new state of matter all together, just as different from the crystalline state as from the state of an ordinary isotropic liquid.
The author (R. BRAUNS) of the article under discussion concludes as follows :
"Because on the subject of liquid crystals there is still much to be explained, it is recommended to let the theories of the space lattice structure, which are so well founded for the case of solid crystals, come first."
In the next document we continue our preparations with respect to the coming exposition of the crystal analogy.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-15.