

e-mail :

The present document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Special and General Categories, Generality of Symmetry and Causality.
In this document, and in many hereafter, we will consider certain definite symmetries as they occur in natural bodies such as organisms and crystals (with respect to the latter we will expound it by studying two-dimensional crystals, which are easier to grasp in this respect and yield the same basic principles as could be obtained by studying real, i.e. three-dimensional crystals). But then we could ask ourselves -- when studying these definite symmetries (alongside with definite shapes and promorphs) such as D2 symmetry, C3 symmetry, etc. -- are we not then doing Special Ontology instead of General Ontology? Indeed, general ontology should study only the most fundamental categories ( If / Then constants), which pervade all of Reality, i.e. all Layers of Existence. But this being so, we could extend the notion "General Ontology" to include categories that are, it is true, not maximally general, but are still fairly general nevertheless, in fact general enough to figure in a General Ontology. Such a category is for example that of Causality (a nexus category). If we accept this category as one that can figure in a General Ontology, then we can also accept the category of Symmetry (whatness category) as sufficiently general to figure in such an Ontology, as we will now show :
Causality is considered to be a general category pervading at least a whole Layer of Existence.
Symmetry (and also Promorph) in the geometric sense is also pervading at least a whole Layer of Existence (in fact, the Mathematical, Physical and Organic Layers).
Symmetry as such is, however, not a distinguishing property, as long as the (trivial) group C1 is considered to represent a symmetry as well (For mathematical purposes it is convenient to do so). So we define Symmetry to include all symmetries except the one that is represented by the group C1 . The latter in fact represents asymmetry.
Causality necessarily involves two entities related to each other as cause and effect.
Symmetry involves only one entity at a time.
Not any pair of entities is causally connected, but many are so connected.
Not any entity is symmetric, but many are.
So Symmetry and Causality are indeed of comparable generality, and can both figure in a General Ontology.
What then is a special category?
Well, for example, D2 symmetry, C3 symmetry, etc. Further, pressure--deformation is (an example of) a special case of causality. So it is indeed possible to still distinguish between special and (moderately) general categories. And this is the basis for considering the category of Symmetry as a (moderately) general category, just like Causality.
And in expounding this category of Symmetry by means of (examples of) special symmetries, like D2 , C3 , etc. -- what we will do in the present and following documents -- we're still doing g e n e r a l ontology.
We can even go further than this, where an extension of the notion of "General Ontology" to include moderately general categories ( If / Then constants) is not even necessary. We will explain this in the next Section.
General Ontology, Special Ontology, Shape, Symmetry and Promorph.
In the documents to come we will present a detailed account of Shape, Symmetry and Promorph (and the relations between them) as they occur in natural intrinsic bodies, be they organic or inorganic. They will also be considered as they occur in purely geometrical bodies (including two-dimensional 'bodies'), i.e. as they occur in the Mathematical Layer of Being. While Shape and Symmetry equally occur in the Mathematical and Material Layers (viz., the Inorganic or Physical Layer and Organic Layer), Promorphs are most relevant for objects in the Material Layers, because they involve antimers, and antimers are equal or similar parts of a concrete material body, while they are only formally present in mathematical bodies.
In our General Ontology we have developed a theory of c o n s t i t u t i v e [in contradistinction to m o d a l -- referring to relations between Possible Existence or Non-existence, Actual Existence or Non-existence, and Necessary Existence or Non-existerce] categories or determinants, which (categories) have been presented as different sorts of "If / Then constants".
Now, general ontology should limit itself only to general, universal and fundamental categories or If / Then constants. Such general fundamental constants should, if they are to be really fundamental, apply to the whole of Existence, i.e. to all Layers or Spheres of Being, and that means they should apply to the Mathematical, as well as to the Physical, Organic, Psychic and Superpsychic Layers (or, in HARTMANN's sense, they should apply to the Real as well as to the Ideal Sphere of Being). Such If / Then constants come in the form of Opposites of Being (Seinsgegensätze), for example :
And if all this is correct, then Shape, Symmetry and Promorph are -- as such -- truly fundamental and universal categories, pervading all of Existence, be it Mathematical, Physical or Organic,
because now the only genuine existents or beings of all the non-mathematical Layers are m a t e r i a l t h i n g s, where relations between these things do only exist in virtue of these things which are thus primary. And every thing, every material object, possesses Shape, Symmetry and Promorph. In the Mathematical Layer they are present as properties of geometric bodies and figures. For all this to be so we must include in the concept of (intrinsic) Shape also irregular forms (because although being irregular, they have a shape nevertheless), and we must include in the concept of (intrinsic) Symmetry also asymmetry (because asymmetry can be described by a symmetry group, namely by the Cyclic Group of order One, C1), and, finally, we must include in the concept of Promorph the apromorph (because an apromorphic body or figure can be described by a promorphological family called the Anaxonia (acentra). So indeed Shape, Symmetry and Promorph can be given in the form of Opposites of Being (Seinsgegensätze), viz.
In our discussions of Shape, Symmetry and Promorph we will restrict ourselves to i n t r i n s i c bodies or figures possessing them intrinsically, because they are by far the most fundamental and ontologically significant beings (every non-intrinsic body (random aggregate) ultimately consists of intrinsic bodies. And in the Mathematical Layer the intrinsic and extrinsic coincide, i.e. there this distinction is irrelevant. And indeed, in this sense, i.e. when we include the Psychic and Superpsychic Layers wholly within the Organic Layer, we, when studying -- from an ontological point of view -- Shape, Symmetry and Promorph as such, are doing truly g e n e r a l ontology. And, of course, when studying Shape, Symmetry and Promorph, we must investigate many s p e c i a l examples of them in order to get to grips with their general nature as fundamental categories, i.e. just with Shape, Symmetry and Promorph i n g e n e r a l as some subset of the total set of fundamental categories pervading (in their generality) all of Existence, be it mathematical or material, inorganic or organic.
Let us now, in the present context, i.e. in our assuming there to be only three Layers of Being, viz. the Mathematical, the Physical and the Organic, compare Shape, Symmetry and Promorph to two other categories, namely Element and System (as such taken from HARTMANN, 1940, p. 231), for which we are sure that they really represent truly fundamental categories, together forming a pair of opposites : Element -- System. Every being, be it mathematical or non-mathematical, is either an element or a system. And except for a last indivisible element, every element can itself also be a system of 'smaller' elements, and every system can also be an element of some higher system. A s p e c i a l c a s e of Element -- System could, for instance, be the participating inorganic ions (elements) of the Belusov-Zhabotinsky Reaction (system).
In a comparable way a s p e c i a l c a s e of the property of intrinsic Shape could be, say, a rectangle (for instance an intrinsically rectangular shape of some two-dimensional crystal), while the intrinsic Symmetry of that rectangular crystal could be that of D1 , meaning that despite its rectangular shape (the symmetry of which is according to the group D2) the crystal has (because of its internal structure) only one mirror line (not two, as for D2) as its only true symmetry element. And the Promorph of such a crystal could then be, say, that of the (two-dimensional analogue of the) Allopola pentamphipleura (Other D1 crystals could have a promorph belonging to the Allopola eudipleura, or to the Allopola eutetrapleura, etc.). So here we have s p e c i a l c a s e s of Shape, Symmetry and Promorph, just like we had a special case of Element (ions of the Belusov-Zhabotinsky Reaction) and a special case of System (Belusov-Zhabotinsky Reaction, or for short BZ-reaction).
And as every being in whatever of the three Layers (together making up the totality of Existence) is co-determined by the Element -- System category pair, so is every being in whatever of these three Layers co-determined by the (regular) Shape -- Irregular Form category pair, (and further) co-determined by the (true) Symmetry -- Asymmetry category pair, and also co-determined by the (true) Promorph -- Apromorph category pair.
And as not every being in whatever Layer is co-determined by the Inorganic Ions -- BZ-reaction special category pair, so is not every being in whatever Layer co-determined by the Non-rectangle -- Rectangle special category pair, not every being in whatever Layer co-determined by the Non-D1 -- D1 special category pair, and not every being in whatever Layer co-determined by the Non-allopola pentamphipleura -- Allopola pentamphipleura special category pair.
So all these category pairs, just listed as "special category pairs", are indeed truly s p e c i a l category pairs.
In the same way we could consider special cases of the Shape, Symmetry and Promorph of three-dimensional material objects such as real crystals or organisms.
HARTMANN, 1940, p. 357, considers as one of his fundamental opposites of Being (Seinsgegensätze) the pair consisting of the categories of Quality and Quantity. And he distinguishes within the category of Quality three pairs of opposites :
Crystals and Organisms, Shape, Symmetry and Promorph, Growth Rate Vector Rosette.
After having specified and delimited the investigation concerning special If / Then constants (categories), resulting in an investigation in which we compare crystals and organisms with respect to (intrinsic) Shape, (intrinsic) Symmetry, and Promorph, as some of their intrinsic properties, we now show how we shall deal with them in more detail.
Often it is attempted to more or less equate crystals and organisms ( For example HAECKEL, E., Generelle Morphologie der Organismen, 1866, Kristallseelen, 1917, and PRZIBRAM, H., Die anorganischen Grenzgebiete der Biologie, 1926 ). And indeed there are many similarities between the two :
However, it is generally acknowledged that organic beings differ strongly from inorganic beings (of which the most instructive representatives are crystals) :
We will now discuss a feature, viz. the Growth Rate Vector Rosette, from which we can derive, with respect to crystals as well as with respect to organisms, intrinsic Shape, intrinsic Symmetry, and Promorph. We will discuss it first for crystals and then for organisms.
Crystals can originate and grow from solutions, vapors, melts, and from other crystals. Generation from solutions is for us the most important one, because it is most suitable for a comparison with organismic bodies.
In the case of crystallization from a solution we have to do with two phases, viz. the dissolved phase and the crystalline phase.
Under different temperature/pressure conditions the stability of one phase or another can be different. Say we have a solution of some chemical substance, and, say, the mentioned thermodynamic and concentration conditions are such that the dissolved phase has become unstable (while the crystalline phase is stable), then crystallization will occur along the following lines :
The creation of a crystal must start from a 'seed', i.e. a very small fragment of the crystalline material belonging to the same substance that is dissolved, or it must start from some substitute of such a seed. Let us consider the former.
First we should (in order for a crystal to be formed) have the accidental formation of an embryo (that's how we will call the just mentioned seed) in the solution. This is in principle possible because in the solution the particles of the dissolved substance constantly bump into each other, bounce away, etc. So among the many temporary configurations (arrangements) there will from time to time appear a configuration having the structure of the type to be crystallized. If such an embryo is of a sufficient size the surface energy of that embryo, which (embryo) can now be called a (crystallization) nucleus, does not cause the total free energy of the nucleus to increase when it grows, but to decrease, and consequently the nucleus will grow, resulting in a crystal.
The intrinsic Shape of the growing crystal will now be determined by the different atomic aspects as presented to the nutrient environment by the several crystal faces. This atomic aspect consists of two factors :
The internal structure, describable by the Space Group + Chemical Composition, is itself directly caused by the relevant (fully physically interpreted) crystallization law, which is the dynamical law of the dynamical system that consists of the growing crystal in its growing environment. This dynamical law is metaphysically interpreted as the Essence of the crystals, i.e. the essence of any individual (single) crystal (that is) generated according to that particular dynamical law (Other crystal species are associated with different dynamical laws).
In order to explain all this (i.e. about growth rates and Shape in crystals) we will (a little further down) reproduce some material from two documents from the First Part of Website, viz. from The Morphology of Crystals, and from The Internal Structure of Crystals.
Chemical nature of the atomic aspect, determining growth rate.
Forms
If we take a face of a crystal of a particular symmetry Class, a face, cutting off certain distances of the corresponding system of crystallographic axes, and if we subject it to all the symmetry elements (rotation axes, mirror planes, center of symmetry) of that Class, then this face will produce copies of itself according to the symmetries of that Class (If we happened having to do with the Asymmetric Class, or if the prevailing symmetry elements (of some other Class) do have a special orientation to it, then the face will not be so multiplied). This set of copies we call a Form (in the crystallographic sense), and the constituent faces of such a Form are crystallographically equivalent (More about these Forms, see the above mentioned document The Morphology of Crystals). Some Forms are closed, i.e. their faces together form a polyhedric figure, like a cube or a tetrahedron. Others are open, like pyramids (without their base), prisms (without their top and bottom faces), or are just a set of two parallel faces, or just one face. While the closed Forms can exist as real crystals, the open ones must be combined with other Forms (of the same crystal Class) such that a closed figure is resulting. But also closed Forms can combine with each other, one cutting off the corners of the other. So we can think of a crystal as consisting of one or more Forms of the corresponding crystal Class to which the crystal belongs. This boils down to imagining a crystal as made up of faces.
How the above concept of (basic crystallographic) Form has its foundation in the crystal's internal structure.
One might wonder why we can so easily speak of faces that together build up a Form, consisting of the same type of face, i.e. consisting of equivalent faces. Surely Crystals are the product of some "Lego" set of faces, that can be attached to each other. But, no, crystals are not hollow structures, but 'filled' solids without container walls.
In order to explain why the above 'constructions' are nevertheless conceptually possible and founded in real state of affairs, let us consider a certain fictitious two-dimensional crystal, consisting of two different sorts of constituents, say two different species of ions (= electrically charged atoms or groups thereof) with opposite electrical charge. Let us represent those ions by two kinds of disks, gray ones and red ones. Because like charges repel each other and opposite charges attract each other, each negatively charged ion wants to collect as many positive ions as its nearest neighbors as possible, and each positively charged ion wants to collect as many negative ions as its nearest neighbors as possibe. And every ion avoids a position next to any ion having a charge of the same sign.
The following crystalline structure will be the result of this (in this figure we depict only the internal structure and not its external boundaries, so we depict just an arbitrary fragment of the 'crystal') :
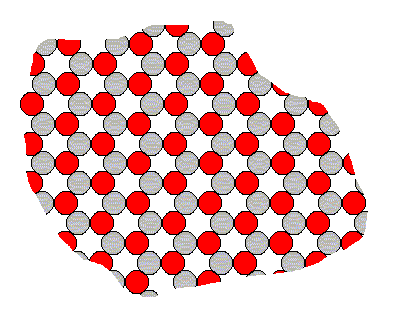
Figure 1. Internal structure of a two-dimensional ionic crystal (consisting of two different sorts of ions of opposite electrical charge).
The total symmetry of this structure is according to the Plane Group P3m1. Its Point Group ( = Crystal Class) is 3m (isomorphic to D3). To study this Plane Group geometrically, click HERE for the document where it is discussed (First Part of Website, Internal Structure of Crystals, Part V).
This structure allows several kinds of flat faces to be developed. Each type of face presents a different atomic aspect to the growing environment (the nutrient environment). In the next figure we show that the structure under consideration allows three different types of faces, A, B and C, corresponding to three atomic aspects to the environment. The blue lines indicate these possible faces, and we must interpret the aspects as true aspects in so far as they are facing outwardly, i.e. towards the environment.
Figure 2. Examples of the three different kinds of faces allowed by the structure, according to the three different atomic aspects pictured below :
Figure 3. Three different atomic aspects of the structure of the figures 1 and 2.
When we look to aspect A we see that six faces are possible, i.e. six faces differing in orientatation but showing the same aspect to the growing environment. The nutrient material cannot distinguish among these six. When conditions in the environment are the same around the entire crystal, all six faces will grow at the same rate. And if they are the only faces appearing, then the 'ideal crystal' will have the shape of a regular hexagon, as shown in the next figure, and will not reveal the lower symmetry of the structure which has the symmetry of an equilateral triangle, not of a regular hexagon.
Figure 4. Regular hexagon bounded by A-faces only. This hexagon does not however possess the full symmetry of a regular hexagon. One set of mirror lines is suppressed, and the rotation axis is three-fold, not six-fold.
To show this clearly let us look to a (two-dimensional) structure which has the full symmetry of the hexagon :
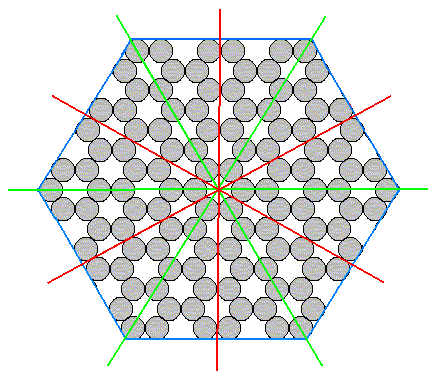
Figure 5. A structure showing the full hexagonal (two-dimensional) symmetry.
This structure is that of a two-dimensional crystal consisting of only one atomic species. It has full hexagonal two-dimensional symmetry, namely a six-fold rotation axis and two sets of mirror lines (each set consisting of three equivalent mirror lines).
The structure of Figure 4, on the other hand, has a three-fold rotation axis instead of a six-fold one. It lacks one set of mirror lines, namely the red ones. Therefore this structure is analogous to a hemihedric Form from the domain of three-dimensional crystals. Such a (less dimensional) Form can only combine with (other such) Forms belonging to the same symmetry Class. So our hexagonal Form as depicted in Figure 4 can only combine with a triangular Form. Such a triangular Form could be bounded by three B-faces -- the B-faces alone, can only form triangles because only three of them (having different orientations) are possible in our structure (as depicted in the Figures 1 and 2), if indeed these three faces grow slowly enough to appear.
Figure 6. Triangular Form, possessing the full symmetry of an equilateral triangle. It has the same symmetry as the hexagon of Figure 4 and can therefore be combined with it.
The fact that faces that grow "slowly enough" will appear and remain, while fast growing faces disappear quickly, sounds a little paradoxical, but let me explain this, before we continue with the possible combinations of Forms.
The growth rate of a crystal face depends, in so far as only the crystal is concerned, on the atomic aspect s.str. the face presents to the nutrient environment ( It can further depend on external influences, for example on the presence of certain chemicals -- impurities -- in that environment. A second factor determining the growth rate is the geometry of the lattice of the given crystal, see below). Now, the slower the face grows, the more likely it will survive, while relatively fast growing faces will ultimately disappear, as the next Figure illustrates :
Figure 7. Successive stages in growth of an imaginary two-dimensional crystal. Growing faster than the x-faces, the y-faces may finally disappear.
So when the A-faces (of the structure depicted in the Figures 1 and 2) appear, and the B-faces grow slowly enough for them also to appear, then the hexagon(al outline) will be mixed with a triangle, i.e. we get a combination of two Forms (both having the same symmetry) :
Figure 8. The combination of two Forms in a two-dimensional crystal. Here three corners of the hexagon are cut off by a triangle, and thus revealing the structure's true symmetry.
But it could also be that the B- and C-faces both grow very slowly relative to the growth rate of the A-faces. The latter will disappear. In this case we will get a combination of two triangles. And because the aspect to the nutrient environment is different in both cases (B-aspect and C-aspect, see Figure 3) the faces will almost certainly grow at a different rate, resulting in triangles of different sizes, and in this way again reflecting the lower symmetry of the structure, i.e. lower than the full symmetry of a regular hexagon. See the next Figure.
Figure 9. Combination of two unequally developed triangles in a two-dimensional crystal. The triangles cut off each others corners.
So for two-dimensional crystals we have now explained the growth of faces and the combinations of Forms. For three-dimensional crystals, i.e. for real crystals, the case is similar, and can thus finally be understood.
Let us give an example from real crystals showing a geometrical symmetry which is higher than the true symmetry, i.e. than the crystallographic symmetry :
The mineral Pyrite, FeS2, can be found in the form of a cube. But, often the faces of such a cube show growth stripes (striae) parallel to the edges of the cube (See Figure 10). Because of this the six secondary mirror planes of the highest symmetrical Class of the Isometric System (Cubic System) are suppressed. So the pyrite cube possesses a lower symmetry than a fully symmetrical cube like the ones of common salt, NaCl (in Nature occuring as the mineral Halite). A common salt cube possesses the full symmetry of a geometrical cube and it has an equal stripe pattern, generally expressing its cleavability. So in contradistinction to Halite, Pyrite belongs to a lower symmetry Class (of the same Crystal System).

Figure 10. Partial suppression of the geometrical cube symmetry, because of absense of the secondary mirror planes, visible by the direction of striae in the mineral Pyrite.
A fine example of why some chemical aspects imply a higher growth rate than other such aspects is the growth of a common salt crystal (NaCl). Such a crystal consists of positively charged Sodium ions ( Na+ ), and negatively charged Chlorine ions ( Cl - ). This crystal contains potential octahedral and cubic faces, i.e. a combination of two Forms. The octahedral faces are parallel to layers of positive Na-ions or negative Cl-ions, so growth consists of adding a layer of Na-ions onto a layer of Cl-ions, then a layer of Cl-ions, then Na-ions again, then Cl-ions, etc. Growth should be very fast, because a layer of Na-ions attracts Cl-ions, and a layer of Cl-ions attracts Na-ions. Moreover such layers represent unsatisfied chemical bonds and so their surface energy is high. This means that adding a new layer of the oppositely charged ions reduce the energy level, satisfying the old layer. Then a new layer is added, satisfying the previous layer, etc. The growth of such faces implies a greater energy reduction than other faces that are electrically neutral, so growth is fastest with respect to the charged faces (Because all natural systems tend to change in directions that minimize their energy level). In contrast the cubic faces have equal numbers of positive Na-ions and negative Cl-ions and are therefore electically neutral, and lack a net electrical attraction for ions in the solution. Adding a new positive Na-ion to the face, for example, depends on random movement of a Na-ion in solution to a position close to the face where the Na-ion can be attracted and bonded by the local negative charge of a Cl-ion. The growth rate therefore is relatively slow. See Figure 7, where the x-faces can represent the cubic faces, and the y-faces can represent the octahedral faces. We see that the octahedral faces eventually disappear, resulting in a cubic shape of the crystal.
Geometric nature of the atomic aspect, determining growth rate.
The pattern of growth rates in several directions (that is the growth rates of the possible crystal faces) determines the intrinsic shape of the crystal (as one of the features of the crystal). The growth rate of a possible face depends on its atomic aspect that it presents to the growing environment. This aspect itself is determined by the density of lattice nodes that are intersected by that face (See Figure 11) and the chemical composition of the crystal, especially which chemical units border on the growing environment.

Figure 11. Besides the chemical composition (chemical aspect presented to the environment) the growth rate of a face is inversely proportional to the number of lattice nodes that are encountered by that face.
The figure shows a primitive rectangular point net (The argument to come also applies to a 3-D point lattice). The intersections of the lines making up the rectangular cells (meshes) are lattice nodes (These nodes represent the locations of chemical units).
Four possible faces are indicated by a, b, c and d. The arrows indicate their respective directions of growth (At the same time there is also a corresponding growth in the opposite directions of the arrows). Generally the slowest growing faces become the most prominent faces on the crystal. The fastest growing faces quickly grow themselves out of existence.
This Figure -- which concerns the growth rates of faces -- only pays attention to one feature of the atomic aspect (The atomic aspect determines the growth rate of a face), namely the density of nodes encountered by the crystal face in question (The other feature refers to the chemical composition of the crystal).
The slowest growing face (on the basis of the feature mentioned) is face b, because here the density of nodes (encountered by that face) is highest.
Next comes face c, and then a.
The fastest growing face is d.
So the faces b and c will become the most prominent faces. The other faces will eventually grow themselves out of existence.
Because the faces b and c are perpendicular to each other the faster growing face of these two, namely c, will not grow itself out of existence. It keeps on growing, and keeps on growing faster than b, so the crystal will finally adopt a rectangular shape with its longest dimension oriented vertically.
Growth Rate Vector Rosette (Which here is always the relative Growth Rate Vector Rosette)
The (relative) Growth Rate Vector Rosette indicates how the growth rates of the possible faces of a crystalline structure differ from each other, and as such directly determines the intrinsic Shape of the crystal (its habitus).
If we now consider Figure 4 we have (for the sake of explanation) a two-dimensional ionic crystal, in which the nature of the ions is assumed to be such that the A-faces are the slowest growing faces (slower than the B- and C-faces), resulting in a hexagonal shape.
To draw and determine the Growth Rate Vector Rosette we must indicate by vectors (originating from the center of the crystal) the rate of growth and the direction of growth of every actual and potential face of the given crystal. The relative rate of growth, i.e. relative to the growth of the other faces, is indicated by the length of the arrow representing the vector (In the next Figure, where we have done so for the 2-D crystal of Figure 4, we did not draw the heads of the arrows, because they could obscure details of the structure. We let the same apply to the other Figures to come).
Figure 12. Growth Rate Vector Rosette of the crystal of Figure 4 (vectors originating from crystal center, heads of arrows not drawn). Only the independent pure vectors, are drawn, i.e. the vectors perpendicular to the possible faces that the structure admits.
To what faces those vectors belong is indicated (A, B, or C). The atomic aspects of these faces are shown in Figure 3. In this crystal the atomic aspects of all the faces are such that face A has the slowest growth rate.
Inspecting the central motif of the crystal we can see two non-equivalent types of directions, which we can call r a d i a l and i n t e r r a d i a l. In fact, in the present case, these directions, radial and interradial, suffice for a Growth Rate Vector Rosette to indicate the Shape of the crystal.
In the above Figure of the 'hemihedric' hexagon we see that the lines BC (composed of two opposite growth vectors) can be interpreted as (promorphological) axes, cross-axes, and that each such cross-axis consists of a radius and an interradius (i.e. a radial part and an interradial part). We call such a cross-axis a semi-radial cross-axis.
The next Figure gives the simplified Growth Rate Vector Rosette for the crystal of Figure 12.
Figure 13. Simplified Growth Rate Vector Rosette of the crystal of Figure 12.
In the hexagon of the above Figures we can distinguish radial areas and interradial areas :
Figure 14. Radial (blue) and Interradial (white) areas in the 'hemihedric' hexagon, representing a two-dimensional ionic crystal ( The boundaries are, of course, more or less arbitrary).
The next Figure indicates the three antimers of the above crystal.
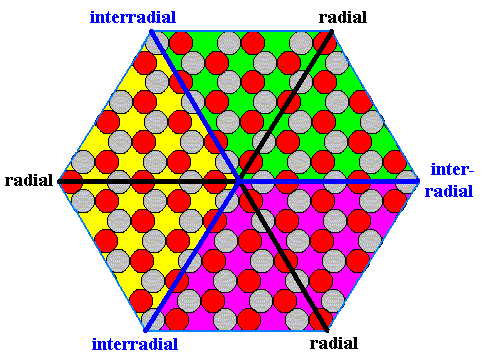
Figure 15. The three antimers of the hexagonal ionic 2-D crystal.
After removing text and some lines, the antimers come out more clearly :
Figure 16. The three antimers of the hexagonal ionic 2-D crystal.
In fact a crystal cannot have antimers : Because of its internal periodicity, the boundaries (and their surroundings) as they are drawn in Figure 15 and 16 to represent (boundaries between) antimers, are not unique :
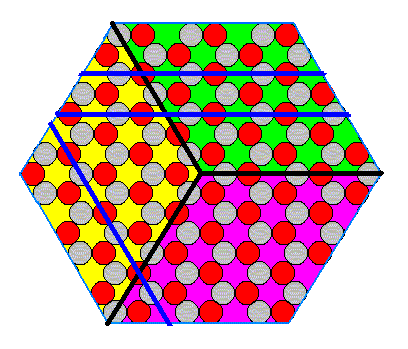
Figure 17. The boundaries of the alledged antimers are not unique.
Moreover, when we -- as a two-dimensional homunculus -- find ourselves in a radial area (say at point a in the next Figure) of our hexagonal crystal, and are, without knowing it, transported to a comparable location in the interradial area (say at point b in the next Figure), then we could not detect that we have been transported, because those areas are not intrinsically distinct :
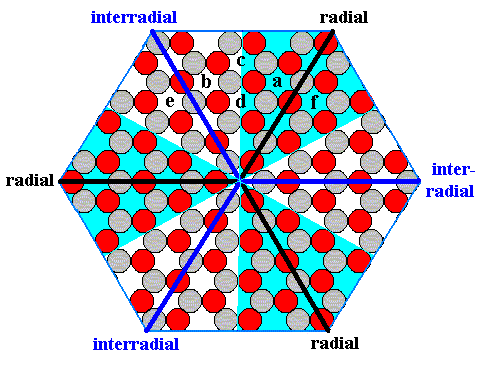
Figure 18. The points a, b, c, d, e, f are wholly equivalent, without regard as to their position being in a radial or in an interradial region of the crystal.
Any complete set of equivalent points of the structure under consideration can be interpreted as the complete set of nodes of a hexagonal lattice underlying the crystal's structure :
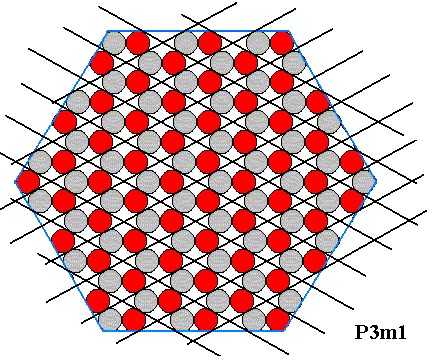
Figure 19. Hexagonal lattice, underlying the structure of the above hexagonal crystal. The motifs, placed in this lattice, and their orientation, determine the total symmetry of the pattern to be that of the Plane Group P3m1. The next two Figures highlight four such motifs.
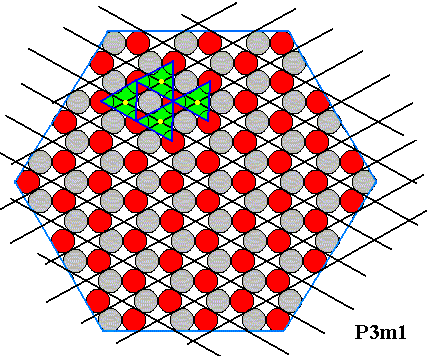
Figure 20. Four motifs (triangles), associated with four lattice points (yellow) are indicated in the internal structure of the hexagonally shaped 2-D ionic crystal.
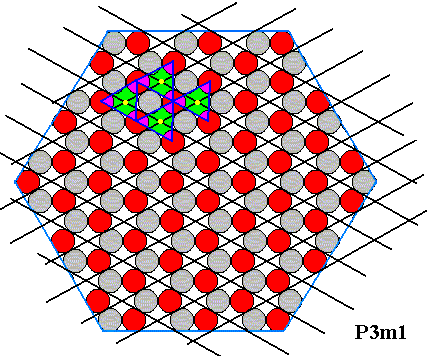
Figure 21. Some colors changed to alternatively highlight the four motifs indicated in the previous Figure.
But although we cannot just like that distinguish antimers in a crystal (like we can perfectly well in organisms), we can nevertheless do so on theoretical grounds, as we have explained in the Series on the Promorphology of Crystals in Second Part of Website. The reader can refer to this Series for full comprehension. For a recollection we here repeat a particular section of those considerations (Recall that the antimers of an organismic body are its counterparts, i.e. identical or similar body parts that are regularly arranged around the body's main axis, and which play an important role in determining the Promorph) :
For O r g a n i s m s we have erected a Form System that is fully inspired by the shapes (i.e. outer forms) and structure (i.e. inner form) of existing organisms. Their structure is t e c t o l o g i c a l, i.e. consisting of definite macroscopical parts that are repeated non-periodically. Every b a s i c f o r m of an organismic individual and also of their subordinate individuals (cells, organs, antimers, etc.) is represented by a geometrical solid displaying the symmetry of that organismic individual.
C r y s t a l s on the other hand, have a p e r i o d i c structure : A certain microscopic unit is repeated periodically in three different spatial directions, which means that microscopic translations are involved in the crystal structure. So (single) crystals do not have macroscopical parts that are repeated non-periodically (while certain twinned crystals do), which means that they, in particular, do not possess a n t i m e r s, so important and determining with respect to the assessment of the stereometric basic form (promorph).
But when we conceptually eliminate all translations inherent in crystals, i.e. eliminate all translational symmetry -- which in turn means that we eliminate (1) simple translations, (2) the translational component of every glide plane, and (3) the translational component of every screw axis -- then we are left with just one c h e m i c a l m o t i f, formed by the superposition of motifs in the lattice. I.e. when we 'telescope' the crystal back, we end up with the p o i n t s y m m e t r y only, represented by the (one) mentioned chemical motif. Consequently, this motif is the result of the superposition of all the point environments of the lattice. Such an environment consists of the whole set of chemical elements (in the sense of parts or particles) associated with a lattice point. Because of the superposition of the lattice points (by means of eliminating all simple translations), we are left with one such an environment. But in addition to simple translations there can be the translational elements of glide planes and screw axes. Also these translations should be eliminated. This can result in the mentioned environment to be telescoped further back, resulting in a smaller motif. This finally resulting motif corresponds either with one formula unit of the substance involved, or with a multiple thereof. In Ice this finally resulting motif consists (as far as my knowledge goes) of one hexagonal ring of six water molecules. Well, this final motif indeed has a t e c t o l o g i c a l structure, and because of this the crystal can be promorphologically assessed after all. How do we do this? (This is explained in the mentioned Series of documents).
For the System of Promorphs See the Series on BASIC FORMS in Second Part of Website. And for the significance of Promorphs see our introductory document within the Group Theory Series (Subpatterns and Subgroups Part XIII).
So, based on these arguments we will distinguish antimers in crystals, and assess the crystal's Promorph (stereometric basic form) based on the number, the geometical nature and arrangement of those antimers (for fictious 2-D crystals as well as for real, i.e. 3-D crystals).
If in Figure 14, we look to the center of the crystal, we see a three-fold motif, in which we can discern radial and interradial parts. As a result we can assess three corners of the hexagon as representing radii, while the remaining corners can be interpreted as representing interradii. Indeed, the two-dimensional Promorph of the crystal is that of the Anisopola triactinota, because the motif has D3 symmetry. [ In the present case we have to do with a two-dimensional crystal, which is a 'hemihedric' hexagon. The corresponding 6-fold pyramid represents the hemihedric 3-D crystal (with its sides alternatively different, say striped and non-striped). The corresponding three-fold pyramid, based on the three antimers, represents the Promorph of the corresponding three-dimensional crystal, which (crystal) belongs to the Class 3m. This 3-fold pyramid has the same symmetry as the depicted 'hemihedric' hexagon, namely D3 ]. See next Figure.
Figure 22. Promorph of the crystal of Figure 14, and, equivalently, of Figure 16.
In the next document we continue investigating the Growth Rate Vector Rosette of crystals, and again focussing -- for the sake of simplicity and explanation -- to their two-dimensional analogues.
To continue click HERE for further study of the Theory of Layers, Part V.
e-mail : 