

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Regular Gyroid Dihexagon
We will now investigate two-dimensional crystals with an intrinsic shape according to a regular gyroid dihexagon (twelve sides, C6 configuration) as to their possible promorphs, but, as in the foregoing, limiting ourselves to holomorphic crystals, which means that we will only investigate crystals of which their intrinsic symmetry is the same as the symmetry of their intrinsic shape. In the present case this means that our regular gyroid dihexagonal crystals will have C6 intrinsic symmetry (while in other cases -- meromorphic crystals -- this symmetry could be lower, namely according to the group C3 , or according to C1 (the Asymmetric Group), depending on the crystal's internal structure). The periodically stacked building blocks of crystals with intrinsic symmetry according to the group C6 must be 60/1200 rhombi, forming a hexagonal net. The next Figure depicts this net.
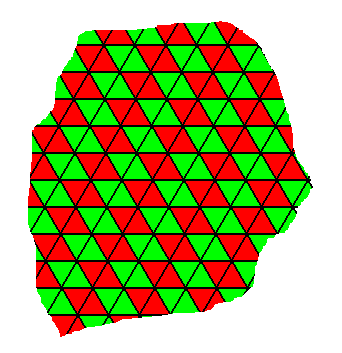
Figure above : Hexagonal net consisting of identical equilateral triangles, non-periodically repeated. Every two such triangles, side to side, form a 60/1200 building block (red, green) that generates the hexagonal net (lattice) by its being periodically stacked.
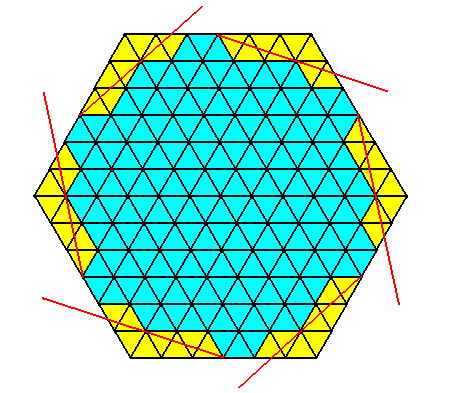
Figure above : Construction of a two-dimensional C6 crystal with intrinsic shape according to a regular gyroid dihexagon, from a regular hexagon built up by the periodic stacking of 60/1200 rhombic building blocks.
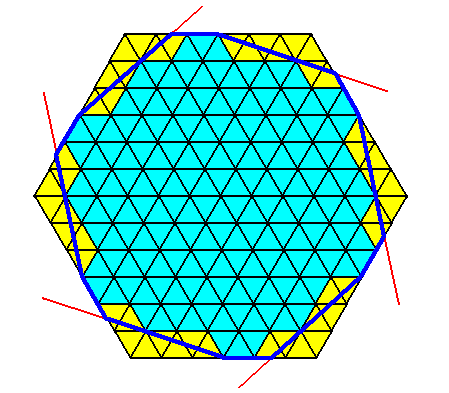
Figure above : The emerging outline ('faces', dark blue lines) of the two-dimensional C6 crystal with intrinsic shape according a regular gyroid dihexagon, under construction from a regular hexagon built up by the periodic stacking of 60/1200 rhombic building blocks.
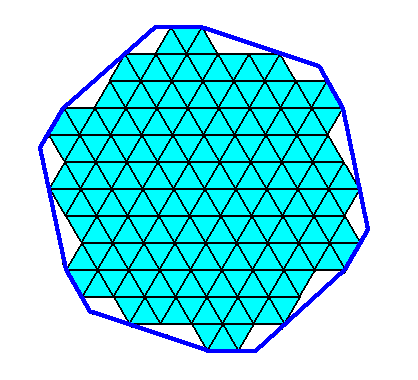
Figure above : The resulting two-dimensional C6 crystal with intrinsic shape according a regular gyroid dihexagon.
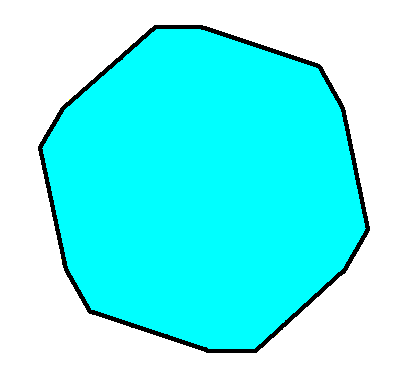
Figure above : Macroscopic view of the two-dimensional C6 crystal with intrinsic shape according a regular gyroid dihexagon, obtained by the removal of lattice connection lines.
The next Figure gives the pattern of symmetry elements of our crystal.
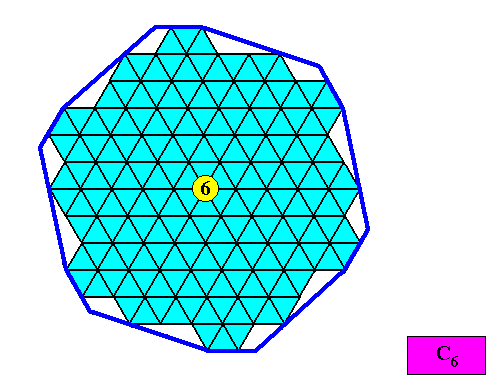
Figure above : Pattern of symmetry elements of our C6 regular gyroid dihexagonal two-dimensional crystal. It consists of one 6-fold rotation axis only, passing through the crystal's center.
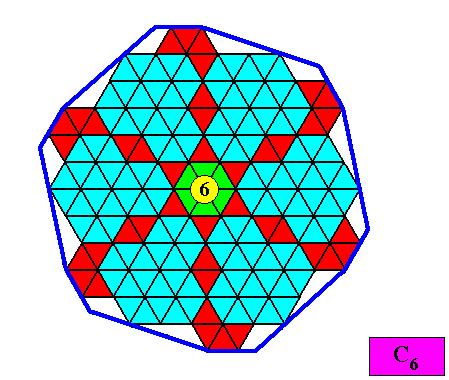
Figure above : Illustration of the crystal's six-fold rotation axis.
Two crystallographic Forms are needed to conceptually construct the outline of the crystal.
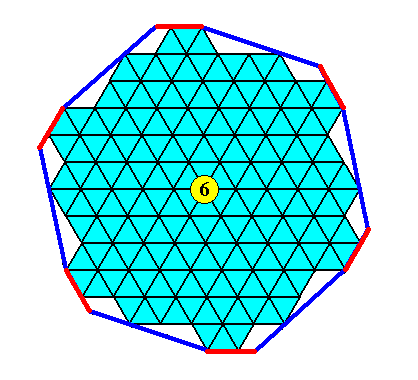
Figure above : Two crystallographic Forms are needed to construct the twelve faces of our regular gyroid dihexagonal C6 two-dimensional crystal : An initially given face (dark blue) implies five other faces in virtue of the 6-fold rotation axis, together making up a closed Form consisting of six faces (regular hexagon). Then another initially given face (red), not parallel to the first one, also implies five more faces, in virtue of that same rotation axis, together making up a second closed Form also consisting of six faces (regular hexagon). The two Forms combine to give our regular gyroid dihexagonal crystal.
As was the case with the C3 crystal of the previous document, the drawings still involve half rhombi (equilateral triangles) in the construction of the crystal, while in fact only complete (60/1200) rhombic building blocks should participate in the crystal's built up. The next Figure shows the half rhombi still involved.
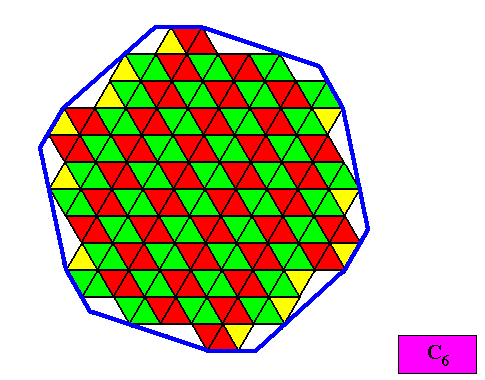
Figure above : Microscopic view of the two-dimensional C6 crystal with intrinsic shape according a regular gyroid dihexagon. Half rhombi (yellow) cannot in fact participate in the crystal's built up. Complete rhombic building blocks are marked either red or green.
Removing these half building blocks gives the following :
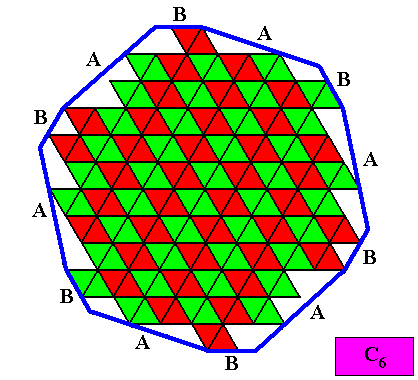
Figure above : Microscopic view of the two-dimensional C6 crystal with intrinsic shape according a regular gyroid dihexagon. Crystal built up only by complete rhombic building blocks (marked either red or green). The two types of sides of the regular gyroid dihexagonal outline of the crystal are indicated (A, B).
The next Figure depicts the nature of face A as it shows itself in the upper left and bottom right of the previous Figure. It illustrates how its direction is determined.
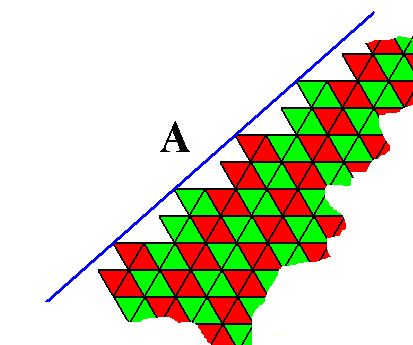
Figure above : The face A as given in the previous Figure. As such it is one of the possible faces allowed by the hexagonal lattice. (i.e. the periodic stacking of 60/1200 rhombic building blocks).
The next Figure depicts the nature of face A as it shows itself left and right in that same Figure. It illustrates how its direction is determined.
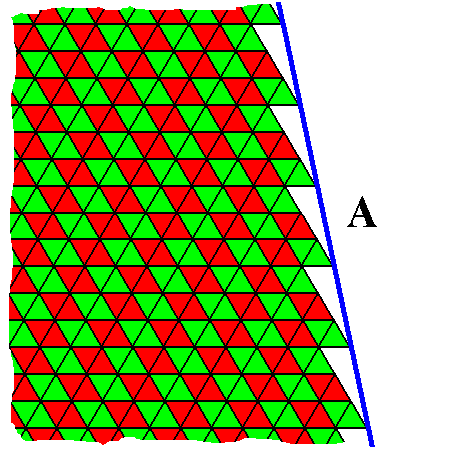
Figure above : The face A as given in the Figure just referred to, and as showing itself left and right in that Figure. As such it is one of the possible faces allowed by the hexagonal lattice. (i.e. the periodic stacking of 60/1200 rhombic building blocks).
Bringing the colors (red, green, in the above Figure displaying the whole crystal) back to light blue (as was used in the Figures further above) gives our regular gyroid dihexagonal crystal consisting of whole (rhombic) building blocks only :
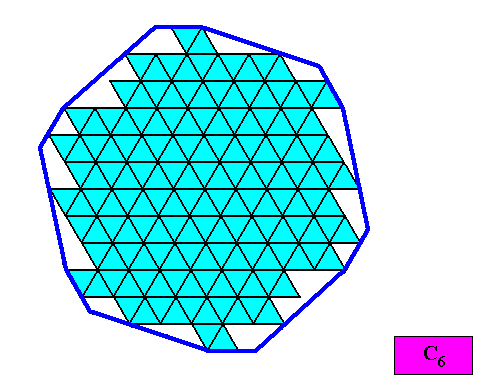
Figure above : Microscopic view of the two-dimensional C6 crystal with intrinsic shape according a regular gyroid dihexagon. Only whole (rhombic) building blocks.
As explained in the previous document, we will nevertheless use drawings where, in addition to complete (rhombic) building blocks, also half rhombic building blocks (provided these halves show themselves as equilateral triangles (and not as just isosceles triangles)) are allowed in the (conceptually) building up of our regular gyroid dihexagonal C6 two-dimensional crystal. Indeed we can see in the Figure above that the faces of the crystal drawn in such a way that only complete rhombic building blocks are allowed are not six by six equivalent, while this is the case where half rhombs (when they are equilateral triangles) are allowed, as can be seen in the Figure we have drawn earlier . Indeed in that Figure there are only two types of faces in the strictest sense, and they are six by six equivalent (and indeed, the crystal outline only needs two (crystallographic) Forms as was shown above ). The next Figure illustrates the six by six equivalence of the crystal faces of our crystal when drawn such that equilateral triangles are allowed to participate in the construction of the faces.
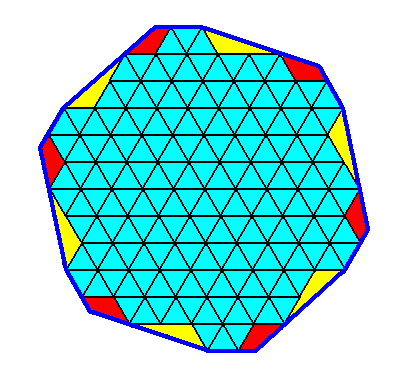
Figure above : Illustration of the six by six equivalence of the faces of our regular gyroid dihexagonal C6 two-dimensional crystal (light blue), drawn such that half rhombic building blocks, when they appear as equilateral triangles, are allowed to participate in the constitution of the crystal faces.
Possible antimer configurations of holomorphic two-domensional crystals with an intrinsic shape of a regular gyroid dihexagon.
A two-dimensional crystal with intrinsic C6 symmetry can have either six equal antimers, or a multiple of six antimers, in which case they are similar. This number of antimers depends on the morphology of the translation-free residue (which we can call the motif).
Six antimers.
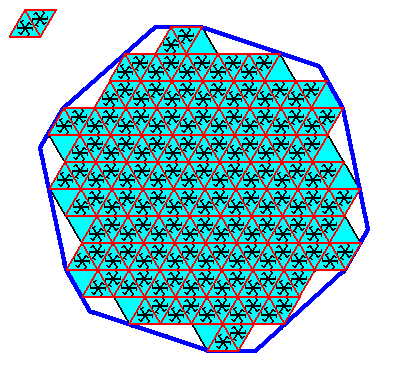
Figure above : Construction of a C6 two-dimensional crystal with an intrinsic shape according to a regular gyroid dihexagon. Two C6 motifs (black) with six equal antimers are inserted in each rhombic building block of the hexagonal net.
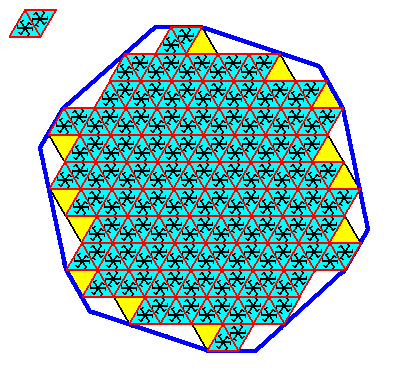
Figure above : Same as previous Figure. The remaining half rhombic building blocks (which are equilateral triangles) that are not yet filled in, are highlighted (yellow).
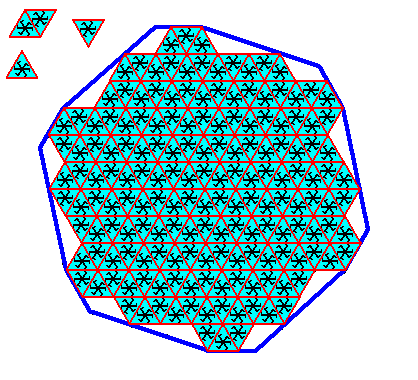
Figure above : Completion of the construction of the C6 two-dimensional crystal with an intrinsic shape according to a regular gyroid dihexagon. The left-over equilateral triangles are now also provided with a C6 motif (black). So now every equilateral triangle of the hexagonal net is provided with a C6 motif. The intrinsic symmetry of this crystal is now explicitly C6 and its total symmetry is according to the plane group P6.
And restoring the lines (dark blue) that indicate the faces of the crystal :
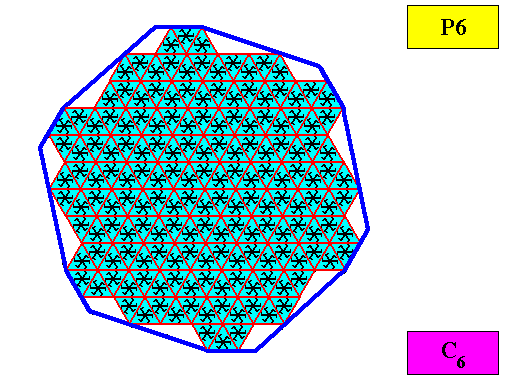
Figure above : The C6 two-dimensional crystal with an intrinsic shape according to a regular gyroid dihexagon. Its C6 motifs have six equal antimers.
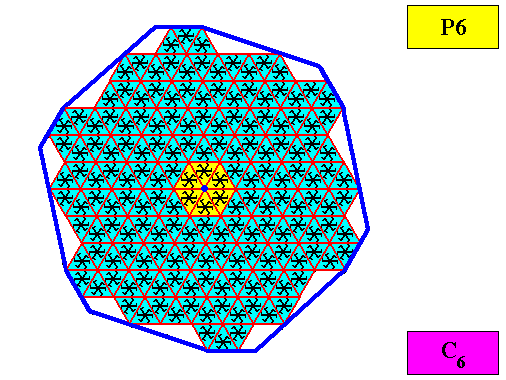
Figure above : Same as previous Figure. One can see that the motifs and their distribution are completely compatible with a 6-fold rotation axis of the crystal, and that they forbid the presence of any mirror line. So indeed this crystal has C6 symmetry.
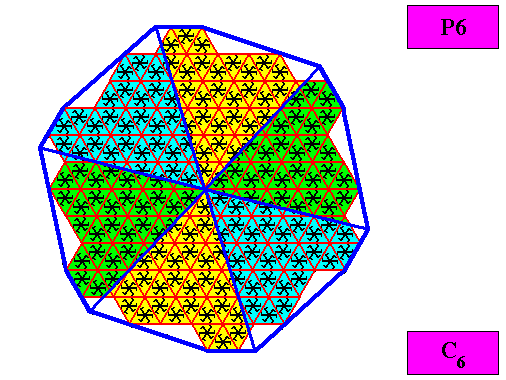
Figure above : The regular gyroid dihexagonal C6 two-dimensional crystal of the previous Figures. The case of s i x equal (and in themselves asymmetric) antimers (green, yellow, blue). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a C6 motif (black) inside each equilateral triangle of the hexagonal net. It is -- or represents -- an atomic configuration such that six equal, and in themselves asymmetric, antimers, relating to each other by a 6-fold rotation axis), can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests 12 similar (and in themselves asymmetric) antimers, while in fact there are six equal antimers present.
Removing the lattice connection lines and the motifs in the above Figure, results in a macroscopic view of the crystal :
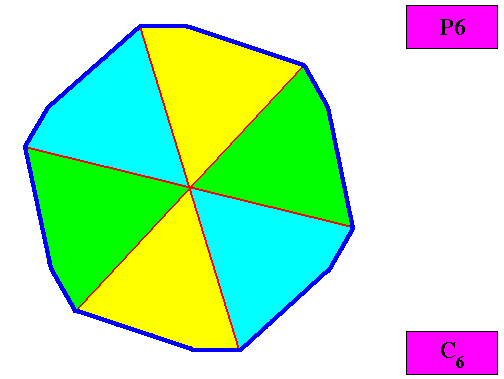
Figure above : Macroscopic view of the regular gyroid dihexagonal C6 two-dimensional crystal of the previous Figure.
The promorph of our regular gyroid dihexagonal crystal with intrinsic C6 symmetry belongs (as a two-dimensional analogue) to the Homogyrostaura hexamera and is depicted in the next Figure.
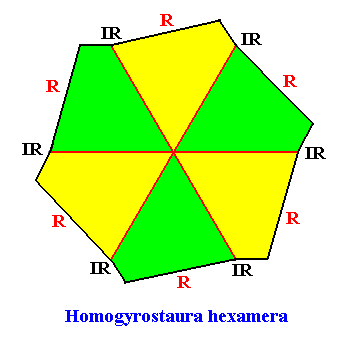
Figure above : The promorph of the regular gyroid dihexagonal C6 crystal with six equal but asymmetric antimers. It is a regular gyroid six-fold polygon with six antimers, and as such the two-dimensional analogue of the regular gyroid six-fold pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the similar shapes of the promorph (regular gyroid six-fold polygon) and the crystal (regular gyroid dihexagon). In fact the above drawing of the crystal could be used to represent this promorph. In the present drawing, however, the gyroid nature is more conspicuously displayed. Radial (R) and interradial (IR) directions are indicated.
Twelve antimers.
The next case to be considered is the presence of 12 similar antimers that are six by six equal. And this is based on the morphology of the C6 translation-free residue (motif) which itself is supposed to consist of 12 similar antimers, six by six equal. Such a motif could look like this :
Figure above : A possible motif as translation-free residue of a C6 two-dimensional crystal. The motif has 12 similar antimers, six by six equal, and its symmetry is according to the group C6 .
In the next Figure we suppose such motifs (C6 symmetry, 12 antimers, six by six equal) to be present in the crystal, but depict the latter directly as it is macroscopically seen ( Because the motifs cannot properly be drawn in the triangles of the hexagonal net we have used above).
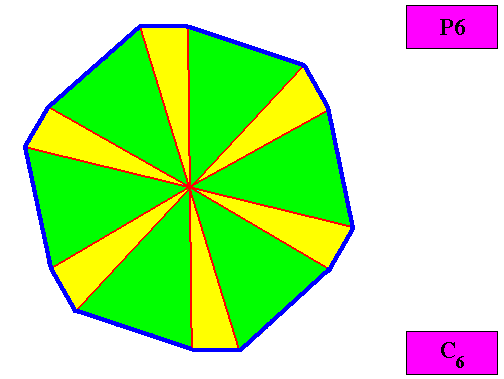
Figure above : Macroscopic view of a regular gyroid dihexagonal C6 two-dimensional crystal. The case of t w e l v e similar (and six by six equal) antimers (green, yellow). There is a correspondence between the morphology of the (microscopic) motif (as translation-free residue, not shown) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. The crystal is eupromorphic because its intrinsic shape suggests 12 similar (and six by six equal) antimers, which are indeed present.
The promorph of our regular gyroid dihexagonal crystal with intrinsic C6 symmetry belongs (as a two-dimensional analogue) to the Homogyrostaura dihexamera and is depicted in the next Figure.

Figure above : The promorph of the regular gyroid dihexagonal C6 crystal with 12 similar (six by six equal) antimers. It is a regular gyroid six-fold polygon with twelve antimers, and as such the two-dimensional analogue of the regular gyroid six-fold pyramid with 12 antimers, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the similar shapes of the promorph (regular gyroid six-fold polygon) and the crystal (regular gyroid dihexagon). In fact the above drawing of the crystal could be used to represent this promorph. In the present drawing, however, the gyroid nature is more conspicuously displayed. The red lines are interradial cross axes.
This concludes our exposition of the thirteen regular crystal shapes of our list (as given in Part XVI ) that were studied with respect to intrinsic symmetry and promorph in holomorphic two-dimensional crystals having these shapes intrinsically.
Irregular Polygon
There is one type of two-dimensional shape that can, like the foregoing shapes, be considered to be a complex shape. It is the totally irregular polygon. Two-dimensional crystals having such a shape are consistent with all crystallographic principles. The 'atomic' aspects (including motifs and lattice geometry), presented to the growing environment, by such a crystal could be such that no repetition whatsoever of them occurs, neither by rotation nor by reflection. If this is the case, no intrinsically symmetric growth will take place, resulting in an irregular polygon, having no symmetry elements whatsoever (i.e. no mirror lines and no rotation axes). Group theoretically such a shape is described by the Asymmetric Group C1 .
Because here we only consider holomorphic (two-dimensional) crystals, the intrinsic symmetry of our crystals, intrinsically having such a shape, i.e. intrinsically having the shape of an irregular polygon, must be according to the group C1 .
Like we saw with respect to other symmetries, many different shapes, all having the same symmetry, are possible, for instance holomorphic D1 crystals (i.e. crystals with one mirror line only) can come in many different shapes : Bilateral Octagon, Bilateral Hexagon, Bilateral Pentagon, Bilateral Tetragon, Bilateral Trigon, etc. Every such shape has D1 symmetry.
Precisely the same is the case with C1 symmetry (total asymmetry) : Holomorphic C1 crystals can come in many different shapes, i.e. many different irregular shapes. But in this case it is sufficient to consider only one of them, representing all other irregular shapes.
So our next and final two-dimensional crystal to be studied is a crystal having as its intrinsic shape that of an irregular hexagon (as such representing all irregular polygons) and with intrinsic symmetry according to the group C1 . Such a crystal has no symmetry elements. It either has no antimers at all, or two similar (not congruent) antimers.

Figure above : Microscopic view of a two-dimensional crystal with an intrinsic irregular shape, in the present case that of an irregular hexagon. The crystal is made up of parallelogrammatic building blocks, periodically repeated. Each building block (parallelogrammatic mesh of the oblique net or (oblique) two-dimensional point lattice) is provided with an asymmetric motif (black). The intrinsic point symmetry of the crystal is therefore according to the Asymmetric Group C1 , while its total symmetry (i.e. including translational symmetry) is according to the plane group P1. And because the symmetry of the crystal's intrinsic shape is also according to that group, the crystal is holomorphic. Every possible crystal face represents a different aspect to the growing environment (because of the asymmetry of the motifs), resulting in non-symmetric growth rates, which in turn result in an irregular polygonal shape of the crystal.
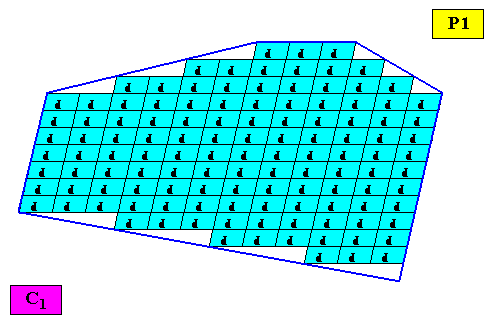
Figure above : Same as previous Figure : The two-dimensional irregular hexagonal C1 crystal (as representing all irregular two-dimensional crystals). The faces of the crystal are indicated (thin dark blue lines). Its hexagonal outline is now clear.
By removing the lattice connection lines and the motifs, we obtain a macroscopic view of this crystal :
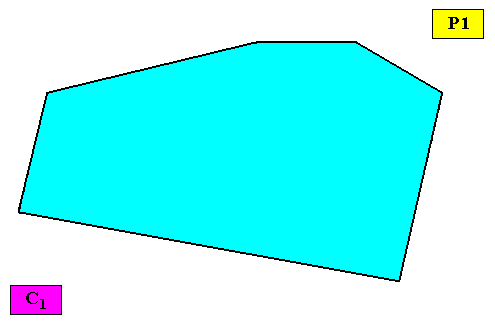
Figure above : Macroscopic view of the above irregular hexagonal C1 two-dimensional crystal of the previous Figure.
Six (crystallographic) Forms are needed to construct the outline of the crystal under investigation :
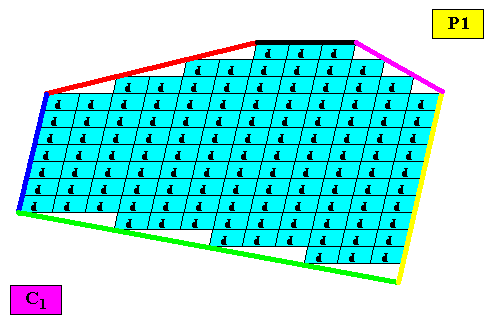
Figure above : Six crystallographic Forms are needed to construct the six faces of our irregular hexagonal C1 two-dimensional crystal : Any initially given face does not imply more faces, because there are no symmetry elements (apart from the trivial 1-fold rotation axis). So such a face is a Form. Six such Forms (from six initially given faces (red, black, purple, yellow, green, dark blue)) combine to give our irregular hexagonal crystal.
In our example there are some parallel faces. Such faces, however, do not relate to each other by any symmetry element (for instance a reflection line). They are independent, and represent different aspects to the growing environment.
Possible antimer configurations of holomorphic two-dimensional crystals with an intrinsic shape of an irregular hexagon (representing all irregular two-dimensional crystal shapes).
No antimers.
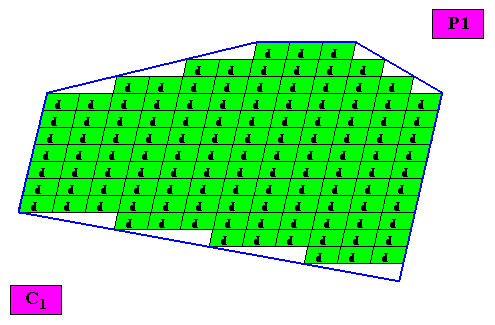
Figure above : Microscopic view of an irregular hexagonal two-dimensional C1 crystal.
The case of no antimers being present.
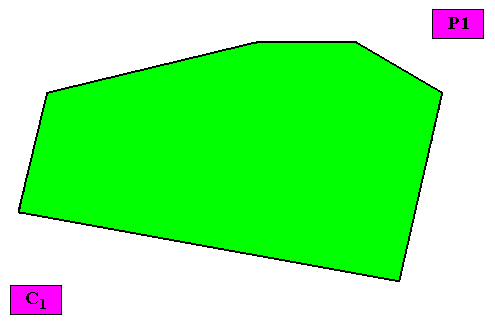
Figure above : Macroscopic view of the crystal of the previous Figure. No antimers are present.
Two antimers.
An irregular hexagonal two-dimensional C1 crystal could, depending on the morphology of the translation-free residue (motif), have two similar (not congruent) antimers, as the next Figure illustrates.

Figure above : Microscopic view of an irregular hexagonal two-dimensional C1 crystal.
The case of t w o similar antimers.
Removing the lattice connection lines and motifs, results in a macroscopic view of the crystal :
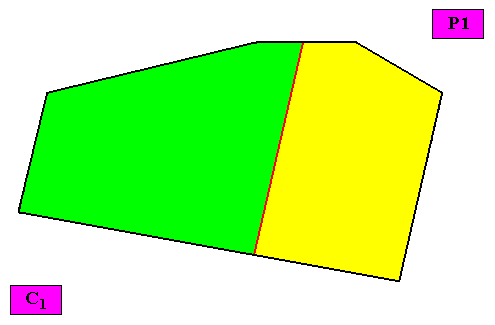
Figure above : Macroscopic view of the crystal of the previous Figure. Two similar antimers are present.
The next Figure (two images) gives the possible promorphs (and their names) of such an irregular hexagonal crystal (representing all irregular two-dimensional crystals). The promorph is either (left image) half an isosceles triangle (and, equivalently, a quarter of a rhombus), representing the case of no antimers, and is as such the two-dimensional analogue of a quarter of a rhombic pyramid, or (right image) an irregular triangle, indicating two unequal antimers (yellow, green), and is as such the two-dimensional analogue of an irregular pyramid (or, equivalently, a 1-fold pyramid).
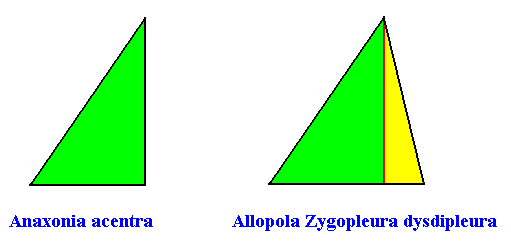
This, finally concludes our study of more complex intrinsic shapes of two-dimensional holomorphic crystals, with respect to symmetry and promorph.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX.