General Ontology XXIXm1aaa




(Takes a little while loading the images)

General Ontology Cosmos and Nomos

Theory of Ontological Layers and Complexity Layers

Part XXIX (Sequel-17)

Crystals and Organisms

Theory of intrinsic Shape, intrinsic Symmetry and Promorph

e-mail :

Back to Homepage

Sequel-17 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).

This document (Part XXIX Sequel-17) further elaborates on the analogy between crystals and organisms.

Sequel to the Preparations (V) to the Repertoire of the Crystal Analogy

The natural crystallographic laboratory and experimentation center

Because crystallization obviously plays such an important part in the crystal analogy (to be systematically outlined later on), it is necessary to delve deeper in the many special form features that especially sterro-crystals (solid crystals) can exhibit. For this we need an extensive laboratory where crystals under many different conditions are grown, observed and analysed. Such a laboratory, however, is expensive and is only available to some professional researchers. But in fact there is an extensive 'experimental laboratory' at hand for everyone. It is a laboratory that experiments with only one substance. This experimentation center is, of course, the earth's atmosphere and surface. We already have discussed extensively its crystallographic products, snow, depth hoar, hoarfrost, etc. And indeed this one substance, H₂O, seems quite sufficient to inform us about crystallization in general.
In the present document we will investigate a number of special forms of snow crystals, which are puzzling but at the same time interesting, and express the complexity and holistic nature of the crystallization process in general. Such an investigation also means a further exploration into the form-potential of ice, and with it of crystals in general. Insight into this form-potential is important for our theory of organic lattices.

Because of the enormous diversity of growth conditions in the atmosphere and on the earth's surface, a corresponding diversity of form features (branches, sectored plates, twinnings, trigonal forms, defects, etc) of ice is to be expected and does indeed occur. But, as far as my knowledge goes, most of these features have not been explained, or at least not sufficiently so. Surely we have to do here with a high degree of complexity in growth and form. Still the most baffling feature is the neat six-fold repetition of complex (and, consequently, unstable) structures around the c-axis of the snow crystal. For this there is no reductionistic and universally accepted explanation yet found :

A continuing mystery about dendritic snowflakes is why all six of their branches seem to be more or less identical [...]. The theory of dendritic growth explains why the side branches will develop at certain angles, but it contains no guarantee that they will all appear at equivalent places on different [ main ] branches, or will grow to the same dimensions. Indeed, these branching events are expected to happen at random. Yet snowflakes can present astonishing examples of coordination, as if each branch knows what the other is doing. One hypothesis is that vibrations of the crystal lattice bounce back and forth through the crystal like standing waves in an organ pipe, providing a degree of coordination and communication in the growth process. Another is that the apparent similarity of the arms is illusory, a result of the spatial constraints imposed because all the branches grow close together at more or less the same rate. But for the present, the secret of the snowflakes endures.

( BALL, Ph., H₂O, a biography of water, 1999, p.177, 179 )

As remarked in the above quote, the structures that appear on a (main) branch, appear by random causes that are super-local (i.e. restricted to almost a point-sized volume of space). It is, therefore, out of the question that such a random condition repeats itself six times around the crystal's main axis.
In earlier documents we have drawn some philosophical conclusions from this mysterious coordination within a single crystal. But here we will concentrate on the particular structures themselves that are so repeated. The reason to do so is to understand more of the crystallization process in general and so prepare better for the coming systematic exposition of the crystal analogy.
The most fruitful way to come close to an understanding of the special form features of snow crystals, especially the flat forms, is to see their internal structure as projected along the c-axis, resulting in two-dimensional crystals based on a hexagonal two-dimensional lattice or net. Such a net (which was already depicted on earlier occasions) consists of a tiling of the plane by equal-sized equilateral triangles in two opposite orientations. This necessarily results in a periodic stacking of 60/120⁰ rhombs (each consisting of two adjacent and oppositely oriented triangles), or (a periodic stacking) of some larger units, namely hexagons. See next Figure.

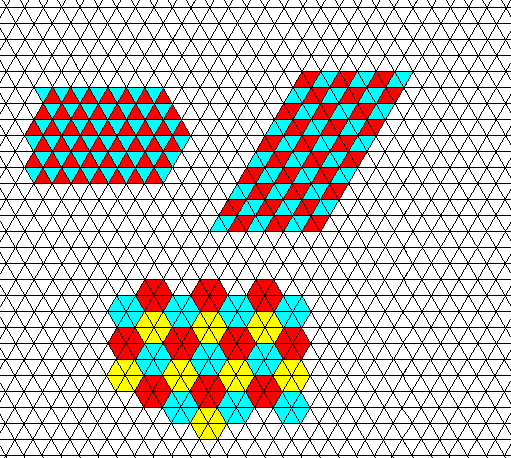
Figure above : The hexagonal net can be interpreted as a periodic stacking, either of rhombs or of hexagons. It is not a periodic stacking of triangles, but only a plane-filling tiling of such triangles ( This is because the triangles do not all have the same orientation).

Sectored-plate snow crystals

Sectored plates are flat extensions of certain snow crystals. They either take the place of the branches as they occur in stellar crystals, or grow at the tips of such branches. It is obvious that their appearance on the growing crystal reflects some change in the crystal's growth regime. Sectored plates are not especially rare, but they only form in mild conditions -- not too warm, not too cold, not too much or too little humidity. Like stellar dendrites, they are large, thin plates that only form right around the magic temperature of -15⁰C (5⁰F). If the humidity is high (effecting fast growth), dendritic branching occurs and the crystal becomes a stellar dendrite. If it's a bit lower, the branching will be less and sectored plates will appear (LIBBRECHT, p.72). The next Figures provide examples of sectored plates.

Figure above : Two examples of sectored plates in snow crystals.
(After BENTLEY & HUMPHREYS, Snow Crystals, 1931.)

Figure above : This branched snow crystal has sectored plate extensions with well-defined ridges. Similar ridges can often be seen in all types of stellar snow crystals. The smooth aspect of the crystal depicted here is caused by its having undergone some evaporation before being photographed. Most snow crystals (except in places like the Antarctic) come to us at a temperature that is not very far below ice's melting point. Therefore the equilibrium vapor pressure, i.e. the escaping tendency of water molecules from the ice, is relatively high, allowing substantial evaporation of such a crystal (i.e. it takes relatively much evaporation before equilibrium has been reached, halting net evaporation). Therefore snow crystals should be photographed at very low temperatures (See the Figure in the previous document , depicting antarctic snow crystals). The mentioned smoothing or rounding off could be the beginning of equitemperature metamorphism, already taking place during the snowfall or immediately thereafter.
(Photograph by Patricia RASMUSSEN, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : Snow crystal with large sectored plates, and slightly curved lateral ridges.
(Photograph by Patricia RASMUSSEN, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

When we have a snow crystal that is just a thin hexagonal plate and nothing more, we in fact have a very flat hexagonal prism. The six facets of such a prism appear as lines when the crystal is projected along the c-axis, i.e. along its main axis onto a plane parallel to the prim's top and bottom faces. If we only consider such projections (resulting in two-dimensional crystals) then the six lines, which are now the six sides of a regular hexagon, represent slowest growing faces of teh crystal. The directions of growth of these faces are perpendicular to them. The directions that point from the center of the (hexagonal) crystal to its corners represent directions of fast growth. Here the corresponding crystal faces no longer exist, but their growth directions are manufested by the corners. Next I reproduce two drawings from Part XXIX Sequel-15 to illustrate these directions in the context of the underlying hexagonal net.

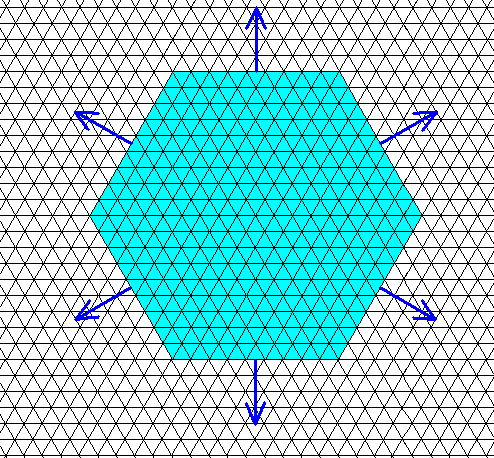
Figure above : The directions of growth of the actual existing (slowest growing) faces of the hexagonal (two-dimensional) crystal are indicated by arrows.

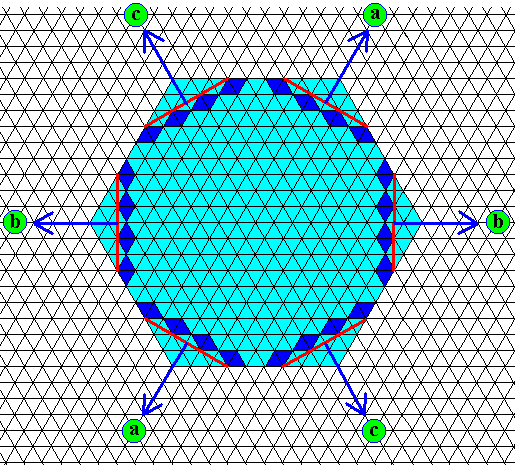
Figure above : Fast growing possible faces of the crystal are indicated (red) together with their directions of growth (arrows), a, b, c (including their opposites). These directions will be materialized by branchings, when further growth of the crystal is (very) fast. These branches, and also their side-branches (standing off at 60⁰) represent the effective molethynes of the snow crystal. As such the molethynes obviously determine the shape of a fast growing snow crystal. But they also determine the shape of the crystal (as seen in the mentioned projection) in the case of slow growth, i.e. they are also responsible for the hexagonal shape of plate-like snow crystals. In this case (of slow growth) the fast growing faces diminish gradually until they have vanished altogether and thus have been transformed into corners.

The next Figure shows a hexagon-shaped snow crystal in which the effective molethynes are materialized in the form of ridges. It is a crystal that is one sectored plate.

Figure : Hexagonal sectored plates are small and uncommon. This tiny example is only 0.3 mm (0.01 inches) in size. We here have a hexagonal crystal with its six effective molethynes (lines of directional forces) materialized as ice ridges (three different directions + opposites). We assume that these materialized molethynes are in fact crystal faces, albeit very small faces, corresponding to the growth direction as indicated by the molethyne, or, in other words, such a materialized molethyne is a growth trail of the corresponding very small but fast growing crystal face.
(Photograph by Patricia RASMUSSEN, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Until now two types of possible faces are identified in a projection along the c-axis of a snow crystal. But of course such a crystal admits of other possible crystal faces (i.e. faces along other directions than the ones just considered), as long as they are microscopically consisting of a regular sequence of whole building-block steps.
A fully grown crystal thus contains a number of growth directions of possible faces. The slowest growing directions (and, in addition to these, directions, fast or slow, that are not flanked by tapering slow growing faces) correspond to surviving crystal faces. The fast growing directions, when flanked by tapering slow growing faces, are, when the crystal is fully developed, not represented by genuine faces anymore. But they can, it seems, still be represented by ridges, and this is what we see in sectored plates (also in the rare cases where the whole snow crystal is itself one sectored plate). Normally these ridges are straight, but there are many cases where they are curved. As such this is an interesting and important phenomenon, because its adds substantially to the form potential of ice. Here we see that curved intrinsic form features are not limited to organisms, but can also be generated not only in rheo-crystals (liquid crystals), but in sterro-crystals (solid crystals) as well.
We wish to explain these curved ridges in sectored plates. But we realize that we, until now, only can make a good (or bad) guess. Let's give it a try. To do this we first depict these ridges as they occur in some snow crystals, i.e. as they occur in the plate-like extensions of certain snow crystals (and because of these ridges, that are radially ordered within such a plate, the latter is called a sectored plate).

Figure above : A s e c t o r e d p l a t e of a snow crystal (two different magnifications and cutouts). In the crystal from which this plate was taken, it is exactly repeated six times around the c-axis (which must be thought to be perpendicular to the plane of the photograph). The c u r v e d lateral ridges of the plate are clearly visible. The median ridge is straight.
(Taken from a photograph by Patricia RASMUSSEN in The Snowflake, 2003, by Kenneth LIBBRECHT.)

To see another sectored plate click HERE . The subscript of this Figure should read : Sectored plate of a snowcrystal. (Taken from a photograph by Patricia RASMUSSEN in The Snowflake, 2003, by Kenneth LIBBRECHT.)

About the curved ridges in sectored-plate snow crystals LIBBRECHT, K., The Snowflake, 2003, p.72, writes the following :

A curious feature of sectored-plate crystals is that the ridges are sometimes curved or at odd angles, particularly with sectored plates growing on the ends of dendritic arms. It almost looks like the crystal structure has been bent, but this is not the case. The ice molecules are still all lined up with the usual crystalline symmetry.
A ridge is created at the corner between adjacent facets on the plate, and thus the ridge delineates the history of where the corner was at previous times. Adjacent facets don't always grow at the same rate, so the ridges can grow in some odd directions. If the relative growth rates of the facets changes with time, the ridges can become curved.

With respect to the last sentence of the above quote we should realize that the relative growth rate of faces can -- if we exclude any bias in the local supply of nutrient material at the different sites of the growing crystal -- only become different when these faces are crystallographically non-equivalent. The faces that can be seen in the form of the (outer) edges of a sectored plate crystallographically represent the prism faces of the crystal, and these are crystallographically equivalent. Click HERE to see these faces and their directions. The directions are vectors (but in the Figure their true lengths are not indicated), so we can shift all vectors such that their origin coincides with the center of the crystal, in this way obtaining a vector rosette. So because these faces that are expressed by a sectored plate (namely their edges) are all equivalent, their intrinsic growth rates are the same, so that there can be no change in their relative growth rates (as was -- in my opinion -- incorrectly assumed, or at least not adequately specified, in the above quote). A change in relative growth rates of faces of a crystal, bringing with it a habitus change, normally happens when the environment is biased in some way, i.e. when it is different at different sites of the given crystal. But LIBBRECHT, in the above quote, means environmental changes that take place uniformly all over the crystal (because the six sectored plates of the same crystal with their curved ridges are identical). Such changes, however, can only bring about a habitus change when non-equivalent faces are involved. Indeed we learned in Part XXIX Sequel-6 that the habitus of ice crystals can change when the temperature changes, and this change means a change in the relative growth rates of basal faces on the one hand and prism faces on the other (which -- basal and prism -- are indeed non-equivalent). So the curved forms of the ridges of the sectored plates must somehow involve non-equivalent possible crystal faces parallel to the crystal's c-axis. When the temperature changes the relative growth rates of these faces changes. But where are these (non-equivalent) faces?
In a sectored-plate snow crystal, when we look down along its c-axis, we see three important features, viz., (1) edges, which represent the slow growing prism faces, (2) broad areas, which represent the top face of the prism (together with the corresponding bottom face these two faces are called basal faces), and (3) ridges (often flanked with grooves).
What then is a ridge?
Well, I assume that a ridge in a sectored plate not only represents a direction of some fast growing possible crystal face, but that it also is that face itself, albeit a very small face, equal to the width of the ridge, as we see it also in the case of slender branches and side branches in stellar snow crystals. Because it is a fast growing 'face' it will not fully develop, because extension of its surface is denied by the two adjacent tapering slower growing faces. This 'face' has its (very small) surface of course perpendicular to the ridge, i.e. perpendicular to its growing direction. I further assume that a (very) local temperature change takes place which effects a corresponding change in the relative growth rates of this 'face' and other non-equivalent fast growing potential faces. So another fast growing 'face' takes over. In this way a small ongoing more or less smooth increase in local temperature (that is to say the temperature at the particular ridge) results in a take-over sequence of one 'face' after another, and this brings about a curvature of the ridge. All this is happening initially at one specific site of the crystal, but it is then immediately copied according to the symmetry group D₆ (which is the symmetry of the projection of a snow crystal down along its c-axis), which means that it is -- when analysed -- reflected in the nearby mirror line of the crystal and the result then rotated in steps of 60⁰ about the c-axis, resulting in twelve curved ridges, that is to say, resulting in six sectored plates, each with one straight median ridge and two lateral curved ridges (because not only the curved ridge but also the whole plate is multiplied). The latter event (reflection and rotation of the initial ridge and its plate) is, of course a description after the fact, resulting from mathematically analysing this fact. In the actual process these partial events take place almost simultaneously, on the basis of some internal communication and coordination.
The next four Figures depict possible crystal faces in a snow crystal (as seen in projection), and how we should imagine the structure of a ridge (or materialized molethyne) to be.

Figure above : Apart from the actually existing faces of the regular hexagon (the edges of the hexagon, of which two are visible in the Figure, there are several other possible faces, as indicated. The next Figures study the 'yellow' face.

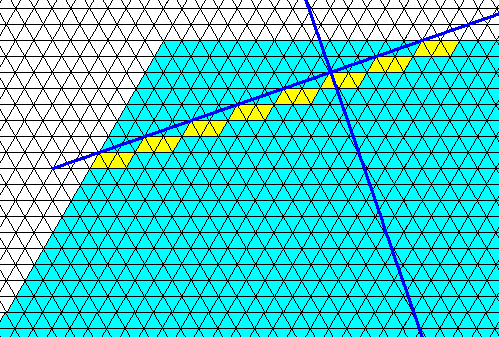
Figure above : The 'yellow' (possible) face of the previous Figure is highlighted, and its growth direction (which is perpendicular to it) is indicated.

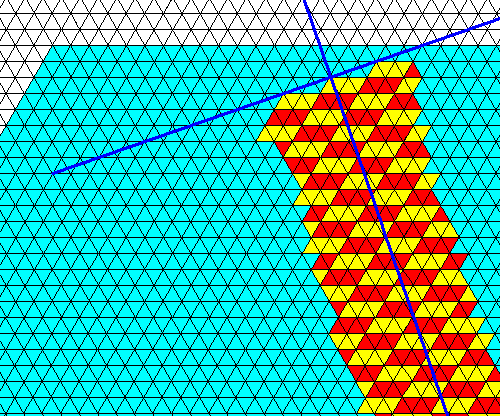
Figure above : The 'yellow' (possible) face does not develop into a genuine crystal face but into a ridge, or materialized molethyne.

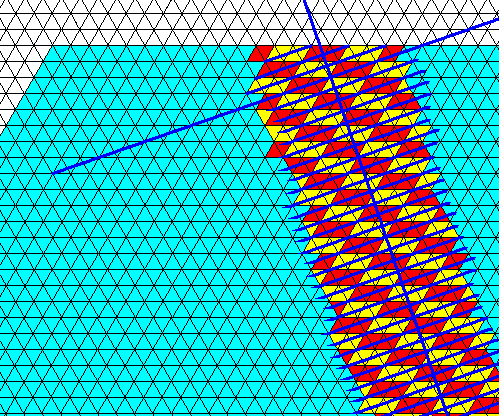
Figure above : Same as previous Figure. The succesive layers of the 'yellow' face are indicated. The surface of the face remained very small while the crystal grew, resulting in a ridge. This ridge is further extended up to the crystal's boundary. Because only one face (and its corresponding direction) is involved, the ridge is (macroscopically seen) straight, i.e. not curved.

If, while such a 'face' (marterialized molethyne) is growing, the temperatur changes to a new value, then the relative growth rates of the (relevant) possible faces, (some of) which are depicted above ), change (because the faces are non-equivalent), resulting in a take-over by another 'face'. If the temperature again changes, another 'face' takes over (because of again altered relative growth rates), etc., resulting in a curved ridge. See next Figure.

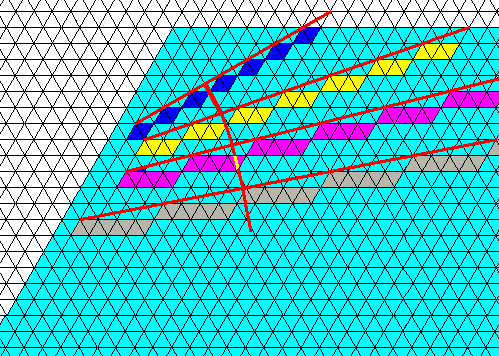
Figure above : Because of a gradual temperature change, the relative growth rates of non-equivalent possible faces change, resulting in the growing ridge (the successive cross sections of which represent these faces one after another) to follow a curved course.

In the next two Figures we see a crystal with large sectored plates, such that the crystal shape approaches that of a plain hexagon. As one can see, the six plates, although of a same type, are not exactly identical. The ridges, forming the materialized rosette of effective molethynes, are clearly visible. They stand out, and are straight.

Figure above : Snow crystal with large sectored plates, and 'vestiges' of slightly curved lateral ridges.
(Photograph by Patricia RASMUSSEN, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

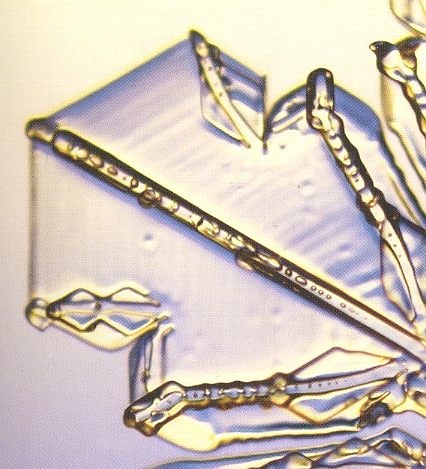
Figure above : Upper left part of the snow crystal depicted in the previous Figure. One can clearly recognize (top of Figure) the two faces (seen as edges) belonging to the set of slowest growing faces, separated by a vestige of a curved ridge. These two faces are crystallographically equivalent, meaning that their intrinsic growth rates are the same, and will always be the same, when nutrient supply is uniform. This implies that the curved state of the ridge separating them cannot have been caused by a change of relative growth rate of these two (mentioned) adjacent faces (as was suggested by LIBBRECHT, as indicated earlier). It must be caused by the ridge being itself a growth trace of successive fast growing faces, as explained above.
(Taken from a photograph by Patricia RASMUSSEN, in The Snowflake, 2003, by Kenneth LIBBRECHT.)

One could wonder why those ridges that coincide with the effective molethynes, i.e. the ridges ending up at the hexagon's corners, always seem to be straight, i.e. not curved. It is hard to answer this question. It could read as follows : The ridges ending up at the corners of the hexagon (which are the materialized effective molethynes) lie on a mirror line of the crystal, so they cannot become asymmetrical by curving. The actually curved ridges, on the other hand, do not lie in an area that is crossed by a mirror line, so they can become asymmetric by becoming curved. See next Figure.

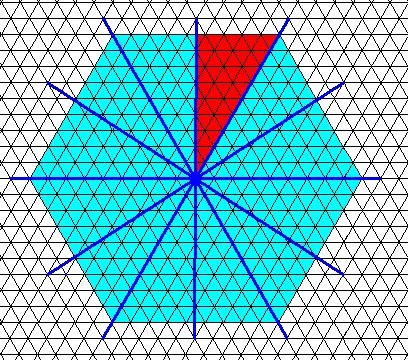
Figure above : Projection down along the c-axis of a simple hexagon-shaped snow crystal. The six mirror lines are indicated. Their point of intersection is the site of the six-fold rotation axis (perpendicular to the plane of the drawing). One of the areas where the curved ridges (not shown) of a sectored-plate crystal normally reside is indicated (red). The whole regular hexagon is generated when this asymmetric area is multiplied according to the symmetries of the hexagon : reflection in the vertical mirror line, and multiplying the result by rotations of 60⁰ about the c-axis (which runs through the center of the hexagon, perpendicular to the plane of the drawing). This asymmetric area allows asymmetric structures within its confines, and thus it can legitimately harbour a curved ridge.

In the next document we will continue the discussion of special features in sterrocrystals. (Still with snow crystals as examples).

e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-18.