

(Takes a little while loading the images)
e-mail :

Sequel-20 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-20) further elaborates on the analogy between crystals and organisms.
Sequel to the Preparations (VIII) to the Repertoire of the Crystal Analogy
Sequel (III) to Special Features of Crystals
Sequel to triangular snow crystals. Face-ditrigon
Having thus analysed the angle-ditrigonal shape and its relation to trigonal crystals (previous document), we will now analyse the face-ditrigon, also with respect to trigonal crystals. See for the face-ditrigon the Figure in Part XXIX Sequel-19 (previous document) (upper right image) , and also the photograph in Part XXIX Sequel-19 (previous document) .
Figure above : Crystallographic construction of the face-ditrigon.
While the initial face generating Form A of the Figure in previous document as well as the initial face generating Form B of that Figure have special orientations with respect to the D3 symmetry elements (mirror lines and 3-fold rotation axis), the inital face c that generates the face-ditrigon has a general orientation with respect to the mentioned symmetry elements.
If the initial face c is subjected to the vertical mirror line, a second face, c' is generated. If this pair of faces, c and c' , is now subjected to the 3-fold rotation axis, the faces c'', c''', c'''' and c''''' are generated, resulting in the face-ditrigon. So the whole face-ditrigon is generated from one single initial face in virtue of the action of the D3 symmetry elements, implying that the face-ditrigon is itself one single (crystallographic) Form (consisting of six faces).
The face-ditrigon here constructed is but one of many possible. As long as the orientation of the initial face is general with respect to the D3 symmetry elements (mirror lines, 3-fold rotation axis), the result will be a face-ditrigon.
It appears that snow crystals having the shape of a face-ditrigon are not very common. We already have depicted two of them above (this photograph in previous document ). Here are some more of them





I have not found any photograph of a face-ditrigonal snow crystal that consists of one single face-ditrigonal plate.
Let us construct this face-ditrigon with a hexagonal net.
Before doing so, it is perhaps instructive to show that in addition to the faces with special orientation with respect to the trigonal mirror lines, or, more generally, with respect to the three crystallographical axes of hexagonal (s.str.) and trigonal two-dimensional crystals (where these axes are set such that they coincide with three mirror lines), that were depicted in the previous document, there is yet another direction that is special with respect to these axes or mirror lines. See next two Figures.
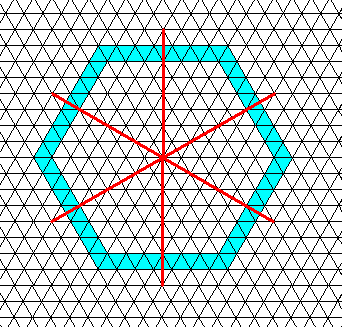
Figure above : Two-dimensional hexagon-shaped crystal, based on a hexagonal net. The orientation of the faces with respect to the three crystallographic axes (coinciding with mirror lines) is the same as we had them in the trigonal Forms of the Figure given earlier .
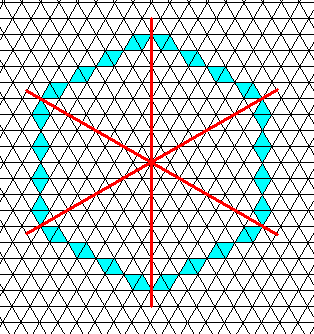
Figure above : Two-dimensional hexagon-shaped crystal, based on a hexagonal net. The orientation of the faces with respect to the three crystallographic axes (coinciding with three equivalent mirror lines) is different as we had them in the trigonal Forms of the Figure given earlier . In the present case the faces are parallel to the crystallographic axes. See also the Figure in Part XXIX Sequel-18 (where the blue lines represent the three crystallographic axes (normal to them is the c-axis, figuring in the corresponding three-dimensional crystals).
The next Figure indicates a possible general direction of a crystal face, and compares it with directions considered earlier.
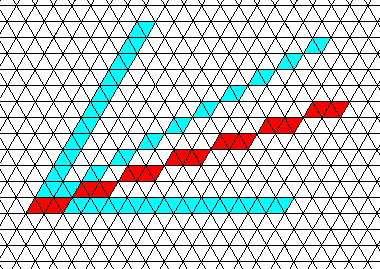
Figure above : Possible general direction (red) in a hexagonal net, as compared with some directions discussed earlier. Orientation of crystallographic axes (that coincide with mirror lines) as in the previous two Figures. If we subject such a face to the symmetry elements of two-dimensional trigonal crystals (three equivalent mirror lines and one 3-fold rotation axis in their point of intersection), then this face is multiplied, resulting in a face-ditrigon, which is therefore one single crystallographic Form of this trigonal two-dimensional Class (crystallographically denoted as 3m ).
This general direction can generate either a face-dihexagon or a face-ditrigon, depending on the given symmetry. Let us illustrates both cases.
Face-dihexagon.
If we subject an initial face having this general direction (with respect to the three crystallographic axes perpendicular to the c-axis, which are set such that they coincide with three equivalent mirror lines) to the symmetry elements of D6 symmetry (3 + 3 mirror lines, one 6-fold rotation axis), then we obtain a face-dihexagon, which is one single Form of the Class corresponding to the D6 symmetry (crystallographically denoted as 6mm (two-dimensional Class)). The next Figures illustrate this.
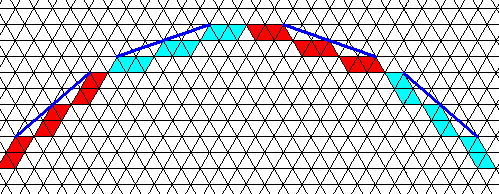
Figure above : Generation (explained below) of some faces of the face-dihexagon, by subjecting an initial face with general orientation with respect to the symmetry elements of the (two-dimensional) Class 6mm (and thus with a symmetry according to the group D6). Equivalently, this subscript can also read : Generation of all the 12 faces of the face-hexagon (four of these faces shown). A face-hexagon is generated because the (1) the intial face has a general orientation, and (2) because the symmetry is supposed to be D6 . See also next Figure.
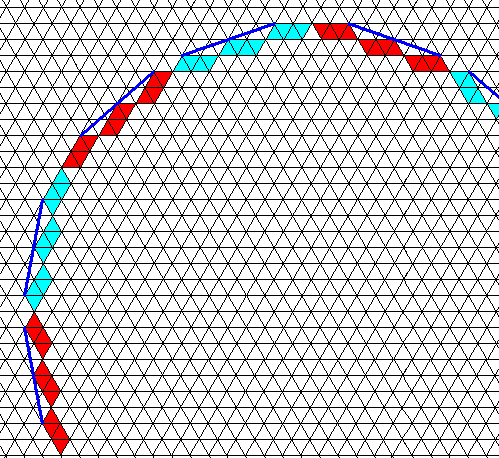
Figure above : Generation (explained below) of some more faces of the face-dihexagon, still by subjecting an initial face with general orientation with respect to the symmetry elements of the (two-dimensional) Class 6mm (D6) to these symmetry elements. The dihexagon has 12 equal faces (and unequal but alternating angles). Its generation is further explained, and its overall shape displayed, in the next Figures.
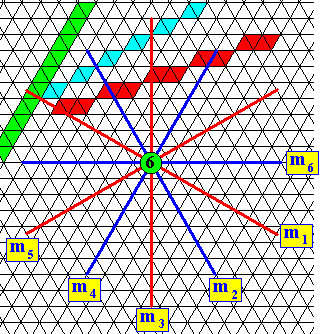
Figure above : Three possible initial faces (green, blue, red), and their orientations with respect to the symmetry elements of the Class 6mm (two-dimensional), which symmetry is according to the group D6 . These symmetry elements are : six mirror lines (three of them coinciding with the three crystallographic axes (red)) and a 6-fold rotation axis at their point of intersection.
The orientation of the green face is special : It is perpendicular to the m1 mirror line. Therefore this mirror line will not duplicate this face.
The orientation of the blue face is also special : In addition to it being parallel to the m5 mirror line, it is perpendicular to the m2 mirror line. Therefore this latter mirror line will not duplicate this face.
The orientation of the red face, on the other hand, is general. It is neither perpendicular, nor parallel to any of the mirror lines. Any mirror line of the set of D6 symmetry elements is oblique with respect to its orientation, and will therefore duplicate it. See also next Figure.
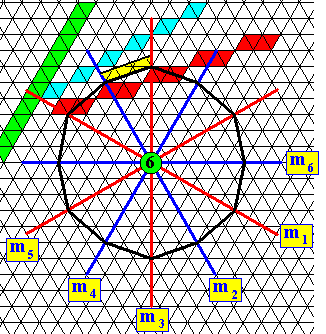
Figure above : When the red face is subjected to the D6 symmetry elements, a dihexagon will be produced. Initial face is highlighted. This face is duplicated by the vertical mirror line (m3), resulting in a face adjacent to it. This face pair is now duplicated by the mirror line m4 resulting in four faces, etc., etc. We could also say that the first pair of faces -- the initial face and the one generated by its reflection in m3 -- is now multiplied by the 6-fold rotation axis, resulting in all the 12 faces of the face-dihexagon.
The next two Figures once more illustrate this dihexagon, in order to get insight in its geometric properties.
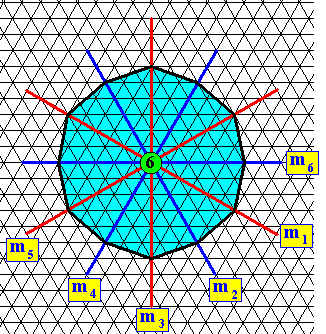
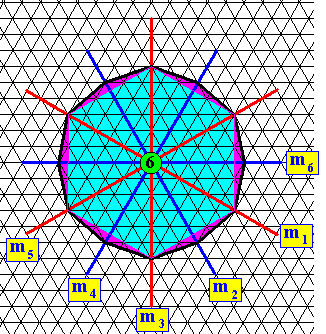
Figure above : Face-dihexagon. Inscribed is a regular hexagon in order to highlight the geometry of the face-dihexagon.
Face-ditrigon.

Figure above : Generation of all six faces of the face-ditrigon by subjecting an initial face with a general orientation with respect to the three crystallographic axes (coinciding with the three equivalent mirror lines) of the (two-dimensional) Class 3m (D3) to the symmetry elements of this Class (three equivalent mirror lines and one 3-fold rotation axis). The face-ditrigon is therefore one single (crystallographic) Form of the Class 3m.

Figure above : Same as previous Figure. (Directions of) faces of the face-ditrigon highlighted.

Figure above : Same as previous two Figures. Shape of the face-ditrigon highlighted.
The ditrigon has three-fold symmetry and possesses (three) mirror lines. It cannot, therefore, be generated by the symmetry elements of D6 symmetry (which implies 6-fold symmetry). It is therefore trigonal, belonging to the Class 3m having D3 symmetry.
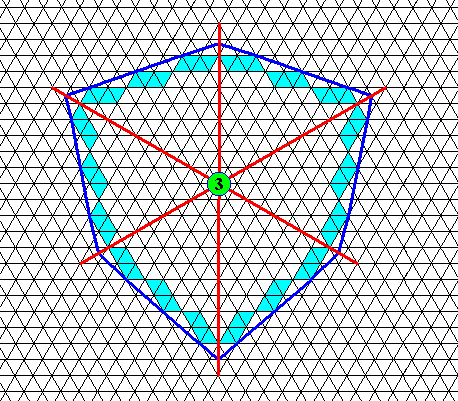
Figure above : Face-ditrigon of the previous Figures. It has three equivalent mirror lines and one 3-fold rotation axis at their point of intersection. It can be generated by taking one face as the initial face and then subjecting this face to an adjacent mirror line, resulting in a pair of adjacent faces. This pair is now multiplied by the 3-fold rotation axis resulting in all six faces of the face-ditrigon.
The next two Figures express the trigonality of the face-ditrigon at the molecular level by differentiating between the two halves (triangles) of the rhomb-shaped unit mesh of the hexagonal lattice.
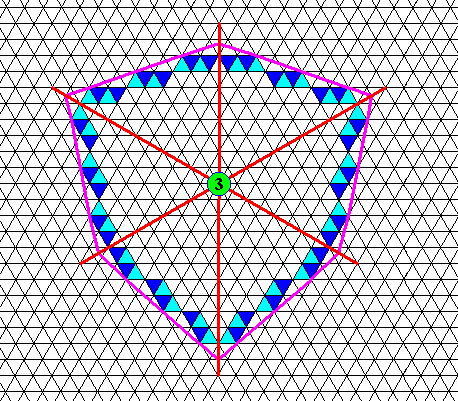
Figure above : Face-ditrigon of the previous Figures.
The trigonality at the molecular level is indicated in the outer layer of the face-ditrigonal two dimensional crystal. Each rhomb-shaped unit mesh contains two different or differently oriented chemical entities, expressed by the different colors (dark blue, light blue) of the two triangles constituting such a unit mesh. See also next Figure.
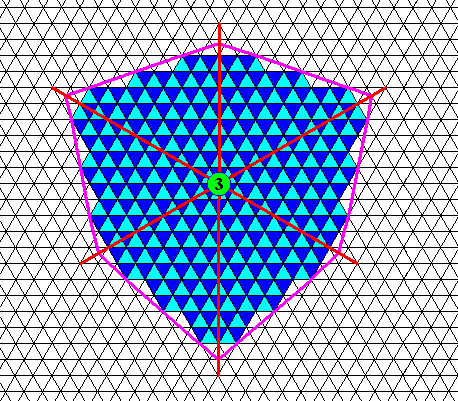
Figure above : Face-ditrigon of the previous Figures.
The trigonality at the molecular level is indicated in all unit meshes of the face-ditrigonal two-dimensional crystal. Compare with the (same) trigonal structure that was exemplified by a trigonal crystal having the shape of a regular hexagon HERE in the previous document .
The next three Figures indicate the layering in the face-ditrigonal two-dimensional crystal of the above Figures.
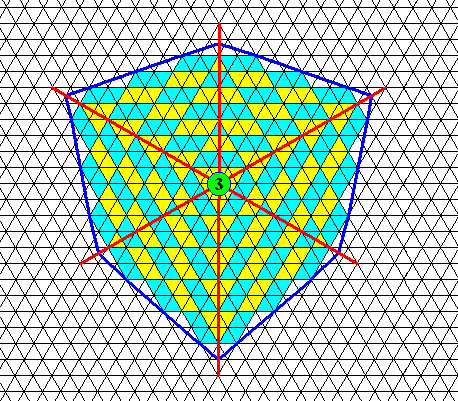
Figure above : Face-ditrigon of the previous Figures.
The layering of the face-ditrigonal crystal is indicated by the colors blue and yellow. See also next Figure.

Figure above : Face-ditrigon of the previous Figures.
The layering of the face-ditrigonal crystal is indicated by the colors blue and red. See also next Figure.
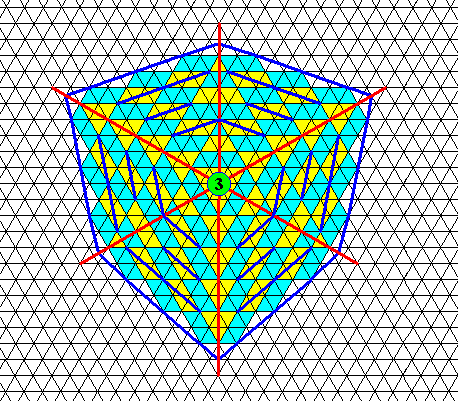
Figure above : Face-ditrigon of the previous Figures.
The layering of the face-ditrigonal crystal is indicated by the colors blue and yellow, and by parallel lines.
Now we have learned enough about the geometry and symmetry of the face-ditrigon. Compare the above drawings with especially the first and the last photographs of triangular snow crystals depicted above.
It seems that a face_ditrigonal two-dimensional crystal (or a projection of a corresponding three-dimensional crystal along its c-axis) begins with a small triangle, just like we saw it in the case of an angle-ditrigonal crystal. Compare this Figure in the previous document .
So it seems that in both cases of triangular snow crystals -- angle-ditrigonal and face-ditrigonal -- the crystal begins as a small triangle. And we know that a triangle cannot, as intrinsic shape, exist in crystals that have a 6-fold rotation axis, as snow crystals generally have.
In the next two documents I propose a solution to the just mentioned problem and present a summary, conclusion and survey concerning triangular snow crystals.
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-21.