

(Takes a little while loading the images)
e-mail :

Sequel-21 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-21) further elaborates on the analogy between crystals and organisms.
Sequel to the Preparations (IX) to the Repertoire of the Crystal Analogy
Sequel (IV) to Special Features of Crystals
Triangular snow crystals, theory, summary and overview (I).
Theory of triangular snow crystals
While crystals having an intrinsic shape of an equilateral triangle must be trigonal-hemihedric (three mirror lines, one 3-fold rotation axis), and not holohedric (six mirror lines, one 6-fold rotation axis), because a 600 rotation about the center of an equilateral triangle does not produce an image that is exactly superimposed upon the original image, crystals having an intrinsic shape of a regular hexagon are most often holohedric, but others, intrinsically having this same (hexagonal) shape, can nevertheless be trigonal, i.e. trigonal-hemihedric, even with the same growth rates of their six faces, as is clear from the next Figure.

Figure above : A trigonal-hemihedric two-dimensional crystal having the shape of a regular hexagon. Its six faces all present the same atomic aspect to the growing environment, so they are equivalent. There are no mirror lines connecting opposite centers of the faces (so these faces are asymmetric in themselves), but there are mirror lines connecting opposite corners of the hexagon, which means that the faces are not six rotational repetitions of one such face. See next Figure.
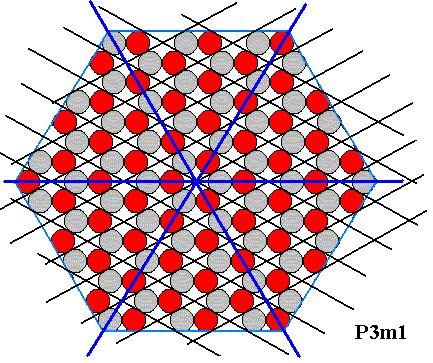
Figure above : Same as previous Figure : A trigonal-hemihedric two-dimensional crystal having the shape of a regular hexagon. It has mirror lines (blue) connecting opposite corners of the hexagon. Each face is asymmetric in itself and adjacent (asymmetric) faces are reflections of each other in the mirror line between them. So the six faces of this crystal are not six rotational repetitions. The rotation axis at the point of intersection of the mirror lines is, therefore, not a 6-fold rotation axis but a 3-fold one. The crystal is crystallographically generated by subjecting an initial face to the action of an adjacent mirror line, resulting in a pair of faces. When this pair is now subjected to the action of the 3-fold rotation axis we obtain the whole crystal (i.e. all of its six faces), which consequently represents one single crystallographic Form of the Class to which the crystal belongs, namely Class 3m (having D3 symmetry). The plane group symmetry (that is to say its total symmetry, including translational symmetries) of this crystal is P3m1.
So although certain (two-dimensional) crystals have the regular hexagon as their intrinsic shape, the intrinsic symmetry of such crystals can nevertheless be lower than that of the regular hexagon, or, in other words, they can still be (only) trigonal-hemihedric, i.e. belong to the Class 3m (of the 2-dimensional Hexagonal Crystal System) instead of 6mm (holohedric Class of the 2-dimensional Hexagonal Crystal System). We can compare such two-dimensional crystals of the trigonal-hemihedric or of the holohedric Class with projections of snow crystals along their c-axis. Now we know that the structure of ice (3-dimensionally) has 6/m 2/m 2/m point group symmetry, implying that the projection of this structure along the direction of its c-axis has (two-dimensionally) 6mm symmetry ( group theoretically denoted as D6 ). So these projections must have the structure, not as that of the trigonal-hemihedric hexagon-shaped crystal as depicted above , but as that of the holohedric crystal depicted in the next Figure :
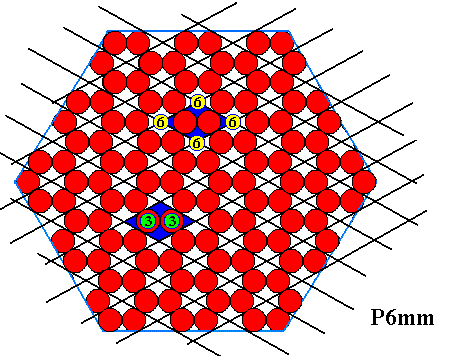
Figure above : Two-dimensional hexagon-shaped crystal belonging to the holohedric Class (6mm) of the two-dimensional Hexagonal Crystal System. Its plane group symmetry is P6mm.
So it seems clear that all snow crystals -- as seen in projection -- must have D6 symmetry and as such belong to the holohedric Class (6mm) of the two-dimensional Hexagonal Crystal System. This means that where ever trigonality in the crystallographic sense occurs in certain snow crystals, it must be considered to be a distortion or anomaly. Trigonality seems, where it occurs in snow crystals, be present at the beginning, i.e. in the initial growth states, of the crystal, as is evident by the fact that truly triangular snow crystals, i.e. plate-like snow crystals where the plate has the shape of an equilateral triangle, are always very small, so they represent the very beginnings of growth in some snow crystals. That trigonality in snow crystals often is connected with earlier growth states, is also evident in many hexagon-shaped or angle-ditrigonal-shaped snow crystals as the next Figure (and many others to come) shows.

In order to determine the (point group) symmetry present in snow crystals, we look to certain morphological features, such as can be seen in the center of the crystal just depicted. These features are, as they are in themselves, not intrinsic with respect to ice, i.e. they do not necessarily belong to, and are not necessarily implied by, the ice structure. They are grooves, ridges or channels, that happen to develop when crystal growth is fast. The intrinsic symmetry of the crystal, however, is evident in virtue of the r e g u l a r r e p e t i t i o n of such randomly occurring features. This repetition is evidently dictated by the intrinsic symmetry of the crystal.
With triangular snow crystals, i.e. snow crystals seemingly having a trigonal symmetry, the following could be the case :
Because of the accidental shape features of dust grains or other nucleation entities, some snow crystals begin trigonally. But this is certainly a distortion as compared with the normal holohedric case, and holds as such more energy, causing it to be less stable. Soon after some growth of this trigonal-hemihedric crystal kernel, the crystal re-establishes itself by adopting holohedric symmetry from the kernel onwards. And holohedric symmetry in ice holds less energy (judging from the fact that the molecular ice structure is holohedric as far as this is observed), so an ice structure with this symmetry is more stable. The kernel, however, remains trigonal-hemihedric, because a snow crystal falling from the sky did not have had sufficient time to let its interior rearrange from trigonal-hemihedric to holohedric (i.e. from 3m to 6mm with respect to point-group symmetry).
What has been said so far seems to fit at least (1) all (small) truly triangular snow crystals (which are then supposed to be wholly trigonal because they represent initial growth states), as in the next Figure :

(2) (the theory seems to fit further) all hexagon-shaped snow crystals with trigonal markings at their center ( like in the above Figure ), and, finally (3), (seems to fit) all angle-ditrigonal snow crystals as in the next Figure :

Figure above : An angle-ditrigonal snow crystal. The crystal started out as a triangular form. It tends to adopt a hexagonal shape while growing.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)
Some hexagon-shaped snow crystals, however, could be wholly trigonal-hemihedric as suggested by the crystal in the next Figure :

Figure above : A hexagon-shaped snow crystal with trigonal markings at its beginning but also at its periphery. This perhaps indicates that the whole crystal is trigonal-hemihedric.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)
In Part XXIX Sequel-19 we considered the growth of an angle-ditrigonal two-dimensional crystal (See HERE for the Figure ). It was assumed (just for the sake of the discussion) that the crystal is wholly trigonal-hemihedric, and this was graphically indicated in the last (growth) layer of the crystal only. The next Figure shows this same crystal, where its complete trigonal-hemihedric nature is indicated in all layers of the crystal :

Figure above : A two-dimensional trigonal-hemihedric crystal having the shape of an angle-ditrigon. The trigonality is expressed by differentiating, in all rhomb-shaped meshes of the hexagonal net, between the two triangles constituting such a mesh.
The next Figure depicts this same crystal, but now assuming (according to the theory just expounded) that generally trigonality in snow crystals is limited to a central region of the crystal only (where the Figure is now supposed to represent such a snow crystal), indicating a trigonal beginning of the crystal.
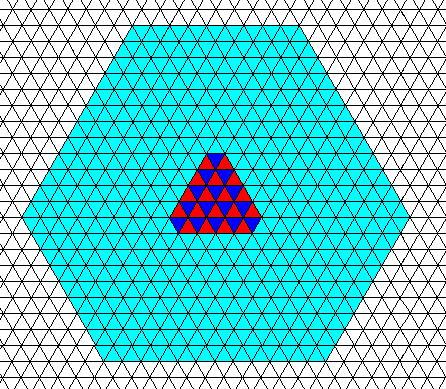
Figure above : An angle-ditrigonal crystal (as in the previous Figure) of which it is assumed that it started trigonally (3m), but soon switched to holohedric symmetry (6mm).
In those areas of it where the crystal is holohedric (in the example from the triangular kernel onwards, i.e. in the light blue area), the content of the two triangles, constituting a rhomb-shaped mesh of the hexagonal net, is identical (morphologically as well as orientationally), whereas in the trigonal kernel it is not.
While (1) truly triangular snow crystals, (2) hexagon-shaped snow crystals with trigonal markings in the crystal's central region, and (3) angle-ditrigonal snow crystals, are more or less explained by the above theory of Class switching (from 3m to 6mm, or, three-dimensionally, from 6-m2 to 6/m 2/m 2/m ), face-ditrigonal snow crystals cannot, it seems, be explained this way.

Figure above : A face-ditrigonal snow crystal
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : A face-ditrigonal snow crystal
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)
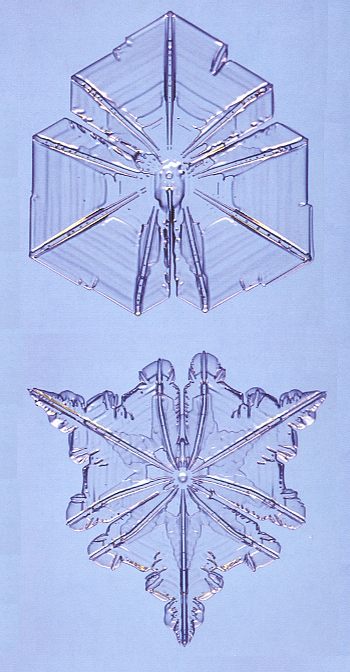
Figure above : Snow crystals with three roughly identical branches are unusual, and nice specimens tend to be small. These two each span about 0.6 mm (0.02 inches).
Note the curved ridges, especially in the bottom image.
(Photograph by Patricia Rasmussen, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
The next Figure depicts diagrammatically such a face-ditrigonal (already depicted earlier), indicating the trigonality at the molecular level.
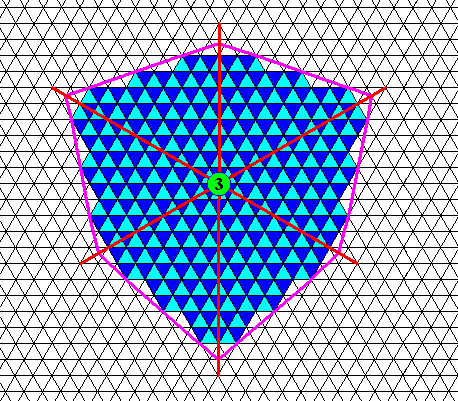
Figure above : Face-ditrigonal crystal.
The trigonality at the molecular level is indicated in all unit meshes of the face-ditrigonal two-dimensional crystal. Compare with the (same) trigonal structure that was exemplified by a trigonal crystal having the shape of a regular hexagon HERE in Part XXIX Sequel-19 .
As indicated by LIBBRECHT, 2003, The Snowflake (See the subscript of the above two photographs ), such (face-di)trigonal crystals are very small indeed, and so probably represent initial (trigonal) growth stages only (After further growth the crystal could switch classes, i.e. it continues its growth with holohedric symmetry rather than with trigonal-hemihedric symmetry with which it began).
This concludes our theory of triangular snow crystals.

Figure above : Most symmetrically developed snow crystals show their features (ridges, grooves and the like) to be almost exactly copied according to six-fold symmetry, even when these features are quite complex.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : In otherwise perfectly symmetrical snow crystals sometimes slight anomalies occur, not complying to the six-fold symmetry (D6 in projection) of the rest of the crystal.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : This snow crystal has a clear trigonal (D3) beginning (i.e. its initial growth stages are clearly trigonal), finally resulting in an angle-ditrigonal shape, after switching to holohedric symmetry (i.e. D6 symmetry).
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : This snow crystal seems to be trigonal throughout, or having just switched to holohedric symmetry.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)


Figure above : An almost completely trigonal snow crystal with hexagonal shape. Subtle structures in the central region of the crystal are repeated three times. Structures at the crystal's periphery are repeated six times, marking the beginning of holohedric symmetry.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)



Figure above : Some otherwise perfectly symmetrical snow crystals show anomalies not compatible with the symmetry of the rest of the crystal.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : Extensive trigonal influence almost throughout the whole snow crystal.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : Another example of what we see in most snow crystals that have symmetrically developed at all : a six-fold repetition of even very complex features.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : A hexagon-shaped snow crystal that is largely trigonal.
The three-fold configuration of the set of bar-like features, is truly, i.e. crystallographically, three-fold, because in the alternating sectors where they are absent there was enough space for them to form, but in spite of that they didn't.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)


As one can see, there are many snow crystals that show clearly trigonal initial growth stages. The exact three-fold repetition of sometimes complex features -- which are each for themselves more or less accidental -- cannot be accidental, i.e. it cannot be extrinsic with respect to the structure of the given crystal. It is astonishing that even crystals that, while growing, undergo switching from one symmetry class to another, still look harmonious. Again evidence for the great form potential of crystalline H2O.
Let us continue to present photographs of snow crystals and comment on them.

Figure above : Asymmetry in snow crystals is, one could say, the rule. It is, however, an extrinsic feature of them, caused by some bias in the growing environment, for example more supply of material (water molecules) at one side of the growing crystal than at the other. But whatever inequalities in the environment there may be, causing corresponding asymmetries, the types of arms on any given individual branched snow crystal is always the same (i.e. the same within a single crystal). Apart from possible microscopic defects in the crystal lattice, the intrinsic symmetry of the crystal's structure is definitely present and, by definition, not affected by a bias in the environment. And for ice this symmetry is according to a group that itself is a higher symmetry group than the (totally) Asymmetric Space Group P1. This symmetry of the internal structure of the crystal (i.e. its space group symmetry) necessarily implies the corresponding intrinsic crystallographic point group symmetry (i.e. its crystal Class), and this in turn implies, provided the bias (local inequalities) in the environment is not too strong, the corresponding intrinsic macroscopic morphological (point group) symmetry as a feature of the crystal's (external) shape. If the environmental bias is too strong, then, (still) in the case of snow crystals, extrinsic macroscopic asymmetry will develop, as it did in the crystal of the present Figure.
If we look at the radial internal macroscopic morphological features in a hexagon-shaped snow crystal, or at the arms of a branched snow crystal, we see, going from crystal to crystal, an infinity of different types of radial- or arm-structures. We might attribute this diversity to a corresponding diversity of micro-environments, but then the question remains why, in one and the same snow crystal individual the type of radial feature or arm is always the same for all six of them. We could assume that the micro-environment immediately around such a crystal is the same (while it is different for other (fellow) crystal individuals), accounting for the equality of the type of radial structure or of arm in one and the same crystal. But this does, according to me, not hold water, because this micro-environment is often different around one and the same crystal individual, as the often occurring asymmetric snow crystals (as shown in the present and next Figure) show. These crystals, i.e. especially the asymmetric branched crystals, seem to demonstrate that a local bias of the micro-environment around one and the same crystal individual produces longer or shorter arms, but does not result in different t y p e s of arms in one and the same crystal.
I assume, as expounded earlier, that a certain type of arm is initiated by one or another random event, and then amplified, 'exaggerated' (in virtue of the competition for water molecules) and at the same time m u l t i p l i e d according to the intrinsic D6 symmetry of the crystal, i.e. of the projection of the snow crystal along its c-axis. This multiplication is : Reflection of the randomly generated structure in a mirror line, resulting in a pair of adjacent structures, followed by a 6-fold rotational multiplication of this pair in virtue of the action of the 6-fold rotation axis.
So the crystal behaves holistically : its development is not solely governed by local factors and events within the crystal, but also by global factors within that same crystal, factors spanning beyond the range of molecular forces, factors having to do with overall coordination throughout the developing crystal : One arm 'knows' what the other is doing.
And this is why we must take the cases of observed three-foldness in snow crystals seriously, which means that we should not attribute them to merely extrinsic and external accidental factors, save for the very initiation of trigonality in and from the crystal seed. Three-foldness in snow crystals is then, although initiated accidentally, itself true crystallographic trigonality.
(Present Figure after a Photograph by Patricia Rasmussen in The Snowflake, 2003, by Kenneth LIBBRECHT.)

Figure above : Another example of extrinsic asymmetry in snow crystals. Also here we see that all six arms, although different in length, are of the same morphological type. (Photograph by Patricia Rasmussen in The Snowflake, 2003, by Kenneth LIBBRECHT.)


Figure above : A perfectly 6-fold snow crystal. As has been said earlier, the vast majority of snow crystals that got the chance to develop an external symmetry at all (not too strong a bias in the crystal's immediate growing environment), is six-fold, and, more specifically, six-fold throughout the whole crystal, i.e. from its very beginnings.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)



Figure above : A snow crystal with a holohedric (i.e. 6-fold) beginning, then, apparently, switching to trigonal-hemihedric (evident in the angle-ditrigon), finally resulting in a somewhat distorted hexagonal plate.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)





Figure above : Snow crystal with trigonal beginning and biased growth of extensions. Also here we cannot speak of outgrowth (arms) of different types within the same crystal. Four of them didn't develop at all (In the present case the possibility is not excluded that they simply have broken off from the crystal plate, for example as a result of collision with other snowflakes during their fall).
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)
The next document continues depicting relevant snow crystals and concludes the investigation of triangular snow crystals.
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-22.