

e-mail :

We continue the investigation of Vector Rosettes of Actual Growth in crystals, focussing for the time being on 2-D crystals.
Recall that in the foregoing we've found out that we can, with respect to crystals, determine the Vector Rosette of Actual Growth that is necessary and sufficient for indicating the Shape of the given crystal, by giving only the vectors that point, from the center of that crystal, to its corners. Some of these vectors can be composed vectors (composed from the original growth vectors of the individual faces, which are perpendicular to the latter), indicating the effective relative growth, and (like all growth vectors) indicating the accomplished growth.
Let us give some more examples of a Vector Rosette of Actual Growth in two-dimensional crystals.
While in the previous document the crystals -- chosen as example -- were based on a hexagonal lattice, which consists of rhombusses, the next crystals are based on an oblique lattice, which consists of parallelograms ( The latter is a generalization of a rhombus).
Plane Group P2, Point Group ( = Crystal Class) 2 (isomorph to C2).
Two-dimensional crystals of this Class possess as their only symmetry a two-fold rotation. A possible Form of the Class is a set of two parallel faces. Two (or more) such Forms can combine to form a crystal.
We depict the lattice without explicit motifs. In fact the lattice itself represents a repetition of motifs (here represented by the relevant areas associated with each lattice node) of the highest symmetry that is compatible with this lattice. These motifs have a symmetry 2 (isomorph with the group C2). Although, as has just been said, the bare lattice represents the highest symmetry that is compatible to that lattice, we let the areas, associated with the nodes of this bare lattice, represent chemical motifs with point symmetry C2. But such motifs still allow for different (even) number of antimers, and thus allow for several possible Promorphs.
Figure 1. (Symbolized) Chemical motifs, both having C2 symmetry (i.e. their only non-identity symmetry transformation is a rotation of 1800 about their main axis), but having two, resp. four antimers.
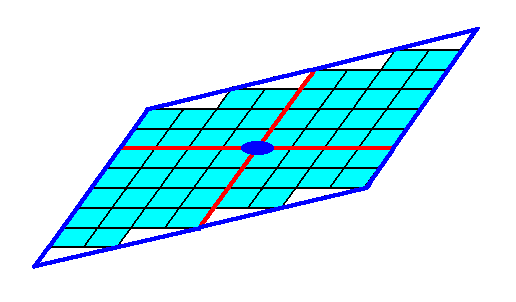
Figure 2. A combination of two possible Forms of the 2-D Crystal Class 2.
Because this combination is closed it can represent a (2-D) crystal. The red lines signify the two crystallographic axes, while the small blue solid ellipse signifies a 2-fold rotation axis, as the only point symmetry element of the crystal.
Of course the building blocks are imagined to be utterly small, resulting in the faces always to be smooth macroscopically.
The next Figure shows the same 2-D crystal, without indication of crystallographic axes and the 2-fold rotation axis. The crystal shape emerges from a combination of two Forms : one Form consisting of the two faces d, the other Form consisting of the faces e.
Figure 3. Two-dimensional crystal.
Heavy solid blue lines indicate faces.
Figure 4 shows the same crystal without the auxiliary lines indicating faces. The nodes of the lattice are at the intersections of the lines outlining the building blocks. These nodes indicate the periodic repetition of motifs, and are equivalent.
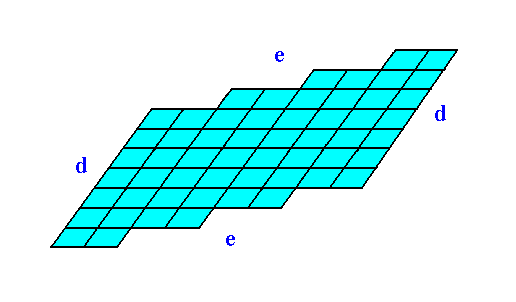
Figure 4. The two-dimensional crystal, drawn without any auxiliary features.
Figures 3 and 4 show that if the faces d were chemically and physically like the faces e they would grow slower than the latter, because more nutrient material must be imported from the growing environment to complete a layer of motifs on the (growing) crystal. But, as can be seen from the shape of the resulted crystal, other factors -- of a chemical or physical nature -- have superseded this effect.
As established earlier, we can determine the (necessary and sufficient) Vector Rosette of Actual Growth of the above crystal by indicating the growth vectors that originate in the center of the crystal and go to its corners.
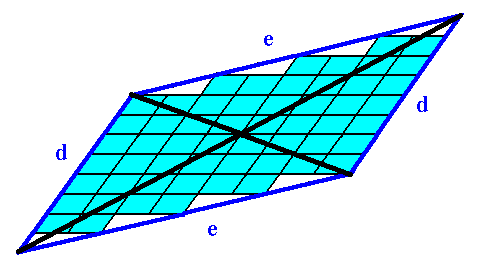
Figure 5. Vector Rosette of Actual Growth of the 2-D crystal depicted in the previous Figures.
The next Figure indicates radial and interradial areas in the crystal, where it is supposed that the chemical motif, that remains after elimination of all translations, has two antimers.
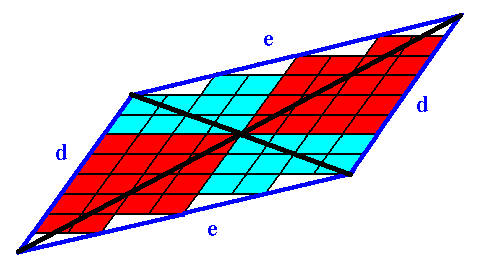
Figure 6. Radial (red) and interradial (blue) areas of the 2-D crystal of Figure 3. Of course we could equally well call the blue areas radial and the red areas interradial. Also their boundaries are more or less arbitrary.
The next Figure depicts the two antimers of the crystal.
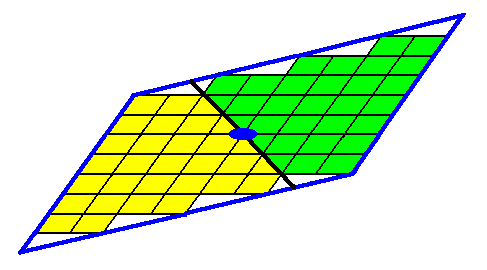
Figure 7. The two antimers of the 2-D crystal of Figure 3.
The boundary separating the antimers is dependent on the structure of the translation-free chemical motif.
From the above Figure we can assess the Promorph. It is represented by the base of a two-fold amphitect gyroid pyramid. The Promorph of the crystal is consequently the 2-D analogue of the (3-D) Heterogyrostaura dimera.
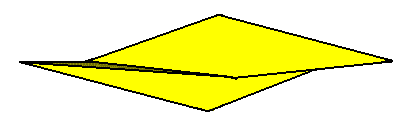
Figure 8. Slightly oblique top view of a two-fold amphitect gyroid pyramid representing the Heterogyrostaura dimera. This promorph represents natural gyroid bodies, compressed perpendicular to their main axis, and having two antimers. The symmetry is, as it is (also) in the Heterogyrostaura tetramera (see below), that of the symmetry group C2 .
In fact an amphitect (gyroid) pyramid can only be (2n+2)-fold, where n = 1, 2, 3, . . . . Speaking about a ' 2-fold (gyroid) pyramid ' indicates that we're dealing with a promorph (represented by this pyramid) of an object which has two antimers.
The next Figure indicates the two antimers of the gyroid pyramid of the previous Figure.
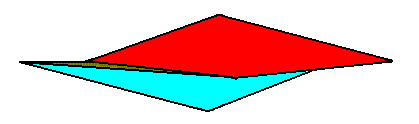
Figure 9. The body parts of the 2-fold amphitect gyroid pyramid (which is the promorph of the Heterogyrostaura dimera), that can represent the two antimers, are indicated (red, blue). But, of course, we could, in the present case, let the antimers coincide with other body parts that are equally adequate. One should realize that this pyramid, as a purely g e o m e t r i c body, represents the promorph of some other body (for example a crystal or an organism).
If, on the other hand, we assume that the translation-free chemical motif has four antimers, then the radial and interradial areas of the crystal could look like this :
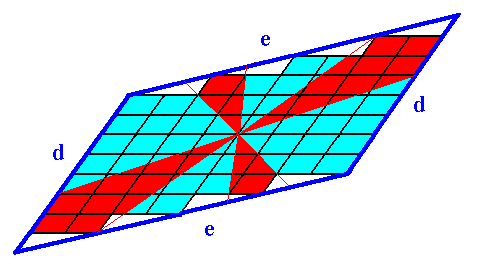
Figure 10. Possible radial (red) and interradial (blue) areas of the above 2-D crystal.
Its four antimers could look like this :
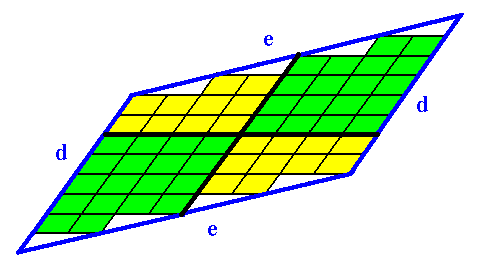
Figure 11. The four antimers, as assumed for the crystal of the previous Figure.
From the above Figure we can assess the Promorph. It is represented by the base of a four-fold amphitect gyroid pyramid. The Promorph of the crystal is consequently the 2-D analogue of the (3-D) Heterogyrostaura tetramera.
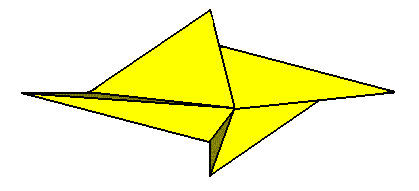
Figure 12. Slightly oblique top view of a four-fold amphitect gyroid pyramid representing the Heterogyrostaura tetramera. This promorph represents natural gyroid bodies, compressed perpendicular to their main axis, and having four antimers. The symmetry is that of the symmetry group C2 .
The next Figure shows the four antimers of the amphitect gyroid pyramid of Figure 12 (One should realize that a purely geometric pyramid does not have unequivocally defined antimers, because the latter are based on a certain definite external and internal sub-structures, like we can see them in atomic complexes or organisms. The 'antimers' of the present geometric pyramid represent antimers in some other (structured) bodies).
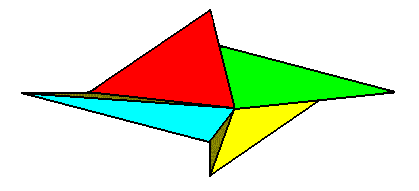
Figure 13. Four-fold amphitect gyroid pyramid representing the Heterogyrostaura tetramera. This promorph represents natural gyroid bodies, compressed perpendicular to their main axis, and having four antimers. The symmetry is that of the symmetry group C2 . The body parts of the pyramid representing the four antimers are indicated (red, green, yellow, blue).
So the 2-D crystal, having been discussed, admits of at least two Promorphs, dependending on the structure of the translation-free chemical motif. The Crystal Class implied by the Plane Group P2 (which -- Plane Group -- is the total symmetry of our just discussed 2-D crystal) is 2 (isomorphic with the group C2). And the symmetry of a crystal class (point symmetry) is always equal to the translation-free residue of the corresponding Plane Group (or Space Group). So this point symmetry directly implies the Promorph of the corresponding crystal to belong to the Heterogyrostaura (amphitect gyroid pyramids). But this is (still) a general Promorph, that can be specified further when the number of antimers of the translation-free chemical motif is known (See Figure 1).
The next example considers a crystal from the same Plane Group (P2) and the same 2-D Crystal Class (2), but consisting of a combination of four Forms.
Figure 14. Construction of a 2-D crystal from a combination of four Forms.
The crystallographic axial system, and the 2-fold rotation axis representing the point symmetry of the crystal, are indicated. The final result of the construction is given in the next Figure.
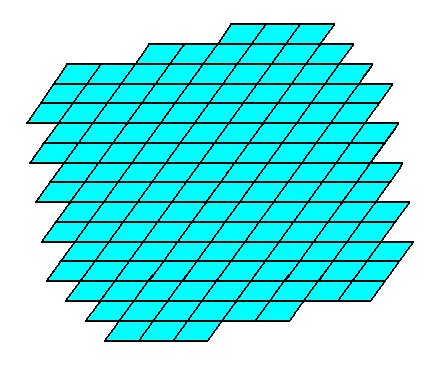
Figure 15. A two-dimensional crystal constructed from the four Forms mentioned above.
Let's first compare some actual growths (i.e. material expansions), here between the 'faces' d and e of the previously discussed crystal on the one hand, and those of the present crystal on the other. The ratio between those growths for the previous crystal is given in the next Figure.
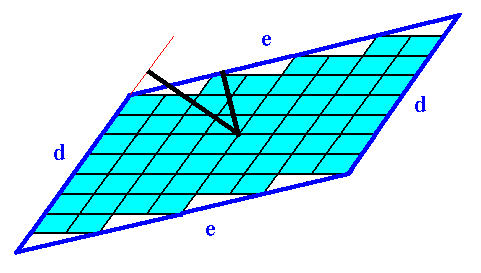
Figure 16. Ratio of growth of the d and e faces of the previously discussed 2-D crystal.
The ratio of the growths between the corresponding faces of the present crystal (Figure 14) is indicated in the next Figure.
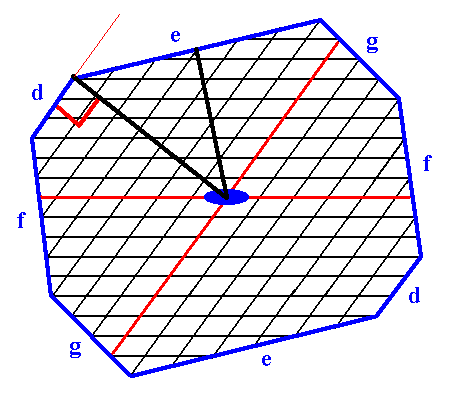
Figure 17. Ratio of growths of the faces d and e of the 2-D crystal of Figure 14.
The ratio's clearly differ (d/e = 1.75 and 1.29 resp.), so although we have to do with two crystals of the same Plane Group (and by implication the same Point Group), they must differ chemically (in an analogous sense, because we here have to do with 2-dimensional crystals).
The Vector Rosette of Actual Growth of the crystal of Figure 14 is given in the next Figure.
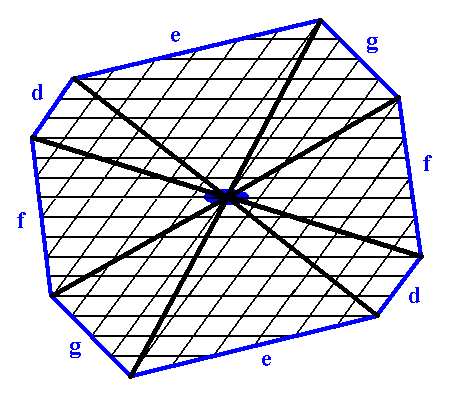
Figure 18. Vector Rosette of Actual Growth of the 2-D crystal of Figure 14 (Plane Group P2, Point Group 2 [ = C2] ).
Radial and interradial areas could be like those given in the next Figure if we assume that the translation-free chemical motif has two antimers.
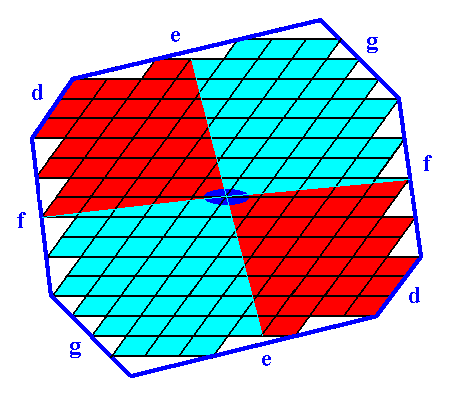
Figure 19. Radial (red) and interradial (blue) areas of the 2-D crystal of Figure 14.
Of course the red areas can also be interpreted as interradial, while the blue areas are then radial. The boundaries between these areas -- as they are drawn -- are more or less arbitrary.
The two antimers of the crystal are indicated in the next Figure.
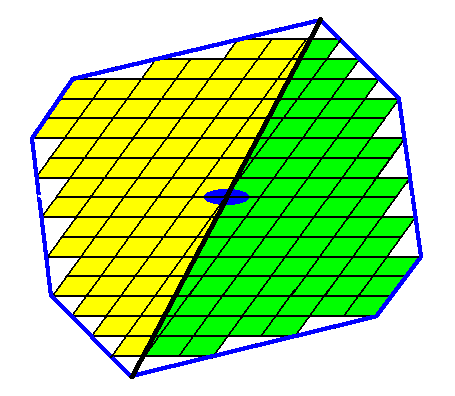
Figure 20. The two antimers of the crystal of Figure 14 are indicated.
According to Figure 20 we can determine the Promorph of the crystal as belonging to a 2-D analogue of the Heterogyrostaura dimera, represented by a two_fold amphitect gyroid pyramid. See Figure 8.
If, on the other hand, we assume that the translation-free chemical motif of the crystal of Figure 14 has four antimers (instead of two), then the radial and interradial areas of that crystal could look like this :
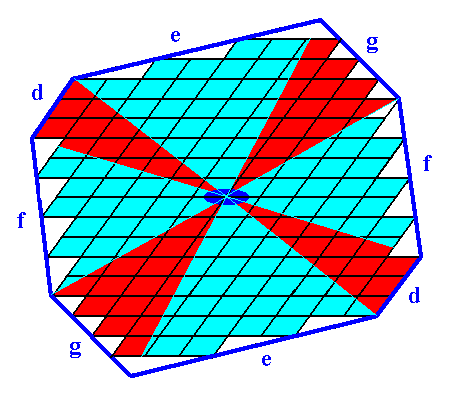
Figure 21. Radial (red) and interradial (blue) areas of the crystal of Figure 14.
Of course the interpretation as to the radial or interradial nature of the areas could be the other way around. The boundaries between these areas are more or less arbitrary.
The four antimers of the crystal are given in the next Figure.
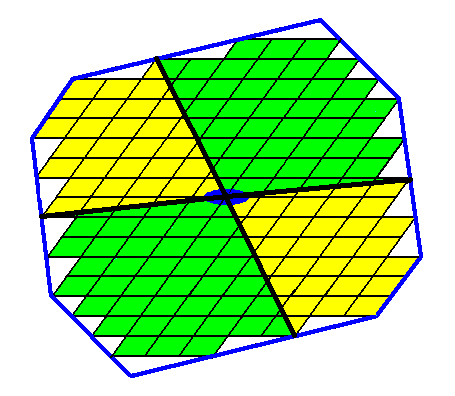
Figure 22. The four antimers of the crystal of Figure 14, if it is assumed that the translation-free chemical motif has four antimers.
According to Figure 22 we can determine the Promorph of the corresponding crystal as belonging to a 2-D analogue of the Heterogyrostaura tetramera, represented by a four_fold amphitect gyroid pyramid. See Figure 12.
The next Figure again depicts the Plane Group P2, but now with motifs explicitly indicated : Motifs with C2 symmetry (implying the possible 2-D crystals to belong to the 2-D Crystal Class 2). Each motif consists of a pair of commas, related to each other by a 2-fold rotation axis. Clearly such a motif, the symmetry of which (together with the proper surroundings) is the translation free residue of the Plane Group P2, has two antimers.

Figure 23. Periodic pattern of motifs representing the Plane Group P2 . One motif (s.str.) is highlighted (circle). The motifs consist of two antimers, and represent the translation-free chemical motif, determining the Promorph of a crystal, having this (internal) structure, to be that of the Heterogyrostaura dimera. A unit cell (unit mesh) is indicated (blue). The yellow and green areas represent group elements. The point lattice is an oblique net consisting of parallelograms.
The next Figure depicts a possible crystal having the above structure.
Figure 24. A possible crystal based on the oblique lattice (net) provided with motifs as given above. Each motif consists of two commas, which in turn are the antimers of the motif.
In the above Figures we have placed the motifs (s.str.) wholly inside the meshes of the net (point lattice). Alternatively we could place them at the nodes of the net. This "inside the mesh, or at the nodes" does not make a difference : When we have placed the motifs wholly inside the meshes, we can still conceive that each node of the net is associated with a motif (which in this case is a motif consisting of four parts of the motif originally conceived as a motif). See next Figure.
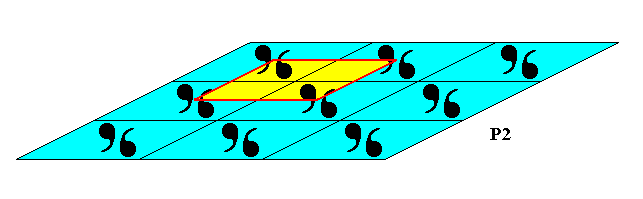
Figure 24a. Alternative interpretation of the motif (s.str.). In this alternative interpretation there is a motif s.str. associated with each lattice node. One such motif is indicated by the yellow area surrounding a particular node of the net. Those parts of the commas that fall within the yellow area together form the alternative motif (associated with a lattice node).
The next Figure shows the Vector Rosette of Actual Growth .
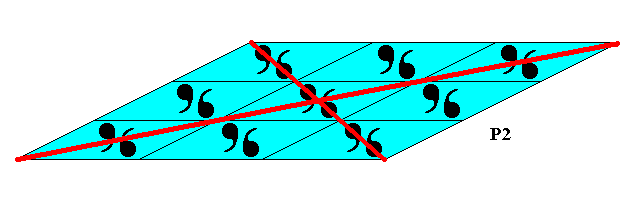
Figure 25. Vector Rosette of Actual Growth of the crystal of Figure 24.
The next Figure illustrates the radial and interradial areas of the crystal of the previous Figures.
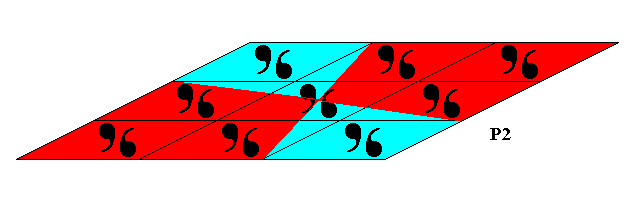
Figure 25a. Radial (red) and interradial (blue) areas of the crystal of the Figure 24. An interpretation of the blue areas as radial and the red areas as interradial is equally valid. The boundaries delineating these areas are more or less arbitrary.
The two antimers of the crystal are indicated in the next Figure.
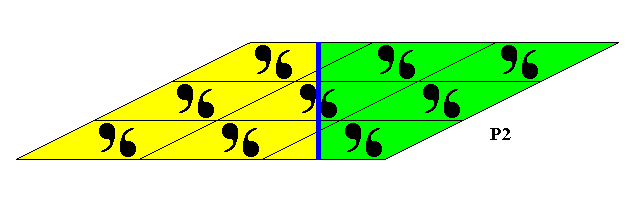
Figure 26. The two antimers of the 2-D crystal of the previous Figures. These antimers are based on the tectological structure of the translation-free 'chemical' motif.
According to Figure 26 we can determine the Promorph of the corresponding crystal as belonging to a 2-D analogue of the Heterogyrostaura dimera, represented by a two_fold amphitect gyroid pyramid. See Figure 8.
If, on the other hand, the translation-free chemical motif is such that we must interpret it as consisting of four antimers, as in the next Figure, then the Promorph of the corresponding crystal would be a 2-D analogue of the Heterogyrostaura tetramera.

Figure 26a. A motif having C2 symmetry (i.e. having, as its only symmetry element, a two-fold rotation axis, like the motifs of the previous three Figures), and consisting of f o u r antimers (instead of two).
Instead of the crystal of Figure 24 we should now have the following crystal (still having planegroup symmetry P2, and point group symmetry 2 [isomorphic with C2] ) :
Figure 26b. A two-dimensional crystal having the same point and plane symmetry as the crystal of Figure 24, but of which the translation-free motifs are composed not of two, but of four antimers.
The next Figure illustrates the radial and interradial areas of the crystal of Figure 26b.
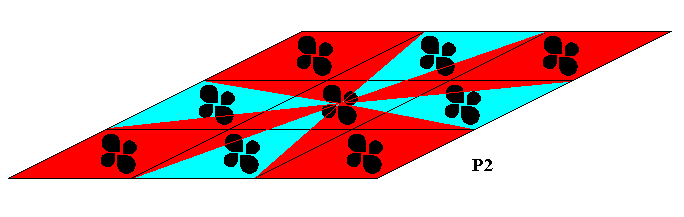
Figure 26c. Radial (red) and interradial (blue) areas of the crystal of Figure 26b. An interpretation of the blue areas as radial and the red areas as interradial is equally valid. The boundaries delineating these areas are more or less arbitrary.
The next Figure illustrates the four antimers of the crystal.
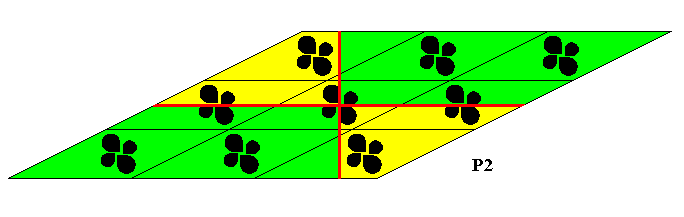
Figure 26d. The four antimers of the crystal of Figure 26b.
So according to Figure 26d the crystal of Figure 26b belongs promorphologically to the 2-D analogue of the Heterogyrostaura tetramera (amphitect gyroid pyramids with four antimers).
The relative growths of the possible faces could, however, such that the horizontal faces grow more slowly than the oblique faces, resulting for example in the following crystal (with the same internal symmetry) :
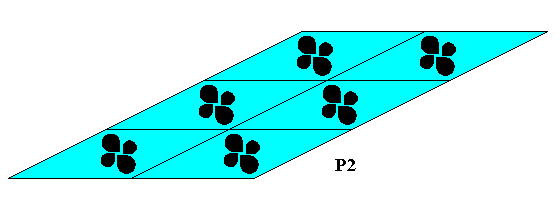
Figure 26e. A two-dimensional crystal, having the same internal symmetry as the crystal of Figure 26b, but differing in structure in the sense that the motif, although having the same point symmetry, is 'chemically' different resulting in different atomic aspects presented to the nutrient environment by the possible faces. This chemical diference is here supposed to entail that the horizontal faces grow more slowly than the oblique faces, resulting in a different shape of the crystal.
The antimers of such a crystal can be depicted as follows :
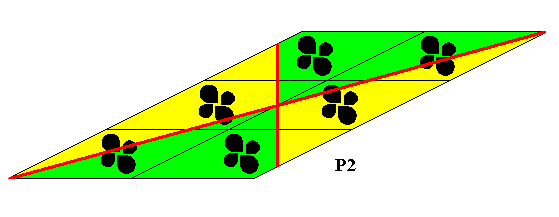
Figure 26f. The four antimers of the crystal of Figure 26e.
The next Figure gives a 2-D pattern according to the Plane Group P1.

Figure 27. A two-dimensional pattern representing the Plane Group P1. The pattern is based on an oblique lattice provided with motifs (s.str.). Each such motif is a comma. The lattice consists of parallelograms. Such a parallelogram plus motif constitutes a unit cell (unit mesh) of the pattern. It also represents a group element.
The next Figure shows a possible crystal having the structure (oblique lattice plus motifs) of the pattern of the previous Figure.
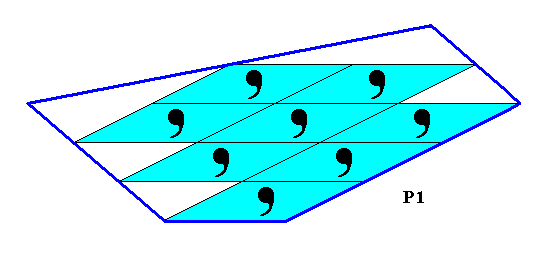
Figure 28. A possible two-dimensional crystal based on the above P1 pattern, and belonging to the 2-D Crystal Class 1. It consists of five Forms (i.e. it is a combination of five Forms, each of which is one 'face), and does not possess antimers, because the translation-free motif does not have antimers.
The Vector Rosette of Actual Growth of the crystal of Figure 28 is given in the next Figure.
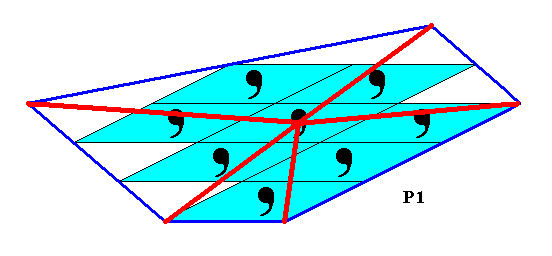
Figure 29. Vector Rosette of Actual Growth of the 2-D crystal of Figure 27. They originate from some arbitrary point that can stand for a possible center of the crystal.
Because (1) the translation-free motif (represented by the comma) does not have antimers, and (2) that translation-free motif does not have a unique center, the Promorph of the crystal belongs to a two-dimensional analogue of the Anaxonia acentra, i.e. bodies without symmetry (With respect to the latter it belongs to the (asymmetric) symmetry group C1), and without a genuine body center.
In the next document we will continue the study of Structure, (intrinsic) Shape, (intrinsic) Symmetry, and Promorph of two-dimensional crystals, as a prelude to some insight of these properties in three-dimensional crystals, and to compare the latter with organisms in those respects.
To continue click HERE for further study of the Theory of Layers, Part XXXII.
e-mail : 