

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Amphitect Hexagon
We will now investigate two-dimensional crystals with an intrinsic shape according to an amphitect hexagon as to their possible promorphs, but, as in the foregoing, limiting ourselves to holomorphic crystals, which means that we will only investigate crystals of which their intrinsic symmetry is the same as the symmetry of their intrinsic shape. In the present case this means that our amphitect hexagonal crystals will have D2 intrinsic symmetry (while in other cases -- meromorphic crystals -- this symmetry could be either according to D1 , or C2 , or C1 , depending on the crystal's internal structure).
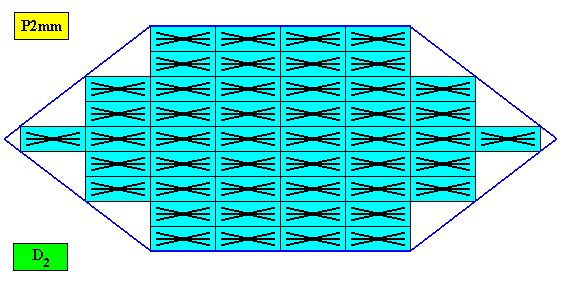
Figure above : Microscopic view of a two-dimensional amphitect hexagonal D2 crystal consisting of the periodic stacking of rectangular building blocks, explicitly provided with D2 motifs. These D2 motifs represent the translation-free residue of the crystal (all the same whether it belongs to the plane group P2mm, P2mg, P2gg or C2mm), and in this example the residue has six antimers. So the crystal of this example itself has six antimers and is thus eupromorphic (because the six antimers are already evident in the crystal's intrinsic shape). Because the building blocks are in fact very small (i.e. in crystals they have microscopic dimensions), all the crystal faces are macroscopically smooth.
The next Figure presents a macroscopic view of the crystal of the previous Figure, obtained by removing all lattice connection lines (indicating building blocks) and all motifs.
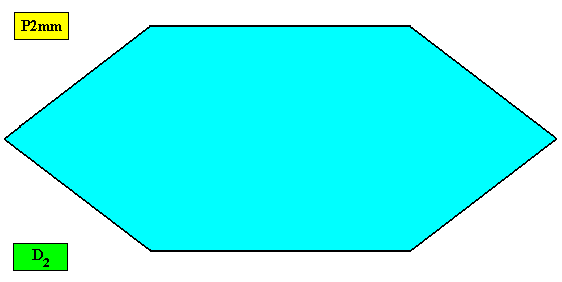
Figure above : Macroscopic view of the two-dimensional amphitect hexagonal D2 crystal of the previous Figure.
The pattern of symmetry elements (with respect to the point symmetry) of our amphitect hexagonal D2 two-dimensional crystal is given in the next Figure.
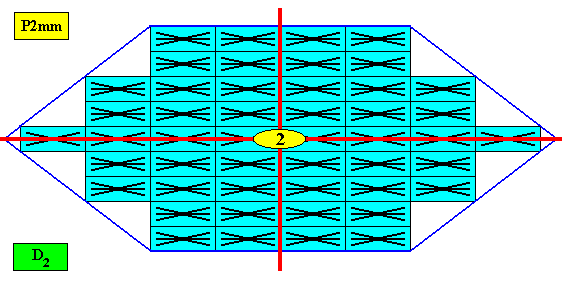
Figure above : Pattern of symmetry elements of the above given amphitect hexagonal D2 two-dimensional crystal. Its consists of two mirror lines (red) perpendicular to each other, and a 2-fold rotation axis (small yellow ellipse) at their point of intersection.
Two crystallographic Forms are needed to construct the outline of the amphitect hexagonal crystal, as the next Figure shows.
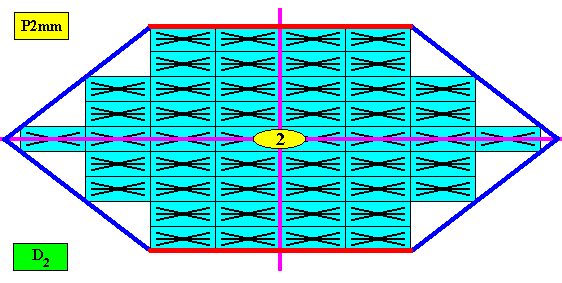
Figure above : Two crystallographic Forms are needed to construct the faces of our amphitect hexagonal D2 two-dimensional crystal : An initially given oblique face (dark blue, not parallel to either mirror line) implies three more faces in virtue of the symmetry elements, resulting in one Form consisting of four faces (dark blue). This is a closed Form, and as such can represent a crystal. However, this crystal has the shape of a rhombus, and not that of an amphitect hexagon. So one more Form is needed : An initially given face (red) parallel to one of the mirror lines, implies one more face in virtue of the symmetry elements, resulting in a Form (red) consisting of two parallel faces. Combined with the first Form it yields our amphitect hexagonal crystal.
Possible a n t i m e r c o n f i g u r a t i o n s for holomorphic amphitect hexagonal two-dimensional crystals. (Shown by crystals somewhat shorter than the ones depicted above, but still being amphitect hexagonal).
Six antimers.
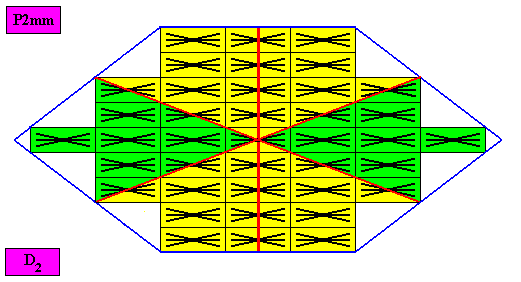
Figure above : An amphitect hexagonal D2 two-dimensional crystal. The case of s i x similar antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue of the crystal) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers, is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D2 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that six antimers can be distinguished in it. The crystal is eupromorphic because its intrinsic shape suggests six antimers, which indeed are present. These six antimers are indicated in the next Figure by numerals.
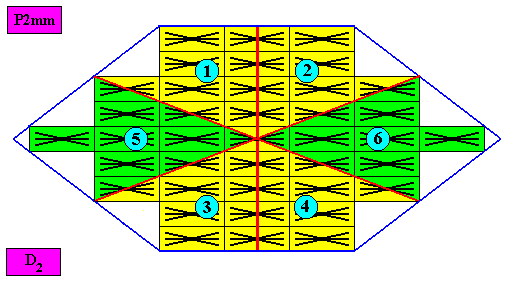
Figure above : Same as previous Figure. The six antimers are indicated by numerals.
Or, using a different coloration (to indicate the six antimers) :
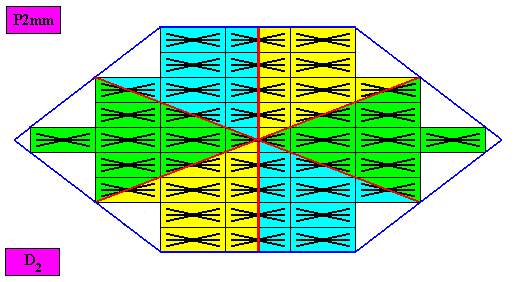
Figure above : Same as previous Figure. The six antimers are indicated by the colors green, yellow and blue.
The next Figure gives a macroscopic view of the crystal of the previous Figure, obtained by removing lattice lines and motifs.
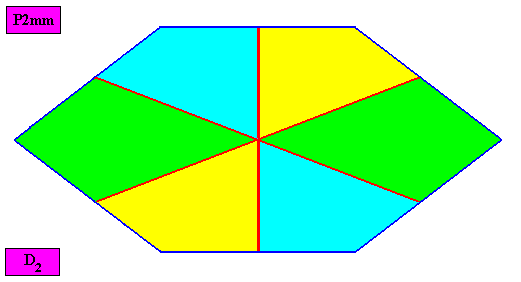
Figure above : Macroscopic view of the amphitect hexagonal D2 two-dimensional crystal of the previous Figure.
The next Figure depicts the six antimers in an equivalent way (In fact the internal structure of the crystal is turned by 900 and then its dimensions reorganized) :
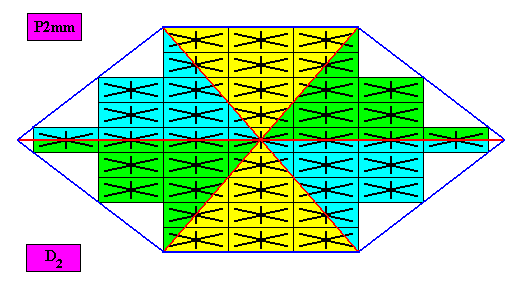
Figure above : An amphitect hexagonal D2 two-dimensional crystal. (Still) the case of six similar antimers (green, yellow, blue). Note again the correspondence between the morphology of the motif (as translation-free residue) and the arrangements of the (macroscopic) antimers of the crystal. So again, in this way the promorph, and in particular the number of antimers, is based on the morphology of the (mentioned) translation-free residue of the crystal. This residue is explicitly given in the form of a D2 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that six antimers can be distinguished in it. The crystal is eupromorphic because its intrinsic shape suggests six antimers, which indeed are present.
The next Figure gives a macroscopic view of the crystal of the previous Figure, obtained by removing lattice lines and motifs.
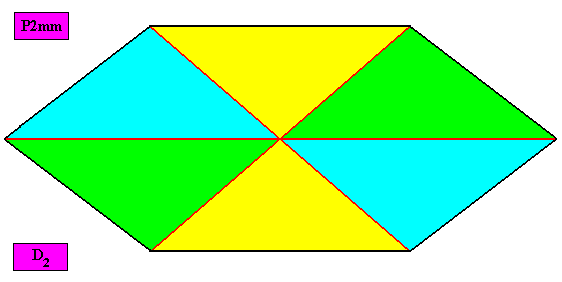
Figure above : Macroscopic view of the amphitect hexagonal D2 two-dimensional crystal of the previous Figure.
The promorph of the above amphitect hexagonal eupromorphic crystal is (as two-dimensional analogue) belonging to the Autopola Oxystaura hexaphragma. This promorph is depicted in the next Figure.
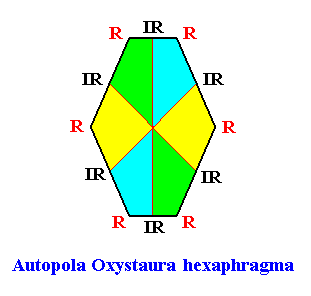
Figure above : The promorph of the amphitect hexagonal crystal with six antimers. It is a 6-fold amphitect polygon (amphitect hexagon) and as such the two-dimensional analogue of the 6-fold amphitect pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Radial (R) and interradial (IR) directions (seen from the center of the polygon) are indicated.
Four antimers, radial configuration.
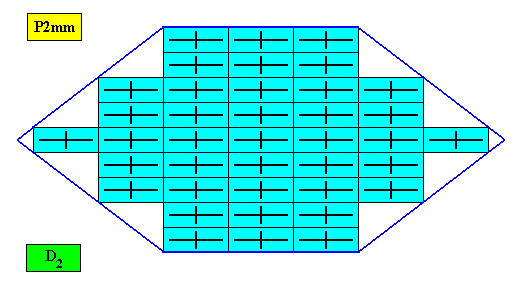
Figure above : A two-dimensional amphitect hexagonal crystal with intrinsic D2 symmetry. Its D2 motifs (black) have four antimers in radial configuration. Microscopic view.
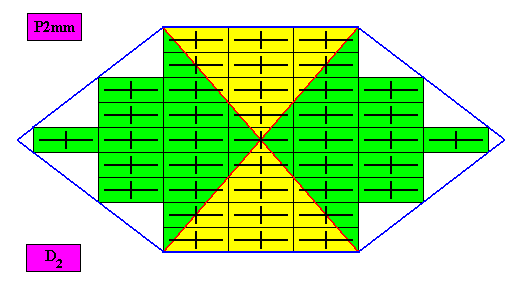
Figure above : The amphitect hexagonal D2 two-dimensional crystal of the previous Figure. The case of f o u r similar antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D2 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that four antimers can be distinguished in it. The four antimers of this (microscopic) atomic configuration are radially arranged (perpendicular directional cross axes passing through antimers), which will reflect itself in the promorph of the crystal. The crystal is non-eupromorphic because its intrinsic shape suggests six antimers, while in fact there are only four of them.
The next Figure gives the macroscopic view of the crystal of the previous Figure, obtained by removing lattice lines and motifs.
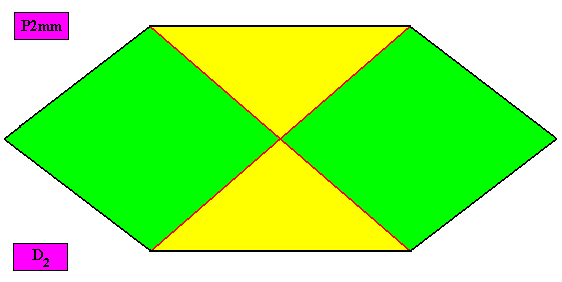
Figure above : Macroscopic view of the amphitect hexagonal D2 two-dimensional crystal with four radially arranged antimers, of the previous Figure.
The promorph of the above amphitect hexagonal non-eupromorphic crystal is (as two-dimensional analogue) belonging to the Autopola Orthostaura Tetraphragma radialia. This promorph is depicted in the next Figure.
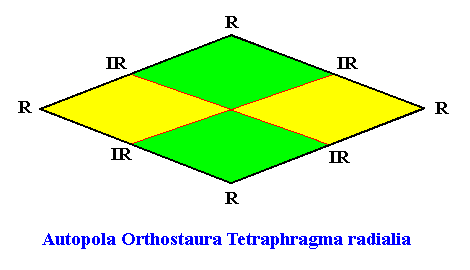
Figure above : The promorph of the amphitect hexagonal crystal with four antimers. It is a 4-fold amphitect polygon (rhombus) and as such the two-dimensional analogue of the rhombic pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the difference in shape between this promorph (rhombus, amphitect tetragon) and that of the crystal (amphitect hexagon) of which it is the promorph.
The above promorph (Autopola Orthostaura Tetraphragma radialia) can be expressed in a more general way than was done in the previous Figure, to express the possible non-congruity (and thus non-equality) of the antimers (only two by two equal). In the previous Figure, which depicted a representation of this promorph, the antimers were (drawn) equal. The more general representation is depicted in the next Figure.
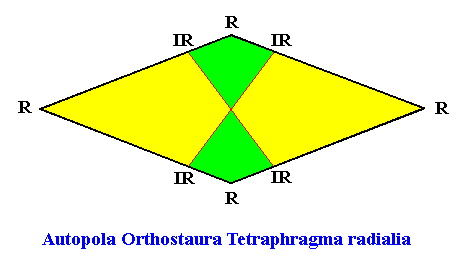
Figure above : Slightly different representation of the promorph (Autopola Orthostaura Tetraphragma radialia) of the amphitect hexagonal crystal with four antimers in radial configuration. It also is a 4-fold amphitect polygon (rhombus), but now expresses the unequality of the antimers as they are in the above amphitect hexagonal crystal.
Four antimers, interradial configuration.
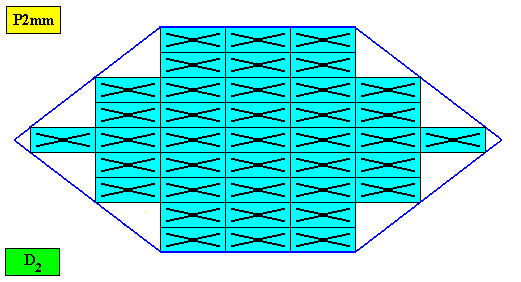
Figure above : A two-dimensional amphitect hexagonal crystal with intrinsic D2 symmetry. Its D2 motifs (black) have four antimers in interradial configuration. Microscopic view.
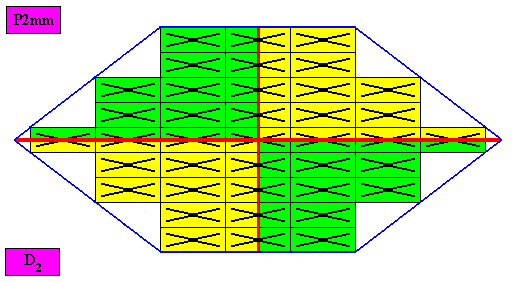
Figure above : The amphitect hexagonal D2 two-dimensional crystal of the previous Figure. The interradial case of f o u r congruent (two by two equal) antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D2 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that four congruent antimers can be distinguished in it. The four antimers of this (microscopic) atomic configuration are interradially arranged (perpendicular directional cross axes lying between antimers), which will reflect itself in the promorph of the crystal. The crystal is non-eupromorphic because its intrinsic shape suggests six antimers, while in fact there are only four of them.
The next Figure gives the macroscopic view of the crystal of the previous Figure, obtained by removing lattice lines and motifs.
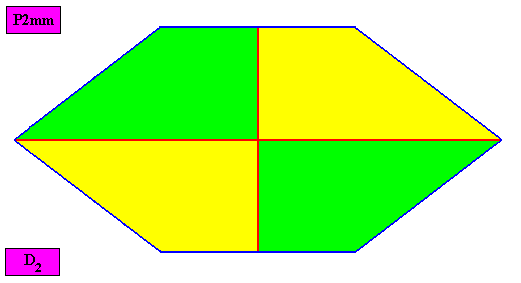
Figure above : Macroscopic view of the amphitect hexagonal D2 two-dimensional crystal with four interradially arranged antimers, of the previous Figure.
The promorph of the above amphitect hexagonal non-eupromorphic crystal is (as two-dimensional analogue) belonging to the Autopola Orthostaura Tetraphragma interradialia. This promorph is depicted in the next Figure.
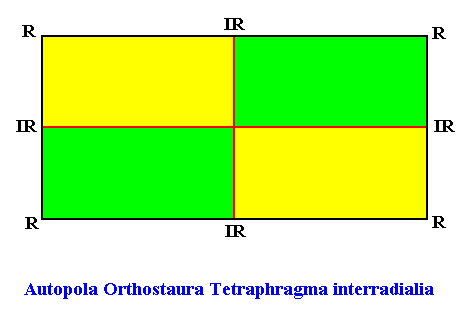
Figure above : The promorph of the amphitect hexagonal crystal with four antimers. It is a rectangle and as such the two-dimensional analogue of the rectangular pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the difference in shape between this promorph (rectangle, rectangular amphitect tetragon) and that of the crystal (amphitect hexagon) of which it is the promorph.
The above promorph (Autopola Orthostaura Tetraphragma interradialia) can be expressed in a more general way than was done in the previous Figure, to express the possible non-equality (but still congruity) of the antimers (only two by two equal, and two by two symmetric). In the previous Figure, which depicted a representation of this promorph, the antimers were (drawn) equal. The more general representation is depicted in the next Figure.
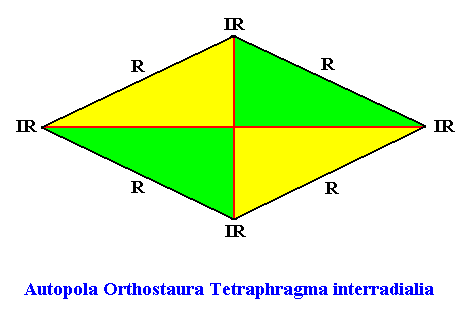
Figure above : Slightly different representation of the promorph (Autopola Orthostaura Tetraphragma interradialia) of the amphitect hexagonal crystal with four antimers in interradial configuration. It is now a rhombus (not a rectangle), and expresses the overall non-equality (but still congruity -- two by two equal, and two by two symmetric) of the four antimers (green, yellow) as they are in the above amphitect hexagonal crystal. Compare with the representation of the Autopola Orthostaura Tetraphragma radialia as depicted above .
Two antimers.
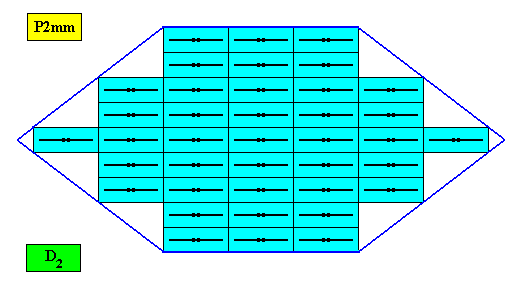
Figure above : A two-dimensional amphitect hexagonal crystal with intrinsic D2 symmetry. Its D2 motifs (black) have two equal antimers (They relate to each other by a half-turn). Microscopic view.
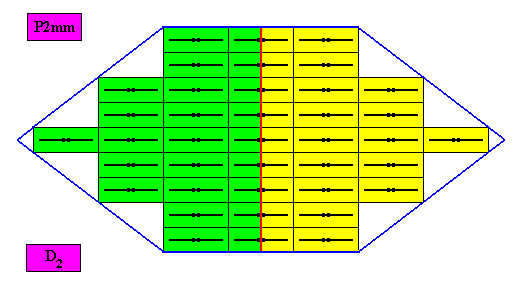
Figure above : The amphitect hexagonal D2 two-dimensional crystal of the previous Figure. The case of t w o equal antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a D2 motif (black) inside each rectangular building block. It is -- or represents -- an atomic configuration such that two antimers can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests six antimers, while in fact there are only two of them.
The next Figure gives the macroscopic view of the crystal of the previous Figure, obtained by removing lattice lines and motifs.
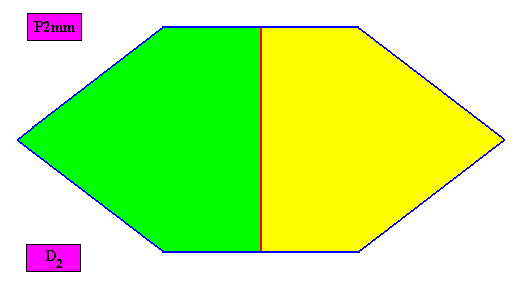
Figure above : Macroscopic view of the amphitect hexagonal D2 two-dimensional crystal of the previous Figure with two equal antimers.
The promorph of the above amphitect hexagonal non-eupromorphic crystal is (as two-dimensional analogue) belonging to the Autopola Orthostaura diphragma. This promorph is depicted in the next Figure.
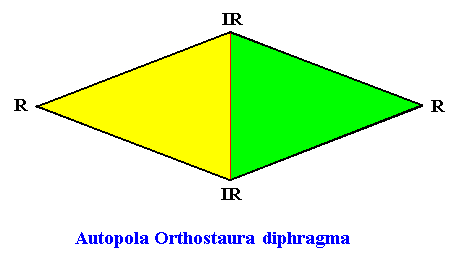
Figure above : The promorph of the amphitect hexagonal crystal with two antimers. It is a 2-fold amphitect polygon (rhombus, in the present case -- as '2-fold' -- expressing two antimers) and as such the two-dimensional analogue of the 2-fold rhombic pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the difference in shape between this promorph (rhombus, amphitect tetragon) and that of the crystal (amphitect hexagon) of which it is the promorph.
In the next document we will discuss the fourth crystal shape of our list (as given in Part XVI ) , viz. the amphitect octagon, with respect to intrinsic symmetry and promorph in holomorphic two-dimensional crystals having this shape intrinsically.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XIX.
e-mail : 