

For a Summary of our Noëtic Theory of Evolution, see further below.
Answering Questions about Producible Numbers by Consulting TNT
We continue from where we left things at the end of the first intermezzoing document (still following Hofstadter). There it was said that " TNT seemed, to all appearances, to have captured all valid mathematical thinking processes in one single, compact system."
Could it be, therefore, that the means with which to answer any question about any formal system lies within just a single formal system -- TNT ? It seems plausible. Take, for instance this question :
Finding the answer is equivalent to determining whether 30 is a MIU-number (that is, a MIU-producible number) or not. [30 is the overall Gödel number of the string MU which overall Gödel number resulted by assigning (arbitrary) numbers -- Gödel numbers -- to the symbols of the MIU-system, as was established in the first intermezzoing document.]. Because it is a statement of number theory (N), we should expect that, with some hard work, we could figure out how to translate the sentence "30 is a MIU-number" into TNT-notation, in somewhat the same way as we figured out how to translate other number-theoretical sentences into TNT-notation. I should immediately caution the reader that such a translation, though it does exist, is immensely complex. If you recall, I [Hofstadter] pointed out in Chapter VIII [in this website largely reproduced in the previous document] that even such a simple arithmetical predicate "b is a power of 10" is very tricky to code into TNT-notation -- and the predicate "b is a MIU-number" is a lot more complicated than that! Still, it can be found, and the numeral SSSSSSSSSSSSSSSSSSSSSSSSSSSSSS0 [30 S's and 0] can be substituted for every b (where it appears in the resulting TNT-string). This will result in a MONstrous string of TNT, a string of TNT which speaks about the MU-puzzle. Let us therefore call that string "MUMON". Through MUMON and strings like it, TNT is now capable of speaking "in code" about the MIU-system. [According to me (JB) this is not entirely true. And this has interesting and significant consequences for our noëtic theory of evolution. See for this my POSTSCRIPT at the end of the present document.]
["MUMON" stands for "30 is an MIU-number" in TNT-notation. So we now have done the following :
First we had the question : "Is MU a theorem of the MIU-system?"
Then we transcribed this question into number theory : "Is 30 an MIU-number?",
and finally we translated the question into TNT-notation : "MUMON?" (that is, "Is MUMON the case?", or, equivalently -- see directly below -- "Is MUMON a theorem of TNT?"). If the number-theoretical statement "30 is an MIU-number" (= the meaning of MUMON) is true, then it must -- when properly translated into TNT-notation -- result in MUMON -- appear as a theorem in TNT.]
The Dual Nature of MUMON
In order to gain some benefit from this peculiar transformation of the original question, we should have to seek the answer to a new question :
[And if 30 is indeed an MIU-number (a number producible by the MIU-system), which is a number theoretical proposition, then MUMON must be a theorem of TNT. And if 30 is not an MIU-number, then MUMON is not a theorem of TNT]
All we have done is replace one relatively short string (MU) by another (the monstrous MUMON), and a simple formal system (the MIU-system) by a complicated one ( TNT ). It isn't likely that the answer will be any more forthcoming even though the question has been reshaped. In fact, TNT has a full complement of both lengthening and shortening rules, and the reformulation of the question is likely to be far harder than the original. One might even say that looking at MU via MUMON is an intentionally idiotic way of doing things. However, MUMON can be looked at on more than one level.
In fact, this is an intriguing point : MUMON has two different passive meanings [These are isomorphic to one another]. Firstly, it has the one which was given before :
But secondly, we know that this statement is tied (via isomorphism) to the statement
So we can legitimately quote this latter as the second passive meaning of MUMON. It may seem very strange because, after all, MUMON contains nothing but plus signs, parentheses, and so forth -- symbols of TNT. How can it possibly express any statement with other than arithmetical content? [Indeed, saying that "MU is a theorem of the MIU-system" is saying something about some typographical structure.]
The fact is, it can. Just as a single musical line may serve as both harmony and melody in a single piece. Just as "BACH" may be interpreted as both a name and a melody [the tunes being B-A-C-H]. Just as a single sentence may be an accurate structural description of a picture by Escher, of a section of DNA, of a piece by Bach, and of the dialogue in which the sentence is embedded, so MUMON can be taken in (at least) two entirely different ways. This state of affairs comes about because of two facts :
[Number theory can (by means of Gödel numbers), in terms of the formal language of TNT, make propositions about every other formal system, for example the MIU-system (See, however, our POSTSCRIPT ). MUMON is a TNT-string saying something about MU which also can be expressed in TNT by translating its Gödel number -- 30 -- into TNT-notation. Thus, a TNT-string can say something about another TNT-string. But MUMON is not a MIU-string, and therefore we have not a MIU-string saying something about another MIU-string.]
Codes and Implicit Meaning
Now it could be objected here that a coded message, unlike an uncoded message, does not express anything on its own -- it requires knowledge of the code. But in reality there is no such thing as an uncoded message. There are only messages written in more familiar codes, and messages written in less familiar codes [Conventional signs standing for natural signs (concepts)]. If the meaning of a message is to be revealed, it must be pulled out of the code by some sort of mechanism, or isomorphism. It may be difficult to discover the method by which the decoding should be done. But once that method has been discovered, the message becomes transparent as water. When a code is familiar enough, it ceases appearing like a code. One forgets that there is a decoding mechanism. The message is identified with its meaning.
Here we have a case where the identification of message and meaning is so strong that it is hard for us to conceive of an alternate meaning residing in the same symbols. Namely, we are so prejudiced by the symbols of TNT towards seeing number-theoreticl meaning (and only number-theoretical meaning) in strings of TNT, that to conceive of certain strings of TNT as statements about the MIU-system is quite difficult. But Gödel's isomorphism compels us to recognize this second level of meaning on certain strings of TNT.
Decoded in the more familiar way, MUMON bears the message :
This is a statement of number theory (where common -- not formalized -- language is used), gotten by interpreting each sign in the conventional way [that is, translating the TNT-symbols one by one (and where in turn one knows what "is a MIU-number" means, and of course, what "number" means).].
But in discovering Gödel-numbering and the whole isomorphism built upon it, we have in a sense broken a code in which messages about the MIU-system are written in strings of TNT. Gödel's isomorphism is a new information-revealer, just as the decipherments of ancient scripts were information-revealers. Decoded by this new and less familiar mechanism, MUMON bears the message
The moral of the story is one we have heard before : that meaning is an automatic by-product of our recognition of any isomorphism. Therefore there are at least two passive meanings of MUMON [a meaning concerning natural numbers, and one concerning typographical features of strings] -- maybe more!
[To further work out our [JB] "noëtic theory of evolution", it is perhaps instructive to analyze the discovered ability of number theory (and with it its formalization [representing its essence]) to express things of other formal systems such as the MIU-system.
In thinking about the assumed formal system of noëtic strategy-strings (FSNSS) in the Implicate Order, we take the MIU-system to represent a rough (and utterly simplified) analogy of it. Like FSNSS, the MIU-system has obtained its specific whatness, its typical nature, not from number theory (and thus also not from its formalization), even when natural numbers are assigned to its symbols (and consequently to its strings) and when its production rules are arithmetized. Indeed, the typical nature of FSNSS, especially of its rules, is extrinsic to number theory and thus extrinsic to the Implicate Order : it must come from the Explicate Order, because the strings to be derived in FSNSS are strategies of how to exist in the Explicate Order. So although we know that the MIU-system can be encoded, and thus embedded, in number theory, and thus (now ontologically thinking) that FSNSS is so encoded and embedded, the specific content of their (now) arithmetical rules, that is, the specific combination in these rules of elementary arithmetic operations, cannot come from number theory ("number theory" here seen as the objectively existing natural numbers and their properties [and studied by a branch of mathematics (also) called "number theory"]). This deserves some further exploration and explicitation, but, in order not to interrupt the present course and discussion in Hofstadter's Chapter, we postpone it until this course and discussion has come to a close (The end of the present document). If the reader, during rereading perhaps, whishes to further focus on the matter of the origin of the rules of formal systems encoded in number theory, he or she may click HERE .]
The Boomerang : Gödel-numbering TNT
Of course things do not stop here. We have only begun realizing the potential of Gödel's isomorphism. The natural trick would be to turn TNT's capability of mirroring other formal systems back on itself. In order to do this, we will have to Gödel-number TNT itself, just as we did the MIU-system, and then "arithmetize" its rules of inference. The Gödel-numbering is easy to do. For instance, we could make the following correspondence :
Symbol Codon
0 ........... 666
S ........... 123
= ........... 111
+ ........... 112
 ........... 236
........... 236
( ............ 362
) ............ 323
< ........... 212
> ........... 213
[ ............ 312
] ............ 313
a ........... 262
' ............ 163
 ......... 161
......... 161
 ......... 616
......... 616
==> ...... 633
- .......... 223
 .......... 333
.......... 333
 .......... 626
.......... 626
: ........... 636
punc. ....... 611
Each symbol of TNT is matched up with a triplet composed of the digits 1, 2, 3, and 6, in a manner chosen for mnemonic value. I shall call each such triplet of digits a Gödel codon or codon for short. Notice that I have given no codon for b, c, d, or e. We are using austere TNT. [thus a' in the austere version stands for b of the less austere version. a'' for c, etc.]. There is a hidden motivation for this, which you will find out about in Chapter XVI. [In that Chapter Hofstadter is going to compare (and match) TNT with the DNA molecular biology : There, among other things, the 20 amino acids are compared with the symbols of TNT, and, indeed, by using austere TNT, we have exactly 20 TNT-symbols (apart from punctuation).]
I will explain the bottom entry, "punctuation", in Chapter XIV.
Now we can rewrite any string or rule in TNT in the new garb. [Until now, the rules being rewritten only as to the numerals that occur in them. For their complete arithmetization, see below]. Here, for instance, is Axiom 1 (of TNT ) in the two notations, the old below the new :
626,262,636,223,123,262,111,666
 a : - S a = 0
a : - S a = 0
Conveniently, the standard convention of putting in a comma every third digit happens to coincide with our codons, setting them off for "easy" legibility. [meaning that these commas in fact do not belong to the transcription]
And here is the Rule of Detachement, in the new notation :
Rule : If x and 212x633y213 are both theorems, then y is a theorem.
[In (not complete) TNT-notation it was : If x and < x ==> y > are both theorems, then y is a theorem]
[As to complete arithmetization of the Rules of TNT, see below]
Finally, here is an entire derivation taken from last Chapter (here, from the previous document), given in austere TNT and also transcribed into the new notation. But before we do so we reproduce the derivation made in the previous document :
 a :
a :  b : (a+Sb) = S(a+b) (axiom 3)
b : (a+Sb) = S(a+b) (axiom 3)
 b : (S0+Sb) = S(S0+b) (specification, S0 for a )
b : (S0+Sb) = S(S0+b) (specification, S0 for a )
 a : (a+0) = a (axiom 2)
a : (a+0) = a (axiom 2)
 a :
a :  a' : (a+Sa') = S(a+a') (axiom 3)
a' : (a+Sa') = S(a+a') (axiom 3)
 a' : (S0+Sa') = S(S0+a') (specification, S0 for a )
a' : (S0+Sa') = S(S0+a') (specification, S0 for a )
 a : (a+0) = a (axiom 2)
a : (a+0) = a (axiom 2)
 a :
a :  a' : (a+Sa') = S(a+a')
a' : (a+Sa') = S(a+a')
 a' : (S0+Sa') = S(S0+a')
a' : (S0+Sa') = S(S0+a')
 a : (a+0) = a
a : (a+0) = a
TNT-Numbers : A Recursively Enumerable Set of Numbers
Looked at this way, the preceding derivation of the theorem "362,123,666,112,123,666,323,111,123,123,666" is a sequence of highly convoluted number-theoretical transformations, each of which acts on one or more input numbers, and yields an output number, which is, as before, called a producible number, or, to be more specific, a TNT-number. Some of the arithmetical rules take an old TNT-number and increase it in a particular way, to yield a new TNT-number. Some take an old TNT-number and decrease it. Other rules take two TNT-numbers, operate on each of them in some odd way, and then combine the results into a new TNT-number -- and so on and so forth. [As an example of the latter transformation we can see the Rule of Joining : If x and y are theorems of the system (Here [that is, not in the Propositional Calculus, but in TNT ], if x and y are TNT-numbers), then so is the string < x y > (a TNT-number)]. And instead of starting with just one known TNT-number, we have five initial TNT-numbers -- one for each (austere) axiom (where b is replaced by a'), of course. Arithmetized TNT [recall that TNT originally is purely typographic !] is actually extremely similar to the arithmetized MIU-system, only there are more rules and axioms, and to write out arithmetical equivalents explicitly would be a big bother -- and quite unenlightening, incidentally. If you followed how it was done for the MIU-system (previous-previous document), there ought to be no doubt on your part that it is quite analogous here.
y > (a TNT-number)]. And instead of starting with just one known TNT-number, we have five initial TNT-numbers -- one for each (austere) axiom (where b is replaced by a'), of course. Arithmetized TNT [recall that TNT originally is purely typographic !] is actually extremely similar to the arithmetized MIU-system, only there are more rules and axioms, and to write out arithmetical equivalents explicitly would be a big bother -- and quite unenlightening, incidentally. If you followed how it was done for the MIU-system (previous-previous document), there ought to be no doubt on your part that it is quite analogous here.
There is a new number-theoretical predicate brought into being by this "Gödelization" of TNT : the predicate
[This is a sentence about TNT. It means : "The Gödel number, that here is succinctly indicated by 'a', is, within the Gödelization of TNT, producible". This sentence will also be expressible in TNT-notation.]
For example, we know from the preceding derivation that 362,123,666,112,123,666,323,111,123,123,666 is a TNT-number, while on the other hand, presumably 123,666,111,666 is not a TNT-number [the latter is in TNT-notation : S0 = 0 ("one equals zero"), which is not a theorem of TNT].
Now it occurs to us that this new number-theoretical predicate is expressible by some string of TNT with one free variable, say a. We could put a negation sign in front, and that string would express the complementary notion
Now if we replaced all the occurrences of a in this second string [as it is assumed to be fully translated in the language of TNT, in which translation a will obviously repeatedly occur] by the TNT-numeral for 123,666,111,666 -- a numeral which would contain exactly 123666111666 S's, much too long to write out -- we would have a TNT-string which, just like MUMON, is capable of being interpreted on two levels. In the first place, that string would say
But because of the isomorphism which links TNT-numbers (TNT-producible numbers) to theorems of TNT, there would be a second-level meaning of this string, which is :
[It is instructive also to consider the affirmative version in this respect :
because (of course) the duality of meaning is also present in it. If we specify a to be, for example, 362,123,666,112,123,666,323,111,123,123,666 (which means : (S0+S0) = SS0, which in turn means : "one plus one equals two"), and which is produced by TNT, then we have :
362,123,666,112,123,666,323,111,123,123,666 is a TNT-number.
This sentence is a number-theoretical statement (that is, a statement in N) about 362,123,666,112,123,666,323,111,123,123,666, namely that this number can be produced from the Gödelized axioms of TNT (which are then not TNT-strings, but just numbers) and the Gödelized and arithmetized production rules of TNT.
And if we now replace the number 362,123,666,112,123,666,323,111,123,123,666 by 362123666112123666323111123123666 S's followed by a 0 (and thus having transcribed the number in TNT-notation), and if we also express the rest of this statement "is a TNT-number" in TNT-notation (difficult, but possible), then we obtain a pure TNT-string with two passive meanings :
SSSSSSSSSSSSSSS................S0 is a TNT-number ("is a TNT-number" in TNT-notation).
Thus, this TNT-string says something about another TNT-string, namely (S0 + S0) = SS0, namely that it is a theorem of TNT.
TNT tries to Swallow Itself
This unexpected double-entendre demonstrates that TNT contains strings which talk about other strings of TNT. In other words, the metalanguage in which we, on the outside, can speak about TNT, is at least partially imitated inside TNT itself [This "partially" probably points to the fact that not the complete meta-TNT can be mirrored in TNT]. And this is not an accidental feature of TNT. [While, as we saw above, TNT can speak about other formal systems such as the MIU-system ( but see POSTSCRIPT below ), it now turned out that it can also speak about itself.]. It happens because the architecture of any formal system can be mirrored inside N (number theory). It is just as inevitable a feature of TNT as are the vibrations induced in a record player when it plays a record. It seems as if vibrations should come from the outside world -- for instance, from jumping children or bouncing balls. But a side effect of producing sounds -- and an unavoidable one -- is that they wrap around and shake the very mechanism which produces them. It is no accident. It is a side effect which cannot be helped. It is in the nature of record players. And it is in the nature of any formalization of number theory that its metalanguage is embedded within it.
We can dignify this observation by calling it the Central Dogma of Mathematical Logic, and depicting it in a two-step diagram :
In words : A string of TNT has an interpretation in N. And a statement of N may have a second meaning as a statement about TNT.
[The above Central Dogma of Mathematical Logic can be expressed more comprehensively :
For example (from top to bottom) :
[For us, here on this website, this phenomenon of the -- still weak form of -- self-reference by the system (namely that some of its strings speak about other strings of it) is very important, because we now may safely assume that all other comparatively strong formal systems will possess this capability too, and so thus also the formal system of noëtic strategy-strings in the Implicate Order, meaning that strategies can speak about other strategies. But for Mathematics and Logic the next to be discussed intensification of self-reference of TNT is more important, because Gödel's theorem follows from it. In what way this might have important implications also for our ontologized formal system of noëtic strategy-strings I do not yet know. I doubt that it has much importance, but it has still to be investigated. And for an understanding of formal systems in general Gödel's theorem is important (and interesting) anyway.]
G : a String Which Talks about Itself in Code
This is intriguing yet it is only half the story. The rest of the story involves an intensification of the self-reference. We are now at the stage where [Hofstadter referring to the dialogue preceding the Chapter] the Tortoise was when he realized that a record could be made which would make the phonograph playing it break [by resonance] -- but now the question is : "Given a record player, how do you actually figure out what to put on the record?" That is a tricky matter.
We want to find a string of TNT -- which we'll call 'G' -- which is about itself, in the sense that one of its passive meanings is a sentence about G. In particular the passive meaning will turn out to be
I should quickly add that G also has a passive meaning which is a statement of number theory. Just like MUMON it is susceptible to being construed in (at least) two different ways. The important thing is that each passive meaning is valid and useful and doesn't cast doubt on the other passive meaning in any way. ( The fact that a phonograph playing a record can induce vibrations in itself and in the record does not diminish in any way the fact that those vibrations are musical sounds !)
G's Existence Is What Causes TNT 's Incompleteness
The ingenious method of creating G, and some important concepts relating to TNT, will be developed in Chapters XIII and XIV. For now it is just interesting to glance ahead, a bit superficially, at the consequences of finding a self-referential piece of TNT. Who knows? It might blow up ! In a sense it does. We focus down on the obvious question :
Let us be sure to form our own opinion on this matter, rather than rely on G's opinion about itself. After all, G may not understand itself any better than a Zen master understands himself. Like MUMON, G may express a falsity. Like MU, G may be a nontheorem. We don't need to believe every possible string of TNT -- only its theorems. Now let us use our power of reasoning to clarify the issue as best we can at this point.
We will make our usual assumption : that TNT incorporates valid methods of reasoning, and therefore that TNT never has falsities for theorems. In other words, anything which is a theorem of TNT expresses a truth. So if G were a theorem, it would express a truth, namely : "G is not a theorem". The full force of its self-reference hits us. By being a theorem, G would have to be a falsity. Relying on our assumption that TNT never has falsities for theorems, we'd be forced to conclude that G is not a theorem. This is all right. It leaves us, however, with a lesser problem. Knowing that G is not a theorem, we'd have to concede that G expresses a truth. Here is a situation in which TNT doesn't live up to our expectations -- we have found a string which expresses a true statement yet the string is not a theorem. And in our amazement, we shouldn't lose track of the fact that G has an arithmetical interpretation too -- which allows us to summarize our findings this way :
A string of TNT has been found. It expresses, unambiguously, a statement about certain arithmetical properties of natural numbers. Moreover, by reasoning outside the systm we can determine not only that the statement is a true one, but also that the string fails to be a theorem of TNT. And thus, if we ask TNT whether the statement is true, TNT says neither yes nor no.
Recall, from the previous-previous document that the MIU-system is a typographic formal system consisting of the symbols M, U, and I, the given string (axiom) MI, and the following typographical rules by which other strings (theorems) can be derived :
and by arithmetizing its rules :
As a number-theoretical statement it reads :
where "a MIU-number" means "a MIU-producible number".
Of course, number theory does not a priori know what "a MIU-producible number" is. So in the number-theoretical statement this must be described. Let us try to do so by using the transcribed axiom and the arithmetized rules of the MIU-system :
First we do this in a global way :
If we take the number 31 (transcribed axiom of the MIU-system) and take into account the arithmetical rules I and II, then we can produce the number 31010.
And now in a more detailed version, using some logical symbols :
 rule I
rule I  rule II > ==> 31010 >
rule II > ==> 31010 >And because number theory does not know what these rules are, we must put things in a still more detailed way (where 'x' means 'times') :
< < 31  < 10m + 1 ==> 10 x (10m + 1) >
< 10m + 1 ==> 10 x (10m + 1) >  < 3x10m + n ==> 10m x (3x10m + n) + n > > ==> 31010 >
< 3x10m + n ==> 10m x (3x10m + n) + n > > ==> 31010 >
But the value of the variable m is in the present case different in the application of the two rules. To apply rule I, m must be specified as 3, while to apply rule II, m must be specified as 2. So we have to name this variable differently, we chose m and m' :
< < 31  < 10m + 1 ==> 10 x (10m + 1) >
< 10m + 1 ==> 10 x (10m + 1) >  < 3x10m' + n ==> 10m' x (3x10m' + n) + n > > ==> 31010 >
< 3x10m' + n ==> 10m' x (3x10m' + n) + n > > ==> 31010 >
The variable n does not appear in rule I, but it does so in rule II. Its value must be 10.
So specifying the variables m, m', and n, with respectively 3, 2, and 10, we get :
< < 31  < 30 + 1 ==> 10 x (30 + 1) >
< 30 + 1 ==> 10 x (30 + 1) >  < 3x102 + 10 ==> 102 x (3x102 + 10) + 10 > > ==> 31010 >
< 3x102 + 10 ==> 102 x (3x102 + 10) + 10 > > ==> 31010 >
and further worked out we get :
< < 31  < 31 ==> 310 >
< 31 ==> 310 >  < 310 ==> 100 x 310 + 10 > > ==> 31010 >
< 310 ==> 100 x 310 + 10 > > ==> 31010 >
And still further worked out we, finally, get :
 < 31 ==> 310 >
< 31 ==> 310 >  < 310 ==> 31010 > > ==> 31010 >
< 310 ==> 31010 > > ==> 31010 >So this is the full number-theoretic statement saying that 31010 is a MIU-producible number, and, according to its second-level meaning, saying that MIUIU is a theorem of the MIU-system.
However, this conclusion is a bit rash, as the following considerations will show.
The last formula is in effect the following statement :
It is directly evident that this statement, so formulated, is true (according to the Rule of Detachment : if x and < x ==> y > are both theorems, then y is a theorem) [ The statement expresses only a special case, that is, a particular instance, of what the Rule of Detachment expresses generally]. And thus the TNT translation of the above string -- < < 31  < 31 ==> 310 >
< 31 ==> 310 >  < 310 ==> 31010 > > ==> 31010 > -- must appear as a theorem of TNT. And when we see this theorem (among all the other theorems of TNT ) we immediately recognize the fact that 31010 is a MIU-producible number, because (1) we recognize "31" as the (transcribed) axiom of the MIU-system, (2) we recognize "< 31 ==> 310 >" as Rule I of that same system (see ABOVE ), and (3) we recognize "< 310 ==> 31010 >" as Rule II of that system. We in fact see that MIUIU is a theorem of the MIU-system.
< 310 ==> 31010 > > ==> 31010 > -- must appear as a theorem of TNT. And when we see this theorem (among all the other theorems of TNT ) we immediately recognize the fact that 31010 is a MIU-producible number, because (1) we recognize "31" as the (transcribed) axiom of the MIU-system, (2) we recognize "< 31 ==> 310 >" as Rule I of that same system (see ABOVE ), and (3) we recognize "< 310 ==> 31010 >" as Rule II of that system. We in fact see that MIUIU is a theorem of the MIU-system.
But although TNT can see that 31010 necessarily follows from a given 31 and the two implications, and thus having the whole statement
(when properly translated into TNT-language) as one of its theorems, it cannot recognize the number "31" as the axiom of precisely the MIU-system, nor can it recognize that "< 31 ==> 310 >" is (an instance of) Rule I of precisely that system, and it can also not recognize "< 310 ==> 31010 >" as (an instance of) Rule II of that system. So we cannot hold that there is a TNT-string that says :
Let us illustrate this further. If we had the following statement :
 < 31 ==> 310 >
< 31 ==> 310 >  < 310 ==> 3101010 > > ==> 3101010 >
< 310 ==> 3101010 > > ==> 3101010 >then (when transcribed into TNT-notation) it would also be one of the theorems of TNT (according to that same Rule of Detachment). But in this case "< 310 ==> 3101010 >" does not correspond with any rule of the MIU-system. But this cannot be discerned by TNT. And indeed, 3101010 is not an MIU-producible number. Also this TNT cannot discern.
Yet another example might be following :
If we had the statement :
 < 30 ==> 300 >
< 30 ==> 300 >  < 300 ==> 3 > > ==> 3 >
< 300 ==> 3 > > ==> 3 >
we would recognize in "< 30 ==> 300 >" Rule II of the MIU-system. Likewise we would recognize in "< 300 ==> 3 >" Rule IV of the MIU-system. But we would also directly see that "30" is not the axiom of the MIU-system, and neither can it be a theorem ( This we are sure of, because we know that MU is not a theorem of the MIU-system.). Also 3, although it follows from < 30  < 30 ==> 300 >
< 30 ==> 300 >  < 300 ==> 3 > > (Rule of Detachment), is not an MIU-producible number ( M is not a theorem [neither is it an axiom] of the MIU-system). But all this cannot be detected by TNT.
< 300 ==> 3 > > (Rule of Detachment), is not an MIU-producible number ( M is not a theorem [neither is it an axiom] of the MIU-system). But all this cannot be detected by TNT.
The here established fact that TNT cannot speak about the MIU-system (because it cannot distinguish between things belonging to this system and those that do not) (and generally about any other formal system different from TNT itself) runs counter some of Hofstadter's assertions. Let us reproduce what he said in this respect (already produced at the beginning of the present document) :
Could it be, therefore, that the means with which to answer any question about any formal system lies within just a single formal system -- TNT ? It seems plausible. Take, for instance this question :And we -- the author of this website -- had found out that TNT is not capable of "speaking in code about the MIU-system". Although I am not a professional mathematician or logician, I think that my conclusion is valid or, in any case, I take into account that it might be correct. Of course TNT contains all the derivations in the MIU-system, but cannot distinguish them from derivations in other systems. So we may perhaps say that TNT speaks about the MIU-system (only) implicitly (and in so far Hofstadter is right). It is in fact we [the knowing subject] who recognize that it does so.
Is MU a theorem of the MIU-system? Finding the answer is equivalent to determining whether 30 is a MIU-number (that is, a MIU-producible number) or not. [30 is the overall Gödel number of the string MU which overall Gödel number resulted by assigning (arbitrary) numbers -- Gödel numbers -- to the symbols of the MIU-system, as was established in the first intermezzoing document.]. Because it is a statement of number theory (N), we should expect that, with some hard work, we could figure out how to translate the sentence "30 is a MIU-number" into TNT-notation, in somewhat the same way as we figured out how to translate other number-theoretical sentences into TNT-notation. I should immediately caution the reader that such a translation, though it does exist, is immensely complex. If you recall, I pointed out [...] that even such a simple arithmetical predicate "b is a power of 10" is very tricky to code into TNT-notation -- and the predicate "b is a MIU-number" is a lot more complicated than that! Still, it can be found, and the numeral SSSSSSSSSSSSSSSSSSSSSSSSSSSSSS0 [30 S's and 0] can be substituted for every b (where it appears in the resulting TNT-string). This will result in a MONstrous string of TNT, a string of TNT which speaks about the MU-puzzle. Let us therefore call that string "MUMON". Through MUMON and strings like it, TNT is now capable of speaking "in code" about the MIU-system.
On the other hand, when we 'Gödelize' TNT itself (and arithmetize its rules) then we find (with Hofstadter) that TNT can speak about itself. It then speaks by its metalanguage, and its metalanguage is embedded within it. And it is clear that the metalanguage of TNT cannot be such that in and through it it can speak about another formal system.
So what we have found is that although TNT, and thus number theory itself, cannot in its strings explicitly speak about other formal systems, it can speak about itself.
If we now think of the "formal system of noëtic strategy-strings" (FSNSS) residing in the Implicate Order, we can hold that --like it was the case with the MIU-system -- (the essence of) number theory (as the objectively existing natural numbers and their properties) cannot speak about FSNSS. It cannot recognize its axioms and especially not its production rules. And while the axioms can come from within the Implicate Order (without them being recognized as such by that Order) the rules are, like the rules of the MIU-system, extrinsic to (ontological) number theory, and therefore as regards their origin, extrinsic to the Implicate Order. They must therefore come from the Explicate Order.
We can analyze the relation between the MIU-system and TNT still further :
Above we had the true statement
 < 31 ==> 310 >
< 31 ==> 310 >  < 310 ==> 31010 > > ==> 31010 >
< 310 ==> 31010 > > ==> 31010 >
In it the elements < 31 ==> 310 > and < 310 ==> 31010 > are not "logical", that is, not any of the Rules of TNT (which are [its] logical rules) legitimizes these two transformations, that is a transformation of 31 into 310, and of 310 into 31010 ( They are legitimized not by logical or rational reasons but by the particular rules of the MIU-system). But the derivation 31010 from 31 is logical (is rational), because, given 31, and given both < 31 ==> 310 > and < 310 ==> 31010 >, logically implies that then 31010 will be obtained (according to the logical Rule of Detachment). So within the (arithmetized) MIU-system the derivation of the number 31010 from the number 31 is logical or rational in its nature, and consequently also the derivation of the string MIUIU from the string MI. These derivations are therefore ultimately based on TNT, that is, on TNT's logical production rules. This is precisely the way the MIU-system is implemented in number theory. The same, then, can be said of our supposed "formal system of noëtic strategy-strings", residing in the Implicate Order : This system has its own rules (ultimately coming from the Explicate order) but is nevertheless implemented in ontological number theory, meaning that the derivations in it of (everytime) a strategy-string from another are logical, that is, take place according to logical rules (namely those of ontological TNT ).
This may suggest that the logical rules of TNT are, or reflect, the basic structure of the Implicate Order (and thus not only reflect the basic structure of mathematical number theory). That is, if we suppose that there is indeed something like "ontological number theory" -- the objectively existing natural numbers and their properties -- (studied by "mathematical number theory" by means of its formalization, TNT ), and if we suppose, moreover, that the Implicate Order is in fact ontological number theory, then we must admit that the logical rules of TNT are, or more or less reflect, the basic structure of the Implicate Order. So, although the particular form in which mathematicians created TNT and its rules of inference does not necessarily need to be the form in which it really exists in the Implicate Order, it is at least a possible representation (of ours) of the basic logical structure of the Implicate Order [Perhaps, because no human knowledge is considered here, we may replace "logical structure" by "rational structure"]. And in this sense we can legitimately speak of "ontological TNT ". And because we do not know the particular form in which TNT (as the essence of ontological number theory) actually exists in the Implicate Order, all we can do is simply assume that the form in which TNT is created by mathematicians actually is the from in which it exists in the Implicate Order. There is, probably a small number of slightly different forms in which number theory is, and was, formalized by mathematicians, but that is not really important. We chose the form in which it is presented by Hofstadter, and which is expounded in the previous document. Being so, we can then assume that the very rules of TNT, as formulated by Hofstadter, are actually present in the Implicate Order as to their very content. And as to what specific symbols are chosen here, such as S, 0, <, >,  ,
,  , ==>, a, ', [, ],
, ==>, a, ', [, ],  ,
,  , -, :, etc., is not substantial. It is not known, but also not important, what symbols actually figure in ontological TNT.
, -, :, etc., is not substantial. It is not known, but also not important, what symbols actually figure in ontological TNT.
So we can say that the very basic structure of the Implicate Order is ontological TNT and its logical rules, as we see them in Hofstadter's presentation of them.
In our noëtic theory we have taken the freedom to assume that there are objectively existing structures (ranging from immaterial to material) that are, in their overall general structure, that is, as to their type, completely isomorphic with a typographical formal system as such systems are forged in conventional mathematics and mathematical logic. [ That is, we hypothetize that certain formal systems, or certain types of formal systems, as they have been created in mathematics and in mathematical logic, do actually exist in rerum natura (in the real world), and thus appear not only in the usual cognitive fashion but also appear ontologically.] For many a researcher this may sound too hypothetic to swallow. I can imagine that. But I want to place organic evolution in precisely such a metaphysical context (by assuming the Implicate and Explicate Orders) in order to account for all of the 'sophisticated' adaptations, typogeneses and anageneses ('higher-developments') that are encountered in it. Many, if not all, of such adaptations, typogeneses, and anageneses, seem to defy any explanation in terms of the material world alone (and that is, in terms of random genetic mutations and natural selection). I did not, however, seek for one or another mystical explanation by assuming some deity-like "higher order" that allegedly had forged all this : The Implicate and Explicate Orders are not supposed to be ontologically completely separate domains : they are in constant interaction by the assumed processes of injection and projection (that is, 'traffic' across their common boundary). Indeed, we had just established that the derivational rules of the formal system of noëtic strategy-strings (FSNSS) cannot have been originated (derived) from the Implicate Order itself, but must in some way have come from the Explicate Order, that is, from the material space-time world.
With this background, now we are in a position to draw an elaborate comparison between F. Crick's "Central Dogma of Molecular Biology" (.DOGMA I ) upon which all cellular processes are based, and what I, with poetic license, call the "Central Dogma of Mathematical Logic" (.DOGMA II ), upon which Gödel's Theorem is based. The mapping from one onto the other is laid out in the next chart, forming the Central Dogmap. [where mRNA = messenger RNA, N = number theory, TNT = formalized number theory, and meta-TNT is the language in which TNT speaks about itself.]
.DOGMA I .DOGMA II
(Molecular Biology) (Mathematical Logic)
strands of DNA <====> strings of TNT
strands of mRNA <====> statements of N
proteins <====> statements of meta-TNT
proteins which act on proteins <====> statements about statements of meta-TNT
proteins which act on proteins which act on proteins <====> statements about statements about statements of meta-TNT
transcription ( DNA ==> RNA ) <====> interpretation ( TNT ==> N )
Translation ( RNA ==> proteins) ==> Arithmetization ( N ==> meta-TNT )
Crick <====> Gödel
Genetic Code (arbitrary convention) <====> Gödel Code (arbitrary convention)
codon (triplet of bases) <====> codon (triplet of digits)
amino acid <====> quoted symbol of TNT used in meta-TNT
self-reproduction <====> self-reference
sufficiently strong cellular support system to permit self-rep <====> sufficiently powerful arithmetical formal system to permit self-ref
All this will certainly provide inspiration to further develop the ontologization of certain relevant formal systems, in order to increase our understanding of things inside the Implicate Order and of its relationship with the Explicate Order. We will do that in future documents. In the second half of part IIIaa in Sixth Part of Website (on palaeo-entomology), we have summarized, slightly amended, and further worked out all what has been said about formal systems and the reception of some of them in our noëtic theory of evolution in the parts LXa, LXb, and LXc of the present series of documents.
Summary of Noëtic Theory (so far developed)
It is perhaps instructive to take stock of our findings in our noëtic theory of evolution as we now have it.
And because it is a summary that is presented here, it is natural that some earlier insights are presented in a transformed state, while others are simply repeated. Our theory is about organisms, their morphology, physiology, and behavior, and especially their evolution. All these typically organic features are placed and integrated in a broader metaphysical context in order to "rationalize" them, because the latter cannot, it seems, be accomplished when only one range of Being -- the material world -- is assumed.
The very element in our noëtic theory of organic evolution that will be expected to be the most controversial in the scientific establisment is the fact that I consider Reality to consist, not of one, but of two (interacting) Orders of Being, viz., the Explicate Order (the whole World or Universe of most scientists) and the Implicate Order (an extra Order assumed to exist by scientists such as BOHM and [in some form] by SHELDRAKE). So we must present good arguments in favor of such a supposition, that is, in favor of the objective existence of the Implicate Order. And in fact, in all the foregoing of the present Main Part of Website (Fifth Part) we have taken the facts of evolution (and the failure of Neodarwinism to explain it) as a strong indication of the existence of a noëtic order (Implicate Order) alongside a material order (Explicate Order). But not only the evolution of organisms provides such an indication, but also their very constitution, in the sense of representing the Organic World as such, and that is, Life as such. In Fourth Part of Website we discussed the possible layering of Reality into, not ontological, but complexity layers. The First Layer was the "Mathematical Layer", and from this most fundamental Layer the other Layers (such as the Physical [s.str.] and the Organic Layer) succesively originated by a discontinuous process of "functional complexification". And already there we said that the "Mathematical Layer" might be equivalent to (a modified version of) HARTMANN's Ideal Sphere of Being, and also to (a modified version of) BOHM's Implicate Order. Each complexity Layer was (in Fourth Part of Website) characterized by its own set of special "determinants" : "categories" or (equivalently), "If / Then constants" (in addition to the set of common -- fundamental -- such determinants). In Fourth Part of Website we extensively investigated the fundamental (or almost fundamental) categories concerning SHAPE, SYMMETRY, and PROMORPH of intrinsic beings in the mathematical as well as in the physical and organic layers.
If we go, not actually, but formally, from one such layer to the one 'above it', that is, from a less complex one (i.e. one which sustains only less complex beings) to a fundamentally more complex one (one that sustains more complex beings), we have to assume a so-called NOVUM to appear, that is, some totally new category, that 'over-forms' many of the other categories that cross over into this 'higher' layer from the lower one. This 'theory of the NOVUM' not only appears in our theory of Complexity Layers, but in fact in any theory that purports to give an account of the origin of Life from inorganic beginnings. And for us, it is this NOVUM that points us to the Implicate Order.
So in order to provide the present summary of our noëtic theory of evolution with an extra argument in favor of the existence of the Implicate Order, let us reproduce here what we have written in part XXIX Sequel-1 of Fourth Part of Website :
On the Transformation of the Organic into the Inorganic :
The Inorganic as the result of a
h o l i s t i c s i m p l i f i c a t i o n of the Organic.
The theory of Layers of Being, as presented on this website (and inspired by, and partly based on, the philosophy of Nicolai HARTMANN ), can still be discussed further, as to its general validity or falsity, when we concentrate on the division between the Inorganic and the Organic. These can be related to each other in four different ways, that is, viewpoints :
The Theory of the Implicate Order is extensively considered in Third Part of Website .
The theory boils down to the assumption that all things, apparently separated in space and / or time, are manifestations of one single dynamic whole, like the waves of an ocean. These things are projections from that whole -- which is called the Implicate Order -- into their states of separatenes, which collectively is called the Explicate Order. The mentioned things can also return from the Explicate (unfolded) Order to the Implicate (enfolded) Order, which is called injection. The Explicate Order is our observable world of things, space and time. What we see happening in this Order are physical processes and transformations. But these are only manifestations of a much more fundamental 'process', namely the dynamics of sustained projection and injection of aspects of the Implicate order. So all things in the Explicate Order are connected with each other in subtle ways via the Implicate Order. The way of being of this Implicate Order is not that of a material world with things separated in space and / or time, but a world in which everything is folded together, i.e. a world in which every 'thing' interpenetrates every other 'thing'. We will call this way of being noëtic which means 'thought-like'. We can think of it as being some kind of proto-intelligence. We can also compare it to Nicolai HARTMANN's Ideal Sphere of Being (See Part I of the present Series [ Fourth Part of Website] ) or to our Mathematical Layer of Being (See also Part I of the present Series). So all the transformations that take place within the Implicate Order are 'thought-like'. Moreover, we assume them to be timeless (especially with respect to our (physical) time). So in fact those transformations are of a logical nature, not of a physical one. At its most fundamental, the Implicate Order is represented by the 'Holomovement' which is absolute unity.
This whole philosophical idea is mainly from the quantum physicist David BOHM, and it is, in its bottom line, very akin (though not mentioned by him) to the metaphysics of the Greek philosopher PLOTINUS in the third century A.D. In the latter metaphysics it is assumed that from "The One", which is unity in an absolute sense, some lower 'hypostases' (reality levels) emanate, ending up in the lowest 'hypostasis', namely that of the material world. So also here we see that the lower forms evolve from higher forms.
Well, the above assumed transition from Organic to Inorganic, cannot, as established above, take place within the physical universe, which we now can translate as such a transition not being possible in the Explicate Order (which is, it is important to realize, just an aspect of the Whole). But it can take place in the Implicate Order, because a transition from Organic to Inorganic can now be seen as a (logical) d e r i v a t i o n , namely by just eliminating the NOVUM and (automatically) with it, all that it entails. This we call Holistic Simplification from the Organic to the Inorganic, i.e. the Inorganic is a holistic simplification of the Organic (as was first proposed by MEYER-ABICH, A., in Naturphilosophie auf neuen Wegen, 1948). This simplification is thus a noëtic process, taking place in the Implicate Order in a space- and timeless fashion. The explicitation of this process, i.e. its appearance in the Explicate Order, must take place in r e v e r s e order : namely from Inorganic to Organic, because (as we now assume) the explicate Organic presupposes explicate Inorganic : To become explicate Organic, the implicate Organic needs an appropriate material substrate. This latter substrate must already be present in the Explicate Order and can now be over-formed by the implicate Organic, resulting in explicate Organic. So what we see in the Explicate Order (observable world) is the apparent emergence of the Organic from pre-existent Inorganic, while in fact the Inorganic was derived from the Organic in the Implicate Order by Holistic Simplification. In this way we have circumvented the problem of the NOVUM (but, of course, at a price of introducing a hypothetical entity, the existence of which must be demonstrated).
Because Holistic Simplification will play an important role in the ensuing discussion, let us give some instructive examples :
We can never derive the corresponding colored version from a given black-and-white picture (that intended to express a scene that originally had certain colors). The corresponding colored picture is more than its black-and-white version . We can, however, easily derive the black-and-white version from the corresponding colored picture, namely by taking a photograph of the latter with a black-and-white film. The latter process -- from colored picture to black-and-white version -- is a genuine holistic simplification.
A second example of holistic simplification concerns geometry. See next Figure.
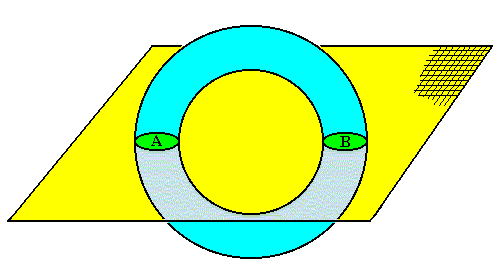
Figure above : A three-dimensional donut-shaped solid object (blue) is intersected by a plane (yellow). The product of the intersection is two areas A and B, which are each two-dimensional. While one cannot unequivocally derive the donut-shaped object from the areas A and B (they give us not enough information as to what the corresponding three-dimensional object will be), we can derive the areas A and B from the donut-shaped object, because those areas are already implicitly present in that object. If we intersect this object by a plane containing its axis of rotation, we obtain the areas A and B. This operation is nothing less than obtaining the areas A and B by holistic simplification of the donut-shaped object. Also here the latter is more than the former, and cannot be derived from it.
The general line of argument here is in fact the following : If it can be shown that the Organic cannot in any way be reduced to the Inorganic, which here should mean not only epistemologically, but also ontologically, then we must assume the appearance of a NOVUM when we formally go from the Inorganic to the Organic. In all this we must realize what precisely "cannot in any way be reduced" means, a slogan that is often enough heard, without, however, any discussion about what such a position entails. One speaks about dynamical systems that are self-organizing, and create patterns and structures that are not to be found in the initial conditions of the system. Such patterns are called emergent. And of course the Organic contains such emergent properties which are absent in the Inorganic. But when these properties have ultimately been produced from inorganic dynamical systems, they can be called "emergent" but they do not represent a genuine NOVUM, because they have (physically) been derived from the dynamical system, i.e. totally from within the dynamical system, which means that such properties were already present in the Inorganic, albeit only implicitly so. And in this case, of course, the Organic -- as represented by its emergent properties -- is reducible to the Inorganic, because it was actually produced by (and thus derived from) the Inorganic (which was represented by the dynamical system that produced these properties). So if one claims to adhere to a true holism, i.e. to an anti-reductionism, in the case of organisms, as many authors do, then they must admit the appearance of a genuine NOVUM when we formally change from the Inorganic to the Organic. But then we must also admit that the Organic cannot have been evolved from the Inorganic, despite the fact of the many indications that it did so originate. We thus have a problem, but this problem can be solved by assuming the above mentioned Implicate Order. So if we are forced to assume a genuine NOVUM to appear when formally going from the Inorganic to the Organic, and if the only outcome from the then implied dilemma is the assumption of something like an Implicate Order (where the holistic simplification takes place), then we have a fairly good argument in favor of the existence of such an Implicate Order.
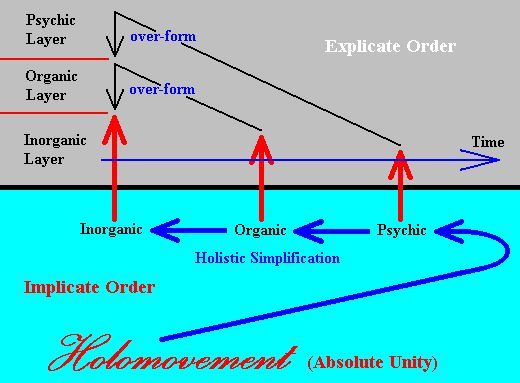
What we actually see in our observable world is a manifestation of a dynamics of continuous projection (from the implicate into the explicate), injection (from the explicate into the implicate), re-projection and re-injection. Only the explicate condition of Being is accessible to observation. We then see (or can deduce from theory and observation) successive stages of processes, for example crystallization, individual organic development, phylogenetic sequences, etc.
| Before we continue the present quotation from Fourth Part of Website, it is perhaps instructive to dwell a little longer on the subject of the NOVUM as it appears in the Organic Layer (when we conceptually pass over into the latter from the Inorganic Layer). As long as we remain in the Explicate Order (that is, as long as we exclude from our consideration the Implicate Order and the holistic simplication taking place there) we indeed encounter in the Organic Layer a NOVUM in its categorical make-up as compared to that of the Inorganic Layer. We had said that this NOVUM might be a general entitative constant or category determining in any intrinsic being of the Organic Layer the implication of its ability to discriminate between SELF and NOT-SELF. But this ability must be inherent in the dynamical law (which is a nexus category) that determines the succession of stages of individual development (morphogenesis). While in bacteria and the like there are hardly any such stages at all, there are many of them in the embryological and post-embryological development of multicellular organisms. Further we may say that such a dynamical law can be generalized, and then calling it the (general) "nexus organicus". And as such it may be an over-forming of the general dynamical law that causally connects the entities or beings of the Inorganic Layer, a law that might be called the (general) "nexus anorganicus". So we can, to begin with, assume the existence of a truly general inorganic nexus category, general in such a way as to not discriminate between continuous and discrete processes. When this general nexus category is over-formed it results in a general organic nexus category that generally determines organic development. We can further assume that this general organic nexus category contains, in addition to rather dominant discrete aspects, also continuous aspects. If this is correct the over-forming indeed involves general categories, that is to say, not only is the organic nexus a general category (of the Organic Layer), but the inorganic nexus category, of which it is an over-forming, is a general category as well, this time of the Inorganic Layer. And in this way we indeed have a truly general inorganic category that is over-formed, resulting in a truly general organic category, where in both cases "general" means general with respect to the given Layer, which in turn means that every concrete entity in such a Layer, is, without exception, subject to this category.
In First Part of Website we have argued that the dynamical law of the dynamical system that generates a b e i n g is equivalent to the ESSENCE of that being ["essence" in the metaphysical sense]. In fact such a dynamical law is, when that being is an organism, a special case of the (general) Nexus Organicus. So the Nexus Organicus is the g e n e r a l ESSENCE of an organism, which in fact means its being alive. So indeed the Nexus Organicus is the genuine NOVUM of the Organic Layer, because it is the l i v i n g condition. The kernel of this Nexus Organicus is the General Inorganic (discrete) Nexus Category. As over-forming of the latter the Nexus Organicus is the NOVUM of the Organic Layer of Being. And every special case of this (general) Nexus Organicus is the law, the special nexus-category, that determines the successive stages in the development of an individual of a given organismic species. And this individual development can only succeed when the law is such that it can discriminate between the SELF of the developing organism and the NOT-SELF. Only then it can select the proper causal factors and integrate them, and only them, in the initial conditions and the subsequent system-states of it.
|
|
Let us now summarize things concerning the categorical determination of organisms as strategies, and add a few more connections between concepts earlier established.
The dynamical law of the dynamical system that generates and maintains a given organism in the Explicate Order constitutes the Essence of that organism, where that "Essence" here forms the ontological kernel of every individual organism of the species to which this essence is typical, and where every organic individual is a true Substance in the metaphysical sense (in addition to inorganic Substances). This dynamical law is inherent in the ultimate elements of the dynamical system, that is, inherent in the particular (as always in the Explicate Order) initial condition of the developing organic individual, and that is again : inherent in the initial configuration of the system-elements. All this has been worked out in detail in First Part of Website .
For a further elaboration of the categorical NOVUM appearing in the Organic Layer, see part XXIX Sequel-24, in Fourth Part of Website . |
W'll now continue with our original quotation from part XXIX Sequel-1, also from Fourth Part of Website.
[...]
The introduction of the Implicate Order (and interpreted as the Mathematical Layer), as contrasted with the Explicate Order (consisting of the Inorganic, Organic, etc. Layers), brings our ontological scheme still more closer to that of HARTMANN : For him, our Mathematical Layer was a separate sphere of Being, the Ideal Sphere, which has its own way of being (its own modality), different from that of his "Real Sphere of Being" which, according to him consists of four Layers of Being, viz., the Inorganic, Organic, Psychic and Super-psychic Layers. Well, by identifying our Mathematical Layer with the Implicate Order, we now, like HARTMANN, contrast it with all the rest of Existence (i.e. the temporal Layers) taken together. And indeed, the Mathematical Layer, also in the form of the Implicate Order, has a fundamentally different way of being (a different modality), namely t i m e l e s s, i.e. different from that of the other Layers taken together, because these are t e m p o r a l.
We must realize that when it would unequivocally turn out that science is finally able to entirely reduce organisms to inorganic entities (and psychic organisms to non-psychic organisms), the idea of ontological Layers and the idea of the Implicate Order probably become superfluous, and should be abandoned. What is left at the most is the Mathematical Layer and the Time Layer, i.e. the former non-mathematical Layers taken together. And within the latter we still can see, it is true, some layering, but only in the form of complexity l e v e l s without ontological significance. Moreover, the Mathematical Layer then probably loses its ontological status : It will become just a way of description of Reality. Quite frankly, I personally am inclined to consider r e d u c t i o n i s m as being a way of seeing things closest to the truth, and thus adhering to an ontological reductionism (where the NOVUM turns into reductionistic complexification). There is, however, no hard evidence for it, apart from the fact that we know for sure that, as a temporal sequence, the Inorganic was first, while only after it the Organic had appeared (and, even later, the Psychic).
We should further realize, that r e d u c t i o n i s m is the only m e t h o d by which natural science can proceed, because a genuine u n d e r s t a n d i n g of any observed phenomenon is reducing it to simpler phenomena. In the individual development of organisms, and also in crystal growth, there are some indications of n o n - l o c a l i t y (distant parts being somehow correlated, however not by any sort of chemical or physical signal), implying w h o l e n e s s. Such phenomena are not intelligible (at least not when they occur in the macroscopic realm). And in such cases, altering the relevant scientific theories and methods will not help. The only thing one can do is to place the (reductionistic) scientific theories and methods in a broader philosophical or metaphysical context that admits of wholeness to be the case, and concede that all scientific theories are always, and in principle, no more than approximations, because they are necessarily reductionistic in character. A possible metaphysical context, fully allowing for Wholeness, is the Theory of the Implicate Order, as outlined above, and in the mentioned Third Part of Website.
( End of quotation from part XXIX Sequel-1 of Fourth Part of Website )
For more details the reader should consult this part as it is in Fourth Part of Website and which can be reached by the LINK just given.
Although in principle trying to comply with the tenets of current natural science, and thus to adhere as much as possible to a reductionistic interpretation of Reality, I found out, in Fourth Part of Website, that not only organisms possess a holistic constitution but also even some inorganic beings, namely crystals (as we saw it in snow crystals for instance). And such holistic features, if they truly exist, even in certain inorganic beings, go against a reductionistic interpretation of Reality, and point to the existence of the Implicate Order as did our findings concerning the formal transition from the inorganic to the organic. The holistic features found in snow crystals (and thus in all crystals) can also be explained by assuming the existence of the Implicate Order and the process of holistic simplification taking place there, and, upon projection, the reverse order -- reductionistic complexification -- of this process in the Explicate Order. But also here it is not in fact a reductionistic complexification but the appearance of a NOVUM -- now of a more special kind. And also here, as soon as we assume it to be in fact the result of holistic simplification in the Implicate Order, it is not a genuine NOVUM. And, also already in Fourth Part of Website, we found that the appearance of such more special NOVA takes place in organic evolution as well. So in the present Summary of our Noëtic Theory of Organic Evolution it will be instructive to quote from part XXIX Sequel-4 of Fourth Part of Website :
In Part XXIX Sequel-1 we have exemplified all this with the structural relationships between the Inorganic and the Organic : As we go, in the Explicate Order, from Inorganic to Organic, we encounter the appearance of a categorical NOVUM. This NOVUM, then modifies all or at least many of the other categories that have entered the Organic Layer from the Inorganic. And in this way clearly lets stand out the Organic Layer with respect to the Inorganic Layer.
All this is based on the discovery of holistic features in organisms, to which we were led by the strong indication of the impossibility of a complete reduction of the Organic to the Inorganic.
It turns out, however, that such non-reducibility also crops up within the Inorganic itself. As an example we have come up with the generation of snow crystals. And what we had found for snow crystals probably holds for all solid crystals whatsoever. We have found that the point symmetry of snow crystals is not just an implication of their Space Group (just by eliminating from the latter all translational elements) -- as such it is crystallographic point symmetry. The point symmetry of these crystals is not just the symmetry of the translation-free chemical motif, but also morphological point symmetry like we see in organisms (Organisms do not have Space Group symmetry, nor crystallographic point symmetry, but only morphological point symmetry). The structure of an organism is not based on a periodic point lattice, and so its point symmetry is not the symmetry of the translation-free residue of its structure. It is morphological point symmetry, expressing itself by the presence of macroscopically defined antimers (i.e. antimers with genuine, macroscopically visible, boundaries, which are not translationally repeated [as they are in crystals, and as metamers are in organisms] ).
It seems that snow crystals (but also crystals in general) and organisms are somehow subjected to a certain holistic feature : a form-equilibrium. This form-equilibrium then is a NOVUM, meaning that the overall intrinsic structure of an organism or of a crystal (generally of an intrinsic being) is not completely derivable from the interactions of its components or elements. These components, i.e. the system of interacting components, is a holistic simplification of this overall structure, taking noëtically place in the Implicate Order, while what we s e e m to see in the Explicate Order is the reductionistic complexification, i.e. it looks as if the overall structure of the organism or of a crystal is the result of the interaction of its material parts (and nothing more). But what we a c t u a l l y see in the Explicate Order is the appearance of a NOVUM, when changing from material parts, or elements, to overall structure. But because of the underlying holistic simplification (as it occurs in the Implicate Order) this NOVUM is in fact not a novum. And whether we experience it as a novum or not, it is, in any case, some specific form-equilibrium, that dominates the development of the organism or crystal, in the form of a global controlling feature, a holistic factor. The kind of NOVUM that is, for instance, represented by the form-equilibrium of a snow crystal (here "form-equilibrium" is equivalent to the parts of such a crystal being correlated, guaranteeing a growth in unison of the crystal) differs from the kind of NOVUM that is involved at the (formal) transition from Inorganic to Organic : While the latter kind of NOVUM entails the modification of most other categories that pass over into the Organic while coming from the Inorganic (Space [inorganic] ===> Umwelt [organic], Increase of Size [inorganic] ===> Growth [organic], Inorganic intrinsic being ===> Organic Individual, etc.), the NOVUM involved in crystallization, and all other such NOVA, (because they are specific, i.e. less encompassing) do not entail modification of other categories, and so do not result in the appearance of a new Layer of Being. Such a NOVUM -- as is visible in the Explicate Order -- is correlated to a corresponding Holistic Simplification in the Implicate Order. Also within the Organic Layer we see -- in the Explicate Order -- a transmutation (usually called "evolution", which term is deceptive in the present context) of lower (i.e. less complex) organisms, resulting in higher (i.e. more complex) organisms. And it is well-known that the actual derivation (as is attempted in science) of higher life forms from lower ones proves to be difficult. In fact what we see, in every such case, is the appearance of a NOVUM, a NOVUM of the same type as we have found it in snow crystals, which means a NOVUM that does not entail modifications of other categories. And the appearance of such a NOVUM, in the evolution of higher life forms from lower such forms, corresponds directly to a holistic simplification noëtically taking place in the Implicate Order. Then, in the Explicate Order the existing lower life forms are over-formed, resulting in higher life forms.
It is to be expected that, in addition to the appearance of such NOVA, also instances of Reductionistic Complexification take place. There we see an increase of complexity without the appearance of a NOVUM : The complex result is totally reducible to the simple initial structure from which it has emerged. And this reduction is just a simplification, not a holistic simplification. And if we change from the initial structure to this complex result, we have to do with just a reductionistic complexification (i.e., ex hypothesi, not with the appearance of a NOVUM).
In that same document of Fourth Part of Website the reader can find a long discussion concerning holistic beings in the Explicate Order and the explanation of them in terms of the Implicate Order.
In part XXIX Sequel-25 of Fourth Part of Website in the window "NOVUM or Unfolding of the Preformed?" the reader can find a further -- and final -- discussion of the NOVUM (the 'new'), that is, a layer-specific categorical NOVUM allegedly appearing in each Layer above the Inorganic Layer. It is investigated there in detail what, in the context of category-layers and the concreta of the categories, in fact "new" here is supposed to mean.
As we saw above, the problem of having to accept the idea of a NOVUM, in first of all the Organic Layer, may be circumvented by assuming "holistic simplification" to take place in the Implicate Order and then projected into the Explicate Order in reverse order resulting in the merely apparent emergence of genuine novelty (anagenesis) and its determining categorical novum. This position, however, brings with it two problems : (1) Concerning organic evolution, a number of highest-level initial noëtic strategies (dynamical laws) must be assumed, implying that evolution in the Explicate Order will not be open-ended : It will end with the projections of these highest-level noëtic strategies. See diagram BELOW . (2) The mentioned alleged nexus-reversal (holistic simplification ==> apparent reductionistic complexification) is a rather ad hoc assumption, just to get rid of a true NOVUM. So we must also investigate how things go without the assumption of holistic simplification (and its reversal upon projection). This is done in the mentioned part XXIX Sequel-25 in Fourth Part of Website, of which we here give a very succinct summary -- while also adding some alterations -- concentrating on the transition from inorganic to organic (in the context of the history of Being). And it has turned out that there is no need to drop the assumption of holistic simplification. On the contrary, it is much better to hold on to it.
The Explicate Order's Layers of Inorganic and Organic (and also the other Layers coming after them) are, first of all category-layers, that is, they are layers, first of all characterized by their categorical content (i.e. their determinative content). However, any category whatsoever does not apply, that is, does not 'exist', in the absence of its corresponding concretum in the Explicate Order. So in this way also the concreta belong to the corresponding category-layer. We do not suppose (constitutive) categories to be present in the Implicate Order because, in the absence there of individuals and individual cases and circumstances, there do not exist true whatness categories because the intrinsic whatness of a noëtic pattern is identical to that pattern itself. Also nexus-categories do not exist there because they too are identical with their 'concreta' viz. the noëtic derivations according to noëtic rules. There we cannot say that such a rule applies to "all relevant individual cases", because, as has been said, in the Implicate Order there are no such cases.
A categorical NOVUM determines, i.e. implies, the (coming into) existence, in the history of Being, of genuine novelty which we may call N. So the structure of a categorical NOVUM, that is a new category, and thus a new If / Then constant, generally is
In the Organic category-layer this is the Nexus Organicus (taken generally) that determines, as a category, the typically organic concretum-concretum determination, and which is an over-forming of causality (which is the general nexus-category of the Inorganic category-layer).
But although N is (ex hypothesi) genuine novelty, the categorical-NOVUM is not. It is a categorical constituent of the Organic category-layer (here, as has been said, still concentrating on the transition from inorganic to organic). But assuming the category " If X, then N ", in fact means that if and where the condition X is satisfied, N, the novelty, will follow. And this in turn implies that the potential of the emergence of Life is present all the time, and especially, was already present in the initial phases of the evolving Universe. But this boils down to the position of a reductionistic constitution of the real world : All phenomena, including Life, can be traced back to the potential already present in the overall dynamical law (= some set of complex differential equations perhaps) of the Universe, as is assumed by the " Theory of Everything " being worked on by perhaps too confident scientists. So indeed the category If X, then N is not a novum, it was there from the beginning, and neither is N a genuine novelty, even when it appears only later when the condition X is satisfied. It is just the outcome of the unfolding of the overall dynamical law assumed in the Theory of Everything.
But the Theory of Everything assumes in fact the g r e a t e s t n o v e l t y of all to occur : According to it the Universe came into being from simply Nothing. So whether we accept or do not accept such a Theory of Everything we must assume novelty to appear. And in all this it is perhaps more realistic to spread out the necessary amount of true categoric novelty over all of the Explicate Order's category-layers, where, for example, then the organic categorical novum only appears after the inorganic world has been fully developed (with all its moderate- and low-temperature chemistry), and the still higher-layer categorical novae also only appear after the concreta of the previous category-layer have been fully formed. This then will significantly lower the amount of initial novelty having to appear at the origin of the Universe from Nothing, i.e. the potential of the primordial Universe can be assumed to be less than is done in the Theory of Everything : The total, that is, the complete, potential will then come about by successive, and incremental appearance of true categorical novelty during the evolution of the Universe (which is the development of Being). But in all this it is difficult to assume the successive emergence, not just of concreta -- things, patterns -- but of the very categories as well, categories (the categorical NOVA) that determine the emergence of these new concreta. So the categorical NOVUM should, first of all, have the following general structure :
The general structure of a category ( If / Then constant) can be depicted as follows :
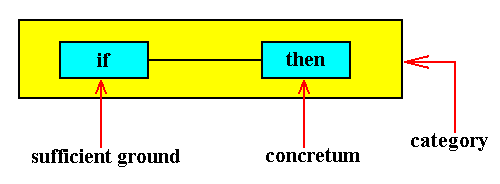
And in our just discussed case we have a special nexus category, which here is a special case of the general nexus organicus. And the concretum of this category is a special concretum-concretum determination, namely the determination of the next (intrinsic) state of a given organism by its previous state. So this state-state determination is itself determined by a special nexus-category, i.e. stands under this category. Here the materially interpreted dynamical law (some special law, that is) is the phenotypically expressed Essence of a given organism (while the not-yet materially interpreted law is its 'genotypical' Essence). As such, its presence, that is the presence of the concrete starting condition or the presence of some one concrete (intrinsic) state of the organism somewhere on the course of the (organism's) dynamic trajectory, implies the generation of the next (intrinsic) state of that organism. See next Figure.
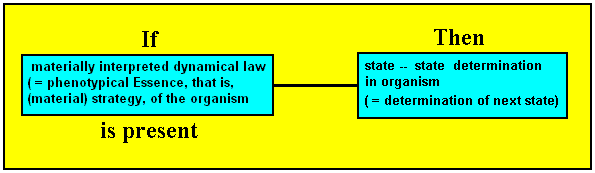
Figure above : A diagram depicting a special nexus category, determining the state-state succession of a given organism. That is, this category determines the intrinsic strategy of this organism to exist and persist (the latter especially refers to reproduction).
Having said all this, let us now consider directly the specific instances of the nexus organicus as they appear in the Explicate Order, and begin with the temporally first instance which is responsible for the very origin of Life (that is, carbon-based life). We have then to specify the general organic nexus category expressed as the If / then constant
where N is the concretum of this general category. And this concretum is itself a concretum-concretum determination of some general type (which we are going to specify), that is, it is the general organic strategy as is found in the morphology, physiology, genetics, and typical behavior of organisms. And the category determines this strategy as to what it is. Let us now then specify.
The condition X of the category is the state of matter in the Explicate Order such that in one or more places in the Universe the thermodynamic conditions are in turn such that liquid water is present and (even) complex carbon-compounds are stable, so that chemical reactions between already existing carbon-compounds can take place in an aquatic medium, resulting in ever more complex (but not necessarily already functionally complex) carbon-compounds.
The concretum N of the category is a special concretum-concretum determination, i.e. a specific dynamical system, such that it does not pick up noise (from its emvironment) in its course. It accomplishes this by actually recognizing it as noise, that is, by recognizing it as ' non-self ' and then not accepting it, that is, neither letting it enter into its initial condition nor letting it enter into subsequent system-states, and in this way avoiding perturbation (which could send the system to quite different end-states), and so rendering it repeatable ( From here on, organisms originate, as it seems (see below), exclusively from organisms as a result of new strategies, themselves determined (as to what they are) by categories of the sort just depicted).
As long as the category If X, then not-N applies, N is not ontologically presupposed in the Explicate Order, and thus not potentially present there. It is only so presupposed 'after the fact', that is, when If X, then N applies, and it m a y so going to apply when N, which is a particular strategy, pre-existing, it is true, in the Implicate Order as a noëtic pattern, is actually projected (into the Explicate Order) and when X is satisfied in the Explicate Order. So the "potentially already present" of N is now removed from the Explicate Order, but it is -- noëtically -- present in the Implicate Order.
In this way the category If X, then N is a genuine categorical NOVUM : the category as well as its concretum are new in the Explicate Order. And this is the same thing as saying that the Explicate Order alone, as it really is, does not support a reductionistic explanation of the origin of life, because it alone cannot bring it fourth. It is the Implicate Order that supplies the first organic strategy by projecting the most simple noëtic strategy-string into the Explicate Order. But this projection does not all by itself 'cause' the local transmutation of the existing category If X, then not-N into a special case of the category If X, then N : This transmutation or categorical flipping may occur repeatedly at any points in time, but as long as the condition X is not satisfied the new category will not apply and therefore will not even exist, meaning that the transmutation did actually not take place. And although the condition X, even when satisfied, is still indifferent with respect to the actual origin of Life (that is, of the first living organisms), the new category may now apply. As long as it does not apply (i.e. when the category If X, then not-N still universally applies), then even when X is satisfied no life will appear in the Explicate Order (while in the Implicate Order Life is, of course, always absent). So the condition X does not, all by itself, possess the potential of developing into living organisms (that's why all the physico-chemical theories of the origin of life have failed!). And thus the origin of Life fully depends upon the emergence of the category If X, then N, that is, on the emergence of the genuine categorical NOVUM.
The subsequent evolution of Life from this primordial beginning (or beginnings) now merely depends on (1) the presence of this primordial beginning (at the place where this evolution is supposed to get started), which now constitutes the extended condition X, and (2) the successive projection of new strategies noëtically derived in the Implicate Order. And here, i.e. in evolution, we have, with respect to categories, to do with a similar state of affairs as with the origin of life every time when there is going to appear, in evolution, a new type of organism, because such a new type is in fact a new strategy, a novelty that is, because it cannot fully be derived from the previous strategy. And if we still adhere to the above theory of holistic simplification (in the Implicate Order) and its subsequent reversal in the Explicate Order, then we can say that every time the new strategy, new with respect to its appearance in the Explicate Order, cannot be derived from the previous one, even in the Implicate Order. There, a previous strategy is derived from the next strategy (where "previous" and "next" refer to their states in the Explicate Order), that is, upon projection, the consecutive order of noëtic derivation becomes, as consecutive order, reversed, resulting in the successive order of appearance in the Explicate Order.
And so in evolution, every new organic strategy, as we see it in the Explicate Order, is a new concretum-concretum determination, itself determined (by a category-concretum determination) by a new, and again, special, nexus-category, that is, a categorical novum, as again a special case of the (general) nexus organicus. And thus we have now to do with the subsequent special instances of the (general) nexus organicus. This is why organic evolution is intrinsically unpredictable, but also why evolution cannot be sustained by the Explicate Order alone. This fact was already anticipated by the phenomenon, encountered in the systematics of organisms (their phyletic classification) and in paleontology, of more or less persistent cross-specialization of features of organisms, visible by the very often encountered fact that a candidate precursor of some given organic type, a candidate that is, on the basis of the derivability of certain features of the later type from features of this candidate precursor, proves itself to be in a derived condition with respect to that later type on the basis of other features of it, and so, following Dollo's Law of the non-reversibility of the evolution of complex (sub)structures, that later type cannot have been evolved from the candidate precursor. So what we, in organic genealogic classification and in paleontology, actually have is only the fact of successive appearance of organismic types in the course of geologic time. And this successive appearance of organismic types in the Explicate Order is just a reflection of the consecutive noëtic derivations in the Implicate Order (and subsequent reversal in the Explicate Order) going hand in hand with the appearance in the Organic Layer of categorical nova. And although the appearance of the first organic categorical novum effects and characterizes the emergence of a new category-layer, the Organic Layer ('on top' of the Inorganic Layer), the subsequent appearances of the other organic categorical nova do not create additional new category-layers. They all are (new) categories of the Organic Layer.
That the Explicate Order alone cannot accomplish organic evolution is also clear when we consider the many sophisticated adaptations as we see them having developed in all organisms, again implying that the Neodarwinian model of organic evolution is inadequate. Below we will consider this in some more detail.
Having thus now given the extra arguments in favor of the existence of the Implicate Order (as we already found out in Fourth Part of Website), and integrated with it the Theory of Categories, that is, the theory of determinative elements of the Explicate Order (also developed in Fourth Part of Website), we can now -- in the present summary -- proceed further in the context of the evolution of organisms and its bearing on the existence of the Implicate Order as we have found out things in the present Part of Website.
In organisms we encounter a host of extremely sophisticated mechanisms in their cells and in their bodies. We also encounter the many 'clever' adaptations to their environment and especially to other organisms. And also we find intricate behavioral patterns such as in the sociality and social parasitism in many insects. In addition to this we see the existence of many 'types' or 'designs' of organisms often not directly related to survival or adaptation. They look more like different 'styles' created for just the sake of diversification. But the diversification of Life might constitute one of the guarantees for its persistence (In this way Life can survive major catastrophes). Anyway, we see that Life has evolved clever strategies to be able, not only to exist, but also to persist.
So there is much evidence against the neodarwinian vision of organic evolution, and little to support it. But because in assuming Reality to be of only one 'sort' -- physical reality -- neodarwinism is the only meaningful theory of evolution, but nevertheless failing miserably -- we must entertain the possibility that Reality is not ontologically homogeneous, that is, does not consist of only one fundamental way of being, and that is, (it being) not strictly monistic. In short, this argument reads :
In a world assumed to be ontologically homogeneous, and, especially, assumed to be wholly physical (s.l.), neodarwinism represents the only possible (i.e. reasonable) theory of evolution. But neodarwinism fails. So the world is not wholly, and not exclusively, physical (s.l.). but must include a non-physical range or aspect.
There must exist, alongside the physical, that is, the material, a second, different, domain of Reality, namely a non-physical immaterial domain of Being. However, this should not allure us to assume some deity-like domain or entity that 'created all things'. For this is not at all an explanation, or even a serious attempt to it, but just a mere intellectual concession leading to cessation of all enquiry. Also we cannot assume the existence of some Platonic realm of immaterial 'Ideas' in some utterly transcendent domain of Being, because such a vision runs into trouble as regards (bridging) the gap that forbids a qualitative relationship between the Ideas on the one hand and the material things on the other.
Having taken all this into account, I have looked for a possibility to place organisms and their evolution, not in one single ontologically homogeneous domain of Being (the material world), and also not in two separate and mutually transcendent domains of Being, but in a single, but, nevertheless, ontologically broader [than just material] context.
I found it in the idea of the "Explicate and Implicate Orders of Reality", first proposed by David Bohm (See Third Part of Website ) in the 1980's (but subsequently modified by me). This, for the reader now familiar idea lets Reality consist of two Orders, viz., the Explicate or unfolded Order, i.e. material space, and the Implicate or enfolded Order, i.e. noëtic space. By the process of 'projection' immaterial patterns of the Implicate Order are unfolded (back) along space- and time-dimensions, resulting in material individual things in space and time. On the other hand, by the process of 'injection' all material things and patterns of the Explicate Order are folded (back) along the space- and time-dimensions (of the Explicate order), resulting in immaterial patterns in the Implicate Order. So the two reality-Orders are in constant interaction (this being not physical), and thus are, despite their being ontologically different (the one is material, the other immaterial), not in an absolute sense transcendent with respect to each other. So in fact there is only one single reality, but consisting of two different, but interacting, domains of Being.
And we point to the Implicate Order as the ultimate seat of the forging of the mentioned sophisticated strategies of organisms, -- however, a forging not without the help and cooperation of the Explicate Order.
The main mechanism and reason of 'projection' of immaterial patterns from the Implicate Order into the Explicate Order is the fact of their becoming -- upon projection -- ontologically complete : They, initially being just pure Forms, acquire matter as their substrate, and become individual, temporal, and spatial. So all immaterial patterns (as they reside) in the Implicate Order strive to become ontologically complete, that is, to become material ( This is contrary to the general attitude in classical Greek philosophy).
However, while most simple patterns, like crystal-structures and other inorganic entities, can be directly projected, and can maintain themselves in the Explicate Order simply there (in that Order) where thermodynamic conditions are such that these patterns are stable or at least metastable, complex noëtic patterns, on the other hand, cannot, generally, be so projected, because many will be incompatible with the general structure or existential conditions of the Explicate Order, that is, material space.
In order for (certain) complex noëtic patterns to be projected, they must be 'strategies', that is, they must be themselves prescriptions telling them how to exist in the Explicate Order. And when they are indeed such strategies they -- upon projection -- appear, in the Explicate Order, as organisms : They are individual, complex, patterns, existing far from thermodynamic equilibrium, which condition they must actively maintain.
While in the Implicate Order these strategies are mere immaterial patterns in the form of descriptions (descriptions of themselves as strategies to exist in the Explicate Order) and thus being in the form of 'strings of symbols' of some kind, these strategies are, when having been unfolded along the spatial and temporal dimensions, that is, having been projected into the Explicate Order, represented by organismic species. And indeed every plant or animal species not only has a strategy to exist and persist, but is this very strategy, now materialized. This material strategy consists of all the aspects of the given organic species : its genome and other species-specific molecular biology, its specific physiology, its morphology, the behavior -- especially the tactics of reproduction -- of the individuals representing that given species. Many of these strategies are very complex and sophisticated indeed, such as those of many species of ants and bees. They invariably involve the strategies of other organismic species as well. So they are -- in the Explicate Order -- essentially ecological structures.
As has been said, in the Implicate Order these strategies are represented by immaterial noëtic patterns in the form of descriptions (not made by someone or something). And they can, even 'before' they are true material strategies, noëtically interact with each other and with other (non-strategy) noëtic patterns, resulting in new strategies. And that indeed purely immaterial reactions or derivations have a great potential to generate complex and intricate patterns is shown by many mathematical systems being prescriptions that generate intricate fractal objects such as the Mandelbrot Set. We must see such a noëtic interaction or reaction as some sort of logical or mathematical derivation of one strategy from another one (or two). And the best way to visualize all this is to assume that the noëtic strategies -- themselves being strings of symbols -- together form a formal 'typographical' system, with a certain number of given strings ('axioms') from which other strings ('theorems') can be derived (and are derived) by following a definite set of noëtical rules, 'production rules'. In this way, from initially given symbol-strings many others will be derived, resulting in a branched sequence ("branched", because often two or more rules can be applied to some given string) of consecutive derivations. And upon projection of this sequence we see -- in the Explicate Order -- the evolution of the organic world, where the temporal succession of appearing organic species corresponds with the timeless consecutiveness of the formal derivations in the Implicate Order. This is true with respect to the corresponding lines of noëtic derivations in the Implicate Order on the one hand, and the lines of evolution in the Explicate Order on the other. That is, there is a one-to-one correspondence between the noëtic strategy-strings of a given line in the Implicate Order on the one hand, and the organic species in the other line in the Explicate Order, but the consecutive order in the 'explicate line' is the other way around with respect to that order in the 'implicate line', that is, upon projection of a sequence of noëtic derivations the derivational order is reversed, resulting in the temporal order of appearance of organismic species in evolution. As explained above (referring to our findings in Fourth Part of Website), the continued noëtic derivation of one noëtic strategy-string from another is in fact a holistic simplification where thus simple ('lower') strategies are derived from noëtically pre-existing more complex ('higher') strategies. And upon projection into the Explicate Order we see the origin of higher forms from lower ones.
But how is it that indeed many of the noëtic immaterial patterns in the Implicate Order (noëtic space) are such strategies, strategies that is, that are precisely geared to conditions in the Explicate Order? The fact of their being so must somehow come from the Explicate Order itself, that is, not from the Implicate Order, because these noëtic strategies reflect conditions and relationships as they typically are in the Explicate Order. To understand this, it is assumed that the formal system of noëtic strategies is in fact an arithmetical system implemented on the substrate of 'number theory'. By "number theory" we here mean 'ontological number theory', that is, the objectively existing natural numbers (positive integers and zero) and their properties (and studied in mathematics as number theory-proper (N)), existing that is, in the Implicate Order.
The formal system of noëtic strategy-strings (FSNSS) is encoded in natural numbers, and the rules of this formal system are ultimately not typographical, but arithmetical. That means that the derivations of one strategy-string from another are, ultimately, arithmetical processes.
But while the basic elements of the rules of FSNSS are the elementary arithmetic operations (such as addition and multiplication), having these rules implemented in ontological number theory, the specific combinations of these elementary arithmetical operations, as these combinations constitute these rules, cannot come from ontological number theory itself, that is, cannot come from the Implicate Order, because although ontological number theory does contain the theorems of FSNSS, it cannot 'recognize' them as belonging to some formal system other than its own formalization, TNT, the latter being its essence. In our case, it cannot 'recognize' them as theorems of FSNSS. Ontological number theory cannot recognize, neither create, the specific production rules of FSNSS ( I have demonstrated this by using a rough and simplified analogue of FSNSS, called the 'MIU-system', a concocted typographical formal system that can be embedded in number theory (as all formal systems can),-- a formal system that was, as we have seen, created by Hofstadter.
So the specific nature of the essentially arithmetic rules of our formal system of noëtic strategy-strings, FSNSS, cannot come from the Implicate Order. In some way or another, information about the structure and conditions of the Explicate Order must be present 'somewhere' in the Implicate Order. Or, in other words, the Implicate Order 'knows' about the Explicate Order. And this is accomplished by the phenomenon of 'injection'. As has been said, the Explicate and Implicate Orders interact with each other by incessant 'projection' and 'injection' of patterns. And injection is the process of re-enfolding of physical and biological structures, re-enfolding that is, back along the space and time dimensions, resulting in becoming noëtic immaterial structures again. And by 'injection', information about the Explicate Order becomes encoded in the rules of FSNSS, and that's why these rules can transform initial strings into Explicate-Order-directed strategies and these in turn into other such strategies. And therefore these strategy-strings are really prescriptions of how these very prescriptions themselves can exist and persist in the Explicate Order and so attain ontological completion. In fact this injection of information into the Implicate Order can be seen as a 'local' over-forming of ontological number theory, an over-forming that is, of the basic TNT-structure. As has been said, the noëtic prescriptions (strategies) appear -- upon projection -- in the Explicate Order as organismic species, each fully adapted to a certain existing ecological niche, resulting in their being relatively stable. And the noëtic derivations of one strategy-string from another are reflected in the Explicate Order as organic evolution, but then in reverse order.
The branching sequence of organic species along evolutionary lines of descent does not, therefore, take place in the Explicate Order (where indeed we encounter a [at least high degree of] polyphyletic development [see where we discussed the evolution of the Order Diptera] ), but in the Implicate Order, where we have called the branching sequence of derivations the "noëtic trajectory". And perhaps the course of this trajectory can be revealed by the method and theory of "Phylogenetic Systematics" in the sense of Willi Hennig, expounded in detail on this Website ( Present Main Part of Website [from part XXV-B onwards of the present Series on evolution). As has been said, the (branching) sequence of noëtic derivations corresponds to a reversed branching sequence in organic evolution in the Explicate Order. But this latter sequence is largely in fact not more than a temporal one, expressing the appearance of organismic species in the course of geologic time. And because simultaneous appearance of different (but related) organismic species is perfectly possible, this sequence is also 'branched'. In the Explicate Order we must read the resulting 'genealogical trees' of Phylogenetic Systematics along the time dimension, while in the Implicate Order we must read them in the reversed order of noëtic derivations (which are atemporal).
See next diagram.
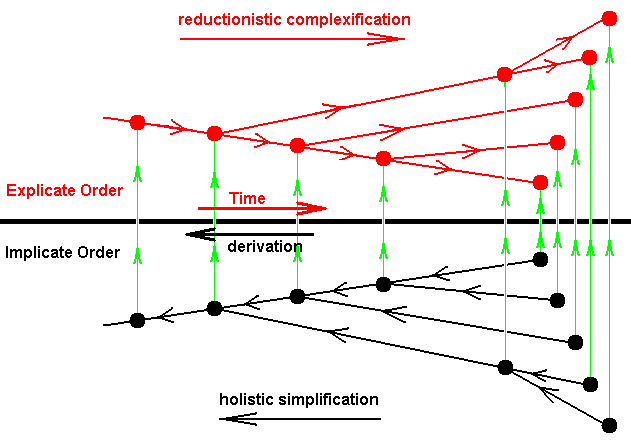
Figure above : Diagram depicting the consecutive noëtic derivation of strategy-strings (symbolized by discs) in the Implicate Order (lower half of diagram), and, upon order-reversal, the projection of these strings into the Explicate Order resulting in the branched evolutionary sequence of organisms (upper half of the diagram), but which sequence in fact is nothing more than the temporal order of their appearance in the Explicate Order. See next Diagrams.
While being merely immaterial strategy-strings in the Implicate Order, they are, upon projection, material strategies (= organic species) in the Explicate Order. Each such a material strategy contains the determined succession of states of the organic individual. And this succession of states is dictated by the special dynamical law (= instance of the nexus organicus or general organic nexus-category) which (law) is the Essence or ontological kernel of the organic individual and commonly possessed by all individuals of the given species. In the Implicate Order this material strategy is present in the form of an immaterial noëtic string of symbols forming a description and prescription of the strategy, and this description in turn is in fact the just mentioned dynamical law, but here not yet materially implemented.
The red lines, connecting the material strategies in the Explicate Order emphasize the correspondence between the noëtic derivation of strategy-strings and their successive appearance, as material strategies, in the Explicate Order. But that's all these lines signify. So they can best be omitted as is done in the next diagram.
Figure above : Same as above. Omitting the lines connecting the material strategies (red discs) with each other emphasizes the fact that in the Explicate Order the only thing that takes place is the successive appearance of new material strategies (new organic species or types). And this successive appearance is a reflection of, or is based on, the consecutive noëtic derivation of immaterial strategy-strings in the Implicate Order and their subsequent projection into the Explicate Order.
Evolution -- as seen in the Explicate Order -- as no more than a succession (and, at times, intermittent simultaneism) of organic species or types is even more emphasized in the next diagram :
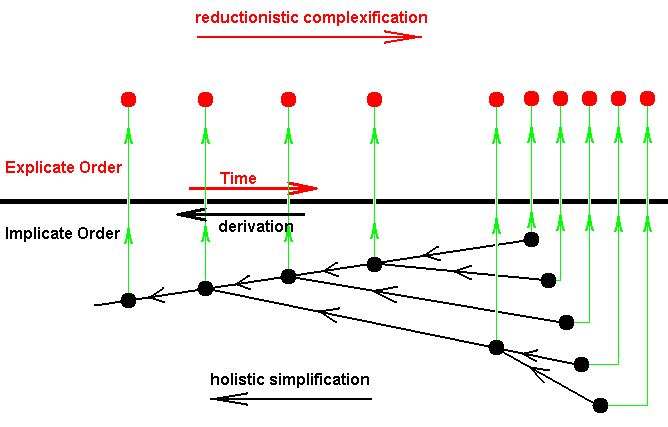
Figure above : Same as above. Based on the consecutive noëtic derivation in the Implicate Order, the strategies appear in the Explicate Order in a definite morphological (s.l.) order [order of structural plans and behavior] and temporal order. And, in the Explicate Order, generally a later appeared strategy (organismic species or type or structural plan) cannot be derived from previous appeared strategies. And if some such strategies nevertheless can, that is, are formally derivable one from the other, that does not necessarily mean that they have, in the Explicate Order, actually and materially originated one from the other.
Our extended noëtic theory may be hyper-succinctly summarized as follows :
It is important to realize the nature of the noëtic derivations of strategies from one another as depicted in the above diagrams.
The noëtic strategies are, in the Implicate Order, not generated one after the other by the mentioned formal system of noëtic strategy-strings (FSNSS). No, they 'were' there already. But they stand, in virtue of their intrinsic nature, in certain relationships to one another, that is, in certain different types of relationship. One of these types of relationship is their formal derivational possibility : Together they form the FSNSS. With FSNSS they can, as it were, be classified in virtue of their formal derivability. And it is this given formally possible derivation, via rules -- rules as it were, determined 'after the fact' -- that is expressed in organic evolution as we see it in the Explicate Order. Thus, in the Implicate Order the different strategies do not actually originate from one another by the formal system of which they are elements : They together just form a derivability structure, indicated by the "noëtic trajectory", which is, consequently, static in the strictest sense. It has only a consecutive nature, that is, it formally orders the strategies as to their noëtic derivability.
The noëtically existing strategies, formally ordered by the FSNSS, also stand in other relationships to one another, namely as products of noëtic reactions : Each strategy by itself is the product of a noëtic reaction, or a chain of such reactions, of (other) strategies with one another and/or with other noëtic entities. And this in fact constitutes the "noëtic ecology" as it is present in the Implicate Order. So it is by way of noëtic reactions that the strategies are actually noëtically constructed (which construction is, of course not a process proceeding in Time). And only then, that is, 'after' their construction, they turn out to be (also) related to one another by formally possible noëtic derivations of them from one another, that is, from (noëtically) existing other strategies, that is, only then they happen intrinsically to form together a formal system, the FSNSS, with what might be called 'axioms' and 'production rules'. And it is this particular system -- a system of formal derivations -- that is expressed in evolution in the Explicate Order. So while the various adaptations (later to be seen as biological and ecological adaptations), as constituents or essential aspects of the various strategies, are forged by noëtic reactions in the Implicate Order, the actual successive appearance of the various strategies -- organic species -- in the Explicate Order, -- the evolutionary sequence, is based on the (reverse) formal derivational structure of the system of noëtic strategies in the Implicate Order.
As has been said, the large collection of strategies -- in their noëtic form -- results from a great many noëtic reactions. Of course not every product of such reactions is a genuine strategy. It often is just a noëtic pattern without any relevance to existential conditions in the Explicate Order. Such a pattern, such a Form, will not enjoy ontological completion, that is, it will never be projected into the Explicate Order. Other products will turn out to be true strategies, but some of them might not fit into the formal system of noëtic strategy-strings because they cannot in any way be derived directly or indirectly from that system's 'axioms'. But they might be part of another formal system of noëtic strategy-strings having different rules and axioms, that is to say they might yield to another formal classification than that represented by our original formal system. So from this it is clear that there might exist -- in the Implicate Order -- not just one, but several different formal systems of noëtic strategy-strings and their respective derivational order and the reversed order of appearance of their strategies in the Explicate Order. This means that Life as such might have been originated in several different ways, that is, in one way on the planet Earth, and in others on other planets. Or in several ways on Earth but followed by extinction of all but one.
We may suppose that a given noëtic strategy-string will only be projected into the Explicate Order when it fits precisely in some pre-existing conditions (in the Explicate Order), that is to say, when and where this strategy is indeed a true strategy. And in evolution every newly appearing strategy (organismic species) has a fore-runner, which is either a direct 'ancestor' (in terms of the Explicate Order), or, when it is the very first strategy to appear, the appropriate chemical and thermodynamic conditions to properly receive such a projected first strategy (origin of Life). In both cases such a fore-runner is noëtically represented by precisely that noëtic pattern (representing chemical conditions) or that strategy-string (representing an organismic species) that is being formally derived -- that is, it being formally derivable -- from the given strategy-string (so formally, it is not a 'fore-runner' but a derivative). We may suppose that for the f i r s t appearance (projection) of a given strategy its fore-runner must be present there where, in the Explicate Order, projection of this given strategy is supposed to take place, or, in other words, the presence of the fore-runner is one of the necessary conditions, that is, belongs to the set of necessary existential conditions for the given strategy to be projected for the first time. When this fore-runner later becomes extinct (in the Explicate order) it might then be not an indispensable loss, and in that case the given strategy keeps on existing, without its fore-runner, in the Explicate Order.
And when in a sequence of successive appearances of new strategies one next strategy to be projected (and thus to be projected for the first time) turns out to be not a true strategy with respect to existing conditions in the Explicate Order, it will not be projected. And that means that also the subsequently to be projected series of new strategies will also not be projected as long as the mentioned conditions remain what they were, because the next (next) strategy to be projected (for the first time) will not find its fore-runner anywhere : Here we have to do with a dead-end branch in evolution, as is so often encountered (in paleontology).
In this way, following our noëtic theory of evolution, we must 'read' the successive, and often simultaneous, appearance of new organismic species, representing new strategies, in the Explicate Order.
It is now clear that the very noëtic f o r m a t i o n of strategies -- that is, the formation of Forms such that each one of them describes itself as being a possible strategy of how for itself to exist in the Explicate Order -- lies in the system or systems of n o ë t i c r e a c t i o n s in the Implicate Order, while the derivational o r d e r i n g of the collection of the so-formed strategies is logically subsequent upon their formation. And about this very formation of the strategies (noëtic strategy-strings) we might say the following : Each immaterial Form in the Implicate Order, being ontologically just a Form and nothing more, intrinsically strives after o n t o l o g i c a l c o m p l e t i o n (which consists for it to in-form prime matter, and as a result of that becoming individual, temporal and spatial). And this 'pursuit' largely determines the s p e c i a l a f f i n i t i e s of noëtic patterns to one another insofar as they are reactants of noëtic reactions. As a result of these special affinities, affinities ultimately geared to obtain ontological completion, the subsequent reaction-products will eventually be noëtic strategies, prescriptions that tell them how to exist (upon projection) in the Explicate Order and so obtaining ontological completion. So on ontological grounds it is to be expected that many noëtic reactions or chains of such reactions will eventually lead to the formation of forms that are not just noëtic patterns whatsoever, but genuine noëtic s t r a t e g i e s. And only then they might be p r o j e c t e d into the Explicate Order, but only if they will fit in existing conditions there. And only then they obtain ontological completion. And, as has been said, the order of projection of these strategies, and thus the order of appearance of organismic species and types in the Explicate Order -- evolution -- is determined by the derivational order of the (still noëtic) strategies, which derivational order in turn results from their (logically subsequently) being part of one or another formal system with its specific 'production rules' (which do not actually produce but derive, or better, show derivability of noëtically already existing strategy-strings). And of course, in the Implicate Order, in addition to noëtic strategies getting formed from non-strategy reactants, new strategies may also result from noëtic reactions between already-formed noëtic strategies.
One might think that the system or systems of noëtic reactions are in themselves already enough to give rise -- upon projection -- to evolution, but this cannot be so. The noëtic reactions are not supposed to form one, or more genuine systems (meaning that their elements arrange themselves into certain patterns of elements). They form mere collections of noëtic reactions. Some reactions between two or more strategies may result in one or more simplified strategies, simplified that is, as compared to the reactant-strategies (simplified as a result of loss of parts or elements). But a product-strategy may also be more complex (and nevertheless its many parts being more integrated into the whole) than the reactant-strategies. In evolution, however, we see that the chief direction is toward the development of higher forms, that is, forms being more complex but having their parts still perfectly integrated into the whole. So evolution apparently is a one-way process. Therefore we must assume that, in the Implicate Order, the strategies, resulting from the many noëtic reactions, subsequently organize themselves into an ordered collection, where the order consists of consecutive derivability of one strategy from another. And this order has -- as has been said -- the form of a certain formal system of strategies, that is, the strategies together form a formal system (or more such systems), a formal system inhering of course its own (large) set of 'production rules'. When now these strategies are being projected from the Implicate Order into the Explicate Order, in exactly the reverse order of consecutivity as is their order of consecutive derivability (their order of formal derivation) in the Implicate Order, evolution of organisms will result in which higher forms appear after lower forms.
The next document is the last of the four-document intermezzo on noëtic theory. We will consider there the very reason of the existence, in the Implicate Order, of organic strategies (in the form of noëtic patterns).
e-mail :  ( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
To continue click HERE for the further study of Organic Evolution, Part LXd.
Back to Evolutionary Part XVII
Back to Evolutionary Part XVIII
Back to Evolutionary Part XXII
Back to Evolutionary Part XXIII
Back to Evolutionary Part XXIV
Back to Evolutionary Part XXV-A
Back to Evolutionary Part XXV-B
Back to Evolutionary Part XXV-C
Back to Evolutionary Part XXVI
Back to Evolutionary Part XXVII
Back to Evolutionary Part XXVIII
Back to Evolutionary Part XXVIII-A
Back to Evolutionary Part XXIX
Back to Evolutionary Part XXXI
Back to Evolutionary Part XXXII
Back to Evolutionary Part XXXIII
Back to Evolutionary Part XXXIV
Back to Evolutionary Part XXXV
Back to Evolutionary Part XXXVI
Back to Evolutionary Part XXXVII
Back to Evolutionary Part XXXVIII
Back to Evolutionary Part XXXIX
Back to Evolutionary Part XLII
Back to Evolutionary Part XLIII
Back to Evolutionary Part XLIV
Back to Evolutionary Part XLVI
Back to Evolutionary Part XLVII
Back to Evolutionary Part XLVIII
Back to Evolutionary Part XLIX
Back to Evolutionary Part LIII
Back to Evolutionary Part LVII
Back to Evolutionary Part LVIII