nomos LXI

Organic Evolution in terms of the Implicate and Explicate Orders.

Part LVII

Hymenoptera (wasps, bees, ants) (Sequel)

The evolutionary diversification in the Order Hymenoptera in terms of Strategies (Sequel).

Ectoparasitic Hemi-Familial Phase

The initial (original) relationships, when the larvae of a terebrant lived at the expense of only the egg-stage of the host, later developed in various directions, of which some led to parasitism at the expense of a more or less mature larva of the host (Orthoparasitic Phase).
In the particular case where the body size of the host larva is for several or even many times larger than that of the terebrant, the latter obtained the possibility to establish on the prey a whole family of its ectoparasitic larvae. In this way originated the hemi-familial ectoparasitic line of evolution among chalcidoids and some other forms about which we will speak later on.
In spite of the generally small sizes of chalcidoids, usually armed with a minute ovipositor concealed in their body, relatively large host larvae were nevertheless accessible for them, and with it under rather various conditions. First of all we can reckon here chalcidoids that develop at the expense of larvae of flies, butterflies, and beetles, gnawing channels ("mines") beneath the superficial skin of leaves, grasses, and trees, or in thin stems and twigs. Thus, for instance, the female of Diaulinus begini ASH. (from the family Eulophidae), while wandering over the surface of a leaf, looks for mining larvae of the fly Agromyza in their mines. Having found such a larva, the chalcidoid bores through the skin of the leaf covering the mine, and lays a pair of eggs (sometimes one) onto the body of the miner. The larvae of the parasite, emerging after a day or two from these eggs feed externally on the host larva, which dies when the parasitic larvae are still very small. The larval period of the chalcidoid lasts about a week. Pupation takes place in the mine at some distance from the body of the prey.
As typical hemi-familial parasites in mines develop chalcidoids of the genus Elasmus, belonging to the small family Elasmidae. The female of E. hispidarum FERR. attacks larvae of one of the species of leaf-eating beetles (Chrysomelidae), Promecotheca sp., mining leaves of the coconut palm. Before oviposition she pricks the underside of the leaf and paralyzes the mining larva definitively. Then she lays a heaplet of eggs in the mine, usually 6-18 of them depending on the size of the prey. The hatched larvae of Elasmus crawl inside the mine in search of a paralyzed larva, and, when found, suck themselves on to it. The beetle larva dies in 12 hours after the parasitic larvae began consuming it.
In the neighborhood of the chalcidoids parasitizing in mines we may place, according to their habits, also those that hit preys that are enclosed in cocoons and in such special formations as puparia and cells. The chalcidoid Microplectron fuscipennis ZETT. (of the subfamily Eulophinae [MALYSHEV's text reads : Fulophinae] looks for cocoons of the pine-sawfly (Diprion setiferum GOEFF.), that lie on the soil amidst plant remains, and which contain the sawfly's mature larva, prepupa, or pupa. With the help of its ovipositor the parasite bores through the wall of the cocoon, and lays onto the body of the prey, [resting] within it, 20, 30, or also more, eggs. The larvae, having hatched from these, develop outside the body of the host and from time to time crawl over it. It is reported that from one cocoon of the sawfly maximally 120 adult chalcidoids emerged. In this it is well possible that not all of them were descendants of one and the same mother.
Another chalcidoid, from the family Pteromalidae, Dibrachoides dynastes FOERST. develops in round cocoons of the lucern weevil Phytonomus variabilis HBST., also usually found amidst plant debris on the surface of the soil. The parasite looks for cocoons containing already the prepupa or pupa of the beetle. With a sting by the ovipositor the prey is definitively paralyzed. Eggs, numbering 3-5, are laid onto the ventral side of the victim's thorax. The young larvae, having been in direct contact with the body of the host, directly after emerging suck themselves onto it and remain there until their feeding has been completed. After this, the larvae leave the host and crawl for some time inside the cocoon, and then in it pupate.
The females of this chalcidoid, as do the females of many other terebrants, especially of the family Pteromalidae, feed on saps of the prey. Not having direct contact with the prey's body, covered by a cocoon, they do it with the help of a remarkable adaptation, namely with a special tube which the female directs to the host body. In order to find a suitable place for this, the chalcidoid meticulously explores the surface of the cocoon with her antennae, tries out to sting it in various places and may even with the help of the tip of her ovipositor turn around the prey's body and gets it in the right position. When the sought-for point is found (usually on the back of the prey's abdomen), the ovipositor is driven here through the wall of the cocoon into the host body, whereby the distal end of the ovipositor makes circular movements. Having done this a few times with intervals of 2-3 minutes, the chalcidoid takes out her ovipositor such that only its tip remains in the prey. And all this time a milky-white fluid, which quickly hardens, is poured along the ovipositor down to the very prey. This goes on for up to 30 seconds after which the female lowers her ovipositor as deep as possible. Then the chalcidoid very carefully and slowly withdraws her ovipositor while its white tube remains in place, adhered to the body of the host with its lower end while lightly projecting above the reticulate surface of the cocoon. All this lasts 5-10 minutes. Directly after it, having stepped back a little, the chalcidoid finds by means of its antennae the projecting end of the tube and begins to suck through it saps of the host. Only after having consumed this food, rich in proteins, the chalcidoid is able to begin oviposition on the very same prey from wich it before had sucked. She lives about 2-4 weeks and generally lays about a hundred eggs.
A remarkable behavior during the infection of cocoons of the caterpillars of the eastern moth Monema flavescens WLK. displays Eurytoma monemae RUSCH. Apparently not being able to bore the thick and hard wall of the cocoon, the eurytoma, in order to gain access to the caterpillar, is not after the cocoon itself, but tenaciously goes after another parasite, Chrysis shanchaiensis SMITH., also developing at the expense of this caterpillar. When the chrysid starts painstakingly to gnaw through an opening in the wall of the cocoon, in order to oviposit in it, the chalcidoid patiently waits nearby. But as soon as the chrysid concludes its work and closes the opening made by it, the eurytoma comes close, stings its ovipositor through the rather porous plug, made by the chrysid, and lays in the cocoon its egg. In a single cocoon of the moth may develop several tens (up to 83 pieces) of eurytomas, and all of them bail out through the opening, prepared by the chrysid. In the development of the last generation, when Ch. shanchaiensis does not fly anymore, the eurytoma is able to find cocoons of the moth infected by the chrysid earlier, and now it itself bores through them, apparently also through the opening closed by the chrysid. In this case the new generation of the eurytoma develops on the mature larva of the chrysid, and, consequently, the eurytoma is then already a secondary parasite [that is, a parasite of a parasite (= hyperparasite) ].
Similar conditions, in which the transition from primary parasitism to hyperparasitism takes place, are created for chalcidoids also then when other parasites of the same host have more delicate cocoons or integument than the host itself. The pteromalid Eupteromalus nidulans FOERST. hibernates as a mature larva in nests of Euproctis (Lepidoptera), but also in cocoons of braconids (terebrantia-braconidae) as a secondary parasite. Females of the chalcidoid, emerging in spring penetrate into spun nests of Euproctis and lay eggs onto its small caterpillars, on the outside of which the larvae of the chalcidoid then develop. In two weeks after the beginning of feeding of the Euproctis caterpillars, the parasites conclude their development and the mature chalcidoids leave the nest. In summertime various species of braconids of the genus Apanteles turn out to be very attractive to the chalcidoid, and those, having delicate cocoons, suffer more of it than do species having more firm cocoons.
In the considered group of chalcidoids, is shown, apart from a development as hyperparasites, also another line of evolution, namely as internal parasitism. As an instructive example of this might serve Monodontomerus aereus WLK. (of the family Callimomidae). Attacking a number of primary parasites of the unpaired bombycid [Bombyx (or perhaps Orgyia, Bombycidae, Lepidoptera] and Euproctis (Lepidoptera), such as larvae of Apanteles, Meteorus, and the like, in their cocoons, this chalcidoid develops as familial external parasite. This also occurs where mature tachinid larvae are infected by it in their puparia. If the chalcidoid had to attack an immature puparium in which the larval hypodermis is still attached to the wall of the puparium, then the chalcidoid takes its eggs into the body cavity of the host. In this case only a few emerging larvae of it reach maturity because the living conditions inside the immature puparium, evidently, are not favorable enough. In favorable conditions, on the other hand, 24 chalcidoids may emerge from a single mature puparium of [the tachinid fly] Compsilura. In the same way as internal familial parasite this chalcidoid develops in pupae of the unpaired bombycid and Euproctis.
It is interesting to point to the fact that, according to an indication of a number of authors, in various chalcidoids, taking their eggs into the puparia of flies, there is an instinct of sealing off the place of injection on the wall of the puparium at the conclusion of oviposition.
To the group of chalcidoids laying their eggs into cocoons of hosts, one should reckon also a second species of that same genus, namely Monodontomerus cupreus SM. The females of that chalcidoid, as also other representatives of that same family for that matter, are distinguished by having a well developed ovipositor, with the help of which they may penetrate into places of living of their hosts not accessible to other chalcidoids, such as, for instance, into the pit of plum, surrounded by the fruit flesh, or into the cells of various solitary bees, the cells of whom are closed at all sides. Thus, the mentioned chalcidoid is able to bore with its ovipositor through the mineral walls of the cells of Chalicodoma and Antophora [I hope that I have spelled the names of these two genera correctly], or [through] the firm separating walls made of green wax in the nests of Osmia, and to lay onto the body of the bee larvae, resting in those nests [cells] 15-20 eggs. The larvae, having hatched from these eggs, feed ectoparasitically on the "larva-wet-nurse". The emerging adult chalcidoids gnaw themselves an exit out of their inclusion.
The familial ectoparasitic Phase is represented by yet a third biological group of chalcidoids, namely those that develop on preys free-living on plants. Thus, the chalcidoid Euplectrus bicolor SWED. (family Eulophidae) hits various caterpillars of owls (Lepidoptera) (gamma owl, cabbage owl, and others), living on the surface of stems and leaves. See next Figure.

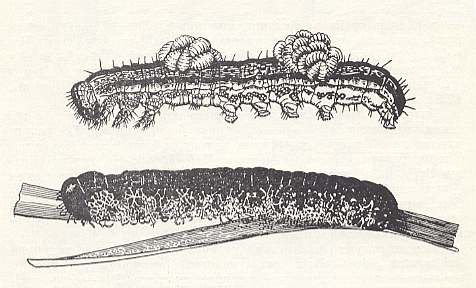
Figure 1 : Two groups of larvae of the chalcidoid Euplectrus on a caterpillar (top), and a number of loosely twined cocoons beneath the caterpillar (bottom).
(From CLAUSEN, 1940, in MALYSHEV, 1966)

Having found such a caterpillar, many times larger than the parasite, the female Euplectrus climbs on it and starts to walk over it, in spite of the fact that the caterpillar in all possible ways resists -- crawling fast, curving, contracting, and even attempting to pour upon the terebrant a foamy mass coming from its mouth. Then the chalcidoid stings the caterpillar 2-3 times with its ovipositor. As a result of this, the movements of the caterpillar slow down and it comes to rest, beit only for a short time. Using this moment, the parasite quickly lays a portion of eggs onto it, on average 15 pieces, distributed usually on the dorsal side of the anterior segments (except the first). Of such egg clutches there are sometimes two or three on a single caterpillar. One female chalcidoid infects not more than two caterpillars with the common number of laid-eggs up to 50.
The eggs are kidney-shaped, on their concave side with a short stalk by which they get firmly attached to the integument of the caterpillar. They are not placed in a compact group, but individually at a distance of 1 mm from each other. Soon after emerging, the larvae gnaw through the skin of the caterpillar, each one on its own spot of attachment, and not changing it until concluding feeding. Proportional to their growth, the larvae automatically crowd each other such that the anterior segments of their body strongly contract, and the individuals that are in the center take a vertical position in these crowding conditions, especially in the case of extraordinary large egg clutches. Some of the larvae (usually the peripheral ones) begin to stay behind in their growth, are on the decline, and may even perish, but a direct struggle among them is nevertheless not observed. In 5-6 days after having begun feeding, the larvae reach their limits of growth. At this time the caterpillar dies. Having left the place of suction, the chalcidoid larvae distribute themselves along the remains of the caterpillar and twine loose cocoons. The whole of the development from egg to the emergence out of the pupa of the winged chalcidoid lasts about a month. It is assumed that in the course of summer three generations develop. The last one hibernates in the adult state.
In the same way, at the expense of free-living caterpillars on leaves (for example the caterpillar of Orgyia antiqua L.), develop as a whole family also the larvae of the chalcidoid Cratotechus longicornis THOMS. (of the nearby subfamily Eulophinae). But they do not form a compact mass on the body of the caterpillar, but are ordered into one series along the sides of its body and therefore do not crowd each other. Having concluded feeding, they are going to lie on their back in a circle near the caterpillar which is sucked empty by them with their heads directed toward it, that is, toward the center [of the circle], and, while not making a cocoon, pupate.
Also free-living on leaves do develop as families the chalcidoid Schizonotus sieboldi RATZ. (of the family Cleonymidae), namely on beetle pupae of the willow multicolored leaf eater Plagiodera versicolora LAICH. and [other] chrysomelids related to it. Having hibernated in the adult stage, this chalcidoid lays some eggs onto the thorax of the pupa of the mentioned beetle between the limbs, and sometimes on its abdomen, and even on its back. The female chalcidoid thereby feeds on fluid (hemolymph) oozing out from the stings applied by her on the back of the pupa of the beetle after oviposition.
Hereto we must also reckon the chalcidoid Scymnophagus townsendi ASHM. (of the Pteromalidae), developing on the outside of pupae of ladybird beetles (Coccinellidae) feeding on aphids. During oviposition the chalcidoid stands up on a projecting region of the back of the pupa and applies a preliminary sting with its ovipositor in order to create a wound for feeding. In the course of several hours she may lick up hemolymph oozing out from the sting wound. After satiation, the chalcidoid again drives its ovipositor usually into the same place but now lowers it totally, through the whole body of the prey, in order to place an egg at the ventral side of the abdomen, or at the wing rudiment, or on a leg. And this feeding and oviposition continues until a heap of 4-6 eggs is laid.
Among chalcidoids of the Phase under discussion we must recognize yet a fourth group of parasites attacking preys that live in hiding places, not totally isolated, whereto females of the parasite may penetrate in order to oviposit directly onto the prey. As an example of this may serve the chalcidoid Eulophus viridulus THOMS. (Eulophidae), parasitizing on more or less fully-grown caterpillars of the corn moth Pyrausta nubilalis HBN. See next Figure.

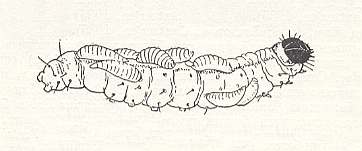
Figure 2 : Larvae of Eulophus viridulus on a caterpillar of the corn moth.
(From SWEETMAN, 1936, in MALYSHEV, 1966)

While making irregularly curved channels in stems of corn, hemp, and a number of other large grassy plants, these caterpillars from time to time gnaw transverse openings in the walls of the stem through which they throw out aggregated wormhole. These openings, apparently, are often used by the eulophus, in order to penetrate to the caterpillar. Having reached the prey, the chalcidoid paralyzes it by stings of its ovipositor, such that all movements of the caterpillar and locomotion along the stem stop forever. Then the chalcidoid lays onto it 15-20 eggs, distributing them along its surface, not at all adhering them to the body of the prey. The larvae develop very fast, and during the course of a few days only an empty skin remains of the caterpillar. Having concluded feeding, the larvae of the parasite crawl a little away and pupate there inside the channel, after having attached themselves with their abdominal end to its wall. In the course of a year three generations develop, and the last one hibernates in the pupal stage inside the channel of the prey. Many found families of the chalcidoid consisted of females only, but in others both sexes were represented in a proportion of two females and one male. Mating takes place, evidently, inside the channel until fly-off from the stem.
The chalcidoid Dibrachys clisiocampae (FITCH.), belonging to the family Pteromalidae, looks for caterpillars of the bee moth, Galleria mellonella L., making spun channels in the waxen constructions of bees. As a result of the stings by the parasite the moth-caterpillars die. The chalcidoid does not place eggs onto them until they die.
To the present (fourth) group of terebrants-ectoparasites we must also reckon the remarkable, occurring in India and China, braconid (Braconidae) Cedria paradoxa WLHN. Having laid onto the caterpillar (Pyralididae, Lepidoptera) that has been paralyzed by it, 30 eggs, C. paradoxa does not leave them, but remains at its developing offspring until they are transformed into pupae and emerge. Then she flies off and searches for a new prey. In this way, C. paradoxa is able to guarantee up to five broods. But the number of eggs to lay by her on the next preys becomes smaller and smaller. Thus, in a number of females, having given four broods, were found in consecutive egg clutches on average 31.4, 20.3, 10.0, and 3.0 eggs. A supposition is made that in normal conditions the female infects just one prey and lays on it all of these eggs. Remaining with the young, the female does not take food, and in summertime her life lasts in total 3 weeks. But hibernating fertilized females may live up to 253 days. It is assumed that, with staying together with the young, C. paradoxa guards [protects] them from chalcidoids.

Onto the present Phase of familial ectoparasitism also step representatives of the bethyloid wasps (Bethyloidea) of the family Bethylidae. [See for the bethyloids, Part XLVII of the present Series on Hymenoptera]. Familial ectoparasitism of larvae of bethylids was, apparentltly, noted for the first time by AUDOUIN, 1842. He observed that in spring the bethylids Goniozus ("Bethylus") formicarius PZ. in large numbers agilely ran on young twigs of grapevine already infested by the vine leaf-roller Tortrix pilleriana SCHIFF. The investigator was convinced that these small wasps attacked the caterpillars of the leaf-rollers. Having grabbed the caterpillar at the anterior part of its body, the bethylid "killed" it quickly. Oviposition was not observed, but in June, on a leaf of the vine a caterpillar of the leaf-roller was found, on the posterior half of which there were eight small legless larvae of a light-green color with their anterior ends sunken between the rings of the caterpillar's body. Having concluded feeding, the larvae abandoned the body of the caterpillar, twined cocoons, and after two weeks adults emerged from them. This concise report was elucidated with beautiful illistrations.
Substantial data about the life and habits of a related species, Goniozus claripennis FORST., reports VOUKASSOVITCH, 1924. Penetrating from behind into the habitation of the caterpillar of the leaf-roller very slowly and carefully not to startle it, the bethylid flings itself onto the prey and paralyzes it with its sting, the stinging act taking 20-30 seconds, and then greedily licks the hemolymph copiously pouring out of the wound. See next Figure.

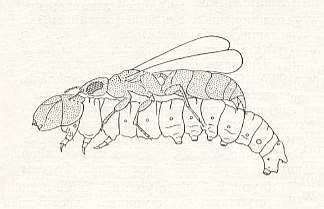
Figure 3 : The bethylid Goniozus claripennis paralyzes a caterpillar of the vine leaf-roller.
(From VOUKASSOVITCH, 1924, in MALYSHEV, 1966)

Then the wasp lays a small number of eggs (1-8), firmly attaching them onto the skin of the prey at determined places, one or two per segment, where also, not leaving the places of adherence, feed its larvae.
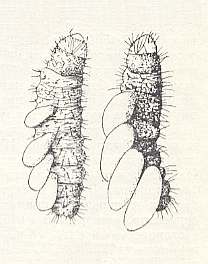
The bethylid Perisierola emigrata ROH. attacks caterpillars of the cotton moth (Pectinophora gossypiella SAUND.) living in the capsules of the cotton plant ("rose worms"), and [attacks] also some others. See next Figure.

Figure 4 : Four larvae of the bethylid Perisierola emigrata placed on a caterpillar. On the right : almost fully-grown. (From CLAUSEN, 1940, in MALYSHEV, 1966)

Having reached the prey, the wasp climbs on its back, walks forward, firmly holds itself with its jaws precisely behind [the prey's] head, bends its body around the caterpillar and stings it from below, behind the mandibles. The second sting is applied at the middle of the prey's body, and a third into the anal segment. Sometimes the caterpillar is hit first at its posterior end, disabling it to bend and bring damage to the parasite. During the stinging the caterpillar strongly swings and fights back, but after that becomes more calm for some five minutes. This is sufficient for the bethylid to oviposit. The eggs are laid onto the underside of the caterpillar, one per segment, usually from 4 to 6, but sometimes -- onto a larger prey -- two times as many. Development proceeds fast. The larvae hatch in the course of 24 hours, and after 2-3 days conclude feeding and then twine cocoons near the remains of the host. Emergence of adults takes place in 10-15 days after oviposition. The males, having emerged first, gnaw openings in the cocoons of the females, penetrate into them and mate there. The oviposition period lasts 1.5 - 2 months, and a female may lay, with interruptions, 150-200 eggs.
Among bethylids, laying a small number of eggs onto the prey, we see also the ability to drag the prey and hide it in some remote place. Substantial observations of this were done already by HALIDAY, 1835, see RICHARDS, 1932. On the fifth of June he spotted a female Bethylus fuscicornis JUR., having thrown itself onto a mature caterpillar of a moth, fallen off from a rose shrub into a depression in the sand. Having grabbed with its jaws the prey, six times as heavy as itself, the bethylid, in the course of 10 minutes, without success attempted to get out of the depression with it, but then climbed up a stalk of straw placed before it and went backwards with the prey. Having gone about a meter, the wasp discovered a piece of a straw stalk projecting from the sand hill, and having, at its base, inserted the caterpillar, began to inspect the surroundings of the hill. Then it descended from the hill and went to the straw stalk. Finally the prey was dragged into the stalk with the head in front. The subsequent course of events was not followed, but it was supplemented by later observations, namely those of FERTON, 1901, who discovered this bethylid on the fifth of June on Corsica in a dry stalk of a blackberry-bush. Here, together with the wasp itself, there were 4 larvae of the wasp, having fed on a green caterpillar, of which almost only its skin had remained.
Similar observations were made by NIELSEN, 1905, on another species -- Bethylus cephalotes FOERST. In an opened twig of blackberry, in which there was an abandoned nest of Pemphredon, at a distance of several centimeters from the entrance to the cavity the investigator spotted this bethylid with a paralyzed caterpillar of a leaf-roller which the wasp was trying to drag further on. A little deeper inside the channel there was another caterpillar -- Tortrix, but this one was almost sucked empty by three larvae of the wasp. In the channel there were no separating walls.
The ability of Bethylus cephalotes to transport the prey was later confirmed by RICHARDS. On the small (10 mm long) paralyzed caterpillar of the night owl the wasp laid 6 eggs, whereby 5 eggs were adhered, one after the other, to the anterior margin of each of the five first abdominal segments, and the first of them, in addition, carried yet a second egg next to the first one. The larvae hatched in 5 days. They had their heads, as turned out later, attached in all cases (except the case of the second egg placed on the first abdominal segment) to the posterior margin of the adjoining segment. In 5 weeks after oviposition emergence of the adults took place.
The method of distributing the eggs on the body of the prey deserves attention in the presently discussed group of bethyloid wasps. They lay their eggs not disorderedly scattered over the body of the prey in different places, as it was noted above for the chalcidoids, but in a rigorously determined way. Let us give some examples of this.
The bethylid Laelius trogodermatis ASHM. (of the Sclerodermini) parasitizes on larvae of Dermestidae and related beetles. In the first days of emergence, the fertilized female Laelius takes to the search for her prey. Having found it, the wasp climbs on its back and firmly holds itself despite strong resistance of the prey. Then, as soon as the beetle larva becomes calmer the parasite moves to its thorax and, having bent its abdomen to the side, drives its sting behind the second or third pair of legs. The sting penetrates, apparently, into one of the thoracic ganglia, because the prey is quickly paralyzed. After this, the bethylid begins to tug the prey at its hairs and legs. During this, the antennae of the wasp vibrate in a characteristic way, as if inspecting the result of the operation. Then the wasp plucks with its mandibles the hairs [of the prey] at the underside of the abdomen and places eggs on the denuded skin of the prey. But before attaching the egg, the wasp drives its sting several times into the given spot, making, apparently, an opening through which the later hatched larva may sink its head into the body of the host. In this way up to 6 eggs are laid. They are oriented longitudinally and are placed in two series along the ventral side of the prey. Sometimes only one egg is laid, but the overall mass of eggs which the bethylid might carry is two times more than its own mass. The whole development takes 30-35 days. Sometimes the wasp develops parthenogenetically [the female then is not fertilized] but then she produces only males.
In the same way, according to the substantial observations of EMDEN, behaves Cephalonomia quadridentata DUCH., belonging to that same group Sclerodermini. See next Figure.

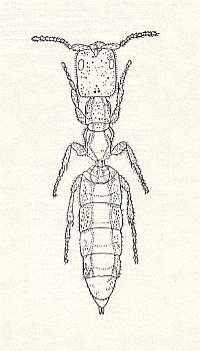
Figure 5 : The bethylid Cephalonomia sp. (From BERLAND, 1951, in MALYSHEV, 1966)

She penetrates into the cocoon containing the larva of a beetle -- the cereal anobiid Stegobium paniceum L. (Coleoptera, Anobiidae) -- and living in it for several days (in favorable conditions 3-4 days), feeds on the saps of the prey. In this time she lays usually four eggs on the body of the prey after having preliminarily smoothed certain places between the segments. Let us add that Cephalonomia tarsalis ASHM., parasitizing on larvae of beetles of the family Cucujidae -- Oryzaephilus surinamensis L., lays in toto two eggs onto the prey, from which one, predestined to develop into a female, is laid on the side of the prothorax, and the second, which always delivers a male, is laid on the metathorax.

Earlier Part XLVII were given comparatively more simple cases of bethylids, [namely those] laying in toto only one egg onto the body of the prey and also on a rigorously determined place and in a determined way. They are characteristic also of a number of other solitarily parasitizing bethylids. Such a type of behavior led, as was already noted, into the direction of development of the habits of higher wasps of the type Tiphia and its relatives. But it, we must assume, gave the start also to the more complex instincts of the just discussed bethylids that lay onto one and the same prey a small number of eggs always in a rigorously determined way. In the higher wasps, vespoids and sphecoids, we already do not encounter such a peculiar method of oviposition -- of a number of eggs in a determined way and onto a single prey. It is clear that this line of familial parasitism of bethylids, in contrast to the solitarily parasitic [line], led them to a dead end, and did not give rise to the habits of the higher wasps.
When the laying of several eggs onto the prey began to take place in an isolated place, it created, as it would seem, the possibility of a prolonged being-together of the mother with her offspring. Such a contact did nevertheless here not take place, evidently because still other necessary prerequisites were missing. By virtue of historically formed conditions, the bethylid-mother belonging to the present group, as we saw, searched for and hit a prey onto which she could lay just a few eggs. Otherwise the offspring would not develop or would turn into dwarfs. In addition, in those cases when the bethylid (for chalcidoids and braconids this is not typical) have to drag the prey [to some place], she, evidently, could not accept extraordinary large larvae [as prey] but only those that surpass her own weight six times and not more, which all by itself limits the size of her egg clutches. But also such a kind of provisioning is, so to say, super-massive, in contrast to usually-massive characteristic of many vespoid and sphecoid wasps, bringing to the cells [i.e. to each cell] a prey sufficient for the nursing of only one larva.
In spite of this, in all considered cases of familial ectoparasitism in chalcidoids, braconids, and bethylids, not for feeding of the mother itself on the body of the prey, nor for a repeated oviposition by her on the same prey, sufficient conditions were created, and therefore the mother could not here stay for long with her offspring even in a remote well-isolated place. All this became realized in the next Phase of evolution in specially formed conditions.

With all this we conclude our exposition of the Ectoparasitic Hemi-Familial Phase of hymenopterous evolution.
In the next document we will -- still on our way to ants -- expound the Familial Ectoparasitic (Hemi-Formicoid) Phase.

Noëtics

Before we turn to this next document continuing with the evolution of ants, we pause for a while to supplement our step by step development of the noëtic theory of evolution.

Every biological adaptation of organisms to other organisms is in fact an internalization, an internalization that is, into the (morphological, physiological, or behavioral) plan of the adapting organism, an internalization of precisely that particular aspect of the plan of an organism to which the adaptation is. For example, the physiology of an endoparasitic larva must be tuned to that of its host, and in this way the parasitic larva has, just by the way it is qualitatively constituted, (evolutionarily) internalized some aspect of the biochemistry and physiology of the host, resulting in its being adapted to the conditions inside a particular species of host. This is how things are (found) in the Explicate Order. In the Implicate Order, on the other hand, we have immaterial noëtic patterns, among which the earlier discussed strategies (A strategy in the Implicate Order is a certain noëtic pattern that is in fact a prescription for it [where "it" is the strategy itself] to (materially) exist in the Explicate Order and then having become ontologically complete), and the mentioned "internalization" is here (in the Implicate Order) represented by a capture, a capture that is, by a given strategy of some part of another strategy, which here means nothing else than the two strategies having some part in common. It is the result of some noëtic reaction, and upon projection we see, in the Explicate Order the presence of the corresponding adaptation involving the mentioned internalization.

Geographic isolation and separation of faunae and florae (playing such an important role in evolution) is an individual state of affairs, and thereore wholly and exclusively belonging to the Explicate Order. For example, in the Implicate Order, a strategy of [as we see it in the Explicate Order] some South American species, can [noëtically] react with that of some Australian species [it is just a reaction of two noëtic patterns]. But course of this reaction cannot be projected into the Explicate Order because no conditions for it exist in the Explicate Order : There can, as a result of the geographic isolation, be no interactions between individuals of the two species.

As has been expounded earlier, a strategy, insofar as it is a noëtic pattern in the Implicate Order, is in fact a description. It is a description, not made by anyone or anything, of how this very description itself may exist and persist in the Explicate Order. Upon existing in this Order the description is, as it were, replaced by its meaning expressed in material biological terms. And a description, as it resides, as a noëtic pattern, in the Implicate Order, is in fact a linear entity, a noëtic string, where the linearity here is not spatially meant, neither temporally, but purely consecutively meant. The parts of the description, just as a description, are ordered logically, and that is here : noëtically ordered. And such a description, such a strategy, such a noëtic string, resides at the noëtically correct 'location' (not spatially meant) in the 'space' (not spatially meant) of the Implicate Order. 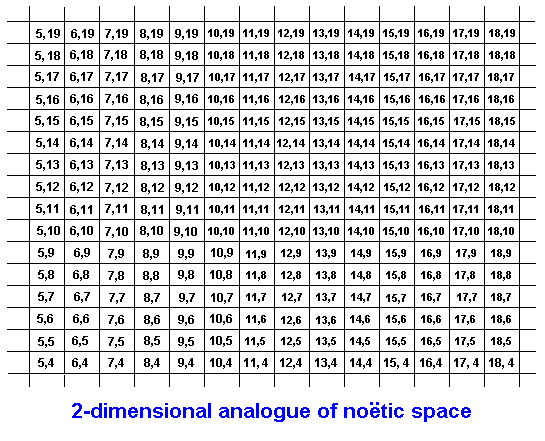We may imagine each entity in the noëtic space having a set of noëtic coordinates expressing its location in that space. They express the noëtic neighborhood of such entities. The noëtic string is in fact a band, and this band represents the noëtic stability field, in the Implicate Order, of that string. It is the noëtic subspace in which the strategy is externally, noëtically, stable. The strategy itself then is a line (or curve) inside this band, meaning that it allows for slight variation within its stability field (The line can assume differnt positions within the band). Evidently the noëtic space is multi-dimensional, so the set of coordinates indicating the location in that noëtic space of some part of a given strategy (or any other noëtic pattern) consists of a more or less large number of elements (Translated in spatial terms the set of coordinates representing a given point in a given space consists of as many numbers as there are dimensions of this space). In expounding our noëtic theory in its generality we simplify things : We present the Implicate Order as a mere two-dimensional space, in which each point has a set of two numerical coordinates. And we represent a strategy by giving only a (relevant) part of it, and thus by giving only the corresponding part of its noëtic stability field, that is, as a part of a band. And each part of such a band, and also each region of the noëtic space for that matter, is represented by the noëtic coordinates of one representative point in it. Let us then draw two bands, each one being just a part of a whole band (strategy stability field), as they are situated in the noëtic space. Let us begin with that space itself. This noëtic space has a g l o b a l analogous [= continuous] structure indicated by the coordinates :

And now two bands situated in it :

These two noëtic strings (bands), A and B, being in each other's noëtic neighborhood, may therefore (noëtically) react with each other. They are then noëtic reactants. In the next example we let the result of this reacion be : Strategy A remains unchanged, while a part of strategy B qualitatively approaches strategy A, resulting in A and B' having some small part in common (represented by the coordinates (11,17) and (12,17)), or, said differently : Strategy B internalizes a part of strategy A (resulting in B becoming B') (upon projection into the Explicate Order this corresponds to a one-sided adaptation of B to A.) :

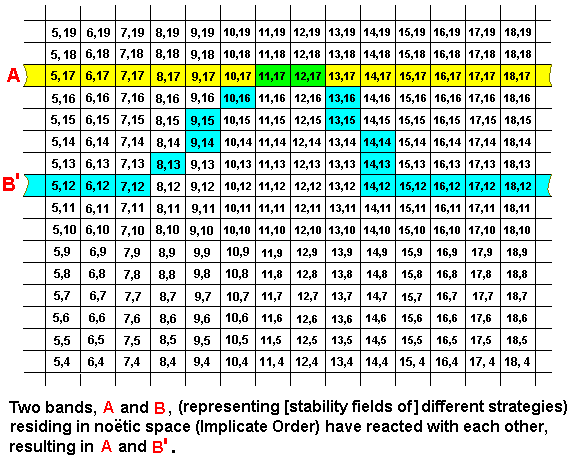
As always in the Implicate Order, the reactants are not exhausted by a reaction : Together with their product or products they remain existing in the Implicate Order. Further, in the present example, the reaction product is not some sort of merged entity : In fact there are two reaction products : (1) the unchanged reactant A, and (2) the changed reactant B (which we can call B'). The overlap of the strategies is only qualitative. They are still two (different) strategies. If we have two (or more) reactants engaging in a noëtic reaction, then the result (product or products) is rigorously determined. For the quality of the ensuing reaction product there are no (several different) options or possibilities, because in the Implicate Order we do not have differing thermodynamic conditions (as we have them in the Explicate Order). There are no such conditions at all in the Implicate Order because they are exclusively implied by the material nature of the entities in the Explicate Order. A noëtic reaction's first (but not yet sufficient) condition is that the reactants must lie in each other's noëtic neighborhood. The other conditions lie in the quality (whatness) of the strategies themselves (that is, they may lie in each other's noëtic neighborhood, but can nevertheless be noëtically incompatible, resulting in the fact that they will not react with each other). In the Implicate Order we must distinguish between noëtic reacions and the noëtic derivations they imply. In the present case we have the noëtic reaction A + B ==> A + B', whereas we have the derivations A ==> A, and B ==> B'. So in this case the noëtic trajectory (we talk about it further, later) stays here in strategy A, and goes from strategy B to strategy B'.

We can also imagine a noëtic reaction between two strategies (represented by bands) in which the adaptation (as seen in the Explicate Order) is mutual (one adaptation and one responding adaptation), that is, both reactants are changed in a corresponding place in their bands :

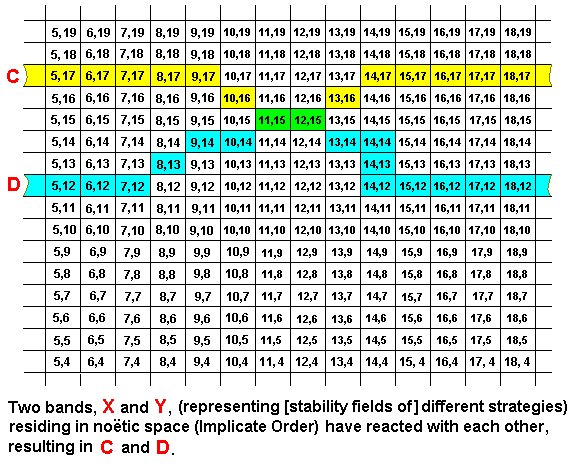
Also here we have two separate reaction products (while the original reactants keep on existing [in the Implicate Order]). They have a small part in common, expressed by the coordinates (11,15) and (12,15). Here the noëtic reaction is X + Y ==> C + D, whereas the implied derivations are X ==> C, and Y ==> D. And here the noëtic trajectory goes from strategy X to strategy C, and from strategy Y to strategy D.

Further, we can imagine that two strategies noëtically react with each other, resulting in, as we see it in the Explicate Order, a mutual adaptation (again, one adaptation and one responding adaptation), but now not at corresponding places in the noëtic string (represented by a band), but at different places :

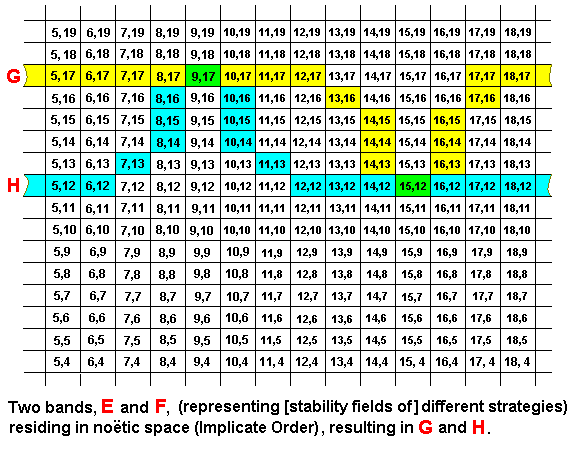
Here the original reactant F has internalized the part of E represented by the coordinates (9,17), resulting in the product H. At the same 'time' the original reactant E has internalized the part of F represented by the coordinates (15,12), resulting in the product G. So the noëtic reaction between E and F resulted in the products G and H, and, as always, the original reactants E and F remain existing in the Implicate Order. In this case we have the noëtic reaction E + F ==> G + H, whereas the implied derivations are E ==> G, and F ==> H. And here the noëtic trajectory goes from strategy E to strategy G, and from strategy F to strategy H.

A noëtic reaction between two strategies can also result in the first reactant having taken over a large part of the second reactant : There exists, for example, a butterfly species that, instead of laying its eggs on the food plant and then letting the caterpillars care for themselves, lets its caterpillars be nursed and guarded by a certain species of ants : As a result of the behavior of the caterpillars they end up near a nest of the ants. Normally the ants will kill any caterpillar they encounter close to the nest and use it as food for their larvae, but this species of caterpillar releases a special ant feromone (a scent) resulting in the fact that the ants recognize it as a larva of their own, carry it into their nest and nurse it like they do with all their larvae, despite its different size and appearance. After having having been fully fed, the caterpillar pupates, and the emerged butterfly leaves the ant nest. So here the mentioned butterfly species 'hijacks' a considerable part of the nursing behavior of that particular ant species, while the behavior of the ants themselves is not altered. Schematically, and generally, we can depict this, again in terms of bands (representing [noëtic stability fields of] strategies), residing, as noëtic patterns (descriptions) in the Implicate Order, that noëtically react with each other such that the first reactant remains the same, while the second reactant internalizes a large part of the first reactant and is therfore itself changed considerably :

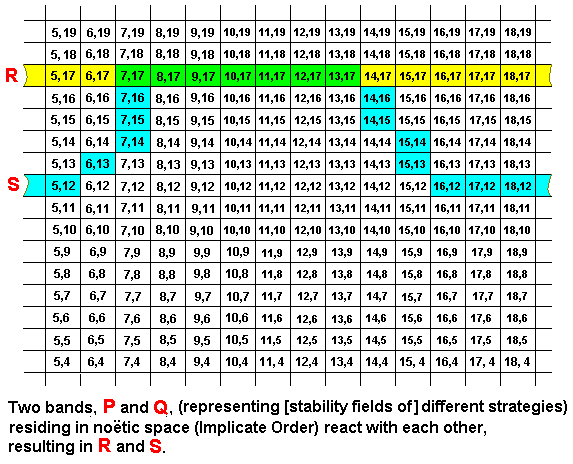
In this case we have the noëtic reaction P + Q ==> R + S, whereas the implied derivations are P ==> R, and Q ==> S. And here the noëtic trajectory goes from strategy P to strategy R, and from strategy Q to strategy S.

Generally we may assume that the driving force of noëtic reactions is the greater noëtic stability of the products.

Apart from two-(or-more)-reactant noëtic reactions, as exemplified above, there are, also in the Implicate Order, so-called one-reactant noëtic reactions, that is, pure derivations. Their counterparts in the Explicate Order are essentially non-adaptive evolutionary changes. They are cases of so-called higher development (anagenesis), that is, a development resulting in a greater integration of the parts of a strategy -- a strategy in the form of a noëtic pattern, as well as in the form of the corresponding material biological strategy (including morphology, physiology and behavior) resulting from projection of the noëtic pattern from the Implicate Order into the Explicate Order. In the afore exemplified two-(or-more)-reactant noëtic reactions the driving force must be the greater noëtic stability of the products (as compared to that of the reactants). However, we cannot speculate about the precise nature of this stability. But we can do so in the case of all one-reactant noëtic reactions, the pure noëtic derivations : Here the driving force (as already explained in earlier documents) is the higher degree of internal, intrinsic, stability of the one product (as compared with the one reactant), resulting from the higher degree of integration of the parts or elements of the strategy (as a noëtic pattern), that is, the higher degree of wholeness of the given strategy (as compared to the one reactant strategy). In a more-than-one-reactant noëtic reaction the derivation of one strategy from another consists in an addition or a subtraction of something to, or from, a reactant strategy. In a one-reactant noëtic reaction (a pure derivation, an anagenesis), on the other hand, generally nothing is added to, or subtracted from, the (one) original reactant : Here we obtain an almost totally new strategy from the old strategy, the derivation driven by just the greater internal noëtic stability of the product. This can sometimes be accompanied by subtraction or addition, it is true, but here not by a subtraction or addition of something from or to a second reactant. In conceived as pure anagenesis there is, in contrast to adaptive reactions, no internalization of something of one reactant by another. Most increases of internal and intrinsic noëtic stability, resulting from anagenesis, do not necessarily involve adaptations, but only 'higher development'. When adaptations turn out to accompany anagenesis, these generally are not true adaptations but simply changes not incompatible with the environment (as is the case in the origin of social insects from solitary ones). 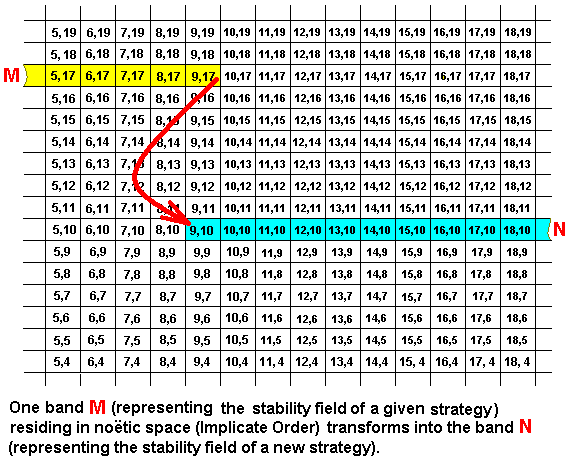We can depict such an anagenetic reaction, such a pure derivation, again in terms of bands (representing [stability fields of] strategies as they reside as noëtic patterns in the Implicate Order : Here the noëtic reaction is M ==> N, and the derivation is (also) M ==> N. And the noëtic trajectory goes from M to N. In the above diagram the one product has nothing in common, it seems, with the one reactant. Of course they must share some general features, such as both being insects and therefore both having six legs. By having the reactant and the product not sharing a part, the diagram expresses the fact that the 'reactant' does not actually participate in the noëtic reaction. It only has a lesser degree of internal noëtic stability than the product has. But because our diagram, like the others, is supposed to show only some small part of the reactant band as well as of the product band, it displays in fact an image of a rather strong 'noëtic microscope'. And this implies that in the above Figure reactant and product do not stand noëtically far away from each other after all, but are, although not 'touching' each other, very close to each other. So the product surely is compatible with the reactant, it cannot originate from just any reactant. Upon projection, we see the counterpart of this noëtic reaction [take place] in the Explicate Order as a new (morphological, behavioral) type of strategy evolutionarily originating in some way from another seemingly unrelated strategy (One of the many instances in Taxonomy of problematic derivation of one group of organisms from another), whereas what we in fact see is merely their being compatible to one another and their temporal consecutiveness. While noëtic space is merely globally and continuously (analogously) ordered by its continuous qualitative dimensions (allowing a system of qualitative noëtic coordinates), the system of noëtic trajectories imposes 'local' and discontinuous order in that same space by everywhere connecting the "derived" from the "original". This system of noëtic trajectories is created by the whole of noëtic reactions, one-reactant as well as more-than-one reactant reactions. In this way, that is, by connecting the various strategies, the noëtic trajectories define a system of noëtic 'ecologies' in the Implicate Order. Upon projection of noëtic patterns from the Implicate Order into the Explicate Order the derivational order is transformed into a time order. The strategies-as-descriptions in the Implicate Order become, upon projection, material biological strategies in the Explicate Order. So it is only upon projection that the pure immaterial Forms become material things and processes. Only then they in-form the Materia Prima (prime matter) of the Explicate Order. Only then they will rest on an ultimate substrate (prime matter) and become physical and individual, and only then, accordingly, they obtain their ontological completion. In the Explicate Order we then see an evolution of organisms : adaptations, diversification, and higher-development. The reactants in both types of the above described noëtic reactions are, of course, also themselves products of some other noëtic reactions. Therefore, in the Implicate Order, many strategies are connected with each other by common parts, indeed creating in this way a network of noëtically ecological relationships. Before we diagrammize this, let us recall that in the above Figures we depicted not strictly the strategy itself (which must be some linear entity, like a line, and be in fact a description) but its band-like noëtic stability field (itself a small subspace of noëtic space). The given strategy can, as noëtic pattern in the Implicate Order, only exist within this field, that is, within its corresponding stability field. And within this field some small variation of the strategy is allowed (expressed by the field's shape and size). Outside this field the strategy cannot exist in the Implicate Order. We showed possible noëtic reactions by letting the reactant and product strategies be represented by their respective noëtic stability fields. And this is completely correct. The strategy is just some linear entity, that we can depict by just a line, running inside the stability field : In the next Figures we will depict only the strategies themselves, and thus draw (curved) lines. Also the system of noëtic coordinates we will not explicitly depict anymore, but assume it, just like the stability fields, to be present nevertheless. 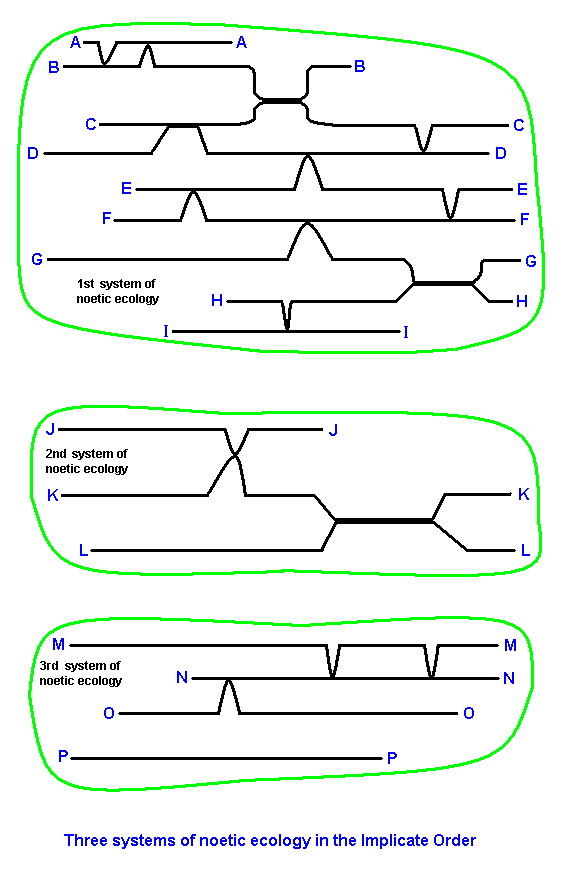Systems of noëtic ecology in the Implicate Order may then be depicted as follows : In the Diagram above, black (straight or/and curved) lines represent (parts of) strategies (indicated by letters), present as linear noëtic entities (descriptions) in the Implicate Order. They are supposed to constitute three systems of noëtic ecology. In these systems we see the connections of strategies with one another being accomplished by local internalizations of a larger or smaller part of one strategy by another, as a result of more-than-one-reactant noëtic reactions. In the Explicate Order they will be ssen as adaptations. In the third system we see the strategy P, assumed to be derived from strategy O, but not by way of a more-than-one-reactant noëtic reaction, and thus not by an adaptive process, that is, not by some form of internalization, but purely as a result of a transition of a strategy with a lower degree of internal noëtic stability (as in O) to a compatible one with a higher degree of such stablity (as in P). This transition we have called anagenesis or higher-development. 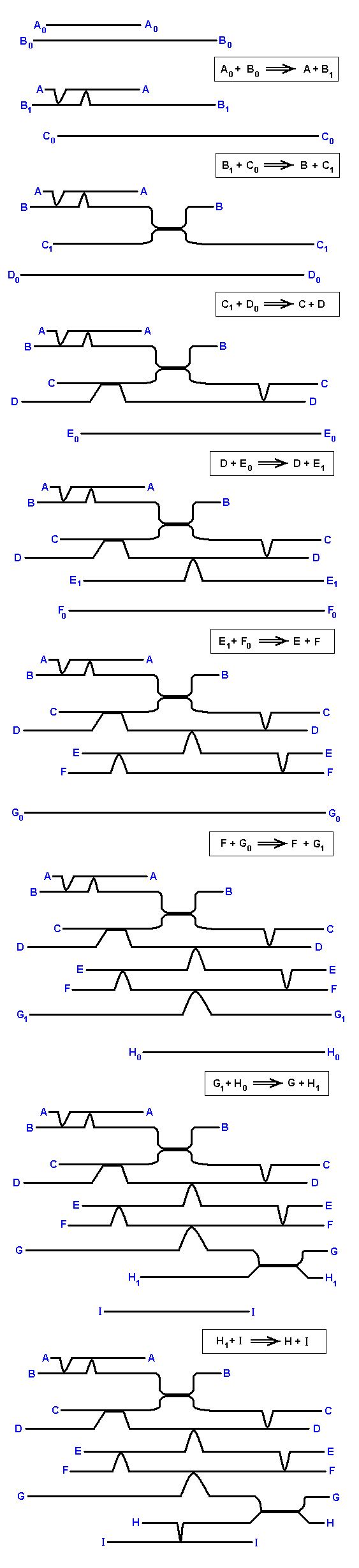Inspecting the first noëtic system, we see the following noëtic reactions between strategies and the corresponding derivations, where the latter trace out noëtic trajectories : In the diagram above it is clear that of the three systems of noëtic ecology their elements (the strategies, A, B, C, D, etc.) are each for themselves already a product of some noëtic reaction. Although the reactants of these reactions do still exist in the Implicate Order (noëtic space), we have not drawn them in the mentioned diagram. But if we want to obtain a full understanding of the noëtic reactions that have given rise to the strategies A, B, C, D, etc (which were drawn) we must include them. In considering them we sometimes have to go back for a few 'generations' of successive noëtic reactions. We will indicate these reactants with a subscript. So, for example, the strategy C has its 'ancestors' (antecedents) C₁, and C₀. Let us now enumerate all the noëtic reactions having given rise to the strategies A, B, C, D, etc. of the first system of noëtic ecology, and after this explain it with the help of a new diagram of that system in which the mentioned reactants are now drawn in. We will write "reactant strategy W + reactant strategy X becomes (as a result of the noëtic reaction) the product strategy Y + the product strategy Z" as : "W + X ==> Y + Z". A₀ + B₀ ==> A + B₁, with the corresponding derivations : A₀ ==> A, and B₀ ==> B₁. B₁ + C₀ ==> B + C₁, with the corresponding derivations : B₁ ==> B, C₀ ==> C₁. C₁ + D₀ ==> C + D, with the corresponding derivations : C₁ ==> C, D₀ ==> D. D + E₀ ==> D + E₁, with the corresponding derivations : D ==> D, E₀ ==> E₁. E₁ + F₀ ==> E + F, with the corresponding derivations : E₁ ==> E, F₀ ==> F. F + G₀ ==> F + G₁, with the corresponding derivations : F ==> F, G₀ ==> G₁. G₁ + H₀ ==> G + H₁, with the corresponding derivations : G₁ ==> G, H₀ ==> H₁. H₁ + I ==> H + I, with the corresponding derivations : H₁ ==> H, I ==> I. Here the full scheme of derivations is : A₀ ==> A. B₀ ==> B₁ ==> B. C₁ ==> C. D₀ ==> D. E₀ ==> E₁ ==> E. F₀ ==> F. G₀ ==> G₁ ==> G. H₀ ==> H₁ ==> H. The next Figure, depicting the complete first system of noëtic ecology, with the 'ancestral reactants' added, explains these noëtic reactions. A given initial strategy, say strategy A₀, not only may noëtically react with strategy B₀ (as we saw above), resulting in strategy A and strategy B₁, where accordingly strategy A₀ was transformed in strategy A (and where B₀ was transformed in B₁), it (that is, strategy A₀) may react with other strategies as well, resulting in a number of additional derivatives of it, all coexisting in the Implicate Order (noëtic space). Many of such derived strategies can together form an iterative series (Just above we already had a few of such series, but there consisting of only two steps). A derivational iterative series consists of a series of items, where each item is derived from the previous one in the series. 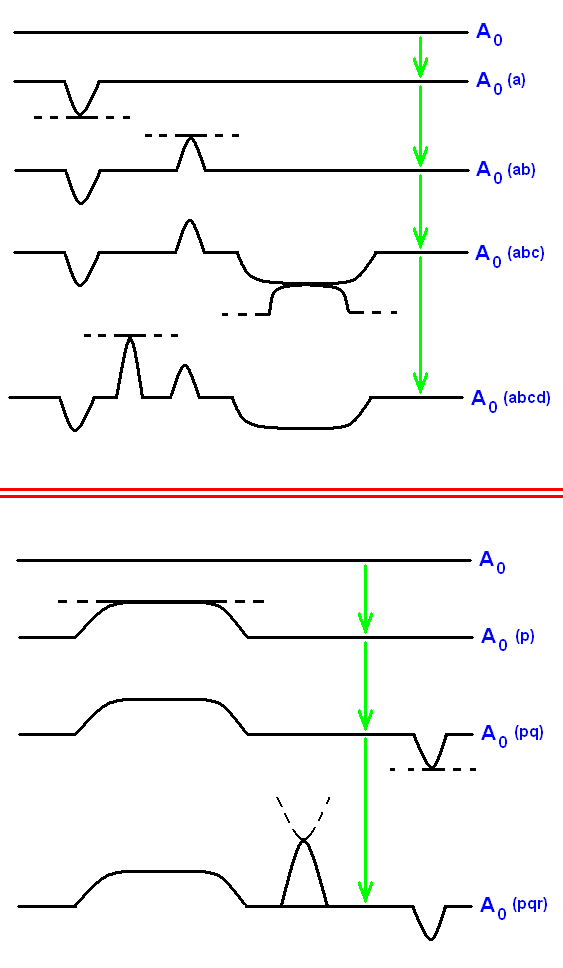So let us set up another few (like the above, also just imaginary) derivative iterative series starting with strategy A₀ (again, each straight and/or curved line represents a given strategy) (and thus extending the first system of noëtic ecology, presented above): And indeed each such derivational iterative series of strategies in the Implicate Order traces out respective segments of the noëtic trajectory, indicated by the green arrows. Now we will analyze the second system of noëtic ecology as it was already given above. 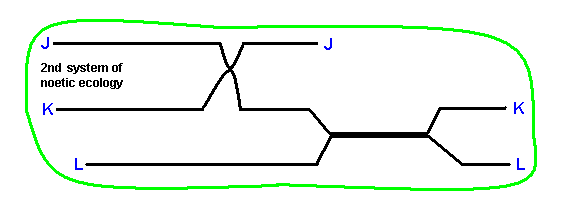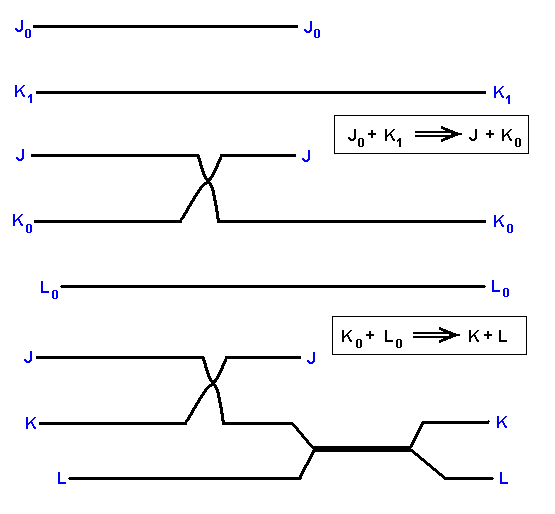To begin with, we depict it again : Analyzing it gives : The derivational sequences are : J₀ ==> J. K₁ ==> K₀ ==> K. L₀ ==> L. They indicate segments of the noëtic trajectory. Finally we will analyze the third system of noëtic ecology as it was already given above. 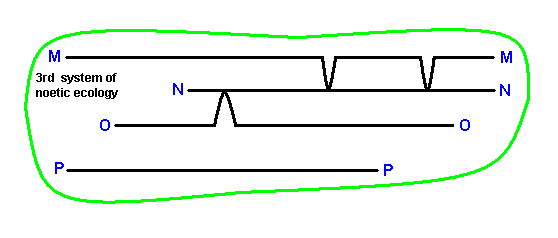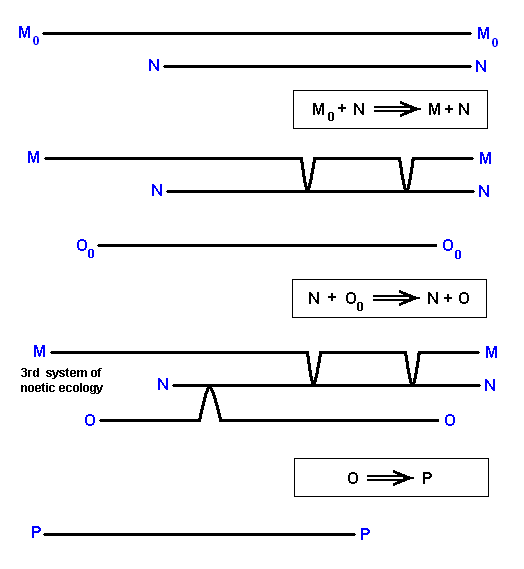To begin with, we depict it again : Analyzing it gives : The derivational sequences are : M₀ ==> M. O₀ ==> O ==> P. The transformation of O into P is supposed to be a one-reactant noëtic reaction, purely driven by the higher degree of internal noëtic stability of P as compared to O (And assumed is, of course, that their noëtic compatibility is such that this transition is possible at all). The mentioned derivational sequences indicate segments of the noëtic trajectory. Recall that in all the above noëtic diagrams each straight and/or curved, more or less horizontally drawn black line segment represents a strategy as that strategy is present in the Implicate Order (noëtic space). And each strategy, only insofar as it resides as a noëtic pattern in the Implicate Order, is in fact a noëtic description : a description of how, for this very description itself, to exist and persist in the Explicate Order, and so obtaining ontological completion. And in our diagrams each one of them, that is, each of the mentioned line segments in it, is supposed to represent only a part of a strategy : The strategy, being a description, is thus a linear (straight and/or curved) noëtic entity, and these diagrams depict only some particular segment of it. The above given systems of noëtic ecology show the one-sided and/or mutual noëtic internalizations of small parts of one strategy by another. Sometimes a large part of a strategy is 'hijacked' by another, as is the case in those represented in the Explicate Order by cuckoo wasps, or by certain butterflies having their larvae nursed and raised by ants, and by the take-over of a whole colony of a social insect species in the case of a social parasite. Smaller, but still substantial parts are hijacked in all cases of specialized individual parasitism, especially the internal parasitism as we see it among terebrants and tachinids, and also in many other parasitic invertebrates. All these cases are the result of noëtic reactions in the Implicate Order : Of course, these reactions, having resulted in the many different strategies, do not take time (because the Implicate Order is timeless). All the possible strategies (and also all the impossible, irrelevant, etc. ones for that matter) -- as long as they are each for themselves a whole and internally non-contradictory -- do exist, as immaterial noëtic patterns, in the Implicate Order. And only when conditions in the Explicate Order are compatible with them they will successively -- according to the noëtic trajectory -- project from the Implicate Order into the Explicate Order. There we see them in the form of the origin and evolution of adaptations (between organisms), and the appearance of new biological and morphological types seemingly coming out of the blue. In the Implicate Order, as has been repeatedly said, no reactants are exhausted in noëtic reactions. Also in the Explicate Order we see many primitive organisms still existing and thriving well. So the mentioned systems of noëtic ecology (drawn above) express the Implicate Order's counterpart of ecological relationships between, often different and taxonomically unrelated species. They show the various internalizations (which in the Explicate Order are expressed as adaptations), and thus how some strategies are derived from others (which did not yet have acquired the given internalizations). And in most cases the reactants of a given noëtic reaction are very different strategies, for example noëtically representing that of a plant species (one reactant) and some insect species (the other reactant). So in such cases there is no way of deriving the one from the other (the given insect species has adapted to the given plant species, but it has evidently not evolved from it). In such cases therefore the noëtic trajectory will not go from one reactant (or from its derivative in the reaction product) of a noëtic reaction directly to the other. But it will go from such a reactant -- a reactant strategy -- to its derivative in the product of the reaction, and in turn from this derivative to the next one, etc., as we had shown it above. So at least many of the derivational relationships are created by the more-than-one-reactant noëtic reactions (which themselves depend on the qualities [whatnesses] of the reactants), and they impose a certain structure onto noëtic space, first of all by the intrinsic internal consistency and wholeness of such a reactant strategy itself, and then by it being a prerequisite (noëtical pre-stage) to another, that is, to its derivative. So all strategies in the Implicate Order are connected to each other by derivational relationships, expressed by the noëtic trajectory (This trajectory evidently is not a single pathway but is branched in many ways, or has even pathways running parallel to each other, that is, are not connected to each other (beit only at their very roots)). But structure in the Implicate Order does not only come from more-than-one-reactant noëtic reactions, but also from so-called one-reactant noëtic reactions. These consist of reactions of the type A ==> B (or O ==> P for that matter, considered above). Here the driving force of the transformation (without exhausting the reactant) is solely the higher degree of internal noëtic stability, as a result of the higher degree of integration of the parts of the product strategy, or higher degree of the latter's wholeness. Upon projection into the Explicate Order we see these transformations as the evolutionary appearance of new, and especially, biologically higher, types of organisms. In addition to the one-reactant noëtic reactions resulting in new types of strategies with a higher degree of internal noëtic stability, there is also another type of one-reactant noëtic reaction, resulting in the Explicate Order in a shift of one or more existing populations of some given organic species to a new environment, say a transition from a terrestrial one to an aquatic one. Here, in the Implicate Order the aquatic strategy (the product) is noëtically derived from the corresponding terrestrial one (the one reactant). So both strategies are already present in the Implicate Order independently of the situation in the Explicate Order. The terrestrial strategy may have already been projected from the Implicate order into the Explicate Order. And then, when conditions in the latter Order are appropriate, the aquatic strategy will also project into the Explicate Order. In the Explicate Order we see all this as follows: The organisms of a certain terrestrial species are present in Nature. Then, at a certain point in geological history one or more populations of this species invade the water, evolutionarily aquiring the necessary adaptations : The species has split in two, one terrestrial and one aquatic. 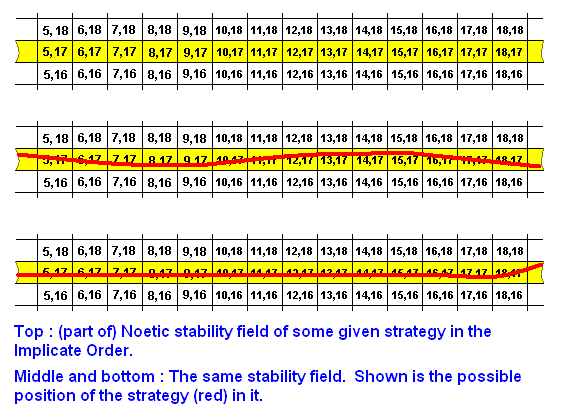Above, we have visualized noëtic space as having qualitative dimensions (there must be many of them, but for simplicity's sake we have drawn only two of them). These qualitative dimensions define noëtic coordinates. See next Figure. The coordinates determine the noëtic position in noëtic space of some given noëtic pattern such as a strategy (itself a noëtic description). But how is such a pattern qualitatively delineated, and thus qualitatively separated, from its noëtic environment? As such this seems impossible because all that we have in noëtic space is continuous variation of quality, expressed by the coordinates. Well, as has been said, the elements of a strategy are not just qualitative parts of noëtic space, not just noëtically continuous parts (they even need not be noëtically continuous at all), but parts that are -- as parts of a description -- logically and rationally connected with each other, like the words in a story. And this means that these parts need not necessarily lie adjacent to each other, but may be separated by parts of noëtic space that do not participate in the description (not participate in the strategy). However, in our above diagrams we have depicted them as c o n t i n u o u s bands, representing the external noëtic stability fields of some given strategy, in which (field) the strategy itself was given as a c o n t i n u o u s line, such as: But this we have only done for simplicity's sake. 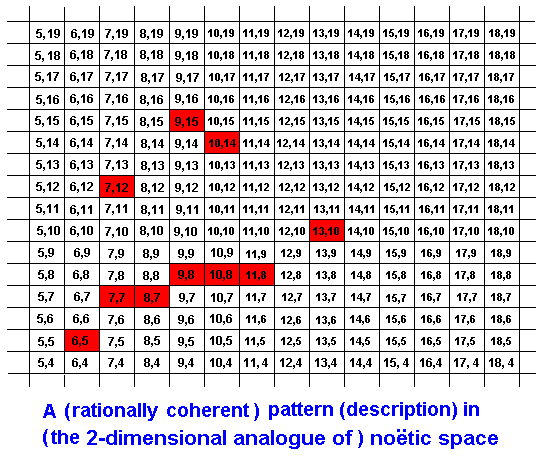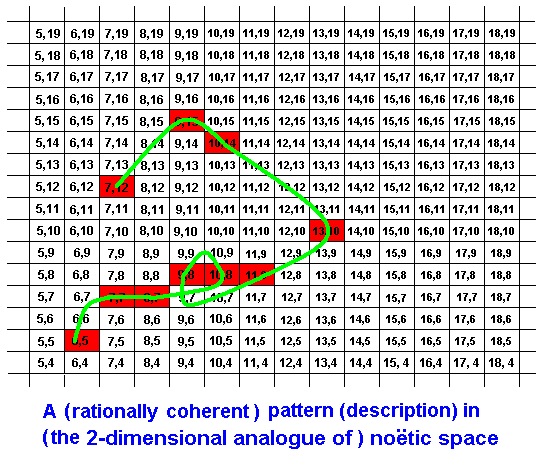In fact the elements of a given strategy (noëtic description) may be scattered over a more or less larger noëtic area in the Implicate Order: The coherence, connecting these elements rationally and logically, might for instance be such: Only those parts of noëtic space do belong to this particular pattern that are marked red. These are the elements of the description (strategy). The rational connecion of these elements is indicated by the green curve. Recall that the noëtic coordinates are not digital but analogous. That is, they are continuous. The coordinates in each rectangle of the diagram represent a single noëtic point, representative of that 'rectangular' element of noëtic space. So between, say, (7,15) and (7,16) there is an infinity of intermediate coordinates : Noëtic space is continuous (and in reality multidimensional). Internalization of some part of a strategy (noëtic description) by another strategy might take place as follows:

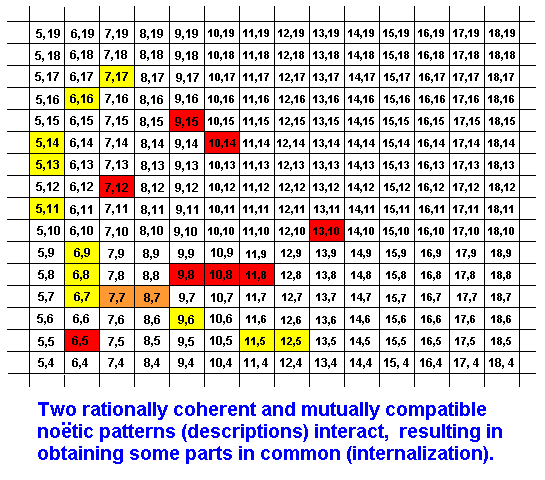
The 'red' strategy has noëtically interacted with the 'yellow' strategy resulting in obtaining parts (orange) common to them. In the Explicate Order we see this as a one-sided or mutual adaptation of two organic species. So the relation between these organisms is not taxonomical (phylogenetic) but ecological. (End of intermezzo on the noëtic theory)

With all this we conclude our further development of the noëtic theory of organic evolution.
In the next document we will -- still on our way to ants -- expound the next Phase of Hymenopterous evolution, the Familial Ectoparasitic (Hemi-Formicoid) Phase.

e-mail :