We had found out that in the Implicate Order (noëtic space) the immaterial patterns -- existing in it -- strive for ontological completion. They can achieve this by being projected into the Explicate Order. Then pure Forms will -- as a result of being unrolled along the space and time dimensions of the Explicate Order -- "inform" Prime matter. Each such a Form will then be manifested as a collection of material "individuals", variable in number and place of occurrence. But projection of a given immaterial pattern -- a Form -- from the Implicate Order into the Explicate Order can only take place if prevailing existential conditions in the Explicate Order are compatible to and receptive for this pattern. So it is expected that most immaterial patterns, noëtic patterns to be sure, -- and especially very complex patterns -- will never be projected, because they have the greatest chance to lack any compatibility with the Explicate Order. But, as we have explained earlier, some such complex patterns will nevertheless manage to be projected, because they are in fact patterns of a special sort :  they are "descriptions", descriptions that is, in a strictly ontological sense, meaning that they are not written down by some one author. And they are not only just descriptions, but each one of them a description of a particular "strategy" of how for this very description itself to exist and persist in the Explicate Order. And, upon projection into the Explicate Order, they appear there materialized as  o r g a n i s m s.  The organism (including its internal chemistry, physiology, morphology, and behavior) is the manifestation or meaning, in the Explicate Order, of that noëtic description. So we must imagine such a "strategy", as it is in the Implicate Order, that is, as it is a noëtic description, to be  a   s t r i n g  (with a definite direction) of consecutive "symbols", a string located in a definite 'place', that is, at a set of definite noëtic coordinates, in noëtic space, as we had already explained in the "noëtics" section of Part LVII of the present Series of Documents :

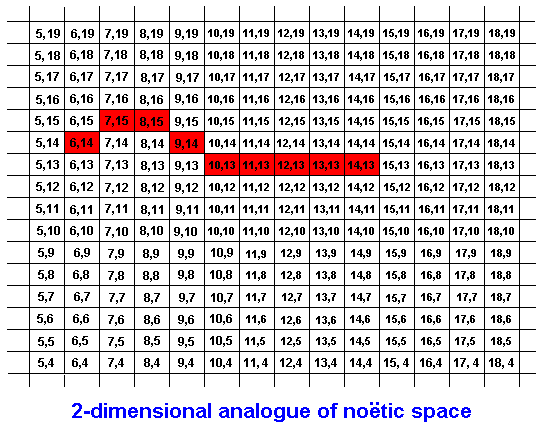
Figure 1 :  Greatly simplified and schematic sketch of a  STRING  in a 2-dimensional analogue of noëtic space (which itself is not spatial and which is multidimensional, where a "dimension" is a scale or range of a given qualitative parameter). Each  red  rectangle represents a symbol of this string. The identity and nature of each symbol is determined by its position in noëtic space, that is, by its noëtic coordinates. The coordinates in any rectangle (white or red) are those of a single representative point of the rectangle (for instance its upper left corner). Here the string possesses only nine different symbols. In reality, however, that is, in noëtic space, it will, when it expresses a strategy, consist of a great many such different symbols of course.

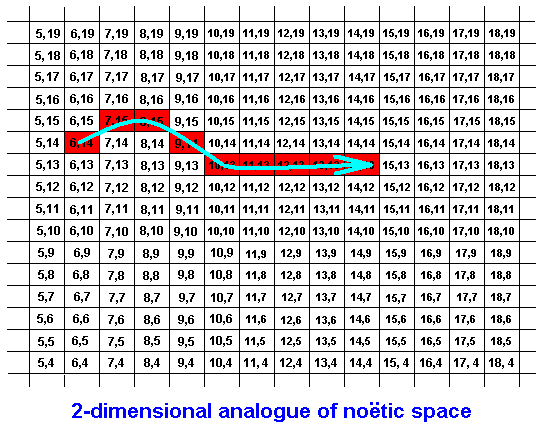
Figure 2 :  Noëtic trajectory.  The fixed direction within a STRING in noëtic space. The fixed consecutiveness of the symbols in the string (resulting from, or representing the STRING's internal direction) can be given by their consecutive (representative) noëtic coordinates :  (6,14), (7,15), (8,15), (9,14), (10,13), (11,13), (12,13), (13,13), (14,13).

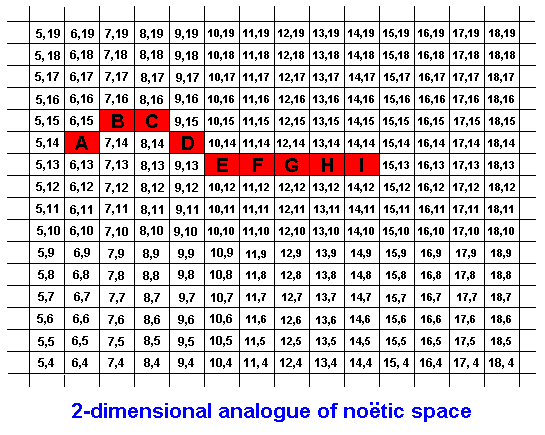
Figure 3 :  The same STRING as in the previous Figure. Here its symbols are represented by the letters A, B, C, D, E, F, G, H, and I.

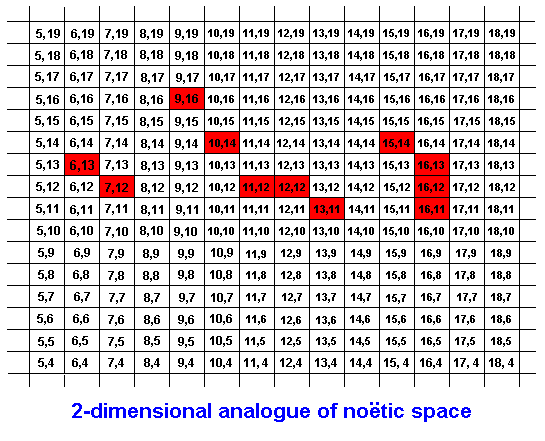
Figure 4 :  A  STRING  of which its elements, its symbols, are not contiguous. Nevertheless it is supposed to be one single string, one single noëtic description (strategy).

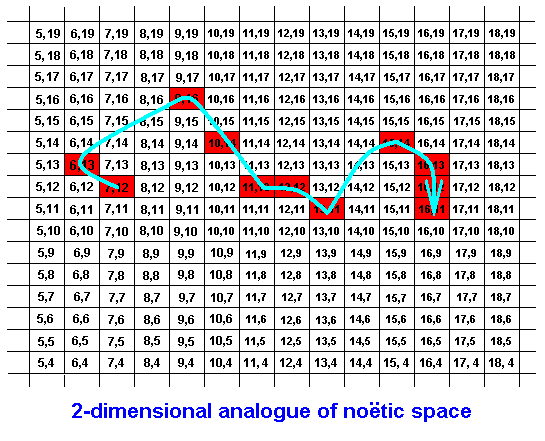
Figure 5 :  Internal direction of the  STRING  of the previous Figure. Following the arrow, the intermediate not-red regions of noëtic space do not belong to this given string.

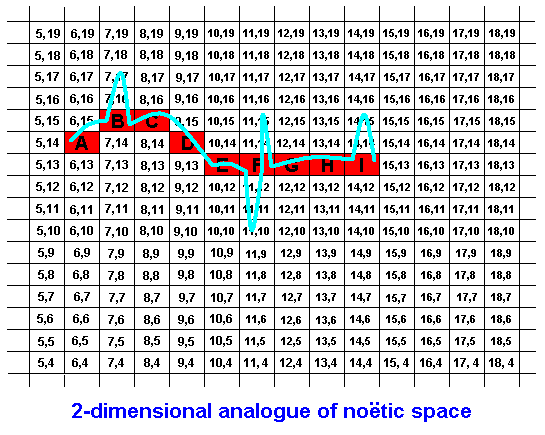
Figure 6 :  The string  ABBCDEFFFGHII  in noëtic space. The blue curve, read from left to right, indicates the consecutive order of the symbols of this string.

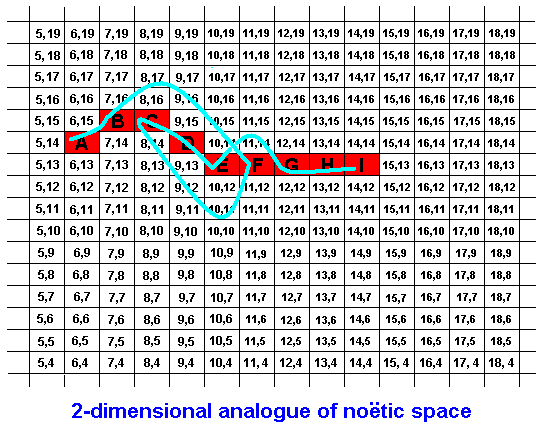
Figure 7 :  The string  ABFCDEGHI  in noëtic space. The blue curve, read from left to right, indicates the consecutive order of the symbols of this string. Also here the intervening white rectangles through which the curve runs do, as all other white rectangles, not belong to this string.

If we speak about noëtic reactions between  strategies  (which upon projection appear as organismic species in the Explicate Order) they always involve -- when the result is seen in the Explicate Order -- adaptations of one strategy to the other. And what exactly IS an "adaptation"? Well, a given organismic species has some aspects of its organization  adapted  to some aspects of the organization of the other species, when the organization of that given species has  internalized  something of the organization of the other species into its own organization. So as a result of this adaptation the organizations of these two (species of) organisms -- their (material) strategies -- have some features in common. In the Implicate Order this means that the two strings, representing their noëtic strategies, also have a larger or smaller part in common. And this is the result of the noëtic reaction between the two strategies. Let us see :

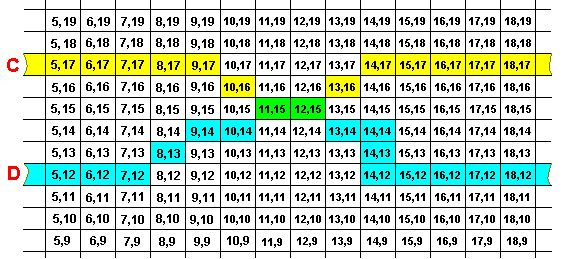
The two products of the noëtic reaction are C and D.  The reaction was A+B ==> B+C.  Here the two strategies have become mutually adapted to each other  [ For example a given organism adapts to the internal environment of another species (the conditions inside the body of its representatives) and thus becomes an internal parasite, living in the host in possibly great numbers, while the host, as a reaction, develops the ability to physiologically recognize the parasite in its body and to produce substances that significantly decreases the number of individuals of the parasite in the host's body, resulting in the parasite infection, while still causing some disease in the host, not to be lethal to the host anymore].
So in this case C has been derived from A, and D from B.
But  IF  the set of derivational Rules of the formal system of our noëtic strings does NOT contain either the rule

[meaning respectively :  If the string A can directly or indirectly be derived from the axiom-strings of the system on the basis of the Rules of the System, that is, if string A is a "theorem" of the System, then string C is also a theorem of the System. And, in the same way, if the string B can directly or indirectly be derived from the axiom-strings of the System on the basis of the Rules of the System, that is, if string B is a "theorem" of the System, then string D is also a theorem of the System.]

or (does not contain) both these rules,  THEN  this particular noëtic reaction cannot take place [the strings A and B may be able to react with each other in some other way (resulting in different adaptations, and so resulting in, say, the strings E and F), but definitely not in the present way]. This means that in that case the string C cannot noëtically exist in the Implicate Order, meaning further that the organismic species corresponding with the noëtic strategy A cannot develop the adaptation that transforms it into another organismic species corresponding with noëtic strategy C.  And in the same way, that the organismic species corresponding with the noëtic strategy B cannot develop the adaptation that transforms it into another organismic species corresponding with noëtic strategy D.  So evolutionary potentialities are ultimately rooted in the derivational Rules of the noëtic formal system of strategies.

Formal systems, as they are defined in the context of mathematical proof theory, that is, as they are formalizing some piece of mathematics (or physics or biology for that matter), are creations of the human mind, either for their own sake, or in order to investigate the general structure and nature of some given existing entity or entities (such as geometry, arithmetic, a physical state of affairs, etc.).
One of the aspects of the mentioned general structure of some given existing entity (broadly conceived) is its consistency (= the absence of contradictory states of affairs in it).  Consistency is about such an existing entity and involves its formalization. When the mentioned entity is consistent it means that no false statement about its elements or larger parts can be found in the formal system in the form of a theorem or axiom (or, said differently, no false statement can be proved to be true by the formal system). So consistency involves the formal system plus its interpretation. We cannot speak of the consistency of the formal system taken alone.
Completeness also involves the formal system plus its interpretation. But here the emphasis is on the formal system. It means that all true statements that can be made about the elements or larger parts of that given existing entity reappear as theorems or axioms in the formal system (of which that given entity is an interpretation). The interpretation or meaning of the formal system, or of its various parts, may be the result of isomorphy found between, on the one hand, the symbols of the system, and the parts or elements of the mentioned existing entity :  isomorphy creates meaning.

Ontologization of formal systems.
So formal systems are creations of the human mind. They need not be arbitrary constructions. They may be geared into some existing structure (whether this is mathematical, physical, or biological), but are mental creations nontheless, and are associated with obtaining knowledge. The status of formal systems is therefore epistemological, not ontological. So if we think that "formal systems" might help us in understanding the generalities of organic evolution still better, thus if we think that the Implicate Order (noëtic space) consists of "formal systems" with their intrinsic Rules of derivation (and so giving a derivational structure to noëtic space), and (if we think) that some of such systems have as their elements, that is, their "strings", the noëtic strategies as they reside in noëtic space, then we must in some way "translate" the epistemological features of formal systems into ontological features. We will now explain how to do so.
The statement or proposition (made by humans) about the three (internal) angles of a triangle -- any triangle -- in Euclidian two-dimensional space (i.e. in the usual flat plane), namely that these three angles together form an angle of 180 degrees, is something epistemological, that is, referring to our knowledge. For such statements it is perfectly relevant to say that they are "true" or "false". The just expressed statement (proposition) about the angles of any triangle is "true".
In ontologizing this, we take into account not the statement about the angles of any triangle, but take exclusively into account the  existing state of affairs with respect to triangles. Here we take "triangles" as objectively existing entities that can be studied. Indeed, the aforementioned statement was about the existence of a certain state of affairs with respect to triangles ("the triangle as such"). An when indeed the described state of affairs (the angles of any triangle adding up to 180 degrees) exists, the statement is true. And if we now ontologize this, then we transpose this "truth" from (what was said about) the statement  to  that state of affairs. So the existence of that state of affairs is ontologically equivalent to the truth of that state of affairs (and not merely to the truth of the mentioned statement about that state of affairs). Indeed, already in the Middle Ages it became established (the philosophers basing themselves on Aristotelian metaphysics) that ontologically (= in the context of the theory of Being, that is, as to Being) "to be a Being" (Ens) is equivalent with "to be True" (Verum) [and also with "to be Good" (Bonum), to be "Beautiful" (Pulchrum), and, finally, with "to be Something" (Aliquid) ]. It was the theory of the transcendentalia.
So upon ontologization, we consider, not the truth or falsity of statements about elements of that particular existential domain which forms the interpretation (meaning) of the formal system, but the existence or non-existence of these elements themselves. The mentioned existential domain might be formed by some subdiscipline of mathematics, such as Euclidean geometry, or by some domain of the physical world, or whatever. In our case it is formed by the system of "material strategies" as we see them in the Explicate Order -- organismic species with all their paraphernalia. The corresponding formal system (or systems) of which the set of material strategies is an interpretation, is thought, not to be created by the human mind (like all other formal systems), but to objectively exist in the Implicate Order (noëtic space), as the set of noëtic strategies and the intrinsic derivational rules by which one noëtic strategy can be formed (derived) from an other. The strategies exist there as noëtic "descriptions" and can thus be imagined as "strings" residing in noëtic space, as shown above. A certain number of these strings (or perhaps only one of them) are the "axioms" of the formal system, while the remainder of the strings are its "theorems". And these theorems can be derived ('produced') directly or indirectly from the axioms by means of the Rules of Derivation of the system (the system possesses a fixed number of these specified rules).
The material strategies of species of organisms (in the Explicate Order) constitute the meanings of the corresponding noëtic strategies in the Implicate Order :  the individual elements of a given noëtic strategy (the "letters" of the [noëtic] description) play, within that noëtic strategy, i.e. within that string, a similar role as do the elements of the (corresponding) material strategy. And this generates  meaning  (of the individual symbols as well as of the strings).
So also here our "ontologization" means that we do not consider statements (made by humans) about those material strategies (organismic species seen in their completeness), but those strategies themselves, as existing states of affairs. And also here it is such that if a given strategy exists (in the Explicate Order) then it is itself true (and thus not only the statement that it exists).
If we, for the time being, suppose that we, with respect to evolution, have to do with just one single formal system noëtically existing in the Implicate Order, and further, certainly legitimately, assume that this system is at least as complex (i.e.at least as strong) as the system of arithmetic, something interesting follows :
If it is so that according to one of GÖDEL's theorems (applied to our noëtic formal system plus interpretation) it is so that there are always (some)  true  material strategies (that is, really existing material strategies) that cannot, as noëtic strategies be legitimately derived from some other noëtic strategy (which either may be an axiom of the system or one of its theorems) of the formal system, then this underivable (noëtic) strategy must itself be a (new) axiom of the formal system. But then there will, in turn, pop up some more existing material strategies that cannot, as noëtic strategies, be derived from the axioms or theorems of the (new) formal system.
This implies that the formal system (of evolution) possesses, not just one, but more than one, or even many, axioms. And this in turn means that the evolution of Life has a strongly  polyphyletic  nature, meaning here that a strong degree of polyphyly, already encountered in the Explicate Order, upon descending along the lines of descent continues to be present also in the Implicate Order.
["Polyphyletic" development of organisms means that organisms evolutionarily develop along lines of descent, many of them such that they, upon descending back into evolutionary history, remain separated from, and thus independent of, each other for quite a long time or even for all their length. And we have found out that this independent course of many such evolutionary lines of descent probably extends well into the Implicate Order, that is, into noëtic space.]
But even when these extra axioms turn out to be only very few in number, and even when they, moreover, have, as to their content (their meaning), little to do with strategies, the fact is that any formal system as strong as or stronger than Number Theory, which our formal system of noëtic strategies certainly is, has the ability to 'speak about itself' :  The need to add extra axioms to the formal system came forth from the fact that in such a system some of its strings could 'speak' about themselves. The possibility of this strongest form of self-reference was a simple consequence of the possibility of a weaker form of self-reference, namely the fact that certain strings of the system may 'speak' about other strings of the system. This means that noëtic strategies are descriptions that may contain 'passages' about other strategies. This is certainly intriguing, and in itself already enough to enquire about the general nature of formal systems while constantly referring to the noëtic space of evolution. Another consequence of the intrinsic nature of (strong) formal systems, already stated, is the fact that  truth  as such is not finitely describable, that is, describable by and within any finite formal system (where the latter can 'say' that a given statement -- being part of the system's meaning, that is about which the system 'speaks' -- is true or false). Gödel's sentence by which he could prove his incompleteness theorem was obtained (and translated into the language of the formal system under enquiry) by thinking about the ancient Paradox of the Liar. This paradox, which was known already to Aristotle, consists of a single sentence L, " This sentence is not true". If  L is true, then L is not true. And if  L is not true, then L is true. There are two odd things about L. The first odd thing is that it is a sentence that refers to itself (the strongest form of self-reference, mentioned above) :  L says, "L is not true". Now, Gödel was able to show that self-reference is not really such a big problem in translating it into arithmetical terms (the language of the formal system enquired into).
So it must be the second odd thing about L that is causing the trouble (in completely and finitely describing some property). It must be that there is no finite mathematical way (coding for sentences) to express the property "truth", or "x" is the code number of a true sentence" (because "true" cannot be finitely described). This is how Gödel came to see that "truth" has no finite mathematical description. The fundamental logical notion of "truth" has no rational definition. And what is for us especially interesting is that there are reasons to believe that ontologically Being and Truth are equivalent (as being two of the so-called "transcendentalia" mentioned above). And if we consider "genuine being" to be "existing in the Explicate Order" (where noëtic patterns acquire ontological completion), then we can say that "existence" (of material strategies for example), so conceived, is not finitely describable. And by what medium are actually or possibly existing organismic species (material strategies) supposed to be described? Well, by that medium of which these material strategies are supposed to be meanings. And this medium, our theory proposes, is the formal system of noëtic strategies in the Implicate Order. So the very existence ('being') of material strategies in the Explicate Order cannot completely be ontologically accounted for by the formal system of noëtic strategies (bringing their meaning forth by having themselves projected into the Explicate Order). This further emphasizes a degree of  transcendence  obtaining between the two Orders of Reality, viz., between the Explicate and Implicate Orders. So again, we indeed should investigate the general nature of  formal systems.

We will do this almost exclusively under the guidance of the relevant texts in the earlier mentioned (in connection with the ant fugue) book "GÖDEL, ESCHER, BACH,  AN ETERNAL GOLDEN BRAID",  written in 1979 by Douglas R. HOFSTADTER. (we here use the text of the 20th-anniversary edition, 2000). As has been said, formal systems (wherever they are described in the professional literature) are man-made, and so are those that are considered in HOFSTADTER's book. Indeed the book is about provability in mathematics, about cognition, about intelligence, and about the possibility of artificial intelligence. And indeed, a formalized version of  X  (where X is a certain part or aspect of the world) serves to know X better, and may show the limits of knowing X, or may show that the formalized version of  X is inconsistent. And, as said above, of the formal systems we're going to deal with, we must "ontologize" all aspects that are as to their nature epistemological, except, of course, those (other) particular epistemological aspects that need to remain epistemological. For aren't we trying to know something about the noëtic space of evolution?
So the formal system that is central to us is the system of noëtic strings (descriptions of strategy) in the Implicate Order. And this system is ontological. It is not a means to investigate the world of existing material strategies (the organismic species, each one in its full spectrum) which is its "meaning".  It is not created by the human intellect for using it as a cognitive tool. It is not created by the human intellect at all, but independently exists in the Implicate Order of Reality. But in order to come to know all features characteristic of a formal system as such (later some of these features being ontologized when necessary) we must study an example of one of them that has not yet been ontologized, that is, one that cannot, for the time being, be considered to independently exist. We do this because formal systems are offered to us by the experts as systems having this epistemological status. And what would in this respect be better than to take as an example a formal system that is, first of all, not too complex, and, secondly, is an independent creation by the mind of an expert (Hofstadter)! The system is even such that it does not suggest any interpretation. So in studying it we will not be distracted by suggestive meanings of its symbols and strings. We can fully concentrate on its being a  formal  system. And this purely formal system is Hofstadter's  MIU-system concocted at pp.33 in his book. And to anticipate things, we will see that every formal system can be embedded in Number Theory (which we call "N", and which is about natural numbers, viz., the numbers 0, 1, 2, 3, ....) and then be questioned in terms of this theory's formalization " TNT " (Theoria Numerorum Typografica), the typographical number theory. So also the formal  MIU-system, but, more interestingly, the formal system of noëtic strings in the Implicate Order, can be questioned by Number Theory. For instance it could be asked whether there are existing material strategies (organismic species) that do not occur as theorems in the noëtic system of strategy-strings, and must therefore be axioms of that system (these strings being underivable from other strings of the system), implying polyphyly also in noëtic evolutionary space. Further it can be questioned about "Being", that is about the nature of "existing in the Explicate Order", and about noëtic strategy-strings expresseing things about other such strings. So, in these enquiries, the formal system TNT, in contrast to the ontological formal system of noëtic strategies, retains its epistemological nature.
Let us now turn to the MIU-system, created by Hofstadter.

This section (of the present document, following HOFSTADTER's text, pp.33), introduces you to a formal system, and moreover, it is my hope that you will want to explore this formal system at least a little. So to provoke your curiosity, I [Hofstadter] have posed a little puzzle.
"Can you produce MU ?"  is the puzzle.  To begin with, you will be supplied with a  string (which means a string of letters). Not to keep you in suspense, that string will be MI. Then you will be told some rules, with which you can change one string into another. If one of those rules is applicable at some point, and you want to use it, you may, but -- there is nothing that will dictate which rule you should use, in case there are several applicable rules. That is left up to you -- and of course, that is where playing the game of any formal system can become something of an art. The major point, which almost doesn't need stating, is that you must not do anything which is outside the rules. We might call this restriction the "Requirement of Formality". In the present Chapter, it probably won't need to be stressed at all. Strange though it may sound, though, I predict that when you play around with some of the formal systems of Chapters to come, you will find yourself violating the Requirement of Formality over and over again, unless you have worked with formal systems before.
The first thing to say about our formal system -- the MIU-system -- is that it utilizes only three letters of the alphabet :  M, I, U. That means that the only strings of the MIU-system are strings which are composed of those three letters.
Below are some strings of the MIU-system :

    MU
    UIM
    MUUMUU
    UIIUMIUUIMUIIUMIUUIMUIIU

But although all of these are legitimate strings, they are not strings which are in your "possession". In fact, the only string in your possession so far is MI. Only by using the rules, about to be introduced, can you enlarge your private collection.
Here is the first rule :

Rule I :  If you possess a string whose last letter is I, you can add on a U at the end.
Thus :   ... I  ==> ... IU

By the way, if up to this point you had not guessed it, a fact about the meaning of "string" is that the letters are in a fixed order. For example, MI and IM are two different strings. A string of symbols is not just a 'bag' of symbols, in which the order doesn't make any difference.
Here is the second rule :

Rule II :  Suppose you have Mx. Then you may add Mxx to your collection.
Thus :   Mx  ==> Mxx

What I mean by this is shown below, in a few examples.

From MIU, you may get MIUIU.
From MUM, you may get MUMUM.
From MU, you may get MUU.

So the letter 'x' in the rule simply stands for any string. But once you have decided which string it stands for, you have to stick with your choice (until you use the rule again, at which point you may make a new choice). Notice the third example above. It shows how, once you possess MU, you can add another string to your collection. But you have to get MU first!  I want to add one last comment about the letter 'x' :  It is not a part of the formal system in the same way as the three letters M, I, and U are. It is useful for us, though, to have some way to talk in general about strings of the system, symbolically -- and that is the function of the 'x' :  to stand for an arbitrary string. If you ever add a string containing an 'x' to your "collection", you have done something wrong, because strings of the MIU-system never contain "x" 's!
Here is the third rule :

Rule III :  If  III occurs in one of the strings in your collection, you may make a new string with U in place of III.
Thus :   ... III ...  ==> ... U ...

Examples :

From UMIIIMU, you could make UMUMU.
From MIIII, you could make MIU (also MUI).
From IIMII, you can't get anywhere using this rule.
     (the three  I's have to be consecutive)
From MIII, make MU.

Don't, under any circumstances, think you can run this rule backwards, as in the following example :

From MU, make MIII.  This is wrong.

Rules are one-way.
Here is the final rule :

Rule IV :  If  UU occurs inside one of your strings, you can drop it.
Thus :   ... UU ...  ==> .......

From UUU, get U.
From MUUUIII, get MUIII.

There you have it. Now you may begin trying to make MU.  Don't worry if you don't get it. Just try it out a bit -- the main thing is for you to get the flavor of this MU-puzzle. Have fun.

The answer to the MU-puzzle appears later in the book [and later in the main Section of the present document]. For now, what is important is not finding the answer, but looking for it. You probably have made some attempts to produce MU.  In so doing, you have built up your own private collection of strings. Such strings, producible by the rules, are called  theorems.  The term "theorem" has, of course, a common usage in mathematics which is quite different from this one. It means [in mathematics] some statement in ordinary language which [statement] has been proven to be true by a rigorous argument, such as Zeno's Theorem about the "unexistence" of motion, or Euclid's Theorem about the infinitude of primes. But in formal systems, theorems need not be thought of as statements -- they are merely strings of symbols. And instead of being  proven,  theorems are merely  produced,  as if by machine, according to certain typographical rules. To emphasize this important distinction in meanings for the word "theorem", I will adopt the following convention in this book :  when "theorem" is capitalized, its meaning will be the everyday one -- a Theorem is a statement in ordinary language which somebody once proved to be true by some sort of logical argument. When uncapitalized, "theorem" will have its technical meaning :  a string producible in some formal system. In these terms the MU-puzzle asks whether MU is a theorem of the MIU-system.
I gave you a theorem for free at the beginning, namely MI.  Such a "free" theorem is callled an  axiom -- the technical meaning being quite different from the usual meaning. A formal system may have zero, one, several, or even infinitely many axioms.
Every formal system has symbol-shunting rules, such as the four rules of the MIU-system. These rules are called either  rules of production  or  rules of inference.  I will use both terms.
The last term which I wish to introduce at this point is  derivation.  Shown below is a derivation of the theorem MUIIU :

(1)  MI ------------------ axiom
(2)  MII ----------------- from (1) by rule II     ( Mx  ==> Mxx)
(3)  MIIII ---------------- from (2) by rule II     ( Mx  ==> Mxx)
(4)  MIIIIU -------------- from (3) by rule I      (... I  ==> ... IU)
(5)  MUIU -------------- from (4) by rule III    (... III ...  ==> ... U ...)
(6)  MUIUUIU --------- from (5) by rule II     ( Mx  ==> Mxx)
(7)  MUIIU ------------- from (6) by rule IV    (... UU ...  ==> ......)

A derivation of a theorem is an explicit, line-by-line demonstration of how to produce that theorem according to the rules of the formal system. The concept of derivation is modeled on that of proof, but a derivation is an austere cousin of a proof [because of its explicit production]. It would sound strange to say that you had  proven  MUIIU, but it does not sound so strange to say you have  derived  MUIIU.

Most people go about the MU-puzzle by deriving a number of theorems, quite at random, just to see what kind of thing turns up. Pretty soon, they begin to notice some properties of the theorems they have made. That is where human intelligence enters the picture. For instance, it was probably not obvious to you that all theorems would begin with M, until you had tried a few. Then, the pattern emerged, and not only could you see the pattern, but you could understand it by looking at the rules, which have the property that they make each new theorem inherit its first letter from an earlier theorem. Ultimately, then, all theorems' first letters can be traced back to the first letter of the sole axiom MI -- and that is a proof that theorems of the MIU-systems must all begin with M.
There is something very significant about what has happened here. It shows one difference between people and machines. It would certainly be possible -- in fact it would be very easy -- to program a computer to generate theorem after theorem of the MIU-system. And we could include in the program a command to stop only upon generating U. You now know that a computer so programmed would never stop. And this does not amaze you. But what if you asked a friend to try to generate U? It would not surprise you if he came back after a while, complaining that he can't get rid of the initial M, and therefore it is a wild goose chase. Even if a person is not very bright, he still cannot help making some observations about what he is doing, and these observations give him good insight into the task -- insight which the computer program, as we have described it, lacks.
Now let me be very explicit about what I meant by saying  this shows a difference between people and machines. I meant that it is possible to program a machine to do a routine task in such a way that the machine will never notice even the most obvious facts about what it is doing. But it is inherent in human consciousness to notice some facts about the things one is doing. But you knew this all along. The difference, then, is that it is possible for a machine to act unobservant. It is impossible for a human to act unobservant. Notice I am not saying that all machines are necessarily incapable of making sophisticated observations. Just that some machines are. Nor am I saying that all people are always making sophisticated observations. People, in fact, are often very unobservant. But machines can be made to be totally unobservant. And people cannot. And in fact, most machines made so far are pretty close to being totally unobservant. Probably for this reason, the property of being unobservant seems to be the characteristic feature of machines, to most people. For example, if somebody says that some task is "mechanical", it does not mean that people are incapable of doing the task. It implies though, that only a machine could do it over and over without ever complaining, or feeling bored.

It is an inherent property of intelligence that it can jump out of the task which it is performing, and survey what it has done. It is always looking for, and often finding, patterns. Now I said that an intelligence can jump out of its task, but that does not mean that it always will. However a little prompting will often suffice.
How well have computers been taught to jump out of the system? I will cite one example which surprised some observers. In a computer chess tournament not long ago in Canada, one program -- the weakest of all the competing ones -- had the unusual feature of quitting long before the game was over. It was not a very good chess player, but it at least had the redeeming quality of being able to spot a hopeless position, and to resign then and there, instead of waiting for the other program to go through the boring ritual of checkmating. Although it lost every game it played, it did it in style. A lot of local chess experts were impressed. Thus, if you define "the system" as "making moves in a chess game", it is clear that this program had a sophisticated, preprogrammed ability to exit from the system. On the other hand, if you think of "the system" as being "whatever the computer had been programmed to do", then there is no doubt that the computer had no ability whatsoever to exit from that system.
It is very important when studying formal systems to distinguish working within the system from making statements or observations about the system. I assume that you began the MIU-puzzle, as do most people, by working within the system, and that you then gradually started getting anxious, and this anxiety finally built up to the point where without any need for further consideration, you exited from the system, trying to take stock of what you had produced, and wondering why it was that you had not succeeded in producing MU. Perhaps you found a reason why you could not produce MU. That is thinking about the system. Perhaps you produced MIU somewhere along the way. That is working within the system. Now I do not want to make it sound as if the two modes are entirely incompatible. I am sure that every human being is capable to some extent of working inside a system and simultaneously thinking about what he is doing. In formal systems, at least, it is important to distinguish between working inside and outside the system.

An observation about this puzzle is that it involves rules of two opposing tendencies -- the lengthening rules and the shortening rules. Two rules (I and II) allow you to increase the size of the strings (but only in very rigid, prescribed ways, of course), and two others allow you to shrink strings somewhat (again in very rigid ways). There seems to be an endless variety to the order in which these different types of rules might be applied, and this gives hope that one way or another, MU could be produced. It might involve lengthening the string to some gigantic size, and then extracting piece after piece until only two symbols are left, or, worse yet, it might involve successive stages of lengthening and then shortening and then lengthening and then shortening, and so on. But there is no guarantee of it. As a matter of fact, we already observed that U cannot be produced at all, and it will make no difference if you lengthen and shorten till kingdom come.
Still the case of U and the case of MU seem quite different. It is by a very superficial feature of U that we recognize the impossibility of producing it :  it doesn't begin with an M (whereas all theorems must). It is very convenient to have such a simple way to detect non-theorems. However, who says that that test will detect all non-theorems? There may be lots of strings which begin with M but are not producible. Maybe MU is one of them. That would mean that the "first-letter test" is of limited usefulness, able only to detect a portion of the non-theorems, but missing others. But there remains the possibility of some more elaborate test which discriminates perfectly between those strings which can be produced by the rules, and those which cannot. Here we have to face the question, "What do we mean by a test?" It may not be obvious why that question makes sense, or is important, in this context. But I will give an example of a "test" which somehow seems to violate the spirit of the word.
Imagine a genie who has all the time in the world, and who enjoys using it to produce theorems of the MIU-system, in a rather methodical way. Here, for instance, is a possible way the genie might go about it :

Step 1 :   Apply every applicable rule to the axiom MI. This yields two new theorems :  MIU,  MII.
Step 2 :   Apply every applicable rule to the theorems produced in step 1. This yields three new theorems :  MIIU,  MIUIU,  MIIII.
Step 3 :   Apply every applicable rule to the theorems produced in step 2.
                This yields five new theorems :  MIIIIU,  IIUIIU,  IUIUIUIU,  IIIIIIII,  MUI.
    .
    .
    .

This method produces every single theorem sooner or later, because the rules are applied in every conceivable order. See next Figure.

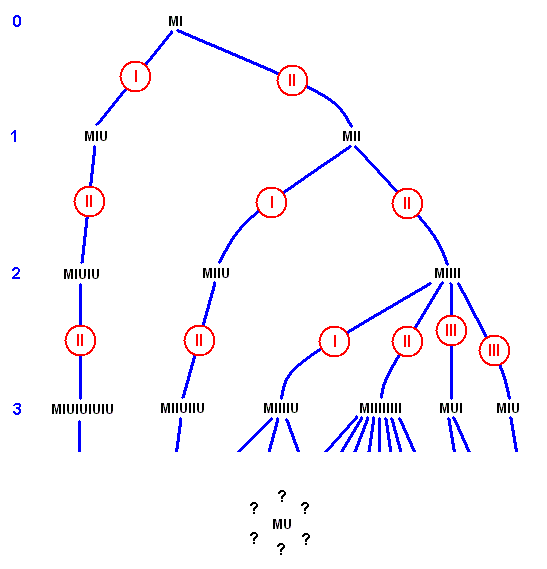
Figure 8 :  A systematically constructed "tree" of all the theorems of the MIU-system. The Nth level down contains those theorems whose derivations contain exactly N steps. The encircled numbers tell which rule was employed. Is MU anywhere in this tree?
[Here we see, by the way, how branching of the course of derivations is possible. It is caused by the fact that the system has more than one "transformation rules" together with the fact that there may be strings that are such that more than one rule may legitimately be applied to them, resulting in more than one new strings.]

Wait until the string in question is produced. When that happens, you know it is a theorem -- and if it never happens, you know that it is not a theorem.

[This is an infinite test. It is mechanical. A decision procedure, on the other hand, is a finite test. It is also mechanical.]
The stated "theoremhood-test" seems ridiculous, because it presupposes that we don't mind waiting around literally an infinite length of time for our answer. This gets to the crux of the matter of what should count as a "test". Of prime importance is a guarantee that we will get our answer in a finite length of time. If there is a test for theoremhood, a test which does always terminate in a finite amount of time, then that test is called a  decision procedure  for the given formal system.
[Here we clearly see the difference between epistemological considerations and ontological ones. Indeed, speaking about a "finite decision procedure" is not speaking about something objectively and independently existing, but about something that can or cannot be applied to something else that IS supposedly independently (of a knower) existing, in order for it to become known. The applicability of a finite decision procedure to some given formal system epistemologically and indirectly expresses a certain objective feature present in that system, a feature that makes it susceptible to such a test.]
When you have a decision procedure, then you have a very concrete characterization of the nature of all theorems of the system. Offhand, it might seem that the rules and axioms of the formal system provide no less complete a characterization of the theorems of the system than a decision procedure would. The tricky word here is "characterization". Certainly the rules of inference and the axiom of the MIU-system do characterize, implicitly, those strings that are theorems. Even more implicitly, they characterize those strings that are not theorems. But implicit characterization is not enough, for many purposes. If someone claims to have a characterization of all theorems, but it takes him infinitely long to deduce that some particular string is not a theorem, you would probably tend to say that there is something lacking in that characterization -- it is not quite concrete enough. And that is why discovering that a decision procedure exists is a very important step. What the discovery means, in effect, is that you can perform a test for the theoremhood of the string, and that, even if the test is complicated, it is guaranteed to terminate. In principle, the test is just as easy, just as mechanical, just as finite, just as full of certitude, as checking whether the first letter of the string is M.  A decision procedure is a "litmus test" for theoremhood.
Incidentally, one requirement on formal systems is that the set of  axioms  must be characterized by a decision procedure -- there must be a litmus test for axiomhood. This ensures that there is no problem in getting off the ground at the beginning, at least. That is the difference between the set of axioms and the set of theorems :  The former always has a decision procedure, but the latter may not.
I am sure you will agree that when looked at the MIU-system for the first time, you had to face this problem exactly. The lone axiom was known, the rules of inference were simple, so the theorems had been implicitly characterized -- and yet it was still quite unclear what the consequences of that characterization were. In particular, it was still totally unclear whether MU is, or is not, a theorem.

[This is, for the time being, all we wanted to say (following Hofstadter) about the MIU-system as a (simple) example of a formal system.  The system is instructive in introducing formal systems as such (as they are created in Logic and Mathematics for example), particularly because it does not hint for some interpretation of it, that is, its symbols M, I, and U, and also its rules of inference, do not suggest any  meanings  attached to them. Other formal systems do suggest possible interpretations, or are even deliberately geared to some particular interpretation, but this is not intrinsic to any formal system.
Next we will discuss another simple formal system that indeed does suggest an interpretation. And precisely because of this (extrinsic) feature it is very instructive for a good understanding of the important concept of meaning, especially how it is induced. While a formal system as such stands on its own feet, independent of any possible meaning, it can figure as a description of something else. And this "something else" then is the system's interpretation. Its symbols then stand for features or things in some world that is supposed or demonstrated to exist somewhere objectively and independently.
And also here, in analyzing the nature of meaning, we will follow again part of the (relevant) text of HOFSTADTER, in the mentioned book of his, from page 46, to begin with.

The formal system in this section is called the pi-system. It is not important to mathematicians or logicians -- in fact, it is just a simple invention of mine [i.e. Hofstadter]. Its importance lies only in the fact that it provides an excellent example of many ideas that play a large role in this book [for us - JB - it is important in explaining the concept of interpretation or meaning].
There are three distinct symbols of the pi-system :

-- the letters p, i, and the hyphen.
The pi-system has an infinite number of axioms. Since we can't write them all down, we have to have some other way of describing what they are. Actually, we want more than just a description of the axioms. We want a way to tell whether some given string is an axiom or not. A mere description of axioms might characterize them fully and yet weakly -- which was the problem with the way theorems in the MIU-system were characterized. We don't want to have to struggle for an indeterminate -- possibly infinite -- length of time, just to find out if some string is an axiom or not. Therefore, we will define axioms in such a way that there is an obvious decision procedure for axiomhood of a string composed of p's, i's, and hyphens.

Definition :   x p - i x -   is an axiom, whenever  x  is composed of hyphens only.

Note that 'x' must stand for the same string of hyphens in both occurrences. For example, --p-i--- is an axiom.
The literal expression   'x p - i x -'   is not an axiom, of course (because 'x' does not belong to the pi-system). It is more like a mold in which all axioms are cast -- and it is called an  axiom schema.
The pi-system has only one rule of production :

Rule :  Suppose  x, y, and z  all stand for particular strings containing only hyphens. And suppose that   x p y i z   is known to be a theorem. Then    x p y - i z -   is a theorem.

For example, take  x  to be '--',  y  to be '---', and  z  to be '-'. The rule tells us :

If   --p---i-   turns out to be a theorem, then so will   --p----i--.

As is typical of rules of production, the statement establishes a causal connection between the theoremhood of two strings, but without asserting theoremhood for either one on its own.
[It is funny, but interesting, that Hofstadter uses here the expression "causal" -- which belongs in fact in the ontological domain -- for the formal derivational relation, or logical implication, between two strings, that is, not between things.]
A most useful exercise for you is to find a decision procedure for the theorems of the pi-system. It is not hard. If you play around for a while, you will probably pick it up. Try it.

I presume you have tried it. First of all, though it may seem too obvious to mention, I would like to point out that every theorem of the pi-system has three separate groups of hyphens, and the separating elements are one  p,  and one  i,  in that order. (This can be shown by an argument based on "heredity", just the way one could show that all MIU-system theorems had to begin with M.)  This means that we can rule out, from its form alone, a string such as  --p--p--p--i--------.
Now, stressing the phrase "from its form alone" may seem silly. What else is there to a string except its form? What else could possibly play a role in determining its properties? Clearly nothing could. But bear this in mind as the discussion of formal systems goes on. The notion of "form" will start to get rather more complicated and abstract, and we will have to think more about the meaning of the word "form". In any case, let us give the name  well-formed string  to any string which begins with a hyphen-group, then has one  p,  then has a second hyphen-group, then an  i,  and then a final hyphen-group.
Back to the decision procedure ... The criterion for theoremhood is that the first two hyphengroups should add up, in length, to the third hyphen-group. For instance,  --p--i----  is a theorem, since 2 plus 2 equals 4, whereas  --p--i-  is not, since 2 plus 2 is not 1. To see why this is the proper criterion, look first at the axiom schema. Obviously, it only manufactures axioms which satisfy the addition criterion. Second, look at the rule of production. If the first string satisfies the addition criterion, so must the second one -- and conversely, if the first string does not satisfy the addition criterion, then neither does the second string. The rule makes the addition criterion into a hereditary property of theorems :  any theorem passes the property on to its offspring. This shows why the addition criterion is correct.
There is, incidentally, a fact about the pi-system which would enable us to say with confidence that it has a decision procedure, even before finding the addition criterion. That fact is that the pi-system is not complicated by the opposing currents of lengthening and shortening rules. It has only lengthening rules.
Any formal system which tells you how to make longer theorems from shorter ones, but never the reverse, has got to have a decision procedure for its theorems [Now, for a short while, we follow formal systems with lengthening rules only, like the pi-system]. For suppose you are given a string [of such a system]. First check whether it's an axiom or not (I am assuming that there is a decision procedure for axiomhood, otherwise things are hopeless). If it is an axiom, then it is by definition a theorem, and the test is over. So suppose instead that it's not an axiom. Then, to be a theorem, it must have come from a shorter string, via one of the rules. By going over the various rules one by one, you can pinpoint not only the rules that could conceivably produce that string, but also exactly which shorter strings could be its forebears on the "family tree". In this way, you "reduce" the problem to determining whether any of several new but shorter strings is a theorem. Each of them can in turn be subjected to the same test. The worst that can happen is a proliferation of more and more, but shorter and shorter, strings to test. As you continue inching your way backwards in this fashion, you must be getting closer to the source of all theorems -- the axiom schemata. You just can't get shorter and shorter indefinitely. Therefore, eventually either you will find that one of your short strings is an axiom [having then shown that the original string under investigaton can be derived from that axiom, and thus that it is a theorem], or you'll come to a point where you're stuck, in that none of your short strings is an axiom, and none of them can be further shortened by running some rule or other backwards [meaning that the origial string cannot be derived from the axioms, and thus that it is not a theorem]. This points out that there really is not much deep interest in formal systems with lengthening rules only. It is the interplay of lengthening and shortening rules that gives formal systems a certain fascination.

Now we come to a central issue of this Section. Perhaps you have already thought to yourself that the pi-theorems are like additions. The string  --p---i-----  is a theorem because 2 plus 3 equals five [it is thus found out to be a theorem by applying to it the decision procedure]. It could even occur to you that the theorem  --p---i-----  is a  statement,  written in an odd notation, whose  meaning  is that 2 plus 3 is 5. Is this a reasonable way to look at things? Well, I deliberately chose 'p' to remind you of  'plus', and ' i ' to remind you of  'is' (in the sense of  'equals') ... So, does the string  --p---i-----  actually  mean  "2 plus 3 equals 5"?
What would make us feel that way? My answer would be that we have perceived an  isomorphism  between  pi-theorems  and  additions.  The term "isomorphism" was earlier defined as an information-preserving transformation. We can now go into that notion a little more deeply, and see it from another perspective. The word "isomorphism" applies when two complex structures can be mapped onto each other in such a way that to each part of one structure there is a corresponding part in the other structure, where "corresponding" means that the two parts play similar roles in their respective structures. This usage of the word "isomorphism" is derived from a more precise notion in mathematics.
It is cause for joy when a mathematician discovers an isomorphism between two structures which he knows. It is often a "bolt from the blue", and a source of wonderment. The perception of an isomorphism between two known structures is a significant advance in knowledge -- and I claim that it is such perceptions of isomorphism which create  meanings  in the minds of people. A final word on the perception of isomorphisms :  Since they come in many shapes and sizes, figuratively speaking, it is not always totally clear when you really have found an isomorphism. Thus, "isomorphism" is a word with all the usual vagueness of words -- which is a defect but an advantage as well.
In this case, we have an excellent prototype for the concept of isomorphism. There is a "lower level" of our isomorphism -- that is, a mapping between the parts of the two structures :

This symbol-word correspondence has a name :  interpretation.
Secondly, on a higher level, there is the correspondence between true statements and theorems. But -- note carefully -- this higher-level correspondence could not be perceived without the prior choice of an interpretation for the symbols. Thus it would be more accurate to describe it as a correspondence between true statements and  interpreted  theorems [If a theorem of the pi-system, say  --p-i---,  is interpreted (by interpreting its symbols) we get the statement :  "two plus one equals three". And because  --p-i---  is supposed to be a theorem of the pi-system, its first two strings of hyphens must add up to the third (which indeed they do), and this fact turns out to be expressed precisely by the interpreted theorem. And thus is the interpreted theorem a true statement (while, strictly speaking, the theorem, all by itself, is not a statement at all, but just a string of symbols)]. In any case we have displayed a two-tiered correspondence, which is typical of all isomorphisms.
When you confront a formal system you know nothing of, and if you hope to discover some hidden meaning in it, your problem is how to assign interpretations to its symbols in a meaningful way -- that is, in such a way that a higher-level correspondence emerges between true statements and theorems. Mathematicians (and also linguists, philosophers, and some others) are users of formal systems, and they invariably have an interpretation in mind for the formal systems which they use and publish. The idea of these people is to set up a formal system whose theorems reflect some portion of reality isomorphically. In such a case, the choice of symbols is a highly motivated one, as is the choice of typographical rules of production. When I [Hofstadter] devised the pi-system, I was in this position. You see why I chose the symbols I chose [In fact Hofstadter chose, in addition to the hyphens, the symbols p and q]. It is no accident that theorems are isomorphic to additions. It happened because I deliberately sought out a way to reflect additions typographically.

You can choose interpretations other than the one I chose. You need not make every theorem come out true. But there would be very little reason to make an interpretation in which, say, all theorems came out false, and certainly even less reason to make an interpretation under which there is no correlation at all, positive or negative, between theoremhood and truth. Let us therefore make a distinction between two types of interpretations for a formal system. First, we can have a  meaningless  interpretation, one under which we fail to see any isomorphic connection between theorems of the system, and reality. Such interpretations abound -- any random choice at all will do. For instance, take this one :

Now  -p-i--  acquires a new interpretation :  "apple horse apple happy apple apple" -- a poetic sentiment, which might appeal to horses, and might even lead them to favor this mode of interpreting  pi-strings! However, this interpretation has very little "meaningfulness". Under interpretation, theorems don't sound any truer, or any better, than nontheorems. A horse might enjoy "happy happy happy apple horse" (mapped onto  iii-p  [clearly a nontheorem]) just as much as any interpreted theorem.
The other kind of interpretation will be called  meaningful.  Under such an interpretation, theorems and truths correspond -- that is, an isomorphism exists between theorems and some portion of reality [and this "reality" might just as well be the world of mathematics]. That is why it is good to distinguish between  interpretations  and  meanings.  Any old word can be used as an interpretation for 'p', but 'plus' is the only  meaningful  choice we've come up with. In summary, the meaning of 'p' seems to be 'plus', though it can have a million different interpretations [So, generally, there are, with respect to symbols of a formal system, many possible interpretations, but only one interpretation will generate meaning].

Probably the most significant fact of the previous subsection, if understood deeply, is this :  the  pi-system seems to force us into recognizing that  symbols of a formal system, though initially without meaning, cannot avoid taking on "meaning" of sorts, at least if an isomorphism is found.  The difference between meaning in a formal system and in a language is a very important one, however. It is this :  In a language, when we have learned a meaning for a word, we then make new statements based on the meaning of the word. In a sense the meaning becomes  active,  since it brings into being a new rule for creating sentences. This means that our command of language is not like a finished product :  The rules for making sentences increase when we learn new meanings. On the other hand, in a formal system, the theorems are predefined, by the rules of production. We can choose "meanings" based on an isomorphism (if we can find one) between theorems and true statements. But this does not give us the license to go out and add new theorems to the established theorems. That is what the Requirement of Formality was warning you of earlier.
In the MIU-system, of course, there was no temptation to go beyond the four rules, because no interpretation was sought for or found. But here, in our new system, one might be seduced by the newly found "meaning" of each symbol into thinking that the string

is a theorem. At least, one might  wish  that this string were a theorem. But wishing doesn't change the fact that it isn't. And it would be a serious mistake to think that it "must" be a theorem, just because 2 plus 2 plus 2 plus 2 equals 8. It would even be misleading to attribute it any meaning at all, since it is not well-formed, and our meaningful interpretation is entirely derived from looking at well-formed strings.
In a formal system, the meaning must remain  passive.  We can read each string according to the meanings of its constituent symbols, but we do not have the right to create new theorems purely on the basis of the meanings we've assigned the symbols. Interpreted formal systems straddle the line between systems without meaning, and systems with meaning. Their strings can be thought of as "expressing" things, but this must come only as a consequence of the formal properties of the system.

And now, I want to destroy any illusion about having found  the  meanings for the symbols of the pi-system. Consider the following association :

Now, --p---i-----  has a new interpretation :  "2 equals 3 taken from 5". Of course it is a true statement [so also under the old interpretation]. All theorems will come out true under this new interpretation. It is just as meaningful as the old one. Obviously, it is silly to ask, "But which one is  the  meaning of the string?" An interpretation will be meaningful to the extent that it accurately reflects some isomorphism to the real world [in most cases this "real world" is the world of mathematics]. When different aspects of the real world are isomorphic to each other (in this case, additions and subtractions), one single formal system can be isomorphic to both, and therefore can take on two passive meanings. This kind of double-valuedness of symbols and strings is an extremely important phenomenon. Here it seems trivial, curious, annoying. But it will come back in deeper contexts and bring with it a great richness of ideas.
Here is a summary of our observations about the pi-system. Under either of the two meaningful interpretations given, every well-formed string has a grammatical assertion for its counterpart -- some are true, some false. The idea of  well-formed strings  in any formal system is that they are those strings which, when interpreted symbol for symbol, yield  grammatical  sentences. (Of course, it depends on the interpretation, but usually, there is one in mind.) Among the well-formed strings occur the theorems. These are defined by an axiom schema, and a rule of production. My goal in inventing the pi-system was to imitate additions :  I wanted every theorem to express a true addition under interpretation. Conversely, I wanted every true addition of precisely two positive integers to be translatable into a string, which would be a theorem. That goal was achieved. Notice, therefore, that all false additions, such as "2 plus 3 equals 6", are mapped into strings which are well-formed, but which are not theorems.

This is our first example of a case where a formal system is based upon a portion of reality, and seems to mimic it perfectly, in that its theorems are isomorphic to truths about that part of reality. However, reality and the formal system are independent. Nobody need be aware that there is an isomorphism between the two. Each side stands by itself -- one plus one equals two, whether or not we know that  -p-i--  is a theorem. And  -p-i--  is still a theorem whether or not we connect it with addition.
You might wonder whether making this formal system, or any formal system, sheds new light on truths in the domain of its interpretation. Have we learned any new additions by producing pi-theorems? Certainly not. But we have learned something about the nature of addition as a process -- namely, that it is easily mimicked by a typographical rule governing meaningless symbols. This still should not be a big surprise since addition is such a simple concept. It is a commonplace that addition can be captured in the spinning gears of a device like a cash register.
But it is clear that we have hardly scratched the surface, as far as formal systems go. It is natural to wonder about what portion of reality can be imitated in its behavior by a set of meaningless symbols governed by formal rules. Can all of reality be turned into a formal system? [meant here should be first of all : can all of reality be described by some formal system? And then one might ask whether (material) reality in fact IS such a system]. In a very broad sense, the answer might appear to be yes. One could suggest, for instance, that reality is itself nothing but one very complicated formal system. Its symbols do not move around on paper, but rather in a three-dimensional vacuum (space). They are the elementary particles of which everything is composed. (Tacit assumption :  that there is an end to the descending chain of matter, so that the expression "elementary particles" makes sense). The "typographical rules" are the laws of physics, which tell how, given the positions and velocities of all particles at a given instant, to modify them, resulting in a new set of positions and velocities belonging to the "next" instant. So the theorems of this grand formal system are the possible configurations of particles at different times in the history of the universe. The sole axiom is (or perhaps  was) the original configuration of all the particles at the "beginning of time". This is so grandiose a conception, however, that it has only the most theoretical interest, and besides, quantum mechanics (and other parts of physics) casts at least some doubt on even the theoretical worth of this idea. Basically, we are asking if the universe operates deterministically, which is an open question.

[With all this, we conclude (p.54) our exposition of Hofstadter's  pi-system. We will now turn to the solution (given by Hofstadter) of the MIU-puzzle, and thus answer the question :  "Is MU a theorem of the MIU-system, that is, can the string MU be derived, ultimately, from the axiom MI by means of the Rules of the system? If so, then it is a theorem of the system. If not, it is still a well-formed MIU-string (because it begins with an M ), but it is not a theorem of the system.
After that we will follow Hofstadter's exposition (pp.260) of how it is possible that some formal systems (but not the MIU-system, and also not the pi-system), especially the formalized number theory "TNT" (formal typographical number theory, which deals with the natural numbers and zero [that is, 0, 1, 2, 3, 4, ...]), can have strings that express something of other strings of the same formal system. It is a self-reference of the system, i.e. the system refers to itself by having some of its strings expressing some property of other strings of it. In Hofstadter the discussion is geared to the exposition (and consequences) of Gödel's Incompleteness Theorem. For this the just mentioned self-reference must be tightened still more : One should find a certain string that expresses something about itself, especially that it is not a theorem. This can be shown to be true, but it is not among the theorems of the formal system under investigation, and therefore that system is incomplete. If that string is subsequently added to the list of the system's axioms, then new such strings will appear that are true but not theorems, etc., etc.
As has been said, for us --- investigating the idea that organic noëtic space contains one (or several) noëtically existing (that is, existing in the Implicate Order) "formal system", with the material organic world in the Explicate Order being its "meaning", that is, its ontological interpretation (and where the isomorphism, generating this meaning, is realized by the fact of  "projection" of "organic strategies" from the Implicate into the Explicate Order --- Gödel's Incompleteness Theorem is perhaps of only limited relevance as to the nature of the Organic Noëtic Formal System :  By having to add extra axioms, this state of affairs emphasizes the strong degree of the polyphyly in evolution even down into the Implicate Order. [By the way, here, with the phrase "ontological interpretation" is definitely not meant an interpretation performed by someone (that is, by a knowing subject), but, so to say, an "interpretation" performed by reality itself :  Upon "projection", the ontological make-up of the beings (entities) involved is changed dramatically : From immaterial non-local to material and individual.]
On the other hand, of much more importance are two possible states of affairs that come out of the fact that all formal systems allow themselves to be "arithmetized" (that is, allow themselves to be mapped onto number theory). First this very fact itself may point to the possibility that the Organic Noëtic Formal System -- of which the "strings" are "strategies", which in turn are noëtic descriptions (consisting of noëtic symbols) -- is ultimately such that the "derivations" of given (noëtic) strategies from other (noëtic) strategies are in fact arithmetical transformations (that make them, by the way, truly noëtical!). Second, the possibility for us (and now thus in a cognitive context) to successfully arithmetize formal systems -- by assigning so-called Gödel-numbers to their symbols, and arithmetize their production-rules -- makes us able to show, following Hofstadter, that, as told, certain strings of a given formal system express something of other strings of the same system. For us this means that a (noëtic) strategy can involve in its intrinsic description other strategies, and this involvement will reappear in the isomorphic material version of it and is a key-feature in ecology.
To explain the mentioned abilities of formal systems (and the subsequent ontologization by us of some of them) will not be easy. Hofstadter, although having cognitive goals in mind, has done very much to make the considerations concerning Formal Number Theory and Mathematical Logic accessible to a broader public. He did this masterly, and at the same time very entertainingly. Thanks to him we can now use these considerations and findings (also) to describe features of the noëtic world of the Implicate Order. And although even Hofstadter's exposition is still difficult and subtle, we will do our best to further explain things, in so far as they have bearing on our noëtic theory of evolution.]

The MIU-puzzle is in fact merely a puzzle about natural numbers in typographical disguise. If we could only find a way to transfer it to the domain of number theory, we might be able to solve it.
If you try counting the numbers of  I's contained in theorems, you will soon notice that it seems never to be 0. In other words, it seems that no matter how much lengthening and shortening is involved, we can never work in such a way that all  I's are eliminated. Let us call the number of  I's in any string the "I-count" of that string. Note that the I-count of the axiom  MI  is 1. We can do more than show that the I-count can't be 0 -- we can show that the I-count can never be any multiple of 3.
To begin with, notice that rules I and IV (see ABOVE ) leave the I-count totally undisturbed. Therefore we need only think about rules II and III. As far as rule III is concerned, it diminishes the I-count by exactly three. After an application of this rule, the I-count of the output might conceivably be a multiple of 3 -- but only if the I-count of the  input  was also. Rule III, in short, never creates a multiple of 3 from scratch. It can only create one when it began with one. The same holds for rule II, which doubles the I-count. The reason is that if 3 divides 2n, then -- because 3 does not divide 2 -- it must divide  n (a simple fact from the theory of numbers). Neither rule II nor rule III can create a multiple of 3 from scratch.
But this is the key to the MU-puzzle! Here is what we know :

• The I-count begins at 1 (the axiom   MI ), and that is not a multiple of 3.
• Two of the rules do not affect the I-count at all.
• The two remaining rules which do affect the I-count do so in such a way as never to create a multiple of 3 unless given one initially.

Not all problems of the type which the MU-puzzle symbolizes are so easy to solve as this one. But we have seen that at least one such puzzle could be embedded within, and solved within, number theory [When we speak of "number theory" (which we often will indicate by "N") we mean its non-formalized version. The language in this version is thus plain English or some other spoken language. Its formalized version is the "Theoria Numerorum Typographica", or "TNT" for short (without quotation marks). Number theory is the "meaning" or (meaningful) interpretation of TNT, that is, TNT describes number theory. Both number theory and TNT concern the positive integers and zero (which are called "natural numbers") and their properties. When setting up TNT, all symbols, operations, quantors, etc. in number theory are translated into special TNT signs, in such a way that a minimum of such TNT signs is obtained.]. We are now going to see that there is a way to embed  all  problems about  any  formal system, in number theory. This can happen thanks to the discovery, by Gödel, of a special kind of isomorphism. To illustrate it, I will use the MIU-system.
We begin by considering the notation of the MIU-system. We shall map each symbol onto a new symbol :

The correspondence was chosen arbitrarily. The only rhyme or reason to it is that each symbol looks a little like the one it is mapped onto. Each number is called the  Gödel number  of the corresponding letter. Now I am sure you can guess what the Gödel number of a multiletter string will be :

It is easy. Clearly this mapping between notations is an  information-preserving transformation. It is like playing the same melody on two different instruments.
Let us now take a look at a typical derivation in the MIU-system, written simultaneously in both notations :

(1)       MI -------------- axiom ---------- 31
(2)       MII ------------- rule II ---------- 311
(3)       MIIII ------------ rule II ---------- 31111
(4)       MUI ------------ rule III --------- 301
(5)       MUIU ---------- rule I ----------- 3010
(6)       MUIUUIU ----- rule II ---------- 3010010
(7)       MUIIU --------- rule IV --------- 30110

The left-hand column is obtained by applying our four familiar typographic rules. The right-hand column, too, could be thought of as having been generated by a similar set of typographic rules. Yet the right-hand column has a dual nature. Let me explain what this means.

We could say of the fifth string ('3010') that it was made from the fourth ('301'), by appending a '0' on the right. On the other hand we could equally well view the transition as caused by an  arithmetical  operation -- multiplication by 10, to be exact. When natural numbers are written in the decimal system, multiplication by 10 and putting a '0' on the right are indistinguishable operations. We can take advantage of this to write an  arithmetical  rule which corresponds to typographical rule I :

Arithmetical Rule Ia :  A number whose decimal expansion ends on the right in '1' can be multiplied by 10.

We can eliminate the reference to the symbols in the decimal expansion by arithmetically describing the rightmost digit :

Arithmetical Rule Ib :  A number whose remainder when divided by 10 is 1, can be multiplied by 10.

Now we could have stuck with a purely typographical rule (also here), such as the following one :

Typographical Rule I :  From any theorem whose rightmost symbol is '1' a new theorem can be made, by appending '0' to the right of that '1'. [Just using numerals instead of letters]

They would have the same effect. This is why the right-hand column has a "dual nature" :  It can be viewed either as a series of typographical operations changing one pattern of symbols into another, or as a series of arithmetical operations changing one magnitude into another. But there are powerful reasons for being more interested in the arithmetical version. Stepping out of one purely typographical system into another isomorphic typographical system is not a very exiting thing to do, whereas stepping clear out of the typographical domain into an isomorphic part of number theory has some kind of inexplored potential. It is as if somebody had known musical scores all his life, but purely visually -- and then, all of a sudden, someone introduced him to the mapping between sounds and musical scores. What a rich, new world! Then again, it is as if somebody had been familiar with string figures all his life, but purely as string figures, devoid of meaning -- and then, all of a sudden, someone introduced him to the mapping between stories and strings. What a revelation! The discovery of Gödel-numbering has been likened to the discovery, by Descartes, of the isomorphism between curves in a plane and equations in two variables :  incredibly simple, once you see it -- and opening onto a vast new world.
Before we jump to conclusions, though, perhaps you would like to see a more complete rendering of this higher level of the isomorphism. It is a very good exercise. The idea is to give an arithmetical rule whose action is indistinguishable from that of each typographical rule of the MIU-system. Of course, the new version of the rules must, just as did the typographical version, apply generally, that is, not only to the derivation given above, where MUIIU was derived from MI.  A solution is given below. In the rules,  m  and  k  are arbitrary natural numbers, and  n  is any natural number which is less than 10^m. In the formulae 'x' means "multiplied by".

Rule I :  If we have made  10m + 1,  then we can make  10 x (10m + 1).
     Example :  Going from line 4 to line 5 (in the above example of a derivation in the MIU-system). Here, m = 30.   301 = 10x30 +1.  And 10x30 +1 ==> (= becomes according to the rule) 10(10x30 + 1) = 3010.  So we've got :  301 ==> 3010.
In this arithmetized rule, the general rule,  m  can take, of course, only values that are relevant here :  If  m  were, say, 1, then our number to which the rule is going to be applied would be 11. But this cannot be the Gödel number of any (well-formed) MIU-string whatsoever. This consideration also applies to the other three arithmetized rules of the MIU-system.

Rule II :  If we have made  3x10^m + n,  then we can make  10^m x (3x10^m + n) + n.  In the first expression,  m  indicates the number of digits after '3' (including the digits represented by  n).
     Example :  Going from line 1 to line 2, where both  m  and  n  equal 1.  31 = 3x10¹ + 1.  And 3x10¹ + 1 ==> 10¹ x (3x10¹ + 1) + 1 = 10 x (3x10 + 1) + 1 = 311.  So we've got :  31 ==> 311.
Another example, where m = 5 and n = 68, reads as follows :  300068 = 3 x 10⁵ + 68 ==> 10⁵ x (3 x 10⁵ + 68) + 68 = 100000 x 300068 + 68 = 30006800000 + 68 = 30006800068.  So we've got :  300068 ==> 30006800068.

Rule III :  If we have made  k x 10^m+3 + 111 x 10^m + n,  then we can make  k x 10^m+1 + n.
     Example :  Going from line 3 to 4. Here, m  and  n  are both 1, and  k  is 3.   3 x 10¹⁺³ + 111 x 10¹ + 1 = 3 x 10⁴ + 111 x 10 + 1 = 30000 + 1111 = 31111. And this becomes  3 x 10¹⁺¹ + 1 = 3 x 10² + 1 = 301.  So we've got :  31111 ==> 301.

Rule IV :  If we have made  k x 10^m+2 + n,  then we can make  k x 10^m + n.
     Example :  Going from line 6 to 7. Here, m = 2,  n = 10,  and k = 301.  So, 301 x 10²⁺² + 10 = 3010000 + 10 = 3010010.  This becomes  301 x 10² + 10 = 30100 + 10 = 30110.  So we've got :  3010010 ==> 30110.  A second example might read :  m = 1,  n = 6,  k = 3. Then we have  3 x 10¹⁺² + 6 = 3006.  And this becomes  3 x 10¹ + 6 = 36.  So we've got :  3006 ==> 36.

Having now arithmetized the MIU-rules, let us not forget to give the axiom in Gödel notation! Without it we can go nowhwere. Therefore, let us postulate that :

Now the right-hand column of the above derivation can be seen as a full-fledged arithmetical process, in a new arithmetical system which we might call the 310-system. This right-hand column will thus be as follows :

(1)       31       given.
(2)       311       rule II   (m = 1, n = 1).
(3)       31111       rule II   (m = 2, n = 11).
(4)       301       rule III   (m = 1, n = 1, k = 3).
(5)       3010       rule I   (m = 30).
(6)       3010010       rule II   (m = 3, n = 10).
(7)       30110       rule IV   (m = 2, n = 10, k = 301).

Notice once again that the lengthening and shortening rules are ever with us in this "310-system". They have merely been transposed into the domain of numbers, so that the Gödel numbers go up and down. If you look carefully at what is going on, you will discover that the rules are based on nothing more profound than the idea that shifting digits to left and right in decimal representations of integers is related to multiplications and divisions by powers of 10. This simple observation finds its generalization in the following  Central Proposition :

If there is a typographical rule which tells how certain digits are to be shifted, changed, dropped, or inserted, in any number represented decimally, then this rule can be represented equally well by an arithmetical counterpart which involves arithmetical operations with powers of ten as well as additions, subtractions, and so forth.

More briefly :

Typographical rules for manipulating  n u m e r a l s  are actually arithmetical rules for operating on  n u m b e r s.

This simple observation is at the heart of Gödel's method, and it will have an absolutely shattering effect. It tells us that once we have a Gödel-numbering for any formal system, we can straightaway form a set of arithmetical rules which complete the Gödel isomorphism. The upshot is that we can transfer the study of any formal system -- in fact the study of  all  formal systems -- into number theory.

Just as any set of typographical rules generates a set of theorems, a corresponding set of natural numbers will be generated by repeated applications of arithmetical rules. These  producible numbers  play the same role inside number theory as theorems do inside any formal system. Of course, different numbers will be producible, depending on which rules are adopted. "Producible numbers" are only producible  relative to a system  of arithmetical rules. For example, such numbers as 31, 3010010, 3111, and so forth could be called  MIU-producible numbers -- an ungainly name, which might be shortened to  MIU-numbers,  symbolizing the fact that those numbers are the ones that result when you transcribe the MIU-system into number theory, via Gödel numbering. If we were to Gödel-number the pi-system and then "arithmetize" its rules, we could call the producible numbers "pi-numbers" -- and so on.
Note that the producible numbers (in any given system) are defined by a recursive method :  given numbers which are known to be producible, we have rules telling how to make more producible numbers. Thus, the class of numbers known to be producible is constantly extending itself, in much the same way that the list of Fibonacci numbers does. [As in any recursive series, there is a non-recursive starting part, followed by the rest -- the recursive part -- according to some rule that is applied to every newly generated number. The Fibonacci series starts with 1, 1, and then each next number must be equal to the sum of the two previous numbers. Thus the series is then :  1, 1, 2, 3, 5, 8, 13, 21, 34, ...]. The set of producible numbers of any system is a  recursively enumerable set.  What about its complement -- the set of nonproducible numbers? Is that set always recursively enumerable? Do numbers which are nonproducible share some common arithmetical feature?
This is the sort of issue which arises when you transpose the study of formal systems into number theory. For each system which is arithmetized, one can ask, "Can we characterize producible numbers in a simple way?" "Can we characterize nonproducible numbers in a recursively enumerable way?" These are difficult questions of number theory. Depending on the system which has been arithmetized, such questions might prove too hard for us to solve. But if there is any hope for solving such problems, it would have to reside in the usual kind of step-by-step reasoning as it applies to natural numbers. And that, of course, was put in its quintessential form in the previous Chapter. [The basics of this Chapter in Hofstadter's book -- where number theory is formalized -- we will reproduce in the next document.]. TNT (= formalized number theory) seemed, to all appearances, to have captured all valid mathematical thinking processes in one single, compact system.

Back to Homepage

Back to Contents

Back to Evolutionary Part XIV

Back to Evolutionary Part XV

Back to Evolutionary Part XVI

Back to Evolutionary Part XVII

Back to Evolutionary Part XVIII

Back to Evolutionary Part XIX

Back to Evolutionary Part XX

Back to Evolutionary Part XXI

Back to Evolutionary Part XXII

Back to Evolutionary Part XXIII

Back to Evolutionary Part XXIV

Back to Evolutionary Part XXV-A

Back to Evolutionary Part XXV-B

Back to Evolutionary Part XXV-C

Back to Evolutionary Part XXVI

Back to Evolutionary Part XXVII

Back to Evolutionary Part XXVIII

Back to Evolutionary Part XXVIII-A

Back to Evolutionary Part XXIX

Back to Evolutionary Part XXX

Back to Evolutionary Part XXXI

Back to Evolutionary Part XXXII

Back to Evolutionary Part XXXIII

Back to Evolutionary Part XXXIV

Back to Evolutionary Part XXXV

Back to Evolutionary Part XXXVI

Back to Evolutionary Part XXXVII

Back to Evolutionary Part XXXVIII

Back to Evolutionary Part XXXIX

Back to Evolutionary Part XL

Back to Evolutionary Part XLI

Back to Evolutionary Part XLII

Back to Evolutionary Part XLIII

Back to Evolutionary Part XLIV

Back to Evolutionary Part XLV

Back to Evolutionary Part XLVI

Back to Evolutionary Part XLVII

Back to Evolutionary Part XLVIII

Back to Evolutionary Part XLIX

Back to Evolutionary Part L

Back to Evolutionary Part LI

Back to Evolutionary Part LII

Back to Evolutionary Part LIII

Back to Evolutionary Part LIV

Back to Evolutionary Part LV

Back to Evolutionary Part LVI

Back to Evolutionary Part LVII

Back to Evolutionary Part LVIII

Back to Evolutionary Part LIX

Back to Evolutionary Part LX