

Typographical Number Theory
Before we, here on the present website, continue our exposition, -- an exposition that will lead us to the demonstration that not only any formal system can be described by number theory (N), but also that in formalized number theory, that is, in typographical number theory (TNT), certain of its strings, TNT-strings, can talk, in code, about other TNT-strings (and even that some of these strings can talk in code about themselves), -- we will first briefly describe some essential features of TNT, in order to provide a better understanding of formalized number theory. For this we again use parts of Hofstadter's mastery exposition of TNT in Chapter VIII (pp.204). The reader can, of course, skip this exposition of TNT, because it is possible to understand the ability of TNT-strings to talk about other TNT-strings (and the ability of number theory, and thus of its formalization, TNT, to code for any formal system) largely without it. But because we, in our noëtic theory, o n t o l o g i z e things found by logicians and mathematicians, including Hofstadter, it remains important to realize that the very status of TNT, originally belonging in the cognitive domain, will be changed under the ontologization. This is explained in the next Introductory Remark.
INTRODUCTORY REMARK concerning the cognitive status and the ontological status of formalized number theory TNT (JB -- author of this website) :
In order correctly to judge the status of number theory (N) and its formalization TNT, especially how MEANING functions in them, it is important to distinguish two viewpoints or contexts, from or in which we see them :
"Ontological" (context, or domain) means "viewpoint from things or patterns as objectively existing" (in the Implicate or Explicate Order), that is, existing independently of being (or not being) known.
"Cognitive" (context, or domain) means "viewpoint from things or patterns insofar as they are, can, or cannot, be known, or insofar as they are mere instruments of knowledge".
In the present exposition we have to do with five systems that are related to each other by MEANING. These systems are :
Both viewpoints should exist side by side, that is, they should not exclude each other. If we pass from one viewpoint to the other, that is, from the cognitive to the ontological viewpoint, or vice versa, MEANING, connecting the mentioned systems, changes its nature (that is : not the meaning (of something) changes, but the very nature of "meaning" itself). Thus, in the cognitive domain MEANING is the statement-decoded, while in the ontological domain MEANING is the (revealed) essence of something objectively existing.
We will explain this further in the next section of this REMARK on the status of TNT :
In Hofstadter's book ( "Gödel, Escher, Bach" ) the expositions about "metamathematics" -- a mathematics that is in fact not just mathematics, but is a b o u t mathematics, in the present case about number theory -- concern how things are with respect to our possible knowledge of the properties of natural numbers. TNT is defined by mathematicians in order to analyse or dissect facts of natural numbers, and thus to analyze true statements about natural numbers, into the most basic ('primitive') constituents. In this sense TNT is devised to speak about number theory -- which we call N -- in terms of the most basic entities. So N is what TNT means for mathematicians. TNT ==> N (TNT means N). It is a cognitive characterization of the relationship between N and TNT.
If we now transpose things from the cognitive domain into the ontological domain (while still preserving the cognitive viewpoint alongside it), we must hold that N as well as TNT are objectively existing (not, conceptual, not man-made) entities in the Implicate Order : N and TNT (stripped from errors of course, and thus consistent) ARE what they ARE in themselves, and, this being so, we must reverse the semantic relationship : TNT itself, that is, all by itself, describes (and thus IS) the very essence of N. Indeed, TNT is precisely what N in fact means. N ==> TNT (N means TNT). So in this context TNT has ontological priority. And if we, in this ontological context, leave out strict self-references in TNT -- [And this is easy to do, because truth or falsity of a symbol-string is attuned to the interpretation of the symbols. But in an ontological context the symbols of TNT do not have any interpretation. They have an interpretation in a cognitive context only. Thus the above given statement on self-reference is relevant in a cognitive context only, i.e. it refers to the cognitive context. So investigating completeness (of a formal system) demands a cognitive context, and thus that TNT ==> N ( TNT means N).] -- that is cases in which a given TNT-string expresses something about itself, especially a string G saying (about itself) "G is not a theorem of TNT", then we can be pretty sure that TNT is complete, that is, TNT is then the complete essence of N.
So, consequently, also in the context of our noëtic theory (in which we have thus "ontologized" certain metamathematical findings of Hofstadter) N -- number theory -- means TNT, that is, TNT is what N in fact is, TNT is the very essence of N (while in the cognitive context [in which TNT is not objectively existing, but devised in order to understand N] the meaning of TNT, that is what its symbols and symbol-strings mean, is to be found in N, that is, in the ordinary language of number theory).
But, still also in the context of our noëtic theory, N has yet another meaning too, a meaning that is stretched out into another direction : The noëtic strategies -- assumed to reside as immaterial patterns in the Implicate Order, where these patterns are held to be 'descriptions' (of strategies of how to be able to exist in the Explicate Order) and thus some sort of typographical strings -- together constitute a formal system (think, as an analogy, of the MIU-system), that is, to begin with, a set of pre-existing, 'primitive', strings (strategies) -- axioms -- and a set of typographical rules. The rest of the strings (theorems) are now derived from the axioms by having the rules applied (About these rules, where they come from, we will speak later on). And -- thinking again of the MIU-system as an analogy -- this noëtic formal system of 'typographical' strings and rules can be isomorphically expressed in number theory -- N -- (by having the strings coded by natural numbers and the rules arithmetized). And in our noëtic context (the Implicate Order) we then hold that this system of strategy-strings IS in fact so coded, which here means that this system IS in fact part of number theory ("number theory" here not taken to be a theory devised by humans, but an existing state of affairs), that is, it means a certain part of number theory, or, said differently, its essence is in number theory. And this in turn implies (as already found out earlier) that the derivations of noëtic strategies from one another are in fact arithmetical transformations. These arithmetical transformations are fully determined by the arithmetized rules of the formal system of noëtic strategy-strings (FSNSS), and are thus specific combinations of the basic arithmetical operations (addition, multiplication, etc.), as we saw it in the arithmetized MIU-system (see HERE in previous document ).
So the o n t o l o g i c a l symbol-meaning relationships between number theory (N), formalized number theory (TNT), and the Formal System of Noëtic Strategy-Strings (FSNSS) (in the Implicate Order), are :
Thus, what happens in the system of noëtic strategy-strings -- derivation of strategy-strings from other such strings -- has its essence in number theory which in turn is essentially TNT.
But the formal system of noëtic strategy-strings (FSNSS) has, in addition to its meaning (residing) in the Implicate Order, also a meaning outside this Order, that is, in the Explicate Order. There the meaning of each noëtic strategy-string is represented by existing material individuals of some definite organic species, characterized by a definite biochemistry, physiology, internal and external morphology, morphogenesis, behavior, and ecology. This meaning is ontologically revealed by the phenomenon of projection (from the Implicate into the Explicate Order). In fact, projection of a given strategy can only take place when an appropriate ecological context actually exists (containing also the evolutionary precursor of that strategy) somewhere in the Explicate Order, and it is thus in fact this ecological context that reveals ('decyphers' or 'decodes') the meaning of that given noëtic strategy-string.
So, in the ontological context we can write :
In terms of ontological priority we can express this as follows :
where we assume that a material strategy -- present in the set of existing organic individuals of a given species -- has ontological priority with respect to the corresponding noëtic strategy, which is ontologically still incomplete.
FSNSS is embedded in N, and, consequently, also in TNT. But there is nothing in N, neither in TNT, that causes or defines FSNSS. The delimitation of FSNSS comes from outside, that is, from outside N or TNT, and thus from outside the Implicate Order. And this means, of course, that the delimitation of FSNSS comes from the Explicate Order.
In the cognitive domain, on the other hand, there is, of course no talk about ontological priority, and the above symbol-meaning relationships (first line of the above two chains) are partly the other way around :
Strings expressing things of other strings of the same system.
"The string MIU is a theorem of the MIU-system"
(because we can produce MIU from the axiom MI )
This whole statement is itself not an MIU-string (because it does not consist solely of MIU-symbols). Thus it is not so that this whole 'MIU-string' expresses something about the (other) MIU-string MIU, because, again, this whole string is not an MIU-string.
The same can be said about the MIU-strings MII, MIIIIU, MUIU, and all other theorems of the MIU-system.
Further we have statements like
"The string MU is not a theorem of the MIU-system"
Also here something is expressed about the MIU-string MU (namely that it is not a theorem). But also here this is not expressed by another MIU-string. It is said by the statement "MU is not a theorem of the MIU-system", but this statement (this series of symbols) is itself not an MIU-string.
And because, us speaking about MIU-strings, expressions about being or not being a theorem are the only expressions in the context of the MIU-system we can think of, it is not possible that in the MIU-system any given MIU-string expresses something about another MIU-string. But in TNT this is possible (as will be shown later). But also no TNT-string can have as its meaning that a given MIU-number expresses something about another MIU-number.
The MIU-system has no interpretation in some part of (physical or mathematical) Reality, but we can see it as an (albeit poor) analogue of FSNSS (formal system of noëtic strategy-strings).
In a cognitive context the typographical MIU-strings and rules together form the meaning of their arithmetic counterparts ("311110" means MIIIIU ), these counterparts obtained by assigning Gödel numbers to the system's symbols and by arithmetizing its production rules.
In an ontological context, on the other hand, the MIU-system and all its derivations can be said to mean some section of number theory ("MIIIIU" means 311110) and thus a corresponding section of TNT, and so essentially being that section of TNT. Nevertheless, pure MIU-strings cannot express things of other MIU-strings, because this system is much too simple. On the other hand, we can expect of FSNSS (formal system of noëtic strategy-strings) that it is rich enough to contain strings that express things about other such strings. And then we can say that these FSNSS-statements in fact mean statements in N, and consequently in TNT. So now we can say that if indeed TNT (which ontologically is basic to N and to FSNSS) turns out to be capable of having several TNT-strings that each express something about other TNT-strings, then we can hold that FSNSS too is so capable.
Embedding of the formal system of noëtic strategy-strings in number theory.
Rule I : If we have made 10m + 1, then we can make 10 x (10m + 1).
Rule II : If we have made 3x10m + n, then we can make 10m x (3x10m + n) + n.
Rule III : If we have made k x 10m+3 + 111 x 10m + n, then we can make k x 10m+1 + n.
Rule IV : If we have made k x 10m+2 + n, then we can make k x 10m + n.
In these rules, m and k are arbitrary natural numbers, and n is any natural number which is less than 10m. In the formulae 'x' means "multiplied by".
We can see that these four numerical transformations are each a certain combination of arithmetical operations. And these latter are just the operations allowed in N and defined in TNT. So the very possibility of these numerical transformations is rooted in number theory, and ultimately in TNT. But the precise combinations of these arithmetical operations (that is, precisely those combinations, and not other potential combinations) are NOT determined nor sanctioned by N, neither are they by TNT, that is, these actually existing combinations fall outside the realm of N or TNT.
So it seems that the general laws and definitions in N and (formalized in) TNT are in some way harnessed by the MIU-system (respectively by FSNSS). The MIU-system (and thus FSNSS) imposes its special structure onto N (and ultimately onto TNT) without violating any of its laws and definitions. So the MIU-system (and thus FSNSS) come from outside N and TNT but is written in their language (that's why we can say that the MIU-system (and thus FSNSS) is "in fact an arithmetical system").
N or TNT cannot cause or express the MIU-system (and thus FSNSS) as to what it specifically is. So although the existence of TNT (and therefore N) implies the existence of natural numbers and their properties, it does not imply any specific combination and recombination of arithmetical operations (addition, multiplication, etc.), and thus does not imply any system such as MIU or FSNSS.
Of course WE can (although it is hard) express in TNT that, say, a given number "is a MIU-producible number", but only when we explicitly specify in TNT what a MIU-producible number in fact is. This can be done only in the cognitive context of TNT.
TNT itself does not define the MIU-system (and so also not FSNSS) neither in a cognitive nor in an ontological context.
In a cognitive context WE take the MIU-system, forged by Hofstadter, and encode it in number theory (by assigning arbitrary Gödel numbers to its typographical symbols, and by arithmetizing its typographical production rules).
In an ontological context, on the other hand, we assume the objective existence of FSNSS (formal system of noëtic strategy-strings) -- and thus, analogously, that of the MIU-system -- and then hold that it is automatically encoded in N, that is, not by us, but by and in noëtic space itself (by a 'method' that is supposed to be more or less similar to that of assigning 'Gödel numbers' and of our arithmetizing the production rules of the system). So FSNSS (and analogously the MIU-system) appears in noëtic space as arithmetized. Thus such a system of noëtic patterns, and all other noëtic systems that might be present in the Implicate Order, ARE in noëtic space essentially arithmetic entities obeying the g e n e r a l laws of TNT (all TNT-laws are general), and also obeying their own s p e c i a l laws (production rules) harnessing these general TNT laws.
So our theory is that noëtic space (the Implicate Order) is in fact "arithmetical space". And this is what makes this space truly "noëtical". The existence of systems like FSNSS in noëtic space gives structure to this space. It is a property of this space itself. And it leads, among other things, to the evolution of organisms in the Explicate Order.
The conventional status of TNT.

Figure 1 : Cognitive picture of formalized number theory, TNT.
Considerable visual symbolism is featured in this diagram of the relationship between various classes of TNT strings. The biggest box represents the set of all TNT strings. The next-biggest box represents the set of all well-formed TNT strings. Within it [that is in the most inner box] is found the set of all sentences of TNT. Now things begin to get interesting. The set of theorems is pictured as a tree growing out of a trunk (representing the set of axioms). The tree-symbol was chosen because of the recursive growth pattern which it exhibits : New branches (theorems) constantly sprouting from old ones. The fingerlike branches probe into the corners of the constraining region (the set of truths), yet can never fully occupy it. The boundary between the set of truths and the set of falsities is meant to suggest a randomly meandering coastline which, no matter how closely you examine it, always has finer levels of structure, and is consequently impossible to describe exactly in any finite way (It is a fractal boundary). The reflected tree (the tree at the right-hand side of the diagram) represents the set of negations of theorems : All of them false, yet unable collectively to span the space of false statements. The bottom part of the right-hand tree represents the set of negated axioms. The black area on the left half of the diagram represents the set of unreachable truths, while the white area on the right half of the diagram represents the set of unreachable falsehoods.
(After HOFSTADTER, 1979)
In an ontological context, on the other hand, TNT only consists of its set of axioms, its transformation rules, and its derived theorems. It is the existing essence of natural numbers an their properties, and, as this essence is in itself, does not contain statements that are neither true nor false, or both true and false for that matter, for if it did, it could not EXIST.
Having now placed TNT in the proper context of our noëtic theory of evolution, we can proceed, following Hofstadter (Chapter VII), to establish what exactly is expressed by formalized number theory, TNT.
(End of Introductory Remark)
Gödel's construction depends on describing the form, as well as the content, of strings of the formal system we shall define in the present Section -- Typographical Number Theory ( TNT ). The unexpected twist is that, because of the subtle mapping which Gödel discovered, the form of strings can be described in the formal system itself. Let us acquaint ourselves with this strange system with the capacity for wrapping around.
Before starting, however, we might ask whether Number Theory -- and a fortiori TNT -- is the same in all conceivable worlds. Although this question is not relevant within an ontological context (where only one single objectively existing world is assumed -- for us a single world consisting of two interacting Orders, the Implicate and Explicate Orders) it is certainly important within the cognitive viewpoint, or, we might say, within pure mathematics. If we assume that at least logic is part of every conceivable world --- however, "Intentional Logic", as defined and expounded in the "Logic Series" (Formal Elements of Cognition, Part II--VII) of the present (Part of) Website, is fully geared to the objectively existing world and only this world --- is that all? That is, are the other logic-related or mathematical disciplines not part of every conceivable world, but more or less change when we go from one world to another? Concerning Number Theory, is it really conceivable that, in some worlds, there are not infinitely many primes (In standard number theory it is indeed proved that there are infinitely many prime numbers)? Would it not seem necessary that numbers should obey the same laws in all conceivable worlds? Or ... is the concept "natural number" better thought of as an undefined term, like "POINT" or "LINE"? In that case, number theory would be a bifurcated theory, like geometry (where we have one standard -- euclidian -- and several non-euclidian geometries) : there would be standard and nonstandard number theories. But there would have to be some counterpart to absolute geometry : a "core" theory, an invariant ingredient of all number theories which identified them as number theories rather than some completely other theory. It seems to be the consensus of most modern mathematicians and philosophers (so Hofstadter, 1979, reports on p.100) that there IS such a core number theory, which ought to be included, along with logic, in what we consider to be "conceivable worlds". This core of number theory, the counterpart to absolute geometry, -- is called Peano arithmetic, and formalized it is known as TNT. Also, it is now well established -- as a matter of fact as a direct consequence of Gödel's Theorem -- that number theory IS a bifurcated theory, with standard and nonstandard versions. Unlike the situation in geometry, however, the number of "brands" of number theory is infinite, which makes the situation of number theory considerably more complex.
What We Want to Be Able to Express in TNT (Hofstadter, pp.204)
We'll begin by citing some typical sentences belonging to number theory. Then we will try to find a set of basic notions in terms of which all our sentences can be rephrased. Those notions will then be given individual symbols. Incidentally, it should be stated at the outset that the term "number theory" will refer only to properties of positive integers and zero (and sets of such integers). These numbers are called the natural numbers. Negative numbers play no role in this theory. Thus the word "number", when used, will mean exclusively a natural number. And it is important -- vital -- for you to keep separate in your mind the formal system (TNT) and the rather ill-defined but comfortable old branch of mathematics that is number theory itself. This I call "N".
Some typical sentences of N -- number theory -- are :
1' There do not exist numbers a and b, both greater than 1, such that 5 equals a times b.
2' There does not exist a number b, such that b times b equals 2.
3' There exist numbers b and c, such that b times b times b, plus c times c times c equals 1729.
4' For all numbers b and c, greater than 0, there is no number a such that a times a times a equals b times b times b plus c times c times c.
5' For each number a, there exists a number b, greater than a, with the property that there do not exist numbers c and d, both greater than 1, such that b equals c times d.
6' There exists a number e such that 2 times e equals 6.
This analysis has gotten us a long way towards the basic elements of the language of number theory. It is clear that a few phrases reappear over and over :
for all numbers b
there exists a number b, such that ...
greater than
equals
times
plus
0, 1, 2, ...
Most of these will be granted individual symbols. An exception is "greater than", which can be further reduced. In fact, the sentence "a is greater than b becomes
there exists a number c, not equal to 0, such that a equals b plus c.
Numerals
We will not have a distinct symbol for each natural number. Instead, we will have a very simple, uniform way of giving a compound symbol to each natural number -- very much as we did in the pi-system. Here is our notation for natural numbers :
zero : 0
one : S0
two : SS0
three : SSS0
four : SSSS0
etc.
The symbol S has an interpretation -- "the successor of". Hence, the interpretation of SS0 is literally "the successor of the successor of zero".
Strings of this form are called numerals.
Variables and Terms
Clearly, we need a way of referring to unspecified, or variable, numbers. For that, we will use the letters a, b, c, d, e. But five will not be enough. We need an unlimited supply of them, just as we had of atoms in the Propositional Calculus [that is, Propositional Logic, which is about statements (as its atoms). It is established there what the truth-value (0 or 1, that is, false or true) of compound statements (statements connected to each other by "and", "or", or "if then", or statements connected with "not") will be, given the truth-values of the constituent individual statements.]. We will use a similar method for making more variables : tacking on any number of primes (which here are commas, not to be confused with prime numbers!). For instance :
e
d'
c''
b'''
a''''
are all variables.
In a way it is a luxury to use the first five letters of the alphabet when we could get away with just a and the prime (thus only two symbols). Later on, I will actually drop b, c, d and e, which will result in a sort of "austere" version of TNT -- austere in the sense that it is a little harder to decipher complex formulas. But for now we'll be luxurious.
Now what about addition and multiplication? Very simple : we will use the ordinary symbols ' + ' and ' . ' . However, we will also introduce a parenthesizing requirement (we are now slowly slipping into the rules which define well-formed strings of TNT ). To write "b plus c" and "b times c", for instance, we use the strings
(b + c)
(b . c)
There is no laxness about such parentheses. To violate the convention is to produce a non-well-formed formula ("Formula"? I use the term instead of "string" because it is conventional to do so. A formula is no more and no less than a string of TNT ).
Incidentally, addition and multiplication are always to be thought of as binary operations -- that is, they unite precisely two numbers, never three or more. Hence, if you wish to translate "1 plus 2 plus 3", you have to decide which of the following two expressions you want :
(S0 + (SS0 + SSS0))
((S0 + SS0) + SSS0)
The next notion we'll symbolize is equals. That is very simple : we use ' = ' . The advantage of taking over the standard symbol used in N -- nonformal number theory -- is obvious : easy legibility.
All numerals and variables are terms.
Atoms and Propositional Symbols
All the symbols of the Propositional Calculus ( Hofstadter, Chapter VII ) except the letters used in making atoms (P. Q, and R) will be used in TNT, and they retain their interpretations :
"-" means negating all what comes after it, that is, negating the whole statement : "it is not so that ... (statement)". (negation).
"... ==> ..." means ... implies ... . (implication, if ... then ...). It is a connective.
For the other connectives "and" and "or" we use the symbols conventionally used in logic :  means "and",
means "and", 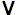 means "or". Of course here "and" does not mean "plus", but connects entire well-formed strings.
means "or". Of course here "and" does not mean "plus", but connects entire well-formed strings.
< ... > includes a compound, such as "x and y", "x or y", or "x ==> y", thus, < x and y >, < x or y >, < x ==> y >.
The role of atoms will be played by strings which, when interpreted, are statements of equality, such as S0 = SSO (which is a false statement) or (S0.S0) = S0 (which is a true statement).
Now we have the equipment to do a fair amount of translation of simple sentences into the notation of TNT :
2 plus 3 equals 4 : (SS0 + SSS0) = SSSS0
2 plus 2 is not equal to 3 : - (SS0 + SS0) = SSS0
If 1 equals 0, then 0 equals 1 : < S0 = 0 ==> 0 = S0 >
The first of these strings is an atom. The rest are compound formulas.
Free Variables and Quantifiers
All the well-formed formulas above have the property that their interpretations are sentences which are either true or false. There are, however, well-formed formulas which do not have that property, such as this one :
Its interpretation is "b plus 1 equals 2". Since b is unspecified, there is no way to assign a truth value to the statement. Because it is neither true not false, such a formula is called open, and the variable b is called a free variable.
One way of changing an open formula into a closed formula, or sentence (proposition), is by prefixing it with a quantifier -- either the phrase "there exists a number b such that ...", or the phrase "for all numbers b". In the first instance, you get the sentence
Clearly this is true. In the second instance, you get the sentence
Clearly this is false.
We will now give the translations of these "N-things" into the formal language of TNT. We introduce symbols for both of these quantifiers.
The above sentences are translated into TNT-notation as follows :
 b : (b + S0) = SS0 ( "
b : (b + S0) = SS0 ( " " stands for "exists".)
" stands for "exists".)
 b : (b + S0) = SS0 ( "
b : (b + S0) = SS0 ( " " stands for "all".)
" stands for "all".)It is very important to note that these statements are no longer about unspecified numbers. The first one is an assertion of existence, and the second one is a universal assertion. They would mean the same thing, even if written with c instead of b :
 c : (c + S0) = SS0
c : (c + S0) = SS0
 c : (c + S0) = SS0
c : (c + S0) = SS0A variable which is under the dominion of a quantifier is called a quantified variable. The following two formulas illustrate the difference between free variables and quantified variables :
 b : (b.b) = SS0 (closed, a sentence of TNT )
b : (b.b) = SS0 (closed, a sentence of TNT )
The second formula means : "It is not so that there is a b such that b times b equals two".
The first formula expresses a property which might be possessed by some natural number. Of course, no natural number has that property. And that is precisely what is expressed by the second formula. It is very crucial to understand this difference between a string with a free variable, which expresses a property, and a string where the variable is quantified, which expresses a truth or falsity. The English translation of a formula with at least one free variable -- an open formula -- is called a predicate. It is a sentence without a subject (or a sentence whose subject is an out-of-context pronoun). For instance,
are non-arithmetical predicates. They express properties which specific entities might or might not possess. One could as well stick on a "dummy subject", such as "so-and-so". A string with free variables is like a predicate with "so-and-so" as its subject. For instance,
is like saying " 1 plus 1 equals so-and-so". This is a predicate in the variable b. It expresses a property which the number b might have. If one were to substitute various numerals [such as 1, 2, 3, etc] for b, one would get a succession of formulas, most of which would express falsehoods. Here is another example of the difference between open formulas and sentences :
 b :
b :  c : (b + c) = (c + b)
c : (b + c) = (c + b)The above formula is a sentence representing, of course, the commutativity of addition. On the other hand,
 c : (b + c) = (c + b)
c : (b + c) = (c + b)is an open formula, since b is free. It expresses a property which the unspecified number b might or might not have -- namely of commuting with all numbers c.
Translating Our Sample Sentences
This completes the vocabulary with which we will express all number-theoretical statements! It takes considerable practice to get the hang of expressing complicated statements of N in this notation, and conversely of figuring out the meaning of well-formed formulas. For this reason we return to the six sample sentences given at the beginning, and work out their translations into TNT. By the way, don't think that the translations given below are unique -- far from it. There are many -- infinitely many -- ways to express each one.
Let us here reproduce these six number theoretic sample sentences :
1' There do not exist numbers a and b, both greater than 1, such that 5 equals a times b.
2' There does not exist a number b, such that b times b equals 2.
3' There exist numbers b and c, such that b times b times b, plus c times c times c equals 1729.
4' For all numbers b and c, greater than 0, there is no number a such that a times a times a equals b times b times b plus c times c times c.
5' For each number a, there exists a number b, greater than a, with the property that there do not exist numbers c and d, both greater than 1, such that b equals c times d.
6' There exists a number e such that 2 times e equals 6.
( To read the translations that follow, recall that a point in TNT means "times", so (a.b) means "a times b" )
 e : (SS0.e) = SSSSSS0
e : (SS0.e) = SSSSSS0Note the necessity of the quantifier. It simply would not do to write
alone. The interpretation of the latter string is of course something that is neither true nor false. It just expresses a property which the number e might have.
It is curious that, since we know multiplication is commutative, we might easily have written
 e : (e.SS0) = SSSSSS0
e : (e.SS0) = SSSSSS0instead. Or, knowing that equality is a symmetrical relation, we might have chosen to write the sides of the equation in the opposite order :
 e : SSSSSS0 =(SS0.e)
e : SSSSSS0 =(SS0.e)Now these three translations of "6 is even" are quite different strings, and it is by no means obvious that theoremhood of any one of them is tied to theoremhood of any of the others. (Similarly, the fact that --p-i--- was a theorem had very little to do with the fact that its "equivalent" string -p--i--- was a theorem. The equivalence lies in our minds, since, as humans, we almost automatically think about interpretations, not structural properties of formulas.).
We can dispense with sentence 2 : "2 is not a square", almost immediately :
 b : (b.b) = SS0
b : (b.b) = SS0However, once again, we find an ambiguity. What if we had chosen to write it this way?
 b : - (b.b) = SS0
b : - (b.b) = SS0
The first way says, "It is not the case that there exists a number b with the propery that b's square is 2", while the second way says, "For all numbers b, it is not the case that b's square is 2".
Once again, to us, they are conceptually equivalent -- but to TNT, they are distinct strings.
Let us proceed to sentence 3 : "1729 is a sum of two cubes". This one will involve two existential quantifiers, one after the other, as follows :
 b :
b :  c : SSSSSS ...... SSSSSSSS0 = (((b.b).b) + ((c.c).c))
c : SSSSSS ...... SSSSSSSS0 = (((b.b).b) + ((c.c).c))[where there are 1729 S's in the formula]
There are alternatives galore. Reverse the order of the quantifiers. Switch the sides of the equation. Change the variables to d and e. Reverse the addition. Write the multiplications differently. Etc., etc. However, I prefer the following two translations of the sentence :
 b :
b :  c : (((SSSSSSSSSS0.SSSSSSSSSS0).(SSSSSSSSSS0) + ((SSSSSSSSS0.SSSSSSSSS0).SSSSSSSSS0)) = (((b.b).b) + ((c.c).c))
c : (((SSSSSSSSSS0.SSSSSSSSSS0).(SSSSSSSSSS0) + ((SSSSSSSSS0.SSSSSSSSS0).SSSSSSSSS0)) = (((b.b).b) + ((c.c).c))
and
 b :
b :  c : (((SSSSSSSSSSSS0.SSSSSSSSSSSS0).SSSSSSSSSSSS0) + ((S0.S0).S0)) = (((b.b).b) + ((c.c).c))
c : (((SSSSSSSSSSSS0.SSSSSSSSSSSS0).SSSSSSSSSSSS0) + ((S0.S0).S0)) = (((b.b).b) + ((c.c).c))
In these two translations the way the number 1729 is written out already expresses the fact that it is the sum of two cubes : respectively 103 + 93 (= 1729) and 123 + 13 (= 1729).
Now let us tackle the related sentence 4 : "No sum of two positive cubes is itself a cube". Suppose that we wished merely to state that 7 is not a sum of two positive cubes. The easiest way to do this is by negating the formula which asserts that 7 IS a sum of two positive cubes. This will be just like the preceding sentence involving 1729, except that we have to add in the proviso of the cubes being positive. We can do this with a trick : prefix the variables with the symbol S as follows :
 b :
b :  c : SSSSSSS0 = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))
c : SSSSSSS0 = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))
You see, we are cubing not b and c, but their successors, which must be positive, since the smallest value which either b or c can take on is zero. Hence the right-hand side represents a sum of two positive cubes. Incidentally, notice that the phrase "there exist numbers b and c such that ...", when translated ( b :
b :  c :), does not involve the symbol
c :), does not involve the symbol  which stands for "and". That symbol is used for connecting entire well-formed strings, not for joining two quantifiers.
which stands for "and". That symbol is used for connecting entire well-formed strings, not for joining two quantifiers.
Now that we have translated " 7 is a sum of two positive cubes", we wish to negate it. That symply involves prefixing the whole thing by a single negation sign " - ". (Note : you should not negate each quantifier, even though the desired phrase runs : " There do not exist numbers b and c such that ..."). Thus we get :
 b :
b :  c : SSSSSSS0 = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))
c : SSSSSSS0 = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))Now our original goal was to assert this property not of the number 7, but of all cubes. Therefore, let us replace the numeral SSSSSSS0 by the string ((a.a).a), which is the translation of "a cubed" :
 b :
b :  c : ((a.a).a) = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))
c : ((a.a).a) = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))At this stage, we are in possession of an open formula, since a is still free. The formula expresses a property which a number a might or might not have -- and it is our purpose to assert that all numbers do have that property. That is simple -- just prefix the whole thing with a universal quantifier :
 a : -
a : - b :
b :  c : ((a.a).a) = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))
c : ((a.a).a) = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))An equally good translation would be this :
 a :
a : b :
b :  c : ((a.a).a) = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))
c : ((a.a).a) = (((Sb.Sb).Sb) + ((Sc.Sc).Sc))In austere TNT, we could use a' instead of b, and a'' instead of c, and the formula would become :
 a :
a : a' :
a' :  a'' : ((a.a).a) = (((Sa'.Sa').Sa') + ((Sa''.Sa'').Sa''))
a'' : ((a.a).a) = (((Sa'.Sa').Sa') + ((Sa''.Sa'').Sa''))What about sentence 1 : "5 is prime"? We had reworded it in this way : " There do not exist numbers a and b, both greater than 1, such that 5 equals a times b". We can slightly modify it, as followes : " There do not exist numbers a and b such that 5 equals a plus 2, times b plus 2". This is another trick -- since a and b are restricted to natural number values, this is an adequate way to say the same thing. Now "b plus 2" could be translated into (b + SS0), but there is a shorter way to write it -- namely, SSb. Likewise, "c plus 2" can be written SSc. Now, our translation is extremely concise :
 b :
b :  c : SSSSS0 = (SSb.SSc)
c : SSSSS0 = (SSb.SSc)
Without the initial negation-symbol, it would be an assertion that two natural numbers do exist, which, when augmented by 2, have a product equal to 5. With the negation-symbol in front, that whole statement is denied, resulting in an assertion that 5 is prime. We have used the expressions SSb and SSc (instead of just b and c) in order to be sure that the alleged factors are greater than 1.
So we have now successfully translated sentence 1.
If we wanted to assert that d plus e plus 1, rather than 5, is prime, the most economical way would be to replace the numeral for 5 by the string (d + Se) :
 b :
b :  c : (d + Se) = (SSb.SSc)
c : (d + Se) = (SSb.SSc)Once again, an open formula, one whose interpretation is neither a true nor a false sentence, but just an assertion about two unspecified numbers, d and e. Notice that the number represented by the string (d + Se) is necessarily greater than d, since one has added to d an unspecified but definitely positive amount. Therefore, if we existentially quantify over the variable e, we will have a formula which asserts that :
There exists a number which is greater than d and which is prime.
 e : -
e : - b :
b :  c : (d + Se) = (SSb.SSc)
c : (d + Se) = (SSb.SSc)Well, all we have left to do now is to assert that this property actually obtains, no matter what d is. The way to do that is to universally quantify over the variable d :
 d :
d :  e : -
e : - b :
b :  c : (d + Se) = (SSb.SSc)
c : (d + Se) = (SSb.SSc)That's the translation of sentence 5 ! It read : " There are infinitely many prime numbers".
[For our noëtic theory of organic evolution -- as it is so far developed on this website -- it is important to realize the following : Our theory assumes that the set of noëtic strategies, existing as string-patterns in the Implicate Order, constitutes a formal system with its own production rules, a system that is, however, essentially arithmetic, with its symbols standing for natural numbers and its production rules being, to this system, intrinsic and unique combinations of arithmetical operations. These operations are the 'usual' arithmetical operations, that is, addition, multiplication, and carrying-to-a-higher-power (which is special case of multiplication), as they are defined -- and ontologically, as they naturally are what they are -- in the theory of natural numbers, and, again, ontologically, in the objectively existing system of natural numbers and their properties : The rules of the noëtic system of strategy-strings harness the laws of objective 'ontological' number theory. So the noëtic system of strategy-strings, although it has its own typical nature, is rooted in (ontological) number theory. But this 'harnessing' coming -- it must be stressed -- from outside number theory, that is, from the Explicate Order.
How to Distinguish True from False?
At this juncture, it is worthwhile pausing for breath and contemplating what it would mean to have a formal system that could sift out the true ones from the false ones. This system would treat all these strings -- which to us look like statements -- as designs having form, but no content. And this system would be like a sieve through which could pass only designs with a special style -- the "style of truth". If you yourself have gone through a number of TNT formulas, trying to translate them, and have separated the true from the false by thinking about meaning, you will appreciate the subtlety that any system would have to have, that could do the same thing -- but typographically! The boundary separating the set of true statements from the set of false statements (as written in the TNT-notation) is anything but straight. It is a boundary with many treacherous curves, see Figure 1, above, a boundary of which mathematicians have delineated stretches, here and there, working over hundreds of years. Just think what a coup it would be to have a typographical method which was guaranteed to place any formula on the proper side of the border!
The Rules of Well-Formedness
It is useful to have a table of Rules of Formation for well-formed formulas. This is provided below. There are some preliminary stages, defining numerals, variables, and terms. Those three classes of strings are ingredients of well-formed formulas, but are not in themselves well-formed. The smallest well-formed formulas are the atoms. Then there are ways of compounding atoms. Many of these rules are recursive lengthening rules, in that they take as input an item of a given class and produce a longer item of the same class. In this table, I use 'x' and 'y' to stand for well-formed formulas, and 's', 't', and 'u' to stand for other kinds of TNT strings. Needless to say, none of these five symbols is itself a symbol of TNT.
Numerals
Variables
a is a variable. If we're not being austere, so are b, c, d and e.
A variable followed by a prime is also a variable.
Examples : a b' c'' d''' e''''
Terms
All numerals and variables are terms.
A term preceded by S is also a term.
If s and t are terms, then so are (s+t) and (s.t).
Examples : 0 b SSa' (S0.(SS0 + c)) S(Sa.(Sb.Sc))
Terms may be divided into two categories
Atoms
If s and t are terms, then s = t is an atom.
Examples : S0 = 0 (SS0+SS0) = SSSS0 S(b+c) = ((c.d).e)
If an atom contains a variable u, then u is free in it. Thus there are four free variables in the last example.
Negations
A well-formed formula preceded by a negation symbol is well-formed.
Examples : -S0 = 0 - b : (b+b) = S0 - < 0 = 0 ==> S0 = 0 > -b = S0
b : (b+b) = S0 - < 0 = 0 ==> S0 = 0 > -b = S0
The quantification status of a variable (which says whether the variable is free or quantified) does not change under negation.
Compounds
If x and y are well-formed formulas, and provided that no variable which is free in one [formula] is quantified in the other, then the following are all well-formed formulas :
< x y >, < x
y >, < x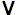 y >, < x ==> y >.
y >, < x ==> y >.
Examples : < 0 = 0 - 0 = 0 > < b = b
- 0 = 0 > < b = b 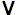 -
-  c : c = b > < S0 = 0 ==>
c : c = b > < S0 = 0 ==>  c : -
c : - b : (b+b) = c >
b : (b+b) = c >
The quantification status of a variable doesn't change here.
Quantifications
If u is a variable, and x is a well-formed formula in which u is free, then the following strings are well-formed formulas :
 u : x and
u : x and  u : x
u : x
Examples :  b : < b = b
b : < b = b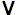 -
- c : c = b >
c : c = b >  c : -
c : - b : (b+b) = c -
b : (b+b) = c - c : Sc = d
c : Sc = d
Open formulas contain at least one free variable.
Examples : -c = c b = b <  b : b = b
b : b = b -c = c >
-c = c >
Closed formulas (sentences) contain no free variables.
Examples : S0 = 0 - d : d = 0
d : d = 0  c : <
c : <  b : b = b
b : b = b -c = c >
-c = c >
This completes the table of Rules of Formation for the well-formed formulas of TNT [And these rules are thus not the production Rules of TNT which will be given later].
And this also concludes the exposition of the notation of TNT. The whole purpose of TNT is to figure out if and how it is possible to characterize the true strings typographically.
The First Rules of TNT and its five Axioms (Hofstadter, pp.215)
Our formal system, TNT, will have axioms, and rules of inference (production rules).
Firstly, all of the Rules of the Propositional Calculus [propositional logic] (where propositions are the atoms, and which is about the truth or falsity of combined propositions) are taken over in TNT. Therefore, one theorem of TNT will be this one :
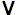 -S0 = 0 >
-S0 = 0 >
which can be derived in the same way as < P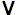 -P > can be derived in the Propositional Calculus, where P stands for a proposition.
-P > can be derived in the Propositional Calculus, where P stands for a proposition.
Let us now give the rules of inference of the Propositional Calculus, which, as has been said, also belong to TNT (They are taken from Hofstadter p.187) :
Joining Rule : If x and y are theorems, then < x y > is a theorem.
y > is a theorem.
Separation Rule : If < x y > is a theorem, then both x and y are theorems.
y > is a theorem, then both x and y are theorems.
Double negation Rule : The string '- -' (not-not) can be deleted from any theorem. It can also be inserted into any theorem, provided that the resulting string is itself well-formed.
Fantasy Rule : If y can be derived when x is assumed to be a theorem, then < x ==> y > is a theorem. [Here, x need not be a theorem, we have here : If x, then y]
Carry-over Rule : Inside a fantasy [if ... then ...], any theorem from the "reality" one level higher can be brought in and used. [things established before the fantasy constitute the "reality-one-level-higher"]
Rule of Detachment : If x and < x ==> y > are both theorems, then y is a theorem.
Contrapositive Rule : < x ==> y > and < -y ==> -x > are interchangeable.
De Morgan's Rule : < -x -y > and - < x
-y > and - < x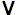 y > are interchangeable.
y > are interchangeable.
Switcheroo Rule : < x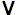 y > and < -x ==> y > are interchangeable.
y > and < -x ==> y > are interchangeable.
For all these rules it must be kept in mind that the symbols 'x' and 'y' always stand for well-formed strings of the system. The rules that appear for the first time in TNT (that is, are not part of the Propositional Calculus) will be given later.
Before we give these rules, let us give the five axioms of TNT :
Axiom 1 :  a : -Sa = 0
a : -Sa = 0
Axiom 2 :  a : (a+0) = a
a : (a+0) = a
Axiom 3 :  a :
a :  b : (a+Sb) = S(a+b)
b : (a+Sb) = S(a+b)
Axiom 4 :  a : (a.0) = 0
a : (a.0) = 0
Axiom 5 :  a :
a :  b : (a.Sb) = ((a.b)+a)
b : (a.Sb) = ((a.b)+a)
(In the austere versions, use a' instead of b)
All these axioms are very simple to understand. Axiom 1 states a special fact about the number 0. Axioms 2 and 3 are concerned with the nature of addition. Axioms 4 and 5 are concerned with the nature of multiplication, and in particular with its relation to addition.
The Five Peano Postulates
By the way, the interpretation of Axiom 1 -- " Zero is not the successor of any natural number" -- is one of the five famous properties of natural numbers first explicitly recognized by the mathematician and logician Giuseppe Peano, in 1889. In setting out his postulates, Peano was following the path of Euclid in this way : he made no attempt to formalize the principles of reasoning, but tried to give a small set of properties of natural numbers from which everything else could be derived by reasoning. Peano's attempt might thus be considered "semiformal". Peano's work had a significant influence, and thus it would be good to show Peano's five postulates. Since the notion of "natural number" is the one which Peano was attempting to define, we will not use the familiar term "natural number", which is laden with connotation. We will replace it with the undefined term djinn, a word which comes fresh and free of connotations to our mind. Then Peano's five postulates place five restrictions on djinns. There are two other undefined terms : Genie, and meta. I will let you figure out for yourself what usual concept each of them is supposed to represent [With "Genie", think of zero, with "meta" think of "what comes directly after it"]. The five Peano postulates are then :
New Rules of TNT : Specification and Generalization
Now we come to new [production] rules of TNT. Many of these rules will allow us to reach in and change the internal structure of the atoms of TNT. In that sense they deal with more "microscopic" properties of strings than the rules of the Propositional Calculus, which treat atoms as indivisible units. For example, it would be nice if we could extract the string -S0 = 0 from the first axiom. To do this we would need a rule which permits us to drop a universal quantifier, and at the same time to change the internal structure of the string which remains, if we wish. Here is such a rule :
Rule of Specification : Suppose u is a variable which occurs inside the string x. If the string
 u : x is a theorem, then so is x, and so are any strings made from x by replacing u, wherever it occurs, by one and the same term.
u : x is a theorem, then so is x, and so are any strings made from x by replacing u, wherever it occurs, by one and the same term.( Restriction : The term which replaces u must not contain any variable that is quantified in x )
The rule of specification allows the desired string -S0 = 0 to be extracted from Axiom 1. It is a one-step derivation :
 a : -Sa = 0 (axiom 1)
a : -Sa = 0 (axiom 1)
-S0 = 0 (specification)
Notice that the rule of specification will allow some formulas which contain free variables (i.e. open formulas) to become theorems. For example, the following strings could also be derived from Axiom 1, by specification :
-Sa = 0
-S(c+SS0) = 0
Both formulas are predicates (not assertions) because they contain a free variable. Therefore, the translation of, for example, the first expression is not "It is not so that the successor of a equals zero", but (in the ordering of natural numbers according to increasing value) "not standing before zero". The same applies to the second expression.
There is another rule, the rule of generalization, which allows us to put back the universal quantifier on theorems which contain variables that became free as a result of usage of specification. Acting on the second string, for example, generalization would give :
 c : -S(c+SS0) = 0
c : -S(c+SS0) = 0
Generalization undoes the action of specification, and vice versa. Usually, generalization is applied after several intermediate steps have transformed the open formula in various ways. Here is the exact statement of the rule :
Rule of Generalization : Suppose x is a theorem in which u, a variable, occurs free. Then
 u : x is a theorem.
u : x is a theorem.( Restriction : No generalization is allowed in a fantasy [if ... then ...] on any variable which appeared free in the fantasy's premise)
The need for restrictions on these two rules will shortly be demonstrated explicitly. Upon following mathematical proofs such as Euclid's proof about the infinitude of primes [i.e. prime numbers] we already can see how the symbol-manipulating rules are starting to approximate the kind of reasoning which a mathematician uses.
[When we look to the rules of TNT that are shared with the Propositional Calculus (see ABOVE ), and also to the new rules of TNT, the ones that have been given until now, and all the ones that will come a little later on, we see that these rules formalize steps of the reasoning process. So the formal system TNT consists of axioms from which (and from theorems already derived from the axioms) we can derive all the theorems of TNT by using these rules, that is by the allowed reasoning steps. So the rules of TNT are not entities that objectively exist somewhere, or, perhaps better expressed, not entities that are objectively inherent in the set of natural numbers and their properties. We assert that the axioms and theorems, and only the axioms and theorems, of TNT should express the fundamental and objectively existing properties of natural numbers. We expect that the rules of TNT, as established (and later, when needed, perhaps partly amended) by the enquiring subject (= "we", that is, mathematicians and logicians), lead us to these existing properties.
On the other hand, the rules in the supposed "formal system" of noëtic strategies existing in the Implicate Order (which rules are ultimately special combinations of arithmetical operations) are not held to be principles of human reasoning. They are fully ontological (i.e. independent of any [general and individual] knowing-subject) and contribute to the special features of the Implicate Order.]
The Existential Quantifier
These past two rules told how to take off universal quantifiers and put them back on. The next two rules tell how to handle existential quantifiers.
Rule of Interchange : Suppose u is a variable. Then the strings
 u : - and -
u : - and - u : are interchangeable anywhere inside any theorem.
u : are interchangeable anywhere inside any theorem.
For example, let us apply this rule to Axiom 1 :
 a : -Sa = 0 (axiom 1)
a : -Sa = 0 (axiom 1)
- a : Sa = 0 (interchange)
a : Sa = 0 (interchange)
By the way, you might notice that both these strings are perfectly natural renditions, in TNT, of the sentence "Zero is not the successor of any natural number". Therefore it is good that they can be turned into each other with ease.
The next rule is, if anything, even more intuitive. It corresponds to the very simple kind of inference we make when we go from "2 is prime" to " There exists a prime". The name of this rule is self-explanatory :
Rule of Existence : Suppose a term (which may contain variables as long as they are free) appears once, or multiply, in a theorem. Then any (or several, or all) of the appearances of the term may be replaced by a variable which otherwise does not occur in the theorem, and the corresponding existential quantifier must be placed in front.
Let us apply the rule to -- as usual -- Axiom 1 :
 a : -Sa = 0 (axiom 1)
a : -Sa = 0 (axiom 1)
 b :
b : a : -Sa = b (existence)
a : -Sa = b (existence)
You might now try to shunt symbols, according to the rules so far given, to produce the theorem - b :
b :  a : Sa = b. [The derivation is] :
a : Sa = b. [The derivation is] :
 a : -Sa = 0 (axiom 1)
a : -Sa = 0 (axiom 1)
 b :
b : a : -Sa = b (existence)
a : -Sa = b (existence)
 b :
b : a : -Sa = b (double negation)
a : -Sa = b (double negation)
 b : -
b : - a : -Sa = b (interchange)
a : -Sa = b (interchange)
 b : -
b : - a : -Sa = b (4)
a : -Sa = b (4)
 b : - -
b : - - a : Sa = b (interchange)
a : Sa = b (interchange)
 b :
b :  a : Sa = b (double negation)
a : Sa = b (double negation)
Rules of Equality and Successorship
We have given rules for manipulating quantifiers, but so far none for the symbols " - " and "S". We rectify that situation now. In what follows, r, s, and t all stand for arbitrary terms.
Rules of Equality :
SYMMETRY : If r = s is a theorem, then so is s = r.
TRANSITIVITY : If r = s and s = t are theorems, then so is r = t.
Rules of Successorship :
ADD S : If r = t is a theorem, then Sr = St is a theorem.
DROP S : If Sr = St is a theorem, then r = t is a theorem.
Now we are equipped with rules that can give us a fantastic variety of theorems. For example, the following derivations yield theorems which are pretty fundamental.
 a :
a :  b : (a+Sb) = S(a+b) (axiom 3)
b : (a+Sb) = S(a+b) (axiom 3)
 b : (S0+Sb) = S(S0+b) (specification, S0 for a )
b : (S0+Sb) = S(S0+b) (specification, S0 for a )
 a : (a+0) = a (axiom 2)
a : (a+0) = a (axiom 2)
 a :
a : b : (a.Sb) = ((a.b)+a) (axiom 5 )
b : (a.Sb) = ((a.b)+a) (axiom 5 )
 b : (S0.Sb) = ((S0.b)+S0) (specification, S0 for a )
b : (S0.Sb) = ((S0.b)+S0) (specification, S0 for a )
 a :
a :  b : (a+Sb) = S(a+b) (axiom 3 )
b : (a+Sb) = S(a+b) (axiom 3 )
 b : ((S0.0)+Sb) = S((S0.0)+b) (specification, (S0.0) for a )
b : ((S0.0)+Sb) = S((S0.0)+b) (specification, (S0.0) for a )
 a : (a+0) = a (axiom 2 )
a : (a+0) = a (axiom 2 )
 a : (a.0) = 0 (axiom 4 )
a : (a.0) = 0 (axiom 4 )
Illegal Shortcuts
Now here is an interesting question : "How can we make a derivation for the string 0 = 0 ?" It seems that the obvious route to go would be first to derive the string  a : a = a, and then to use specification. So, what about the following 'derivation' of
a : a = a, and then to use specification. So, what about the following 'derivation' of  a : a = a ... What is wrong with it? Can you fix it up?
a : a = a ... What is wrong with it? Can you fix it up?
 a : (a+0) = a (axiom 2 )
a : (a+0) = a (axiom 2 )
 a : a = (a+0) (symmetry)
a : a = (a+0) (symmetry)
 a : a = a (transitivity, lines 2, 1 )
a : a = a (transitivity, lines 2, 1 )
 a : (a+0) = a (axiom 2 )
a : (a+0) = a (axiom 2 )
 a : a = a (generalization)
a : a = a (generalization)
Why Specification and Generalization Are Restricted
Now let us see why there are restrictions necessary on both specification and generalization. (See for these restrictions HERE ). Here are two derivations. In each of them, one of the restrictions is violated. Look at the disastrous results they produce :
[With "push" is meant that we enter a fantasy, consisting of an assumption (a premise), A, and something, B, derived from it. We then obtain : A ==> B according to the Fantasy Rule. With "pop" is meant that we leave the fantasy.]
 a : a = 0 (generalization [Wrong!] )
a : a = 0 (generalization [Wrong!] )
 a : < a = 0 ==> Sa = 0 > (generalization)
a : < a = 0 ==> Sa = 0 > (generalization)
 a : a = a (previous theorem)
a : a = a (previous theorem)
 b : b = Sa (existence)
b : b = Sa (existence)
 a :
a :  b : b = Sa (generalization)
b : b = Sa (generalization)
 b : b = Sb (specification [Wrong!] )
b : b = Sb (specification [Wrong!] )
 b :), and thus cannot figure in a specification.
b :), and thus cannot figure in a specification.So now you can see why those restrictions are needed.
Here is a simple puzzle : translate (if you have not already done so) Peano's fourth postulate into TNT-notation, and then derive that string as a theorem.
Fourth postulate of Peano :  a :
a :  b : < -a = b ==> -Sa = Sb >
b : < -a = b ==> -Sa = Sb >
Its derivation :
 a :
a :  b : < -a = b ==> -Sa = Sb > (generalization)
b : < -a = b ==> -Sa = Sb > (generalization)
Something is Missing
[In this and the four following sections we prepare, and finally state, the last rule of TNT, the rule of induction, that allows us to prove, that when the first member of an infinite cascade of strings is found to be a theorem, and the pass-on pattern is also a theorem, all members of the cascade are theorems. This "all" we cannot prove by successively derive every next member from the previous member of the cascade because the cascade contains infinitely many members. The rule of induction allows such a proof. To apply this rule we need to have two theorems, because the rule, if it is to be applied, assumes two strings to be a theorem. In the next sections these two strings will be stated and proved to be theorems.]
Now if you experiment around for a while with the rules and axioms of TNT so far presented, you will find that you can produce the following pyramidal family of theorems (a set of strings all cast from an identical mold, differeing from one another only in that the numerals 0, S0, SS0, and so on have been stuffed in) :
etc.
As a matter of fact, each of the theorems in this family can be derived from the one directly above it, in only a couple of lines. Thus it is a sort of "cascade" of theorems, each one triggering the next.
Let us do some of such derivations :
 a : (a+0) = a (axiom 2 )
a : (a+0) = a (axiom 2 )
 a :
a :  b : (a+Sb) = S(a+b) (axiom 3 )
b : (a+Sb) = S(a+b) (axiom 3 )
 a :
a :  b : (a+Sb) = S(a+b) (axiom 3 )
b : (a+Sb) = S(a+b) (axiom 3 )
 a : (0+a) = a
a : (0+a) = a
[Do not confuse this string with axiom 2, which is :  a : (a+0) = a ]
a : (a+0) = a ]
Yet with the rules so far given, this string eludes production. Try to produce it yourself if you don't believe me. [It will be proved with the new and last rule of TNT]
You may think that we should immediately remedy the situation with the following
(Proposed) Rule of All : If all the strings in a pyramidal family are theorems, then so is the universally quantified string which summarizes them.
The problem with this rule is that it cannot be used in the M-mode [= Mechanical mode, that is, not by intuitive reasoning, but by actually producing that summarizing string from the axioms an rules of TNT so far given (in the present text)]. Only people who are thinking about the system can ever know that an infinite set of strings are all theorems. Thus this is not a rule that can be stuck inside any formal system.
[Problematic, accordingly, is the first part of the above proposed rule : This first part cannot be established from within, and thus we cannot obtain the second part of the rule.]
OMEGA-Incomplete Systems and Undecidable Strings
So we find ourselves in a strange situation, in which we can typographically produce theorems about the addition of any specific numbers, but even such a simple string as the one above,  a : (0+a) = a, which expresses a property of addition in general, is not a theorem. The expressive capability of TNT being so very strong, why can it not produce it as a theorem (with the means yet at hand)? If the string above is not a theorem, then we will have good reason to consider TNT to be defective. As a matter of fact, there is a name for systems with this kind of defect -- they are called OMEGA-incomplete ( The prefix "OMEGA" [written with the Greek letter] comes from the fact that the totality of natural numbers is sometimes denoted by "OMEGA"). Here is the exact definition :
a : (0+a) = a, which expresses a property of addition in general, is not a theorem. The expressive capability of TNT being so very strong, why can it not produce it as a theorem (with the means yet at hand)? If the string above is not a theorem, then we will have good reason to consider TNT to be defective. As a matter of fact, there is a name for systems with this kind of defect -- they are called OMEGA-incomplete ( The prefix "OMEGA" [written with the Greek letter] comes from the fact that the totality of natural numbers is sometimes denoted by "OMEGA"). Here is the exact definition :
A system is OMEGA-incomplete if all the strings in a pyramidal family are theorems, but the universally quantified summarizing string is not a theorem.
Incidentally, the negation of the above summarizing string
 a : (0+a) = a
a : (0+a) = ais also a nontheorem of TNT. This means that the original string is undecidable within the system. If one or the other were a theorem, then we would say that it was decidable. Although it may sound like a mystical term, there is nothing mystical about undecidability within a given system. It is only a sign that the system could be extended. For example, within absolute geometry, Euclid's fifth postulate is undecidable. It has to be added as an extra postulate of geometry, to yield Euclidean geometry. Or conversely, its negation can be added, to yield non-Euclidean geometry. If you think back to geometry, you will remember why this curious thing happens. It is because the four postulates of absolute geometry simply do not pin down the meanings of the terms "point" and "line", and there is room for different extensions of the notions. The points and lines of Euclidean geometry provide one kind of extension of the notions "point" and "line". The POINTS and LINES of non-Euclidean geometry, another. However, using the pre-flavored words "point" and "line" tended, for two millenia, to make people believe that those words were necessarily univalent, capable of only one meaning.
Non-Euclidean TNT
We are now faced with a similar situation, involving TNT. We have adopted a notation which prejudices us in certain ways. For instance, usage of the symbol "+" tends to make us think that every theorem with a plus sign in it ought to say something known and familiar and "sensible" about the known and familiar operation we call "addition". Therefore it would run against the grain to propose adding the follwing "sixth axiom" :
 a : (0+a) = a
a : (0+a) = aIt doesn't jibe with what we believe about addition. But it is one possible extension of TNT, as we have so far formulated TNT. The system which uses this as its sixth axiom is a consistent system, in the sense of not having two theorems of the form x and - x. However, when you juxtapose this "sixth axiom" with the pyramidal family of theorems shown above, you will probably be bothered by a seeming inconsistency between the family and the new axiom. But this kind of inconsistency is not so damaging as the other kind (where x and - x are both theorems). In fact, it is not a true inconsistency, because there is a way of interpreting the symbols so that everything comes out all right.
OMEGA-Inconsistency Is Not the Same as Inconsistency
This kind of inconsistency, created by the opposition of (1) a pyramidal family of theorems which collectively assert that all natural numbers have some property, and (2) a single theorem which seems to assert that not all numbers have it, is given the name OMEGA-inconsistency. An OMEGA-inconsistent system is more like the at-the-outset-distasteful-but-in-the-end-acceptable non-Euclidean geometry. In order to form a mental model of what is going on, you have to imagine that there are some "extra", unsuspected numbers -- let us not call them "natural", but supernatural numbers -- which have no numerals. Therefore, facts about them cannot be represented in the pyramidal family. ( This is a little bit -- [Hofstadter referring to the dialogue introducing his present Chapter] -- like Achilles' conception of GOD -- as a sort of "superdjinn", a being greater than any of the djinns. This was scoffed at by the Genie, but it is a reasonable image, and may help you to imagine supernatural numbers.)
What this tells us is that the axioms and rules of TNT, as so far presented, do not fully pin down the interpretations for the symbols of TNT. There is still room for variation in one's mental model of the notions they stand for. Each of the various possible extensions would pin down some of the notions further. But in different ways. Which symbols would begin to take on "distasteful" passive meanings, if we added the "sixth axiom" given above? Would all of the symbols become tainted, or would some of them still mean what we want them to mean? I will let you think about that. In any case, we will not follow this extension now, but instead go on to try to repair the OMEGA-incompleteness [instead of -inconsistency] of TNT [and not making the system OMEGA-inconsistent by adding the 6th axiom].
The Last Rule
The problem with the " Rule of All " was that it required knowing that all the lines of an infinite pyramidal family are theorems -- too much for a finite being. But suppose that each line of the pyramid can be derived from its predecessor in a patterned way. Then there would be a finite reason accounting for the fact that all the strings in the pyramid are theorems. The trick, then, is to find the pattern that causes the cascade, and show that that pattern is a theorem in itself. That is like proving that each djinn passes a message to its meta, as the children's game of " Telophone". The other thing left to show is that Genie starts the cascading message -- that is, to establish that the first line of the pyramid is a theorem. Then you know that GOD will get the message!
In the particular pyramid we were looking at, there is a pattern, captured by lines 4-9 of the derivation below.
 a :
a :  b : (a+Sb) = S(a+b) (axiom 3)
b : (a+Sb) = S(a+b) (axiom 3)
 b : (0+Sb) = S(0+b) (specification, 0 for a )
b : (0+Sb) = S(0+b) (specification, 0 for a )
The first line of the pyramid is also a theorem. It follows directly from Axiom 2. All we need now is a rule which lets us deduce that the string which summarizes the entire pyramid is itself a theorem. Such a rule will be a formalized statement of the fifth Peano postulate.
[ Let us summarize things we now have] :
We now have :  b : < (0+b) = b ==> (0+Sb) = Sb >. ( The whole implication, obtained from the above derivation, may be generalized [while the premise may not.] )
b : < (0+b) = b ==> (0+Sb) = Sb >. ( The whole implication, obtained from the above derivation, may be generalized [while the premise may not.] )
And we have (0+0) = 0, the 'starting signal' of the cascade, the first line of the pyramid.
But we have not :  b : (0+b) = b (because the premise of a fantasy [the assumption of an implication] may not be generalized). So we have not a theorem that generally speaks about the whole pyramid of strings.
b : (0+b) = b (because the premise of a fantasy [the assumption of an implication] may not be generalized). So we have not a theorem that generally speaks about the whole pyramid of strings.
We do have : (0+S0) = S0, that is, a concrete case. (See for the derivation of this string and of the next strings of the pyramid ABOVE )
And we have also : (0+SS0) = SS0, that is, every time we have only a concrete case).
To express that rule [as desired above], we need a little notation. Let us abbreviate a well-formed formula in which the variable a is free by the following notation :
( There may be other free variables, too, but that is irrelevant). Then the notation X{Sa/a} will stand for that string but with every occurrence of a replaced by Sa. Likewise, X{0/a} would stand for the same string, with each appearance of a replaced by 0.
A specific example would be to let X{a} stand for the string in question : (0+a) = a. Then X{Sa/a} would represent the string (0+Sa) = Sa, and X{0/a} would represent (0+0) = 0. ( Warning : This notation is not part of TNT. It is for our convenience in talking about TNT.)
With this new notation, we can state the last rule of TNT quite precisely :
Rule of Induction : Suppose u is a variable, and X{u} is a well-formed formula in which u occurs free. If both
 u : < X{u} ==> X{Su/u} > and X{0/u} are theorems, then
u : < X{u} ==> X{Su/u} > and X{0/u} are theorems, then  u : X{u} is also a theorem.
u : X{u} is also a theorem.
This is about as close as we can come to putting Peano's fifth postulate into TNT.
[Let us, that is, the author of this website, 'translate' the Rule of Induction, as it is precisely stated by Hofstadter above, into more plain language in order to understand it as best as possible :
IF (1) to every u applies that when u is a free variable of a well-formed formula implying that in it u may be replaced by Su, and (2) when (now without conditions) in the well-formed string u may be replaced by 0, that is, when the string with 0 instead of u is a theorem,
THEN for every u applies that the well-formed string (formula) with u is a theorem, that is,  u : X{u} is a theorem, and consequently X{u} is a theorem (specification), X{0/u} is a theorem (specification), X{0S/u} is a theorem (specification), X{0SS/u} is a theorem (specification), X{0SSS/u} is a theorem (specification), etc.
u : X{u} is a theorem, and consequently X{u} is a theorem (specification), X{0/u} is a theorem (specification), X{0S/u} is a theorem (specification), X{0SS/u} is a theorem (specification), X{0SSS/u} is a theorem (specification), etc.
Now let us use the Rule of Induction to show that  a : (0+a) = a is indeed a theorem in TNT. Emerging from the fantasy in our derivation above, we can apply the fantasy rule, to give us
a : (0+a) = a is indeed a theorem in TNT. Emerging from the fantasy in our derivation above, we can apply the fantasy rule, to give us
10. < (0+b) = b ==> (0+Sb) = Sb > (fantasy rule)
11.  b : < (0+b) = b ==> (0+Sb) = Sb > (generalization)
b : < (0+b) = b ==> (0+Sb) = Sb > (generalization)
This is the first of the two input theorems required by the induction rule. The other requirement is the first line of the pyramid, which we have. Therefore, we can apply the rule of induction, to deduce what we wanted :
 b : (0+b) = b
b : (0+b) = b
Specification and generalization will allow us to change the variable from b to a. Thus  a : (0+a) = a is no longer an undecidable string of TNT.
a : (0+a) = a is no longer an undecidable string of TNT.
[We have not added this formula as an axiom, but have added a rule by which the formula can be proved.]
[Here we continue the derivation of  a : (0+a) = a from line 11 above. That is, we show how the induction rule is applied] :
a : (0+a) = a from line 11 above. That is, we show how the induction rule is applied] :
(0+b) = b will be denoted as X{b}. Then X{0/b} stands for the string (0+0) = 0 (which is a theorem).
11.  b : < (0+b) = b ==> (0+Sb) = Sb > . This we can denote as :
b : < (0+b) = b ==> (0+Sb) = Sb > . This we can denote as :  b : < X{b} ==> X{Sb/b} > (which is a theorem).
b : < X{b} ==> X{Sb/b} > (which is a theorem).
So we now have obtained both theorems necessary for the Induction Rule :
 b : < X{b} ==> X{Sb/b} >
b : < X{b} ==> X{Sb/b} >
and
X{0/b}
It then follows from this rule :  b : X{b}, and this stands for the string
b : X{b}, and this stands for the string  b : (0+b) = b, and through specification and generalization we get :
b : (0+b) = b, and through specification and generalization we get :
 a : (0+a) = a.
a : (0+a) = a.
In the in-between piece of the Chapter Hofstadter gives a long derivation in TNT of the commutativity of addition
 d :
d :  c : (c+d) = (d+c)
c : (c+d) = (d+c)
Formal Reasoning versus Informal Reasoning
I would have preferred to show how to derive Euclid's Theorem (the infinitude of primes) in TNT, but it would probably have doubled the length of the book. Now after this theorem, the natural direction to go would be to prove the associativity of addition (a + b) + c = a + (b + c), the commutativity and associativity of multiplication, and the distributivity of multiplication over addition a.(b + c) = a.b + a.c. These would give a powerful base to work from.
As it is now formulated, TNT has reached "critical mass" (perhaps a strange metaphor to apply to something called " TNT "). It is of the same strength as the system of Principia Mathematica [a voluminous treatise about founding mathematics on logic, written in the beginning of the 20th century]. In TNT one can now prove every theorem which you would find in a standard treatise on number theory. Of course, no one would claim that deriving theorems in TNT is the best way to do number theory. Anybody who felt that way would fall in the same class of people as those who think that the best way to know what 1000x1000 is, is to draw a 1000 by 1000 grid, and count all the squares in it ... No. After total formalization, the only way to go is towards relaxation of the formal system. Otherwise, it is so enormously unwieldy as to be, for all practical purposes, useless. Thus, it is important to embed TNT within a wider context, a context which enables new rules of inference to be derived, so that derivations can be speeded up. This would require formalization of the language in which rules of inference are expressed -- that is, the metalanguage. And one could go considerably further. However, none of these speeding-up tricks would make TNT any more powerful. They would simply make it more usable. The simple fact is that we have put into TNT every mode of thought that number theorists rely on. Embedding it in ever larger contexts will not enlarge the space of theorems. It will just make working in TNT -- or in each "new, improved version" -- look more like doing conventional number theory.
Number Theorists Go out of Business
Suppose that you didn't have advance knowledge that TNT will turn out to be incomplete, but rather, expected that it is complete -- that is, that every true statement expressible in the TNT-notation is a theorem. In that case you could make a decision procedure for all of number theory. The method would be easy : if you want to know whether N-statement X is true or false, code it into TNT-sentence x. Now if X is true, completeness says that x is a theorem. And conversely, if not-X is true, then completeness says that - x is a theorem. So either x or - x must be a theorem, since either X or not-X is true. Now begin systematically enumerating all the theorems of TNT, in the way we did for the MIU-system. You must come to x or - x after a while. And whichever one you hit tells you which of X and not-X is true ( Did you follow this argument? It crucially depends on your being able to hold separate in your mind the formal system TNT and its informal counterpart N. Make sure you understand it) [So a theorem of a formal system can never in itself be true or false. If it is really a theorem, then (one of) its interpretation(s) (its meaning) is true, and only its interpretation.]. Thus, in principle, if TNT were complete, number theorists would be put out of business : any question in their field could be resolved, with sufficient time, in a purely mechanical way. As it turns out, this is impossible, which, depending on your point of view, is a cause either for rejoicing, or for mourning.
Hilbert's Program
The final question which we will take up in this Chapter is whether we should have as much faith in the consistency of TNT as we did in the consistency of the Propositional Calculus. And, if we don't, whether it is possible to increase our faith in TNT, by proving it to be consistent. One could make the same opening statement on the "obviousness" of TNT's consistency as Imprudence did [Hofstadter referring to the dialogue preceding the Chapter] in regard to the Propositional Calculus -- namely, that each rule embodies a reasoning principle which we fully believe in, and therefore to question the consistency of TNT is to question our own sanity. To some extent, this argument still carries weight -- but not quite so much weight as before. There are just too many rules of inference, and some of them just might be slightly "off". Furthermore, how do we know that this mental model we have of some abstract entities called "natural numbers" is actually a coherent construct? Perhaps our own thought processes, those informal processes which we have tried to capture in the formal rules of the system, are themselves inconsistent! It is of course not the kind of thing we expect, but it gets more and more conceivable that our thoughts might lead us astray, the more complex the subject matter gets -- and natural numbers are by no means a trivial subject matter. So Prudence's cry for a proof of consistency has to be taken more seriously in this case. It's not that we seriously doubt that TNT could be inconsistent -- but there is a little doubt, a flicker, a glimmer of a doubt in our minds, and a proof would help to dispel that doubt.
But what means of proof would we like to see used? Once again, we are faced with the recurrent question of circularity. If we use all the same equipment in a proof about our system as we have inserted into it, what will we have accomplished? If we could manage to convince ourselves of the consistency of TNT, but by using a weaker system of reasoning than TNT, we will have beaten the circularity objection! Think of the way a heavy rope is passed between ships (or so I read when I was a kid) : first a light arrow is fired across the gap, pulling behind it a thin rope. Once a connection has been established between the two ships in this way, then the heavy rope can be pulled across the gap. If we can use a "light" system to show that a "heavy" system is consistent, then we shall have really accomplished something.
Now on first sight one might think there is a thin rope. Our goal is to prove that TNT has a certain typographical property (consistency) : that no theorems of the form x and - x ever occur [occur both at the same time]. This is similar to trying to show that MU is not a theorem of the MIU-system. Both are statements about typographical properties of symbol-manipulation systems. The visions of a thin rope are based on the presumption that facts about number theory won't be needed in proving that such a typographical property holds. In other words, if properties of integers are not used -- or if only a few extremely simple ones are used -- then we could achieve the goal of proving TNT consistent, by using means which are weaker than its own internal modes of reasoning.
[When we would use properties of integers (and, more specificly, of natural numbers), the consistency of TNT would already be presupposed. And that the consistency of TNT is just a mere typographical property of it, becomes clear when we realize that in saying that no theorems of the form x and -x occur together we did not produce one string or another. The only thing that was said is that certain strings cannot be produced by the system.]
This is the hope which was held by an important school of mathematicians and logicians in the early part of the 20th century, led by David Hilbert. The goal was to prove the consistency of formalizations of number theory similar to TNT by employing a very restricted set of principles of reasoning called "finitistic" methods of reasoning. These would be the thin rope. Included among finitistic methods are all of propositional reasoning, as embodied in the Propositional Calculus, and additionally some kinds of numerical reasoning. But Gödel's work showed that any effort to pull the heavy rope of TNT's consistency across the gap by using the thin rope of finitistic methods is doomed to failure. Gödel showed that in order to pull the heavy rope across the gap, you can't use a lighter rope. There just isn't a strong enough one. Less metaphorically, we can say : Any system that is strong enough to prove TNT's consistency is at least as strong as TNT itself. [And the consistency of such a system is then as hard to prove as of that of TNT]. And so circularity is inevitable.
We have now concluded the exposition on formalized number theory, by following closely Hofstadter in his Chapter VIII, where he has wonderfully accomplished the task to render these esoteric matters accessible to a broader public, and thus, also accessible to us.
In the next document we will investigate -- again following Hofstadter -- the ability of TNT-strings to express things about other TNT-strings. This ability is then also expected in the Formal System of Noëtic Strategy-Strings (FSNSS) which is implemented on (embedded in) number theory (which we equate here with the objectively existing domain of natural numbers and their properties, of which formalized number theory, TNT, purports to represent [in its axioms and theorems] the essence).
e-mail :
 ( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
To continue click HERE for the further study of Organic Evolution, Part LXc.
Back to Evolutionary Part XVII
Back to Evolutionary Part XVIII
Back to Evolutionary Part XXII
Back to Evolutionary Part XXIII
Back to Evolutionary Part XXIV
Back to Evolutionary Part XXV-A
Back to Evolutionary Part XXV-B
Back to Evolutionary Part XXV-C
Back to Evolutionary Part XXVI
Back to Evolutionary Part XXVII
Back to Evolutionary Part XXVIII
Back to Evolutionary Part XXVIII-A
Back to Evolutionary Part XXIX
Back to Evolutionary Part XXXI
Back to Evolutionary Part XXXII
Back to Evolutionary Part XXXIII
Back to Evolutionary Part XXXIV
Back to Evolutionary Part XXXV
Back to Evolutionary Part XXXVI
Back to Evolutionary Part XXXVII
Back to Evolutionary Part XXXVIII
Back to Evolutionary Part XXXIX
Back to Evolutionary Part XLII
Back to Evolutionary Part XLIII
Back to Evolutionary Part XLIV
Back to Evolutionary Part XLVI
Back to Evolutionary Part XLVII
Back to Evolutionary Part XLVIII
Back to Evolutionary Part XLIX
Back to Evolutionary Part LIII
Back to Evolutionary Part LVII
Back to Evolutionary Part LVIII