

The non-functional aspects in the family- (or superfamily-) groundplans in Diptera, and their bearing on the theory of evolution, as this theory is ultimately in terms of the Implicate / Explicate Orders and noëtic reactions.
If we look to a dipterous family, or, when things allow it, a superfamily or any other group of closely related families, we can note that the representatives of such a taxon are (morphologically) built on the basis of a particular groundplan, that is, a complete 'family design' not of only the wing-venation but of the insect as a whole and including its developmental stages (larva). Indeed, we often can relatively easily recognize a given fly as being a representative of a certain particular family, superfamily, or a certain group of families. And generally there is much agreement about the definition and content of most dipterous families. Although the particular wing-venation often is one of the characteristics of a given family, other features can be such characters too, such as mouthparts and other structures of the adult or the structure of the larva.
Note on Acalyptrates :
The Acalytrates form, together with the Calyptrates, the group of the highest evolved Diptera. The Acalyptrates are in many cases small and more or less naked flies such as the fruitflies and drosophilids, while the Calyptrates are more robust, bristly and buzzy flies such as the housefly and the bluebottle. These two groups (acalyptrates and calyptrates) take their names from the absence or presence respectively of the calypter, or squama (or scale), that is, a (thoracic) lobe at the base of the wing that covers the halteres when it is well developed. As usual, there are exceptions in each group, but the division of the families into these two sections (family-groups) is nevertheless a natural and convenient one (OLDROYD, 1964, p. 170).
The Acalyptrate group of flies consists of a large number of families of which we mention :
Lauxaniidae (=Sapromyzidae), Celyphidae, Dryomyzidae, Helomyzidae, Chiromyiidae, Coelopidae (seaweed-flies), Sepsidae, Piophilidae, Clusiidae, Agromyzidae, Micropezidae (=Calobatidae, =Tylidae), Borboridae (=Sphaeroceridae), Sciomyzidae, Milichiidae, Carnidae, Chamaemyiidae, Ephydridae, Diopsidae, Chloropidae, Trypetidae (fruitflies), Otitidae (=Ortalidae), and Drosophilidae.
(The Calyptrate group consists of only a few families such as the Muscidae, Tachinidae, Calliphoridae, etc.)
Although the corresponding ecological niches (as occupied by members of the several different complexes -- Tipuloids, Syrphids, Acalyptrates) are not exactly the same, their differences are too small as to account for the very different groundplans of the mentioned complexes : For example, suppose that the ecological niches A(1), B(1), C(1), and D(1), are each occupied by certain representatives of the tipuloid complex, while the ecological niches A(2), B(2), C(2), and D(2), are occupied by certain representatives of the Syrphidae, and the ecological niches A(3), B(3), C(3), and D(3), are occupied by certain representatives of the Acalyptrata. Suppose further that the ecological niche A(x) is generally characterized (but not yet fully defined) by "rotting wood". We can then say that each of the mentioned complexes (tipuloids, syrphids, acalyptrates) has members occupying the general ecological niche "rotting wood", but that the respective narrowly taken ecological niches A(1), A(2), and A(3), all referring to living in rotting wood, are not exactly identical : They will differ either in the degree of advancement of the rotting process chosen by the larvae of the respective complexes, or in different products of this process being utilized by the larvae of different complexes, or in the same products being differently processed by them, etc. Something similar can be said about the ecological niches B(1), B(2), B(3), of C(1), C(2), C(3), and of D(1), D(2), D(3).
This non-correspondence between family-groundplan and ecology is a feature that is widely distributed throughout Diptera (and certainly also throughout virtually every other insect Order). This highly interesting feature has not as yet been considered in this website. The clarification of its evolutionary meaning and significance must at least be attempted in any discussion about organic evolution. It is precisely because of the lack of functional and ecological (adaptational) relevance of (the features of) the groundplan that the very fact of the existence of the many different groundplans in Diptera (as in almost any insect Order) seems utterly inexplicable, and indeed a major challenge for evolutionary theory, including our own interpretation of organic evolution ultimately in terms of the Implicate / Explicate Orders and noëtic reactions.
Let us now investigate two of the above mentioned complexes of dipterous families as to their groundplan, morphology, and ecology, namely the Tipuloids and the Acalyptrates. These groups are about at both ends of the evolutionary scale of Diptera : The Tipuloids being close to the first Diptera, while the Acalyptrates being (together with the Calyptrates) a more or less recent development in Diptera. While Tipuloids are known already from the lower Jurassic, the Acalytrates are only known since the beginning of the Tertiary period. And, as we saw in the previous document (click HERE ), every family, or group of closely related families, has a characteristic wing-venation, in the sense that the venation of every representative can be derived from a particular venational groundplan. So we can say that the overall groundplan of a dipterous family or group of related families is, in a way, expressed in the wing-venation.
(The latter statement brings back the question whether the wing-venation in Diptera is functional or just formal. In itself the statement suggests non-functionality, because it connects the wing-venation with the overall (family-)groundplan which itself was found to be non-functional (It is only functional in a most general sense, namely that it must comply with the general conditions of insect life). Preliminarily we could say that the various wing-venations as we actually encounter them in the various representatives of a given dipterous family go parallel with the various overall morphologies as we actually encounter them in these representatives. Except in the most primitive members of the family, we have to do, not with groundplans but with derivatives of a single groundplan, a groundplan, that is, respectively of the wing-venation and of the overall morphology of the body. And it is the groundplan -- the family-body-groundplan as well as the family-venational-groundplan -- that has been found to have no connection with a specific function or specific adaptation).
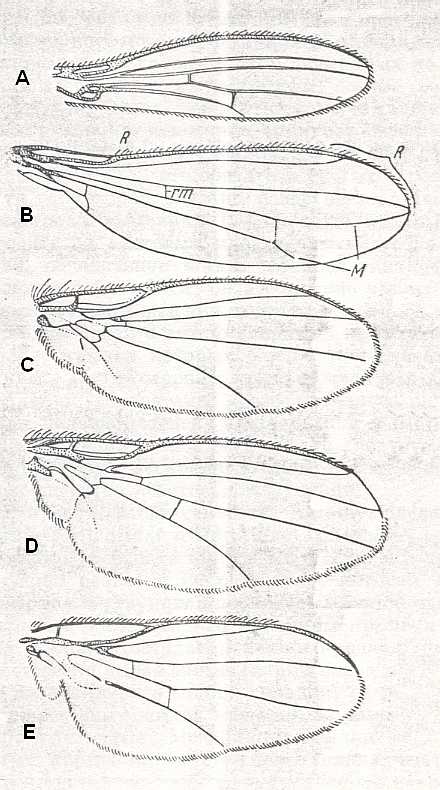
Adult tipuloids are medium- to large-sized diptera, all belonging to the suborder Nematocera, with long and slender body, long legs, long narrow wings, and -- as most Nematocera -- long multisegmented antennae. The tipuloids ( Tipulidae, Limoniidae, Cylindrotomidae, Ptychopteridae, Trichoceridae, Tanyderidae, and Pachyneuridae) have a characteristic wing-venation. Below we depict that of the first five families (the tipuloid nature of the last mentioned two families is more or less uncertain) :
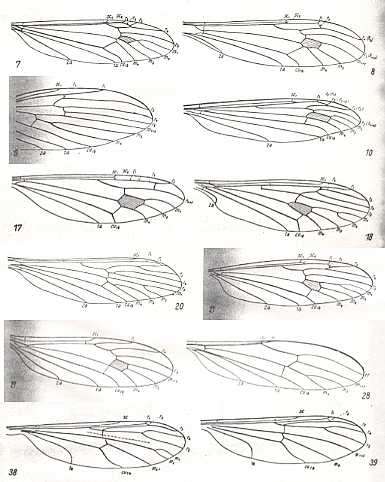
Figure 1 : Wing-venation of a number of representatives of the families Tipulidae, Cylindrotomidae, Trichoceridae, Limoniidae and Ptychopteridae ( = Liriopeidae).
Reading from left to right and from top to bottom :
7 -- Pales dorsalis FABR. (Tipulidae).
8 -- Idiotipula confluens ALEX. (Tipulidae).
19 -- Molophilus flavoscutellatus LACKSCH. (Limoniidae).
10 -- Phalacrocera replicata L. (Cylindrotomidae)
17 -- Stibadocerella albitarsis De MEIJ. (Cylindrotomidae).
18 -- Trichocera regelationis L. (Trichoceridae).
20 -- Tricyphona protea ALEX. (Limoniidae).
21 -- Limnophila ferruginea MEIG. (Limoniidae).
27 -- Atarba picticornis O.S. (Limonidae).
28 -- Toxorhina muliebris O.S. (Limonidae).
38 -- Liriope scutellaris MEIG. (Ptychopteridae [=Liriopeidae] ).
39 -- Bittacomorphella nipponensis ALEX.. (Ptychopteridae [=Liriopeidae] ).
(From HENNIG, 1954)
The next three Figures depict the typical habitus (body-shape) of tipuloids :
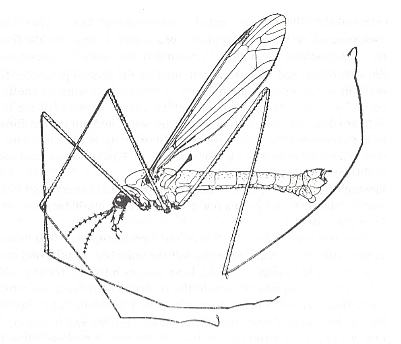
Figure 2 : Tipula paludosa Meigen ( Tipulidae, male), general view ( length of body 20 mm).
(After Lindner, 1928.)
Figure 2 depicts a typical member of the Tipulomorpha. It belongs to the family Tipulidae, that is, the long-palped crane-flies or 'daddy-long-legs'.
The next figure depicts a member of the family Ptychopteridae :
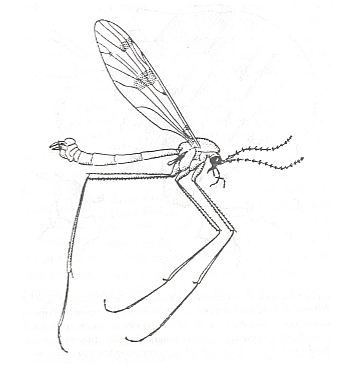
Figure 3 :
Ptychoptera contaminata L., Ptychopteridae, male, general view (length of body 9 mm).
(After LINDNER, 1928.)
The next Figure depicts a member of the relict family Tanyderidae :
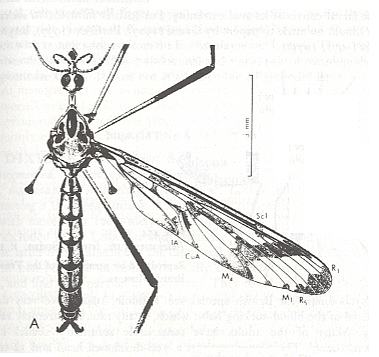
Figure 4 : Eutanyderus oreonympha, Tanyderidae.
The length-measure (vertical line segment) expresses : 5 mm.
(After COLLESS, in RICHARDS & DAVIES, Imm's General Textbook of Entomology,
10th edition, 1977.)
The next Figure depicts the wing-venation of another member of the family Tanyderidae :
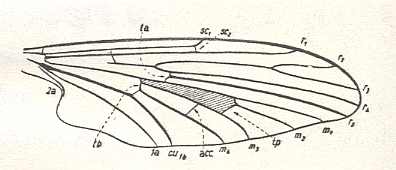
The next Figure depicts the wing-venation of a member of the isolated family Pachyneuridae considered to be more or less closely related to tipuloid flies :
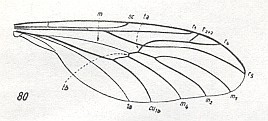
Next we depict the wing-venation of a fly considered to belong to the Ptychopteridae :
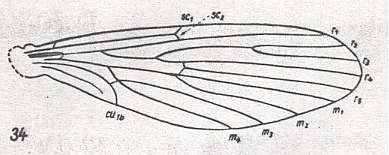
Figure 7 :
Wing of Nemopalpus zelandiae ALEX. ( Liriopeidae [ = Ptychopteridae] ).
[According to ROHDENDORF, 1964, Nemopalpus belongs to the family Nemopalpidae].
Interpretation of wing-venation according to HENNIG, 1954.
(From HENNIG, 1954, after ALEXANDER, 1927.)
Finally, the next two Figures again depict the habitus (body-shape) of some tipuloids :
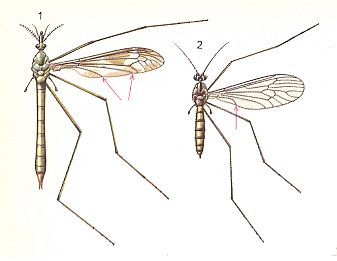
Figure 8 :
1 -- Tipula maxima PODA ( Tipulidae).
2 -- Trichocera annulata MEIGEN ( Trichoceridae).
(After CHINERY, Elseviers Insektengids voor West-Europa, 1983)
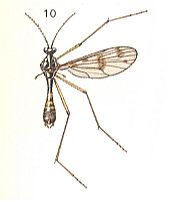
Figure 9 :
10 -- Ptychoptera contaminata L. ( Ptychopteridae).
(After CHINERY, Elseviers Insektengids voor West-Europa, 1983)
For a fly, which is not a tipuloid, but the adult of which nevertheless looks like one, click HERE .
The larvae of the tipuloids are not maggots (as they truly are in all acalyptrates). They have a well-differentiated head (capsule) which is provided with the original set of mouthparts or a set derivable from them. But, as all dipterous larvae, they do not possess true legs.
Click H E R E to see some larvae of the families Limoniidae (the largest family of tipuloids), the Tipulidae, the Cylindrotomidae, the Trichoceridae, the Tanyderidae, and the Pachyneuridae.
Adult acalyptrates are small- to medium-sized flies. Their body-shape often, but not always, is rather compact. Head relatively broad. Antennae short, consisting of three segments only. The third antennal segment bears a long bristle (arista). Wings often with a rounded apex. Anterior medial vein straight, that is, its distal part not with a conspicuous, forwardly directed, bent as we do have it in most calyptrates. The acalyptrates belong to the suborder Cyclorrapha.
The next five figures depict the habitus (body-shape) of a number of acalyptrates :


Figure 12 :
3 -- Melieria omissa MEIGEN ( Otitidae [ = Ortalidae] ).
4 -- Urophora cardui L. ( Trypetidae [ = Tephritidae] ).
5 -- Calliopum aeneum FALLEN ( Lauxaniidae).
6 -- Tetanocera elata FABR. ( Sciomyzidae).
7 -- Platystoma seminationis L. ( Platystomidae).
8 -- Dryomyza flaveola FABR. ( Dryomyzidae).
9 -- Coelopa frigida FABR. ( Coelopidae).
10 -- Psila rosae FABR. ( Psilidae).
11 -- Trepidaria petronella L. ( Micropezidae [ = Calobatidae, = Tylidae] ).
12 -- Chamaemyia aridella FALLEN ( Chamaemyiidae).
13 -- Lonchaea chorea FABR. ( Lonchaeidae).
14 -- Sepsis punctum FABR. ( Sepsidae).
15 -- Piophila casei L. ( Piophilidae).
(After CHINERY, Elseviers Insektengids voor West-Europa, 1983)

Figure 13 :
1 -- Helomyza spec. ( Helomyzidae).
2 -- Anthomyza gracilis FALLEN ( Anthomyzidae).
3 -- Trichiaspis similis COLLIN ( Sphaeroceridae [ = Borboridae] ).
4 -- Opomyza germinationis L. ( Opomyzidae).
5 -- Psilopa nigritella STENHAMMAR ( Ephydridae).
6 -- Oscinella frit L. ( Chloropidae).
7 -- Thaumatomyia notata MEIG. ( Chloropidae).
8 -- Lipara lucens MEIG. ( Chloropidae).
9 -- Meonura obscurella FALLEN ( Milichidae).
10 -- Carnus hemapterus NITZSCH ( Milichidae).
12 -- Drosophila funebris FABR. ( Drosophilidae).
13 -- Phytomyza ilicis CURTIS ( Agromyzidae).
(After CHINERY, Elseviers Insektengids voor West-Europa, 1983)
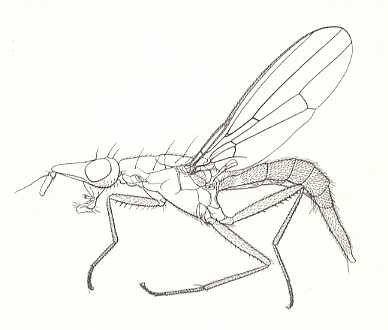
Figure 14 : Ozaenina diversa, Otitidae [ = Ortalidae] (subfamily Richardiinae).
(After OLDROYD, 1964)
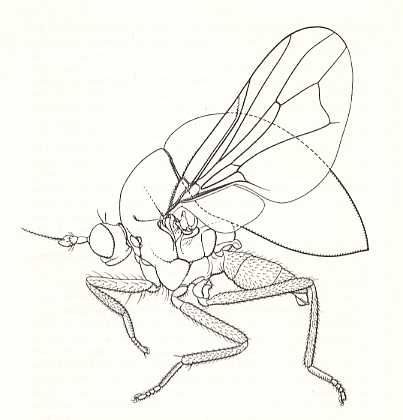
Figure 15 : A beetle-fly, belonging to the family Celyphidae.
The enormous scutellum (posterior dorsal shield of thorax) of the second thoracic segment
completely covers the abdomen. This enlarged scutellum also acts as a fixed cover for the wings in the resting position.
(After OLDROYD, 1964)
The wing-venation of acalyptrate flies is fairly constant and typical throughout this whole group. Here we present the wing-venation of representatives of the following acalyptrate (except two) families and subfamilies :
Family Drosophilidae (Drosophilinae, Periscelidinae, Canaceinae, Asteiinae and Sphaeroceratinae).
Family Lauxaniidae.
Family Tylidae.
Family Agromyzidae (Agromyzinae).
Family Chloropidae
Family Sciomyzidae
Family Trypaneidae
Family Ephydridae (Ephydrinae).
Family Sepsidae
Family Anthomyiidae (Calyptrates)
Family Phasiidae (Calyptrates)
Family Trypetidae
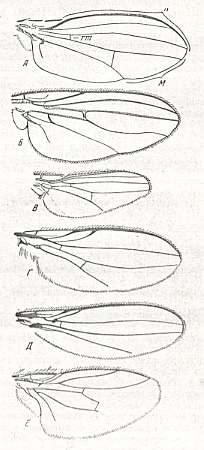
Wings of acalytrate flies. |
Wings of acalytrate flies. |
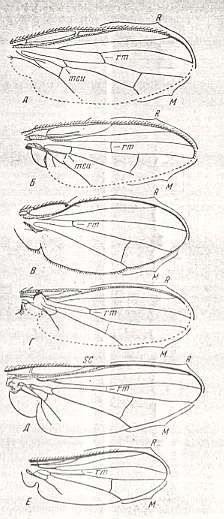
Wings of acalytrate flies. |
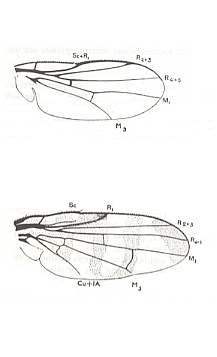
Wings of acalytrate flies. |
The last two wings in the left column of the above Figure respectively belong to the Anthomyiidae and Phasiidae. Although these two families do not belong to the Acalyptrates (but to the Calyptrates) the depicted representatives are nevertheless interesting because their wing-venation is really very close to that of the acalyptrates.
The larvae of the acalyptrates are all true maggots (as also those of the calyptrates). They do not have a head that is clearly differentiated from the rest of the body. They have a truly worm-like shape, that is to say, they do not in any way resemble caterpillars. The mouthparts consist of sclerotized hooks.
Tipuloids and Acalyptrates ecologically compared.
So we have now shown the two groups of families, the tipuloids and the acalyptrates.
They clearly represent two very different overall groundplans. The respective groundplans of these two groups are difficult to exactly define, but their existence should be clear after inspection of all the above figures (and from consulting other sources, and from observations in the field). And we also see that the difference of groundplans and the homogeneity in each is fairly well reflected in the wing-venation of the two groups. This indicates that the wing-venation is not only an integral part of the groundplan (which itself is considered to be non-functional) but formally seems to represent it in toto.
In what follows we will investigate whether or not the mentioned difference of the respective groundplans of tipuloids and acalyptrates matches with the difference of the respective ecologies of them, and also whether the magnitudes of the deviations from the groundplan-in-its-pure-state as we see them within each group reflect the different ecologies as we see these within each group. And although the ecology of many species is unknown, what we do know might well be sufficient to be able to draw some general conclusions about the functional significance or insignificance of the overall groundplan.
We can confidently say that, apart from a number of exceptions, the larval habitat (i.e. the type of environment where we can find the larva) of a given fly species contains most of the ecological niche of that species (this is especially true of the tipuloids and acalyptrates). The habits (feeding, moving around, etc.) of the adult fly merely follow from, that is, are determined by, the feeding habits of the larva, i.e. determined by the amount, quality and chemical nature of larval food. The habitat of the larva generally indicates the possible feeding habits of the larva and thus generally indicates, although not the precise ecological niche of the given fly species, its ecological zone.
Let us now compare the larval habitats, indicating the ecological zones, of species of tipuloids and of acalyptrates (see also in Organic Evolution Part V : Biology of the larvae of Diptera) :
| Tipuloids | Larval Habitat | Acalyptrates |
| Dictenidia, Tanyptera, Phoroctenia, Ctenophora, Tipula ( Tipulidae). Pachyneura ( Pachyneuridae), Epiphragma, Libnotes ( Limoniidae). |
Living in Rotting wood and its products (such as sap and fungi), habitat of many vegetable scavengers (saprophagous insects). | Clusiidae, Lonchaeidae, Tylidae [ = Calobatidae, = Micropezidae], Elachiptera (Chloropidae). |
| Trichoceridae [ = Petauristidae]. | Compost ( = decaying vegetable matter of a compost-like nature). | Lauxaniidae ( = Sapromyzidae), Helomyzidae, Elachiptera (Chloropidae). A few Drosophilidae (Diastata, Camilla, Parascaptomyza). |
| Tipulidae (mainly species of Tipula), Lauxaniidae [ = Sapromyzidae]. Certain species of Limonia ( Limoniidae). | Forest-litter. | |
| In the body of fungi large semi-transparent larvae of Metalimnobia quadrimaculata ( Limoniidae) are common. | Fungi. | Some Helomyzidae. Minute oval larvae of Drosophilidae, and yellowish larvae of Sphaeroceridae [ = Borboridae] develop in masses in the caps (including the hymenophor) as well as in the stem of the fruiting bodies of edible mushrooms. |
| Libnotes undulata ( Limoniidae). | Fermenting saps (from trees, fruits, etc.). | Drosophilidae. |
| Tipula ( Tipulidae), certain Limoniidae. | Feeding on living plants (including mosses) : their roots. | |
| Liogma, Cylindrotoma (Cylindrotomidae). | Feeding on living plants : their tissue. | |
| Leaf-miner : Limonia (Dicranomyia) kauaiensis ( Limoniidae). |
Feeding in living plants : galls, mines or otherwise. | Leaf-miners : all Agromyzidae, certain Trypetidae, Lauxaniidae [ = Sapromyzidae] (Halidayella [or Calliopum] aenea mines in leaves of clover and makes a gall in the flowers of viola), Psilidae, Drosophilidae, Ephydridae. Galls : some Trypetidae. Plant-feeders (not necessarily mining of making galls) : Chloropidae (such as Oscinella frit, Chlorops pumilionis (=taeniopus), and many other Chloropids). Trypetidae (fruits, flowers, seed-pods). |
| Certain Limoniidae and Tipulidae. Ptychoptera, Bittacomorpha ( Ptychopteridae). Protoplasa ( Tanyderidae). On banks and in deposits of mud at the bottom one can encounter larvae of Limoniidae and Tipulidae. | Living in fresh stagnant water. | Ephydridae (mining in aquatic plants). |
| Antocha ( Limoniidae). Rather common in small sources in deposits of mud are the large grayish larvae of Pedicia rivosa ( Limoniidae). In sources and brooks, in accumulations of wet wood develop some Limoniidae, e.g. Lipsothrix errans. | Living in fresh, flowing and well-aerated water (rivers, streams, sources). | |
| Geranomyia ( Limoniidae) (feeding on algal growth, diatoms, etc). | Living (temporarily) in or near sea water (intertidal zones, beaches, salt-marshes, salt-pans). | Coelopidae (seaweed flies or kelp flies), Sphaeroceridae [ = Borboridae] (namely Thoracochaeta zosterae). |
| Hexatomini and Pediciini of the Limoniidae. | Carnivorous larvae in fresh water. | Sepedon, Dictya (Sciomyzidae-Tetanocerinae, also carnivorous on land). |
| Terrestrial Carnivores (larvae). | Chamaemyiidae, some Drosophilidae (Gitona, Acletoxenus). | |
| Animal scavengers (i.e. eating all kinds of animal left-overs). | ||
| Living in nests of social insects (termites, bees, wasps, ants). | Rioxa termitoxena ( Trypetidae) breeds in the burrows of the Australian tree-living termites Mastotermes darwiniensis and Calotermes irregularis. Cacoxenus indagator ( Drosophilidae) lives as a larva in the nests of various carpenter bees and mason wasps ; it is a scavenger. |
|
| Living in nests or burrows of vertebrates (mostly those of birds). | some Sphaeroceridae [ = Borboridae], Milichiidae (scavengers), Carnidae (scavengers) (such as Carnus hemapterus). | |
| Dung-feeders. | some Helomyzidae, Sepsidae, Sphaeroceridae [ = Borboridae], Milichiidae, Carnidae. | |
| Carrion-feeders ( = necrophagous larvae). | some Helomyzidae, Sepsidae, Piophilidae (Piophila, drier carrion), some Ephydridae, certain Milichiidae. Larvae of Palloptera usta ( Pallopteridae [or Lonchaeidae] ) mainly feed on corpses of larvae and on beetles, and rarely prey upon other animals. | |
| Internal parasites of invertebrates. | some Sciomyzidae-Sciomyzinae (parasites [and with it killers] of snails), Discomyza incurva (parasite of land-snails [Helix] and belonging to the Ephydridae), Oscinosoma and Siphonella (Chloropidae, parasitic in the egg-masses of spiders as well as attacking certain beetles). Cryptochaetum ( Drosophilidae) is an internal parasite of scale-insects. |
As we can see in the above Table both tipuloids and acalyptrates are present in the following ecological zones :
A significant complex of Diptera is for individual development connected with disintegrating wood and the materials coming forth from it. Members of this complex can be encountered within such wood as well as under its bark, in mouldered wood [present] in hollows, or in a fermenting sap. To this complex belong the larvae of Dictenidia BRUL., Tanyptera LATR., Phoroctenia COQ., Ctenophora MEIG. (family Tipulidae) [Nematocera-Tipulomorpha], Hyperoscelididae [Nematocera-Bibionomorpha], Axymyiidae [Bibionomorpha], Pachyneuridae [Tipulomorpha or Bibionomorpha], Hesperinidae [Bibionomorpha], Clusiidae [(suborder) Brachycera-Cyclorrapha or, more or less equivalently, (infraorder) Myiomorpha], Lonchaeidae [Myiomorpha], many Bibionidae [Bibionomorpha], Sciaridae [= Lycoriidae] [Bibionomorpha], Ceratopogonidae [ = Heleidae] [Nematocera-Tipulomorpha], and, finally, Stratiomyidae [Asilomorpha].
Also from such a case (of which there are many others) we can see that the difference of existing groundplans is not ecologically expressed. So a change from one groundplan to another is not equivalent to a change of adaptation (that is, an adaptation to a new ecological zone or niche). Apart from very general ecological and physiological constraints and demands that are always forced upon any groundplan, the latter has no special functional or ecological meaning. It is just a pattern. And of course this pattern can and will be provided with the necessary adaptations in order for it to be able to exist in certain ecological niches or zones. So a given species of fly always consists of a non-adaptive structural core (the family- or superfamily-groundplan) encrusted or overformed as it were with adaptive structures. The nature of the latter partly depends on the nature of the groundplan (a given groundplan is not compatible with just any kind of adaptation overforming it, but only with some of them), and partly (it depends) on the nature of the ecological zone or niche to which representatives of the groundplan will become adapted.
Such an assumed overall structure -- adaptive periphery and non-adaptive core -- is impossible to describe in purely biological terms ; that is to say, the non-adaptiveness of the mentioned core (i.e. groundplan), and the evolutionary appearance of ever more new non-adaptive structures (new groundplans) cannot be explained by standard biological theory (random genetic mutations, natural selection). And we know that even already most adaptations as we see them in organisms cannot be explained by this theory. That was the reason for us to invoke the Implicate Order, that is, for us to widen the standard concept of Reality as it generally is held to be something exclusively physical and material, by letting it consist, not of one single Order, but of two interconnected Orders, namely the Explicate Order (= physical and material reality) and the Implicate Order (= enfolded reality). The Implicate Order can also called the Noëtic Order. And, indeed, all the many 'smart' adaptations as we see them in organisms can at least be rationally described (not yet explained) in terms of the Implicate Order and noëtic reactions. And now we must attempt to do the same with respect to the mentioned non-adaptive groundplans and their successive appearance in evolutionary history :
Because a given groundplan (and that goes for every groundplan individually considered) has no specific ecological meaning, their differences, as these turn up when comparing one groundplan with another, and their connections, that is, their mutual relationships, cannot be a matter of the Explicate Order, they must be a matter of the noëtic order, that is, of the Implicate Order.
We therefore assume that all the possible dipterous groundplans are together present in the Implicate Order as a result of the noëtic derivation of one from another. They exist there as noëtic entities or patterns. We assume further that they are contained there within noëtic stability fields. Outside its stability field a groundplan exists in the Implicate Order only in a metastable noëtic condition or is totally noëtically unstable and does not exist there. When it is stable it can be projected into the Explicate Order and is seen there as a successful groundplan. When it is metastable it can also be projected into the Explicate Order but is seen there as less successful and in a state of evolutionary decline. When it is unstable it cannot be projected into the Explicate Order. With all this we must realize that a groundplan cannot as such, that is, on its own, be projected : Only a (noëtic) reaction-product resulting from the noëtic reaction between the noëtic content of such a groundplan and the noëtic content of one of the potential ecological niches as determined by that groundplan can be projected from the Implicate Order into the Explicate Order. As we will express it later : An organic groundplan, as it (stably or at least metastably) exists as a noëtic entity in the Implicate Order, can only (be) project(ed) into the Explicate Order if it carries with it not only the general conditions for existence in this Order but also all the specific conditions for living in some existing ecological niche.
As has been said, we must visualize the groundplans as having their fields of stability in the Implicate Order. The stability conditions of the groundplans in that Order are not thermodynamic, nor are they ecological. They are noëtic stability conditions. Thermodynamic and ecological stability conditions are matters of the Explicate Order.
The "fields" of stability of the different groundplans are, of course, not spatial fields : we are in the noëtic Order. The term "field" is used only metaphorically. This is, because the stability here is not a function of dimensional variables (as we have them in the Temperature/Pressure stability diagrams of physical phases), but a function of noëtic variables.
Evolution of Diptera (as the evolution of any group of organisms), as it is seen in the Explicate Order (and deduced from fossils, comparative morphology and evolutionary theory), is in fact a trajectory through the noëtic stability landscape in the Implicate Order. This trajectory is in some noëtic ranges multiple-branched and in other ranges consisting of a collection of individual trajectories not connected with each other. A given period or point in time of the evolution of a certain group (of Diptera) corresponds to a definite locational point in the noëtic stability landscape in the Implicate Order, where "locational point" has no spatial meaning but a noëtic meaning. The evolutionary state of another group corresponds with another such point in that landscape. The individual evolutionary histories of these groups correspond to individual trajectories in that same landscape.
On the basis of this we can say the following :
All the above is an attempt to account for the fact that organisms turn out to be distributed into a relatively small number of groundplans, and that these groundplans do not have -- apart from some very general -- ecological significance, that is, a groundplan is not an adaptive structure. And non-adaptive structures cannot be explained or even only described as such in physical and biological terms. So we had to invoke the Implicate Order, as we already had to do for all cases of so-called 'smart adaptations'. We must attempt to describe the succession of groundplans, as we see it in the Explicate Order, in terms of the Implicate Order, and try to describe the transition of one family-groundplan into another (for instance the transition of the rhagionoid groundplan into the empidoid groundplan) in terms of stability and instability. When a given groundplan transforms into another, then we may say that this happened because the former had become unstable. And why had it become unstable? We had tried to answer this by saying that when a family somewhere in its evolutionary history cannot longer continue to colonize more and more diverse ecological niches (or zones), its groundplan will become unstable. However, it is not evident why a groundplan becomes unstable when it has occupied all its potential ecological niches. Further, we have made the stability of the groundplan dependent on ecological factors, while earlier it was found that the groundplan has no ecological significance. So this attempt will certainly not solve our problem (that is, the problem of the non-adaptive groundplans). Nevertheless the reader might find it instructive to read the attempt anyway, and can do it by clicking HERE .
The stability conditions of the groundplans cannot reside in the Explicate Order. Organic groundplans -- being non-adaptive -- are a matter of the Implicate Order. So these stability conditions cannot be ecological factors, and the stability or instability of a given groundplan is not determined by the ecological situation of its representatives. In fact, as we have outlined above, the ecological situation, or perhaps better, the evolutionary situation in the Explicate Order is a physical expression of the underlying degree of noëtical stability of the respective groundplans in the Implicate Order.
Physical analogue of the noëtic stability landscape of organic groundplans.
The stability, instability, metastability and equilibrium of family groundplans in the Implicate Order can tentatively be approached and understood only by using physical analogues : The stability, instability, etc. of physical and mineral phases depending on the external conditions of temperature and pressure in which these phases find themselves. Such phases are, for example, the three physical phases of water : ice, liquid water, and steam, or the set of mineral phases of carbon : diamond and graphite. They are expressed in so-called phase diagrams or stability diagrams. For every system there is one phase diagram, thus one diagram for, say, the system "H2O" (water) having at least three different phases, and another for, say, the system "SiO2" (silica) having at least six different phases. Each phase of a system has its stability field, that is a set of temperature and pressure conditions at which that phase can thermodynamically exist, that is, at which that phase is thermodynamically stable. When pressure and temperature are such that we are right on the boundary between two stability fields the two corresponding phases can thermodynamically coexist, they are in thermodynamic equilibrium with each other. In many cases a phase can exist even outside its stability field in the adjacent stability field of the other phase. It is then provisionally stable, metastable. A light disturbance, however, lets it transform into the proper phase in whose stability field it finds itself. For example, liquid water at atmospheric pressure is stable between 0 and 100 degrees Celcius but can be supercooled below 0 degrees without becoming ice.
In many cases two phases belonging to different systems can also thermodynamically coexist because their stability fields coincide or overlap.
Noëtic stability landscape of organic grounplans in the Implicate Order.
With this physical analogue in mind we can think of the organic groundplans -- while morphologically expressed in the Explicate Order as families, superfamilies, or family groups of organisms -- as actually being 'phases' existing in the Implicate Order. As such they are then not physical or mineral phases but noëtical phases. In some 'regions' in the Implicate Order the noëtic conditions are such that a particular groundplan can noëtically exist. Such a region is the noëtic stability field of that groundplan. It borders at the stability fields of other related groundplans. Right on such a boundary between two fields the two (related) groundplans ('phases') belonging to these fields can noëtically coexist. They are in noëtic equilibrium. Also here, noëtically related groundplans form a system, and so also here two or more different groundplans belonging to different systems -- that is, groundplans standing noëtically far away from each other -- can noëtically coexist when their respective noëtic stability fields coincide or overlap (See HERE ).
Stability Diagrams of physical and mineralogical systems
It is now time to discuss in yet more detail some physical and mineralogical systems, that is, discuss their respective stability diagrams (phase diagrams), in order to obtain a good understanding of how diagrams of this kind can serve as analogues of the noëtic stability landscapes of the groundplans as these plans reside in the form of noëtic contents (purely qualitative contents) in the Implicate Order (and can be projected into the Explicate Order).
Every chemical element or compound can, depending on temperature or pressure, enter in different physical states or phases, which can be gaseous, liquid or solid. The solid state is in the majority of cases a crystalline state, which means that the molecular or atomic constituents are ordered, forming a crystal lattice. The gaseous and liquid states are disordered in this respect. While there is for any given substance only one gaseous state or phase (if the substance does not disintegrate at the required temperature) there often exist more than one liquid state and especially several different solid states (crystalline phases) (When in a given system there exist several different kinds of crystals or several different kinds of liquids we can use the term phases also in this case). If the system consists of only one substance, for example H2O (water) one speaks of a one-component system. If a system consists of two substances, for example Iron (Fe) and Sulfur (S), one speaks of a two-component system or binary system, etc. Components are the independent chemical parts of a system. So in the one-component system of silica the compound SiO2 is its only component (and this component can appear, in addition to a SiO2 melt and a SiO2 vapor, in different SiO2 crystalline forms, that is, (mineral) phases, such as low(temperature)-quartz, high(temperature)-quartz, tridymite, etc.), while in the two-component system Fe-S the iron and sulfur are the components, and in the three-component system K2O-Al2O3-SiO2 the molecular groups K2O, Al2O3 and SiO2 are the components of the system (thus not the individual atoms).
For using such physical systems as physical analogues of noëtic systems (groundplans) one-component systems are by far the more important because they can serve as analogues of systems of noëtically related groundplans, groundplans that is to say that can can be noëtically derived from each other in just the same sense that in the SiO2 system -- a one-component system -- high-quartz can be formed from low-quartz (by increasing the temperature above 5730C ). The two quartzes are of course closely related because they both are SiO2 (Silicium dioxide). They are just different polymorphs of the same substance. So in what follows later on we will concentrate on one-component systems.
The ranges of possible existence of the phases of a system (these ranges generally depending on temperature, pressure, and often concentration-relationships) are called their stability fields. They are depicted in stability diagrams. The conditions (such as temperature, pressure and concentration) insofar as they are conceived as variables are called degrees of freedom.
The phase rule introduced by Willard Gibbs, which is now thermodynamically well-based and called phase law, makes it possible to exactly predict the number of phases that can occur in a given system under known physico-chemical conditions.
The maximal number of different phases P in a given system of components that can coexist and thus can be in thermodynamic equilibrium with each other is given as the total number of components K plus the number 2 and this subtracted by the number of degrees of freedom (generally the number of condition variables) :
which is eaquivalent to
In many mineralogical systems, especially in volcanic rocks and the like, where the condition variables pressure and temperature vary significantly, the number of coexistent phases is equal to the number of mineral species, and generally also to the number of different substances. So here the number of degrees of freedom is two, F = 2, so P = K.
I assume that because of the high degree of possible variation of either temperature or pressure in such (mineralogical) systems variations in relative concentrations are comparatively small and concentrations can be considered as constant.
If, on the other hand, one variable, for instance pressure or temperature, is considered to be fixed, then one more phase can be added to the one or ones already existing : F = 1, so P = K + 1 ( K + 1 phases of the system can coexist).
If, finally, both temperature and pressure are considered to be fixed, that is, F = 0, then yet one more phase can be added : P = K + 2 ( K + 2 phases of the system can coexist).
While gases are always completely miscible, many liquids are not, and especially many crystals are not miscible. So in many-component systems we can often see, at a certain P / T condition, the simultaneous presence of several different solid phases, in which the various crystalline modifications are stable only within definite P / T ranges. When such a range is crossed (as a result of increase or decrease of temperature and/or pressure) the modifications transform themselves, or pass over into a different state of aggregation, that is, they melt, evaporize, or become glassy (and in the case of liquids, they solidify or evaporate) [A glass is an amorphous solid, i.e. a solid with a disordered internal structure]. When the transformation sequence proceeds rapidly, a phase transition in the solid state generally takes place at once. When, on the other hand, the transformation sequence proceeds slowly, a given phase can, under certain circumstances, continue to exist unstably for a long time (that is, the phase transition is delayed).
And so we can see that trigonally crystallizing Quartz (SiO2) (low-quartz) upon heating up to 5730C transforms in hexagonal Quartz (SiO2) (high-quartz). This transformation proceeds without delay and is manifested by a sudden change of the symmetry properties. Upon cooling low quartz is at once formed at 5730C. Such a phase transition is called enantiotropic or reversible. On the other hand, a phase transition that can proceed only in one direction is called monotropic or irreversible. A mineralogical example of monotropic phase transition is the formation of Calcite (CaCO3) from Aragonite (CaCO3) when, as a dry substance, it is heated up to 400-500 degrees Celcius.
We will now discuss several physico-chemical one-component systems where different phases of the same substance (aggregation phases and mineral phases) have different P / T stability fields (in a stability diagram -- P/T diagram) and can be transformed into one another when temperature (T) and/or pressure (P) are changed.
H2O system
Apart from the aggregation states solid, liquid and gaseous, H2O has a relatively large number (up to 12) of different mineral phases, that is to say it has up to twelve different modifications of its solid state -- ice. Ice-I is the common modification of ice, while all the others are rather exotic, they are stable only at very low temperatures and/or very high pressures. The next Figure depicts the stability diagram (phase diagram, P/T diagram) of H2O. The temperature scale is set in the horizontal direction (abscissa) and the pressure in the vertical direction (ordinate) :
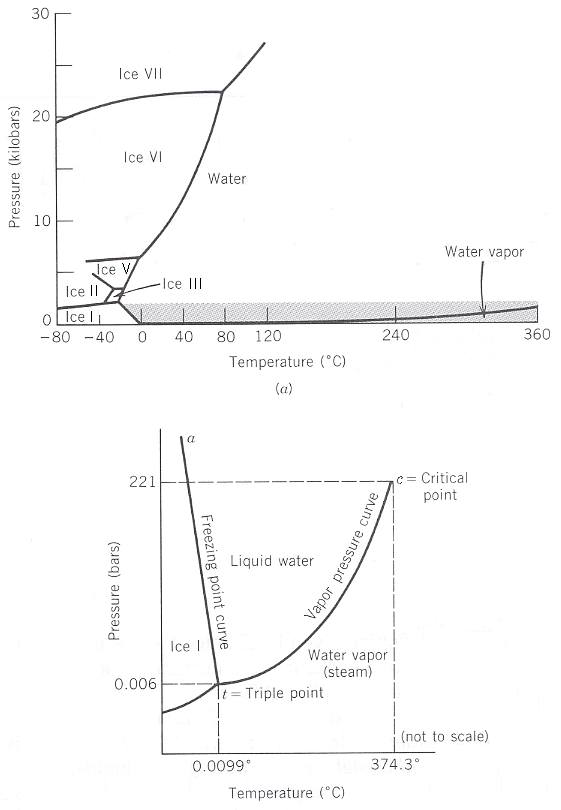
Figure 16
Top image : P-T diagram for H2O. Six polymorphic modifications of ice are indicated by I, II, III, V, VI, and VII. For clarity the water-steam curve has been offset slightly toward higher pressure. The shaded region is enlarged but not to scale in the bottom image. Pressure in kilobars.
Bottom image : P-T diagram for H2O, only for a short range of pressures, that is, only for moderate pressures. Pressure in bars.
Pressure units : 1 kilobar (kbar) = 1000 bar, 1 bar = 0.987 atmosphere.
(After KLEIN & HURLBUT, 1999, Manual of Mineralogy)
In the present existential fields of Liquid water, Water vapor (steam), IceI, Ice II, Ice III, Ice V, Ice VI and Ice VII, pressure and temperature can be varied at will. So here only one phase is stable : The number of degrees of freedom is two, F = 2. The number of components of the system is one, K = 1, so, according to the phase rule P (number of phases) = K + 2 - F, we have P = 1 + 2 - 2 = 1, that is, in these fields only one phase of the system is stable. In this case the system is bivariant, changing the P and T conditions one is moving in a plane, the existential field (stability field) of a possible phase.
We can tell some more about the polymorphs of ice (taken from BALL, Ph., 1999, "H2O, A BIOGRAPHY OF WATER" ) :
Ice -- that is, normal ice, Ice-I, consists of an ordered arrangement (crystal lattice) of interconnected water molecules. The structure of the ice lattice is such that it contains a lot of empty space. This makes ice a most unusual solid. In most solid materials the molecular or atomic constituents are packed densely, to make the most of the attractive interactions between them. This means that there is little scope for rearrangements, and all that happens if the solid is squeezed is that the atomic or molecular constituents get a little closer together. When the pressures get really big, however, a crystal may change its structure abruptly to some totally new atomic or molecular arrangement. This is a phase transition, taking place between two alternative solid forms of the same substance. And, as has been said, for ice there is much space to get more densely packed, especially by adopting crystal structures (the rearrangement of molecules) that pack its constituents more densely. Typically, solids may exhibit perhaps two or three different crystal structures at different pressures, but ice is much more versatile -- so far, twelve different crystal structures have been identified when ice is compressed. Ice-I is, as has been said, the normal type of ice, stable under winter conditions. When Ice-I is squeezed, there is so much space (between the water molecules of the crystal lattice) to take up the strain that it faces many more options than other solids of how to arrange its component parts. And the hydrogen bonds that hold the crystal lattice together are weak enough to be bent, stretched and shortened substantially under pressure. Each phase transition corresponds to a change of internal scene. These transformations augment the map of water's different phases (states). Its stability diagram (see Figure 16, top image ) becomes a veritable patchwork of stability fields.
When Ice-I is compressed to pressures of 3500 atmospheres we can see it jolt twice into new states : Ice-II and Ice-III. At a pressure of at least 6500 atmospheres Ice-VI is stable. It seems to remain solid up to at least 800C ('hot ice'). Ice-VI transforms to Ice-VII at around 22000 atmospheres, and Ice-VII is the really hot ice : you can heat it to well above 1000C without melting it, provided that the pressure is stepped up too. If the pressure is released while the ice is still below 00C, Ice-VII reverts to Ice-I [that is, jumps all the way to Ice-I ]. Only if it is kept very cold indeed -- below about minus 1700C -- does Ice-VII survive at atmospheric pressure. All these forms of ice contain the tetrahedral bonding arrangement of Ice-I, but in various distorted or reorganized forms. But the very-high-pressure phases of ice -- Ice-VI, VII, and VIII -- have a density almost twice as great as Ice-I. Twice as many molecules are packed into the same volume of space. No amount of bending or splaying will fill this much empty space. Instead, these internal arrangements of crystal constituents are dramatically innovative.
A curious feature of the patchwork of Ice States in the stability diagram of H2O is that it contains no territory marked "Ice-four", even though there is Ice-five, Ice-six and so on. Ice-IV does exist - it was identified in 1935 -- but it is a will-o'-the-wisp, a tentative, ghostly form of ice. It is formed under conditions in which Ice-V is the more stable form, and so it cannot persist indefinitely but transforms gradually to Ice-V. Ice-IV is metastable, that is, only provisionally stable [Normally a metastable state lies -- in the stability diagram -- a little outside the proper stability field of that state. Only inside that field it is really stable. The Ice-IV state, however, does not have such a field, so its existence is always transient. It persists only so long as an energy barrier prevents its conversion to the more stable state which here is Ice-V ].
New states of ice are still being found out in the frozen part of water's stability landscape. In 1998 a twelfth structure of ice -- Ice-XII -- was reported. Like Ice-IV , this phase appears at pressures and temperatures for which Ice-V is usually observed, and it too is metastable. It would not be at all surprising if still more forms of ice are discovered as it becomes possible to extend the search down to lower temperatures and out to higher pressures. There is no telling what lies out there.
H2O glasses
When a melt of a given substance or mineral is cooled so suddenly, so rapidly, that the atomic or molecular constituents have no time to arrange themselves into a low-energy configuration (crystal lattice) an internally disordered solid is the result, which is called a glass or amorphous solid. The molecules or atoms of the melt are stopped right in their tracks before they have a chance to take up regimented positions. Glasses are common in volcanic rocks originated by the sudden solidification of molten material reaching the earth's surface during volcanic eruptions. And indeed, when we rapidly cool molten sand (the chief mineral content of which is quartz (SiO2)) we obtain window glass. But the internal disordered configuration of a glass has a higher energy than the corresponding crystal lattice would have when the molten substance had been allowed to cool slowly giving it the time to settle in crystalline form. This means that all glasses are not truly stable phases, they are metastable.
Also H2O can occur as a glass. In fact it has two glass modifications. When water vapor is suddenly cooled below minus 1400C disorderly ice -- a glass -- is formed. If amorphous ice is warmed up above minus 1400C, its molecules can just about start to move again. The result is an extremely peculiar form of liquid water, which is about as viscous as asphalt. In such frigid conditions this viscous water exists in a highly precarious state : once the temperature exceeds minus 1200C the molecules have enough mobility to rearrange themselves into the crystalline ice lattice, and the stuff freezes to regular old Ice-I.
Water has yet a second glassy form in addition to the one just described : When Ice-I is squeezed to 10000 atmospheres at a temperature of minus 1960C, it 'melts' not into a liquid but into an amorphous ice with a greater density than that of the first form. The greater density indicates that the water molecules in this material are packed together more closely : the structure, while still disorderly, is different.
These glasses (like all glasses) are, as has been said, not truly stable phases : like Ice-IV and Ice-XII they are only provisionally stable, and the only thing that prevents them from transforming into a crystalline form is that the molecules are so cold they can barely move.
Supercooled water
Water can be cooled at least 380C below zero without freezing to ice. Liquid water below its freezing point is said to be supercooled.
Supercooled water is a liquid in Solidland, a liquid that has strayed over the border. This means that supercooled water is another metastable state, persisting in conditions that favor a different state.
Supercooled water is fairly common : many clouds, including altocumulus, altostratus, cirrocumulus, cirrostratus, and cirrus, are composed at least partly of supercooled water. Air temperatures at altitudes of greater than two kilometers are usually low enough to freeze water. And yet clouds consisting of tiny water droplets can be found up to altitudes of around thirteen kilometers. The water droplets in these clouds are typically between about 5 and 200 micrometers across. And it gets more and more difficult to grow ice crystals in progressively tinier droplets of water. The chances of enough water molecules coming together at random in the right orientation to form a 'nucleus' of ice become ever smaller. Cloud droplets generaly have to be colder than about minus 150C before they'll freeze, and even then a particle of mineral dust is usually needed to 'seed' the ice. Seed particles such as dust are the first places where freezing happens when a liquid is cooled below its freezing point. So to supercool water, you need to be assiduous in removing such impurities. Even then, supercooled water is poised on the brink of freezing : Below freezing point, there is a chance that a nucleus will form and ice will start to grow even without a seed. Even a slight agitation of the liquid might trigger crystallization.
On polymorphism in minerals.
In the exposition of the next one-component systems we will only consider the solid phases. These phases are possible polymorphs of a single substance. To understand that the possible polymorphs of such a substance differ structurally from each other -- they are embodiments of different qualitative contents -- it is necessary to say something more about polymorphism in minerals (KLEIN & HURLBUT, 2000, 153-158) :
The ability of a specific chemical substance to crystallize with more than one type of structure (as a function of changes in temperature, pressure, or both) is known as polymorphism. The various structures of such a chemical element or compound are known as polymorphic forms, or polymorphs [or modifications].
Three major types of mechanisms are recognized by which one polymorphic form of a substance can change to another. These are reconstructive, displacive, and order-disorder polymorphism.
The reason why a constant chemical composition may have different structural arrangements is that some structural configurations represent greater (or lesser) internal (structural) energies (E) than others. The relative internal energy of a specific polymorph may be a function of temperature, pressure, or both. A higher internal energy, as a function of increasing temperature, is caused by higher frequencies of vibrations of the atoms. We can expect abrupt differences in the relative internal energy levels as a function of temperature in polymorphs that are related by reconstructive transformations. And we can further expect that the respective structures of these polymorphs are completely different from each other.
If, on the other hand, the increase in internal energy level in one polymorph as a function of increasing temperature, until at a specific temperature the transformation takes place, is continuous, we have to do with displacive transformation, as a function of increasing temperature.
Pressure can also be a major driving force in polymorphic transformations. Increasing pressure favors the development of structural arrangements that result in an increase in the density of atomic packing (as reflected in increased density or specific gravity of the material) and a decrease in molar volume.
In a reconstructive polymorphic reaction the internal arrangement in going from one form to another is extensive. It involves the breaking of atomic bonds and a reassembly of the structural units in a different arrangement. This type of transformation requires a large amount of energy, is not readily reversed, and is sluggish. An example of such a polymorphic reaction is the change from Tridymite or Cristobalite to low Quartz. All three are polymorphs of SiO2.
In a displacive polymorphic reaction the internal adjustment in going from one form to another is very small and requires little energy. The structure is generally left completely in tact, and no bonds between ions (= electrically charged atoms or atomic groups) are broken. Only a slight displacement of atoms (or ions) and readjustment of bond angles ("kinking") between ions is needed. This type of transformation occurs instantaneously and is easily reversible. An example is the cooling of the high Quartz form of SiO2 to below 5370C at atmospheric pressure. It rearranges its structure to that of low Quartz. The difference between the two forms of Quartz is expressed by their Space Groups (= internal symmetry) ( high Quartz, P6222, low Quartz, P3221 ). The structural arrangement in the low-temperature form is slightly less symmetric and somewhat more dense than in the high-temperature form. The transition from high to low Quartz can be viewed as the result of "kinking" of atomic bonds in the original high Quartz structure.
Yet another type of polymorphism is referred to as order-disorder transformation. To appreciate this transformation, it should be noted that perfect order occurs only at absolute zero (00Kelvin, which is aequivalent to minus 273.150Celcius). An increase in temperature disturbs the perfect order of a structure, until at some high temperature a totally disordered (totally random) state is obtained. As such, there is no definite transition point between perfect order and complete disorder. In a state of perfect order, the atoms in a structure are arranged in specific crystallographic site locations. At high temperatures, close to but below the melting point of a substance, atoms (or ions) tend to become completely disordered and are ready to break away from the structure. Slow cooling of a mineral structure will permit the original randomized ions (at high temperatures) to select specific sites in the structure and become more ordered. If we have, say, an alloy of composition AB with 50 percent of atoms of kind A and 50 percent of atoms of kind B, then total disorder, on an atomic scale, implies equal probability of finding A or B in a specific site in the structure. In other words, the probability of a given atomic site being occupied by one type of atom instead of another equals 1.
An example of order-disorder polymorphism in a mineral is shown by Potassium feldspar ( KAlSi3O8 ), in which Al (aluminum) occupies a structural position identical with and replacing Si (silicon) in the mineral. The high-temperature form, Sanidine, with Space Group (= internal symmetry) C2/m, shows a disordered distribution of Al in the alumino-silicate framework. The low-temperature K-feldspar, low Microcline with Space Group C1*, however, shows an ordered distribution of Al in the alumino-silicate framework. States of intermediate order (which are equivalent to intermediate disorder) are present between that of high-temperature Sanidine and low-temperature Microcline.
We are now ready to continue our exposition of stability diagrams of one-component systems.
The Al2OSiO4 system
The next one-component system of which we study the stability diagram is that of the substance Al2OSiO4 (Aluminum silicate). Here we only consider the solid phases of the system. Aluminum silicate can occur in three different crystalline forms (three mineral phases), Sillimanite, Andalusite and Kyanite. The stability of these phases depends on temperature and pressure and can be depicted in a stability diagram.
Here some data concerning the symmetry structure of these three minerals :
Sillimanite : Crystal Class : Orthorhombic, 2/m 2/m 2/m. Space Group : Pbnm.
Andalusite : Crystal Class : Orthorhombic, 2/m 2/m 2/m. Space Group : Pnnm.
Kyanite : Crystal Class : Triclinic, 1*. Space Group : P1*. [a " * " after a number -- in the Crystal Class symbol or in the Space Group symbol -- stands for a score above that number (as it is done in current symbolism) ].
We see that they all differ with respect to their Space Group, meaning that their internal symmetry -- and thus their structure -- is different, despite their identical chemical formula, Al2OSiO4. They are the three different solid phases (mineral phases) of this substance.
Stability diagram of the Al2OSiO4 system.
Before we discuss the stability diagram of this system we first tell something about stability diagrams in general, namely where they in fact come from, that is, why they are what they are. We have taken it from NESSE, W. Introduction to Mineralogy, 2000, p. 75-76.
We know that the stability of a given phase (and of anything whatsoever) is a matter of that phase having the lowest energy possible in the present situation. It tends to spontaneously adopt an internal configuration that has this lowest energy, because then it is 'free from stress'. [While the stability of a mineral is thus determined by the energy of its internal structure, mechanical stability of some physical body is determined by its potential energy (energy of place)].
The measure of energy with which to judge the stability of minerals is Gibbs free energy, whose symbol is G. The term "free energy" expresses the energy in excess of the internal energy. This is the excess energy which is needed to drive a chemical reaction. To compare the Gibbs free energy of two possible mineral arrangements of the same chemical elements to decide which is more stable, it is necessary to have a common basis for comparison. The widely adopted convention in chemistry is to compare Gibbs free energy levels based on the free energy of formation from the elements, DELTA Gf. The free energy of formation from the elements is the energy difference between the chemical elements in their standard states (e.g. 2980K and 1 atm pressure) and these elements-chemically-bonded to form a mineral at the temperature and pressure of interest. Given two minerals with the same composition, such as Quartz and Tridymite (both SiO2), the stable mineral under specified temperature and pressure conditions is the mineral with the lowest DELTA Gf. Because DELTA Gf varies as a function of both temperature and pressure, under some conditions Quartz has lower Gibbs free energy and is more stable, and under others Tridymite has lower Gibbs free energy and is more stable.
Mineral transformations involve a conversion of one mineral or set of minerals to form another mineral or set of minerals. They are chemical reactions and can be dealt with using the normal conventions of chemistry. The polymorphic transition of Tridymite to form Quartz can be written
A more complex reaction is the formation of K-feldspar and Sillimanite at the expense of Muscovite and Quartz at fairly high temperatures in metamorphic rocks such as mica schist :
Both reactions are chemically balanced. The number of atoms of each element is the same on reactant and product sides of the reaction. The stability of a chemical reaction (including all mineral phase transitions -- same substance, different mineral phases) can be expressed in terms of Gibbs free energy :
that is, the free energy of a reaction is the difference in the free energy of formation of the product minerals and the reactant minerals. If, at a specific temerature-pressure condition, DELTA Greaction is smaller than 0,
then DELTA Gf (products) is smaller than DELTA Gf (reactants) and thus the products are more stable than that from which they are produced, and the reaction can spontaneously proceed. If, on the other hand, DELTA Greaction is greater than 0, then DELTA Gf (products) is greater than DELTA Gf (reactants) and thus the reactants are more stable (than their products). Minerals to the right of the <==> sign in chemical reaction notation would break down to form the reactant assemblage. The equilibrium condition is obtained if DELTA Greaction = 0. The products and reactants have the same free energy and no net reaction will proceed. [NESSE, 2000, p. 76]
It is convenient to illustrate the stability of minerals -- that is, solid crystalline phases -- and mineral reactions using various diagrams. The simplest are temperature-pressure (T-P) diagrams (stability diagrams, phase diagrams) [as had been used above for the mineral [ice] and aggregational phases of H2O (water) ]. Such diagrams are, as we now know, used to show the stability fields of minerals. The present example will concern the system of aluminum silicates. The mineral phases of this system are, as has been said, Sillimanite. Andalusite and Kyanite (the latter also known as Disthene). They are polymorphs with the chemical formula Al2OSiO4 (also written as Al2SiO5). They are common minerals in mica schists produced by metamorphism of shale. The free energy of formation of each of these minerals from their elements, that is, from aluminum [= aluminium] (Al), Silicon (Si), and Oxygen (O), varies as a function of both temperature and pressure. See top image of next Figure :
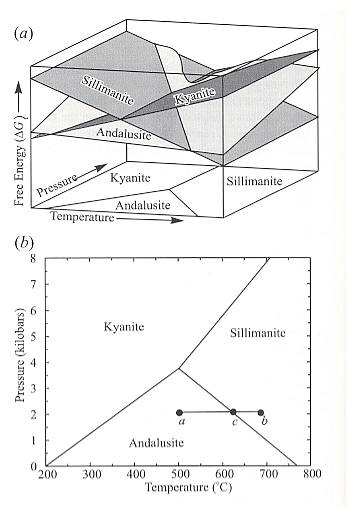
Figure 17 : Aluminum silicate stability relations.
Top image (a) : Schematic illustration of Gibbs free energy of formation of Andalusite (light), Sillimanite (intermediate), and Kyanite (dark) as a function of pressure and temperature. The mineral with the lowest free energy at a specific temperature-pressure condition is the stable phase at those conditions.
Bottom image (b) : Temperature-pressure stability fields of the aluminum silicate minerals Andalusite, Sillimanite, and Kyanite.
(From NESSE, 2000)
Under some conditions of temperature and pressure, Andalusite has the lowest energy, and under others Sillimanite or Kyanite is the lowest energy form of Al2OSiO4.
The SiO2 system
The substance SiO2 is Silicon dioxyde. It is widely distrubuted in and on the earth's crust, that is is sand and surfase rocks. Like that of ice, the crystal structure of SiO2 minerals is fairly open. So also here we can expect a number of high-pressure modifications, that is, these (and related) minerals tend not to be stable at high pressures and will convert to other modifications. Some SiO2 modifications (polymorphs) are Quartz, Tridymitem and Cristobalite. They have their own distinctive structures and conversion from one to the other requires that chemical bonds be broken -- they are reconstructive polymorphs. In addition, the structures of Quartz, Tridymite, and Cristobalite are each represented by ALPHA (low) and BETA (high) varieties. The ALPHA nd BETA varieties of each mineral are displacive polymorphs, related to each other by a distortion in the crystal lattice. In each case the BETA polymorph has higher symmetry and is stable at higher temperature than the ALPHA polymorph.
In addition to the vapor and liquid phase there are at least nine modifications of solid SiO2 :
| Polymorph | Crystal System and Class (point symmetry) |
Space Group (translational symmetry) |
| ALPHA-Quartz ( low Quartz ). |
Hexagonal (rhombohedral), 32. | P3221 (or P3121). |
| BETA-Quartz ( high Quartz ). |
Hexagonal (hexagonal), 622. | P6222 (or P6422) . |
| ALPHA-Tridymite ( low Tridymite ) |
Monoclinic or Orthorhombic, 2/m, m, or 222. |
Monoclinic : C2/c (or Cc). Orthorhombic : C2221. |
| BETA-Tridymite ( high Tridymite ) |
Hexagonal, 6/m 2/m 2/m. | P63/mmc. |
| ALPHA-Cristobalite ( low Cristobalite ) |
Tetragonal, 422. | P41212 (or P43212). |
| BETA-Cristobalite ( high Cristobalite ) |
Isometric (= cubic), 4/m 3* 2/m. | Fd3m. |
| Coesite. | Monoclinic, | C2/c. |
| Stishovite. | Tetragonal, | P42/mnm. |
| Keatite. | Tetragonal, | P41212 (or P43212). |
As we can see, all SiO2 polymorphs have different Space Groups (except low Cristobalite and Keatite), so their structures are different, that is, they represent different qualitative contents ( Low Cristobalite and Keatite have different specific gravities, pointing to a different structure).
Let us describe the successive appearance of these polymorphs when the temperature and/or pressure are progressively increased (STRÜBEL, 1977, Mineralogie, pp. 219). To begin with, we present the SiO2 stablity diagram, obtained from two sources :
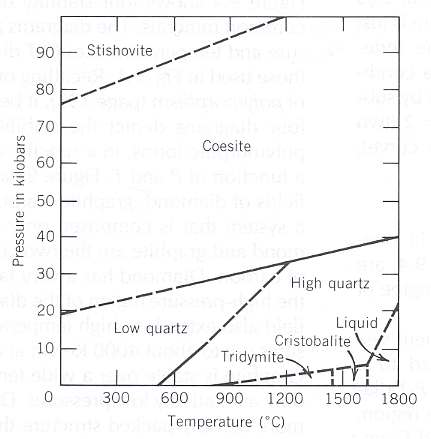
Figure 18 : Mineral stability diagram (P-T diagram) of the system SiO2.
When curves, or lines, are solid their locations have been determined with certainty. When they are dashed, their location is less well known.
A kilobar = 1000 bars. 1 bar = 0.987 atmosphere.
(From KLEIN & HURLBUT, 1999)
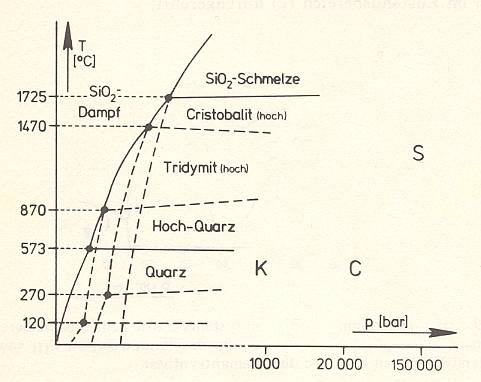
Figure 19 : Mineral stability diagram (P-T diagram) of the system SiO2 with the fields of existence (stability fields) of the low-pressure modifications and the ranges of formation of the high-pressure modifications Keatite = K, Coesite = C, and Stishovite = S.
(After STRÜBEL, 1977)
At room temperature and atmospheric pressure the trigonal-trapezohedric low Quartz is stable. It transforms without delay and reversibly into the hexagonal-trapezohedric high Quartz when heated up to 5730C. This transformation goes with a discontinuous change of properties.
The high-pressure modification of SiO2, the monoclinic Coesite, is stable at 8000C and at about 35000 atmosphere. It, however, also has the ability to keep on existing metastably at atmospheric pressure and room temperature. Coesit evidently has a great density because of the extreme high-pressure condition of its formation. A marked highest-pressure modification of SiO2, Stishovite, has been produced at 10000C and at about 100000 atmospheres. Finally, a middle-pressure modification Keatite is known, which appears tetragonally in hydrothermal conditions at about 1000 bar.
The Carbon system
The chemical element Carbon (C) shows, in addition to a liquid and vapor phase, three different solid phases : Diamond, Graphite, and Carbon III.

Figure 20 : Mineral stability diagram (P-T diagram) of the system C (= Carbon).
When curves, or lines, are solid their locations have been determined with certainty. When they are dashed, their location is less well known.
A kilobar = 1000 bars. 1 bar = 0.987 atmosphere.
(From KLEIN & HURLBUT, 1999)
The above Figure shows the stability fields of Diamond, Graphite, Carbon III, and liquid, for a system that is composed only of Carbon (C). Diamond and Graphite are the two common polymorphs of Carbon. Diamond has a very large stability field in the high-pressure region of the diagram. The diamond field also extends to high temperature at certain pressures (up to about 40000K at about 150 kilobars). Graphite is stable over a wide temperature range but only at relatively low pressures. Diamond has a much more densely packed structure than Graphite. As such, Diamond would be expected to be the high-pressure phase, as shown in the stability diagram. The polymorphic reaction in transforming Diamond to Graphite, and vice versa, is reconstructive. In such reconstructions, chemical bonds must be broken, and the structure must be reassembled. This requires large amounts of energy (activation energy), and because of this, Diamond is very stable under ordinary pressures and temperatures (atmospheric conditions) even though thermodynamically the diagram shows that Graphite is the stable phase under atmospheric conditions. The conversion rate of Diamond to Graphite, at atmospheric conditions, must be infinitely slow, and cannot be detected.
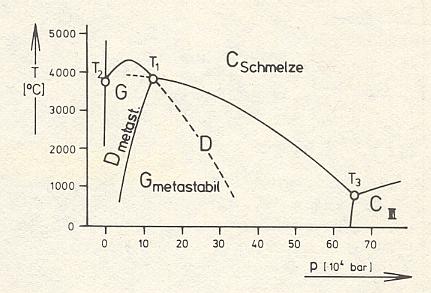
Figure 19 : Mineral stability diagram (P-T diagram) of the one-component system C (Carbon) with the fields of existence (stability fields) of Diamond (D), Graphite (G) and a high-pressure modification CIII.
(After STRÜBEL, 1977)
The invariant triple point T1 in which Graphite, Diamond, and Carbon melt coexist lies at 39000C. A further triple point T2 lies at atmospheric pressure at 38000C, where Graphite, liquid Carbon, and Carbon vapor coexist together, and finally there is a third triple point T3 at 10000C and a pressure of 630 kbar, where Diamond, liquid Carbon, and a highest-pressure modification of Carbon (which has metallic properties) coexist. Graphite (G) as well as Diamond (D) can exist metastably to the right respectively left of their common phase boundary. (STRÜBEL, 1977, p. 218/9).
The CaCO3 system
In this system the only substance is CaCO3 (Calcium carbonate), and it shows two different solid phases, Calcite and Aragonite.
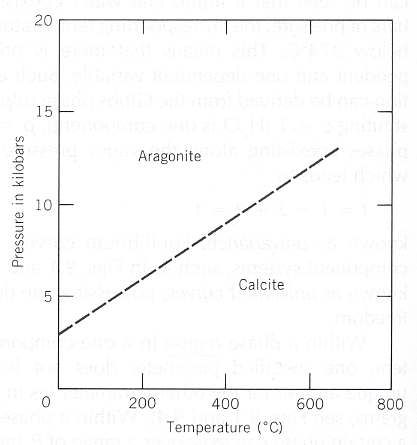
Figure 21 : Mineral stability diagram (P-T diagram) of the system CaCO3 .
When curves, or lines, are solid their locations have been determined with certainty. When they are dashed, their location is less well known.
A kilobar = 1000 bars. 1 bar = 0.987 atmosphere.
(From KLEIN & HURLBUT, 1999)
Calcite crystallographically belongs in the Hexagonal Crystal System and in the Class 3*2/m. Its Space Group is R3*c.
With this we have come to an e n d of our exposition of the stability of phases in one-component physical and mineralogical systems.
In the next document we will apply the mineral-stability-diagram-analogue of the situation as it is in the Implicate Order with respect to dipterous groundplans to the evolution of families, superfamilies and groups of families of the insect Order Diptera as this evolution physically takes place in the Explicate Order.
e-mail :
 ( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
To continue click HERE for the further study of Organic Evolution, Part XXV.
Back to Evolutionary Part XVII
Back to Evolutionary Part XVIII
Back to Evolutionary Part XXII
Back to Evolutionary Part XXIII