

[As done earlier, in these enquiries into the wing-venation and its transformations in Diptera-Nematocera we will consider the subcostal vein (Sc) at most only occasionally. This vein, especially its terminal branches (Sc1, Sc2), is -- in Diptera -- often difficult to discern.]
Introduction
We have seen that phylogenetic systematics collects species together as a monophyletic group, basing itself on a decided-upon synapomorphy (= common possesion of derived character states) or synapomorphies in these species. Several monophyletic groups can in turn form -- also based on synapomorphy -- a monophyletic group of higher rank. In this way phylogenetic research results in (proposed) cladistic schemes or phylogenetic trees. And we ourselves have found out that the resulting cladistics does not reside in the Explicate Order, but in the Implicate Order. There it is the branched noëtic trajectory that visits successive stablility fields of organic groundplans, resulting in fact in the formal derivation of one groundplan from another. The first, but not yet sufficient, condition for such a groundplan to be projected into the Explicate Order is that it has indeed been visited by the noëtic trajectory. The second condition for it to be projected is that it carries with it the appropriate existential conditions ( 'existential ' with respect to the Explicate Order), that is, conditions for its integration in an ecological niche that does actually exist in the Explicate Order. In this sense projection depends on the Explicate Order. While in the Implicate Order we have to do with formal derivations (of one noëtic pattern from another), in the Explicate Order it is a matter of physical existence, determined by ecological factors.
In the present document we will concentrate on the possible or impossible formal derivations of venational patterns in Nematocera (= lower Diptera). Phylogenetic systematics tries to establish these formal derivations as character-transformations, and on the basis of this looks for synapomorphies. In Nematocera there are of course, in addition to venational characters, many characters that are involved in such transformations. If it wishes to establish phylogenetic relationships between subgroups of a given group it should concentrate on non-adaptive characters, because adaptive characters or character-transformations are much more liable to evolve convergently in the presence of similar ecological demands than non-adaptive ones are. One type of such characters is provided by the wing-venation. Indeed, wing-venation is only adaptive in a very general sense : It must in all cases be compatible with wings that can serve as flight-organs (except in species that are becoming flightless). And more precisely, it must comply with the demands of the specific flight-regime that belongs to a given group as part of what this group essentially is. But apart from these general demands the wing-venation is non-adaptive, and that means that its transformations are formal transformations, formal derivations. And these derivations are supposed to take place first of all in the Implicate Order. Upon projection they can be observed in the Explicate Order.
However, if we trace these venational derivations within a given group, and with it trace possible phylogenetic lines within that group, we will see that there is no one single line that connects all the members of the group, even when that group contains a rich scale of primitive and derived subgroups. Generally one expects that the preservation of primitive or ancient subgroups (subgroups that have little changed since their origin) bears witness to the history of the whole group, so that one can derive one subgroup from another, especially with respect to their non-adaptive characters. Certainly such ancient subgroups (and indeed also fossil representatives of the group) can be of much help to establish the nature and direction of relevant character-transformations (and so establish apomorphies and synapomorphies). But we will see that many character-transformations -- not in the least those of the wing-venation -- are very convoluted and apt to take place convergently (that is, one and the same character-transformation has taken place several times independently even within a single group of organisms). We will show this in the wing-venation of the dipteran family Limoniidae ( Tipulomorpha).
Venational derivation in the Limoniidae ( Diptera-Nematocera, Tipulomorpha)
We will investigate the wing-venation of the following limoniid genera each provided with a number (for later reference) :
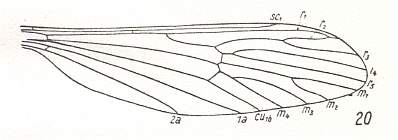
Figure 1 : Wing of Tricyphona protea ALEX., Limoniidae. Although the anterior branch of the Radial Sector ends up in R1, it is not crossvein-like and we will count it as a normal branch of the Radial Sector. Of the limoniid wings without discoidal cell this wing is the most primitive.
(After ALEXANDER, 1927, from HENNIG, 1954)
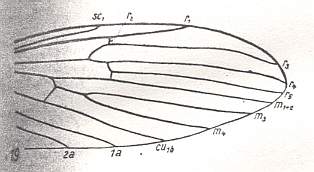
Figure 2 : Wing of Molophilus flavoscutellatus LACKSCH., Limoniidae.
(After HENNIG, 1954)

Figure 3 : Wing of Orimarga attenuata WALK., Limoniidae.
(From LINDNER, Die Fliegen der palaearktischen Region)
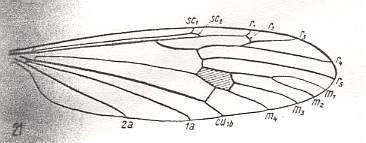
Figure 4 : Wing of Limnophila ferruginea MEIG., Limoniidae. The shaded region (that is, the region drawn shadedly) is the discoidal cell. Of the limoniid wings with a discoidal cell this wing is the most primitive.
(After HENNIG, 1954)
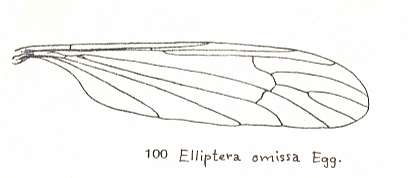
Figure 5 : Wing of Elliptera omissa EGG., Limoniidae.
(From LINDNER, Die Fliegen der palaearktischen Region)
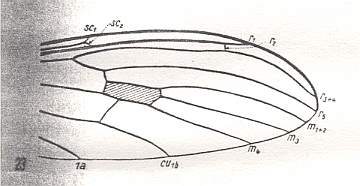
Figure 6 : Distal part of the wing of Dicranoptycha livescens Lw., Limoniidae.
(After HENNIG, 1954)
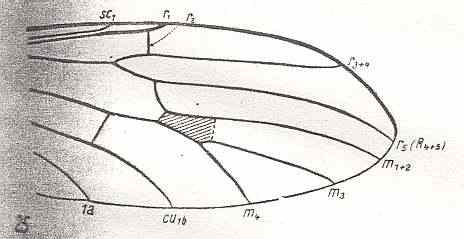
Figure 7 : Distal part of the wing of Antocha alpigena MIK., Limoniidae. the cross-vein tp drawn here as an interrupted line is absent in this species, but present in other species of this genus. R2 is very weak.
(After HENNIG, 1954)
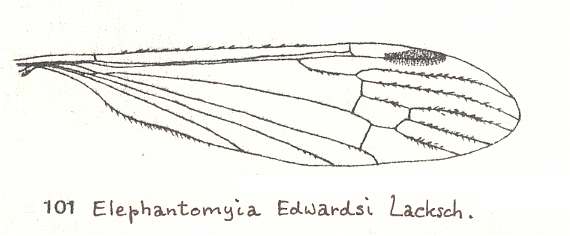
Figure 8 : Wing of Elephantomyia edwardsi LACKSCH., Limoniidae.
(From LINDNER, Die Fliegen der palaearktischen Region)
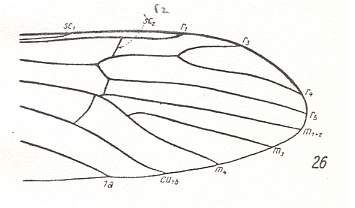
Figure 9 : Distal part of the wing of Empeda nubila SCHUMM., Limoniidae. The veinlet pointed to is R2 (not Sc2).
(After HENNIG, 1954)
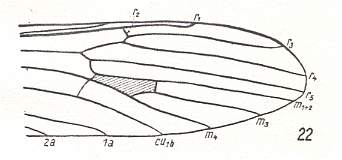
Figure 10 : Distal part of the wing of Erioptera trivialis MEIG., Limoniidae.
(After HENNIG, 1954)
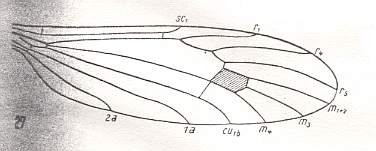
Figure 11 : Wing of Atarba picticornis O.S., Limoniidae.
(After ALEXANDER, 1942, from HENNIG, 1954)
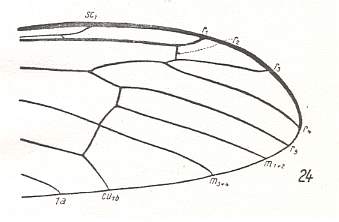
Figure 12 : Distal part of the wing of Hexatoma bicolor MEIG., Limoniidae.
(After HENNIG, 1954)
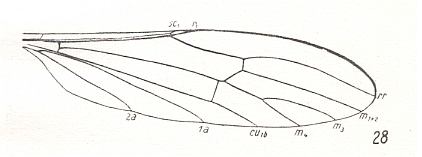
Figure 13 : Wing of Toxorhina muliebris O.S., Limoniidae.
(After HENNIG, 1954)
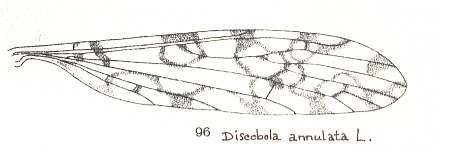
Figure 14 : Wing of Discobola annulata MEIG., Limoniidae.
(From LINDNER, Die Fliegen der palaearktischen Region)
For a wing with almost identical venation, but belonging to a representative of a different genus (of the same family), see next Figure :

Figure 14a : Wing of Rhipidia maculata MEIG., Limoniidae.
(From LINDNER, Die Fliegen der palaearktischen Region)
Analyzing the transformations of wing-venation in the family Limoniidae we concentrate on three features :
We now characterize the fourteen genera by the condition of these three features (discoidal cell, Radial Sector, Media). We first give the number (arbitrarily) assigned to the genus, then the name of the genus, and finally the condition of the three features ( The reader can click on the genus name to check these conditions) :
1. Tricyphona . No discoidal cell, 4Rs, 2+2 M.
2. Molophilus . No discoidal cell, 3.5 Rs, 1+2 M.
3. Orimarga . No discoidal cell, 2.5 Rs, 1+2 M.
5. Elliptera . No discoidal cell, 1Rs, 2+1 M.
12. Hexatoma . No discoidal cell, 3.5 Rs, 1+1 M.
13. Toxorhina . No discoidal cell, 1Rs, 1+2 M.
7. Antocha . No discoidal cell, 2.5 Rs, 1+1+1 M.
9. Empeda . No discoidal cell, 3.5 Rs, 1+2 M.
8. Elephantomyia . Discoidal cell present, 2Rs, 1+1+1 M.
14. Discobola . Discoidal cell present, 2.5 Rs, 1+1+1 M.
4. Limnophila . Discoidal cell present, 3.5 Rs, 2+1+1 M.
6. Dicranoptycha . Discoidal cell present, 2.5 Rs, 1+1+1 M.
11. Atarba . Discoidal cell present, 2Rs, 1+1+1 M.
10. Erioptera . Discoidal cell present, 3.5 Rs, 1+1+1 M.
--------------------------------------------------------------------------------------------
We now determine which limoniid genus, that is here : which limoniid venation, allows formally to be derived from which other, and to which (which can be more than one) it allows formally to lead.
Whether some given venational configuration A can be formally derived from a configuration B (= B can lead to A), or can formally lead to a configuration C (= C can be derived from A) depends on an important presupposition. If we translate the in fact noëtic concepts "formally derive from" and "formally lead to" into the respective biological concepts "evolutionarily descend from" and "evolutionarily develop into", then the mentioned presupposition is in fact DOLLO's Law of Irreversibility in evolution. The law (based on observations in paleontology) in fact says that no structural change (in especially morphology) having taken place in evolution can be reversed to its original condition. In interpreting wing-venation in insects one first of all assumes (based on comparison of recent and fossil forms) that the original venation was rather rich, which here means that the main five vein-systems (apart from the Costa : Subcostal-, Radial-, Medial-, Cubital-, and Anal-system) were each originally rich in branches. Subsequent evolution of the venation then consisted in reduction of veins or shift of them, resulting in the various specialized wing-venations. This tendency of reduction and shift can be observed in all subgroups of insects all the way down to, say, dipteran families. So in the course of evolution the Radial Sector (which itself is a branch of the Radius) can lose one or more of its branches, or one or two of them take a different course in the wing, or change into a mere fold or groove of the wing-membrane. Also the Media can lose several of its branches. Often reduction of a vein takes place by two initially parallel veins forming first a fork, the stalk of which is then subsequently shortened until the two veins are completely coalesced with each other, forming just a single vein. It is supposed that all these processes (reduction more so than mere shift), once having taken place in evolution, cannot be reversed again (in the same group of organisms).
The transformation of insect wings and their venation is partly functional : The Diptera arose from ancient mecopteroids (scorpion-flies and their allies) which fly by 'rowing' : their long venation-rich wings produce a weak lifting power -- their wingbeat-frequency is relatively low -- and a rather strong traction-force. The first Diptera that led to the tipuloids (such as Limoniidae) retained the long and venation-rich wings. But their wings specialized by becoming petiolate. As a result the lifting-force and traction-force somewhat increased (because the wings can easily rotate around their longitudinal axis during the up-down beats). But flight remained rather weak with little maneuverability (as we see it in daddy-longlegs). Later in evolution, beyond the tipuloids, the wings became shorter with less veins and a mechanically worked-out extreme wing-base and loss of the petiole (wing stalk). As a result the wingbeat-frequency could be increased and more lifting power and maneuverability obtained. The Limoniidae are well within the tipuloids with their long petiolated wings. All the venational changes within the family can safely be considered non-adaptive, that is, purely formal.
In primitive Limoniidae the Media -- to take an example -- is originally 4-branched (that is, a 4-branched Media is present in the venational groundplan of the family Limoniidae). There are also limoniids in which the Media has (evolutionarily) become 3-branched. Now we cannot assume that this 3-branched condition will ever evolutionarily revert to a 4-branched condition. Noëtically expressed : a 4-branched Media cannot be derived from a 3-branched Media, wheras the latter can be derived from the former. The same goes for the Radial Sector (and other veins). In the Limoniidae the discoidal cell is a primitive feature. It has come about by the presence of the intermedial cross-vein tp (which closes the cell distally). This discoidal cell can, in the course of evolution, disappear as a result of the vanishing of the mentioned cross-vein. And also here the reverse process cannot take place, that is the formation again of the lost cross-vein tp, and with it the re-emergence of the discoidal cell.
Such presuppositions (summarized as 'Dollo's Law') are made by most authors (including HENNIG) and I think for good reasons. In what follows we also follow Dollo's Law. And under these restrictions not all venational derivations are possible.
We will now list all formal derivations which are allowed in the venation (with respect to the discoidal cell, the Radial Sector, and the Media) of the representatives of the 14 limoniid genera. Thereby we first mention a genus by giving the number that is assigned to it, and then list all the genera (from our collection of 14 genera), by giving their respective numbers, from which it can venationally be derived. And after this we list all the genera whereto its venation can formally lead. Then we take a second genus from our collection and do the same with it, etc., until we have done all fourteen of them (the reader may click on the numbers to see the respective figures of the venation of the genus) :
1 FROM : none.
1 TO : 2 , 3 , 5 , 12 , 13 , 9 .
2 FROM : 1 , 9 4 , 10 .
2 TO : 3 , 12 , 13 , 9 .
3 FROM : 1 , 2 , 7 , 9 , 14 , 4 , 6 , 10 .
3 TO : 13 .
4 FROM : none.
4 to : 8 , 14 , 6 , 11 , 10 , 2 , 3 , 5 , 12 , 13 , 7 , 9 .
5 FROM : 1 , 7 , 8 , 14 , 4 , 6 , 11 , 10 .
5 TO : none.
6 FROM : 14 , 4 , 10 .
6 TO : 14 , 8 , 11 , 3 , 5 , 13 , 7 .
7 FROM : 14 , 4 , 6 , 10 .
7 TO : 3 , 5 , 13 .
8 FROM : 14 , 4 , 6 , 11 , 10 .
8 TO : 11 , 5 , 13 .
9 FROM : 1 , 2 , 4 , 10 .
9 TO : 2 , 3 , 12 , 13 .
10 FROM : 4 .
10 TO : 11 , 6 , 14 , 8 , 9 , 7 , 13 , 12 , 5 , 3 , 2 .
11 FROM : 8 , 14 , 4 , 6 , 10 .
11 TO : 8 , 13 , 5 .
12 FROM : 1 , 2 , 9 , 4 , 10 .
12 TO : none.
13 FROM : 1 , 2 , 3 , 7 , 9 , 8 , 14 , 4 , 6 , 11 , 10 .
13 TO : none.
14 FROM : 4 , 6 .
14 TO : 8 , 6 , 11 , 3 , 5 , 13 , 7 .
From the above list of allowed formal derivations (allowed at least with respect to the discoidal cell, the number of branches of the Radial Sector, and the structure of the Media) we can deduce some important things :
1 is, within the confines of the Limoniidae, a venational starting point. Apparently it is a starting point of a derivational series of limoniid venational patterns without a discoidal cell.
4 also is, within the confines of the Limoniidae, a venational starting point. But, apparently, it is a starting point where at least initially a discoidal cell is present.
5 is, at least within our 14 genera, a venational end point. So also is 12 and 13 .
4 and 1 together lead eventually to all the other venational patterns of our group of fourteen.
1 leads, among others, to end points 5 and 13 .
4 leads, among others, to end points 5 , 12 , and 13 .
3 leads only to 13 which is an end point.
The next diagram summarizes which ones of our 14 venational patterns can be derived from the starting point 1 , and which ones from the starting point 4 :
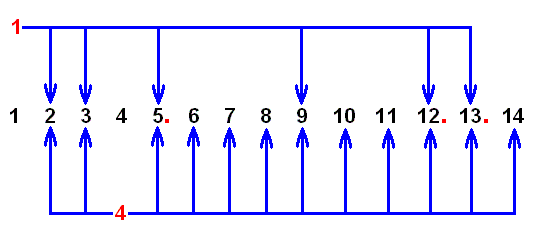
Figure 15 : 2 , 3 , 5 , 9 , 12 , and 13 can be derived from 1 , while all members of our collection of fourteen, except 1 (and 4 ), can be derived from 4 . See the above list of allowed formal derivations .
A red point after a number indicates that this number represents an end point.
Looking to the above diagram we could think that from the starting point 1 there arise six parallel independent derivations, and that from the starting point 4 there arise twelve parallel independent derivations. But this is of course not so, because some derivations can be intermediate. For example, 1 can lead to 13 , but it can do so via 9 , so 1 ==> 9 and 1 ==> 13 are not parallel derivations. Nevertheless we expect a number of parallel independent derivational lines to exist. These lines must be separated by pairs of limoniid venational patterns -- represented by our numbers -- that cannot be derived from each other along neither direction, that is, if we have such a pair, consisting of the patterns A and B, then A cannot be derived from B, and B cannot be derived from A. Such a pair, the members of which thus show specialization-crossing, can be indicated by ( A | B ) (= "A-vertical bar-B"). It is not necessary to determine all such pairs. For our theoretical discussion it is sufficient to show that there exist at least many of them. By inspecting the above list of allowed formal derivations we can determine at least a minimum number of such pairs, and we can do this as follows :
|
2 ==> 3 2 ==> 12 2 ==> 13 2 ==> 9 |
3 ==> 13 |
6 ==> 14 6 ==> 8 6 ==> 11 6 ==> 3 6 ==> 5 6 ==> 13 6 ==> 7 |
7 ==> 3 7 ==> 5 7 ==> 13 |
|
8 ==> 11 8 ==> 5 8 ==> 13 |
9 ==> 2 9 ==> 3 9 ==> 12 9 ==> 13 |
10 ==> 11 10 ==> 6 10 ==> 14 10 ==> 8 10 ==> 9 10 ==> 7 10 ==> 13 10 ==> 12 10 ==> 5 10 ==> 3 10 ==> 2 |
11 ==> 8 11 ==> 13 11 ==> 5
14 ==> 8 |
From all this we can isolate the following pairs of which the members cannot be derived from each other, that is, members with specialization-crossing :
| ( 1 | 4 ) | ( 7 | 8 ) | ( 2 | 8 ) | ( 3 | all but 13 ) |
| ( 6 | 2 ) | ( 6 | 9 ) | ( 6 | 12 ) | ( 7 | 2 ) |
| ( 7 | 9 ) | ( 7 | 11 ) | ( 8 | 3 ) | ( 8 | 9 ) |
| ( 8 | 12 ) | ( 9 | 5 ) | ( 9 | 11 ) | ( 9 | 14 ) |
| ( 11 | 2 ) | ( 11 | 3 ) | ( 11 | 12 ) | ( 14 | 2 ) |
| ( 14 | 12 ) | ( 2 | 5 ) |
What do these derivational 'interruptions' mean?
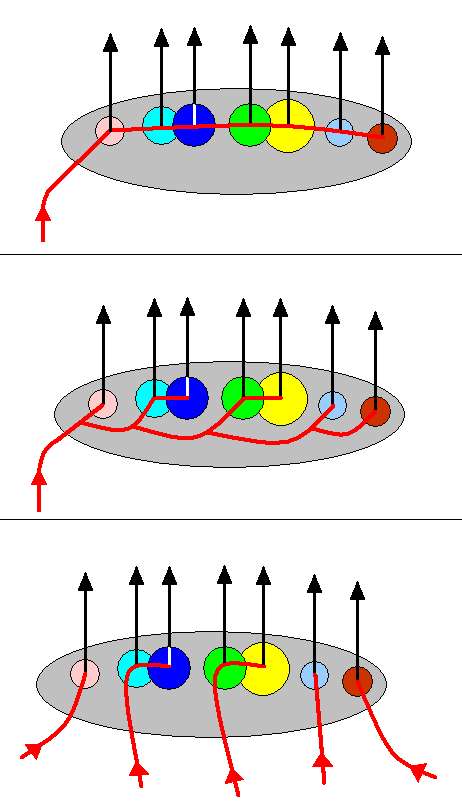
Figure 16 : Diagram depicting several possibilities of the course of the noëtic trajectory (trajectories) (red) in the Implicate Order through the stability field of a family-groundplan (brown ellipse) containing its genus-groundplans (circular subregions). The black vertical arrows represent the projections of the genus-groundplans (carrying their existential conditions) from the Implicate Order into the Explicate Order.
Top image : The noëtic trajectory enters the stability field of the family-groundplan and then succesively visits its genus-groundplans. Here it is assumed that the genus-groundplans can formally be derived directly from one another, that is, it is assumed that between every two genus-groundplans there is no specialization-crossing.
Middle image : The noëtic trajectory enters the stability field of the family-groundplan and then successively visits those of its genus-groundplans, but not directly so : Specialization-crossing between every two successive genus-groundplans forces us to assume that the noëtic trajectory bifurcates before entering a genus-groundplan. One branch of it enters a genus-groundplan while the other proceeds to the next genus-groundplan, or to the next pair of genus-groundplans.
Bottom image : The noëtic trajectory is here in fact five independent trajectories, each one of them, after having entered the family-groundplan, proceeds to only a single genus-groundplan, or to two genus-groundplans.
As has been said, the above diagrams are general. The number of genera assumed there is arbitrary. So these diagrams do not specifically depict possible situations of the family Limoniidae, but show general possibilities that could, in their generality also apply to that family. This also goes for the next diagram.
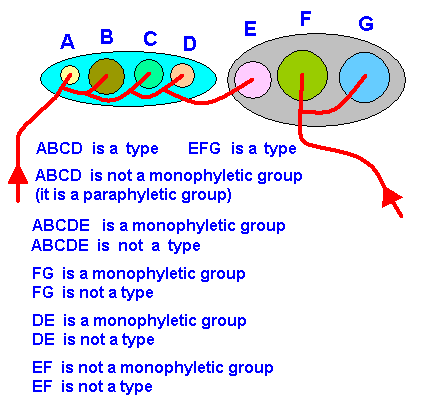
Figure 17 : Diagram depicting the fact that evolution is a matter of genealogic cladistics (monophyletic groups) as well as a succession of types (groundplans). There are two successions of generic types : A ==> B ==> C ==> D ==> E, and F ==> G, if the temporal succession of projections is indeed respectively A, B, C, D, E, and F, G. And with A, B, C, D, E we have a succession of two family-groundplans : Upon projection, the first family-groundplan appears in the Explicate Order with species of four genera. Then the second family-groundplan appears with species of one of the family's genera.
Red curves : Noëtic trajectories. Ellipses : noëtic stability fields of family-groundplans. Circles : noëtic stability fields of genus-groundplans.
A concrete example of the involvement in evolution of both "types" and "clades" is the following :
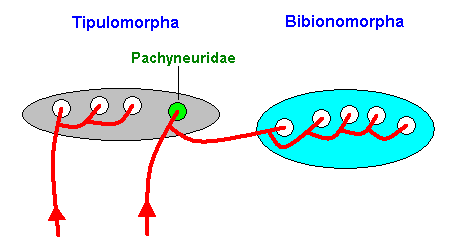
Figure 18 : Diagram depicting the allocation of the family Pachyneuridae to type and clade : Phylogenetically the family Pachyneuridae belongs to the Bibionomorpha (and in it to the Fungivoriformia). Typologically, on the other hand, it belongs to the Tipulomorpha. The (stability fields of the) high-level groundplans Tipulomorpha and Bibionomorpha are depicted by ellipses. The family-groundplans (their number here is arbitrarily set) are depicted by circles. The red curves are noëtic trajectories. One of these trajectories visits two high-level groundplans (Tipulomorpha and Bibionomorpha). The phylogenetic inclusion of the Pachyneuridae cuts through two different types.
We now return to the family Limoniidae and investigate whether in the wing-venation there are even more restrictions of derivation, by studying not only the number of branches of the Radial Sector but also the very structure of it. Indeed it is possible that a limoniid wing having a 3.5 Rs, that is, a Radial sector with three free branches plus one branch that is very short, crossvein-like, and ending up in R1, and having a 2-branched Media, (see Figure 12 ) can nevertheless not be derived from a limoniid wing also having a 3.5 Rs, and having a 3-branched Media (see Figure 9 ) because the structure of the 3.5 Rs in the former form is, albeit slightly, more primitive, if we indeed assume that the crossvein-like branch of the Radial Sector -- in its process of finally disappearing -- is moving into the direction of the wing-base.
Let us now try to find, in addition to the case just mentioned, more instances of the structure of the Radial Sector in pairs of limoniid genera that forbids derivation.
We assume that in limoniid wings there is a tendency of the anterior fork of the Radial Sector to shift into the apical direction, resulting in its origination from the upper branch of the posterior fork of the Radial Sector :
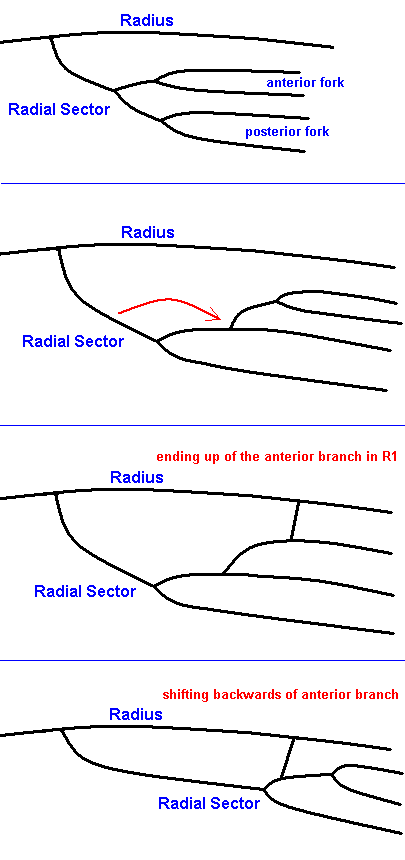
Figure 19 : Possible stages (reading from top to bottom) of development of the Radial Sector in the wings of the family Limoniidae.
In line with these assumptions about the direction and nature of the transformation of the Radial Sector in Limoniidae we find that :
2 cannot be derived from 4 because in the former the origin of the anterior fork of the Radial Sector is still from the common stalk of the Radial Sector, which is a primitive configuration as compared to the situation in 4 . But the reverse derivation is still possible, so this does not yield another derivational interruption (i.e. a pair of which its members cannot be derived from each other in either direction) in addition to the ones we had already found.
2 cannot be derived from 9 because of the same reason as in the previous case (see also the diagram above ). But also here the reverse derivation is possible. So no new pair representing a derivational interruption is found.
Above we already established that 12 cannot be derived from 9 . And also here the reverse derivation is possible. So here too no new pair representing a derivational interruption is found.
2 cannot be derived from 10 again because of the same reason. And also here the reverse derivation is possible. So here too no new pair representing a derivational interruption is found.
ABOVE we found 21 pairs the members of which cannot be derived from each other in either direction. In addition, we also found that all genera cannot be derived from 3 and vice versa, except 13 . This yields another 12 such pairs. So in total we now have 33 pairs representing derivational interruption, meaning that there must be 34 independent lines of evolutionary development within the single family Limoniidae. All this under the assumption of the validity of Dollo's Law of irreversibility in evolution. And even when this estimate (34) turns out much too high, we still can be sure that this family evolved along a number of independent genealogical lines. And this is contrary to the expectations of phylogenetic systematics.
In addition to the above example (limoniid venation) demonstrating problems in phylogenetic systematics, there surely are many more such cases. One such case is the interpretation of apparently spurious veins as we see them in (among others) the nematocerous family Heleidae (= Ceratopogonidae, biting-midges), a family closely related to the Chironomidae (dancing-midges). In contrast to the Limoniidae, the wing-venation in Heleidae is remarkably constant. There is some transformation, it is true, but nearly all members of the family have (evolutionarily) reached the penultimate or ultimate stages of it. But, between the Radial Sector and the Media we see in almost all members of the family a more or less sclerotized and isolated fork. How should we interpret this fork? Is it R4 and R5 of the Radial Sector, or is it a new venational structure? In all the wings depicted below, the Radial Sector has shifted toward the Radius. They touch each other or are even coalesced for a short distance. The branches M1 and M2 of M1+2 form a deep fork. Its bifurcation point lies very close to the cross-vein ta. The cubital fork (branches : M4 and Cu1b) is conspicuously present. Let us depict a number of these wings :
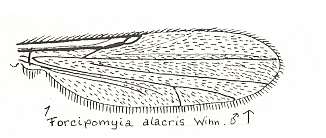
Figure 20 : Wing of Forcipomyia alacris WINN. Male. Family Heleidae.
The mentioned isolated fork between the Radial Sector/Costa and M1 is very weakly present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
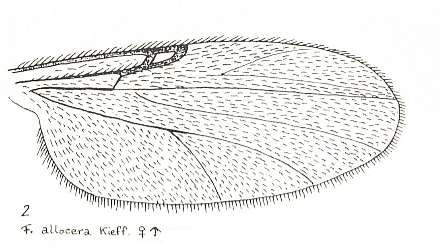
Figure 21 : Wing of Forcipomyia allocera KIEFF. Female. Family Heleidae.
Isolated fork present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
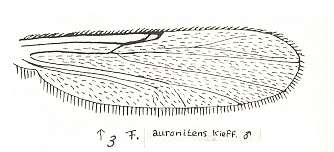
Figure 23 : Wing of Forcipomyia auronitens KIEFF. Male. Family Heleidae.
Isolated fork present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
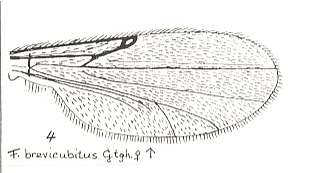
Figure 24 : Wing of Forcipomyia brevicubitus GTGH. Female. Family Heleidae.
Isolated fork very weakly present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
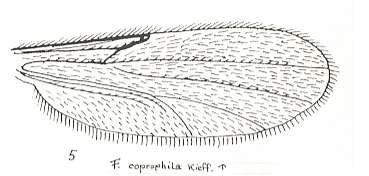
Figure 25 : Wing of Forcipomyia coprophila KIEFF. Family Heleidae.
Isolated fork absent.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
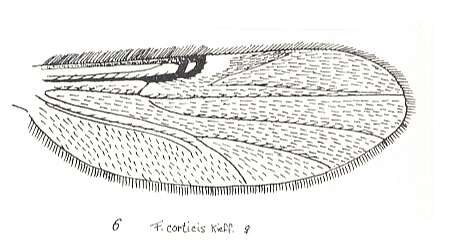
Figure 26 : Wing of Forcipomyia corticis KIEFF. Female. Family Heleidae.
Isolated fork present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
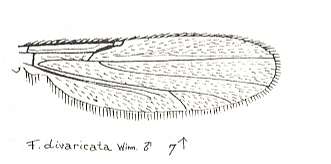
Figure 27 : Wing of Forcipomyia divaricata WINN. Male. Family Heleidae.
Isolated fork very weakly present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
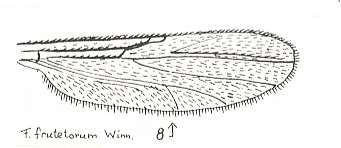
Figure 28 : Wing of Forcipomyia frutetorum WINN. Family Heleidae.
Isolated fork present. Its posterior branch strong.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
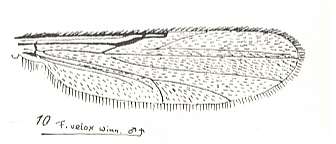
Figure 29 : Wing of Forcipomyia velox WINN. Male. Family Heleidae.
Isolated fork present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
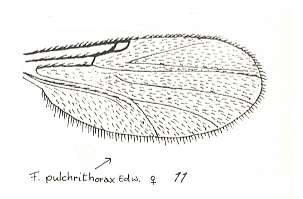
Figure 30 : Wing of Forcipomyia pulchrithorax EDW. Female. Family Heleidae.
Isolated fork present.
(After GOETGHEBUER, from LINDNER, Die Fliegen der palaearktischen Region)
How must we interpret the isolated fork between Radial Sector/Costa and M1? To get more insight into this matter, let us quote HENNIG, 1954, p.283-284 :
Many authors ( f.i. EDWARDS [. . .] ) were troubled when trying to interpret a fork that is present in many H e l e i d a e between the Radial Sector and M1. Here we have not to do with merely folds in the wing membrane, but, evident from coloration and growth of hair, with a genuine vein-like stiffening of the wing membrane. Identification as R4+R5 or MA2 (VIGNON and SÉGUY) would create great difficulties, because then it would remain not-understood why these veins are preserved precisely in the H e l e i d a e, while they were lost in all related forms (also in those that are otherwise primitive). Against such an interpretation also speaks the fact that this fork is present precisely in forms with otherwise relatively apomorphous venation. According to me all difficulties are resolved by the following consideration : Repeatedly it is found that the structure of the wing membrane (folds) has original ties with the course of veins, but that the veins can relatively easily leave these structures behind, while the structure of the wing membrane is preserved more or less tenaciously. Apparently, when needed, the old structures [folds] can be reactivated, without the need thereby to assume that veins that have disappeared or shifted already long ago, reappear or have been miraculously preserved while they have disappeared in all related forms. As has been said, in the H e l e i d a e the development of the venation unequivocally consists of the Radial Sector approaching the Radius. The Media, however, does not follow (this trend). As a result, between the Radial Sector and the Media a relatively wide vein-free field is created, which is detrimental to the stability of the wing membrane. But this does not prevent the shifting of the Radial Sector. Rather the compensation consists in the reactivation of an old fold-structure (or whatever structure) of the wing membrane, which originally lodged the shifted Radial Sector. So one can retrace the fork in many Heleidae back to the Radial Sector, without the need to identify it with determined branches of the Radial Sector, which are present anyway! The fork only indicates the original position (as it were the old, but now in a sense re-occupied bed) of the Radial Sector. Something comparable takes place in the M e l u s i n i d a e (= Simuliidae) in the area between the Media and Cubitus.
This explanation of the extra fork in the wings of many Heleidae is certainly plausible. Only one thing bothers me a bit : The re-activation of the old bed of a part of the original Radial Sector means that now n e w longitudinal veins appear, new that is, if the mentioned part of the Radial Sector is still present elsewhere in the wing, or has disappeared for a long time now (And when finally having disappeared it cannot as such, that is, as that part of the Radial Sector, come back. So if something nevertheless 'reappears' it is not that part of the Radial Sector, but a new venational element). What then are these veins? As far as I know such a phenomenon is very rare in insect wings, but of course the possibility cannot be denied. As HENNIG suggests, the reactivation of the fold structure has a functional meaning (the restoration of the stability of that part of the wing membrane). But as we saw in the Figures above, for example in Figure 25 , the fork can be totally absent, even in the same genus where other species definitely possess it. If the reactivated fork is not functional, but formal, then we have the problem of the appearance of new (longitudinal) veins 'out of the blue'. So it is, for the time being, best to adhere to HENNIG's explanation, that is, that the reactivated fork is just some new functional structure. And these new 'veins' do not belong to the original venational scheme of the insect wing. We might say they are no veins at all.
This concludes our discussion of problems met with in phylogenetic systematics when it uses the wing-venation to find synapomorphies for establishing monophyletic groups. In many cases the identity of veins (that is, their homology) is hard, if not impossible, to determine. As a result it is difficult to establish what exactly happened with the venation in the evolution of some given group. And this in turn implies that it is often difficult to establish apomorphies in characters (derived character states). Further we saw that there must often be cases of parallel evolutionary development even within single families. And if these parallel lines never converge to some common point then phylogenetic systematics is highly troubled or even irrelevant. Anyway, we have seen that cladistics and typology can go together, as is illustrated in Figure 17 and Figure 18 .
In the next document we will pick up our exposition of the phylogeny of the Bibionomorpha. The results obtained there will now be interpreted noëtically.
e-mail :
 ( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
To continue click HERE for the further study of Organic Evolution, Part XXX.
Back to Evolutionary Part XVII
Back to Evolutionary Part XVIII
Back to Evolutionary Part XXII
Back to Evolutionary Part XXIII
Back to Evolutionary Part XXIV
Back to Evolutionary Part XXV-A
Back to Evolutionary Part XXV-B
Back to Evolutionary Part XXV-C
Back to Evolutionary Part XXVI
Back to Evolutionary Part XXVII
Back to Evolutionary Part XXVIII
Back to Evolutionary Part XXVIII-A