In order to deal adequately with the content of the present and following (two) documents, the reader should consult first of all the previous documents concerning the Preparation to the Promorphology of Crystals. And when he or she is not familiar with Crystallography, I recomment to consult the Special Series of the First Part of this website, accessible via back to homepage, especially the introductory document, and all the ones that deal explicitly with all the Crystal Classes (The reader should not necessarily read the documents on the derivation of those Classes).
Introduction
For O r g a n i s m s we have erected a Form System that is fully inspired by the shapes (i.e. outer forms) and structure (i.e. inner form) of existing organisms. Their structure is t e c t o l o g i c a l, i.e. consisting of definite macroscopical parts that are repeated non-periodically. Every b a s i c f o r m of an organismic individual and also of their subordinate individuals (cells, organs, antimers, etc.) is represented by a geometrical solid displaying the symmetry of that organismic individual.
C r y s t a l s on the other hand, have a p e r i o d i c structure : A certain microscopic unit is repeated periodically in three different spatial directions, which means that microscopic translations are involved in the crystal structure. So crystals do not have macroscopical parts that are repeated non-periodically, which means that they, in particular, do not possess a n t i m e r s, so important and determining with respect to the assessment of the stereometric basic form (promorph).
But when we conceptually eliminate all translations inherent in crystals, i.e. eliminate all translational symmetry -- which in turn means that we eliminate (1) simple translations, (2) the translational component of every glide plane, and (3) the translational component of every screw axis -- then we are left with just one c h e m i c a l m o t i f, formed by the superposition of motifs in the lattice. I.e. when we 'telescope' the crystal back, we end up with the p o i n t s y m m e t r y only, represented by the (one) mentioned chemical motif. Consequently, this motif is the result of the superposition of all the point environments of the lattice. Such an environment consists of the whole set of chemical elements (in the sense of parts or particles) associated with a lattice point. Because of the superposition of the lattice points (by means of eliminating all simple translations), we are left with one such an environment. But in addition to simple translations there can be the translational elements of glide planes and screw axes. Also these translations should be eliminated. This can result in the mentioned environment to be telescoped further back, resulting in a smaller motif. This finally resulting motif corresponds either with one formula unit of the substance involved, or with a multiple thereof. In Ice this finally resulting motif consists (as far as my knowledge goes) of one hexagonal ring of six water molecules. Well, this final motif indeed has a t e c t o l o g i c a l structure, and because of this the crystal can be promorphologically assessed after all. How do we do this?
Every Crystal Class (representing the point symmetry of the crystals, i.e. the translation-free residue of the total symmetry -- (in turn) represented by the Space Group) comprises many differently formed crystals. We want to assess the b a s i c c o m m o n f o r m of a given crystal of such a Class. And of course this common form is (already) given by the symmetry content of the given Class, and as such characterizing that Class. To represent this symmetry content ( = the symmetry of the chemical motif that results after telescoping the crystal back, a symmetry, as such representing the mentioned translation-free residue ) promorphologically, we take the simplest geometric solid (body) that fully and exclusively represents purely geometrically the symmetries of the given Crystal Class. Sometimes, however, such a simplest geometric body does not occur (i.e. is not materialized) in a certain Crystal Class, because in crystals the point symmetry is not only represented by the geometrical shape of a crystal but also by some other (non-geometrical) features like luster, etch figures, striations. This can result in a crystal that geometrically shows a higher symmetry than it actually has. In Promorphology, however, we want to express the symmetry content fully by means of the geometry, implying that we will construct figures that so express that symmetry content, figures (shapes) we will not encounter in real crystals.
We will further set, once and for all, that we will mean by "simplest geometric body" a body with the smallest number of faces, but still representing the full symmetry content geometrically. Sometimes, however, we must take a body with more faces than the possible minimum. This we have to do, because we (should) include in the meaning of the term "simplest geometric body" in addition to its having as small a number of faces as possible, the fact that it is not further divisible anymore without losing its specific symmetry, in other words we want a body that is not idem specie divisible anymore. We will explain this (further) in due course. But before we do so we will repeat an exposition (as given in the second document of the Special Series in the First Part of our website) about the Hermann-Mauguin notation expressing the point symmetry of crystals. Further we will give (once more) an overview of all the Crystal Classes and Crystal Systems. After all this is recapitulated, the content of the present (and next two) document(s) on the Promorphology of Crystals will be easier to manage.
Besides by special n a m e s, we can also refer to the Crystal Classes by means of short symbols. One system of symbols widely used is that of C. HERMANN and Ch. MAUGUIN. These symbols enumerate all the non-equivalent symmetry elements of the particular Crystal Class. Each Class embodies a combination of basic symmetry elements (including a 'combination' of only one such symmetry element). As the set of symmetry elements to be used for the symbols one has chosen :
The Hermann-Mauguin symbol of a Crystal Class consists of one, two or three parts, that relate to the following directions [For the Crystal Systems and the crystallographic axes (i.e. a-axis, b-axis, etc.) mentioned in the table, see the OVERVIEW OF CRYSTAL SYSTEMS AND CLASSES bvelow.] :
| Crystal System |
First Part | Second Part | Third Part |
| Monoclinic |
Ortho-axis | - | - |
| Orthorhombic |
a-axis | b-axis | c-axis |
| Tetragonal |
c-axis | a- and b-axis | bisectors between a- and b-axes |
| Hexagonal |
c-axis | a-, b- and d-axis | bisectors betw. a-, b- and d-axes |
| Isometric |
a-, b- and c-axis | body-diagonals | plane-diagonals |
Regarding the Isometric System : Body-diagonals are lines perpendicular to the octahedral faces, while plane-diagonals are lines that are parallel to one of the cube faces.
Regarding the Monoclinic System : The Ortho-axis is the crystallographic axis of the Monoclinic System that is perpendicular to the two other monoclinic crystallographic axes.
Regarding the Triclinic System : It consists of only two Classes, having respectively 1 and 1* as their Hermann-Mauguin symbols.
Let us treat another example.
The symbol 4/m 2/m 2/m refers to a tetragonal crystal (i.e. a crystal belonging to the Tetragonal Crystal System) [ 4 also occurs in the isometric Classes, but (the symbols for) such crystals are directly recognized by the 3 at the second part of the symbol]. This Class has a 4-fold rotation axis along the c-axis and a mirror plane perpendicular to it, so 4/m comes as the first part of the symbol. It has moreover 2-fold rotation axes along the a- and b-axes, each of them having a mirror plane perpendicular to it, so 2/m will figure as the second part of the symbol (there are two such rotation axes (coupled with a mirror plane), but, because they are equivalent they are represented in the symbol by only one "2/m"). Further the Class has two more 2-fold rotation axes along the bisectors of the a- and b-axes, and a mirror plane perpendicular to each one. So they are also represented by 2/m, which however will figure as the third part of the Hermann-Maugin symbol of the Class.
Sometimes the Hermann-Maugin symbols are used in an abbreviated form, namely in those cases where some symmetry elements are implied by others. The implied ones are then omitted if there is no possibility of confusion. On this website we will, however, always use the complete symbols.
Overview of the 32 Symmetry Classes of Crystals
In this Overview we use the following abbreviations and terminology :
cs = center of symmetry.
p. = polar axis.
+ = present.
- = absent.
u [v] = u v-fold rotation axes present.
4* means a 4-fold roto-inversion axis.
An expression like "Hemimorphic of Holohedric" means that the hemimorphic Form is directly derived from the holohedric Form. The same applies to expressions like "hemimorphic of pyramidal hemihedric" which means that the hemimorphic Form is derived from a (in this case pyramidal) hemihedric Form (and consequently not from a holohedric Form).
one + one + one means three items present (for example three mirror planes) but belongong to three different types.
The Hermann-Maugin symbols are written down below each Class name.
(for example, three [4] = three 4-fold rotation axes present).
(for example, one [4*] = one 4-fold roto-inversion axis present).
The next six tables are going to list all the 32 Crystal Classes, one table for each Crystal System.
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Hexakisoctahedric 4/m 3* 2/m |
3 + 6 | three [4] four [3] six [2] |
+ |
| Tetrahedric Hemihedric |
Hexakistetrahedric 4* 3 m |
6 | three [2] four [3] p. |
- |
| Pentagonal Hemihedric |
Duakisdodecahedric 2/m 3* |
3 | three [2] four [3] |
+ |
| Plagihedric Hemihedric |
Pentagonikositetrahedric 4 3 2 |
- | three [4] four [3] six [2] |
- |
| Tetartohedric | Tetrahedric pentagondodecahedric 2 3 |
- | three [2] four [3] p. |
- |
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Ditetragonal-bipyramidal 4/m 2/m 2/m |
1 + (2 + 2) | one [4] two + two [2] |
+ |
| Hemimorphy of Holohedric |
Ditetragonal-pyramidal 4 m m |
2 + 2 | one [4] p. | - |
| Pyramidal Hemihedric |
Tetragonal-bipyramidal 4/m |
1 | one [4] | + |
| Hemimorphy of Pyramidal Hemihedric |
Tetragonal-pyramidal 4 |
- | one [4] p. | - |
| Trapezohedric Hemihedric |
Tetragonal-trapezohedric 4 2 2 |
- | one [4] two + two [2] |
- |
| Sphenoidic Hemihedric |
Tetragonal-scalenohedric 4* 2 m |
2 | one + two [2] | - |
| Sphenoidic Tetartohedric |
Tetragonal-bisphenoidic 4* |
- | one [4*] | - |
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Dihexagonal-bipyramidal 6/m 2/m 2/m |
1 + (3 + 3) | one [6] three + three [2] |
+ |
| Hemimorphy of Holohedric |
Dihexagonal-pyramidal 6 m m |
3 + 3 | one [6] p. | - |
| Pyramidal Hemihedric |
Hexagonal-bipyramidal 6/m |
1 | one [6] | + |
| Hemimorphy of Pyramidal Hemihedric |
Hexagonal-pyramidal 6 |
- | one [6] p. | - |
| Trapezohedric Hemihedric |
Hexagonal-trapezohedric 6 2 2 |
- | one [6] three + three [2] |
- |
| Rhombohedric Hemihedric |
Ditrigonal-scalenohedric 3* 2/m |
3 | one [3] three [2] |
+ |
| Rhombohedric Tetartohedric |
Trigonal-rhombohedric 3* |
- | one [3] | + |
| Trigonal Hemihedric |
Ditrigonal-bipyramidal 6* m 2 |
1 + 3 | one [3] three [2] p. |
- |
| Hemimorphy of Trigonal Hemihedric |
Ditrigonal-pyramidal 3 m |
3 | one [3] p. | - |
| Trigonal Tetartohedric |
Trigonal-bipyramidal 6* |
1 | one [3] | - |
| Hemimorphy of Trigonal Tetartohedric (Ogdohedric) |
Trigonal-pyramidal 3 |
- | one [3] p. | - |
| Trapezohedric Tetartohedric |
Trigonal-trapezohedric 3 2 |
- | one [3] three [2] p. |
- |
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Rhombic-bipyramidal 2/m 2/m 2/m |
1 + 1 + 1 | one + one + one [2] | + |
| Hemimorphy | Rhombic-pyramidal m m 2 |
1 + 1 | one [2] p. | - |
| Hemihedric | Rhombic-bisphenoidic 2 2 2 |
- | one + one + one [2] | - |
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Prismatic 2/m |
1 | one [2] | + |
| Hemimorphy | Sphenoidic 2 |
- | one [2] p. | - |
| Hemihedric | Domatic m |
1 | - | - |
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Pinacoidal 1* |
- | - | + |
| Hemihedric | Asymmetric 1 |
- | - | - |
Now we are ready to continue our p r o m o r p h o l o g y of crystals.

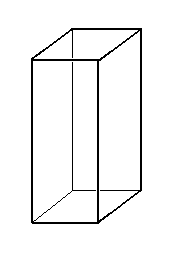
The tetragonal prism has (here as a geometric solid, not as a crystallographic Form) six faces, while the tetragonal bipyramid, also expressing 4/m 2/m 2/m, has eight faces :
But the prism can be divided by any plane perpendicular to the c-axis (along which runs the 4-fold rotation axis) and the resulting parts still possess the full 4/m 2/m 2/m symmetry. This is not possible with the tetragonal bipyramid (= one but the simplest body, i.e. comes next to the tetragonal prism). So we will choose the t e t r a g o n a l b i p y r a m i d as the b a s i c f o r m (promorph) of the Class 4/m 2/m 2/m, and as such it is a member of the I s o s t a u r a o c t o p l e u r a (which is one of the many categories of our Promorphological System).
Antimers
Organic promorphs are assessed mainly on the basis of the h o m o t y p i c n u m b e r (= number of antimers or counterparts), and further on the basis of the form relationships of those antimers and with it (of) the relationships of the axes which they imply and finally on the basis of absence or presence of a main axis and the nature of its poles. Most important are the antimers.
In crystals we would as it initially seems, have to consider the tectology of the c h e m i c a l m o t i f that remains after elimination of all translations. But because the crystal as a whole, i.e. as a macroscopical object, does not possess a tectological structure, and so does not possess true antimers, we cannot determine the promorph on the basis of prevailing antimers. The symmetry of the given Crystal Class leads us to a certain simple geometric body representing this symmetry geometrically. The number of antimers must now be determined from this geometric body, implying that sometimes several numbers of antimers are equally possible, say, six or eight, two or four, etc. In these cases we will give both numbers. So in the case of Crystals we determine the homotypic basic number of (and from) the basic form itself instead of determining it from that real object of which we consider the basic form (promorph). In principle, however, the number of antimers (the homotypic basic number) can be determined from the real object itself, namely from that chemical motif that remains after eliminating all translations. But in most cases such a determination (assessment) will not be easy to carry out successfully and without errors, so we will stick to the assessment of the number of antimers from the basic form itself.
New Promorphological Categories
In some cases we will have to introduce some new promorphological categories in order to accommodate for some crystal classes. Those new categories that -- as far as I can see -- are not materialized in any organism, and are moreover not expected to be materialized ever, will be presented in separate INFRAMES, in order to prevent the Promorphological System to become more or less messy and unwieldy, and in order to keep the system 'organic' (Promorphology is a system of organic forms). When, on the other hand, a new category is -- as to my knowledge -- not materialized in any organism, but could reasonably be expected to be so materialized at some time or place, it will be incorporated and fully integrated into the Promorphological System, but not extensively be dealt with.
When all this is done (below), we will have established a connection between the crystallographic system of crystals and the promorphological system of organic forms. Our motivation for this is to emphasize the u n i t y of the material world : The inorganic world of genuine beings, as represented first of all by (single) crystals is, at a fundamental level, not different from the organic world (We have established this, on the basis of their c o m m o n
o n t o l o g y, in all the philosophical essays (documents) of the First Part of this website, accessible via back to homepage).
Twins
Many crystals occur as t w i n s, i.e. not as single crystals, but as regular and lawful aggregations of several single crystals. Many such twinned crystals have accordingly acquired a t e c t o l o g i c a l structure consisting of genuine antimers. Such (twinned) crystals can be directly promorphologically assessed as to one or another promorphological category.
In the following we will, however, concentrate on single crystals and assess their promorphology.
Each determined p r o m o r p h (= stereometric basic form) can be accessed by clicking on its name. When one does so, one will end up IN the Promorphological System, so that one can see the proper place of the determined promorph within the system.
REMARK : In the Hermann-Mauguin symbol, expressing the symmetry, we use, for typographical reasons, an asterisk (*), for example 3*. A symmetry element denoted by 3* is a 3-fold rotoinversion axis (= rotation of 1200 immediately followed by inversion in a point on that axis). In the crystallographic literature and also in our Figures this asterisk is replaced by a horizontal score above the relevant numeral.
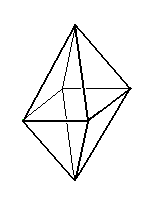
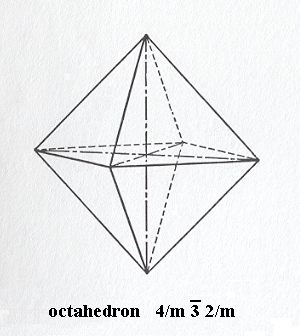
Hexakisoctahedric Class, 4/m 3* 2/m
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Regular Octahedron (Figure 3).
The promorph is accordingly that of the Octaedra regularia (Polyaxonia rhythmica).
Hexakistetrahedric Class, 4* 3 m
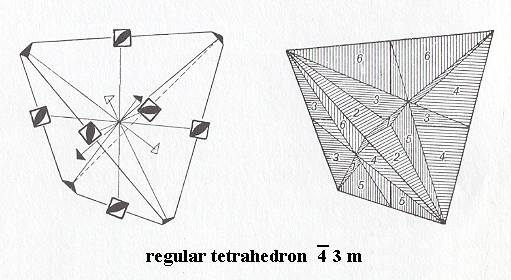
Figure 4. Regular Tetrahedron, Stereometric Basic Form of all the (single) crystals of the Hexakistetrahedric Class of the Isometric Crystal System. Symmetry content is indicated (Small squares with solid oval : 4-fold rotoinversion axis. Small triangles : 3-fold rotation axes. The right image displays the prevailing mirror planes.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
Pentagonicositetrahedric Class, 4 3 2
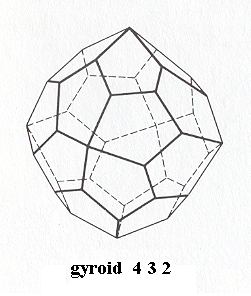
Duakisdodecahedric Class, 2/m 3*
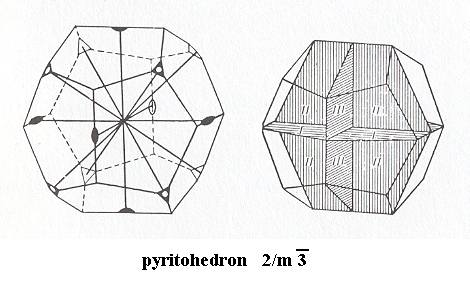
Figure 6. Pyritohedron, Stereometric Basic Form of all the (single) crystals of the Duakisdodecahedric Class of the Isometric Crystal System. Symmetry content is indicated (Small triangles with holes : 3-fold rotoinversion axes. Small black ovals : 2-fold rotation axes. In the right image the prevailing mirror planes are indicated. The next Figure again depicts the Pyritohedron, but without all the indications.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
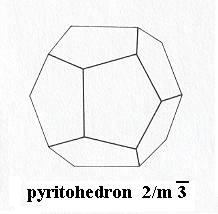
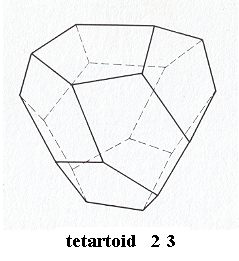
Tetrahedric pentagondodecahedric Class, 2 3
Ditetragonal-bipyramidal Class, 4/m 2/m 2/m
The geometric solid taken (according to the above established criteria) to represent the stereometric basic form (promorph) of all the crystals of this Class is the Tetragonal Bipyramid (Figure 8).
The promorph is accordingly that of the Isostaura octopleura (Stauraxonia homopola).
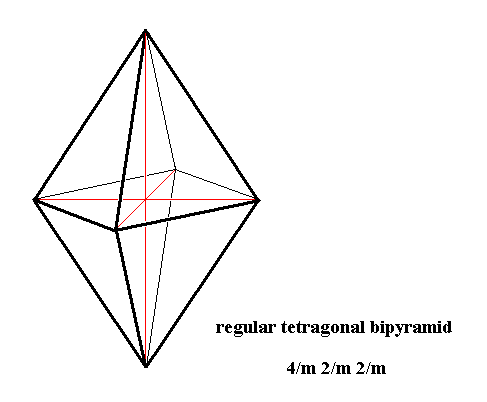
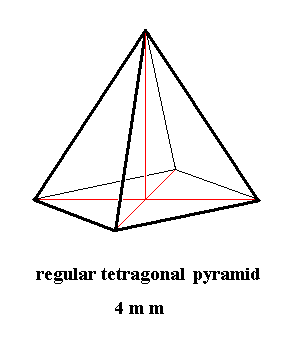
Ditetragonal-pyramidal Class, 4 m m
Tetragonal-bipyramidal Class, 4/m
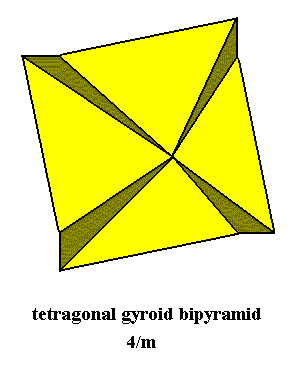
Figure 10. Oblique top view of the Tetragonal (4-fold) Gyroid Bipyramid, Stereometric Basic Form of all the (single) crystals of the Tetragonal-bipyramidal Class of the Tetragonal Crystal System. Because of the view direction the lower pyramid is not visible.
Tetragonal-pyramidal Class, 4
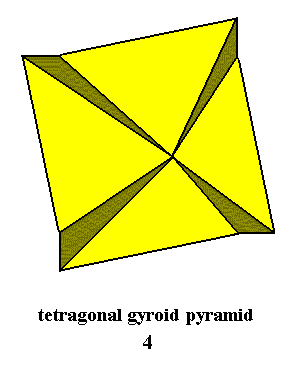
Tetragonal-trapezohedric Class, 4 2 2
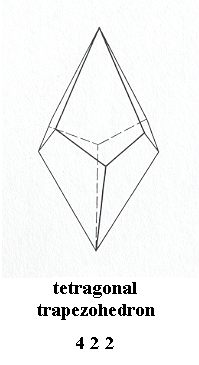
Figure 12. Tetragonal Trapezohedron, Stereometric Basic Form of all the (single) crystals of the Tetragonal-trapezohedric Class of the Tetragonal Crystal System.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
Tetragonal-scalenohedric Class, 4* 2 m
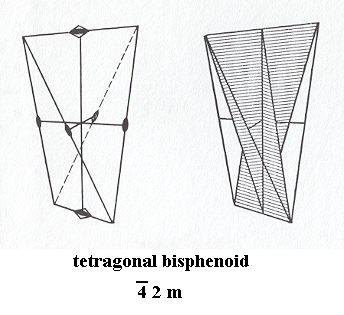
Figure 13. Tetragonal Bisphenoid, Stereometric Basic Form of all the (single) crystals of the Tetragonal-scalenohedric Class of the Tetragonal Crystal System.
Left image : The position of the rotational axes. Small square with solid oval indicates a 4-fold rotoinversion axis. Small oval indicates a 2-fold rotation axis.
Right image : The position of the two mirror planes.
( After HURLBUT, C. & KLEIN, C., 1977, Manual of Mineralogy )
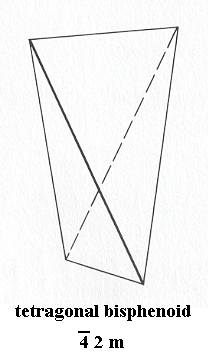
Tetragonal-bisphenoidic Class, 4*
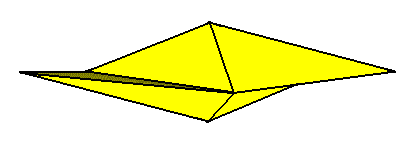
The above Figure depicts a single gyroid 2-fold pyramid. The next Figure depicts an apical 2-fold bipyramid, i.e. two 2-fold gyroid pyramids connected by their tips.
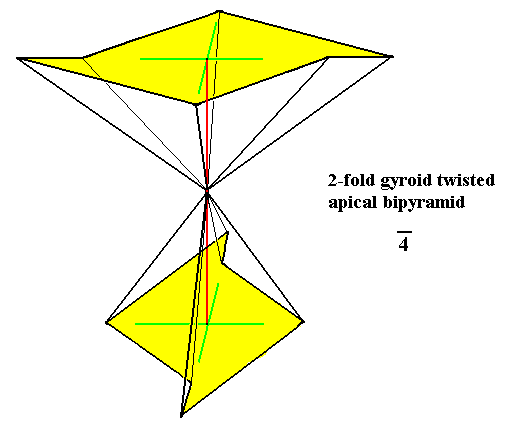
Figure 15. An apical 2-fold gyroid (and twisted) bipyramid, Stereometric Basic Form of the (single) crystals of the Tetragonal-bisphenoidic Class of the Tetragonal Crystal System. It can be considered as to consist of two antimers. The lower and upper parts of each antimer (i.e. the one part of the given antimer lies on one side, while the other part lies on the other side of the equatorial plane (point)) are rotated by 900 with repect to each other. In classifying this form under the Stauraxonia homopola, we ignore the fact that the two pyramids are rotated (by 900) with respect to each other (as a consequence of the rientation of the parts of the antimers just mentioned).
The next Figure again illustrates the symmetry content of our Class, i.e. the Class with symmetry 4*, the Tetragonal-bisphenoidic Class of the Tetragonal Crystal System. This 4* symmetry means the possession of just a 4-fold rotoinversion axis, meaning that the object possessing such an axis will be mapped onto itself when it is rotated by 900 directly followed by inversion in a point on that axis.
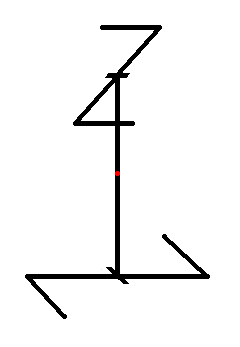
The promorph is accordingly that of the Allosigmostaura pseudobisphenoidea (Stauraxonia homopola sigmostaura) (in calling them "pseudobisphenoidea" we indicate the fact that although crystals of this Class can assume the shape of a bisphenoid, this bisphenoid does not possess all the symmetries of a geometrical bisphenoid (which is 4* 2 m). In crystals we can observe this lesser symmetry by means of features like etch figures. So we, who are looking for a geometrical solid expressing all (but at the same time exclusively) the symmetries of the present Class (Which here is the possession of just a 4-fold rotoinversion axis), cannot use the Bisphenoid. We have used the above bipyramid instead.
To continue click HERE to proceed with the second part of the Promorphology of Crystals.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)
back to Allopola amphipleura and zygopleura
back to the Basic Forms of Cells I
back to the Basic Forms of Cells II
back to the Basic Forms of Organs
back to the Basic Forms of Antimers
back to the Basic Forms of Metamers
back to the Basic Forms of Persons
back to the Basic Forms of Colonies
back to the first Part of the Preparation to the Promorphology of Crystals
back to the second Part of the Preparation to the Promorphology of Crystals
back to the third Part of the Preparation to the Promorphology of Crystals
back to the fourth part of the Preparation to the Promorphology of Crystals
back to the fifth part of the Preparation to the Promorphology of Crystals
back to the sixth part of the Preparation to the Promorphology of Crystals
back to the seventh part of the Preparation to the Promorphology of Crystals
back to the eighth part of the Preparation to the Promorphology of Crystals
back to the ninth part of the Preparation to the Promorphology of Crystals
back to the tenth part of the Preparation to the Promorphology of Crystals
back to the eleventh part of the Preparation to the Promorphology of Crystals
back to the twelfth part of the Preparation to the Promorphology of Crystals
back to the thirteenth part of the Preparation to the Promorphology of Crystals
back to the fourteenth part of the Preparation to the Promorphology of Crystals
back to the fifteenth part of the Preparation to the Promorphology of Crystals
back to the sixteenth part of the Preparation to the Promorphology of Crystals
back to the seveneenth part of the Preparation to the Promorphology of Crystals
back to the first part of the Preparation to the Promorphology of 3-D Crystals
back to the second part of the Preparation to the Promorphology of 3-D Crystals
back to the third part of the Preparation to the Promorphology of 3-D Crystals
back to the fourth part of the Preparation to the Promorphology of 3-D Crystals
back to the fifth part of the Preparation to the Promorphology of 3-D Crystals