Promorphology of Crystals Preparation III

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
3

REMARK : When the reader feels satisfied with our established theoretical foundation (done in the previous two documents) that allows (single, non-twinned) Crystals to be promorphologically assessed, he or she can skip all the following, and directly proceed with The Promorphology of Crystals.

We are concerning ourselves with a theoretical justification to treat single non-twinned Crystals -- figuring as representatives of inorganic genuine beings -- promorphologically, despite their periodic structure, which means that we may determine their stereometric basic form (promorph), just like we did in the case of organic beings, to which the Promorphological System was originally geared. For the purpose of getting this justification it was sufficient that we limited our considerations to 2-dimensional crystals. After we gave some generalities, we demonstrated this justification for 2-D crystals of the Plane Group P4gm. Although all this is sufficient for our purpose, it is nevertheless very instructive to consider ALL 2-dimensional Plane Groups in this respect, i.e. we're going to derive the t e c t o l o g i c a l a s p e c t of 2-D crystals of all the 17 Plane Groups. Recall that a "tectological structure" (in contradistinction to a "periodic structure") relates to the fact that entities that possess such a structure are composed of repeated morphological units that are differently oriented with respect to each other within the overall pattern (In a periodic structure these units all have the same orientation with respect to each other within the overall pattern, and where a tectological structure does nevertheless show repeated parts with the same orientation -- as in the case of possessing equal metamers -- those parts are not repeated such as to fill space. In the case of the mentioned metamers for example those parts are repeated only along one dimension of the organism's three-dimensional space).

Before we proceed we give an overview of the 2-D lattice types, 2-D Point Groups and 2-D Plane Groups.

With respect to the occurrence of glide lines (glide reflections) in 2-D crystals we have three cases :

Glide lines are primarily present. They are then given in the Plane Group symbol.

Glide lines are just implied. They are not given in the Plane Group symbol.

No glide lines are present.

In the last two cases the motif, from which we derive the tectology of the given crystal, is directly given, i.e. it is directly detectable in the planar array, without further elaborations.
In the first case (a case that we have considered extensively by means of the Plane Group P4gm in the previous document) the tectological aspect, and especially its details, is more or less burried beneath the surface. We have to eliminate the translational components of the prevailing glide reflections in order to extract the "complex motif" (as we did for P4gm).
We will now determine the tectological aspect and its details with respect to all the remaining Plane Groups.

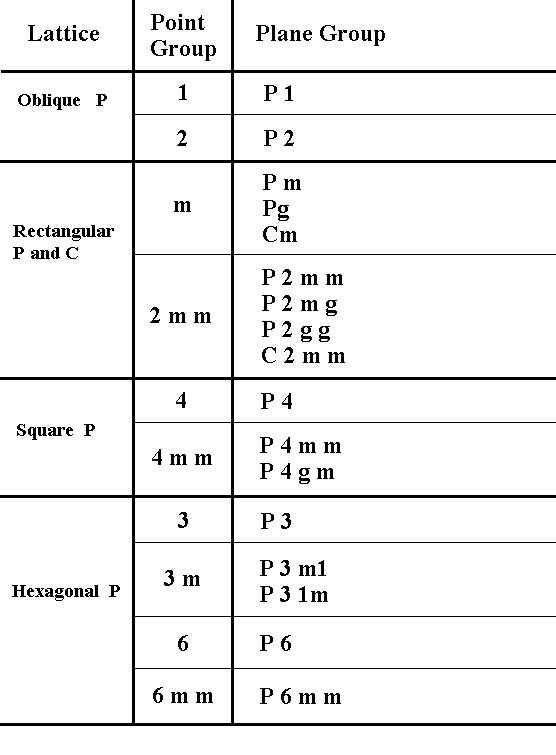
The Plane Group P1
The symmetry of a motif pattern according to the Plane Group P1 is based on (whatever variant of) the Oblique Point Lattice (Net). See the next Figures.

Figure 1. Pattern of motifs according to the Plane Group P1. The pattern must be considered as to be extended indefinitely in 2-D space.
( After KLEIN, C., & HURLBUT, C., 1999, Manual of Mineralogy )

The next Figure shows the underlying Oblique Net.

Figure 2. Pattern of motifs according to the Plane Group P1. The nodes of the net coincide with equivalent points (areas) of the pattern, i.e. points of the pattern that all have identical surroundings.
( Adapted from KLEIN, C., & HURLBUT, C., 1999, Manual of Mineralogy )

If we isolate a unit cell, then we have eliminated all s i m p l e translations (which are responsible for the periodic repetition of a unit cell (For 2-D we can also call it a unit mesh). And because there are no other translations involved in the pattern, the isolated unit cell is identical to the C o m p l e x M o t i f (As is evident from Figure 2, we can choose the nodes of the oblique net to coincide with any element of the pattern. We choose to let them coincide with the eyes of the fishes).

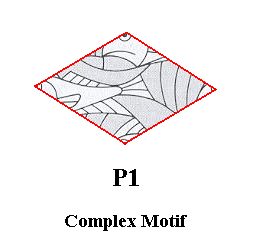
Figure 3. Isolated unit cell of the pattern of Figure 1. It is equivalent to the Complex Motif.

As can be seen in the Figures 2 and 3, the pattern of fishes and boats is not totally accurate with respect to repeating distances. It is however still fully instructive for our purposes. Such small discrepances, by the way, are very common in Nature, and can be interpreted as extrinsic and (therefore accidental) and as such be abstracted, i.e. conceptually removed, from the overall pattern.
The Complex Motif, as is just derived, represents the t e c t o l o g i c a l a s p e c t of the 'crystal' built according to the pattern of Figure 1. There is no symmetry present in this Complex Motif, i.e. its Point Group is 1. The simplest geometric plane figure that represents this symmetry geometrically is an Irregular Trigon or non-equilateral triangle, and this is the 2-D promorph or planimetric basic form of every single non-twinned 2-D crystal with Plane Group P1. The latter is the only Plane Group compatible with the 2-D Crystal Class 1.

Figure 4. Geometric Figure representing the planimetric basic form of all crystals based on Plane Group P1 and thus of the Class 1.

We have not developed a promorphological system of two-dimensional objects, but if we had done so, the triangle of Figure 4 would certainly occupy a definite place in such a system.

The Plane Group P2
Patterns of motifs according to Plane Group P2 are also based on the Oblique Point Lattice (Net). But in this case the pattern has the full symmetry of the empty building block of the Oblique Net, the parallelogram (which has a 2-fold rotation axis). See next Figures.

Figure 5. Pattern according to Plane Group P2. The pattern must be considered as to be extended indefinitely in 2-D space. It has 2-fold rotation axes periodically repeated all over the pattern. See next Figure.

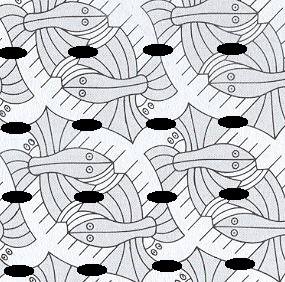
Figure 6. Pattern according to Plane Group P2. It has 2-fold rotation axes (normal to the plane of the drawing) periodically repeated all over the pattern indicated by small black ellipses.

It is most convenient to locate the nodes of the net right on the symmetry elements. So in the present case we locate the nodes of the underlying Oblique Net at 2-fold rotation axes in equivalent places within the pattern (i.e. we only connect only those 2-fold axes which all lie in equivalent places, which means that their surroundings are identical : This is because the nodes of the net must indicate equivalent areas within the pattern. And a net, so constituted, indicates the periodic nature of the pattern).

Figure 7. Pattern according to Plane Group P2. The underlying Oblique Net is inserted such that its nodes coincide with a part of the 2-fold rotation axes present in the pattern. The net indicates the periodic nature of the pattern.

Scrutinizing the pattern of Figure 5, we can, in addition to simple translations, detect only 2-fold rotation axes. No other symmetry elements are present. So the lattice (net) indicating the pattern's periodic nature must be (a version of) the Oblique Net. We have drawn it in Figure 7. There we see that an Oblique Net can -- accidentally -- have the shape of a square net. Indeed the pattern shows the accidental nature of the net being square (or almost square for that matter).
Isolating a unit cell means eliminating all simple translations. And because there are no other translations involved the (most symmetrical) unit cell is identical to the Complex Motif. See next Figure.

Figure 8. Isolated unit cell of the pattern of Figure 5.

The content of this isolated unit cell (as isolated) possesses only one single symmetry element, namely a 2-fold rotation axis at its center. Of course, if the unit cell is repeated indefinitely -- and in this way forming our pattern -- the 2-fold rotation axes present at the unit cell's boundary are genuine 2-fold rotation axes. But as soon we isolate the unit cell, those axes at the boundary are no 2-fold rotation axes anymore. Only the one in the center of the image (the isolated unit cell) is a genuine 2-fold rotation axis. See Next Figure.

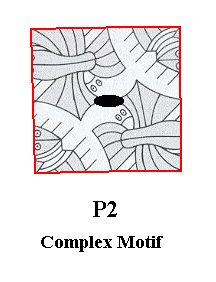
Figure 9. Isolated unit cell of the pattern of Figure 5. As such, i.e. as isolated, it is (now) a pattern possessing as its only symmetry element a 2-fold rotation axis in its center (normal to the plane of the drawing, and indicated by a small black ellipse).

So the Complex Motif (represented by the isolated unit cell) has as its symmetry content just one 2-fold rotation axis. Its Point Groip is therefore 2. The simplest geometric 2-D figure geometrically representing this symmetry is the General Parallelogram. So this General Parallelogram is the promorph or planimetric basic form of all the 2-D crystals belonging to the Plane Group P2 and with it to the 2-D Crystal Class 2. See next Figure.

Figure 10. The promorph or planimetric basic form of all 2-D crystals of the Plane Group P2 and of the Class 2.

The Plane Group Pm
Patterns of motifs according to Plane Group Pm are based on the Primitive Rectangular Point Lattice (Net). The next Figure depicts such a pattern.

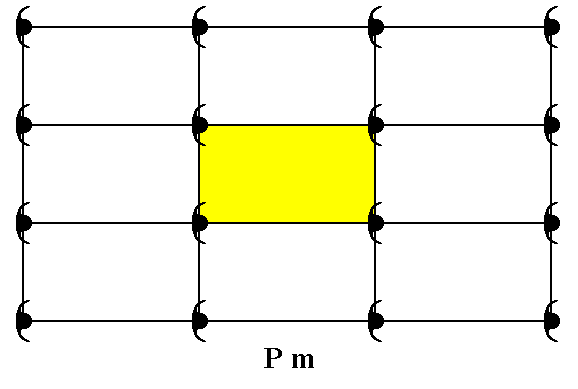
Figure 11. A repetitive pattern, according to Plane Group Pm. The pattern must be considered as to be extended indefinitely in 2-D space. A unit cell (mesh) is chosen (yellow).
This unit mesh has a point symmetry m, and is primitive.

When we isolate the unit cell, we have eliminated all simple translations. Because there are no other translations present in the pattern, our isolated unit cell (as isolated) is identical to the Complex Motif. See next Figure.

Figure 12. Isolated unit cell of the pattern of Figure 11. This unit cell can stand for the Complex Motif of 2-D crystals belonging to the Plane Group Pm and with it to the 2-D Crystal Class m.

The just derived Complex Motif is in itself correct but not very instructive. Alternatively we can take it as the t o t a l m o t i f, which is wholly equivalent to the above chosen unit cell (mesh). This total motif (i.e. the motif s.str. + its proper surroundings, in the Figure indicated with blue) can now figure as the Complex Motif. Its symmetry is directly evident : The only symmetry element it contains is a mirror line, so its point symmetry is m. See for this total motif, at the same time representing the Complex Motif, the next Figure.

Figure 13. A total motif ( = the whole content of the red rectangle ). It consists of one whole motif s.str. plus its homogeneous surroundigs (background) within the red rectangle, and is equivalent to the above chosen unit cell.

Isolating the total motif yields the Complex Motif :

Figure 14. An isolated total motif. As such it can represent the Complex Motif.

We can see that the symmetry content of the Complex Motif is : one mirror line, as indicated in the next Figure.

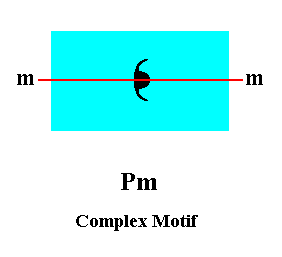
Figure 15. The symmetry content of the Complex Motif is one mirror line (m) as indicated.

So the Complex Motif, representing the translation-free residue of the periodic pattern of Figure 11, belongs, with respect to its symmetry, to the 2-D Point Group m. The simplest geometric figure that displays this symmetry geometrically is the Isosceles Triangle. This isosceles triangle represents the promorph or planimetric basic form of all the 2-D crystals of the Plane Group Pm, and with it of the 2-D Crystal Class m.

There are two more Plane Groups that have the Point Group m as their translation-free residue, namely the Plane Groups Pg and Cm. So also their Complex Motif will have the same symmetry : m.

The next Figure depicts the Isosceles Triangle.

Figure 16. The promorph or planimetric basic form of all the 2-D crystals of the 2-D Crystal Class m.

To see, and, if you like, to investigate, another 2-D periodic Pm motif pattern, click the small preview image :

In the next document we will go on along the sequence of Plane Groups and derive the corresponding Complex Motifs.

To continue click HERE starting with the next Plane Group : Pg.

e-mail :