
The Homopola sigmostaura are represented by a few sigmoid organisms, for example the diatomean Gyrosigma, which will be depicted below.
The basic form of the Sigmostaura is represented by a homopolar regular or amphitect bipyramid of which the cross axes show a sigmoid form. This implies that the bipyramid, which we will call a g y r o i d b i p y r a m i d, does not possess mirror planes parallel to the main axis. The latter nevertheless is a 2- or more-fold rotation axis, which means that the symmetry of the bipyramid is such that when it is rotated about its main axis by a certain angle it will be mapped onto itself, i.e. the resulting figure remains the same after such a rotation. The only plane of symmetry is the equatorial plane, perpendicular to the main axis and containing its midpoint.

The Homopola sigmostaura divide into two subgroups which are analogues of the Homopola isostaura and the Homopola allostaura, i.e. respectively depending on a regular bipyramid and on an amphitect bipyramid. The next Figures exemplify them with basic forms possessing four antimers.
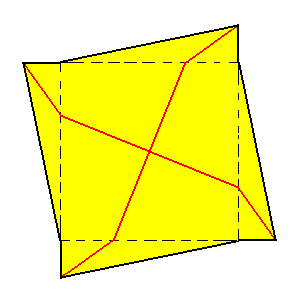
Figure 2. Equatorial plane of a regular gyroid bipyramid with four antimers. The 4-fold rotation axis (main axis) is perpendicular to the plane of the drawing and goes through the center of the image. The two radial s i g m o i d cross axes are shown in red. The form of those axes as drawn, only symbolizes their sigmoid character.
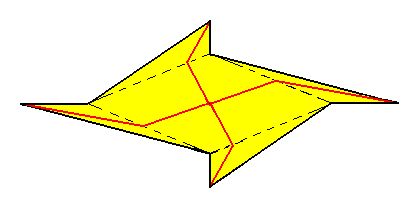
Figure 3. Equatorial plane of an amphitect gyroid bipyramid with four antimers. The 2-fold rotation axis (main axis) is perpendicular to the plane of the drawing and goes through the center of the image. The two radial sigmoid non-equivalent cross axes are shown in red. The shape of these axes as drawn, only symbolizes their sigmoid character.

Figure 4. Equatorial plane of an amphitect gyroid bipyramid with four antimers. Auxiliary lines and cross axes omitted. The 2-fold rotation axis (main axis) is perpendicular to the plane of the drawing and goes through the center of the image.

As has been said, the Homopola sigmostaura can be divided into two subgroups. When based on a regular bipyramid (Figure 2) we will call them Sigmostaura isosigmostaura. When based on an amphitect pyramid (Figure 3, 4 and 5) we will call them Sigmostaura allosigmostaura.
Twisted regular bipyramidal bodies with a homopolar main axis.
The basic forms belonging to this group can be derived from regular bipyramids, by eliminating all mirror planes parallel to the main axis. The main axis remains a rotational axis.
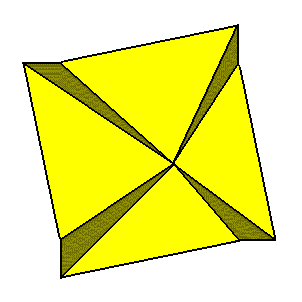
The symmetry of the Isosigmostaura quadrimera (Figure 6) can crystallographically be described as 4/m, meaning the presence of a 4-fold rotation axis normal to a mirror plane, and is the same as that of crystals of the Bipyramidal Class (4/m) of the Tetragonal Crystal System (See the Special Series on the first Part of this website, accessible via back to homepage).
The symmetry of the Isosigmostaura trimera can crystallographically be described as 6* (= 3/m), meaning the presence of a 6-fold rotoinversion axis, which is equivalent to the presence of a 3-fold rotation axis normal to a mirror plane, and (that symmetry) is the same as that of crystals of the Trigonal-bipyramidal Class (6*) of the Hexagonal Crystal System.
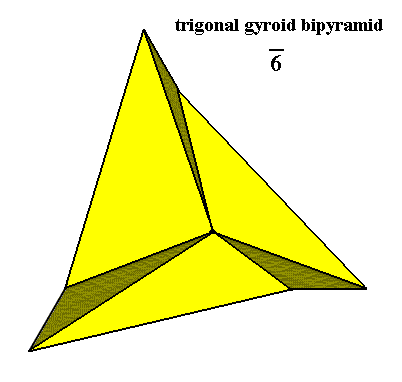
Figure 6a. Slightly oblique top view of a Trigonal (3-fold) Gyroid Biyramid. The lower pyramid is not visible but is present. The only mirror plane present is the equatorial plane connecting the two constituent pyramids.
The symmetry of the Isosigmostaura sextamera can crystallographically be described as 6/m, meaning the presence of a 6-fold rotation axis normal to a mirror plane, and is the same as that of crystals of the Hexagonal-bipyramidal Class (6/m) of the Hexagonal Crystal System.
In the next Figure we indicate, by means of the equatorial plane, how to construct a six-fold gyroid bipyramid, as the basic form of the Isosigmostaura sextamera (Stauraxonia homopola sigmostaura).
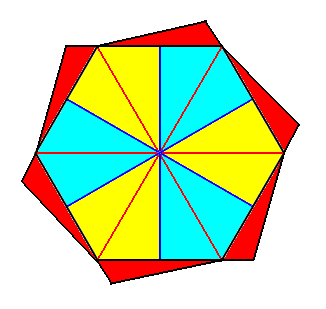
Figure 6a. Construction of a regular six-fold gyroid bipyramid by means of adaptation of the equatorial plane of a regular six-fold bipyramid. Attachment of the red parts, as indicated in the Figure, causes the elimination of the mirror lines inherent in a regular hexagon. For the bipyramid this means the disappearance of all vertical mirror planes, i.e. mirror planes containing the main axis. The 6-fold rotation axis, though, remains.
The next Figure depicts the bipyramid, finally resulting from this construction.
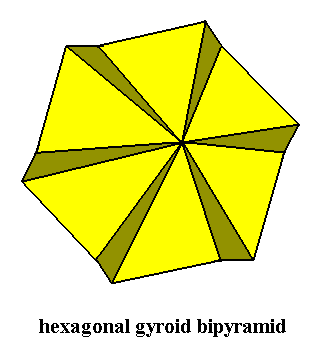
Figure 6b. Regular Hexagonal (i.e. six-fold) Gyroid Bipyramid, occuring as stereometric basic form of (single) crystals of the Hexagonal-bipyramidal Class of the Hexagonal Crystal System. Because of the view direction the lower pyramid is not visible.
The symmetry of the Isosigmostaura pseudorhomboedra can crystallographically be described as 3*, meaning the presence of a 3-fold rotoinversion axis as the only symmetry element, and is the same as that of crystals of the Trigonal-rhombohedric Class (3*) of the Hexagonal Crystal System.
The stereometric basic form of the Isosigmostaura pseudorhomboedra can be depicted as two regular 3-fold gyroid pyramids connected with each other by their tips and rotated 600 with respect to each other. The resulting form is a trigonal (3-fold) gyroid twisted apical bipyramid. See next Figure.
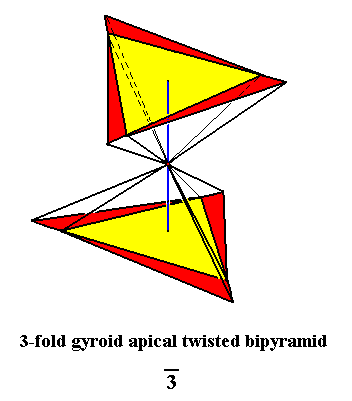
Figure 6c. The Trigonal Gyroid Twisted Apical Bipyramid as the Stereometric Basic Form of the Isosigmostaura pseudorhomboedra (Stauraxonia homopola sigmostaura). In calling them (Stauraxonia) "homopola", we ignore the rotation of the composing pyramids with respect to each other.
For more details about the Isosigmostaura pseudorhomboedra, the document on The Promorphology of Crystals.
Twisted amphitect biyramidal bodies with a homopolar main axis.
These basic forms can be derived from amphitect bipyramids by eliminating all mirror planes parallel to the main axis. This main axis (still) is a 2-fold rotation axis.
The symmetry of the Allosigmostaura can, crystallographically be described as 2/m, meaning the presence of a 2-fold rotation axis perpendicular to a mirror plane (m), and is the same as that of crystals belonging to the Prismatic Class (2/m) of the Monoclinic Crystal System (See the Special Series on the first Part of this website, accessible via back to homepage).
The next Figure depicts a member of the Allosigmostaura with four antimers (it belongs to the Allosigmostaura quadramphimera).

The next Figures depict yet another species of the Allosigmostaura, namely one that belongs to the Allosigmostaura duamphimera. It can be derived from an amphitect four-fold gyroid bipyramid. It possesses two antimers.

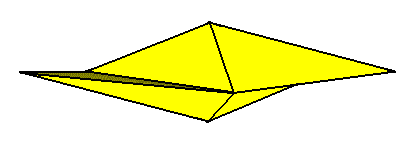
The stereometric basic form of the Allosigmostaura duamphimera is materialized in the diatomean Gyrosigma :

Figure 10. Gyrosigma, a diatomean cell. The 2-fold rotation axis is perpendicular to the plane of the photograph and goes through the center of the cell.
Promorphologically it belongs to the Allosigmostaura with two antimers : Allosigmostaura duamphimera.
(Photograph, after HUSTEDT, F., 1956, Kieselalgen (Diatomeen))
In order to make this basic form clear, we depict yet another geometric body promorphologically wholly equivalent to that of Figure 9.
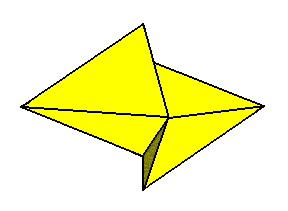
Of course the images of the Figures 9 and 11 also allow for f o u r antimers to be distinguished. However we stipulate them to have t w o antimers when we promorphologically describe an organism that tectologically consists of two antimers, and that is such that its basic form must be described by means of an amphitect gyroid bipyramid that is derivable from a rhombic octahedron or rhombic bipyramid. A similar case we will encounter in the case of the Diphragma (Heterostaura autopola).
The Allosigmostaura allow for still other forms, among which an apical gyroid bipyramid, but such that the gyroid pyramids, composing the bipyramid, are rotated by 900 with respect to each other. As such the resulting symmetry content is that of a single 4-fold rotoinversion axis. Crystals of the Tetragonal-bisphenoidic Crystal Class of the Tetragonal Crystal System have this symmetry. Because no organisms are to be expected to realize this form we will introduce it separately in the inframe below.
To continue click HERE to proceed further with the systematic Promorphology.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Homopola isostaura and allostaura