The form group of the Zeugites or allopolar heterostaurs is the last and most differentiated group, and at the same time the most important and most diverse, of all main groups which we have found by our investigation of the axes of organic forms and their poles. Of the animal kingdom most of the so-called bilateral-symmetric animals belong to the present group, namely all vertbrates, Arthropods, Molluscs, most worms, further a large number of Echinoderms (the so-called irregular Echinoderms), many Coelenterates, etc. Just as common we find this basic form in the plant kingdom, where most of the so-called "irregular flowers", for example of the Grasses, Orchids, Umbellifers, Labiates, Composites and many others, belong to it (The "Composites" have 'flowers' that are composed of many very small flowers -- florets -- and it is these latter that, like all the other mentioned flowers, belong to the form group of the Allopola).
The allopolar heterostauric form obtains its biggest importance as the general basic form of most of the higher organized persons and metamers. But it is also generally basic to the form of antimers and organs, less common to that of cells and colonies (Cormi). So we indeed can indicate this basic form as the most important and most applicable one of all basic forms.

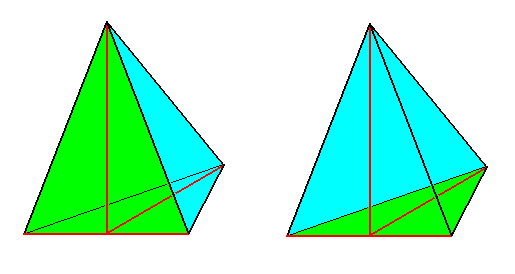
Figure 1.   The basic form of the Heterostaura allopola, illustrated with half a Rhombic Pyramid (which itself is the basic form of the Allopola eudipleura) .
Left image :   bisection face (originated by the bisection of the whole Rhombic Pyramid) emphasized (green).
Right image :   Base emphasized (green).
Main axis (vertical), lateral axis (horizontal) and dorso-ventral axis are indicated in red.

The general morphological properties of the zeugites or centrepipeds are of a very definite nature, implying that when one investigates them closely, their differences from the autopolar heterostaurs, with whom they often are confused, become very clear. In all zeugites the two body halves, that are separated by the median plane, are symmetrically equal or similar, but never congruent. They are each others mirror images and consequently cannot be mapped onto each other by any mechanical operation (like for instance rotation, or translation). In the majority of all centrepipeds these two halves, which we usually distinguish as right and left, are symmetrically equal. So all parts (i.e. morphological elements) are repeated with equal number and magnitude, and with equal relative, but opposite absolute positioning in the opposite body half. The only essential difference between the two halves consists in the fact that the equal distance of the parts from the common median plane is measured in opposite directions in either half. In another part of the centrepipeds on the other hand, as in the Pleuronectids (flatfishes) or the Gastropods that are coiled into a spiral, the two body halves are only symmetrically similar, insofar as one half is more or less stronger developed than the other, while both parts still possess the same (number of) essential organs or predispositions thereof. The right and left halves then are not only opposite, but also unequal, but still more or less similar.
According to this important distinction we can distinguish two divisions within the allopolar heterostaurs, when we indicate the forms that are symmetrically equal as  H o m o p l e u r a,  an the forms that are just symmetrically similar as  H e t e r o p l e u r a.
The just mentioned difference can be reduced to the fact that in the Homopleura both poles of just  o n e  (dorso-ventral) directional axis become unequal, while those of the other directional axis (lateral) remain equal. In the Heteropleura on the other hand both poles of both directional axes become unequal, often in such a degree, that the centrepiped character becomes strongly disturbed, as in the mentioned Pleuronectids and Gastropods.
So the  h o m o p l e u r a l  z e u g i t e s,  or the "strict bilateral-symmetric" organismic forms, distinguish themselves from all other heterostaurs by the fact that from the three unequal euthyni (directional axes) being perpendicular to each other,  o n e  (the lateral axis) is  e q u i p o l a r,  while the other two (dorso-ventral and main axis) are  u n e q u i p o l a r.
In the  h e t e r o p l e u r a l  z e u g i t e s,  in which also left and right differentiate themselves,  a l l  t h r e e  d i r e c t i o n a l  a x e s  a r e  u n e q u i p o l a r.

As important this distinction of homopleural and heteropleural forms seems to be, as insignificant it is for an understanding of the essence of the basic form within practical morphology, because the differentiation of the left and right body halves or of both poles of the lateral axis, will never acquire the same significance for the form as it is generally possessed by the differentiation of both poles of the dorso-ventral axis and those of the main axis.
Strictly speaking, the heteropleural condition is very common in zeugites, because the left and right halves are only seldom equal with respect to the smallest details of their form and magnitude. But these more fine-grained differences are legitimately ignored in any general morphological inquiry. Only those forms are determined as being genuine Heteropleura in which the unequality of the symmetrically similar right and left halves is conspicuous, as in Pleuronectids (flatfishes) and spiral Gastropods.

The number of antimers in zeugites is not considered by researchers just before Haeckel's time, and yet it is of the utmost importance for the assessment and distinction of several zeugite forms, whether they consist of two antimers, as in Vertebrates, Molluscs and Articulates, or of four, as in most worms, or of three antimers, as in Orchids, or of five, as in the irregular Echinoderms. On the basis of these differences we will first of all divide the form group of the Heterostaura allopola into two subgroups, that correspond to the two subgroups of the Autopola.
To the  o r t h o s t a u r i c  a u t o p o l e s  with two or four antimers correspond the  Z y g o p l e u r a l  z e u g i t e s  with two or four antimers, in which only one or two radial, and just as many interradial cross planes are present.
To the  o x y s t a u r i c  a u t o p o l e s  with six, eight or more antimers correspond the  A m p h i p l e u r a l  z e u g i t e s  with three, five or more antimers, in which at least three radial or semiradial cross planes are expressed.
In each of these two divisions homopleural and heteropleural forms can occur. However in the Amphipleura the heteropleural forms are very rare.

The geometric basic form of the  z e u g i t e s  o r  a l l o p o l a r  h e t e r o s t a u r s  is the  b i s e c t e d  a m p h i t e c t  p y r a m i d. This basic form can therefore be obtained by dividing the basic form of the autopolar heterostaurs into two equal halves. The plane of bisection coincides with one of the directional planes. The same applies to the corresponding subgroups of both form groups. In this way the general basic form of the  Z  y g o p e u r a  is half an amphitect pyramid with four sides, i.e. half a Rhombic Pyramid. The general basic form of the  A m p h i p l e u r a  is half an amphitect pyramid with 4+2n sides. But these division laws are strictly speaking only valid for the Homopleura in both form groups, because the unequality of the two lateral halves, that we see in the Heteropleura, impedes a definite determination of a general geometric basic form.
These most differentiated of all basic forms seem first of all, because of their inherent irregularity, to be connected with the lowest of all basic forms, the amorphous bodies or Anaxonia (See HERE for a treatment of these lowest forms). And partially they, like the latter, have indeed been interpreted as totally "irregular" or "asymetric" forms. But we should not forget, that in spite of the strong differentiation of the unequal antimers, and because of that also of the lateral halves, the pyramidal form remains determined in virtue of the number of antimers and of the relationship between the heteropolar main axis and the cross axes. The general basic form of the Heteropleura consequently is the irregular pyramid.

In the case of a  r e a l  bisection of a pyramid, representing a basic form, the number of antimers will be halved.
In the case of an  i d e a l  bisection of a pyramid, representing a basic form, the original number of antimers will be preserved, but some of these antimers will become differentiated from the rest.

On interpreting the configuration of antimers in general, but especially in the case of assessing the Tetraphragma and Tetrapleura, the organic forms, i.e. the concrete organic form individuals, will always constitute our point of reference. As  "a n t i m e r s"  we consider those counter parts -- i.e. discernable parts that group themselves around the center of the given organic form individual -- that show the highest morphological independency, i.e. that show the highest degree of individuality within that given form individual (We say "highest" with respect to all cases where there is some doubt as to whether some part is an antimer or not). When we interpret the result of a bisection we keep following the original antimers while they are in the process of differentiation (ideal bisection) or in the process of a real bisection of the given form individual. This is important for the assessment of the (number of) antimers that are left after the bisection.
In all this we should keep in mind that in the organic world there are seldom -- if any -- two individuals that are exactly identical. And this also applies to  s y m m e t r y - i n d i v i d u a l s,  i.e. to  a n t i m e r s.  And because of the complexity of organic individuals (morphonts) -- of all orders -- and because of the omnipresent  t r a n s i t i o n s,  the science of Promorphology is clearly distinguished from pure Stereometry. Especially in the Allopoles, where, for example, the main axis cannot be geometrically distinguished anymore from the dorso-ventral axis, and where in the heteropleural dipleural allopoles (Dysdipleura) it cannot be so distinguished at all -- to express this fact we could call the latter  T r i a x o n i a -- we must keep the difference of the two disciplines in mind.
The above defined ways of  b i s e c t i o n  of pyramids can be illustrated by means of their  b a s e s  (or equatorial planes for that matter).

We shall first of all -- using the concepts of real and ideal bisection -- derive the Zygopleural zeugites from the orthostauric autopoles. The different colors used to indicate regions in the ensuing drawings are meant to highlight the antimers by distinguishing and, in a way separate them from each other. Different colors neither do mean different types of antimers nor their symmetry relations.
We start with a bisection of a straight rectangular four-sided pyramid (the base of which is a rectangle, and having its tip right above the center of that rectangle, causing the main axis to be a 2-fold rotation axis). This pyramid is supposed to represent an organismic form with four antimers, while both its directional axes are interradial, so it is the basic form of the Autopola tetraphragma interradialia. The next Figure illustrates a  r e a l  b i s e c t i o n  of this basic form (represented by the pyramid's base).

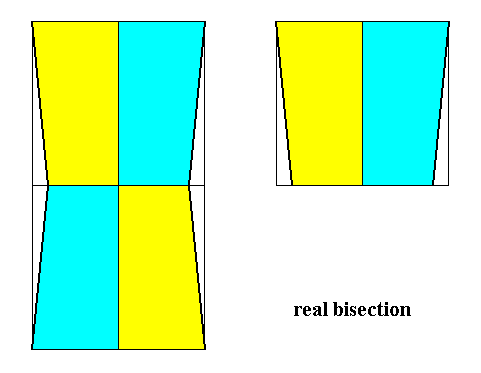
Figure 2.
Left image :   Base of a four-sided rectangular straight pyramid. This base is rectangular. The antimers are indicated by colors (light blue and yellow). The shape of these antimers, as drawn, symbolizes the heteropolarity of the main axis of the pyramid, which here means that each antimer is wholly asymmetric (See next Figure). The rectangular pyramid, here represented by its base, is the basic form of the Tetraphragma interradialia (Autopola).
Right image :   Result of a  r e a l  bisection performed on the left image. The number of antimers is halved. The resulting basic form is an  a l l o p o l a r  form, namely one that belongs to the Eudipleura (Allopola zygopleura), i.e. allopoles with two symmetrically equal, but not congruent, antimers.

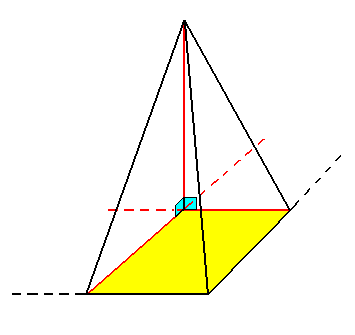
Figure 3.   Antimer of a rectangular pyramid. The vertical main axis (red) is perpendicular to the cross axes (red), implying the asymmetry of the antimer.

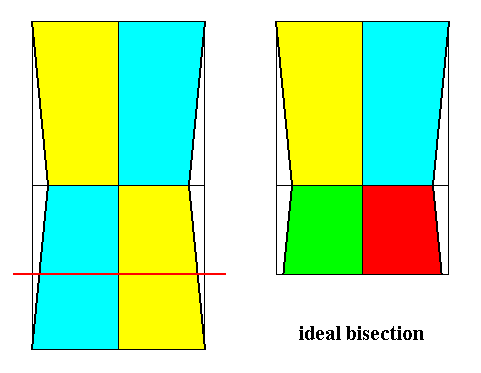
Figure 4.
Left image :   Base of a four-sided rectangular straight pyramid as in Figure 2 (left image). This pyramid is the basic form of the Tetraphragma interradialia (Autopola). An ideal bisection line (in fact just a partition line) is indicated (red) symbolizing ideal bisection, i.e. differentiation of an antimer pair with respect to the other pair.
Right image :   Result of an  i d e a l  bisection performed on the left image. The number of antimers is preserved. The resulting basic form is an  a l l o p o l a r  form, namely one that belongs to the Eutetrapleura interradialia (Allopola zygopleura), i.e. an allopolar form with two unequal pairs of antimers, each pair consisting of two symmetrically positioned antimers.

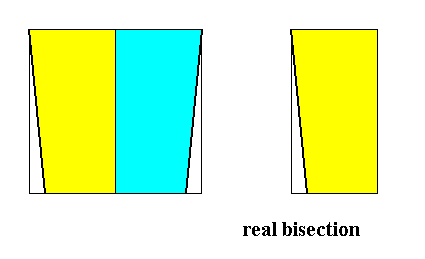
Figure 5.
Left image :   Base of a halved four-sided rectangular straight pyramid, as in Figure 2 right image. This pyramid has two symmetrically positioned antimers. It is the basic form of Zygopleura eudipleura, and as such a homopleural zeugite.
Right image :   Result of a  r e a l  bisection performed on the left image. Initially the number of antimers is halved, which in this case means that there is only one antimer left. But as such it cannot be an antimer anymore, because by definition antimers are counter parts. If we interpret the resulting basic form as a heteropleural zeugite, then it is heteropleural in the strongest sense, which here means that the resulting form is wholly asymmetric. It reflects in a way the shapes that we find in crystals of the Asymmetric Class of the Triclinic Crystal System. Promorphologically the resulted form should belong to the Anaxonia (forms that do not admit of non-arbitrary body axes).

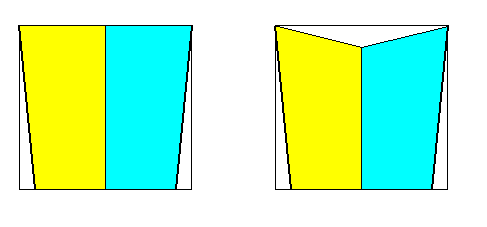
Figure 6.
Left image :   Base of a halved four-sided rectangular straight pyramid, as in Figure 2 right image. This pyramid has two symmetrically positioned antimers. It is the basic form of Zygopleura eudipleura, and as such a homopleural zeugite.
Right image :   A form, wholly equivalent to that of the left image. The image is adapted in order it to be able to express the asymmetry of the right antimer after ideal bisection (See next Figure).

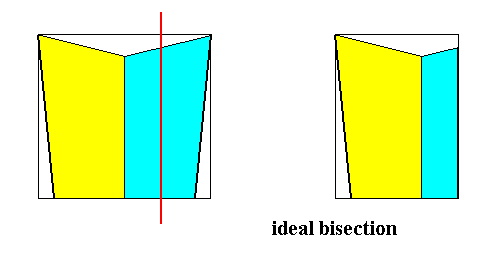
Figure 7.
Left image :   Adapted outline of the base of a halved four-sided rectangular straight pyramid, as in Figure 6 right image. This (halved) pyramid still has two symmetrically positioned antimers. It is the basic form of the Zygopleura eudipleura, and as such a homopleural zeugite. A line (red) of ideal bisection is added.
Right image :   Resulting form after  i d e a l  bisection of the form of the left image. Ideal bisection preserves the number of antimers, while at the same time expressing the differentiation of those antimers. The result is a form with (still)  t w o  antimers. These antimers are different from each other (but are supposed to possess (in the real organismic form) the same predisposition with respect to their parts. The two antimers are not symmetrically equal, nor congruent, but symmetrically similar. We have derived the Dysdipleura (Allopola zygopleura).

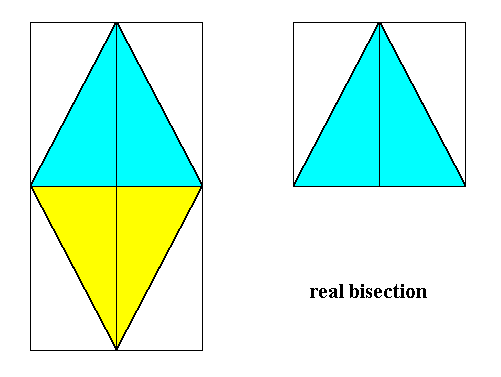
Figure 8.
Left image :   Base of a Rhombic Pyramid with  t w o  antimers. As such it is the basic form of the Diphragma (Autopola). The two antimers are indicated with colors (light blue and yellow).
Right image :   Result of a  r e a l  bisection of the form of the left image. The resulting form consists of one antimer, which is however itself consisting of two symmetrically positioned antimers. We have derived a member of the Eudipleura (Allopola zygopleura).

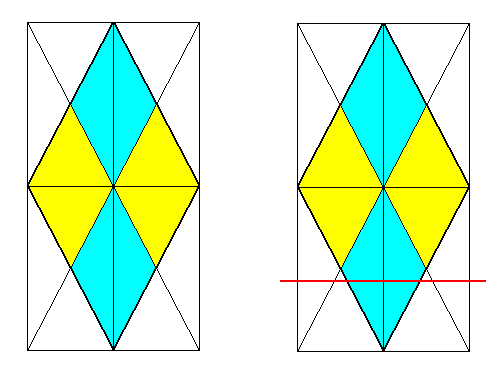
Figure 9.
Left image :   Base of a Rhombic Pyramid with  f o u r  antimers. This pyramid is the basic form of the Tetraphragma radialia (Autopola). The four antimers are indicated by colors (light blue and yellow).
Right image :   Line (red) of ideal bisection added (See the next Figure).

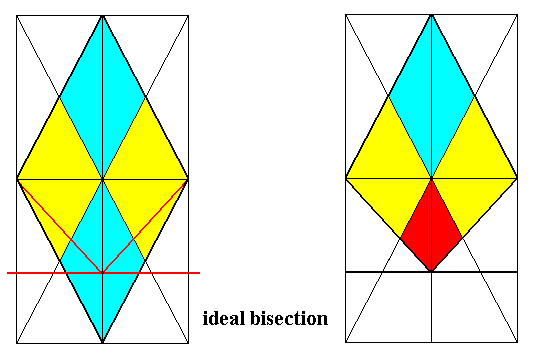
Figure 10.
Left image :   Constuction of an ideally bisected Rhombic Pyramid with  f o u r  antimers, illustrated by its base. The four original antimers are indicated by colors (light blue and yellow).
Right image :   Result of the ideal bisection. The resulting form still has four antimers, but three of them are differentiated with respect to the remaining one. We have constructed a form belonging to the Eutetrapleura radialia (Allopola zygopleura).

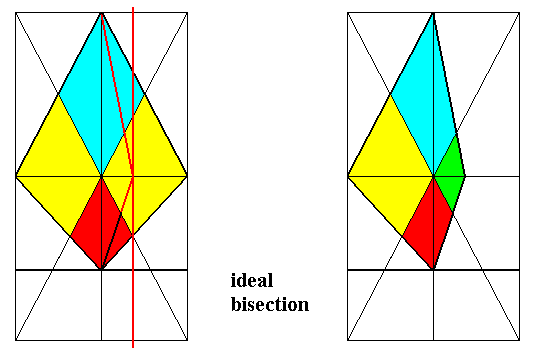
Figure 11.
Left image :   Constuction of an ideally  d o u b l y  bisected Rhombic Pyramid with  f o u r  antimers, illustrated by its base. The four original antimers are indicated by colors.
Right image :   Result of the ideal bisection. The resulting form still has four antimers, but three of them are differentiated with respect to the remaining one. We have constructed a (heteropleural) form belonging to the Dystetrapleura radialia (Allopola zygopleura).

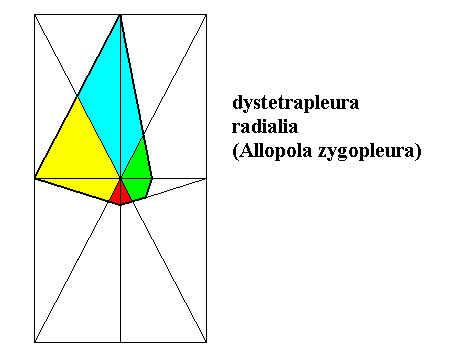
Figure 12. A more extreme version of the form constructed in Figure 11. The resulting form still has four antimers, but three of them are differentiated with respect to the remaining one. Also in this case we have constructed a (heteropleural) form belonging to the Dystetrapleura radialia (Allopola zygopleura).

• From the Tetraphragma interradialia (Autopola orthostaura with four antimers) we derived the Eudipleura (Allopola zygopleura with two antimers) by real bisection (Figure 2).
• From the Tetraphragma interradialia (Autopola orthstaura with four antimers) we derived the Eutetrapleura interradialia (Allopola zygopleura with four antimers) by ideal bisection (Figure 4).
• From the Eudipleura (Allopola zygopleura with two antimers) we in turn derived the Anaxonia, i.e. a totally asymmetric form, by real bisection (Figure 5).
• From the Eudipleura (Allopola zygopleura) we also derived the Dysdipleura (Allopola zygopleura with two antimers) by ideal bisection. They are heteropleural Zeugites (Figure 7).
• From the Diphragma (Autopola orthostaura with two antimers) we derived the Eudipleura (Allopola zygopleura with two antimers) by real bisection (Figure 8).
• From the Tetraphragma radialia (Allopola zygopleura with four antimers) we derived the Eutetrapleura radialia (Allopola zygopleura with four antimers) by ideal bisection (Figure 10).
• From the Eutetrapleura radialia (Allopola zygopleura with four antimers) we in turn derived the Dystetrapleura radialia (Allopola zygopleura with four antimers) by ideal bisection (Figures 11 and 12).

The base ( b a s i s ) of an oxystauric autopolar pyramid is an amphitect polygon consisting of 4+2n sides, i.e. either having 6, or 8, or 12, etc. sides. Those sides are arranged such that the polygon has two mirror lines (its directional axes) perpendicular to each other while their point of intersection coincides with the center of the polygon. All this implies a 2-fold rotational symmetry for the polygon.
When we're going to derive polygones (bases) for amphipleural allopoles from polygones of oxystauric autopoles by means of either bisecting them ideally, or really, we never (conceptually) cut an antimer into separate pieces. In the process of bisecting the antimeres involved either disappear, or become differentiated, or do not change at all. The line of division (bisection) coincides with one of the directional axes in the case of real bisection. In a way this also holds for ideal bisection, because differentiation takes place immediately after the relevant directional axis, i.e. in ideal bisection differentiation takes place in one of the two areas separated by this axis. Because the bisection line is not allowed to run through any antimer (as outlined in the polygon), but only to run between them, some versions of amphitect polygones cannot be subjected to bisection, for example the following version of an eight-sided amphitect polygon :

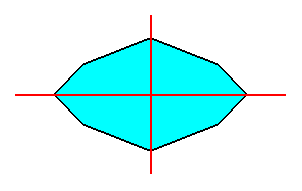
Figure 13.   An eight-sided amphitect polygon, such that its two directional axes both are  r a d i a l.  Such a polygon cannot be bisected, neither really, nor ideally.

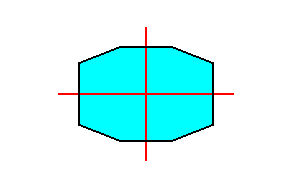
Figure 14.   An eight-sided amphitect polygon, such that its two directional axes both are  i n t e r r a d i a l.  Such a polygon can be bisected, really, as well as ideally.

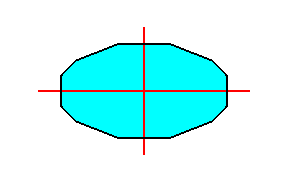
Figure 15.   A twelve-sided amphitect polygon, such that its two directional axes both are  i n t e r r a d i a l.  Such a polygon can be bisected, really, as well as ideally.

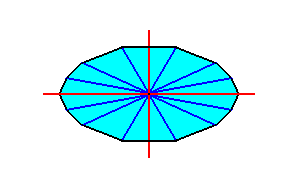
Figure 16.   A fourteen-sided amphitect polygon, such that one of its directional axes is radial and the other interradial. Such a polygon can be bisected, really, as well as ideally, only along the interradial directional axis.

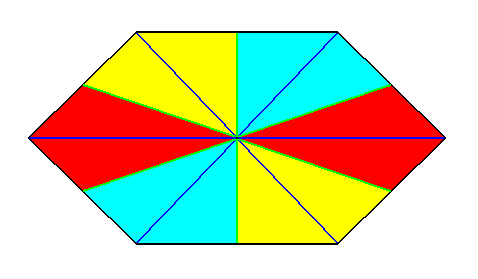
Figure 17.   A six-sided amphitect polygon representing the basic form of the Hexaphragma (Autopola). The six antimers are indicated with colors.  

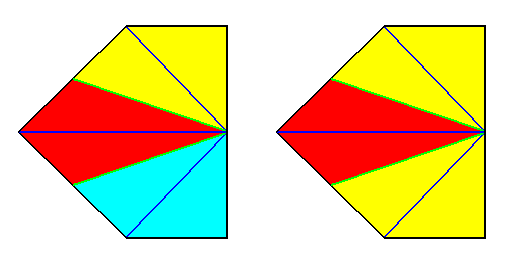
Figure 18.  
Left image :   Result of a  r e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Triamphipleura (Allopola amphipleura with three antimers).
Right image :   After some redistribution of colors, in order to show the symmetry with repect to the lateral axis.

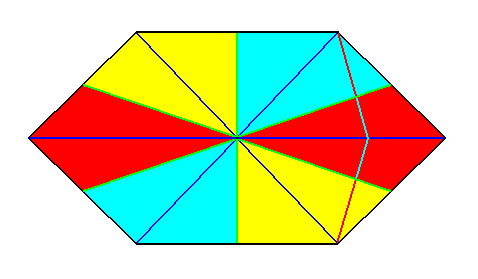
Figure 19.   Indication of an ideal bisection to be performed on the six-sided amphitect polygon. See next Figure.

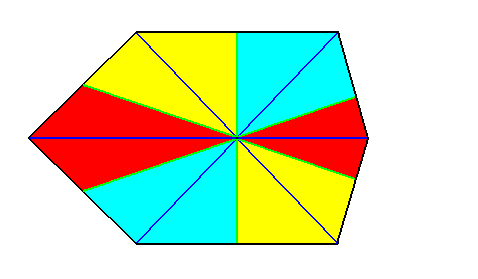
Figure 20.   Result of an  i  d e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Hexamphipleura (Allopola amphipleura with six antimers).

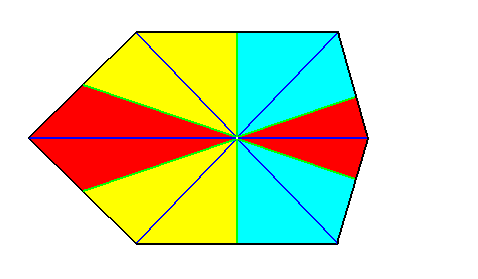
Figure 20a.   The same as the previous Figure, but now after redistributing some colors to express the symmetry with respect to the lateral axis.

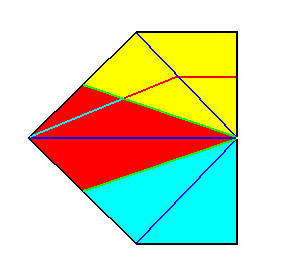
Figure 21.   Indication of an  i d e a l  bisection of the polygon of Figure 18 representing the basic form of the Triamphipleura (Allopola amphipleura with three antimers). See next Figure.

Figure 22.   Result of an  i d e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Dystriamphipleura (Allopola amphipleura heteropleura with three antimers).

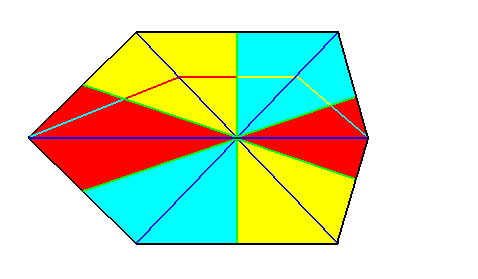
Figure 23.   Indication of an  i d e a l  bisection of the polygon of Figure 20 representing the basic form of the Hexamphipleura (Allopola amphipleura with six antimers). See next Figure.

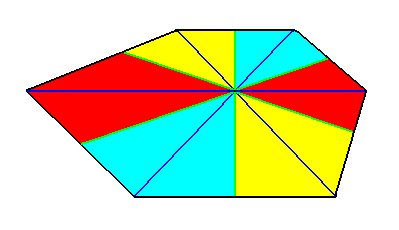
Figure 24.   Result of an  i d e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Dyshexamphipleura (Allopola amphipleura heteropleura with six antimers).

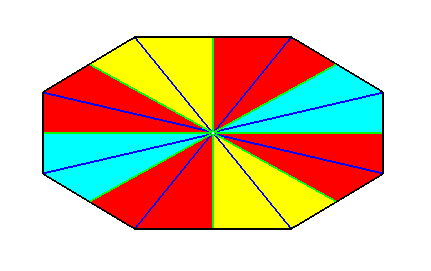
Figure 25.   An eight-sided amphitect polygon, such that its two directional axes both are  i n t e r r a d i a l.  It represents the basic form of the (interradial) Octophragma (Autopola). Such a polygon can be bisected, really, as well as ideally. The eight antimers are indicated by colors.

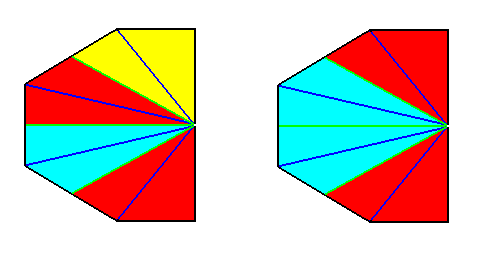
Figure 26.  
Left image :   Result of a  r e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Eutetrapleura interradialia (Allopola zygopleura with four antimers).
Right image :   After redistribution of colors, in order to express the symmetry with respect to the lateral axis.

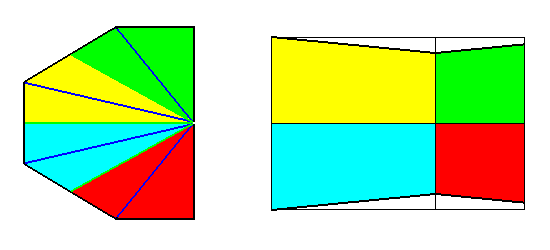
Figure 27.   Two results of the derivation of the Eutetrapleura interradialia (Allopola zygopleura with four antimers). To ease the comparison I have adapted the orientation and the coloring. The two forms are equivalent from a promorphological point of view.

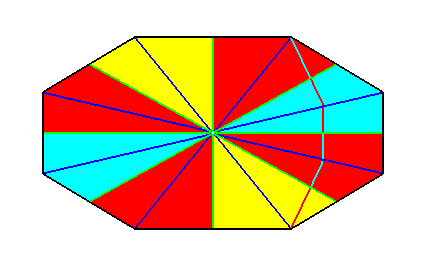
Figure 28.   Indication of an  i d e a l  bisection of the polygon of Figure 25 representing the basic form of the Octophragma (Autopola oxystaura with eight antimers). See next Figure.

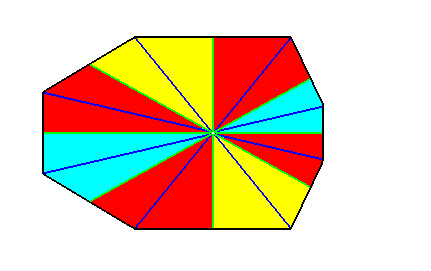
Figure 29.   Result of an  i d e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Octamphipleura (Allopola amphipleura with eight antimers).

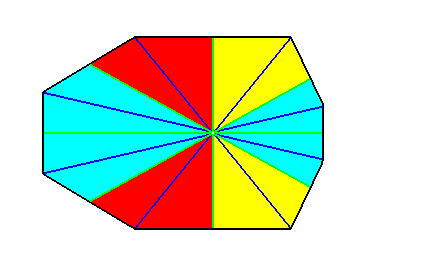
Figure 29a.   The same as the previous Figure, but now after redistributing some colors to express the symmetry with respect to the lateral axis.

We will continue our derivations with the next higher autopolar pyramid, the 10-fold amphitect pyramid, represented by its base.

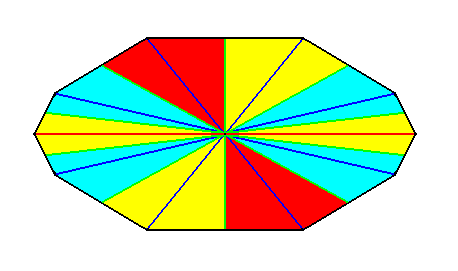
Figure 30.   A ten-sided amphitect polygon, such that one of its directional axes is  i n t e r r a d i a l,  while the other is  r a d i a l.  It represents the basic form of the Decaphragma (Autopola). Such a polygon can be bisected, really, as well as ideally, along the interradial directional axis. The ten antimers are indicated by colors.

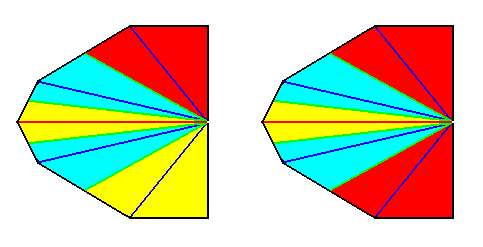
Figure 31.  
Left image :   Result of a  r e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Pentamphipleura (Allopola amphipleura with five antimers).
Right image :   After redistribution of colors, to indicate the symmetry with respect to the lateral axis.

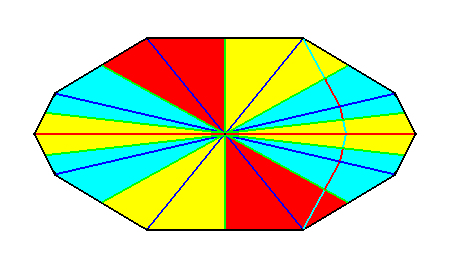
Figure 32.   Indication of an  i d e a l  bisection of the polygon of Figure 30 representing the basic form of the Decaphragma (Autopola oxystaura with ten antimers). See next Figure.

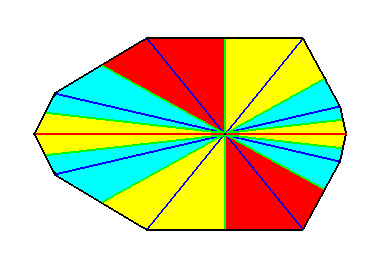
Figure 33.   Result of an  i d e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Decamphipleura (Allopola amphipleura with ten antimers).

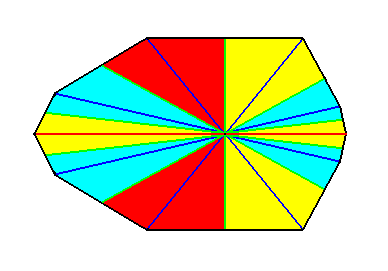
Figure 33a.   The same as the previous Figure, but now after redistributing some colors to express the symmetry with respect to the lateral axis.

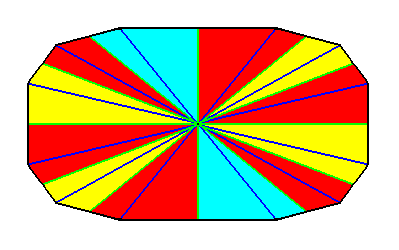
Figure 34.   A twelve-sided amphitect polygon, such that both of its directional axes are  i n t e r r a d i a l.  It represents the basic form of the Dodecaphragma (Autopola). Such a polygon can be bisected, really, as well as ideally, along a directional axis.
The twelve antimers are indicated by colors.

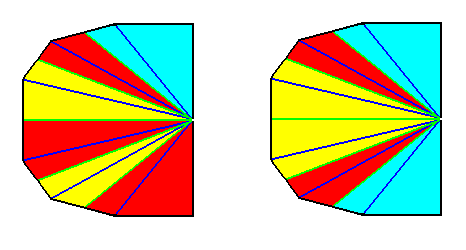
Figure 35.  
Left image :   Result of a  r e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Hexamphipleura (Allopola amphipleura with six antimers).
Right image :   After redistribution of colors, to indicate the symmetry with respect to the lateral axis.

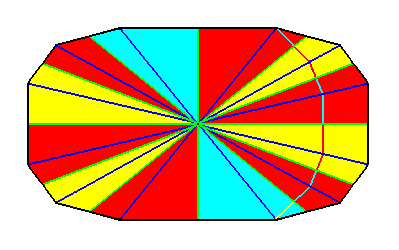
Figure 36.   Indication of an  i d e a l  bisection of the polygon of Figure 34 representing the basic form of the Dodecaphragma (Autopola oxystaura with twelve antimers). See next Figure.

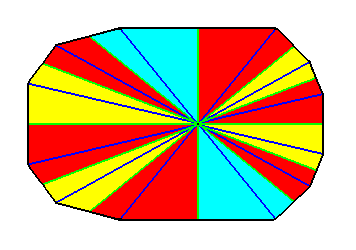
Figure 37.   Result of an  i d e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Dodecamphipleura (Allopola amphipleura with twelve antimers).

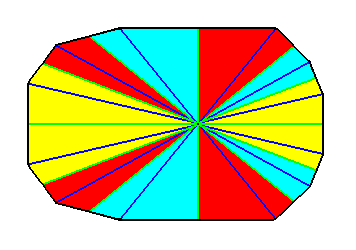
Figure 37a.   The same as the previous Figure, but now after redistributing some colors to express the symmetry with respect to the lateral axis.

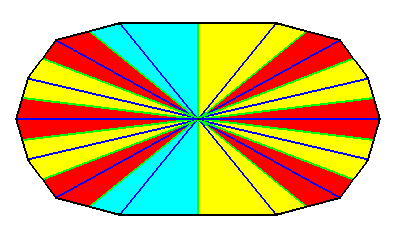
Figure 38.   A fourteen-sided amphitect polygon, such that one of its directional axes is  i n t e r r a d i a l,  while the other is  r a d i a l.  It represents the basic form of the tetrakaidecaphragma (Autopola). Such a polygon can be bisected, really, as well as ideally, along the interradial directional axis. The fourteen antimers are indicated by colors.

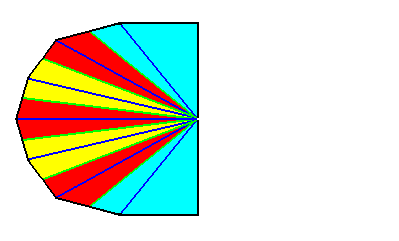
Figure 39.   Result of a  r e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Heptamphipleura (Allopola amphipleura with seven antimers).

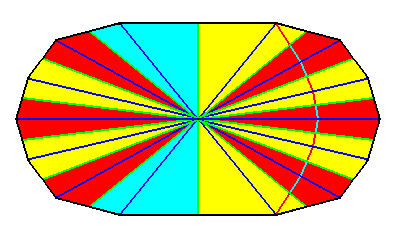
Figure 40.   Indication of an  i d e a l  bisection of the polygon of Figure 38 representing the basic form of the Tetrakaidecaphragma (Autopola oxystaura with fourteen antimers). See next Figure.

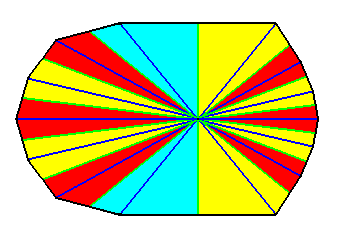
Figure 41.   Result of an  i d e a l  bisection of the polygon of the previous Figure. This result represents (by means of the base of the pyramid) the basic form of the Tetrakaidecamphipleura (Allopola amphipleura with fourteen antimers).

• From the Hexaphragmic autopoles (6 antimers) we derived the Triamphipleura (Allopola amphipleura with three antimers) by real bisection (Figure 18).
• From the Hexaphragmic autopoles (6 antimers) we derived the Hexamphipleura (Allopola amphipleura with six antimers) by ideal bisection (Figures 20 and 20a).
• From the Triamphipleural allopoles (3 antimers) we derived the Dystriamphipleura (Allopola amphipleura heteropleura with three antimers) by ideal bisection (Figure 22).
• From the Hexamphipleural allopoles (6 antimers) we derived the Dyshexamphipleura (Allopola amphipleura heteropleura with six antimers) by ideal bisection (Figure 24).
• From the Octophragmic autopoles (8 antimers) we derived the Eutetrapleura interradialia (Allopola zygopleura with four antimers) by real bisection (Figure 26).
• From the Octophragmic autopoles (8 antimers) we derived the Octamphipleura (Allopola amphipleura with eight antimers) by ideal bisection (Figures 29 and 29a).
• From the Decaphragmic autopoles (10 antimers) we derived the Pentamphipleura (Allopola amphipleura with five antimers) by real bisection (Figure 31).
• From the Decaphragmic autopoles (10 antimers) we derived the Decamphipleura (Allopola amphipleura with ten antimers) by ideal bisection (Figures 33 and 33a).
• From the Dodecaphragmic autopoles (12 antimers) we derived the Hexamphipleura (Allopola amphipleura with six antimers) by real bisection (Figure 35).
• From the Dodecaphragmic autopoles (12 antimers) we derived the Dodecamphipleura (Allopola amphipleura with twelve antimers) by ideal bisection (Figures 37 and 37a).
• From the Tetrakaidecaphragmic autopoles (14 antimers) we derived the Heptamphipleura (Allopola amphipleura with seven antimers) by real bisection (Figure 39).
• From the Tetrakaidecaphragmic autopoles (14 antimers) we derived the Tetrakaidecamphipleura (Allopola amphipleura with fourteen antimers) by ideal bisection (Figure 41).