Promorphology of Crystals Preparation IV

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
4

REMARK : When the reader feels satisfied with our established theoretical foundation (done in the previous two documents) that allows (single, non-twinned) Crystals to be promorphologically assessed, he or she can skip all the following, and directly proceed with The Promorphology of Crystals.

The Plane Group Pg
The symmetry of periodic patterns of motifs according to the Plane Group Pg are based on one or another version of the Primitive Rectangular Point Lattice (Net). See the next Figures.

Figure 1. Pattern of motifs according to the Plane Group Pg. The pattern must be considered as to be extended indefinitely in 2-D space.
( After KLEIN, C., & HURLBUT, C., 1999, Manual of Mineralogy )

The next Figure shows the underlying Primitive Rectangular Net.

Figure 2. Underlying primitive rectangular lattice (net) of the pattern of motifs according to the Plane Group Pg. The nodes of the net coincide with equivalent points (areas) of the pattern, i.e. points of the pattern that all have identical surroundings.
( Adapted from KLEIN, C., & HURLBUT, C., 1999, Manual of Mineralogy )

The pattern of Figure 1 contains g l i d e l i n e s (g) as its only symmetry element (in addition to simple translation). See next Figure.

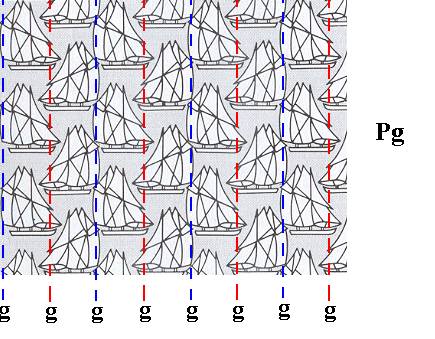
Figure 3. Glide lines (g) of the pattern of Figure 1, indicated by red and blue dashed lines.

One such glide line is clarified in the next Figure.

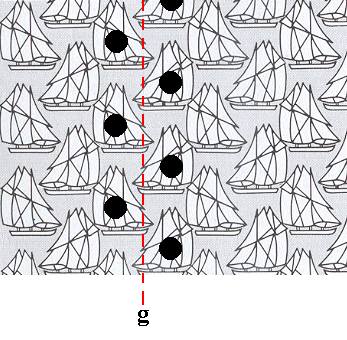
Figure 4. One glide line of the pattern of Figure 1, is clarified.

In Figure 2 we had connected equivalent points in order to obtain the underlying lattice (net). It is clear that we can start to draw such a net from any point of the pattern as long as all the points coinciding with the nodes of the net are fully equivalent. Well in Figure 2 this was done correct. It is however more convenient to align the lines or nodes of the net with some symmetry elements of the given pattern. The result is an identical net. In our case it is convenient to let the vertical lines of the net coincide with glide lines (resulting in half of the glide lines coinciding with the vertical elements of the net). This is done in the next Figure.

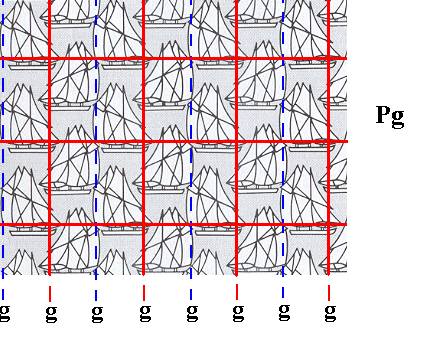
Figure 5. The position of the primitive rectangular lattice (net), underlying the periodicity of the pattern of Figure 1, is chosen such that its vertical elements coincide with glide lines.

Now we must -- in order to derive the Complex Motif -- eliminate the translations involved in the glide lines (glide translations). We can do this in several ways. Let's first try one way. We concentrate on a few unit cells, but of course the operations to be executed must apply to the whole pattern (thought as indefinitely extended in 2-D space) : First we copy a unit cell. Then we shift this copy along the glide line, going through the middle of the unit cell, by a distance of half a simple translation along the vertical edge of the unit cell, i.e. we shift the copy by one half of the vertical side of the unit cell. See next Figure.

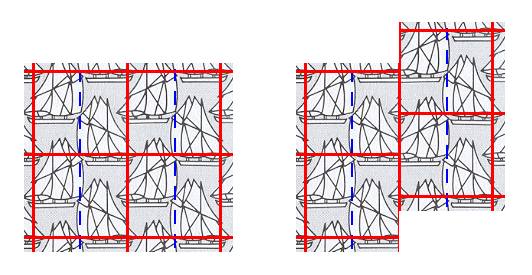
Figure 6. Concentrating on one single unit cell : The lower left unit cell is copied and is placed next to the original at its right side (Left Image). Then that copy is shifted upwards by one-half of the length of the vertical edge of the unit cell, i.e. half a simple translation in that direction.

Now the shifted copy must be laid over the original unit cell without thereby being shifted again, so its superposition involves the upper half of the original unit cell and the lower half of the unit cell directly above the original one. See next Figure.

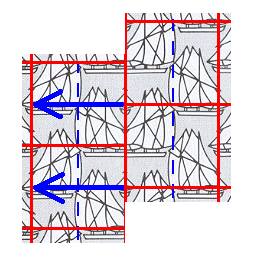
Figure 7. The copied and shifted unit cell should -- according to the arrows -- be placed over the original unit cell (in fact over its upper half and over the lower half of the unit cell directly above the original unit cell).

The two areas that are going to be superimposed upon each other (as indicated by the arrows in Figure 7) are mirror symmetric with respect to each other as the next Figure (more clearly) shows :

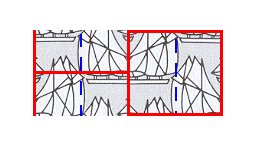
Figure 8. The two areas that are to be superimposed upon each other are mirror symmetric with respect to each other.

Because the images are not transparent, we cannot execute this superposition, but we know the result nevertheless : when two symmetric images are superimposed upon each other, without thereby being shifted parallel to the mirror line in the process, the result will be a mirror symmetric image. The next Figure illustrates this.

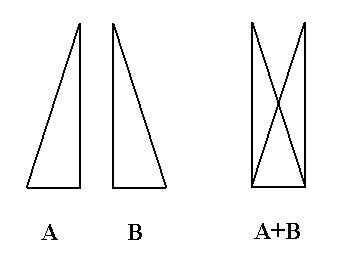
Figure 9. When two planimetric figures, that are mirror symmetric with respect to each other, are superimposed upon each other, the result will be a figure that is itself mirror symmetric .

When the two parts of Figure 8 (i.e. its left and right parts) are actually superimposed, we obtain an area having the same dimensions as a unit cell of the original pattern. This means that we not only have undone the glide translations (in virtue of the executed shift), but also the simple translations (that were responsible for the periodic multiplication of a unit cell of the pattern). Therefore the result of the superposition of the left and right part of the image of Figure 8 will be our sought for Complex Motif. And we know that the symmetry content of this Complex Motif is : one mirror plane (As already related to, we must of course involve the whole pattern in the above operations : We make a copy of it, shift it up by one-half of a vertical side of the unit cell and superimpose this shifted copy over the original).
A second way to eliminate the glide translations is to shift every column to the, say, right of every second glide line (The interleaved glide lines will then automatically be co-involved) upward by half a vertical unit cell length. And if we, after having done that, isolate an earea having the same size and form of the initially chosen unit cell, then we have also eliminated all simple translations, and end up with the Complex Motif, which has one symmetry element, namely a mirror line.
The simplest plane figure that expresses this symmetry geometrically is the Isosceles Triangle (Which we also found with respect to the Plane Group Pm). This isosceles triangle represents the promorph or planimetric basic form of all 2-D crystals of which the symmetry of their internal structure can be described by the Plane Group Pg. And such crystals -- as do those of Plane Group Pm -- belong to the 2-D Crystal class m.

Figure 10. The Isosceles Triangle representing the planimetric basic form (promorph) of all the 2-D crystals of the Plane Group Pg, and with it of the Point Group m.

A note on Glide lines and Unit Cells.
It is probably useful to dwell a little further upon our present subject, i.e. to realize what in fact we are doing. Well, we are still doing P r o m o r p h o l o g y, i.e. we are considering the stereometric basic forms of Organisms. But, in the present documents, we want to integrate the i n o r g a n i c beings within our Promorphological System. This system was originally geared to describe and systematize the stereometric basic forms of o r g a n i s m s. Organisms were investigated as to their inherent and intrinsic symmetries, that could be derived when all accidental and extrinsic form features were subtracted, i.e. left out of consideration. This was done by looking for and finding ideal body axes, investigating the nature of their poles, and determining the geometric nature of their constant and intrinsic body centra, i.e. whether such a centrum was at all present, and if so, whether it was a point, a line or a plane. All this resulted in a stereometric characterization of the given organism. This characterization was then given in the form of a geometric solid (say a pyramid, cylinder, etc.) expressing the basic ideal symmetry content geometrically.
But, inorganic real intrinsic beings -- that are mainly represented by individual c r y s t a l s -- also show definite shapes and symmetries, and, even clearer than most organisms do. So the desire came up to integrate crystals into the promorphological system. But, the promorphology of organisms was based on an important feature of the structure of organisms, namely their TECTOLOGICAL structure, which means that their body is made up of repeating parts, such that the orientation of these parts is not periodic, which means that they normally group themselves around an axis, resulting in their orientation to be different from each other. These parts are called ANTIMERS. Other parts build up the organismic body by repeating such that their orientation is, it is true, the same for al these parts, but then this repetition is a repetition only in one direction. These parts are called METAMERS. Crystals (to be precisely, single non-twinned crystals) on the other hand, are always periodically built : A certain microscopic unit is repeated while maintaining exactly the same orientation, and moreover this repetition always goes along three directions, in such a way that space is completely filled. So if we investigate crystals we do not find antimers and metamers. And especially the antimers played a crucial role in determining the stereometric basic form or promorph of the organism, namely the number, symmetry and configuration of antimers. As has been said, in (single non-twinned) crystals we do not find such antimers, which fact could indicate that crystals do not yield to any promorphological assessment, at most doing so as a vague analogy. So we are only theoretically legitimized to include crystals in our promorphological investigation if they, in spite of their periodic nature possess some t e c t o l o g i c a l a s p e c t that determines in some way their shapes and symmetries in such a way that those symmetries can be promorphologically interpreted. One indication of their tectological aspect is the fact that they are finite bodies with definite intrinsic symmetries (on the basis of which they indeed are attributed to Crystal Classes of which there are thirty-two). But this is not enough. We must explicitly demonstrate that they possess a genuine and intrinsic tectological aspect. Assuming they have this aspect we can assess their promoph on the basis of their intrinsic point symmetry reflected in their belonging to a certain Crystal Class. In accordance with our way of work within organic Promorphology we then look for, and find, the s t e r e o m e t r i c s o l i d that geometrically expresses this symmetry. Not all crystals are such that their geometric shape (even when they have grown undisturbedly in a uniform medium) displays this symmetry. Sometimes we must physically investigate their faces to detect symmetries -- or the lack of symmetries -- for instance by means of etch figures. In these cases we must come up with a geometric solid having a shape that does not as such occur in the crystals involved in those cases.
In the present documents we are concerning ourselves with the demonstration of the tectological aspect in single non-twinned crystals (Thereby we make also use of the geometic properties of 2-D crystals in order to help the understanding of 3-D crystals). We know that crystals are constituted by chemical atoms, ions, atomic or ionic groups. And these chemical entities do have a tectological nature. They are not themselves crystals, i.e. they do not show a full-fledged p e r i o d i c nature. So we know the direction in which to find the tectological aspect in crystals : the c h e m i c a l m o t i f s thay reside in them. Well, we now have to find such a non-periodic motif in every crystal species. How do we do this? We can do this by eliminating everything that is responsible for the crystal's periodic (non-tectological) nature. And it are the TRANSLATIONS that are responsible for that periodic nature. First we have the so-called simple translations. They are responsible for the periodic repetition of the mentioned microscopic entity, the unit cell. The unit cell is a building block of the given crystal furnished with chemical motifs. Then we have the translational components of of certain symmetries : glide planes (in 2-D crystals, glide lines) and screw axes (Because screw axes themselves involve three-dimensional space, they do not occur in 2-D crystals). Screw axes and glide planes (lines) draw as it were the chemical motifs apart, so that parts of them become displaced and separated from each other. This lowers the symmetry of crystals insofar as they are considered microscopially, which here means, insofar as they are p e r i o d i c structures. But in order to find the tectological aspect in crystals we must do away with these translations in order to obtain a motif that has the full symmetry of the crystal as seen macroscopically, a symmetry that is expressed by its Crystal Class. This symmetry is called the crystal's p o i n t s y m m e t r y. It is the translation-free residue of the crystal's total symmetry, which is its point symmetry plus its translational symmetries (simple translations, glide planes (lines) and screw axes). So in finding the motif -- we call it the Complex Motif -- that has a tectological structure we must eliminate all translations. Elimination of a translational component of a glide or screw operation increases the symmetry of the resulting configuration of motif units. But of course when, in the process of elimination of translations, the symmetry of the crystal's Class has been reached, this symmetry cannot be increased any further by still eliminating remainig translations. We will observe that elimination of some translations brings automatically with it the undoing of other translations at the same time. But we have, to be sure, to continue the elimination as long as the symmetry of the Class of the given crystal has not been reached, because the derived Complex Motif must have all the point symmetry that the crystal has in store, otherwise it does not represent this crystal properly.
For two-dimensional crystals -- with which the present documents are dealing, as a preparation for the understanding of how this all works in three-dimensional crystals -- we can state some rules to follow in the systematic elimination of translations. Simple translations speak for themselves, and screw axes do not occur in 2-D crystals, so these rules will only consider the glide translations that we encounter in two-dimensional periodic patterns ('two-dimensional crystals').

First of all, in deriving the Complex Motif, we must take our point of departure from the h i g h e s t s y m m e t r i c u n i t c e l l, guaranteeing that the Complex Motif to be derived from it will possess all the symmetry that the given crystal has in store.
If we have a glide line that is parallel to an existing mirror line, the symmetry of the (complex) motif will not be increased further anymore, so that we do not have to consider this glide line (in deriving the Complex Motif), i.e. we do not have to eliminate (i.e. undo) the glide translation associated with it.

If in a pattern based on a square lattice, we have two diagonal glide lines (diagonal wit respect to a square unit cell) and in addition to them two other glide lines perpendicular to them (i.e. two non-diagonal glide lines), then, having eliminated the glide translations associated to the non-diagonal glide lines, and having accordingly turned these glide lines into mirror lines, then two other mirror lines are automatically implied, which means that the two diagonal glide lines are already transformed into mirror lines. So we then do not have to consider the diagonal glide lines anymore. We then have already reached the maximal symmetry that the (resulting) Complex Motif can attain.

In two-dimensional patterns based on the Hexagonal Net we must take the most symmetric building block, and that is the Hexagon consisting of three rhomb-shaped (smaller) unit cells. If we take such a hexagonal building block together with its content as the (larger) unit cell, then we have a motif that has already the symmetry of the given 2-D Crystal Class. Indeed, in the hexagonal Plane groups where we find glide lines to be present, namely in the Plane Groups P3m1, P31m and P6mm, we find for every glide line an existing mirror line parallel to it. So indeed the elimination of the associated glide lines does not increase the symmetry any further, and consequently we do not have to work on them in order to find the Complex Motif.

The point symmetry inherent in the Plane Groups P2mg, P2gg, P2mm and C2mm, is 2mm. The Complex Motif will have this symmetry. The simplest geometric figure that geometrically expresses that symmetry is the Rectangle or the Rhombus.
In Promorphology these two figures, in spite of their having the same symmetry are different :
The Rectangle expresses the fact that the two d i r e c t i o n a l a x e s (euthyni)-- which are the two axes that are perpendicular to each other and coincide with the mirror lines -- pass b e t w e e n the antimers (i.e. the motif units, which, as counterparts compose the Complex Motif), and so are i n t e r r a d i a l.
The Rhombus on the other hand, expresses the fact that one or both directional axes go right t h r o u g h the motif units that can be interpreted as the Complex Motif's antimers.
In chemical terms we can say that a directional axis either goes between atoms (or between atomic groups), or right through them. All this clearly shows that Promorphology of crystals is different from Crystallography. To determine whether we have to do with radial or interradial directional axes (and also whether we have to do with two or four antimers), we must consult the u l t i m a t e Complex Motif, i.e. the motif that appears when ALL translations, including all glide translations, are eliminated. The latter can be accomplished by our Copy-Shift-Superimpose method.
Because the symmetry of all two-dimensional periodic patterns is based on just 17 Plane Groups we can treat things exhaustively, without any posibility that one day something pops up that ruins all our theoretical findings with respect to the derivation of te Complex Motif.
The above findings with respect to occurring glides will significantly ease our task of deriving the Complex Motif with respect to all the remaining Plane Groups.

In the next document will continue to go along the sequence of Plane Groups and derive the Complex Motif of each of them.

To continue click HERE to derive the Complex Motif of other 2-D periodic patterns.

e-mail :