REMARK : When the reader feels satisfied with our established theoretical foundation (done in the previous two documents) that allows (single, non-twinned) Crystals to be promorphologically assessed, he or she can skip all the following, and directly proceed with The Promorphology of Crystals.
The Plane Group P4gm
REMARK : This Plane Group has been treated of already earlier, namely in Part One and Part Two of the present series of documents. But there we concentrated every time on the immediate vicinity of one and the same lattice point (node) only. In the other Parts, including the present Part (6), we consider the whole pattern based on the different Plane Groups.
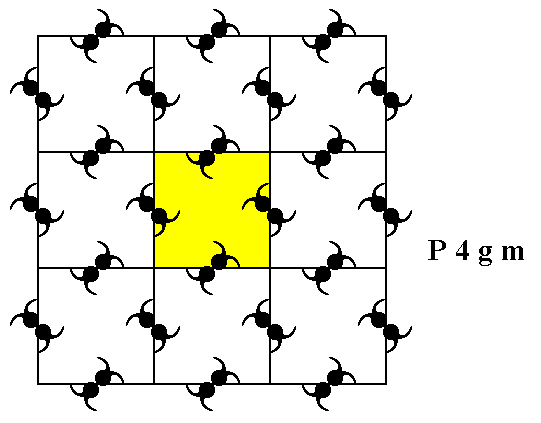
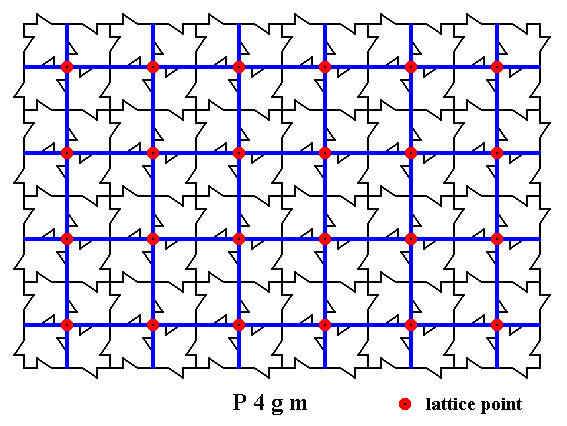
The symmetry of periodic patterns of motifs according to the Plane Group P4gm are based on one or another version of the Square Point Lattice (Net). See the next Figures.

Figure 1. Periodic two-dimensional pattern according to the Plane Group P4gm. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).
In addition to four-fold and two-fold rotation axes the P4gm pattern contains two sets of mirror lines (both in a diagonal direction) and two sets of glide lines, diagonal and non-diagonal. See next Figure.
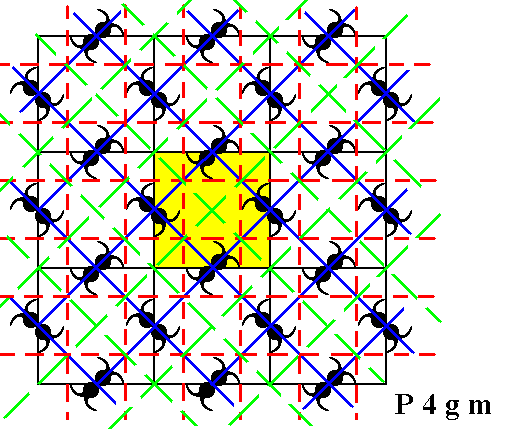
Figure 2. Periodic two-dimensional pattern according to the Plane Group P4gm. The pattern must be considered as indefinitely extended in 2-D space. The pattern contains two sets of mirror lines (dark blue solid lines) and two sets of glide lines : diagonal glide lines indicated by green dashed lines, non-diagonal glide lines (in the horizontal and vertical directions) indicated by red dashed lines.
We're now going to eliminate glide translations till our resulting motif has 4mm point symmetry. It can then represent the Complex Motif. We eliminate a translation involved in a glide, i.e. we undo a glide translation, by copying the motif pattern (taking a part is sufficient, because the pattern is periodic) and shift that copy parallel to the particular glide line of which we want to eliminate the translational component, over half that unit cell dimension that is parallel to the given glide line, and then superimpose the shifted copy onto the original. In this way the structure is telescoped back, and motif units that were separated by the glide line are now again aligned.
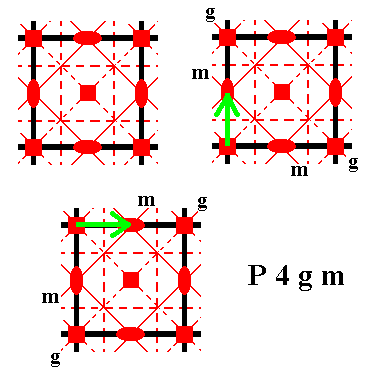
Figure 3.
Top left : The symmetry content of a unit cell of the pattern according to the Plane Group P4gm.
Top right : A vertical copy-shift-superimpose operation in order to undo the vertical glide translations, will copy the mirror line m--m onto the the glide line g--g, turning it into a mirror line.
Bottom : A horizontal copy-shift-superimpose operation in order to undo the horizontal glide translations, will copy the mirror line m--m onto the the glide line g--g, turning it into a mirror line
We will now start to undo the non-diagonal translations of the pattern of Figure 1, a 2-D pattern of motifs, according to the Plane Group P4gm.
The next Figures are about the undoing of the vertical glide lines.
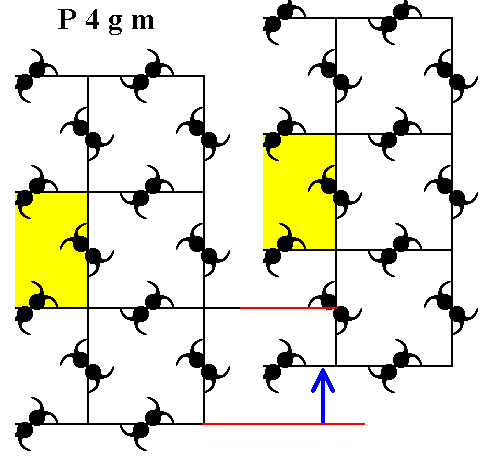
Figure 4. A copy of the pattern is made, and shifted vertically over half the length of a side of the unit cell, indicated by the blue arrow.
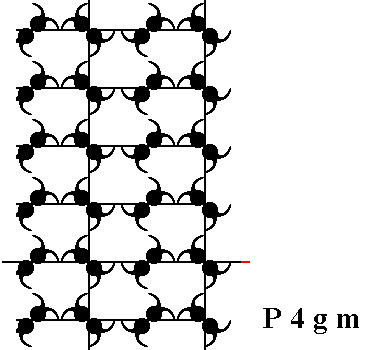
Figure 5. The shifted copy is superimposed onto the original.

Figure 6. The resulted pattern is extended according to its inherent periodicity.
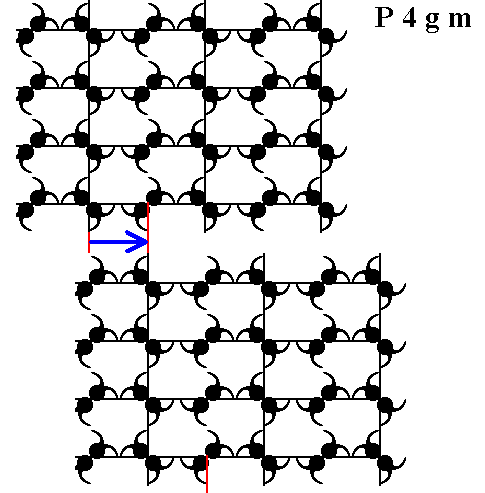
Figure 7. Of the just obtained result (Figure 6) a copy is made, and shifted horizontally according to the arrow over half the length of a side of a unit cell.

The pattern obtained in Figure 8 is still periodic. So we still have to eliminate the simple translations (Recall that simple translations are just translations, they are not associated with a glide line or screw axis). In our result we see black figures being repeated all over. Well, when we isolate one such figure together with its corresponding background, we have obtained the Complex Motif of the P4gm pattern (and because only its point symmetry matters it represents the Complex Motif of e v e r y motif pattern according to P4gm). Indeed our result is the Complex Motif : Because the symmetry of the Crystal Class has already been reached, namely 4mm, we do not have to consider the diagonal glide lines.
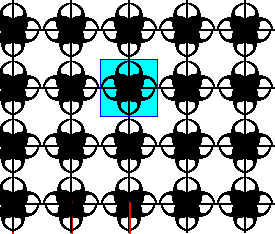
The next Figure, finally, gives the Complex Motif.

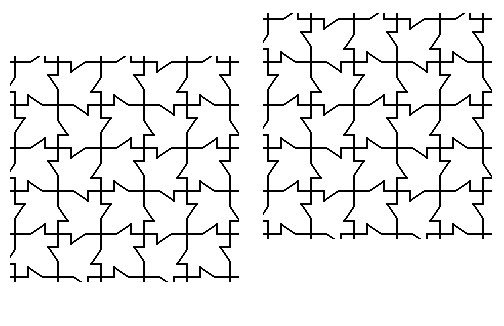
It is instructive to again derive the Complex Motif from a pattern with different motifs but still belonging to the same Plane Group P4gm. It is a two-dimensional pattern of maple leaves, that was considered earlier, namely in Part One and Part Two of the present series of documents. See next Figure.
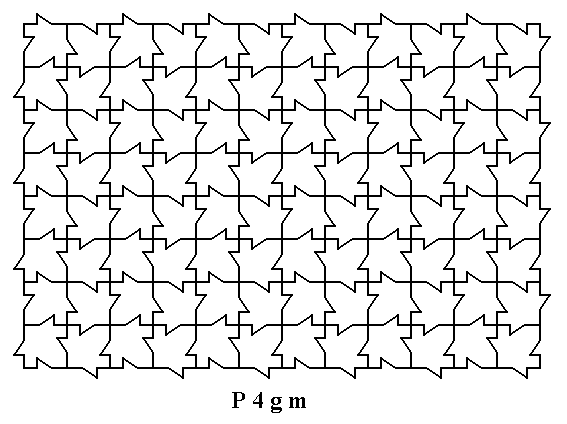
The periodicity of this pattern is based on the Square Net :
The configuration of the glide lines in this maple leaf pattern (and of other symmetry elements) is of course the same as was indicated above : Figure 2.
The result of the superposition is shown in the next Figure.
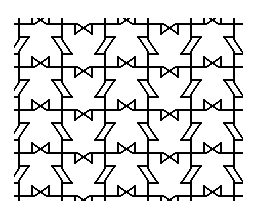
We see that this result is the same as the one that was obtained earlier, in Part Two (Figure 27 there) of the present series of documents. There we concentrated on the immediate surroundings of one lattice node only.
With the obtained result we now do the same (copy-shift-superimpose) with respect to the horizontal glide translations :
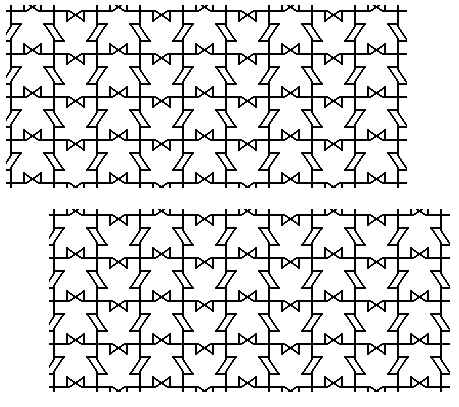
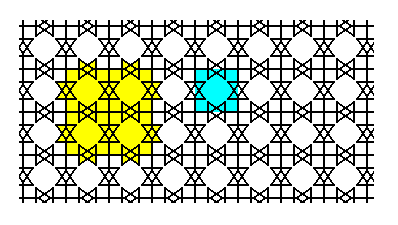
In Figure 18 it is evident that a copy-diagonal-shift-superimpose operation (in which the diagonal shift has the same length as half a unit cell side) will not change the pattern any further, because the shifted copy will coincide with the original.
It is instructive to compare the result of Figure 18 with a result obtained earlier in Part Two (Figure 31a there) of the present series of documents :
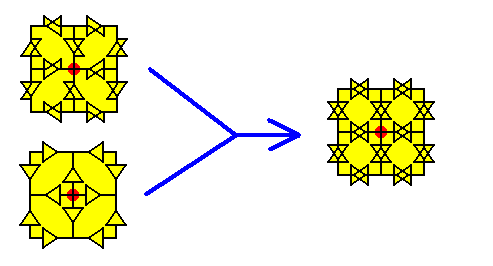
Figure 18a. Result of the explicit elimination of the glide translations of the pattern of Figure 11 (maple leaf pattern, according to P4gm) by sucessively undoing the diagonal, vertical and horizontal glide translations and then superimposing the results, while concentrating on the immediate surroundings of one lattice node only.
We see that the two results are identical, not only with respect to the symmetry (4mm), but also with respect to the shape of the resulting motif. As is evident from Figure 18, we already have reached the 4mm symmetry : Motifs with 4mm symmetry are repeated. When we isolate such a motif plus its corresponding background, i.e. if we eliminate all simple translations, we end up with the Complex Motif.
Above, we executed the copy-horizontal-shift-superimpose operation onto the result of the copy-vertical-shift-superimpose operation. In Part Two (Figure 30 there) of the present series of documents, on the other hand, we eliminated the horizontal translations -- while concentrating on the immediate surroundings of one lattice node only -- not from the result of the elimination of the vertical glide translation, but from the initial pattern (like was done with respect to the vertical glide translations). It is instructive to execute the copy-horizontal-shift-superimpose operation not on the result of the corresponding vertical operation, but on the initial pattern (Figure 11) :
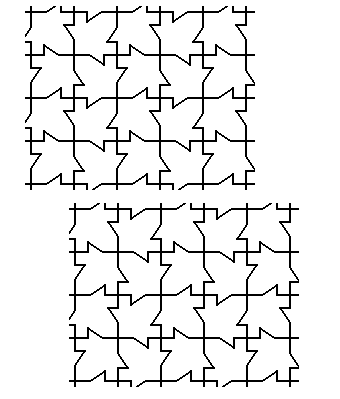
Figure 18b. A copy is made from the pattern (P4gm) of Figure 11. The copy is shifted horizontally by half the length of a side of the unit cell.

Figure 18c. The shifted copy of the previous Figure is superimposed onto the original. An area, within the region where the superposition actually has taken place, is highlighted (blue and green) for comparison with earlier results.
Although we do not need to consider the d i a g o n a l glide translations, it is nevertheless instructive to investigate them.
We begin with the undoing of the diagonal translations from our just obtained result. This means that we copy the pattern of Figure 18, shift the copy by half a unit cell diagonal, and superimpose the shifted copy onto the original. The next Figure gives the result of all this.
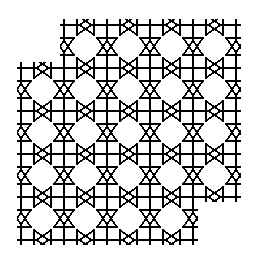
Figure 19. Copy-shift-superimpose operation in the diagonal direction executed on the result obtained in Figure 18. As was to be expected, the pattern doesn't change because the begin and end points that determine the shift vector are equivalent.
The next Figure shows the result of the copy-shift-superimpose operation in the diagonal direction (in which the amount of the shift is equal to half a unit cell diagonal), executed on the initial pattern, i.e. on the pattern of Figure 11.
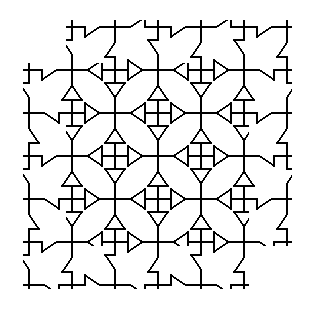
Figure 20. Result of the diagonal copy-shift-superimpose operation, in which the amount of shift is equal to half a unit cell diagonal.
In the next figure we isolate the area that was actually involved in the superposition (in fact of course, always the whole infinite pattern is involved in the superposition).
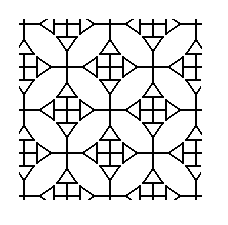
Figure 21. The area actually involved in the above diagonal copy-shift-superimpose operation.
This is the same result as was obtained earlier in Part Two (Figure 23a there) of the present series of documents, where we successively eliminated the NW-SE ( = Northwest-Southeast ) diagonal glide translation and the NE-SW diagonal glide translation, and concentrated on just the immediate surroundings of one particular lattice node. See the next two Figures that compare them :
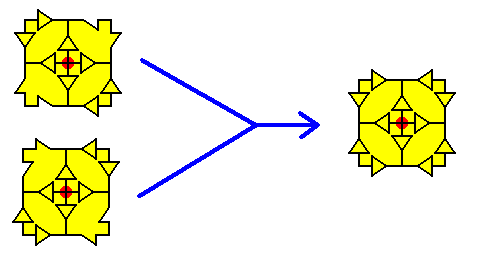
Figure 21a. Earlier result of the successive elimination of the two diagonal glide translations.

Figure 21b. An area highlighted (yellow) in an extension of the image of Figure 21 (i.e. by having executed the operations on a larger initial area of the maple leaf pattern of Figure 11). We see that our earlier result is identical to our present result.
Also here (in Figure 21 of the present document) we have already reached the 4mm symmetry. The resulting motif is, however, different from the one we obtained by eliminating the vertical and horizontal glide translations. Both motifs can equally well yield our sought for Complex Motif.

Figure 22. A larger area of the pattern obtained in Figure 21, in order to clearly detect the repeated unit.
In this larger area we can easily detect equivalent points. When we connect these points we can detect a repeating unit. See next Figure.

Figure 23. In the larger area of the pattern, as obtained in Figure 22, we can detect equivalent points. When we connect these points we get a net which then indicates the repeating unit. One such unit is highlighted (light blue).
Isolating the highlighted motif of Figure 23 eliminates all simple translations, and we finally end up with the Complex Motif. Its symmetry is 4mm. It is the same symmetry as we obtained earlier (Figure 18 but also Figure 10).
The simplest planimetric figure that expresses this symmetry geometrically is the Square. So the Square is the promorph or planimetric basic form of all 2-D crystals belonging to the Plane Group P4gm and with it to the 2-D Crystal Class 4mm.

Figure 24. The Square as the promorph or planimetric basic form of all 2-D crystals belonging to Plane Group P4gm and with it to the Class 4mm.
It is instructive to know that when we subject the result with respect to the diagonal glide translations, as in Figure 22, to the copy-non-diagonal-shift-superimpose operation, the result will be identical to that obtained here in Figure 18 and also to our earlier result in Part Two (Figure 31a there) of the present series of documents, where we successively eliminated the NW-SE diagonal glide translation and the NE-SW diagonal glide translation, the vertical and horizontal glide translations, and concentrated on just the immediate surroundings of one particular lattice node.
Summarizing the present and earlier results, gives the following listing with respect to the elimination of glide translations of the P4gm maple leaf pattern (Figure 11) (All the procedures of the mentioned earlier (Part Two) results concerned one and the same chosen particular, but in no way special, lattice point (node)) :
It is perhaps instructive to indicate equivalent areas in the maple leaf pattern ( Figure 12 ) and the pattern of Figure 1. They are different pattern, but their symmetry is wholly the same : Their Plane Group is P4gm and their Point Group is 4mm. In the next Figure we can see what in the maple leaf pattern corresponds to the motifs s.str. of the pattern of Figure 1.
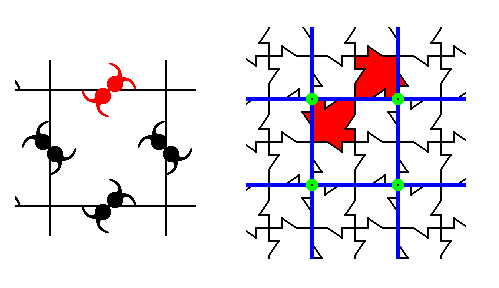
Figure 25. The correspondence of motifs in the pattern of Figure 1 to those of Figure 12 (maple leaf pattern).
Left image : Fragment of the motif pattern of Figure 1. One motif s.str. is highlighted (red).
Right image : Fragment of the maple leaf pattern of Figure 12. A part of it, corresponding to the highlighted motif in the left image, is also colored red.
To continue click HERE to investigate the next Plane Groups with respect to the Complex Motif of 2-D periodic patterns according to those Plane Groups.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola
back to Homostaura anisopola, Heterostaura
back to Autopola oxystaura and orthostaura
back to Allopola (introduction)
back to Allopola amphipleura and zygopleura
back to the Basic Forms of Cells I
back to the Basic Forms of Cells II
back to the Basic Forms of Organs
back to the Basic Forms of Antimers
back to the Basic Forms of Metamers
back to the Basic Forms of Persons
back to the Basic Forms of Colonies
back to the first part of the Preparation to the Promorphology of Crystals
back to the second part of the Preparation to the Promorphology of Crystals
back to the third part of the Preparation to the Promorphology of Crystals
back to the fourth part of the Preparation to the Promorphology of Crystals
back to the fifth part of the Preparation to the Promorphology of Crystals