Although the above discussed homopolar stauraxonians evoke some special interest because their axial systems relate to three Crystal Systems, the Tetragonal, Hexagonal and Orthorhombic Systems, they, and all the forms that we treated of earlier, are not too often discussed (by others), probably because they mainly occur in first- and second-order morphological individuals (cells and organs), and because as basic form of whole organisms they are limited to only a few types of lower orgamisms, mainly Radiolarians. Much more attention, with respect to basic forms is devoted to organismic shapes that belong to the heteropolar stauraxonians, which we will call H e t e r o p o l a for short.
Indeed the heteropola supply the general basic forms to all higher (whole) animals and (whole) plants, and so they provide the largest and most conspicuous shapes of the whole organismic world.
The general properties of the p y r a m i d are known from Stereometry. It is a polyhedron that is enclosed around a polygon as basis, by triangles in such a way that these triangular sides (pleura) all meet in one point (apex).
For the discussions to come it is in many respects more convenient to consider the truncated pyramid as the basic form of the heteropolar stauraxonians instead of the whole pyramid. Such a truncated pyramid is truncated along a plane that is parallel to its base. Because the pyramid only expresses the differentiation of several cross axes and the unequality of the poles of the main axis, it is immaterial whether we signify with the term a p e x or a p i c a l s u r f a c e the pointed far end of the whole pyramid or the surface of truncation of the truncated pyramid. This apex or apical surface we will biologically denote as aboral area ( A r e a a b o r a l i s, A n t i s t o m i u m ). The basis of the pyramid on the other hand we will biologically call oral area ( A r e a o r a l i s, P e r i s t o m i u m ). The axis of the pyramid, i.e. the line going from the top of the pyramid to its bottom (base) in such a way that it is perpendicular to the base, is biologically called the m a i n a x i s or longitudinal axis ( A x i s l o n g i t u d i n a l i s, A x o n p r i n c i p a l i s ) of the body.
The number of lateral sides of the pyramid is equal to the number of antimers of which the body of the heteropolar stauraxonians is composed, and this homotypic basic number is in turn equal to the number of cross axes that meet in the center.
When the homotypic basic number is even (2n), as in Coelenterates (for example in jelly fishes, medusae), or as in the four-fold flowers of higher plants, half of the cross axes (n) is radial, half (n) is interradial. When, on the other hand, the homotypic basic number is uneven (2n-1), as in Echinoderms (starfishes and the like), or as in the three-fold and five-fold flowers of higher plants, all cross axes
(2n-1) are composed of a radial and an interradial part, i.e. they are semiradial. These three sorts of cross axes correspond to the three sorts of meridian planes, that contain the main axis and a cross axis, the radial, interradial and semiradial cross planes, which are already treated of above when introducing the Stauraxonia. Also the construction of the cross axes was already explained there.
The r a d i a l a x i s (Radius, and as such half a cross axis) is simply obtained by drawing a line in the median plane of an antimer perpendicular to the main axis and intersecting its mid-point, while an i n t e r r a d i a l a x i s (Interradius, and as such half a cross axis) is obtained by drawing such a line in the boundary plane between to adjacent antimers. A s e m i r a d i a l c r o s s a x i s is composed of a radius and an interradius lying opposite to each other. See next Figures.

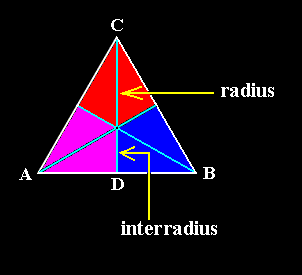
Figure 1. A three-sided regular polygon (Equilateral Triangle) as representing the base of a regular three-fold pyramid (it can also represent a plane, parallel to the base and containing the mid-point of the main axis). The colored areas indicate the three antimers. The three bisectors of the triangle represent the three semiradial cross axes, for example CD. The upper half of the cross axis CD is a r a d i u s, while its lower half is an i n t e r r a d i u s.
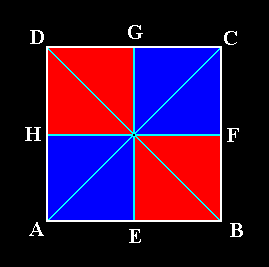
Figure 2. A four-sided regular polygon (Square) as representing the base of a regular four-fold pyramid (it can also represent a plane, parallel to the base and containing the mid-point of the main axis). The colored areas indicate the four antimers. AC and BD represent the radial cross axes, each one composed of two radii. HF and EG represent the interradial cross axes (the planes containing the latter and containing the main axis are the boundary planes between two adjacent antimers). Each interradial cross axis is composed of two interradii.
In the heteropolar as well as in the homopolar stauraxonians the mid-lines of the antimers are clearly indicated by the edges of the pyramid. The boundary lines of the antimers, on the other hand, lie in the lateral sides of the pyramid. As radial area ( A r e a r a d i a l i s ) we can distinguish in many heteropolar stauraxonians a certain part of two adjacent lateral sides of the pyramid (at both sides of the respective edge of the pyramid), for example representing the ambulacra petaloidea of the Echinoderms, or the petals of polypetal higher plants. On the other hand we have the interradial area ( A r e a i n t e r r a d i a l i s ), that extends between two radial areas of the same lateral side of the pyramid, for example representing the interambulacra of the Echinoderms, or the sepals, that alternate with the petals, in higher polypetal plants.
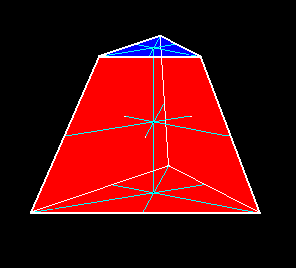
Figure 3. A single straight three-fold truncated pyramid. It consists of five faces ( 4+n, where n = 1 ). The cross axes originate in the center of the pyramidal body, but are redrawn on the top and bottom faces.
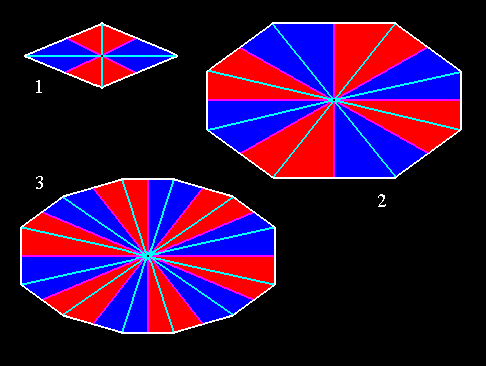
Figure 4. Some amphitect polygons representing bases or equatorial planes of possible amphitect pyramids. Radial and interradial cross axes and antimers are indicated.
(1). Four-sided amphitect polygon (Rhombus). Four antimers.
(2). Eight-sided amphitect polygon. Eight antimers.
(3). Twelve-sided amphitect polygon. Twelve antimers.
Radial cross axes are indicated in blue. Interradial cross axes are indicated in pink. The radial cross planes ( containing the radial cross axes ) are the median planes of the antimers (i.e. in each case of two opposite antimers). The interradial cross planes ( containing the interradial cross axes ) are the planes separating adjacent antimers. The antimers are indicated in red and dark blue.
As we can derive the heteropolar stauraxonians from the homopolar stauraxonians by dividing them up along the equatorial plane of the bipyramid (obtaining two single pyramids), this also applies to both divisions of the homopola and heteropola : The Homopola isostaura (regular bipyramids) are just a union (with their bases) of two congruent individuals belonging to the Heteropola homostaura (regular pyramids), and in the same way we can interpret the Homopola allostaura (amphitect bipyramids) as a twin form consisting of two congruent individuals of the Heteropola heterostaura. We must however qualify this comparison by the fact that only the basic form of the Heterostaura a u t o p o l a is a w h o l e amphitect pyramid, while that of the Heterostaura a l l o p o l a is h a l f an amphitect pyramid. So we must divide an individual of the Homopola allostaura twice in order to obtain a member of the Heterostaura allopola (The mentioned autopola and allopola will be discussed further down).
Our Homostaura correspond to the so-called regular radial animals, i.e. absolutely regular radiates with congruent antimers, for example most medusae (jelly-fishes), star-fishes, etc. Our Heterostaura, on the other hand, partly comprise the majority of so-called "bilateral-symmetric" animals (the [ Homopola ] Allostaura, which are also, in a sense, bilateral-symmetric, excluded), partly the so-called "irregular or symmetric radiate animals", partly, finally, the so-called "biradiate animals".
As in the animal kingdom, also in the plant kingdom the majority of all third- and fifth-order form individuals (antimers and persons) belong to the Heteropola Stauraxonia. Most higher plant persons, the sexually differentiated (flower off-shoots) as well as the sexually non-differentiated leaf off-shoots, allow, as most animal persons, promorphologically to be reduced to the pyramid. The same is true of most antimers that constitute these persons. In contrast to this the heteropolar stauraxon form is less common in fourth- and six-order form individuals, and even more uncommon in first- and second-order form individuals. It is consequently also rare among Protists.
The insight of the fact that indeed the pyramid must be assessed as the stereometric basic form of all Heteropola, and that consequently the overwhelming majority of all animal and plant persons and antimers can be promorphologically reduced to the pyramid as their common basic form (promorphont), is as important, as it is in many cases hard to yield (from a morphological investigation), and indeed until now ( Haeckel, 1866 ) not found. In a relatively simple and certain way one will reach that insight, that explains the difficult form relationships, by a promorphological investigation of the persons of radiate animals, the Echinoderms (star-fishes and the like) as well as the Coelenterates (jelly-fishes and the like). And even here their pyramidal basic form remained hidden ( Haeckel, 1866 ).
Nothing is probably more significant than the critical consideration of the continuous concerns of the great J o h a n n e s M ü l l e r (with whom Haeckel was in contact at the beginning of his career), to understand the basic forms and the homologies of the Echinoderms. Despite his unsurpassed knowledge of this interesting as well as difficult animal group, and despite his remarkable efforts, to establish a morphological insight with respect to these animals, and to yield a true "philosophy of Echinoderms", he did not succeed to find the key of the problem ( Haeckel, 1866 ). This key consists in the insight that the basic form of the regular Echinoderms is a five-fold regular pyramid, while that of the "bilateral-symmetric" Echinoderms is half of a ten-fold amphitect pyramid.


Figure 5. Skeleton, i.e. the internal shell ( "sand-dollar" ) of a "bilateral-symmetric" Echinoderm, a sea urchin.
Top image : dorsal view.
Bottom image : ventral view.
The outline of the skeleton and the texture of its ventral part shows that this sea urchin is not regular.
The next figures show how to determine the stereometric basic form of this sand-dollar.
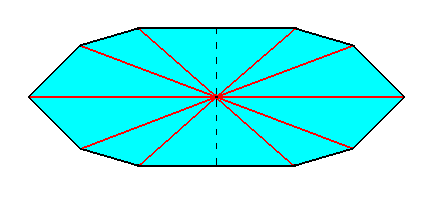
Figure 6. Equatorial plane of a ten-fold amphitect pyramid. The dashed line indicates our next to be executed removal of one half. Radial cross axes are indicated in red
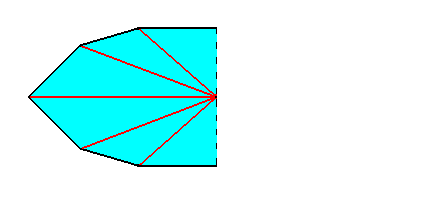
Figure 7. One half of the equatorial plane. It now represents the equatorial plane of half a ten-fold amphitect pyramid.
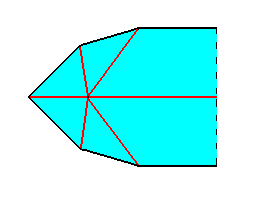
Figure 8. Equatorial plane of half a ten-fold amphitect pyramid, as depicted above. We have shifted the axial system to the left.
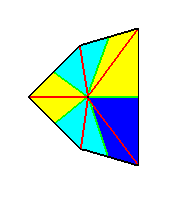
Figure 9. We have altered the above image without altering its symmetry. The five antimers are indicated by coloration.
We can clearly see that in this drawing we correctly express the symmetry (as far as its horizontal axes are concerned) of the above depicted sea urchin according to its internal skeleton. The two images of the skeleton (Figure5) clearly show the heteropolarity of the animal's main axis.
As such the animal's basic form belongs to the Heteropola heterostaura (single whole or half amphitect pyramids). Within this group it belongs to the Heterostaura allopola (half amphitect pyramids), and because it has more than two antimers it belongs to the Allostaura amphipleura, and, finally, because it has precisely f i v e antimers, it belongs to the Allostaura p e n t a m p h i p l e u r a.
In the image of this Figure we see that not all cross axes are straight lines (and thus also some meridian planes are bent), but this is immaterial : we must imagine the axial system to originate from the mid-point of the main axis, and then radiating outward from that point.
Radii are indicated in red. Interradii are indicated in green.
J o h a n n e s M ü l l e r assessed the basic form of the regular Echinoderms, instead of being a five-fold regular pyramid, as being a s p h e r e with a determined axis, the poles of which (Mouth Pole and Apical Pole) are unequal, and that from the mouth pole radiate five radii which, as more or less complete meridians, run to the apical pole. However, such a "sphere" is indeed nothing else than a five-fold regular pyramid, and the five "meridians" or surface radii (Ambulacra) are the five edges of the pyramid.
As soon as one bases oneself on this insight, the difficult homologies of the Echinoderms -- says Haeckel -- will be resolved, clearly and easily.
First and foremost also here, like in all promorphological inquiries, should be the information about the principal axes and their poles. Then should follow an inquiry concerning the differentiation relations between the several axes and their poles, resulting in the construction of the sides of the pyramid. It should strongly be discouraged to base the promorphological inquiry on a consideration of the s u r f a c e q u a l i t y of any one organism without considering the axes and their poles. If one wants to find the basic form of persons or metamers (fifth- and fourth-order form individuals), then first of all information about their composition of a n t i m e r s is needed, and then information about their differentiation. If, on the other hand, an antimer itself is the object of promorphological investigation, then we should first of all look for their composition of similar parts and their spatial relationships. The same holds for any such investigation of second- and first-order form individuals (organs and cells).
Just as clear as in the case of persons of most Echinoderms and Coelenterates, the pyramid, as heteropolar stauraxon form, is expressed in most sexual persons (flower off-shoots) of higher plants. It is expressed by the number of petals (and sepals), i.e. the number of antimers. Much harder, on the other hand, is to extract relevant information from the asexual persons of the higher plants, the leaf off-shoots. If in such cases the stalk clearly is three-fold or four-fold, i.e. showing three, respectively four edges, or when the leaves are clearly arranged in three or four meridian planes (cross planes), then also here it is easy to determine the composition of such a person out of three, repectively four, antimers. Such a clear morphology is, however, often not the case, because the several leaf rings originating from the elongated stalk members of the off-shoot, are not, as in flower offhoots, placed -- with shortened stalk members -- above each other such that the corresponding leaves lie in meridian planes, they lie instead on a spiral. In such cases the cross axes are often hard to detect. Maybe they are in many cases determined by the number of pith radii and -- placed with them in alternation -- the (number of) vascular bundles of the stalk, that, as it seems, in many higher plants divide the stalk in a very regular way into antimers.
The important form group of the homostaur heteropolar stauraxonians, that we will call h o m o s t a u r a for short, comprises the majority of the so-called "radiate forms or regular forms" in that sense at least in which most morphologists use (1866) this equivocal term.
The regular single pyramid, which is the basic form of all Homostaura, is more or less clearly expressed especially in the fifth-order form individuals (Persons), in the majority of the so-called "radiate animals" (in most Coelenterates, and in a large part of the Echinoderms) and of the higher plants. In the case of the mentioned animals of course only the strictly regular radiate forms do belong here, while the "irregular" or bilateral-symmetric Echinoderms must be excluded and relegated to the Heterostaura, and of the Coelenterates all Ctenophora and some others (must be excluded). Of the Protists a part of the Radiolarians belong to the Homostaura. They are not persons but (single) cells. Of the plant kingdom we must reckon the majority of off-shoots in higher plants and in many lower plants to the Homostaura, although here very often a seeming homostaur turns out to be a heterostaur on closer inspection.
The general properties of the regular pyramid are so well known from Stereometry and also partly already considered above, that here we need only succinctly to recapitulate some of the most important characteristics of this basic form in relation to its construction in animal and plant organisms, and to determine how to apply it.
As the b a s e
( A r e a b a s a l i s ) of the regular pyramid, which in the present case always is a regular polygon, we must, in the homostauric animal forms, determine the oral end of the animal's body ( A r e a o r a l i s, P e r i s t o m i u m ), that is to say, for example, in the regular Echinoderms and Coelenterates that region of the body where the mouth is to be found. In the flowers of higher plants it corresponds to the often bell-shaped opening of the flower. Regarding the off-shoots (persons) of all plants we will always interpret its free end (vegetational end) as basal or oral end (Peristomium). And this implies that we, maybe counterintuitively) consistently interpret the opposite end of the plant's root as oral end.
To the A p e x ( A r e a a p i c a l i s ), on the other hand, i.e. to the pointed end of the whole regular pyramid, or to the section, parallel to the base, of the truncted regular pyramid, should, in the homostauric animal forms, correspond the body end that is opposite to its mouth end, and which we will denote as a b o r a l e n d or a n t i s t o m i a l s u r f a c e ( A r e a a b o r a l i s, A n t i s t o m i u m ). In the Echinoderms it is the apical field in which often lies the anus. In the sedentary Coelenterates it is the proximal body end that is attached to some external substrate, while in those that swim freely it is the convex surface that is almost always directed upwards, and that is incorrectly called "back". In those higher plant flowers, and their analogues in lower plants, that have the regular pyramid as their basic form, it is their non-free, attached, often by means of a stalk, end, lying opposite to the oral end, that corresponds to the aboral surface or apex. So in all off-shoots (persons) of all plants we will consistently interpret the sedentary end, i.e. the sedentary pole of the axial organ, as the apical or aboral end (tip of the whole pyramid, or section of the truncated pyramid), that is to say, in the simple shoot or in the main shoot of colonies (Cormi) the root, while in lateral off-shoots their sedentary ends, i.e. the ends by which they are attached to the main shoot.
The homotypic basic number ( = number of antimers) of the Homostaura is determined by the number of sides of the regular polygon that is the basis of the regular pyramid, or by the equal number of sides (lateral faces) of the regular pyramid. This number can be three or more. The lateral faces are all congruent isosceles triangles. The cross axes either are (when the mentioned number is uneven) all equal (They are semiradial), or (when that number is even) alternately equal (radial and interradial). If we consider the t r u n c a t e d regular pyramid as basic form, then the main axis (in Geometry simply called "axis" of the regular pyramid) is a line that connects the centers of the top and bottom faces (i.e. apical and basal planes) of that pyramid. If, on the other hand we consider the w h o l e pyramid as the basic form, then the main axis is the perpendicular running from tip to base, ending up in the center of the latter. In the first case the animers are truncated, while in the second case they are whole four-fold pyramids, of which the base is a trapezoid (See Figure 10).

The edges of the regular pyramid represent the mid-lines of the antimer surfaces, which as such do indeed protrude outwards in most animal and plant forms that belong to the present group. The boundary lines of the antimer surfaces on the other hand, correspond to the mid-lines that halve the lateral faces of the regular pyramid into two congruent rectangular triangles.
The form group of the Homostaura divides in so many subspecies as the number of pyramid sides (and thus according to the homotypic basic number) can be. Although this number is, it is true, a priori unlimited, there are only a few numbers realized in Nature. In the overwhelming majority of homostaurs, in the animal as well as in the plant kingdom, we only see it to be three, four, five, or a low multiple, in most cases a two-fold (duplum) thereof, resulting in six, eight, less common ten, antimers to be present. Much more uncommon, and only as a kind of exception, another homotypic basic number is present, for example seven in some higher plants, and eleven in some star-fishes. In these cases, however, the number is often either not constant within the species, as in some star-fishes, or one can conclude from the individual development or from close relatives having a different number (mostly five) that the number seven, or the other number that is not by division reducible to three, four or five, is not the primitive (i.e. original) homotypic basic number, but secondarily originated from the latter by variation and adaptation. Where higher numbers appear to be present, they either can be derived by consideration of the mentioned conditions, or by a multiplication of three, four or five. And so we can establish all this as an important law of general Promorphology, that reads :
The homotypic basic number, or number of antimers, of the Homostaura (the number of sides of the pyramid) always is three, four or five, or a multiple thereof, mostly a duplum.
When other (prime) numbers seem to occur, we can almost always demonstrate that we either have to do with an inconstancy of the number, or with its secondary nature, i.e. having originated from the three mentioned numbers by abortion.
In many Homostaura, where the number of antimers seems to be a multiple of three, four or five, one can often demonstrate, from the individual development or from the number of certain (especially internal) organs, that the primitive number is in fact the simple three, four or five, and that only later on a multiplication (mostly just a doubling) took place. This is the case in many higher plant flowers, where often in one and the same flower one leaf ring (and thus one metamer) shows the single basic number, while other leaf rings of that same flower show a different multiple of that number. Also in homostauric animals we can observe this phenomenon, for example in many medusae. In all such cases the lowest number seems to be the basic number, while the multiples of it are secondary multiplications.
We must however distinguish these cases from those in which a multiple of three, four or five is the original basic number, that either as such remains simple during all of the organism's life, or is then multiplied. Also this case is very common in animals and plants. Probably it is in all such cases just the duplum (the two-fold), never the triplum (the three-fold) or a higher multiple of three, four or five, that appears as the original primitive number of antimers. Because in such cases already in the initial stadium of the individual development is an aggregate of six, eight, ten antimers, we cannot assess the homotypic basic number as three, four, five, but as the duplum thereof.
The determination of the homotypic basic number in homostauric organisms often encounters difficulties by reason of the fact that this number seems to be different in different metamers of a person (for instance in the different leaf rings of an off-shoot). Very often we see this in higher plant flowers where seldom all leaf rings (sepals, petals, pollen threads, etc) of a flower show the same number, and where especially the female genitals generally are subjected to a greater or lesser reduction. In contrast to the homostauric plants the homostauric animals behave differently in this respect. All their organ rings (metamers) show as a rule the same basic number or a multiple thereof. Numerical reductions in some rings are here rare exceptions and almost always related to the transition from the homostauric basic form into the heterostauric basic form.
On the basis of the above considerations we can reduce the species of the Homostaura, the number of which is in accord with the number of different homotypic basic numbers and as such unlimited, to only a few. Of the many possible basic numbers only remain : three, four, five, six, eight, ten as the genuine determinants of homostauric species, while as rare exceptions seven and nine. Those rare cases in which we encounter a number higher than ten can be grouped together, because in these cases the basic number itself is variable within the (biological) species.
These different species of Homostaura naturally divide into two groups, namely one group characterized by an e v e n basic number, and one characterized by an u n e v e n basic number. This distinction, that as such seems insignificant, is important because certain very important differences in the axial relationships go together with it, exerting much influence on the whole shape. For the time being it can be said that the Homostaura with an uneven homotypic basic number, for example three, five, more often and definitely transform into the heterostauric form and differentiate, than the Homostaura with an even number, for example four, six, do. Among animals it is the five-fold Echinoderms, among plants the three-fold orchids, that show very clearly a series of most remarkable transitions from pure homostauric forms to completely heterostauric forms (bilateral symmetry).
The Homostaura with an e v e n b a s i c n u m b e r (2n) are called I s o p o l a, because in them both poles of each cross axis are equal. Both poles either end up at the mid-line of two opposite antimers, or at the boundary line of two opposite antimer pairs. Because of this, as has been said earlier, there are two types of cross axes and cross planes present, alternating with each other, n radial and n interradial. Each radial cross plane is the median plane of two opposite antimers, each of which is divided into two symmetrically equal three-fold pyramids by that plane. Each interradial cross plane is the boundary plane of two congruent antimer pairs. The most common homotypic basic number that belong to these Isopola is four, then six, then eight. Very seldom ten or more (10+2n).
The Homostaura with an u n e v e n b a s i c n u m b e r (2n-1) can, in contradistinction, be called, A l l o p o l a, because in them the two poles of each cross axis are unequal. One pole ends up at the mid-line of an antimer, the other at the boundary line of the opposite antimer pair. Therefore here all (2n-1) cross axes and cross planes are of one and the same type (semiradial), each one half radial, half interradial (or differently expressed : one half is a radius, the other half an interradius). Each individual semiradial cross plane is for one half the median plane of an antimer, for its other half the boundary plane of the opposite antimer pair. The most common homotypic basic number is five, then three. Very seldom seven, nine or more (9+2n).
On Composite Flowers and the like
Considering the r e g u l a r p y r a m i d as basic form of the Stauraxonia homostaura, certain very common organic structures, that seem to be clear materializations of this basic form, are the sexual persons of higher plants, i.e. f l o w e r s. Their number of petals seems to determine the basic form of those persons. We see three-fold, four-fold and five-fold flowers, and these do not present any difficulty in determining their basic form (promorphont). But in addition to these low-radiate flowers we also know of multiradiate flowers, like daisies or sunflowers. They thus seem morphologically be based on pyramids with many sides, i.e. pyramids with a high homotypic basic number indicating the number of antimers. But on closer inspection each of these multiradiate 'flowers' turns out to be composed of many small flowers -- florets -- that are integrated into one compact whole. Therefore they belong to the plant group called Composites. When we inspect a sunflower (which belongs to that group), we can see how the florets are ordered within the whole. This order is especially clearly visible when the florets have turned into seeds : It seems to consist of several interlaced s p i r a l s . When we want to determine the b a s i c f o r m of such a composite flower, the presence of spirals seems to oppose their having a homostauric basic form. Indeed it is, and will remain difficult to determine its basic form. Haeckel (1866) does not assess them as homostaurs, and maybe he is right.
Let us analyse these composite flowers further (We base our exposition mainly on STEWART, I., 1995, Nature's Numbers, pp. 135.).
The numbers of petals in composite flowers, petals that are placed on the outer circular edge of such a flower, all seem to belong to the following series :
8, 13, 21, 34, 55, 89, 144, etc.
This series is in fact part of a very famous mathematical series of numbers, discovered by Fibonacci in 1202.
The (whole) series can be generated when the numbers 1, 1 are given as starting numbers (i.e. they form the initial condition of the process generating the series). So the first two numbers of the series are 1, 1. Now the actual generation can proceed when we give the appropriate r u l e that should be applied (first) to those initial numbers. This rule reads : Every next number of the series is the sum of the two previous ones. Because this same rule is applied again and again we have to do with a recursive system, generating a series of numbers. Well, in proceeding as described the third number obviously will be 2 (1+1). So we have 1, 1, 2. The fourth number is 3 (1+2), the fifth number is 5 (2+3), etc. In this way we obtain the following series of numbers which is called the F i b o n a c c i S e r i e s :
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
When we examine the giant sunflower we see a ring of conspicuous petals placed around a pattern of florets. These florets are arranged in two intersecting families of spirals, one winding clockwise, the other counterclockwise. In some species of sunflower the number of clockwise spirals is 34, and the number of counterclockwise spirals is 55. Both are Fibonacci numbers, occurring consecutively in the series. These numbers, and also others, but always belonging to two consecutive Fibonacci numbers, not only appear in sunflowers, but also in their relatives, daisies, marguerites and all other flowers of the Composites, but also in pine cones and pineapples. The latter have 8 rows of scales -- the diamond-shaped markings -- sloping to the left, and 13 sloping to the right, again two consecutive Fibonacci numbers. In composite flowers, basically, one conspicuous petal terminates each spiral in just one of the two families (of spirals). So the number of these petals is always one from the Fibonacci series.
If genetics can choose to give a flower any number of petals it likes, or a pinecone any number of scales that it likes, why do we observe such a preponderance of Fibonacci numbers?
It seems reasonable to suggest that there is some dynamics in plant growth by which these numbers arise. Let's see that through.
At the tip of the shoot of a growing plant we can see the bits and pieces from which all the main features of the plant -- leaves, petals, sepals, florets, etc. -- develop. At the center of the tip is a circular region of tissue with no special features, called the "apex" [ In Promorphology it is not the apex, but the base (of the pyramid representing the basic form). It is the peristomial pole or Area oralis. ]. Around that "apex", one by one, tiny lumps form, called p r i m o r d i a. Each primordium migrates away from the apex -- or, more accurately, the apex grows away from the lump -- and eventually the lump develops into a leaf, petal, or the like. Moreover, the general arrangement of those features is laid down right at the start, as the primordia form. So basically all you have to do is explain why you see spiral shapes and Fibonacci numbers in the primordia.
It turns out that while the primordia are generated they (seen after the fact) come to lie on a closely wound spiral, going round some 100 times. This spiral, the g e n e r a t i v e s p i r a l, cannot (in contradistinction to the above mentioned spirals) be seen just like that, but is only evident from countings. The next two Figures depict a part of such a generative spiral.
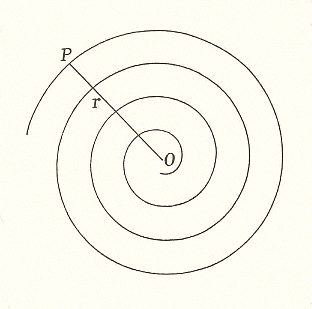
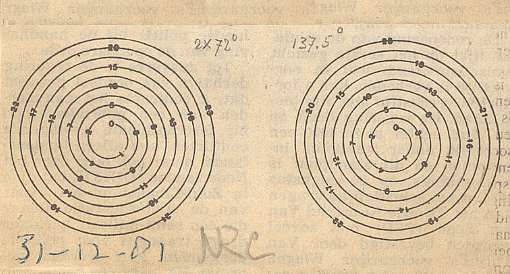
Figure 12. Spiral of Archimedes. Among other things, it is the generative spiral according to the generation and migration of primordia in plants. In the left image the divergence angle between successive primordia is 1440, resulting in a five-fold distribution pattern (of primordia) consisting of five straight radii. In the right image the divergence angle is 137.50, resulting in a five-fold pattern with spiral radii (i.e. one family of five spirals).
The essential quantitative aspect is the angle between successive primordia. When we draw lines from the centers of successive primordia perpendicular to the axis of the shoot we can measure the angles between them. Successive angles turn out to be pretty equal, their common value is called the divergence angle. So the primordia are equally spaced -- in an angular sense -- along the generative spiral. And this divergence angle is usually very close to 137.50. How is this angle related to the Fibonacci numbers, i.e. the number of spirals belonging to one family, and another such number of spirals belonging to the other family, both Fibonacci numbers and moreover consecutive Fibonacci numbers?
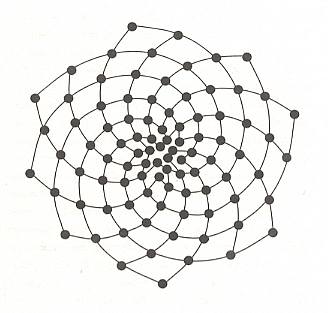
Figure 13. Successive dots arranged at angles of 137.50 to each other along a tightly wound spiral (not shown) naturally fall into two families of loosely wound spirals that are immediately apparent to the eye. Here there are 8 spirals in one direction and 13 in the other -- consecutive Fibonacci numbers.
( After STEWART, I., 1995, Nature's Numbers)
The probable reasons why the golden angle is involved in such plant features can be described as follows : When the primordia (turn out later to) develop into (green) leaves, those leaves together should be maximally exposed to light. So they should not be placed above each other in the sense that they partly or wholly overlap. When, on the other hand, they become florets (which are, however, not totally homologous to leaves) that are going to constitute a single composite flower, it sounds reasonable that they will arrange themselves as compact as possible (into an integrated composite flower). How is such an arrangement possible within the above described way of growing of the off-shoot?
0, 144, 288, 72, 216,
0, 144, 288, 72, 216,
0, 144, 288, 72, 216,
etc.
It is clear that in this way we get five straight radii consisting of primordia or what will become of them. See Figure 12 left image.
In fact, if you use a divergence angle that is a r a t i o n a l multiple of 3600, you always get a system of radial straight lines. So there are gaps between the lines, and the primordia don't pack efficiently. So in order to fill space (within the mentioned way of growing) efficiently, you need a divergence angle that is an i r r a t i o n a l multiple of 3600 -- a multiple by a number that is not an exact fraction ( 90 and 144, that we had just discussed, are rational fractions : 1/4 and 2/5 ). But which irrational number? Numbers are either irrational or not, but -- as STEWART, p.141, says, like "equality" in George Orwell's Animal Farm -- some are more irrational than others. It is already long known that the most irrational number is the golden number. It is "badly approximable" by rational numbers, and if you quantify how badly, it's the worst of them all. So it should be expected that the golden angle should pack the primordia most closely within the context of the way of growing of a plant's off-shoot. It has indeed been found that the golden angle is a consequence of a specific growth dynamics. The time interval of the appearance of the successive primordia is determining in this respect.
Of course in real plants we will not encounter all this in a precise fashion (like it does in models). In particular, in many plants the rate of appearance of primordia can speed up or slow down. In fact, changes in morphology -- whether a given primordium becomes a leaf, a petal, sepal, etc. -- often accompany such variations. So maybe what the genes do is affect the timing of the appearance of the primordia. But plants don't need their genes to tell them how to space their primordia : that's done by the dynamics. Generally, as it seems probable, many organic morphological features, among which the ideal stereometric basic form (promorphont) of organisms and their parts, will be generated by purely physical and chemical forces and mathematical constraints, as do many inorganic analogues. The production and its timing of the specific materials that by themselves exhibit such forces, will be taken care of by the genes of the organism. The visible spirals in the sunflower are such morphological features. They are the effect of a specific type of growth dynamics and are themselves very specific by restricting themselves to Fibonacci numbers.
So, for the time being, we will tentatively assume the r e g u l a r p y r a m i d which is the basic form of the Stauraxonia homostaura, as the one that underlies the f i n a l form of the sunflower and its morphological relatives (other Composites, but also pineapples and pinecones). The homotypic basic number will tentatively be equated with the number of conspicuous petals at the end of the spirals of one of the two families. That number then is one from the Fibonacci number series, and consequently is either even or uneven as the case may be.
As has been said, each of the sunflower's florets is a p e r s o n, i.e. a fifth-order form individual. These individuals are packed together very tightly into a composite flower, which as such turns the single sunflower plant into a colony. And in the case of plants with many off-shoots such a composite flower is a kind of subcolony, because such plants are themselves already colonies (cormi) before considering the composite nature of their flowers.
Although the relevant promorphological matters are not definitively settled here with respect to c o m p o s i t e f l o w e r s, it was necessary to include a discussion and to dwell upon the relevant features a little longer.
A further elaboration of plant phyllotaxis and the definitive assessment of the promorphs they entail, can be found in Part XXIX (Sequel-2) of Fourth Part of Website .
We will now proceed to the two form genera of the Homostaura, the Homostaura isopola and the Homostaura anisopola.
The general basic form or promorphont of all isopolar homostaurs is the r e g u l a r p y r a m i d w i t h a n e v e n n u m b e r o f s i d e s. The characteristic axial relationships of this genus of forms can be succinctly recapitulated as follows :
When the homotypic basic number is 2n, we have n radial cross axes (and cross planes) equal among themselves and as such alternating with n, differing from the latter but equal among themselves, interradial cross axes (and cross planes). Each of the 2n antimers is a (whole or truncated) rectangular four-fold pyramid, the base of which is a double isosceles trapezoid (Figure 10) (i.e. a trapezoid that is divided by one diagonal into two unequal isosceles triangles). Of the four sides of the antimer the two outer adjacent ones are symmetrically congruent, so also the two inner adjacent ones. Each of the four sides of the antimer contains a right angle.
See the next Figure.
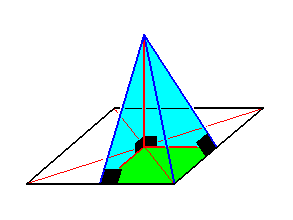
Figure 14. An antimer of a four-fold regular pyramid (basic form of the Isopola tetractinota). The antimer is a rectangular four-sided pyramid. Each side contains a right angle (indicated in black).
Both external sides of the antimer are the halves of two adjacent sides of the regular pyramid. The two internal sides are the halves of two neighboring interradial cross planes.
We divide the form genus of the isopolar homostaurs into five form species, according to whether the homotypic basic number is four, six, eight, ten, or more (10+2n). The smaller that number, the more perfect, generally, is the organization, and the higher the organism.
By the name M y r i a c t i n o t a we group together all isopolar homostaurs having their even basic number greater than ten, i.e. at least twelve, fourteen, sixteen, etc., generally 10+2n. This composition is vindicated on the one hand by the fact that more than ten antimers in homostaurs are rare anyway, and, on the other hand by the fact that if and where they occur, the homotypic basic number within the (biological) species often is variable and only seldom constant. Especially in many such cases, the one individual of the (biological) species possesses an even, and the other an uneven number of antimers. So in the Myriactinote and Polyactinote (multiradiate forms with an uneven basic number) forms we see a direct connection between the Isopola and Anisopola.
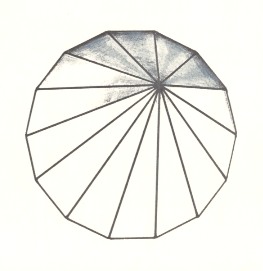
Figure 15. Slightly oblique top view of a 14-fold regular pyramid as a representative of the Isopola myriactinota.
In the plant kingdom no clear examples have been found (1866) ( See however -- i.e. click to -- what we say about that while discussing the Polyactinota ), but in the animal kingdom we see materializations of the myriactinote form : some star-fishes and some lower Hydromedusae. Among star-fishes we find (Haeckel) for example Asteracanthion helianthus with 20 to 30 and even with 40 antimers.
The ten-fold regular pyramid, as the basic form of the isopolar homostaurs with ten antimers, is very seldomly materialized. We can see it in some Hydromedusae.
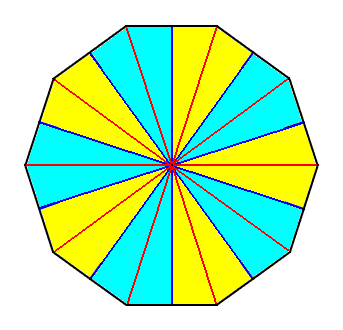
Figure 16. Base (or a plane parallel to it and containing the mid-point of the main axis) of a 10-fold regular pyramid (Such a pyramid represents the basic form of the Isopola decactinota). Radial cross axes are indicated in red. Interradial cross axes are indicated in dark blue. All the cross axes are equipolar. The ten antimers are indicated by colors (light blue, yellow).
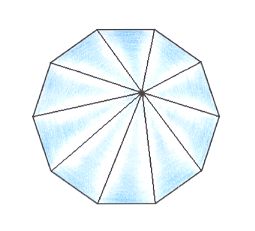
Figure 17. Slightly oblique top view of a ten-fold regular pyramid representing the basic form of the Isopola decactinota.
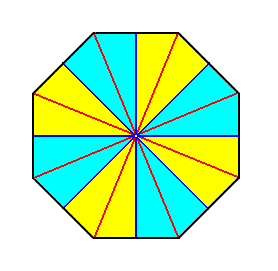
Figure 18. Base (or a plane perpendicular to it and containing the mid-point of the main axis) of an eight-fold regular pyramid representing the basic form of the Isopola octactinota. The radial cross axes are indicated in red. The interradial cross axes are indicated in blue. All the cross axes are equipolar. The eight antimers are indicated by colors (light blue, yellow).
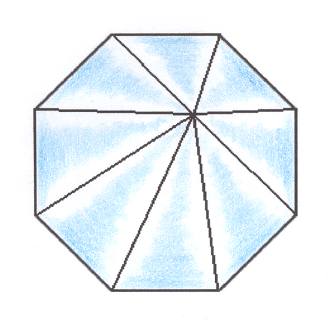
Figure 19. Slightly oblique top view of an eight-fold regular pyramid representing the basic form of the Isopola octactinota.
The basic form of the isopolar homostaurs with eight antimers is much more common and constant than the decactinote form, and is especially important as being the common basic form of all eight-fold polyps (Alcyonarians, Octocorallia)(See next link).
To see (more) real representatives of the Isopola octactinota click HERE, or scroll down to continue with the next promorphological category.
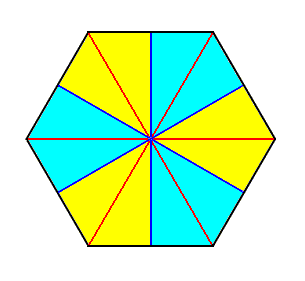
Figure 20. Base (or a plane parallel to it and containing the mid-point of the main axis) of a 6-fold regular pyramid (Such a pyramid represents the basic form of the Isopola hexactinota). Radial cross axes are indicated in red. Interradial cross axes are indicated in dark blue. All the cross axes are equipolar. The six antimers are indicated by colors (light blue, yellow).
The basic form of the regular six-fold pyramid is yet more common than that of the eight-fold. It is the basic form of the majority of polyps, for instance many corals.
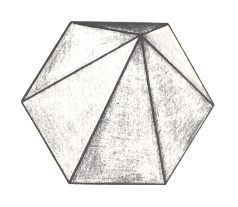
Figure 21. Slightly oblique top view of a 6-fold regular pyramid as a representative of the Isopola hexactinota.
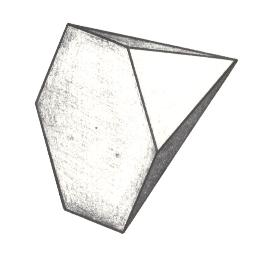
Figure 22. Oblique bottom view of a 6-fold regular pyramid as a representative of the Isopola hexactinota.
Figure 23. Slightly oblique top view of a 6-fold regular pyramid as a representative of the Isopola hexactinota. One antimer is taken out.
The Quadratic Pyramid or half equifacial Octahedron, which is the basic form of the isopolar homostaurs with four antimers, is the most common species of Homostaura isopola. It is the basic form of all higher, and of many lower medusae. A well known species of higher medusae is the jelly-fish Aurelia.
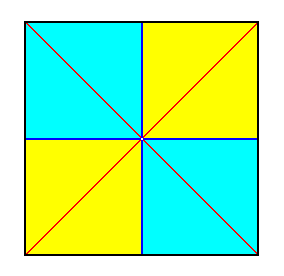
Figure 24. Base (or a plane parallel to it and containing the mid-point of the main axis) of a 4-fold regular pyramid (Such a pyramid represents the basic form of the Isopola tetractinota). Radial cross axes are indicated in red. Interradial cross axes are indicated in dark blue. All the cross axes are equipolar. The four antimers are indicated by colors (light blue, yellow).

Figure 25. Slightly oblique top view of a 4-fold regular pyramid as a representative of the Isopola tetractinota. The four SIDES of the pyramid are indicated by colors. The next Figure indicates the four antimers.
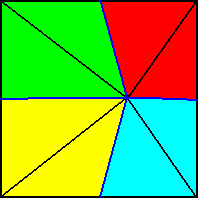
Figure 26. Slightly oblique top view of a 4-fold regular pyramid as a representative of the Isopola tetractinota. The four ANTIMERS of the pyramid are indicated by colors ( See also Figure 14 for one such antimer ).
Among the flowers of higher plants the tetractinote form is often materialized. We could safely assess the majority of dicotyledones with a four-split or four-leaf calyx and with four-split or four-leafed corolla as having the basic form of the Tetractinota, despite the number of pollen threads being four or eight.
The equatorial plane (i.e. the plane, parallel to the base and dividing the main axis into two equal halves) of this basic form is a square. The two radial cross planes, determined by the diagonals of that square, which meet at right angles, can be compared to the two directional planes of the orthostauric autopoles, especially those of the Tetraphragma, with which the present simplest form of the isopolar homostaurs is connected by many transitions in a gradual way. As soon as, like in some medusae, two opposite antimers, by reason of the development of some special organ, become conspicuous with respect to the two other antimers that alternate with them, or (as in Crucifers) by staying behind the latter, the transition from the Quadratic Pyramid of the Tetractinota to the Rhombic Pyramid of the Tetraphragma is accomplished.
( The mentioned form group, the Tetraphragma, will be dealt with further below ).
To continue click HERE to proceed further (Homostaura anisopola, Heterostaura, etc) with the systematic Promorphology.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia