Promorphology of Crystals Preparation VII

Stereometric Basic forms of Inorganic Beings

Promorphology of Crystals
preparation
7

REMARK : When the reader feels satisfied with our established theoretical foundation (done in the previous two documents) that allows (single, non-twinned) Crystals to be promorphologically assessed, he or she can skip all the following, and directly proceed with The Promorphology of Crystals.

The Plane Group P4mm
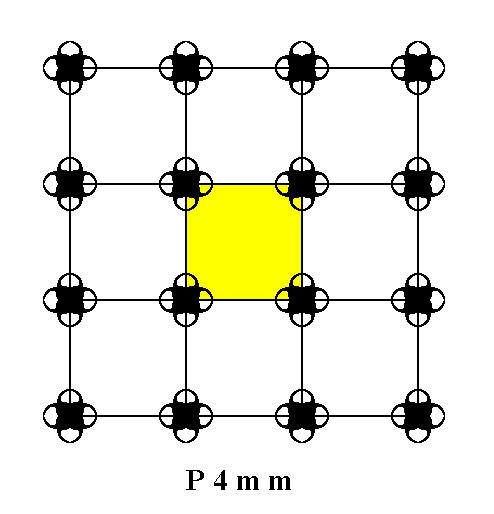
The symmetry of periodic patterns of motifs according to the Plane Group P4mm are based on one or another version of the Primitive Square Point Lattice (Net). See the next Figures.

Figure 1. Periodic two-dimensional pattern according to the Plane Group P4mm. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).

In addition to four-fold and two-fold rotation axes the P4mm pattern contains two sets of mirror lines (both in a diagonal direction), two sets of non-diagonal mirror lines, and two sets of diagonal glide lines parallel to and interleaved with the diagonal mirror lines. See next Figure.

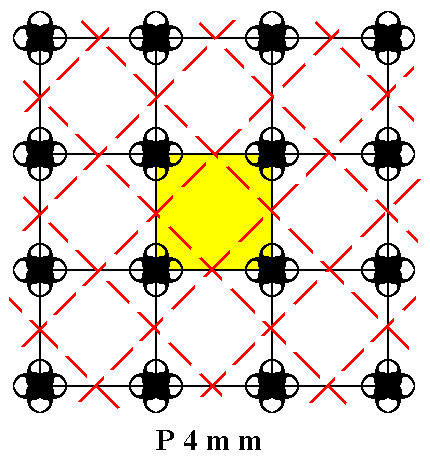
Figure 2. Periodic two-dimensional pattern according to the Plane Group P4mm. The pattern must be considered as indefinitely extended in 2-D space. The pattern contains 2-fold rotation axes (not shown), mirror lines (not shown) and glide lines. The latter are indicated by red dashed lines.

Although it is to be expected that the elimination of the glide translations will not increase the symmetry, meaning that the (penultimate) Complex Motif is already given by the content of a single unit cell, we nevertheless are going to eliminate those translations in order to obtain the ultimate Complex Motif. We will do this with our method of Copy-Shift-Superimpose. See next Figures.

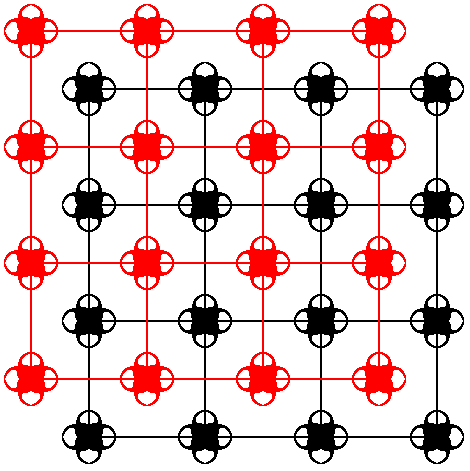
Figure 3. A copy is made of the pattern of Figure 1 and shifted diagonally, SE-NW, by half a unit cell diagonal.

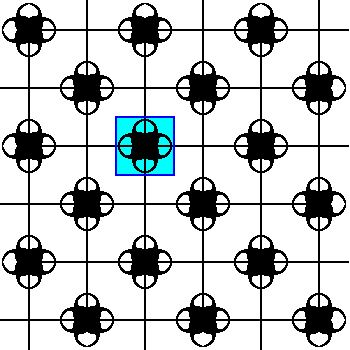
Figure 4. Processed result of Figure 3. The SE-NW diagonal glide translations are eliminated. A repeating unit is indicated. It is repeated according to a square lattice that is 45⁰ rotated with respect to the original lattice. In this new lattice the motifs s.str. can be considered to lie on the nodes of the lattice.

From Figure 4 it is clear that with the elimination of the SE-NW glide translation the SW-NE translations are eliminated (The Copy-SW-NE-shift-Superimpose operation, in which the shift involves a distance equal to half a unit cell diagonal, will not effect any change in the pattern). So we now have eliminated all glide translations. And when we isolate a repeating unit of the just obtained result, which means that now also all simple translations are eliminated, we obtain the ultimate Complex Motif. See next Figure.

Figure 5. The ultimate Complex Motif of the periodic pattern of Figure 1.

As can be seen from Figure 5, the symmetry of the Complex Motif is 4mm, i.e. it has two sets of mirror lines and a 4-fold rotation axis going through their point of intersection. THe planimetric figure that represents this symmetry is the Square, which is accordingly representing the promorph of all 2-D crystals of the Plane Group P4mm and with it of the Crystal Class 4mm. See next Figure.

Figure 6. The Square, representing the promorph or planimetric basic form of all 2-D crystals of the Plane Group P4mm and with it of the Crystal Class 4mm.

The Plane Group P4
The symmetry of periodic patterns of motifs according to the Plane Group P4 are based on one or another version of the Primitive Square Point Lattice (Net). See the next Figure.

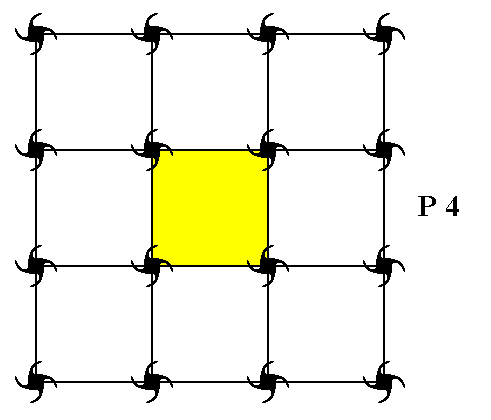
Figure 7. Periodic two-dimensional pattern according to the Plane Group P4. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).

The P4 pattern does not contain glide lines, nor does it contain mirror lines. The only symmetry elements are simple translations (responsible for the repetition of the unit cell), 2-fold rotation axes and 4-fold rotation axes. So the content of a unit cell is already the Complex Motif. This content consists of 4x1/4=1 motif s.str. If we prefer the Complex Motif to be represented by a whole motif s.str., then we take the total motif : the complete surroundings of a lattice point. This total motif, which accordingly consists of one whole motif s.str. plus corresponding background, is fully equivalent to a unit cell, as was chosen in Figure 7. The next Figure depicts such a total motif.

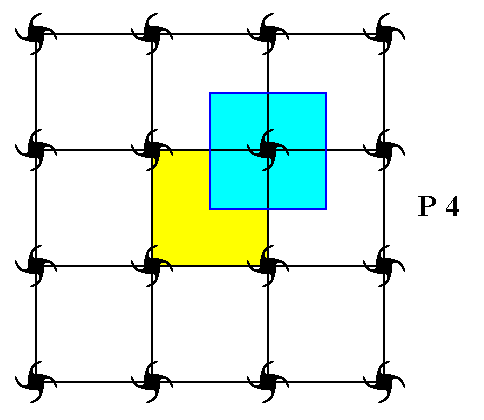
Figure 8. A total motif is indicated (light blue). It is the complete surroundings of the upper right lattice point of the chosen unit cell.

When we isolate this total motif we will automatically have undone the simple translations, and consequently end up with the Complex Motif. See next Figure.

Figure 9. The Complex Motif of the pattern of the periodic P4 pattern of Figure 7.

As can be seen from Figure 9, the Complex Motif has a symmetry of 4, which means that its only symmetry element is a 4-fold rotation axis. The simplest planimetric figure that expresses this symmetry is a Twisted Square. So the Twisted Square represents the promorph of all the 2-D crystals of the Plane Group P4 and with it of the Class 4. See next Figure.

Figure 10. The Twisted Square can represent the promorph or planimetric basic form of all 2-D crystals of the Plane Group P4 and with it of the Class 4.

The Plane Group P3
The symmetry of periodic patterns of motifs according to the Plane Group P3 are based on one or another version of the Primitive Hexagonal Point Lattice (Net). See the next Figure.

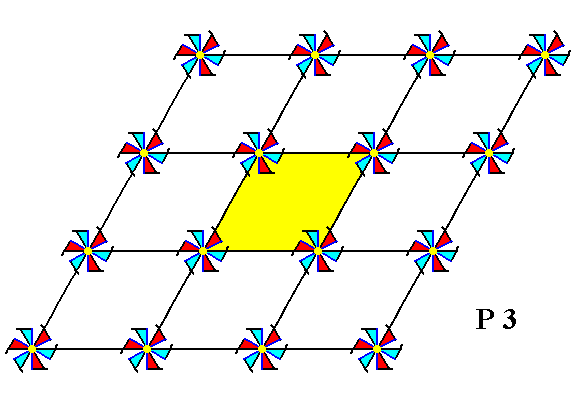
Figure 11. Periodic two-dimensional pattern according to the Plane Group P3. The pattern must be considered as indefinitely extended in 2-D space. A unit cell (mesh) is indicated (yellow).

The P3 pattern does not contain glide lines, nor does it contain mirror lines. The only symmetry elements are simple translations (responsible for the repetition of the unit cell) and 3-fold rotation axes.
First we could think of the Compex Motif being represented by the content of the unit cell as chosen in Figure 11, of even more conveniently, the total motif, i.e. the complete surroundings of a lattice point :

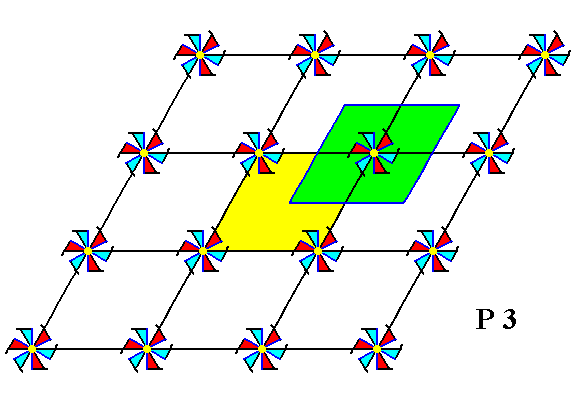
Figure 12. Periodic two-dimensional pattern according to the Plane Group P3. The pattern must be considered as indefinitely extended in 2-D space. In addition of a possible unit cell (yellow), a corresponding total motif is indicated (green). It is the complete surrounding of the upper right lattice point (of the lattice chosen).

When we isolate this total motif, thereby eliminating all simple translations, we obtain the following :

Figure 13. Isolated total motif. It consists of one whole motif s.str. plus its corresponding background.

This total motif, however, cannot represent the Complex Motif (Recall that in addition to the motif s.str. (the tri-radiate figure) its corresponding background (green) including the shape of that background, belongs to the total motif, associated with the given lattice point). From the Plane Group symbol, P3, we can deduce that 3, i.e. the possession of one 3-fold rotation axis as the only symmetry element, is the translation-free residue of the Plane Group P3. So the symmetry of the Complex Motif must be 3.
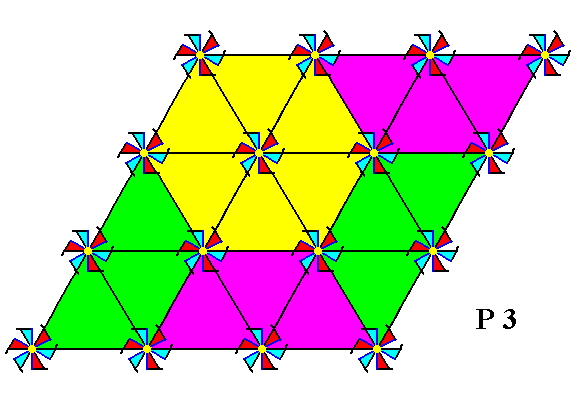
Well, although the symmetry of the motif s.str. within the total motif (Figure 13) is indeed 3, the symmetry of the whole total motif is lower. In fact the total motif has no symmetry at all!
All this implies that we have to look for another unit cell. Earlier we had established that, in order to find the Complex Motif we must start with the most symmetric unit cell choice. Indeed the rhombic unit cell as chosen in Figure 11, is certainly not the most symmetric unit cell. The pattern clearly suggests a h e x a g o n a l u n i t c e l l. And such a unit cell has definitely more symmetry than the rhomb-shaped unit cell has. See next Figure.

Figure 14. An alternatif unit cell choice : The regular hexagon. We obtain it after we have triangulated the net (i.e. we have inserted NW-SE connection lines). One such hexagon is indicated (yellow). The other colors serve to show that the hexagon is indeed a repeating unit (Recall that the net must be imagined as to be extended infinitely in 2-D space).

If we isolate this hexagonal unit cell we get the following :

Figure 15. An isolated hexagonal unit cell of the periodic motif pattern of Figure 11. It can serve as the Complex Motif.

The above isolated unit cell consists of 6x1/3+1=3 motifs s.str. ( = tri-radiate figures). So the Complex Motif consists of three motifs s.str. We can try to isolate just one whole motif s.str. -- one tri-radiate figure -- plus a proper hexagonal background. However, in order for it to be a genuine repeating unit the hexagonal outline of this background must be rotatated by 30⁰ with respect to the hexagonal outline of the unit cell. If we don't do this the result would not be a genuine repeating unit of our pattern (i.e. building up our pattern -- consisting of motifs s.str. plus background -- by its periodic repetition), as the next Figure shows :

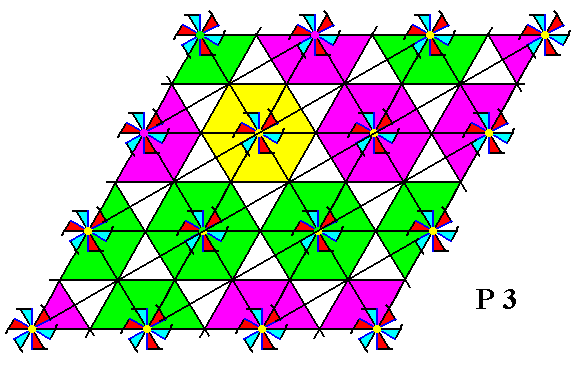
Figure 16. Just o n e motif s.str. plus its proper hexagonal surroundings (background), is not a repeating unit if the hexagonal outline of the background has the same orientation as that of the hexagonal unit cell. As such it does not produce the pattern of Figure 11, consisting of motifs s.str. + background. The units are too small.

If, on the other hand, we choose a hexagonal outline (of the background of each whole motif s.str.) that is rotated 30⁰ with respect to the outline of the hexagonal unit cell, then we get a somewhat larger unit, and, especially a unit that is a genuine repeating unit, as the next Figure shows :

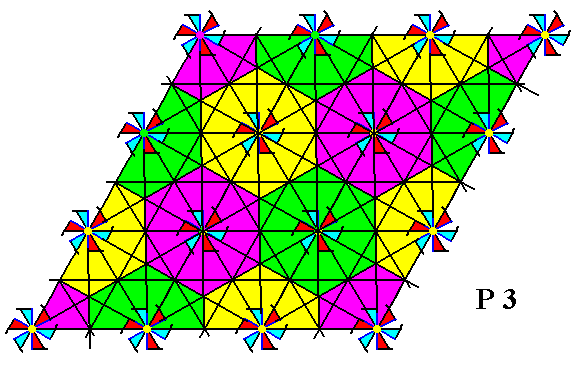
Figure 16a. Just o n e motif s.str. plus its proper hexagonal surroundings (background), as depicted here is a genuine repeating unit, because now the hexagonal outline of the background differs in orientation by 30⁰ with respect to the outline of the hexagonal unit cell, and as such it does produce the pattern of Figure 11, consisting of motifs s.str. + background.

The repeating units as found in Figure 16a, are in fact t o t a l m o t i f s associated with each lattice point. The center of such a total motif coincides with a lattice point. The whole total motif is the complete surroundings of a lattice point.

Although the total motif, as depicted in Figure 16a, is a genuine repeating unit, it is not a p r e f e r a b l e unit cell choice because of the following reason : The corners of the hexagon (As can be seen in Figure 16a) are not equivalent to the central point, because in that point something is present which is absent in the corner points. This implies that the hexagonal net (point lattice) based on such a unit cell is primitive, i.e. the central point -- which is furnished with a motif s.str. -- is not a lattice point. All this further implies that the motifs s.str. do not coincide with the lattice points. Although such a coincidence is theoretically not mandatory it is very convenient and instructive.

When we i s o l a t e a total motif from Figure 16a, we get a p r e f e r a b l e (preferable above that of Figure 15) C o m p l e x M o t i f. See the next Figure.

Figure 16b. The preferable (because smaller) Complex Motif of the periodic P3 pattern of Figure 11. It consists of one whole motif s.str. plus the corresponding background.

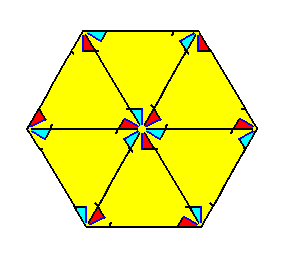
With Figure 15 we had obtained a somewhat larger version of the Complex Motif of our P3 periodic motif pattern. It is a tri-radiate motif (implying that it has three antimers), without mirror lines, so its symmetry is 3. The composition of the Complex Motif out of three congruent antimers is shown in the next Figure :

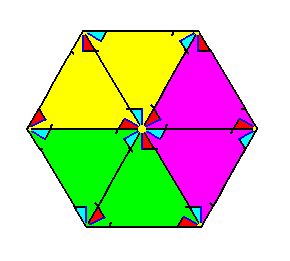
Figure 17. The (larger) Complex Motif consists of three congruent a n t i m e r s. Each antimer is asymmetric. Mirror lines are absent. The number of motifs s.str. is 6x1/3+1=3.

Our preferable Complex Motif consisting of only one motif s.str. also has three antimers and no mirror lines. See next Figure.

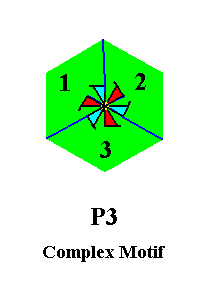
Figure 17a. Also the preferable Complex Motif consists of three congruent a n t i m e r s. Each antimer is asymmetric. Mirror lines are absent. The number of motifs s.str. is 1 (and that is the reason why it is preferable to figure as Complex Motif).

The simplest planimetric figure expressing the symmetry (3) of the Complex Motif is a Twisted Equilateral Triangle. This twisted triangle is accordingly the promorph or planimetric basic form of all the 2-D crystals belonging to the Plane Group P3 and with it to the Class 3. See next Figure.

Figure 18. The Twisted Equilateral Triangle as the planimetric basic form or promorph of all 2-D crystals of the Plane Group P3 and with it of the Class 3.

To continue click HERE to investigate the next Plane Groups in order to find the Complex Motif.

e-mail :