The basic form of the anisopolar homostaurs or heteropolar homostauric stauraxonians with an uneven number of antimers is the r e g u l a r p y r a m i d w i t h a n u n e v e n n u m b e r o f s i d e s, as is established above. The axial relationships of this form genus are characterized by the fact that, because the homotypic basic number is 2n-1, there are just as many cross axes present, being equal among each other, each one consisting of a radius and an interradius. Such an axis is a semiradial cross axis. See next Figure.

Figure 1. Base (or a plane parallel to it and containing the mid-point of the main axis) of a regular 5-fold pyramid. The five semiradial cross axes are indicated, as well as the five antimers.
Each of the 2n-1 antimers is a (whole or truncated) rectangular four-fold pyramid of which the base is a doubly isosceles trapezoid (a trapezoid having its two diagonals perpendicular to each other, and of which there is one that halves the other without itself to become halved). Of the four sides of each antimer, each one containing a right angle, the two inner ones are symmetrically congruent, the same goes for the two outer ones. The two outer sides are halves of two adjacent sides of the regular pyramid, the two inner sides are the interradial halves of two neighboring semiradial cross planes.
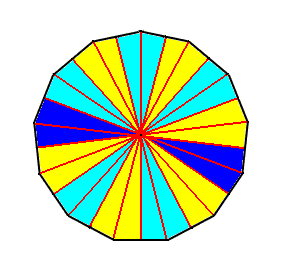
Figure 2. Base ( or a plane parallel to it and containing the mid-point of the main axis ) of a regular 13-fold pyramid. The 13 semiradial cross axes and the 13 antimers are indicated.
In the group of the Polyactinotes we place all those anisopolar homostaurs having their uneven homotypic number larger than nine, i.e. at least 11, 13, 15, etc., generally 9+2n. These homostaurs cannot be clearly distinguished from the Myriactinotes, because in many biological species belonging to the present group the basic number is variable, sometimes even, sometimes uneven. Seldom a number bigger than nine is constant within all individuals of a species. Higher uneven numbers are seldom anyhow, and more seldom than higher even numbers (Haeckel, 1866).
Of all homotypic basic numbers under twelve it seems that nine is the most rare in the organismic world. In a constant or rather almost constant way we find nine antimers in some starfish species.
Figure 3. A regular 9-fold pyramid, as the basic form of the Enneactinota. The main axis and the 9 semiradial cross axes are indicated (their interradial halves are marked by dashed lines). Also one antimer is outlined.
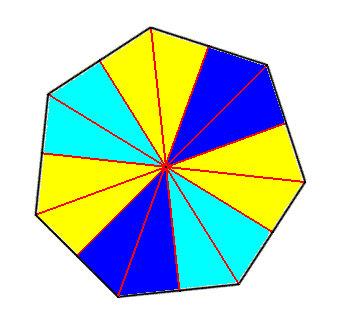
Figure 4. Base of a regular 7-fold pyramid (such a pyramid representing the basic form of the Heptactinota). The 7 semiradial cross axes are indicated. The seven antimers are indicated by coloration.
As remarked earlier the basic numbers nine and seven are of all lower numbers most seldom materialized in organic forms. So the seven-sided regular pyramid is rarily encountered as the clearly expressed basic form of persons in the animal as well as in the plant kingdom. Among animals Haeckel knows of only one example, namely the beautiful seven-radiate starfish Luidia savignyi. Also in plants seven as a constant homotypic basic number is very rare, and only clearly expressed in a few higher plant flowers.

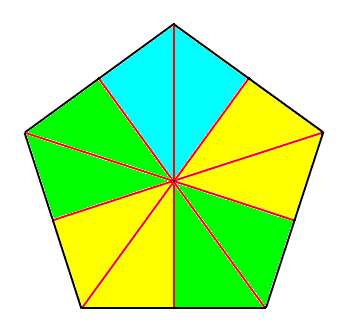
Figure 5. Base of a regular 5-fold pyramid (such a pyramid representing the basic form of the Pentactinota). The 5 semiradial cross axes are indicated. The five antimers are indicated by coloration.
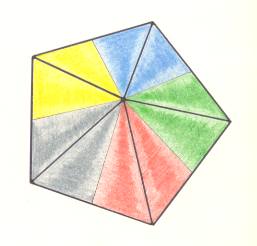
Figure 6. Slightly oblique top view of a five-fold regular pyramid as the basic form of the Pentactinota. The five antimers are indicated by colors.
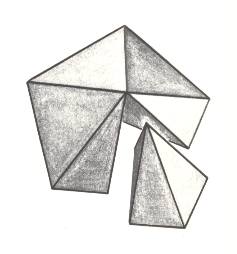
Figure 7. Slightly oblique top view of a five-fold regular pyramid. One antimer is taken out.
The pentactinote form, the basic form of the anisopolar homostaurs with five antimers, is of all regular pyramids with an uneven number of sides the most commonly materialized form in orgamisms. Not only is the large phylum of Echinoderms mainly characterized by the possession of five antimers, but also very many dicotyledone plant flowers are so characterized. However, it is true that in a large part of these two groups the strict regular form transforms into the bilateral-symmetric form (Amphipleura) right into the latter's perfect expression, making it often difficult to determine the line of separation between the five-fold regular and the five-fold amphitect semipyramid (i.e. half of a ten-fold amphitect pyramid).
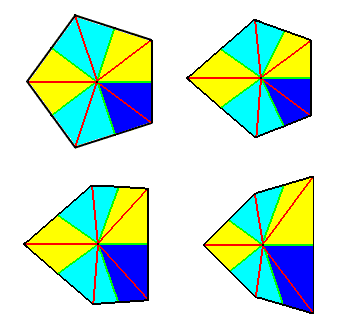
Figure 8. Possible stages of transition from the Pentactinota (Homostaura) (top left image) to Pentamphipleura (Heterostaura) (bottom right image). Radii are indicated in red, interradii in green. The five antimers are indicated by coloration.
The s t r i c t l y r e g u l a r f i v e - s i d e d p y r a m i d is materialized in a part of the phylum of Echinoderms (star-fishes, sea-urchins, etc.). To these absolutely regular Echinoderms a large number of "subregular" forms adjoins, in which the five antimers are congruent when we do not consider one rather unimportant feature (for example an unpaired genital pore, or the excentric anus) that lets an unpaired radius and interradius be unique with respect to the four others.

Figure 8a. Test of a regular sea-urchin (Echinodermata). One can clearly see its five-foldness.
In Coelenterates (jellyfishes, polypes and the like) the pentactinote form seems to be absent (Haeckel, 1866).
Figure 9. Base (or a plane parallel to it and containing the mid-point of the main axis) of a regular three-fold pyramid. The three semiradial cross axes and the three antimers are indicated.
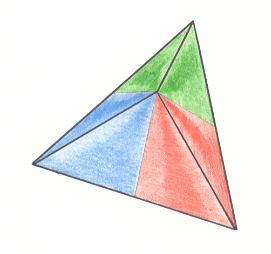
Figure 10. Slightly oblique top view of a three-fold regular pyramid as the basic form of the Triactinota. The three antimers are indicated.
The most simple case of all anisopolar Homostaurs presents itself as a three-sided regular pyramid, as it can be found very often in the plant kingdom, while it is not materialized in any person in the animal kingdom. As basic form of organs, on the other hand, it is present in that kingdom, for example in the three-fold pedicellarians of sea urchins. In Radiolarians this form does occur. Not seldom is the geometric basic form in this Class clearly expressed in the shape of their silica shell as in the genus Lithomelissa.
The heterostauric heteropolar stauraxonians, or H e t e r o s t a u r a as we will call them for short, constitute a very important and extensive form series. It is the most common and most differentiated of all main form groups in which we have divided the basic forms of organisms. The majority of all persons in the animal kingdom, many of them in the plant kingdom, and many antimers, metamers, organs and cells show this basic form. The simplest geometric expression of it is the i r r e g u l a r, and then most often as a m p h i t e c t, p y r a m i d, either the whole, or half of it, and seldom a quarter of the amphitect pyramid.
The character and general properties of the amphitect pyramid (flattened pyramid) were already determined above. It is a straight pyramid (i.e. with its tip precisely above the center of its base) with an even number of sides. Its base is an amphitect polygon. The number of sides can be very different, but must be even. The next Figure depicts some possible bases of amphitect pyramids.
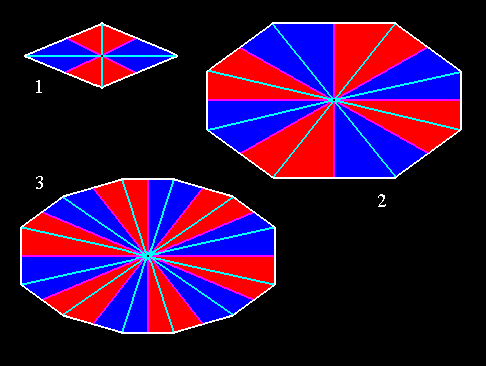
Figure 11. Some amphitect polygons representing bases or equatorial planes of possible amphitect pyramids. Radial and interradial cross axes and antimers are indicated.
(1). Four-sided amphitect polygon (Rhombus). Four antimers.
(2). Eight-sided amphitect polygon. Eight antimers.
(3). Twelve-sided amphitect polygon. Twelve antimers.
Radial cross axes are indicated in blue. Interradial cross axes are indicated in pink. The radial cross planes ( containing the radial cross axes ) are the median planes of the antimers (i.e. in each case of two opposite antimers). The interradial cross planes ( containing the interradial cross axes ) are the planes separating adjacent antimers. The antimers are indicated in red and dark blue.
As an organic example of the 8-sided amphitect pyramid we can indicate the Ctenophores, and for the 4-sided amphitect pyramid we should look among the flowers of Crucifers.
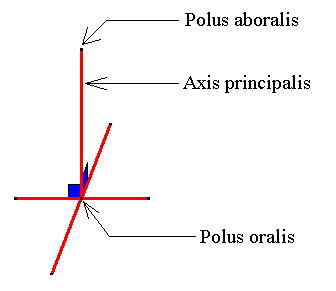
Figure 12. The main axis and the two directional axes (ideal cross axes) of the amphitect pyramid. The directional axes should lie in the equatorial plane, i.e. the plane parallel to the pyramid's base and containing the mid-point of the main axis. But, for convenience the directional axes are imagined to lie in the base of the pyramid.
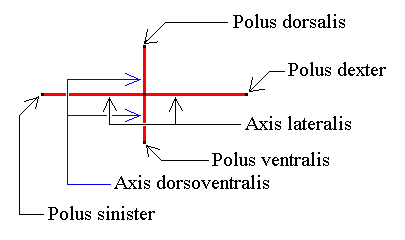
Figure 13. The two directional axes or ideal cross axes lying in the equatorial plane (or in the base for that matter) of the amphitect pyramid. The main axis (not drawn) is perpendicular to both directional axes and contains their point of intersection.
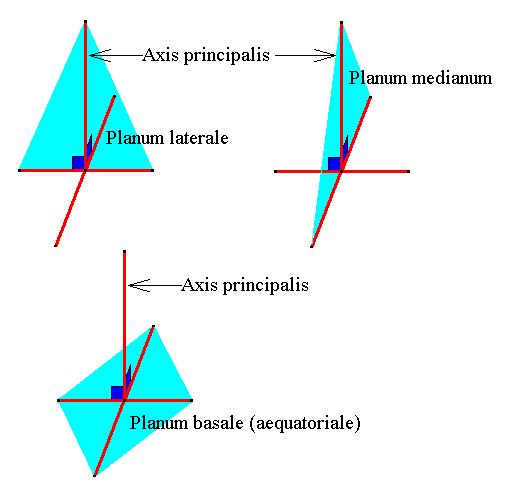
Figure 14. The three directional planes (light blue) :
Lateral plane, median plane, basal plane (equatorial plane).
The (two ideal) cross axes are drawn such that they are contained in the b a s a l p l a n e of the amphitect pyramid for convenience. In fact they should lie in the e q u a t o r i a l p l a n e (which is parallel to the basal plane and containing the mid-point of the main axis.
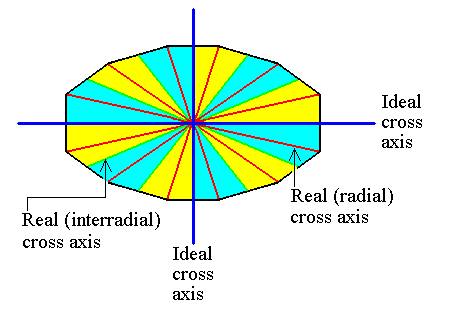
Figure 15. The cross axes, indicated in the equatorial plane of a 12-sided amphitect pyramid. The cross axes can be either i d e a l, and where they are ideal, they are d i r e c t i o n a l axes (Such an axis can be radial or interradial), or r e a l, and where they are real, they can be either radial or interradial.
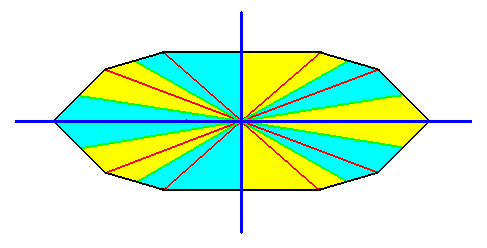
Figure 16.
The cross axes, indicated in the equatorial plane of a 10-sided amphitect pyramid.
Here we have a case that one directional axis (dark blue) is r a d i a l while the other (dark blue) is i n t e r r a d i a l.
Scheme of points lines and planes :
As was the case with most previously considered basic forms, also the whole (or half) amphitect pyramid, which constitutes the common basic form of most Heterostaurs, is not as such recognized by morphologists (1866), because one did not consider at all, or insufficiently so, the determining axes and their poles. Rather one had indicated all forms belonging to our Heterostaura as "bilateral-symmetric" in the broadest sense of the term.
The utmost extensive and diverse form group of the Heterostaura can, first of all be divided into two main divisions, a u t o p o l a and a l l o p o l a, according to both directional axes (ideal cross axes) being homopolar, or at least one of them (seldom both) being heteropolar.
The H e t e r o s t a u r a a u t o p o l a, in which both poles of each of the directional axes are equal, are divided into two congruent halves by each of the two directional planes.
The H e t e r o s t a u r a a l l o p o l a, in which the poles of one directional axis (seldom also those of the other) are unequal, are divided by one directional plane into two unequal parts, by the other directional plane into two symmetrically equal parts (or, when both directional axes are heteropolar, into two symmetrically similar parts).
There is an important difference between these two main divisions of the heterostaura :
While in the Autopola, as in all until now considered Protaxonians, the center of the body is a l i n e, it becomes a p l a n e in the Allopola. If one credits the greatest significance to this quality of the center (of the body), a quality that determines to a great extent the shape of the body, then one should interpret the Autopola as the last and most differentiated division of the C e n t r a x o n i a (Protaxonia, except the Allopola), and oppose them to the Allopola which can be characterized as C e n t r e p i p e d a.
The geometric basic form of the autopolar heterostaurs is the w h o l e, while that of the allopolar heterostaurs is half an amphitect pyramid (seldom, when both directional axes are heteropolar, a quarter of an amphitect pyramid).
In the Autopola the left and right halves are congruent, in the Allopola symmetrically equal (seldom just symmetrically similar). In the Autopola the dorsal and ventral halves are congruent, in the Allopola unequal.
The small, but morphologically especially interesting division of the autopolar heterostaurs is the basic form of Ctenophores and other animals, and of some dicotyledone families, for example the Crucifers. Much more important and larger is the division of the allopolar heterostaurs that provides the basic form to the organismic body as a whole of most higher and many lower animals and plants. To these belong all Vertebrates, Arthropods and Molluscs, most worms, the irregular Echinoderms, further the Grasses, Orchids, Umbellifers and many others.
The interest that can be credited to the autopolar heterostaurs is, in a way, vindicated by the fact that a well-known animal group, the, already mentioned, Ctenophores, was (before 1866) very differently interpreted as to their stereometric basic form (as Haeckel reports), namely either as "purely bilateral-symmetric", "transitions from the bilateral-symmetric to the radial-regular type", or, finally, pure "radiate animals", and, within the latter either as eight-fold, or as two-fold animals.
And yet the characteristic basic form of the autopolar heterostaurs is in all Ctenophora that much clearly expressed, and without any transitions to be present, either to true "bilateral symmetry", or to true "radial" regularity, that a simple inquiry into the axes and their poles, and as soon as one has established the promorphological concepts, directly leads to one and only one possible result.
T h e b a s i c f o r m o f t h e H e t e r o s t a u r a a u t o p o l a i s t h e a m p h i t e c t p y r a m i d, the character of which is expounded above.
As its most certain criterion, characterizing it in a l l c a s e s and definitely distinguishing it from all other pyramids, we can again indicate the fact that the a m p h i t e c t p y r a m i d is divided into four rectangular pyramids by two unequal planes --directional planes -- (and only by these planes) that are perpendicular to each other while their line of intersection coincides with the main axis. Of the four pyramids every two contiguous are symmetrically equal, and every two opposite are congruent.
This property is implied by the fact that the two d i r e c t i o n a l a x e s (Euthyni, or ideal cross axes), that are contained in those directional planes, and that divide themselves and the main axis in equal halves under right angles, are unequal, while both poles (and polar surfaces) of each directional axis are equal.
The next Figure shows that the homopolarity of the axes perpendicular to the main axis, as it is characteristic for the Autopola, strictly only refers to the d i r e c t i o n a l (i.e. ideal) cross axes. For the other cross axes we cannot find any mirror line (or plane, when we consider the whole pyramid and not only its base) that could reflect the parts of the figure (here of the amphitect polygon, and by implication the amphitect pyramid), separated by this line, onto each other, as is indicated in the Figure with respect to the axis RR' and the line SS'. But although the polar areas of such a non-directional cross axis are not (plane) symmetric, they are congruent, and can in orgasms represent repeated organs or other features.
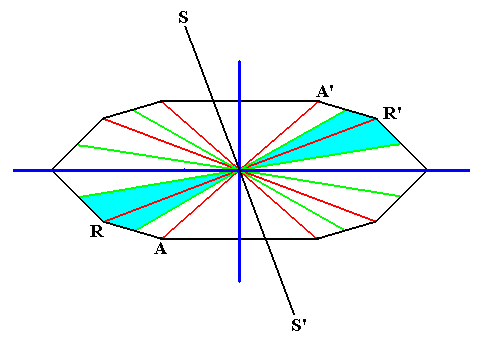
Figure 17.
The cross axes, as indicated in the equatorial plane of a 10-sided amphitect pyramid.
Dark blue : directional axes. Red : real (radial) cross axes. Green : real (interradial) cross axes. The two regions associated with the two poles of every non-directional cross axis are not symmetric with respect to each other, but are congruent. This is shown for the real (radial) cross axis RR' and the line SS' that was supposed to be the mirror line relating the two regions by reflectional symmetry.
The autopolar heterostaurs on the one hand differ from all until now investigated heteropolar stauraxonians, i.e. from the homostaurs, by the unequal length and quality of their radial cross axes (as exemplified by the axes RR' and AA' in the above Figure), and also of their interradial cross axes (within one and the same autopolar body), while they correspond to the Homostaura isopola by the fact that both polar regions of each cross axis are congruent. On the other hand the autopolar heterostaurs differ from the allopolar heterostaurs (to which they correspond in their having unequal cross axes), by the congruence of both poles (and polar regions) of each cross axis.
The difference between all these and related basic forms can be succinctly stated by involving the possible r o t a t i o n a l a x e s o f s y m m e t r y of crystallography (which Haeckel fails to recognize as being instructive). These symmetry axes describe the rotational symmetry of an object as follows : If an object has an n-fold symmetry axis, then the object will be mapped onto itself (i.e. covers itself completely) when it is rotated about that axis by 360/n0, i.e. the image that appears after such a rotation covers the original image completely. For example : If an object has a 3-fold rotation axis, then the object will be left unchanged when it is rotated by 1200 about that axis, i.e. its image after such a rotation will cover the original image completely.
Now we can state the difference between the just mentioned basic forms clearly and succinctly :
The main axis of the Homostaura (regular pyramids) can be a 3-fold, 4-fold, 5-fold, 6-fold, 7-fold, 8-fold, 9-fold, 10-fold, or, generally, n-fold rotation axis, while the main axis of the Heterostaura autopola (amphitect pyramids) is always a 2-fold rotation axis.
We can make this statement more general by including the homopolar stauraxonians (bipyramids):
The main axis of the Homopola isostaura (regular bipyramids) and of the Heteropola homostaura (regular pyramids) can be a 3-fold, 4-fold, 5-fold, 6-fold, 7-fold, 8-fold, 9-fold, 10-fold, or, generally, n-fold rotation axis, while the main axis of the Homopola allostaura (amphitect bipyramids) and of the Heteropola autopola, i.e. Heterostaura autopola (amphitect pyramids) is always a 2-fold rotation axis. This 2-fold rotation axis disappears in the Heterostaura allopola.
As the mentioned features, relating to the cross axes and their poles, position the Autopola between the homostaurs and the allopolar heterostaurs, so does their body center (Centrum). While this centrum becomes a plane (Centrepipeda) in the allopolar heterostaurs, it remains a line in the Autopola as in the Homostaura. But by reason of the differentiation of both directional planes -- that in the latter are always equal, and thus as such in fact not present, there is an approximation to be detected of the Autopola to the Allopola, because there are, so to say, two m e d i a n p l a n e s present coinciding with the two directional planes, while in the Homostaura there are no genuine median planes. But because each one of these median planes (in the Autopola) is divided into two equal halves by the other, the essential character of the allopolar median plane is absent : the composition of two unequal halves, dorsal and ventral half. Therefore we can in the autopolar form all by itself, i.e. without comparing them with related allopoles (allopole organisms, phylogenetically related to the given autopole organisms), never determine which one of the unequal directional axes and directional planes is the dorso-ventral, and which one the lateral. The dorsal side differs as little from the ventral side, as does the right side from the left. Only the main axis is heteropolar.
As we can derive the autopolar heterostauric form (amphitect pyramid) from the corresponding allostauric homopolar stauraxon form (amphitect bipyramid) by dividing the amphitect bipyramid into congruent halves (and proceed to consider only one such half) along its equatorial plane, so we can also derive the two subgroups of the Autopola from the corresponding subgroups of the Homopola allostaura (amphitect bipyramids), by division along their equatorial planes. ( See for the two subgroups within the Homopola allostaura HERE ). In this way we will obtain the A u t o p o l a o x y s t a u r a, in which more than two radial cross axes are present that intersect at acute angles, and the A u t o p o l a o r t h o s t a u r a, in which only two radial cross axes are present, intersecting each other at right angles and therefore coincide with the two ideal cross axes (directional axes).
We can, however, conjecture that, in addition to a 'normal' orthostauric autopolar form type ---- i.e. a form (See left image next Figure) of which the two directional axes are unequal and representing the form's only radial cross axes, that are then perpendicular to each other, (all this) involving four antimers, each of which is symmetric with respect to its median plane ---- there exists yet another autopolar form type (See right image next Figure), also possessing four antimers, each of which is, however, asymmetric with respect to its 'median plane' (it therefore is not a genuine median plane anymore). In the latter case (which Haeckel does not recognize as such), although its having four antimers (and as such it should belong to the orthostauric autopoles), the form's two radial cross axes do not meet at right angles but at obtuse and acute angles (alternating with each other). So this form, not withstanding its having four antimers, seems to fall outside the orthostauric autopoles, but cannot belong to the oxystaurs either, because these all have more than four antimers. We should, however, not be disturbed by this phenomenon (if it occurs at all in the organic world) : The latter form is just an organic m o d i f i c a t i o n of the normal autopolar orthostauric form : the pure geometrical symmetry content of both forms is expressed by the rhombic pyramid : (exclusively) two non-equivalent vertical mirror planes (implying their line of intersection to be a 2-fold rotation axis). Because in this modification both directional axes are interradial, we call it the interradiate modification and the (sub)group which it represents will be called the Autopola tetraphragma i n t e r r a d i a l i a (The Autopola orthostaura consists of two main divisions, namely the Tetraphragma -- rhombic pyramid with four antimers -- and the Diphragma -- rhombic pyramid with two antimers). See the next Figure.
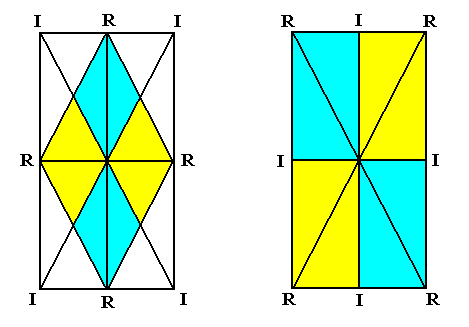
Figure 18. Autopola orthostaura tetraphragma.
Left image : The colored image (within the rectangle) depicts the equatorial plane of the Autopola tetraphragma radialia. The two directional axes are radial and intersect at angles of 900. The four antimers are indicated by coloration. Each antimer is symmetric with respect to the relevant directional plane, containing the corresponding directional axis.
Right image : The colored rectangular image represents the equatorial plane of the Autopola tetraphragma interradialia. The two directional axes are the same as in the left image, but are now interradial. The radial cross axes intersect at angles different from 900 : acute and obtuse angles alternate. The four antimers are indicated by coloring. Each antimer is not symmetric with respect to the relevant radial cross plane containing the corresponding radial cross axis.
Radial cross axes are indicated as R, interradial cross axes as I.
The orthostauric autopoles correspond to the orthogonia or octopleural allostaurs, the halves of which they constitute, and are, like the latter, composed of four antimers (except for the Diphragma, which are composed of two animers).
To continue click HERE to proceed further with the systematic Promorphology.
e-mail :

back to retrospect and continuation page
back to Internal Structure of 3-D Crystals
back to The Shapes of 3-D Crystals
back to The Thermodynamics of Crystals
back to Introduction to Promorphology
back to Anaxonia, Homaxonia, Polyaxonia
back to Protaxonia : Monaxonia
back to Stauraxonia heteropola